Study of the Rolling Friction Coefficient between Dissimilar Materials through the Motion of a Conical Pendulum
Abstract
1. Introduction
2. Materials and Methods
2.1. Principle of Methodology
2.2. Proposed Method: Theoretical Fundamentals
- to the tendency of sliding between the points C1 and C2, the sliding friction force T, parallel and of contrary direction of velocity vC1C2, will oppose;
- to the spinning motion, the spinning torque Ms, normal to the tangent plane and of contrary direction of the angular velocity ωs, will oppose;
- to the angular rolling velocity ωr, the rolling friction torque Mr contained in the tangent plane and of opposite direction of angular velocity ωr, will oppose.
- The normal force N
- The sliding friction force T
- The spinning friction moment Ms
- The rolling friction moment Mr
- The Ox0y0z0 system that has the Oz0 axis in the vertical direction;
- The Ox1y1z1 frame obtained by revolving the frame Ox0y0z0 with an angle α about the axis Oy0 ≡ Oy1. The ball is sustained by the plane Ox1y1;
- The frame Ox2y2z2 obtained by rotating the system Ox1y1z1 around the axis Oz1 ≡ Oz2 with an angle ψ;
- The coordinate system Ox3y3z3 obtained by rotating the frame Ox2y2z2 with an angle (π/2 − δ), as shown in Figure 3, about the axis Oy2 ≡ Oy3;
- The coordinate system Ox′y′z′ obtained by rotating the frame Ox3y3z3 with an angle φ about the axis Oz3 ≡ Oz′.
- The normal reaction N, parallel to k2:
- The friction force T in the support plane and normal to the angular rolling velocity ω:
- The rolling torque Mr, collinear to the angular rolling velocity and of opposite orientation:
- The spin torque from the contact point is zero since the angular velocity lacks a component along the normal to the support plane.
2.3. Experimental Method
2.3.1. Experimental Device
- The plate to be tested, 3, is positioned on top of the duralumin plate, 1;
- The tilting angle of the device to the imposed angle α is obtained by moving the adjusting cylinder, 5 (the cylinder is moved until the short mobile edge of the plate, 1, reaches the height h = l∙sinα);
- The ball, 5, is removed from the equilibrium position by a small ψ0 angle (less than 15deg) and let to oscillate freely while rolling over the plate, 3; it is observed that the angular amplitude of the oscillation decreases in time and finding the manner of the angular amplitude damp in time is the goal of the test;
- The displacement of the wire, 6, with respect to the protractor, 7, is filmed using a camera, 11, focused on the region where the distance of wire–protractor is minimum;
- The film is transferred to a computer and the images are analyzed frame by frame to obtain the values of the extreme elongations and the instants when they occur;
- In the first stage, these experimental values for time and amplitude were measured manually by a human operator, using QuickTime software; this step was time-consuming and tedious;
- To overcome this inconvenience, an image analysis code was developed (presented in Section 2.3.2) and thus the position of the wire, the times and the extreme angular elongations could be accurately found.
2.3.2. Software for Elongation Measurement Using Automatic Image Processing
- detects the moving object, i.e., the wire, partitions it into zones of interest(rectangles) and surrounds the pixels of the wire with a red quadrangle (as shown in Figure 11); due to binarization of image, it is possible that the wire is represented by several disconnected portions, so a number of morphological operations of dilation and erosion are executed;
- in order to establish the orientation of the wire, the coefficients of the regression line passing through the pixels cloud of the wire image in the frame (located in the red polygon on Figure 5) will be determined; these coefficients will be computed based on the coordinates of the wire pixels within the screen (xi, yi); thus, having the equation of the regression line,
- the program establishes for each frame the value of the angular elongation after image processing;
- an estimated value is also determined depending on the value from the previous frame; if the difference in absolute value between the established value and the estimated one is greater than a certain threshold, then the automatic processing stops at this frame, which is displayed together with the graphical representation of the two lines (the regression one and the one corresponding to the estimated value);
- the operator examines the frame at which the processing stopped; if there is a discrepancy between the orientation of the wire and the calculated regression line, the operator can manually select two marks by clicking on the image of the wire, and the program calculates the angular elongation for this frame based on the line passing through the two chosen marks and resumes the automatic processing.
2.4. Experimental Results
3. Discussions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A


References
- Uicker, J.; Pennock, G.; Shigley, J. The World of Mechanisms. In Theory of Machines and Mechanisms, 5th ed.; Oxford University Press: Oxford, UK, 2003; pp. 3–32. [Google Scholar]
- Alaci, S.; Ciornei, C.; Filote, C. Considerations upon a new tripod joint solution. Mechanics 2013, 19, 567–574. [Google Scholar] [CrossRef]
- Johnson, K.; Kendall, K.; Roberts, A. Surface energy and the contact of elastic solids. Proc. R. Soc. Lond. 1971, 324, 301–313. [Google Scholar]
- Persson, B. Rolling friction for hard cylinder and sphere on viscoelastic solid. Eur. Phys. J. E 2010, 33, 327–333. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wang, X.; Yang, W.; Li, H. A numerical study of the rolling friction between a microsphere and a substrate considering the adhesive effect. J. Phys. D Appl. Phys. 2016, 49, 025501. [Google Scholar] [CrossRef]
- Hibbeler, R. Fundamental Concepts. In Fluid Mechanics; Pearson Prentice Hall: Boston, MA, USA, 2015; pp. 3–45. [Google Scholar]
- Hertz, H. Über die berührung fester elastischer Körper (On the contact of rigid elastic solids). In Miscellaneous Papers; Jones, D.E., Schott, G.A., Eds.; J. reine und angewandte Mathematik 92; Macmillan: London, UK, 1896; pp. 146–162. [Google Scholar]
- Johnson, K. Normal contact of elastic solids: Hertz theory. In Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985; pp. 84–106. [Google Scholar]
- Hills, D.; Nowell, D.; Sackfield, A. Elliptical contacts. In Mechanics of Elastic Contact; Butterworth Heinemann Ltd.: Oxford, UK, 1993; pp. 291–319. [Google Scholar]
- Popov, V. Qualitative Treatment of Contact Problems—Normal Contact without Adhesion. In Contact Mechanics and Friction, Physical Principles and Applications; Springer: Berlin/Heidelberg, Germany, 2010; pp. 9–23. [Google Scholar]
- Halme, J.; Andersson, P. Rolling contact fatigue and wear fundamentals for rolling bearing diagnostics—state of the art. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 377–393. [Google Scholar] [CrossRef]
- Popp, K.; Stelter, P. Nonlinear Oscillations of Structures Induced by Dry Friction. In Nonlinear Dynamics in Engineering Systems. International Union of Theoretical and Applied Mechanics; Schiehlen, W., Ed.; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar] [CrossRef]
- Mangeron, D.; Irimiciuc, N. Dinamica miscarii absolute a rigidului. In Mecanica Rigidelor cu Aplicatii in Inginerie. Mecanica rigidului (in Romanian); Editura Tehnică: Bucuresti, Romania, 1978; Volume 1, pp. 233–436. [Google Scholar]
- Cherepanov, G. Theory of rolling: Solution of the Coulomb problem. J. Appl. Mech. Tech. Phys. 2014, 55, 182–189. [Google Scholar] [CrossRef]
- Dzhilavdari, I.; Riznookaya, N. An Experimental Assessment of the Components of Rolling Friction of Balls at Small Cyclic Displacements. J. Frict. Wear 2008, 29, 330–334. [Google Scholar] [CrossRef]
- Dzhilavdari, I.; Riznookaya, N. Measurement of the friction characteristics on materials surfaces using the pendulum microoscillations method. J. Frict. Wear 2007, 28, 446–451. [Google Scholar] [CrossRef]
- Alaci, S.; Ciornei, F.; Ciogole, A.; Ciornei, M. Estimation of coefficient of rolling friction by the evolvent pendulum method. IOP Conf. Ser.: Mater. Sci. Eng. 2017, 200, 0122005. [Google Scholar] [CrossRef]
- Ciornei, M.; Alaci, S.; Ciornei, F.; Romanu, I. A method for the determination of the coefficient of rolling friction using cycloidal pendulum. IOP Conf. Ser. Mater. Sci. Eng. 2017, 227, 012027. [Google Scholar] [CrossRef]
- Ciornei, F.; Pentiuc, R.; Alaci, S.; Romanu, I.; Siretean, S.; Ciornei, M. An improved technique of finding the coefficient of rolling friction by inclined plane method. IOP Conf. Ser. Mater. Sci. Eng. 2019, 514, 012004. [Google Scholar] [CrossRef]
- Zaspa, Y. Internal Synthesis of Motion and the Dynamic Characteristics of External Friction. J. Frict. Wear 2011, 32, 167–178. [Google Scholar] [CrossRef]
- Spiegel, M. Space motion of rigid bodies. In Theoretical Mechanics: Schaum’s Outline Series; McGraw-Hill Education: New York, NY, USA, 1967; pp. 253–281. [Google Scholar]
- Fischer, I. Coordinate transformation. In Dual-Number Methods in Kinematics, Statics and Dynamics; CRC Press: Boca Raton, FL, USA, 1998; pp. 9–40. [Google Scholar]
- McCarthy, J.; Soh, G. Spherical kinematics. In Geometric Design of Linkages (Interdisciplinary Applied Mathematics), 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 179–201. [Google Scholar]
- O’Reilly, O. The dynamics of rolling disks and sliding disks. Nonlinear Dyn. 1996, 10, 287–305. [Google Scholar] [CrossRef]
- Scaraggi, M.; Persson, B. Rolling Friction: Comparison of Analytical Theory with Exact Numerical Results. Tribol. Lett. 2014, 55, 15–21. [Google Scholar] [CrossRef]
- Kopchenova, N.; Maron, I. Approximate Solutions of Ordinary Differential Equations. In Computational Mathematics, 3rd ed.; Mir Publishers: Moscow, Russia, 1984; pp. 198–243. [Google Scholar]
- OpenCV. Open Source Computer Vision Library. Available online: https://github.com/opencv/opencv (accessed on 19 August 2020).
- JavaCV. Java interface to OpenCV, FFmpeg, and more. Available online: https://github.com/bytedeco/javacv (accessed on 19 August 2020).
- Huang, P.; Yang, Q. Theory and contents of frictional mechanics. Friction 2014, 2, 27–39. [Google Scholar] [CrossRef]
- Beer, F.; Johnston, R.; Mazurek, D.; Eisenberg, E. Vector Mechanics For. Engineers: Statics, 9th ed.; McGraw-Hill: New York, NY, USA, 2010. [Google Scholar]
- Wen, S.; Huang, P. Rolling friction and its applications. In Principles of Tribology, 2nd ed.; Tsinghua University Press: Beijing, China; John Wiley & Sons: Hoboken, NJ, USA, 2018; pp. 252–281. [Google Scholar]
- Koczan, G.; Ziomek, J. Research on rolling friction’s dependence on ball bearings’ radius. Engl. Transl. Przegląd Mech. 2018, 1, 21–26. [Google Scholar] [CrossRef]
- Domenech, A.; Domenech, T.; Cebrian, J. Introduction to the study of rolling friction. Am. J. Phys. 1987, 55, 231–235. [Google Scholar] [CrossRef]
- Olaru, D.; Stamate, C.; Dumitrascu, A.; Prisacaru, G. New micro tribometer for rolling friction. Wear 2011, 271, 842–852. [Google Scholar] [CrossRef]
- Sosnovskii, L.; Komissarov, V.; Shcherbakov, S. A Method of Experimental Study of Friction in a Active System. J. Frict. Wear 2012, 33, 136–145. [Google Scholar] [CrossRef]
- Available online: https://www.sciencedirect.com/topics/physics-and-astronomy/tribometers (accessed on 22 October 2020).
- Zhang, X.; Zhang, Y.; Du, S.; Yang, Z.; He, T.; Li, Z. Study on the Tribological Performance of Copper-Based Powder Metallurgical Friction Materials with Cu-Coated or Uncoated Graphite Particles as Lubricants. Materials 2018, 11, 2016. [Google Scholar] [CrossRef]
- ISO 28580-2018. Available online: https://www.iso.org/standard/67531.html (accessed on 27 October 2020).
- SAE J2452-2017. Available online: https://standards.globalspec.com/std/10170311/SAE%20J2452 (accessed on 27 October 2020).
- Minkin, L.; Sikes, D. Coefficient of rolling friction—Lab experiment. Am. J. Phys. 2018, 86, 77. [Google Scholar] [CrossRef]
- Cross, C. Effects of surface roughness on rolling friction. Eur. J. Phys. 2015, 36, 065029. [Google Scholar] [CrossRef]
- Ketterhagen, W.; Bharadwaj, R.; Hancock, B. The coefficient of rolling resistance (CoRR) of some pharmaceutical tablets. Int. J. Pharm. 2010, 392, 107–110. [Google Scholar] [CrossRef] [PubMed]
- Bonhomme, J.; Moll, V. A Method to Determine the Rolling Resistance Coefficient by Means of Uniaxial Testing Machines. Exp. Tech. 2015, 39, 37–41. [Google Scholar] [CrossRef]
- Abdalsalam, M.; Gutierrez, M. Comprehensive study of the effects of rolling resistance on the stress–strain and strain localization behaviour of granular materials. Granul. Matter 2010, 12, 527–541. [Google Scholar] [CrossRef]
- Andersen, L. Rolling Resistance Modelling: From Functional Data Analysis to Asset Management System. Ph.D. Thesis, Roskilde University, Roskilde, Denmark, April 2015. [Google Scholar]


















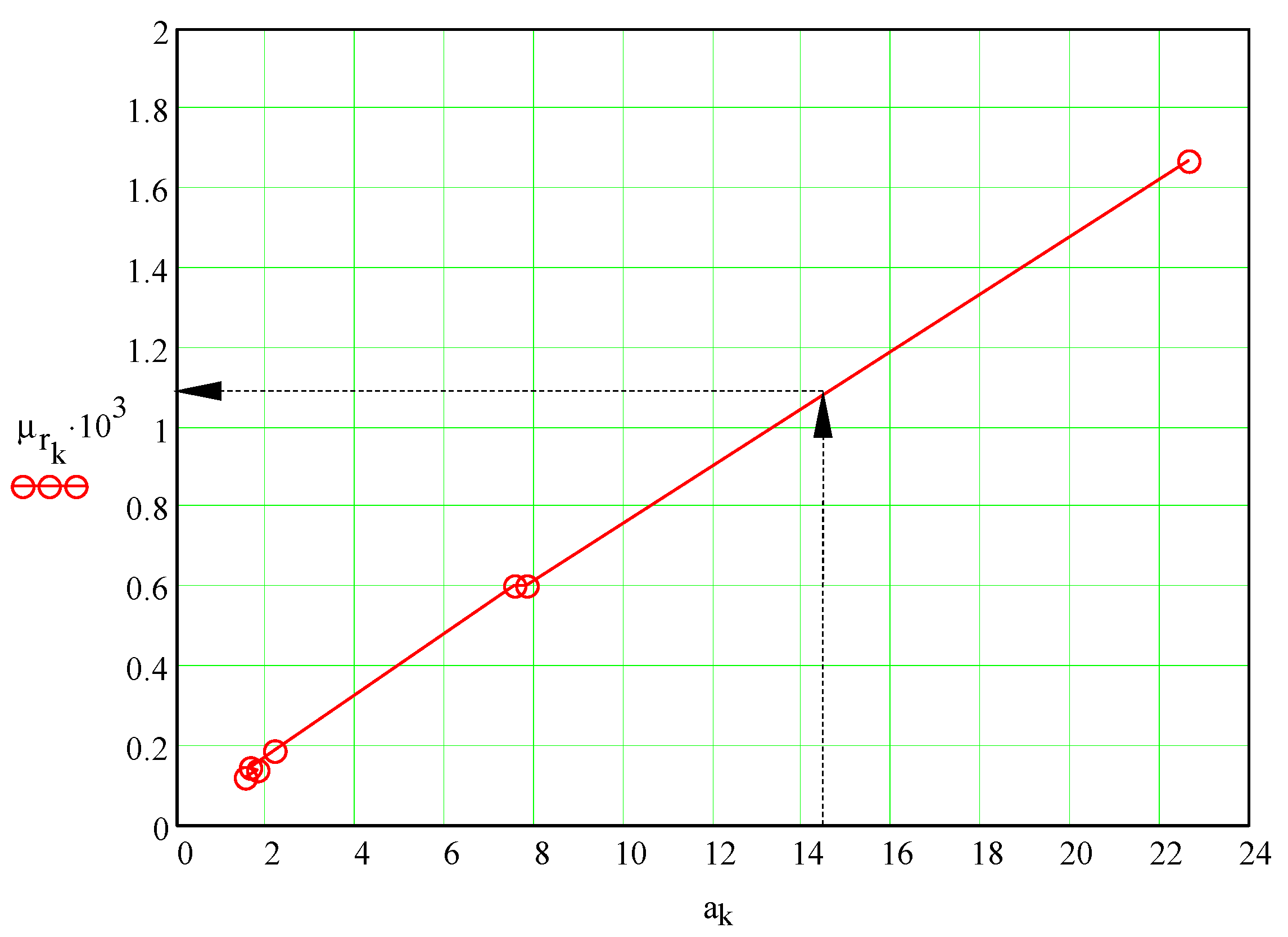
| Material of the Plate | (m) | (-) | (rad/s) |
|---|---|---|---|
| Steel | 4.508 | 0.142 | 1.656 |
| Glass | 3.714 | 0.117 | 1.556 |
| Aluminum | 4.445 | 0.140 | 1.811 |
| Copper | 18.986 | 0.598 | 7.587 |
| Polycarbonate | 18.986 | 0.598 | 7.823 |
| Carbon fiber composite | 5.810 | 0.183 | 2.189 |
| Glass fiber fabric over glass plate | 53.023 | 1.670 | 22.65 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alaci, S.; Muscă, I.; Pentiuc, Ș.-G. Study of the Rolling Friction Coefficient between Dissimilar Materials through the Motion of a Conical Pendulum. Materials 2020, 13, 5032. https://doi.org/10.3390/ma13215032
Alaci S, Muscă I, Pentiuc Ș-G. Study of the Rolling Friction Coefficient between Dissimilar Materials through the Motion of a Conical Pendulum. Materials. 2020; 13(21):5032. https://doi.org/10.3390/ma13215032
Chicago/Turabian StyleAlaci, Stelian, Ilie Muscă, and Ștefan-Gheorghe Pentiuc. 2020. "Study of the Rolling Friction Coefficient between Dissimilar Materials through the Motion of a Conical Pendulum" Materials 13, no. 21: 5032. https://doi.org/10.3390/ma13215032
APA StyleAlaci, S., Muscă, I., & Pentiuc, Ș.-G. (2020). Study of the Rolling Friction Coefficient between Dissimilar Materials through the Motion of a Conical Pendulum. Materials, 13(21), 5032. https://doi.org/10.3390/ma13215032






