Cementitious Composites with High Compaction Potential: Modeling and Calibration
Abstract
1. Introduction
Goals and Structure of the Paper
2. Modeling Cementitious Materials with DEM
2.1. Governing Equations of Motion
2.2. Constitutive Law
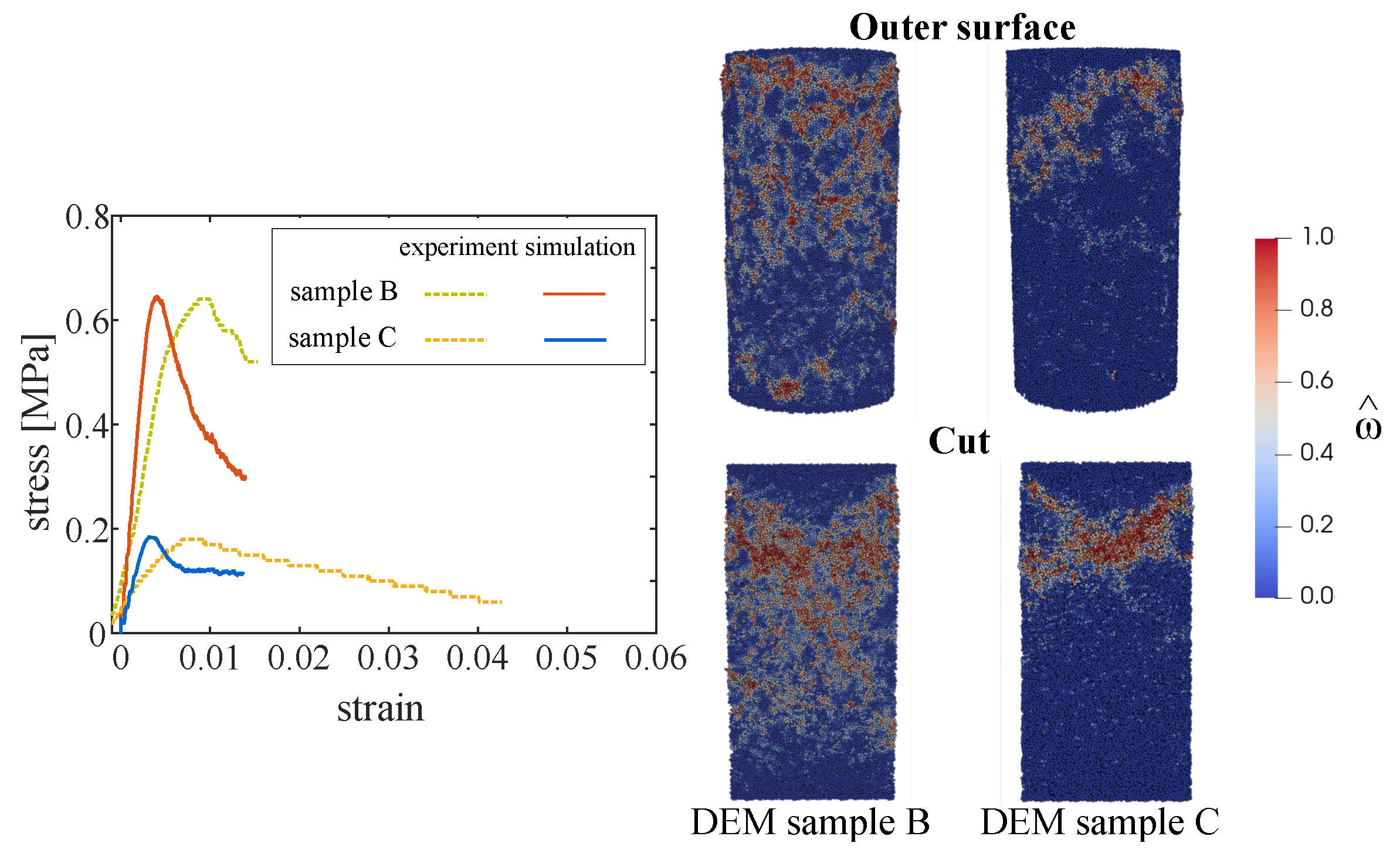
3. Calibration and Validation of the DEM Model Based on Laboratory Experiments
3.1. Experimental Data from Compression Tests on Highly Compressible Composite Grouts
3.2. Calibration of Model Parameters
3.2.1. Calibration Step 1
3.2.2. Calibration Step 2
- Voids with a prescribed volume fraction and size distribution are randomly picked and placed within a cylindrical domain (height = 200 mm, diameter = 100 mm).
- The coordinate and radius of each void particle is recorded.
- Given a dense packing of DEM particles generated in Step 1, the DEM particles lying within the spherical region defined by void position and radius are removed.
3.2.3. Calibration Step 3
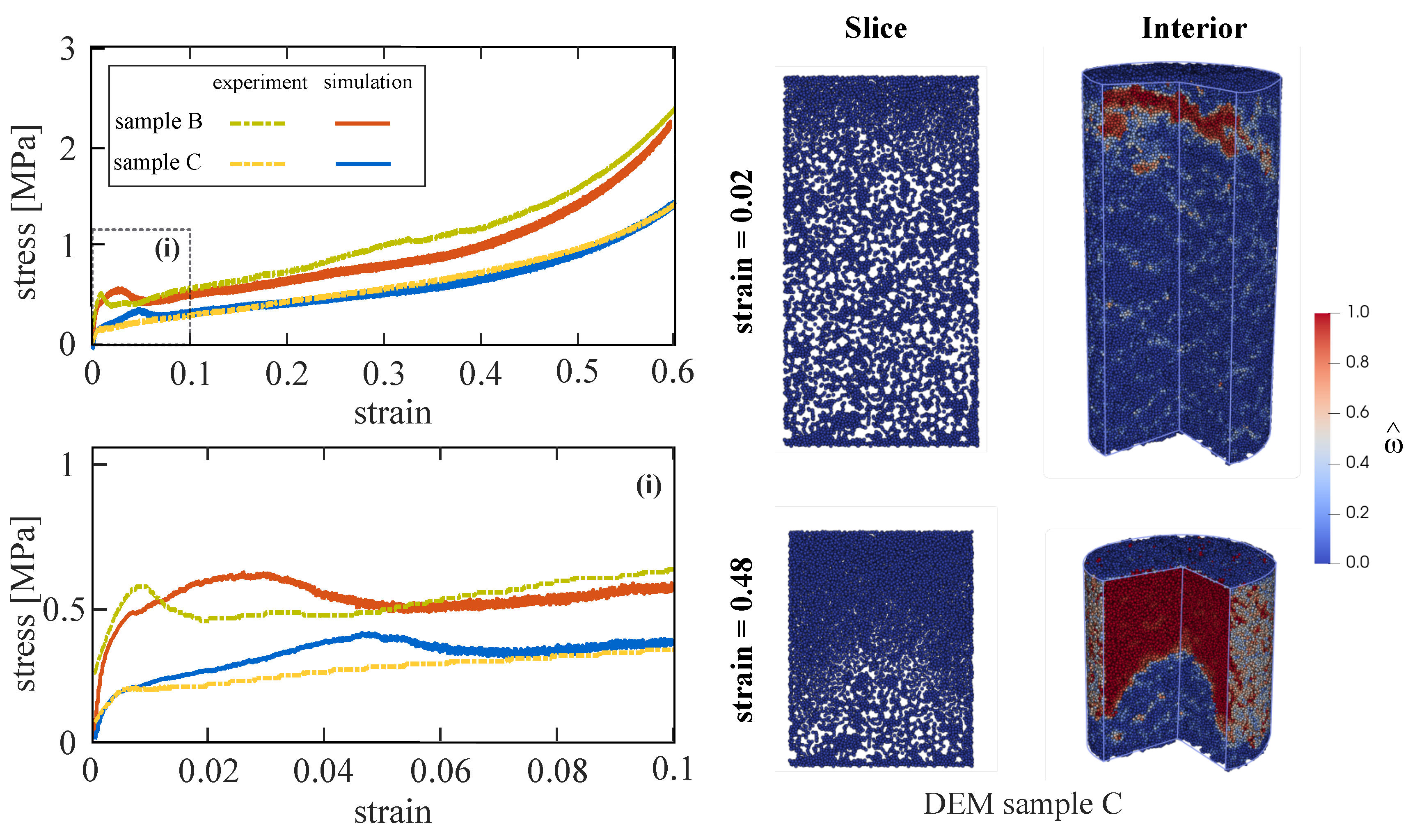
3.3. Validation
4. Conclusions
- Cementitious materials with high-compaction potential can be designed using a combination of weak inclusions and pores.
- Experimental observations and model simulations show the development of compaction gradients during confined uniaxial compression tests.
- Despite the extensive work dedicated to the calibration procedure as well as the high computational cost, DEM has shown its capability to replicate the main physical mechanisms governing the behavior of compressible cementitious composites.
- In order to capture the effect of fine pores with a characteristic size smaller than the DEM discretization, a phenomenological plasticity-type submodel has to be calibrated in addition to the usual inter-particle parameters.
- The proposed calibration procedure offers a good control of the pore structure characteristics, such as void volume fraction, air-void size, and void size distribution. Consequently, the proposed computational model allows to support the design of new materials with specific, customized compaction properties (elastic phase, plateau, and densification). These materials can be used for optimizing the compressibility characteristics of annular gap grouts used to fill the tail void gap in mechanized tunneling in case of tunneling projects in rocks with a high squeezing potential.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| EPS | Expanded polysterene |
| REV | Representative elementary volume |
| FEM | Finite Element Method |
| DEM | Discrete Element Method |
References
- Anagnostou, G.; Pimentel, E.; Serafeimidis, K. Swelling of sulphatic claystones–some fundamental questions and their practical relevance. Geomech. Tunn. 2010, 3, 567–572. [Google Scholar] [CrossRef]
- Steiner, W. Tunnelling in squeezing rocks: Case histories. Rock Mech. Rock Eng. 1996, 29, 211–246. [Google Scholar] [CrossRef]
- Einstein, H. Tunnelling in difficult ground-swelling behaviour and identification of swelling rocks. Rock Mech. Rock Eng. 1996, 29, 113–124. [Google Scholar] [CrossRef]
- Mezger, F.; Ramoni, M.; Anagnostou, G. Some concepts for segmental linings in squeezing rock. In Rapid Excavation and Tunneling Conference 2015 Proceedings; Society for Mining, Metallurgy, and Exploration Inc. (SME): New Orleans, LA, USA, 2015; pp. 646–658. [Google Scholar]
- Cantieni, L.; Anagnostou, G. The interaction between yielding supports and squeezing ground. Tunn. Undergr. Space Technol. 2009, 24, 309–322. [Google Scholar] [CrossRef]
- Nehdi, M.; Khan, A.; Lo, K. Development of deformable protective system for underground infrastructure using cellular grouts. Mater. J. 2002, 99, 490–498. [Google Scholar]
- Schneider, E.; Spiegl, M. Convergency compatible support systems. Tunnels Tunn. Int. 2008, JUN, 40–43. [Google Scholar]
- Mezger, F.; Ramoni, M.; Anagnostou, G. Options for deformable segmental lining systems for tunnelling in squeezing rock. Tunn. Undergr. Space Technol. 2018, 76, 64–75. [Google Scholar] [CrossRef]
- Cucino, P.; Eccher, G.; Castellanza, R.; Parpajola, A.; Di Prisco, C.; SpA, L. Expanded clay in deep mechanised tunnel boring. In Proceedings of the ITA-AITES World Tunnel Congress Bangkok, Bangkok, Thailand, 21–23 May 2012. [Google Scholar]
- Strohhäusl, S. TBM Tunnelling Under High Overburden With Yielding Segmental Linings Eureka Project Eu 1079. In Tunnel Boring Machines: Trends in Design and Construction of Mechanical Tunnelling; CRC Press: London, UK, 1996; pp. 61–68. [Google Scholar]
- Schneider, E.; Rotter, K.; Saxer, A.; Röck, R. Compex support system. Felsbau 2005, 23, 95–101. [Google Scholar]
- Billig, B.; Ebsen, B.; Gipperich, C.; Schaab, A.; Wulff, M. DeCo Grout–innovative grout to cope with rock deformations in TBM tunnelling. In Proceedings of the Underground Space–the 4th Dimension of Metropolises, ITA World Tunnel Congress, Prague, Czech Republic, 5–10 May 2007; pp. 1487–1492. [Google Scholar]
- Amran, Y.M.; Farzadnia, N.; Ali, A.A. Properties and applications of foamed concrete; a review. Constr. Build. Mater. 2015, 101, 990–1005. [Google Scholar] [CrossRef]
- Ramamurthy, K.; Nambiar, E.K.; Ranjani, G.I.S. A classification of studies on properties of foam concrete. Cem. Concr. Compos. 2009, 31, 388–396. [Google Scholar] [CrossRef]
- Olsson, W.A. Theoretical and experimental investigation of compaction bands in porous rock. J. Geophys. Res. Solid Earth 1999, 104, 7219–7228. [Google Scholar] [CrossRef]
- Issen, K.A.; Rudnicki, J.W. Conditions for compaction bands in porous rock. J. Geophys. Res. Solid Earth 2000, 105, 21529–21536. [Google Scholar] [CrossRef]
- Issen, K.A. The influence of constitutive models on localization conditions for porous rock. Eng. Fract. Mech. 2002, 69, 1891–1906. [Google Scholar] [CrossRef]
- Rudnicki, J.W. Shear and compaction band formation on an elliptic yield cap. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef]
- Eshelby, J. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. A 1957, 241, 376–396. [Google Scholar]
- Bernaud, D.; Deudé, V.; Dormieux, L.; Maghous, S.; Schmitt, D. Evolution of elastic properties in finite poroplasticity and finite element analysis. Int. J. Numer. Anal. Methods Geomech. 2002, 26, 845–871. [Google Scholar] [CrossRef]
- Barthélémy, J.F.; Dormieux, L.; Maghous, S. Micromechanical approach to the modelling of compaction at large strains. Comput. Geotech. 2003, 30, 321–338. [Google Scholar] [CrossRef]
- Danas, K.; Aravas, N. Numerical modeling of elasto-plastic porous materials with void shape effects at finite deformations. Compos. Part B Eng. 2012, 43, 2544–2559. [Google Scholar] [CrossRef]
- Jiang, Y.; Fan, H. A micromechanics model for predicting the stress–strain relations of filled elastomers. Comput. Mater. Sci. 2013, 67, 104–108. [Google Scholar] [CrossRef]
- Jiang, Y.; Shi, X.; Qiu, K. A micromechanics-based incremental damage model for carbon black filled rubbers. Compos. Part B Eng. 2015, 75, 11–16. [Google Scholar] [CrossRef]
- Lopez-Pamies, O.; Castañeda, P.P. Homogenization-based constitutive models for porous elastomers and implications for macroscopic instabilities: II?Results. J. Mech. Phys. Solids 2007, 55, 1702–1728. [Google Scholar] [CrossRef][Green Version]
- Ponte Castaneda, P. The effective mechanical properties of nonlinear isotropic composites. J. Mech. Phys. Solids 1991, 39, 45–71. [Google Scholar] [CrossRef]
- Suquet, P. Overall properties of nonlinear composites: A modified secant moduli theory and its link with Ponte Castañeda’s nonlinear variational procedure. C. R. L’Académie Sci. Sér. II Mécanique Phys. Chim. Astron. 1995, 320, 563–571. [Google Scholar]
- Kader, M.; Islam, M.; Saadatfar, M.; Hazell, P.; Brown, A.; Ahmed, S.; Escobedo, J. Macro and micro collapse mechanisms of closed-cell aluminium foams during quasi-static compression. Mater. Des. 2017, 118, 11–21. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, J.; Fan, J.; Wang, Z.; Zhao, L. On crushing response of the three-dimensional closed-cell foam based on Voronoi model. Mech. Mater. 2014, 68, 85–94. [Google Scholar]
- Cundall, P.; Strack, A. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Donzé, F.V.; Richefeu, V.; Magnier, S.A. Advances in discrete element method applied to soil, rock and concrete mechanics. Electron. J. Geotech. Eng. 2009, 8, 44. [Google Scholar]
- Papka, S.D.; Kyriakides, S. Experiments and full-scale numerical simulations of in-plane crushing of a honeycomb. Acta Mater. 1998, 46, 2765–2776. [Google Scholar] [CrossRef]
- Katsman, R.; Aharonov, E.; Scher, H. Numerical simulation of compaction bands in high-porosity sedimentary rock. Mech. Mater. 2005, 37, 143–162. [Google Scholar]
- Hazzard, J.F.; Young, R.P.; Maxwell, S. Micromechanical modeling of cracking and failure in brittle rocks. J. Geophys. Res. Solid Earth 2000, 105, 16683–16697. [Google Scholar]
- Dattola, G.; Di Prisco, C.; Redaelli, I.; Utili, S. A distinct element method numerical investigation of compaction processes in highly porous cemented granular materials. Int. J. Numer. Anal. Methods Geomech. 2014, 38, 1101–1130. [Google Scholar]
- Nguyen, T.T.; Bui, H.H.; Ngo, T.D.; Nguyen, G.D. Experimental and numerical investigation of influence of air-voids on the compressive behaviour of foamed concrete. Mater. Des. 2017, 130, 103–119. [Google Scholar] [CrossRef]
- Nitka, M.; Tejchman, J. Modelling of concrete behaviour in uniaxial compression and tension with DEM. Granul. Matter 2015, 17, 145–164. [Google Scholar]
- Nitka, M.; Tejchman, J. Modelling of concrete fracture at aggregate level using FEM and DEM based on X-ray μCT images of internal structure. Eng. Fract. Mech. 2015, 147, 13–35. [Google Scholar]
- Suchorzewski, J.; Tejchman, J.; Nitka, M. Discrete element method simulations of fracture in concrete under uniaxial compression based on its real internal structure. Int. J. Damage Mech. 2018, 27, 578–607. [Google Scholar]
- Suchorzewski, J.; Tejchman, J.; Nitka, M. Experimental and numerical investigations of concrete behaviour at meso-level during quasi-static splitting tension. Theor. Appl. Fract. Mech. 2018, 96, 720–739. [Google Scholar] [CrossRef]
- Coetzee, C. Calibration of the discrete element method. Powder Technol. 2017, 310, 104–142. [Google Scholar]
- Oñate, E.; Zárate, F.; Miquel, J.; Santasusana, M.; Celigueta, M.A.; Arrufat, F.; Gandikota, R.; Valiullin, K.; Ring, L. A local constitutive model for the discrete element method. Application to geomaterials and concrete. Comput. Part. Mech. 2015, 2, 139–160. [Google Scholar]
- Richardson, D.C.; Walsh, K.J.; Murdoch, N.; Michel, P. Numerical simulations of granular dynamics: I. Hard-sphere discrete element method and tests. Icarus 2011, 212, 427–437. [Google Scholar]
- Mitarai, N.; Nakanishi, H. Hard-sphere limit of soft-sphere model for granular materials: Stiffness dependence of steady granular flow. Phys. Rev. E 2003, 67, 021301. [Google Scholar]
- Šmilauer, V. Cohesive Particle Model Using Discrete Element Method on the Yade Platform. Ph.D. Thesis, Czech Technical University, Prague, Czech Republic, 2010. [Google Scholar]
- Tran, V.; Donzé, F.V.; Marin, P. A discrete element model of concrete under high triaxial loading. Cem. Concr. Compos. 2011, 33, 936–948. [Google Scholar] [CrossRef]
- Šmilauer, V.; Chareyre, B. Yade dem Formulation. Available online: https://yade-dem.org/w/images/e/e0/YadeFormulation.pdf (accessed on 4 November 2020).
- Van Mier, J. Strain Softening of Concrete under Multiaxial Loading Conditions. Ph.D. Thesis, TH Eindhoven, Eindhoven, The Netherlands, 1984. [Google Scholar]
- Šmilauer, V. Woo Documentation. 2016. Available online: https://woodem.org (accessed on 4 November 2020).
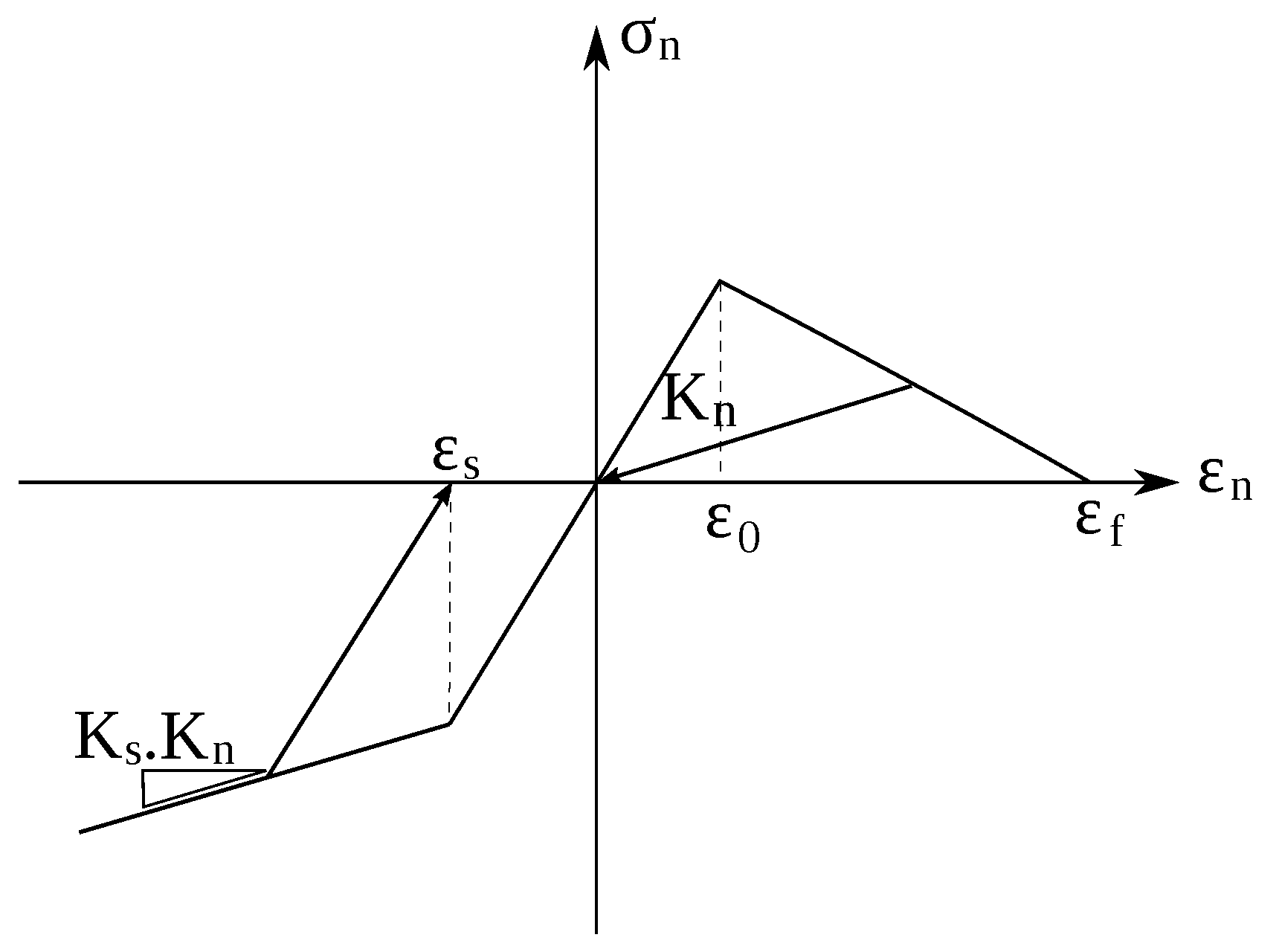



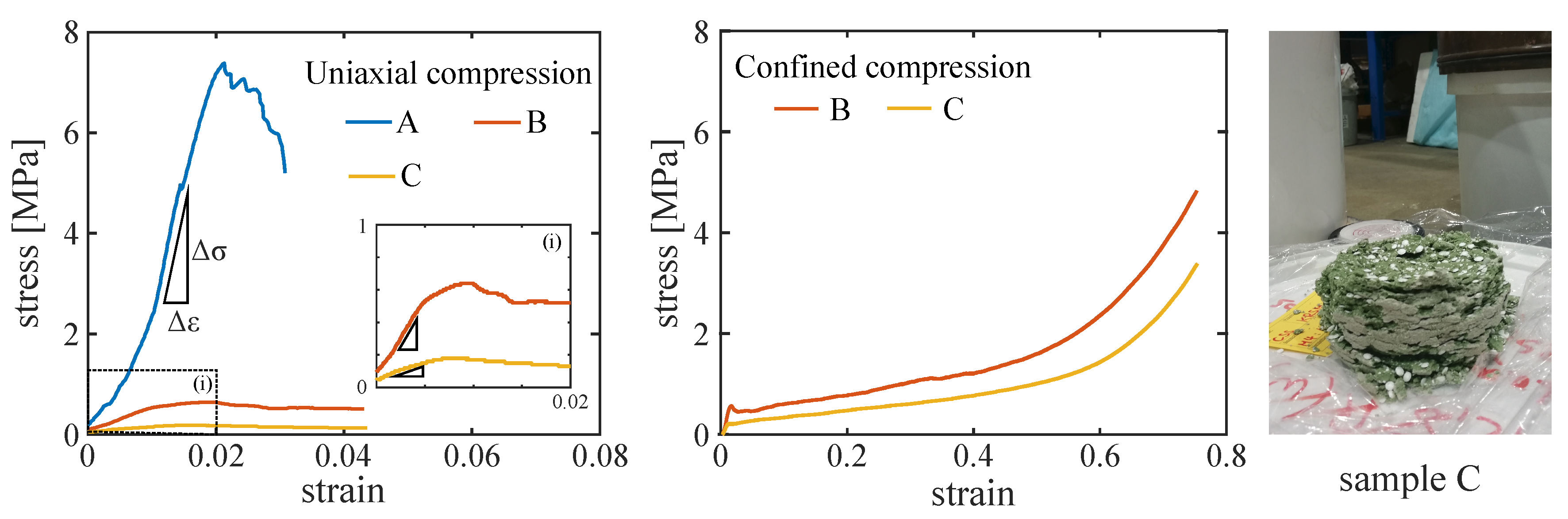
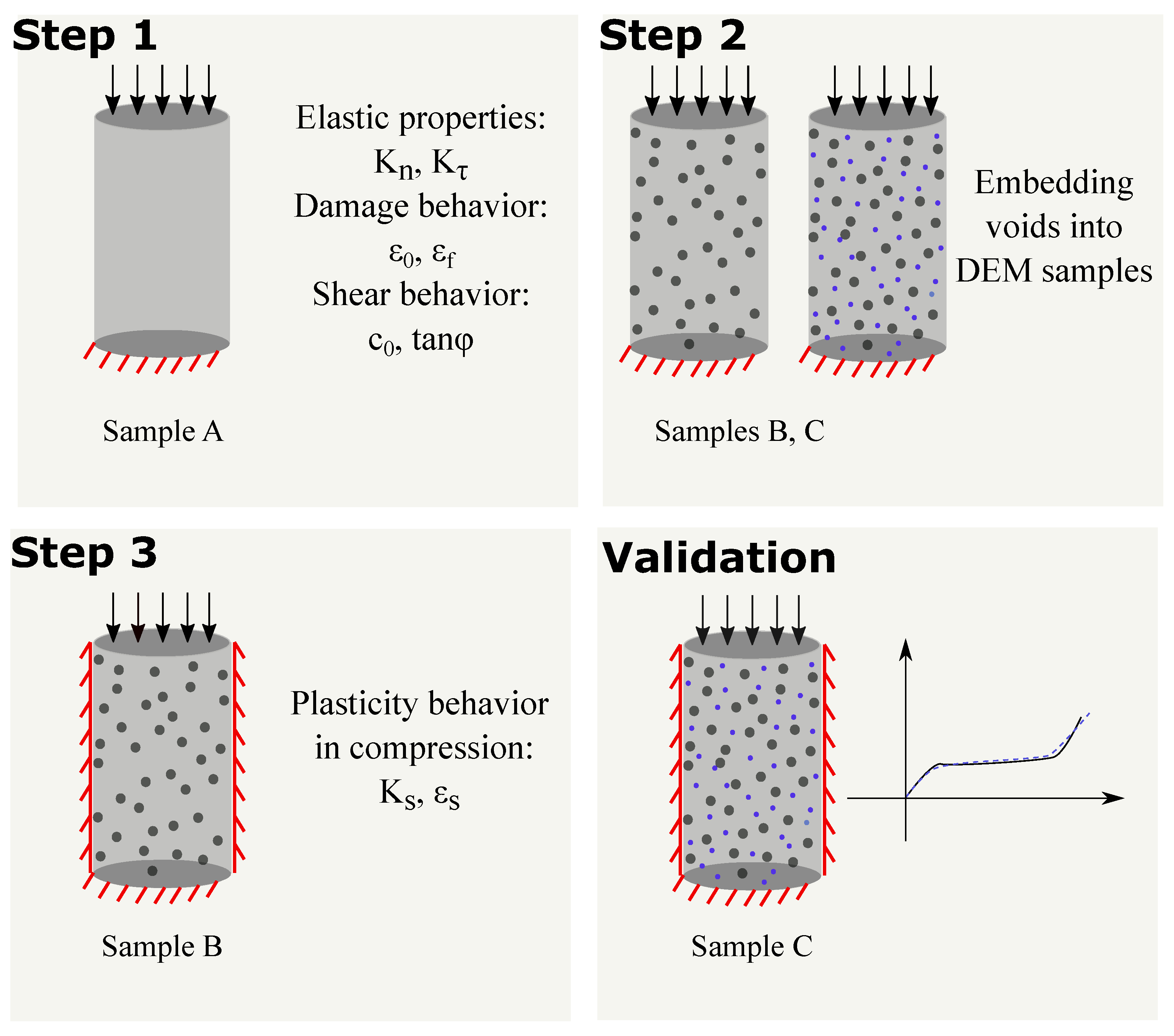

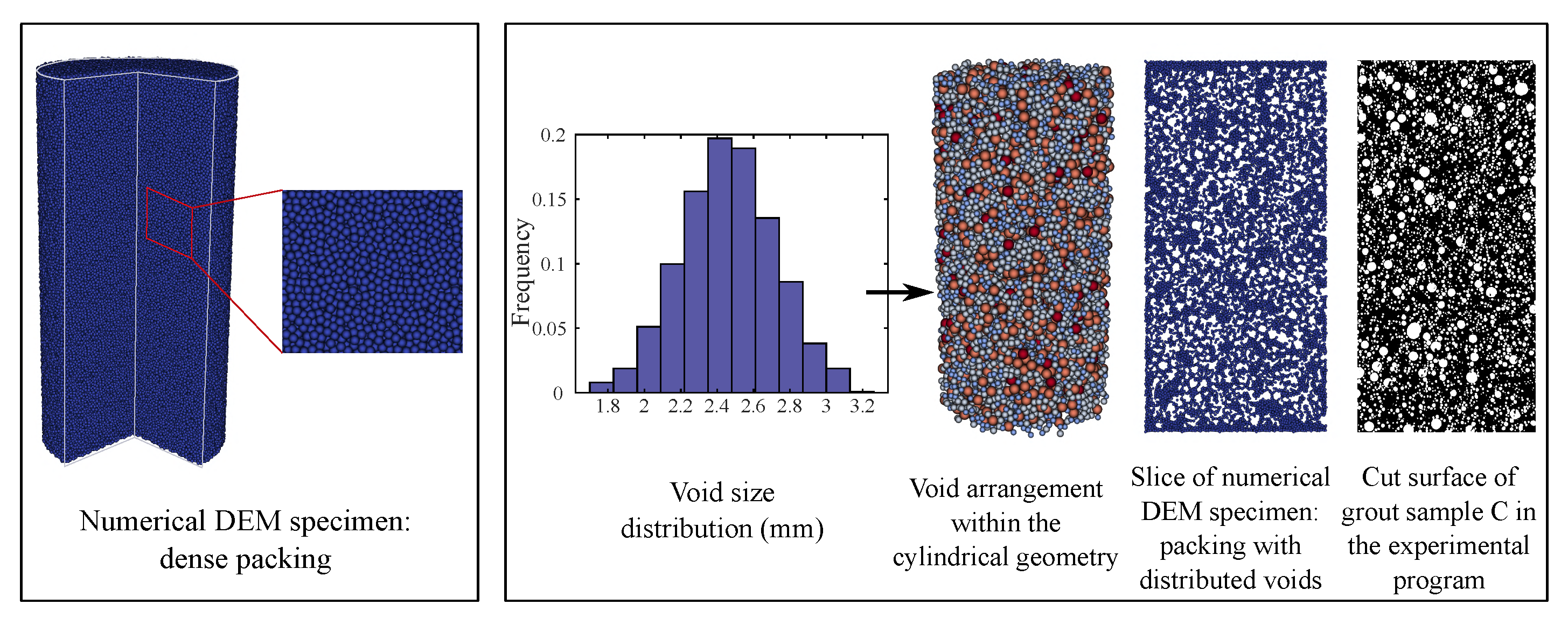
| Elastic parameters | ||
|---|---|---|
| normal modulus | Pa | |
| tangential modulus | Pa | |
| Damage law in tension | ||
| limit elastic strain | ||
| relative ductility | ||
| Elasto-plasticity in shear | ||
| initial cohesion | Pa | |
| frictional angle | ||
| Elasto-plasticity in compression | ||
| plastic strain | ||
| relative hardening modulus | ||
| Mix Designs | A | B | C |
|---|---|---|---|
| Source Materials | Volume | Volume | Volume |
| Cement | 67.6 | 25.9 | 19.4 |
| Slag | 142.0 | 54.5 | 40.8 |
| Filler | 0.0 | 0.0 | 0.0 |
| Bentonite | 21.4 | 8.2 | 6.2 |
| Water | 695.9 | 267.1 | 200.0 |
| Foaming agent | 0.0 | 0.0 | 0.89 |
| EPS 0.5–1 mm | 0.0 | 297.9 | 223.1 |
| EPS 1–2 mm | 0.0 | 123.3 | 92.3 |
| EPS 2–5 mm | 0.0 | 195.2 | 146.2 |
| Activator 1 (Sodium) | 37.6 | 14.4 | 10.8 |
| Activator 2 (Potassium) | 35.5 | 13.6 | 10.2 |
| Calculated Air voids | 0.0 | 0.0 | 250.0 |
| Total | 1000 | 1000 | 1000 |
| Sample | Young’s Modulus (GPa) | Compressive Strength (MPa) | Density (kg/m3) |
|---|---|---|---|
| A | 1.262 | 7.38 | 1430 |
| B | 0.248 | 0.64 | 840 |
| C | 0.12 | 0.18 | 460 |
| Elastic parameters | ||
|---|---|---|
| 0.8 | GPa | |
| 0.2 | ||
| Damage law in tension | ||
| 30 | ||
| Elasto-plasticity in shear | ||
| MPa | ||
| Elasto-plasticity in compression | ||
| Sample | Radius of DEM Particles (mm) | Number of DEM Particles | Void Volume Fraction | Mean Void Radius (mm) | Number of Voids |
|---|---|---|---|---|---|
| B | 0.8 | 253,718 | 42% | 2.5 | 11,567 |
| C | 0.8 | 199,357 | 53.2% | 2.5 | 14,651 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vu, G.; Iskhakov, T.; Timothy, J.J.; Schulte-Schrepping, C.; Breitenbücher, R.; Meschke, G. Cementitious Composites with High Compaction Potential: Modeling and Calibration. Materials 2020, 13, 4989. https://doi.org/10.3390/ma13214989
Vu G, Iskhakov T, Timothy JJ, Schulte-Schrepping C, Breitenbücher R, Meschke G. Cementitious Composites with High Compaction Potential: Modeling and Calibration. Materials. 2020; 13(21):4989. https://doi.org/10.3390/ma13214989
Chicago/Turabian StyleVu, Giao, Tagir Iskhakov, Jithender J. Timothy, Christoph Schulte-Schrepping, Rolf Breitenbücher, and Günther Meschke. 2020. "Cementitious Composites with High Compaction Potential: Modeling and Calibration" Materials 13, no. 21: 4989. https://doi.org/10.3390/ma13214989
APA StyleVu, G., Iskhakov, T., Timothy, J. J., Schulte-Schrepping, C., Breitenbücher, R., & Meschke, G. (2020). Cementitious Composites with High Compaction Potential: Modeling and Calibration. Materials, 13(21), 4989. https://doi.org/10.3390/ma13214989








