Effect of Rotation of the Principal Stress Axes Relative to the Material on the Evolution of Material Properties in Severe Plastic Deformation Processes
Abstract
1. Introduction
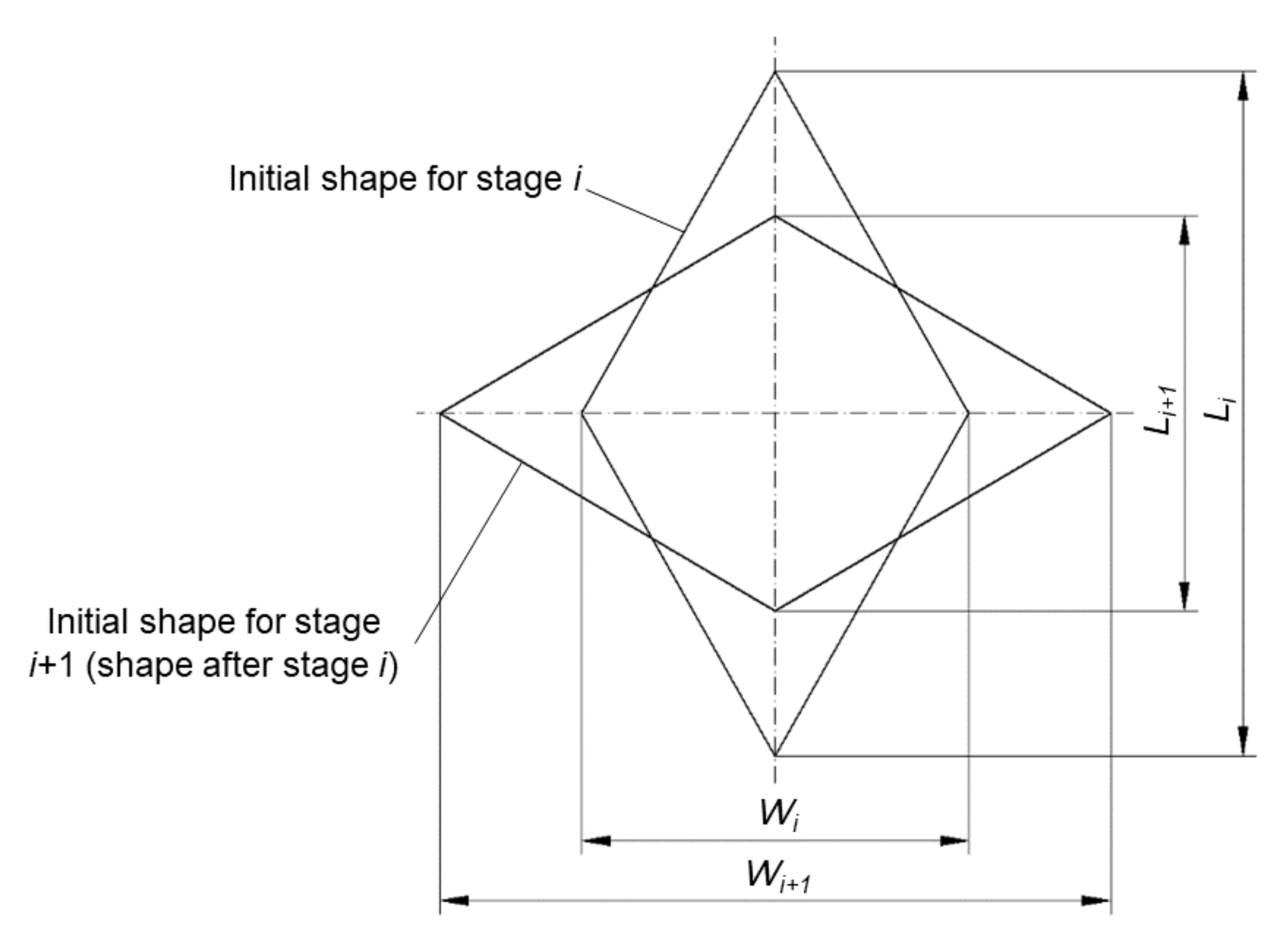
2. General Approach
3. Experimental Procedures
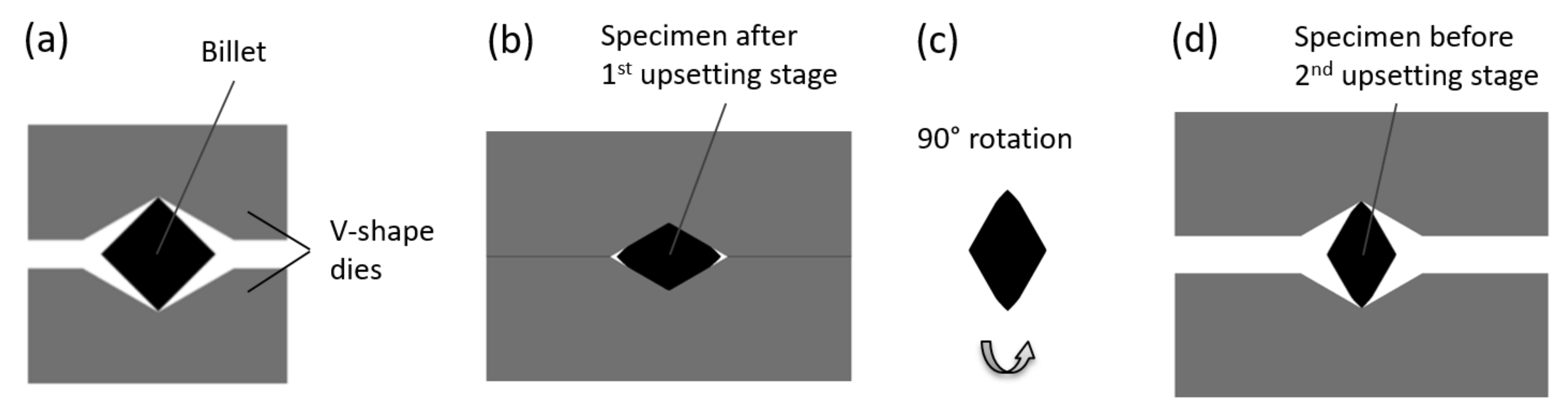
3.1. Deformation Processes
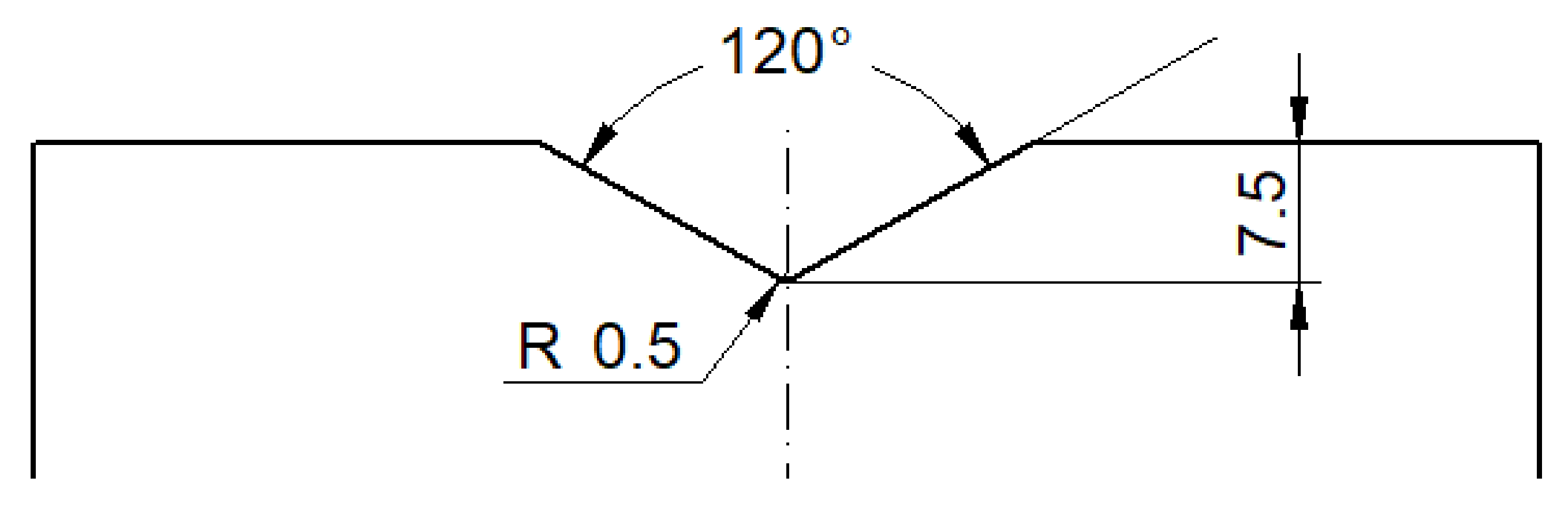
3.2. Specimens
3.3. Measurements
4. Results
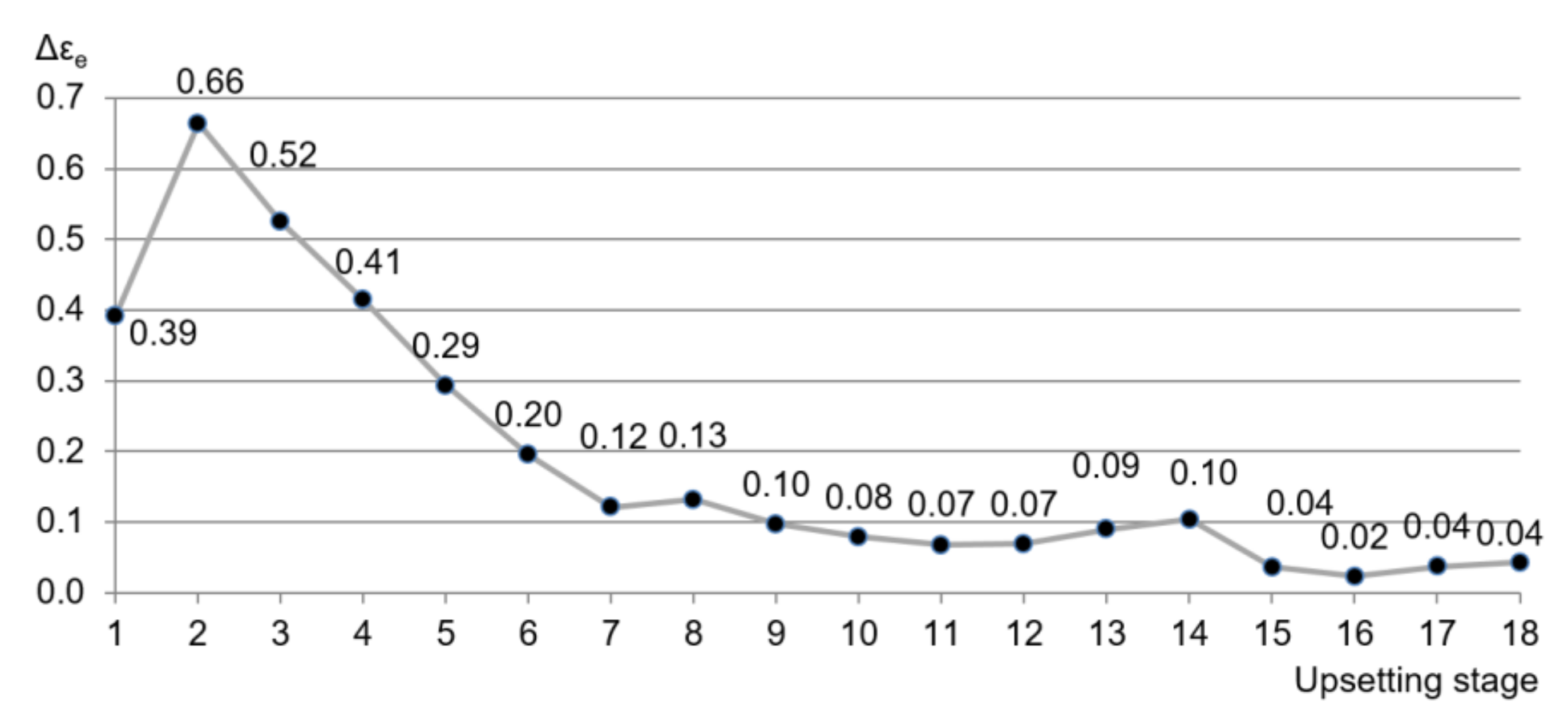
4.1. Strain
4.2. Microstructure
4.3. Microhardness
4.4. SPD Process Versus Rastegaev’s Method
5. Discussion
- The rotation of the principal stress axes does not affect the evolution of microhardness (i.e., the value of microhardness at two points is the same if the value of the equivalent strain at these points is the same) in the case of the two processes studied.
- The rotation of the principal stress axes affects the evolution of microstructure (i.e., parameters that characterize the microstructure at two points are different even if the value of the equivalent strain at these points is the same).
Author Contributions
Funding
Conflicts of Interest
References
- Valiev, R.Z.; Langdon, T.G. The 7th International Conference on Nanomaterials by Severe Plastic Deformation: A report of the International NanoSPD Steering Committee. In Proceedings of the 7th International Conference on Nanomaterials by Severe Plastic Deformation, Sydney, Australia, 2–7 July 2017; pp. 1–10. [Google Scholar] [CrossRef]
- Huang, Y.; Langdon, T.G. Advances in ultrafine-grained materials. Mater. Today 2013, 16, 85–93. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Islamgaliev, R.K.; Alexandrov, I.V. Bulk nanostructured materials from severe plastic deformation. Prog. Mat. Sci. 2000, 45, 103–189. [Google Scholar] [CrossRef]
- Su, L.; Deng, G.; Luzin, V.; Wang, H.; Wang, Z.; Yu, H.; Li, H.; Tieu, A.K. Effect of cryogenic temperature equal channel angular pressing on microstructure, bulk texture and tensile properties of AA1050. Mater. Sci. Eng. A 2020, 780, 139190. [Google Scholar] [CrossRef]
- Alawadhi, M.Y.; Sabbaghianrad, S.; Wang, Y.C.; Huang, Y.; Langdon, T.G. Characteristics of grain refinement in oxygen-free copper processed by equal-channel angular pressing and dynamic testing. Mater. Sci. Eng. A 2020, 775, 138985. [Google Scholar] [CrossRef]
- Bridgman, P.W. On torsion combined with compression. J. Appl. Phys. 1943, 14, 273–283. [Google Scholar] [CrossRef]
- Bridgman, P.W. Effects of high shearing stress combined with high hydrostatic pressure. Phys. Rev. 1935, 48, 825–847. [Google Scholar] [CrossRef]
- Straumal, B.; Kilmametov, A.; Mazilkin, A.; Kogtenkova, O.; Baretzky, B.; Korneva, A.; Zięba, P. Diffusive and displacive phase transformations under high pressure torsion. Acta Metall. Slovaca 2019, 25, 230–252. [Google Scholar] [CrossRef]
- Duan, J.; Wen, H.; Zhou, C.; He, X.; Islamgaliev, R.; Valiev, R. Annealing behavior in a high-pressure torsion-processed Fe–9Cr steel. J. Mater. Sci. 2020, 55, 7958–7968. [Google Scholar] [CrossRef]
- Luo, D.; Huminiuc, T.; Huang, Y.; Polcar, T.; Langdon, T.G. The fabrication of high strength Zr/Nb nanocomposites using high-pressure torsion. Mater. Sci. Eng. A 2020, 790, 139693. [Google Scholar] [CrossRef]
- Chen, Q.; Shu, D.Y.; Lin, J.; Wu, Y.; Xia, X.S.; Huang, S.H.; Zhao, Z.D.; Mishin, O.V.; Wu, G.L. Evolution of microstructure and texture in copper during repetitive extrusion-upsetting and subsequent annealing. J. Mater. Sci. Technol. 2017, 33, 690–697. [Google Scholar] [CrossRef]
- Park, C.H.; Kim, J.H.; Yeom, J.T.; Oh, C.S.; Semiatin, S.L.; Lee, C.S. Formation of a submicrocrystalline structure in a two-phase titanium alloy without severe plastic deformation. Scr. Mater. 2013, 68, 996–999. [Google Scholar] [CrossRef]
- Łyszkowski, R.; Czujko, T.; Varin, R.A. Multi-axial forging of Fe3Al-base intermetallic alloy and its mechanical properties. J. Mater. Sci. 2017, 52, 2902–2914. [Google Scholar] [CrossRef]
- Rusz, S.; Hilšer, O.; Ochodek, V.; Čížek, L.; Kraus, M.; Mareš, V.; Grajcar, A.; Švec, J. Effect of severe plastic deformation on mechanical and fatigue behavior of medium-c sheet steel. J. Min. Metall. Sect. B Metall. 2020, 56, 161–170. [Google Scholar] [CrossRef]
- Kral, P.; Dvorak, J.; Sklenicka, V.; Horita, Z.; Takizawa, Y.; Tang, Y.; Kvapilova, M.; Svobodova, M. Effect of ultrafine-grained microstructure on creep behaviour in 304L austenitic steel. Mater. Sci. Eng. A 2020, 785, 139383. [Google Scholar] [CrossRef]
- Schuh, B.; Mendez-Martin, F.; Völker, B.; George, E.P.; Clemens, H.; Pippan, R.; Hohenwarter, A. Mechanical properties, microstructure and thermal stability of a nanocrystalline CoCrFeMnNi high-entropy alloy after severe plastic deformation. Acta Mater. 2015, 96, 258–268. [Google Scholar] [CrossRef]
- Lu, K.; Hansen, N. Structural refinement and deformation mechanisms in nanostructured metals. Scr. Mater. 2009, 60, 1033–1038. [Google Scholar] [CrossRef]
- Sakai, T.; Belyakov, A.; Miura, H. Ultrafine grain formation in ferritic stainless steel during severe plastic deformation. Metall. Mater. Trans. A 2008, 39, 2206–2214. [Google Scholar] [CrossRef]
- Sakai, G.; Horita, Z.; Langdon, T.G. Grain refinement and superplasticity in an aluminum alloy processed by high-pressure torsion. Mater. Sci. Eng. A 2005, 393, 344–351. [Google Scholar] [CrossRef]
- Zhilyaev, A.P.; Oh-ishi, K.; Langdon, T.G.; McNelley, T.R. Microstructural evolution in commercial purity aluminum during high-pressure torsion. Mater. Sci. Eng. A 2005, 410–411, 277–280. [Google Scholar] [CrossRef]
- Lee, J.C.; Seok, H.K.; Suh, J.Y. Microstructural evolutions of the Al strip prepared by cold rolling and continuous equal channel angular pressing. Acta Mater. 2002, 50, 4005–4019. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Ivanisenko, Y.V.; Rauch, E.F.; Baudlet, B. Structure and deformation behaviour of armco iron subjected to severe plastic deformation. Acta Mater. 1996, 44, 4705–4712. [Google Scholar] [CrossRef]
- Richmond, O.; Devenpeck, M.L. A die profile for maximum efficiency in strip drawing. In Proceedings of the 4th U.S. National Congress of Applied Mechanics, New York, NY, USA, 18–21 June 1962; Rosenberg, R.M., Ed.; ASME: New York, NY, USA, 1962; pp. 1053–1057. [Google Scholar]
- Richmond, O.; Morrison, H.L. Streamlined wire drawing dies of minimum length. J. Mech. Phys. Solids. 1967, 15, 195–203. [Google Scholar] [CrossRef]
- Devenpeck, M.L.; Richmond, O. Strip-drawing experiments with a sigmoidal die profile. J. Eng. Ind. 1965, 87, 425–428. [Google Scholar] [CrossRef]
- Chung, K.; Alexandrov, S. Ideal flow in plasticity. Appl. Mech. Rev. 2007, 60, 316–335. [Google Scholar] [CrossRef]
- Goldstein, R.; Alexandrov, S. A new evolution equation for average grain size in processes of severe plastic deformation. J. Eng. Math. 2013, 78, 67–81. [Google Scholar] [CrossRef]
- Reiss, W.; Pohlandt, K. The Rastegaev upset test—A method to compress large material volumes homogeneously. Exp. Tech. 1986, 10, 20–24. [Google Scholar] [CrossRef]
- Yang, X.; Miura, H.; Sakai, T. Structural development at severely high strain in AZ31 magnesium alloy processed by cold forging and subsequent annealing. Mater. Des. 2013, 44, 573–579. [Google Scholar] [CrossRef]
- Wetscher, F.; Vorhauer, A.; Stock, R.; Pippan, R. Structural refinement of low alloyed steels during severe plastic deformation. Mater. Sci. Eng. A 2004, 387–389, 809–816. [Google Scholar] [CrossRef]
- Horita, Z.; Langdon, T.G. Microstructures and microhardness of an aluminum alloy and pure copper after processing by high-pressure torsion. Mater. Sci. Eng. A 2005, 410–411, 422–425. [Google Scholar] [CrossRef]
- Orlov, D.; Todaka, Y.; Umemoto, M.; Tsuji, N. Role of strain reversal in grain refinement by severe plastic deformation. Mater. Sci. Eng. A 2009, 499, 427–433. [Google Scholar] [CrossRef]
- EN 10084: 2008 Case hardening steels. Technical delivery conditions, IFEK - Ferrous metals: 2008. Available online: https://standards.iteh.ai/catalog/standards/sist/ae668925-3134-4cad-926e-323e6420e641/sist-en-10084-2008 (accessed on 14 June 2015).
- ISO 6507-1:2018(en) Metallic materials—Vickers hardness test, ISO/TC 164/SC 3: 2018. Available online: https://www.iso.org/obp/ui/#iso:std:iso:6507:-1:en (accessed on 3 April 2018).
- ISO 643:2012 Steels — Micrographic determination of the apparent grain size, ISO/TC 17/SC 7: 2012. Available online: https://www.iso.org/standard/61697.html (accessed on 7 May 2018).
- Smallman, R.E.; Ngan, A.H.W. Physical Metallurgy and Advanced Materials, 7th ed.; Butterworth-Heinemann: Oxford, UK, 2007. [Google Scholar] [CrossRef]
- Shin, D.H.; Kim, B.C.; Kim, Y.-S.; Park, K.-T. Microstructural evolution in a commercial low carbon steel by equal channel angular pressing. Acta Mater. 2000, 48, 2247–2255. [Google Scholar] [CrossRef]
- Zhu, J.; Liu, S.; Long, D.; Liu, Y.; Lin, N.; Yuan, X.; Orlov, D. Asymmetric cross rolling: A new technique for alleviating orientation-dependent microstructure inhomogeneity in tantalum sheets. J. Mater. Res. Technol. 2020, 9, 4566–4577. [Google Scholar] [CrossRef]
- Yu, J.; Zhang, Z.; Wang, Q.; Hao, H.; Cui, J.; Li, L. Rotary extrusion as a novel severe plastic deformation method for cylindrical tubes. Mater. Lett. 2018, 215, 195–199. [Google Scholar] [CrossRef]
- Naizabekov, A.; Volokitina, I.; Lezhnev, S.; Arbuz, A.; Panin, E.; Volokitin, A. Structure and mechanical properties of AISI1045 in the helical rolling-pressing process. J. Mater. Eng. Perform. 2020, 29, 315–329. [Google Scholar] [CrossRef]
- Bazarnik, P.; Huang, Y.; Lewandowska, M.; Langdon, T.G. Structural impact on the Hall-Petch relationship in an Al-5Mg alloy processed by high-pressure torsion. Mater. Sci. Eng. A 2015, 626, 9–15. [Google Scholar] [CrossRef]
- Akbaripanah, F.; Fereshteh-Saniee, F.; Mahmudi, R.; Kim, H.K. Microstructural homogeneity, texture, tensile and shear behavior of AM60 magnesium alloy produced by extrusion and equal channel angular pressing. Mater. Des. 2013, 43, 31–39. [Google Scholar] [CrossRef]

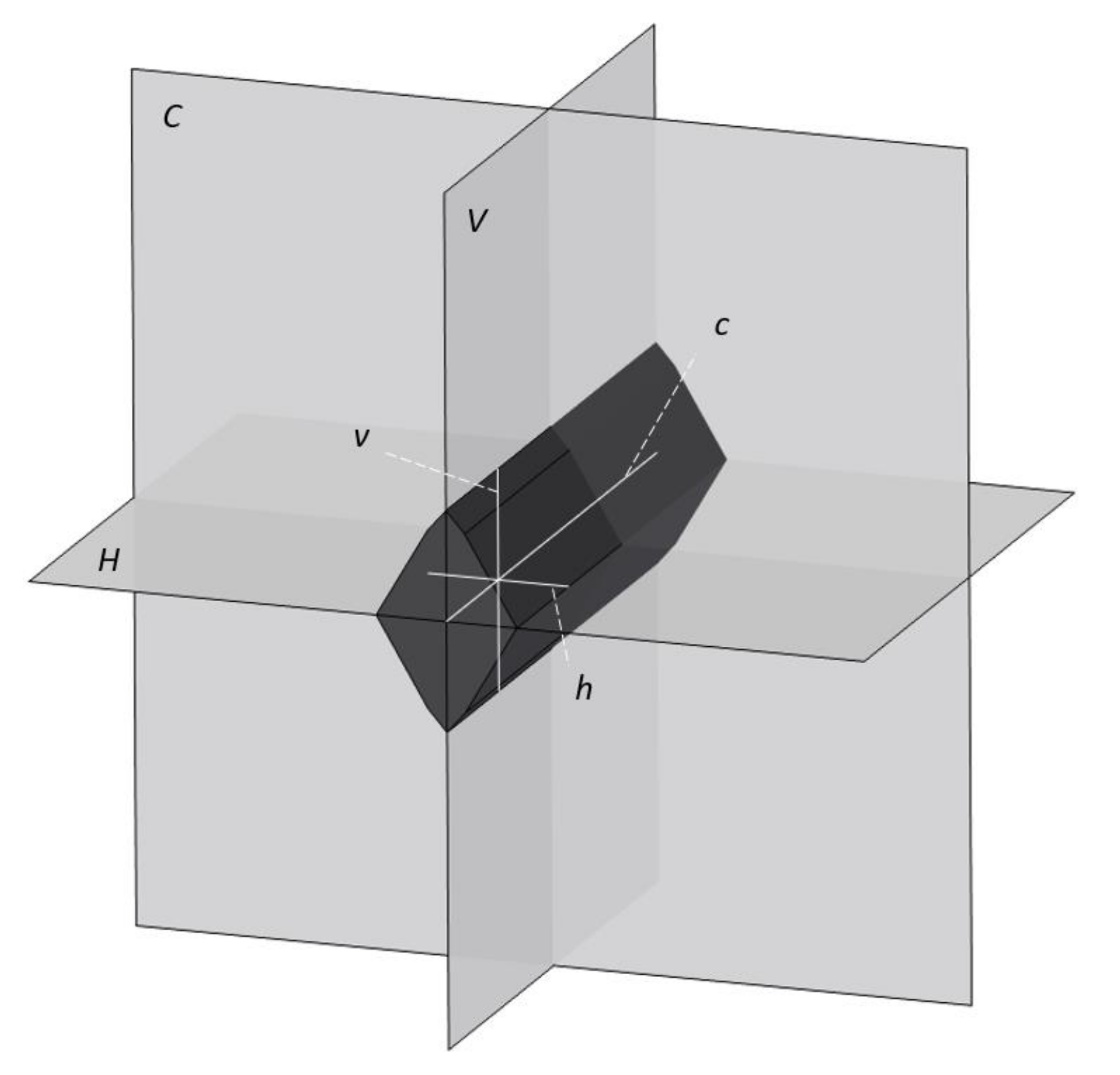






 c-axis,
c-axis,  —2 mm from c-axis,
—2 mm from c-axis,  —4 mm from c-axis,
—4 mm from c-axis,  —6 mm from c-axis).
—6 mm from c-axis).
 c-axis,
c-axis,  —2 mm from c-axis,
—2 mm from c-axis,  —4 mm from c-axis,
—4 mm from c-axis,  —6 mm from c-axis).
—6 mm from c-axis).

| Mass. % | C | Si | Mn | S | Cr | P | Al | Cu | Mo | Ni |
|---|---|---|---|---|---|---|---|---|---|---|
| C15E steel | 0.17 | 0.25 | 0.516 | 0.019 | 0.017 | 0.015 | 0.022 | 0.140 | 0.045 | 0.214 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vilotic, M.; Sidjanin, L.; Alexandrov, S.; Lang, L. Effect of Rotation of the Principal Stress Axes Relative to the Material on the Evolution of Material Properties in Severe Plastic Deformation Processes. Materials 2020, 13, 4667. https://doi.org/10.3390/ma13204667
Vilotic M, Sidjanin L, Alexandrov S, Lang L. Effect of Rotation of the Principal Stress Axes Relative to the Material on the Evolution of Material Properties in Severe Plastic Deformation Processes. Materials. 2020; 13(20):4667. https://doi.org/10.3390/ma13204667
Chicago/Turabian StyleVilotic, Marko, Leposava Sidjanin, Sergei Alexandrov, and Lihui Lang. 2020. "Effect of Rotation of the Principal Stress Axes Relative to the Material on the Evolution of Material Properties in Severe Plastic Deformation Processes" Materials 13, no. 20: 4667. https://doi.org/10.3390/ma13204667
APA StyleVilotic, M., Sidjanin, L., Alexandrov, S., & Lang, L. (2020). Effect of Rotation of the Principal Stress Axes Relative to the Material on the Evolution of Material Properties in Severe Plastic Deformation Processes. Materials, 13(20), 4667. https://doi.org/10.3390/ma13204667








