Effect of Particle Specific Surface Area on the Rheology of Non-Brownian Silica Suspensions
Abstract
1. Introduction
2. Materials and Methods
2.1. Particle Suspensions
2.2. Sample Preparation
2.3. Shear Rheology
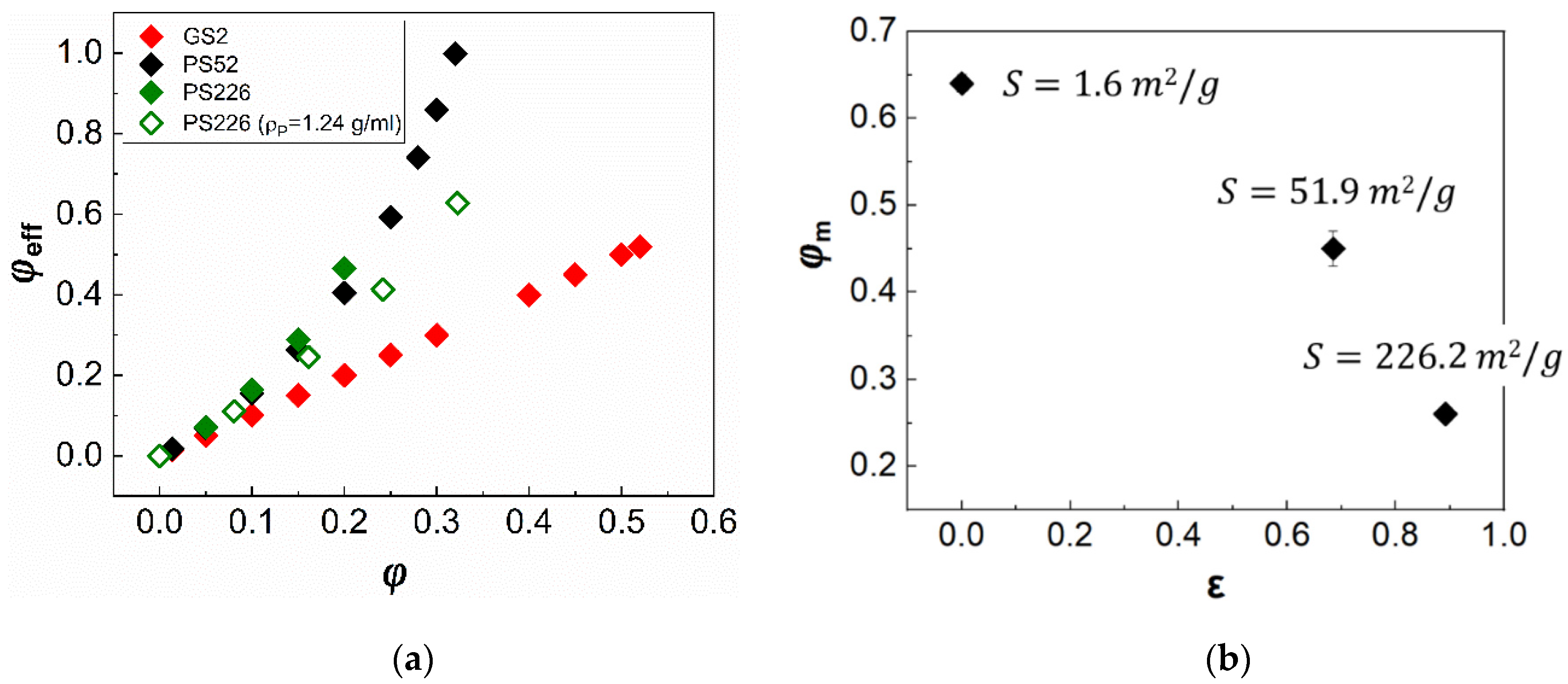
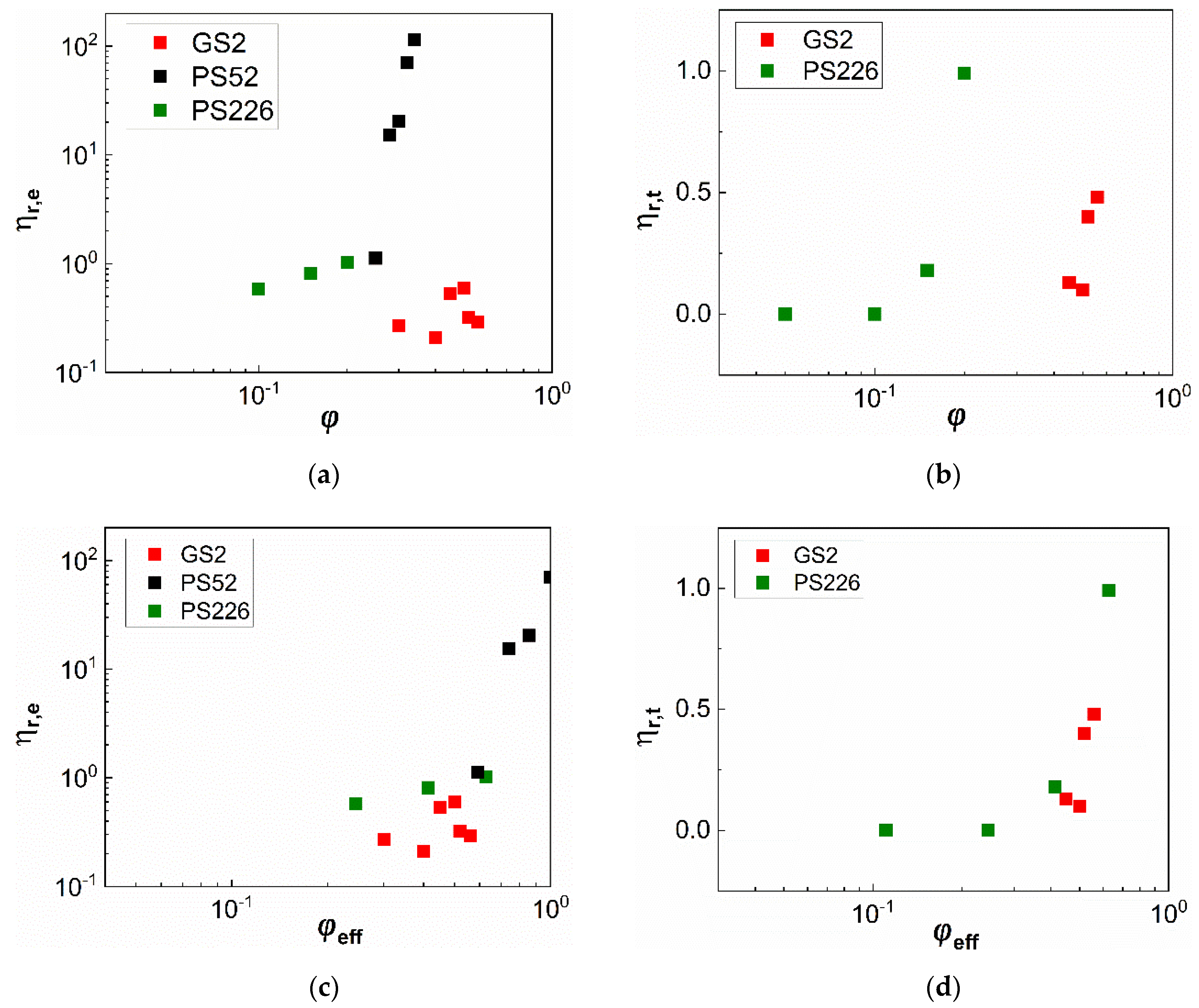
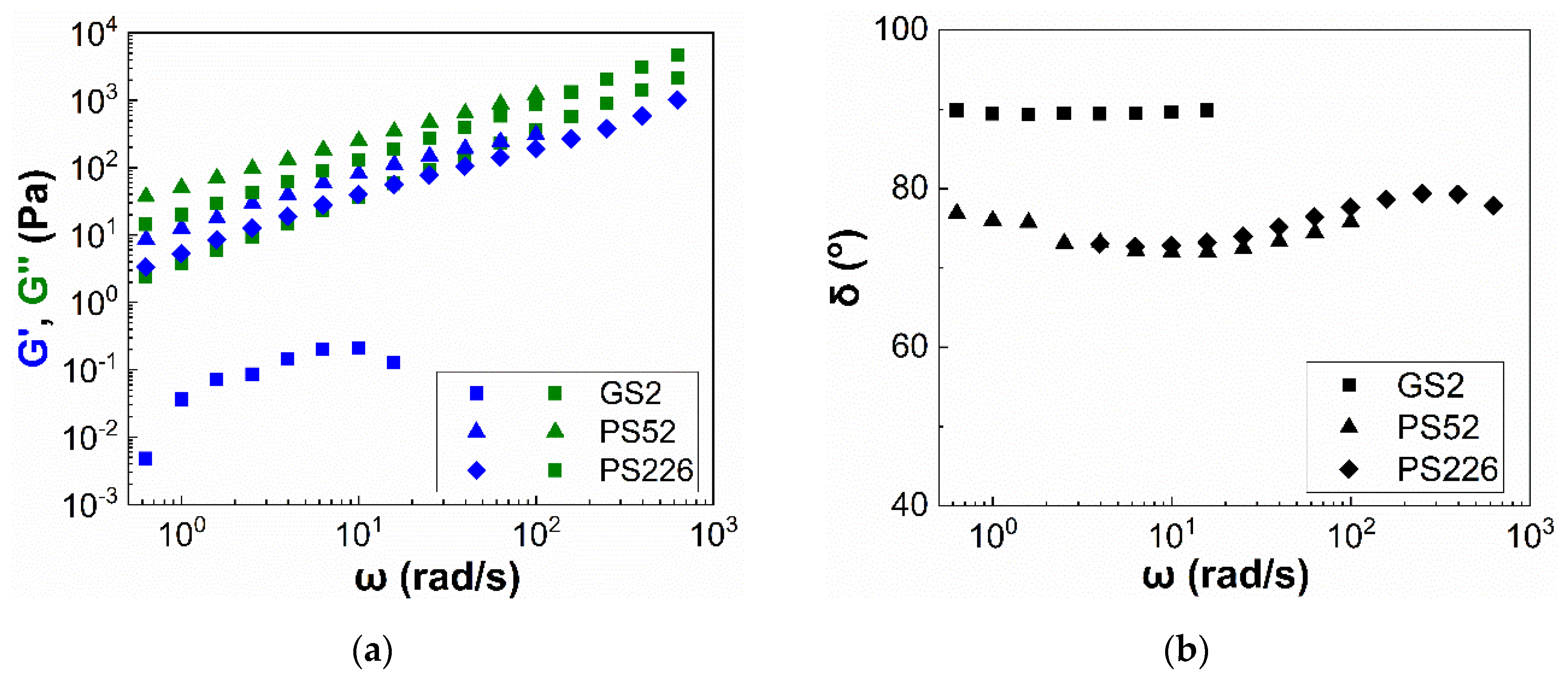
3. Results
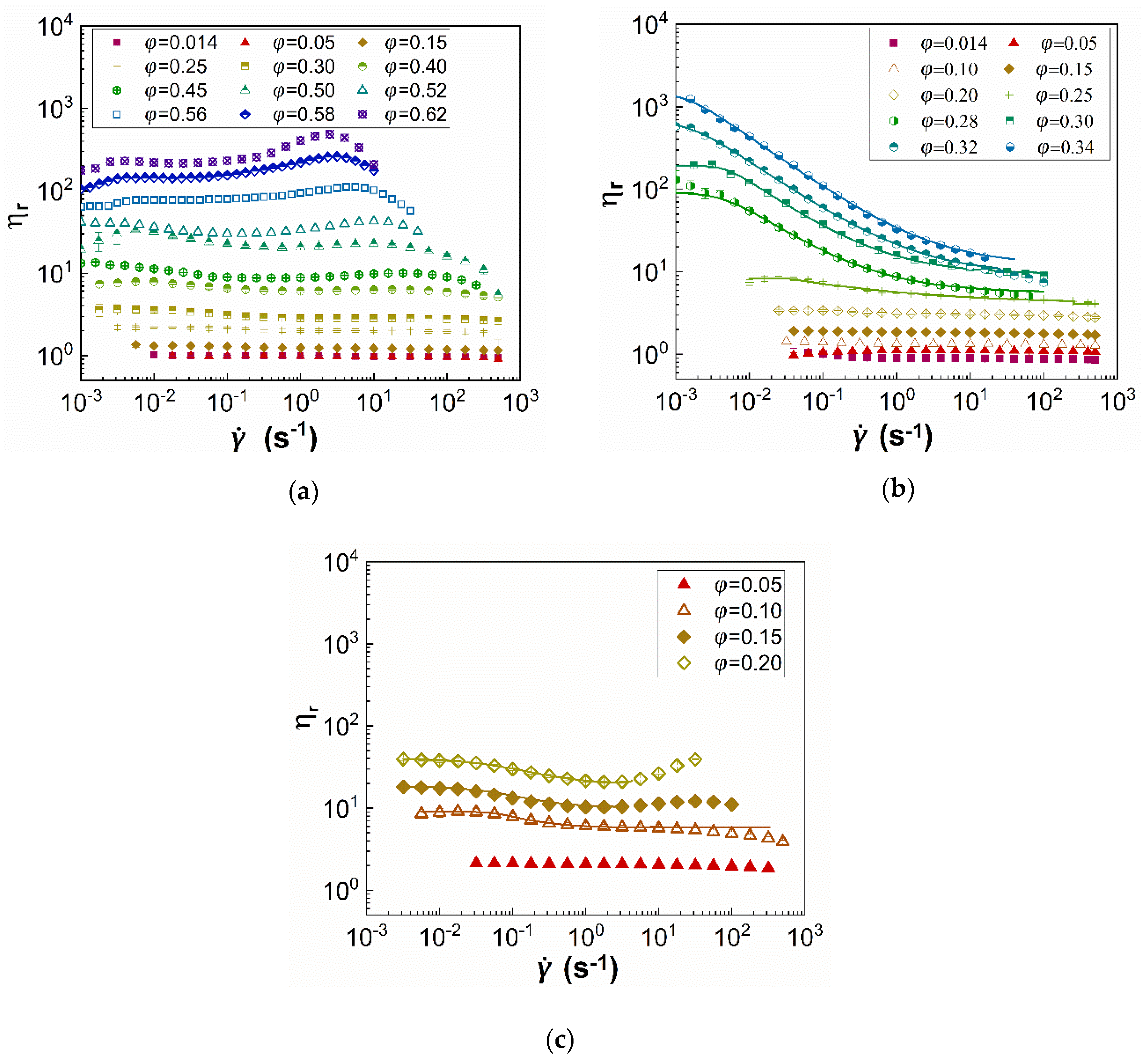
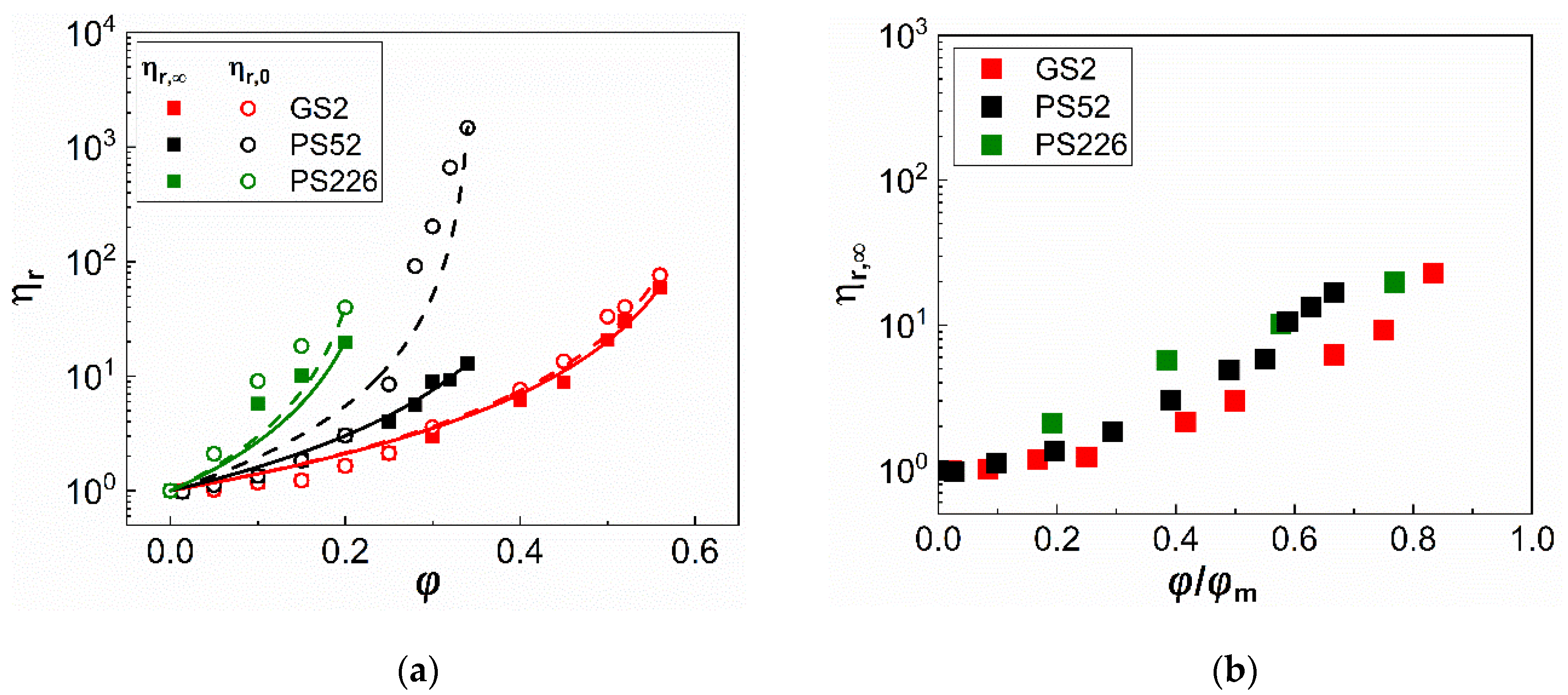
3.1. Steady State Shear Rheology
3.2. Viscoelasticity
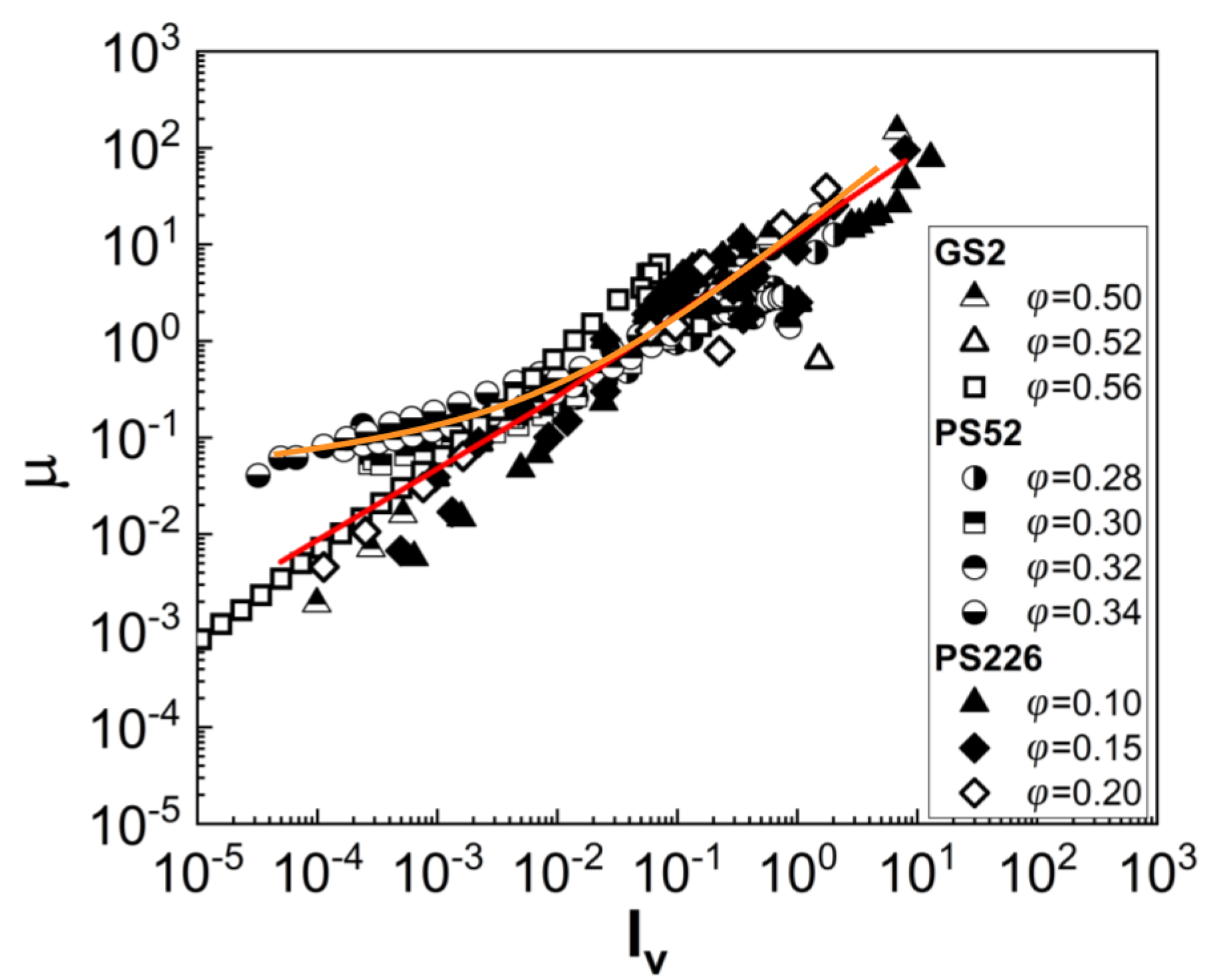
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| 0.10 | 0.15 | 0.20 | |
|---|---|---|---|
| 14.99 | 12.98 | 8.9 | |
| 6.27 | 10.64 | 22.84 | |
| 0.56 | 0.56 | 0.56 | |
| 0.54 | 1.07 | 3.34 |
References
- Genovese, D.B. Shear rheology of hard-sphere, dispersed, and aggregated suspensions, and filler-matrix composites. Adv. Colloid Interface Sci. 2012, 171–172, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Tanner, R.I.; Dai, S. Particle roughness and rheology in noncolloidal suspensions. J. Rheol. 2016, 60, 809–818. [Google Scholar] [CrossRef]
- Moon, J.Y.; Dai, S.; Chang, L.; Lee, J.S.; Tanner, R.I. The effect of sphere roughness on the rheology of concentrated suspensions. J. Nonnewton. Fluid Mech. 2015, 223, 233–239. [Google Scholar] [CrossRef]
- Asija, N.; Chouhan, H.; Bhatnagar, N. Effect of Specific Surface Area on the Shear Rheology of Fumed Silica Dispersions. In Proceedings of the International Conference on Precision Meso, Micro and Nano Engineering, Delhi, India, 10–15 December 2015. [Google Scholar]
- Chen, S.; Øye, G.; Sjöblom, J. Rheological Properties of Aqueous Silica Particle Suspensions. J. Dispers. Sci. Technol. 2005, 26, 495–501. [Google Scholar] [CrossRef]
- Chen, S.; Øye, G.; Sjöblom, J. Rheological properties of silica particle suspensions in mineral oil. J. Dispers. Sci. Technol. 2007, 26, 791–798. [Google Scholar] [CrossRef]
- Raghavan, S.R.; Walls, H.J.; Khan, S.A. Rheology of silica dispersions in organic liquids: New evidence for solvation forces dictated by hydrogen bonding. Langmuir 2000, 16, 7920–7930. [Google Scholar] [CrossRef]
- Hoyle, C.; Dai, S.; Tanner, R.; Jabbarzadeh, A. Effect of particle roughness on the rheology of suspensions of hollow glass microsphere particles. J. Nonnewton. Fluid Mech. 2020, 276, 104235. [Google Scholar] [CrossRef]
- Blanc, F.; D’Ambrosio, E.; Lobry, L.; Peters, F.; Lemaire, E. Universal scaling law in frictional non-Brownian suspensions. Phys. Rev. Fluids 2018, 3, 114303. [Google Scholar] [CrossRef]
- Davis, R.H.; Zhao, Y.; Galvin, K.P.; Wilson, H.J. Solid-solid contacts due to surface roughness and their effects on suspension behavior. R. Soc. 2003, 361, 871–894. [Google Scholar]
- Tanner, R.I.; Ness, C.; Mahmud, A.; Dai, S.; Moon, J. A bootstrap mechanism for non-colloidal suspension viscosity. Rheol. Acta 2018, 57, 635–643. [Google Scholar] [CrossRef]
- Papadopoulou, A.; Gillissen, J.J.J.; Wilson, H.J.; Tiwari, M.K.; Balabani, S. On the shear thinning of non-Brownian suspensions: Friction or adhesion? J. Nonnewton. Fluid Mech. 2020, 281, 104298. [Google Scholar] [CrossRef]
- Gillissen, J.J.J.; Papadopoulou, A.; Tiwari, M.K.; Balabani, S.; Wilson, H.J. Suspension rheology of adhesive particles at high shear-rates. Phys. Rev. Fluids 2020, 5, 053302. [Google Scholar] [CrossRef]
- Pal, R. Viscosity models for concentrated suspensions of solid core-porous shell particles. Can. J. Chem. Eng. 2015, 93, 590–598. [Google Scholar] [CrossRef]
- Olanrewaju, K.O.; Bae, T.H.; Nair, S.; Breedveld, V. The rheology of suspensions of porous zeolite particles in polymer solutions. Rheol. Acta. 2013, 53, 133–141. [Google Scholar] [CrossRef]
- Zhuravlev, L.T.; Potapov, V.V. Density of silanol groups on the surface of silica precipitated from a hydrothermal solution. Russ. J. Phys. Chem. 2006, 80, 1119–1128. [Google Scholar] [CrossRef]
- Gallas, J.-P.; Goupil, J.-M.; Vimont, A.; Lavalley, J.-C.; Gil, B.; Gilson, J.-P.; Miserque, O. Quantification of Water and Silanol Species on Various Silicas by Coupling IR Spectroscopy and in-Situ Thermogravimetry. Langmuir 2009, 25, 5825–5834. [Google Scholar] [CrossRef] [PubMed]
- Zhuravlev, L.T. The surface chemistry of amorphous silica. Zhuravlev model. Colloids Surfaces A Physicochem. Eng. Asp. 2000, 173, 1–38. [Google Scholar] [CrossRef]
- Amiri, A.; Øye, G.; Sjöblom, J. Stability and Flow-Induced Flocculation of Fumed Silica Suspensions in Mixture of Water-Glycerol. J. Dispers. Sci. Technol. 2012, 33, 1247–1256. [Google Scholar] [CrossRef]
- Saint-Michel, B.; Manneville, S.; Meeker, S.; Ovarlez, G.; Bodiguel, H. X-ray Radiography of Viscous Resuspension. Phys. Fluids 2019, 31, 103301. [Google Scholar] [CrossRef]
- Chu, B.; Brady, A.T.; Mannhalter, B.D.; Salem, D.R. Effect of silica particle surface chemistry on the shear thickening behaviour of concentrated colloidal suspensions. J. Phys. D Appl. Phys. 2014, 47, 7. [Google Scholar] [CrossRef]
- Hayashi, H.; Kawaguchi, M. Effects of the degree of surface modification on the rheological responses of precipitated silica suspensions in benzyl alcohol. J. Dispers. Sci. Technol. 2017, 38, 737–742. [Google Scholar] [CrossRef]
- Gao, J.; Mwasame, P.M.; Wagner, N.J. Thermal rheology and microstructure of shear thickening suspensions of silica nanoparticles dispersed in the ionic liquid [C 4 mim][BF 4 ]. J. Rheol. 2017, 61, 525–535. [Google Scholar] [CrossRef]
- Khandavalli, S.; Rothstein, J.P. Large amplitude oscillatory shear rheology of three different shear-thickening particle dispersions. Rheol Acta 2015, 54, 601–618. [Google Scholar] [CrossRef]
- Ma, T.; Yang, R.; Zheng, Z.; Song, Y. Rheology of fumed silica/polydimethylsiloxane suspensions. J. Rheol. 2017, 61, 205–215. [Google Scholar] [CrossRef]
- Varga, Z.; Grenard, V.; Pecorario, S.; Taberlet, N.; Dolique, V.; Manneville, S.; Divoux, T.; McKinley, G.H.; Swan, J.W. Hydrodynamics control shear-induced pattern formation in attractive suspensions. Proc. Natl. Acad. Sci. USA 2019, 116, 12193–12198. [Google Scholar] [CrossRef] [PubMed]
- Gamonpilas, C.; Morris, J.F.; Denn, M.M. Shear and normal stress measurements in non-Brownian monodisperse and bidisperse suspensions. J. Rheol. 2016, 60, 289–296. [Google Scholar] [CrossRef]
- Lobry, L.; Lemaire, E.; Blanc, F.; Gallier, S.; Peters, F. Shear thinning in non-Brownian suspensions explained by variable friction between particles. J. Fluid Mech. 2019, 860, 682–710. [Google Scholar] [CrossRef]
- Foss, D.R.; Brady, J.F. Structure, diffusion and rheology of Brownian suspensions by Stokesian Dynamics simulation. J. Fluid Mech 2000, 407, 167–200. [Google Scholar] [CrossRef]
- Boyd, J.; Buick, J.M.; Green, S. Analysis of the Casson and Carreau-Yasuda non-Newtonian blood models in steady and oscillatory flows using the lattice Boltzmann method. Phys. Fluids 2007, 19, 093103. [Google Scholar] [CrossRef]
- Macosko, C.W. Rheology: Principles, Measurements and Applications, 1st ed.; Wiley-VCH: Hoboken, NJ, USA, 1994. [Google Scholar]
- Quemada, D. Rheological modelling of complex fluids. I. The concept of effective volume fraction revisited. EPJ Appl. Phys. 1998, 1, 119–127. [Google Scholar] [CrossRef]
- Denn, M.M.; Morris, J.F. Rheology of non-Brownian suspensions. Annu. Rev. Chem. Biomol. Eng. 2014, 5, 203–228. [Google Scholar] [CrossRef] [PubMed]
- Stickel, J.J.; Powell, R.L. Fluid mechanics and rheology of dense suspensions. Annu. Rev. Fluid Mech 2005, 37, 129–149. [Google Scholar] [CrossRef]
- Dörr, A.; Sadiki, A.; Mehdizadeh, A. A discrete model for the apparent viscosity of polydisperse suspensions including maximum packing fraction. J. Rheol. 2013, 57, 743–765. [Google Scholar] [CrossRef]
- Chatté, G.; Comtet, J.; Niguès, A.; Bocquet, L.; Siria, A.; Ducouret, G.; Lequeux, F.; Lenoir, N.; Ovarlez, G.; Colin, A. Shear thinning in non-Brownian suspensions. Soft Matter 2018, 14, 865–1070. [Google Scholar] [CrossRef]
- Boyer, F.; Guazzelli, É.; Pouliquen, O. Unifying suspension and granular rheology. Phys. Rev. Lett. 2011, 107, 188301. [Google Scholar] [CrossRef] [PubMed]
- Gallier, S.; Lemaire, E.; Peters, F.; Lobry, L. Rheology of sheared suspensions of rough frictional particles. J. Fluid Mech. 2014, 757, 514–549. [Google Scholar] [CrossRef]
- Sayan, P.; Ulrich, J. The effect of particle size and suspension density on the measurement of ultrasonic velocity in aqueous solutions. Chem. Eng. Process. 2002, 41, 281–287. [Google Scholar] [CrossRef]
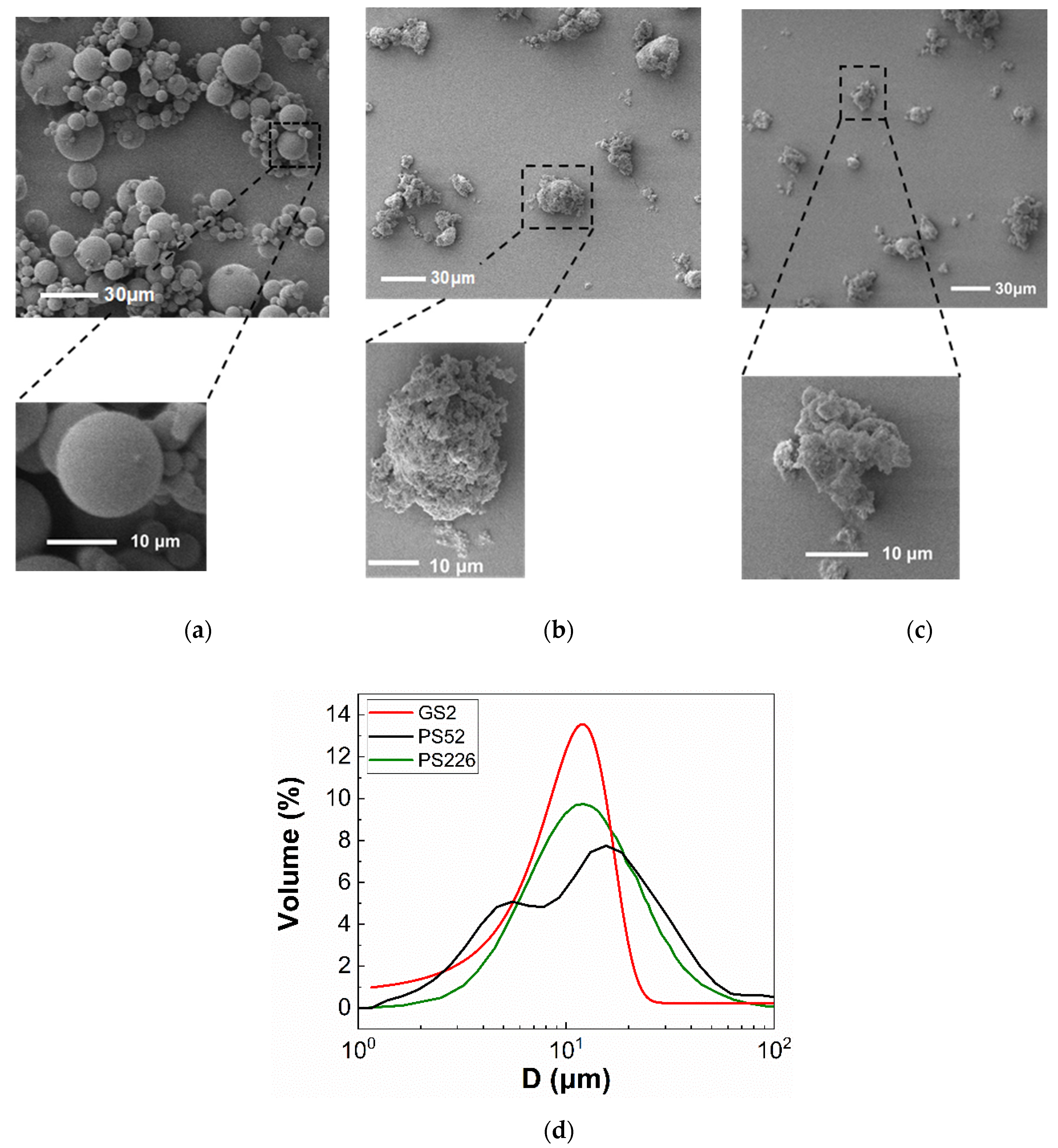
| Particle Properties | GS2 | PS52 | PS226 |
|---|---|---|---|
| Density () | 1.1 | 2.0 | 2.0 |
| Diameter (D, μm) | 11 ± 5.5 | 17.5 ± 15.2 | 12.5 ± 4.0 |
| Specific surface area (S, m2/g) *1 | 1.6 | 51.9 | 226.2 |
| Porosity *1 (ε) | - | 68.5% | 89.2% |
| Fluid properties at 20 °C | Glycerol | ||
| Density () | 1.25 | ||
| Viscosity () | 1.3 ( *2) | ||
| Particles | |
|---|---|
| GS2 | 0.64 |
| PS52 | 0.47 |
| PS226 | 0.26 |
| Particles | |
|---|---|
| GS2 | 0.012 |
| PS52 | 0.40 |
| PS226 | 1.70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papadopoulou, A.; Gillissen, J.J.J.; Tiwari, M.K.; Balabani, S. Effect of Particle Specific Surface Area on the Rheology of Non-Brownian Silica Suspensions. Materials 2020, 13, 4628. https://doi.org/10.3390/ma13204628
Papadopoulou A, Gillissen JJJ, Tiwari MK, Balabani S. Effect of Particle Specific Surface Area on the Rheology of Non-Brownian Silica Suspensions. Materials. 2020; 13(20):4628. https://doi.org/10.3390/ma13204628
Chicago/Turabian StylePapadopoulou, Anastasia, Jurriaan J. J. Gillissen, Manish K. Tiwari, and Stavroula Balabani. 2020. "Effect of Particle Specific Surface Area on the Rheology of Non-Brownian Silica Suspensions" Materials 13, no. 20: 4628. https://doi.org/10.3390/ma13204628
APA StylePapadopoulou, A., Gillissen, J. J. J., Tiwari, M. K., & Balabani, S. (2020). Effect of Particle Specific Surface Area on the Rheology of Non-Brownian Silica Suspensions. Materials, 13(20), 4628. https://doi.org/10.3390/ma13204628





