Lithography-Free Route to Hierarchical Structuring of High-χ Block Copolymers on a Gradient Patterned Surface
Abstract
1. Introduction
2. Materials and Methods
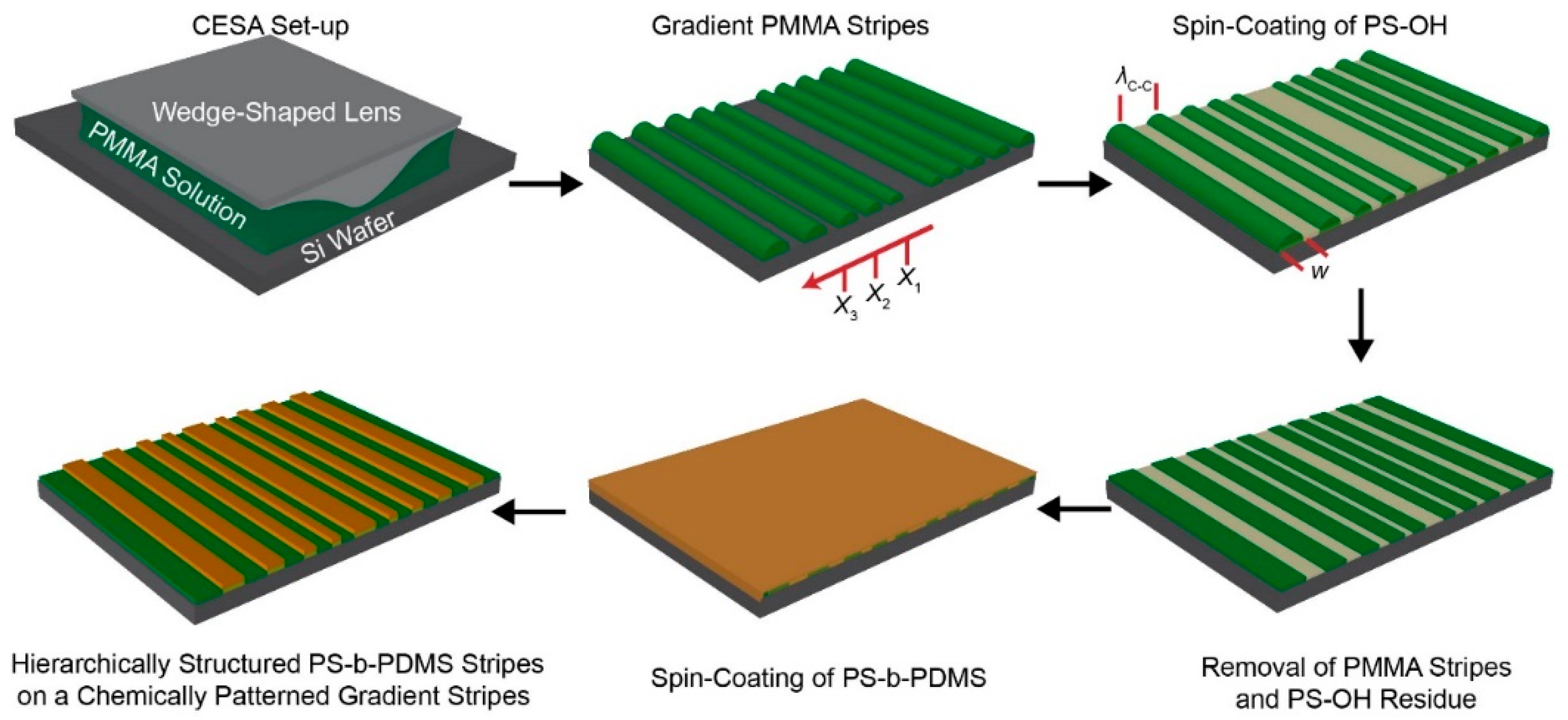
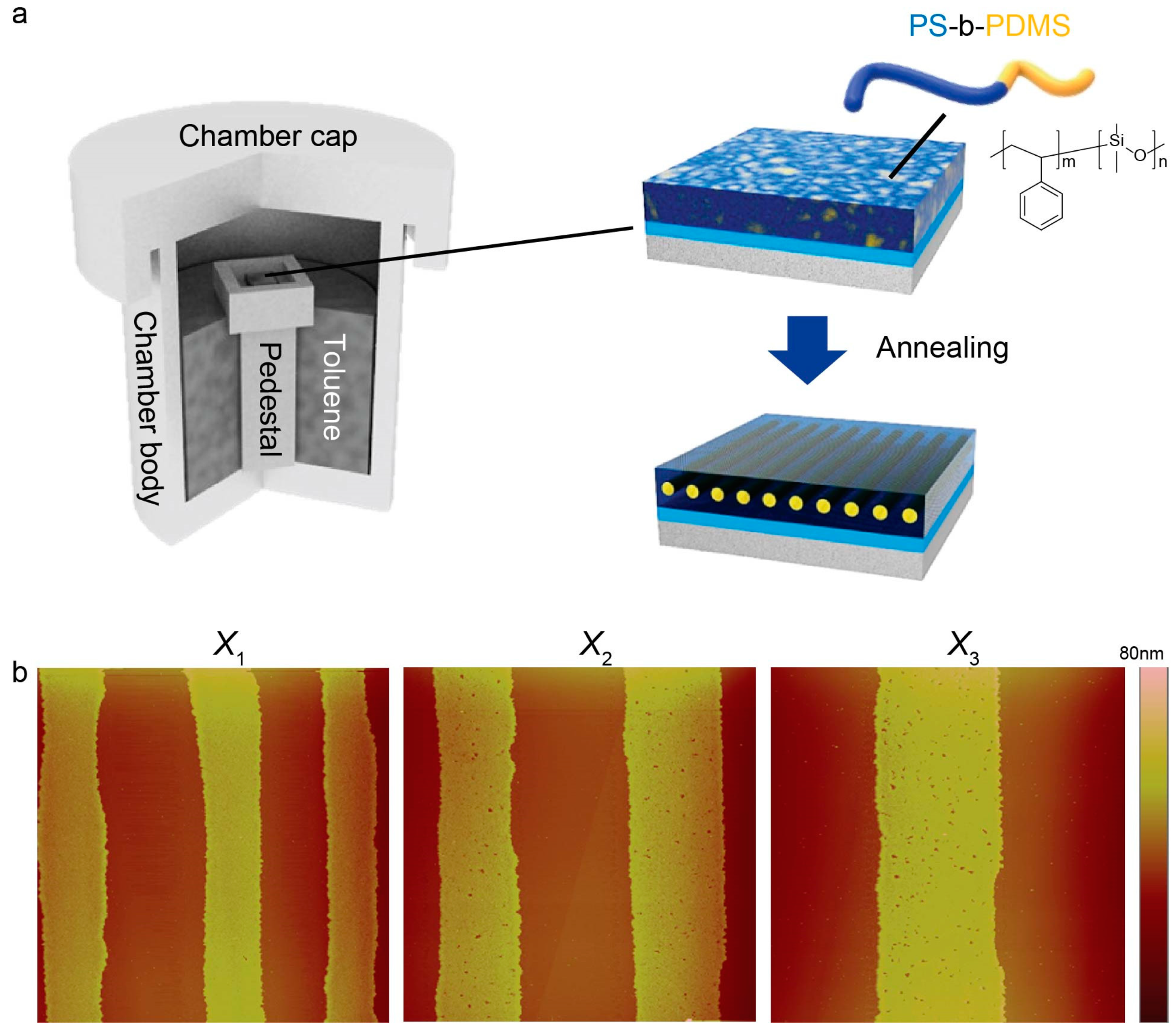
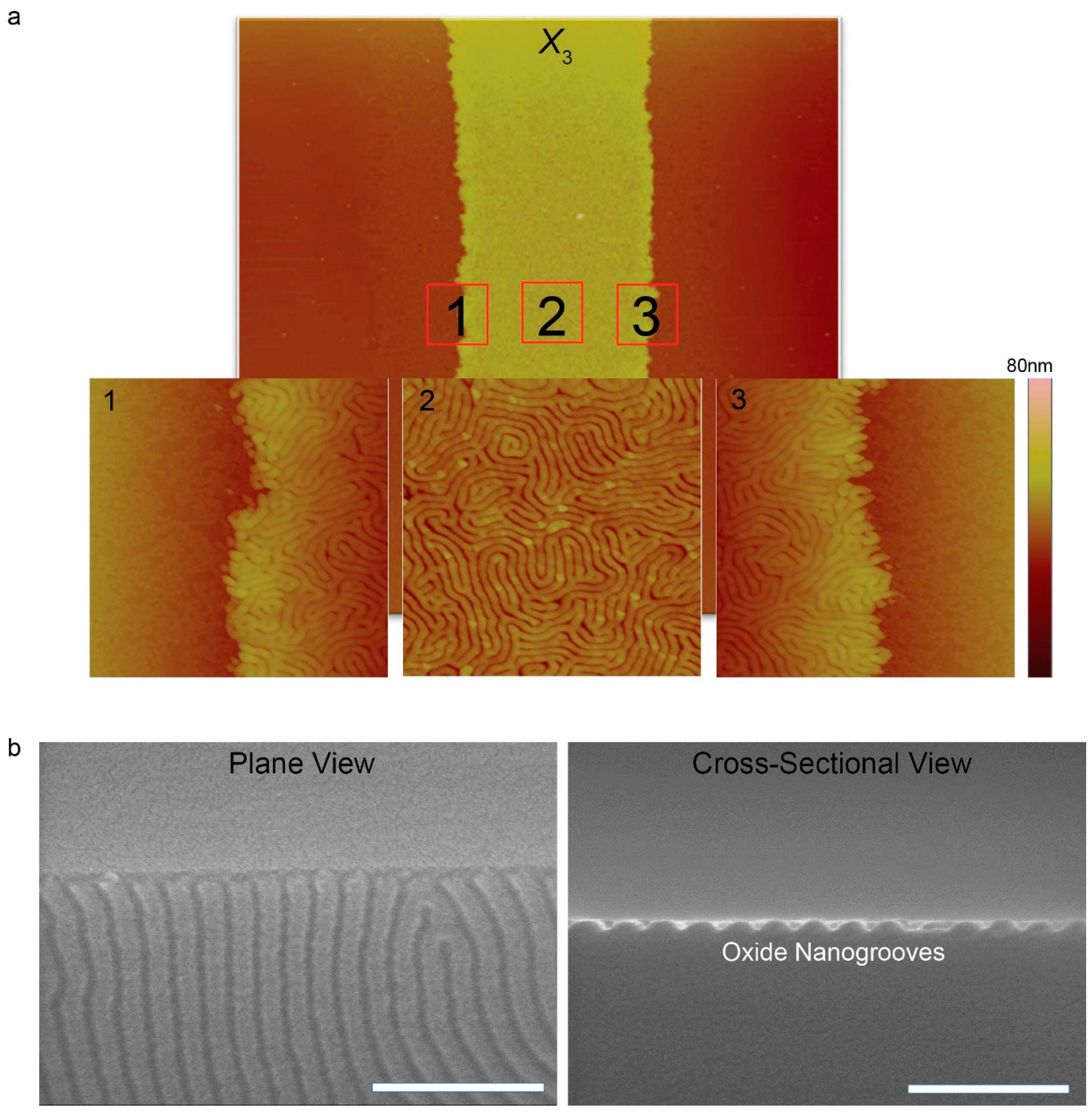
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Deegan, R.D.; Bakajin, O.; Dupont, T.F.; Huber, G.; Nagel, S.R.; Witten, T.A. Capillary Flow as the Cause of Ring Steins from Dried Liquid Drops. Nature 1997, 389, 827–829. [Google Scholar] [CrossRef]
- Adachi, E.; Dimitrov, A.S.; Nagayama, K. Stripe Patterns Formed on a Glass Surface during Droplet Evaporation. Langmuir 1995, 11, 1057–1060. [Google Scholar] [CrossRef]
- Larson, R.G. Twenty Years of Drying Droplets. Nature 2017, 550, 446–467. [Google Scholar] [CrossRef]
- Soltman, D.; Subramanian, V. Inket-Printed Line Morphologies and Temperature Control of the Coffee Ring Effect. Langmuir 2008, 24, 2224–2231. [Google Scholar] [CrossRef]
- Larson, R.G. Transport and Deposition Patterns in Drying Sessile Droplets. AlChE J. 2014, 60, 1538–1571. [Google Scholar] [CrossRef]
- Trantum, J.R.; Wright, D.W.; Haselton, F.R. Biomarker-Mediated Disruption of Coffee-Ring Formation as a Low Resource Diagnostic Indicator. Langmuir 2012, 28, 2187–2193. [Google Scholar] [CrossRef]
- Byun, M.; Bowden, N.B.; Lin, Z. Hierarchically Organized Structures Engineered from Controlled Evaporative Self-Assembly. Nano Lett. 2010, 10, 3111–3117. [Google Scholar] [CrossRef]
- Byun, M.; Han, W.; Qiu, F.; Bowden, N.B.; Lin, Z. Hierarchically Ordered Structures Enabled by Controlled Evaporative Self-Assembly. Small 2010, 6, 2250–2255. [Google Scholar] [CrossRef]
- Byun, M.; Han, W.; Li, B.; Xin, X.; Lin, Z. An Unconventional Route to Hierarchically Ordered Block Copolymers on a Gradient Patterned Surface through Controlled Evaporative Self-Assembly. Angew. Chem. Int. Ed. 2013, 125, 1160–1165. [Google Scholar] [CrossRef]
- Han, W.; Lin, Z. Learning from “Coffee Rings”: Ordered Structures Enabled by Controlled Evaporative Self-Assembly. Angew. Chem. Int. Ed. 2012, 51, 1534–1536. [Google Scholar] [CrossRef]
- Han, W.; Byun, M.; Li, B.; Pang, X.; Lin, Z. A Simple Route to Hierarchically Assembled Micelles and Inorganic Nanoparticles. Angew. Chem. Int. Ed. 2012, 124, 12756–12760. [Google Scholar] [CrossRef]
- Cho, H.R.; Park, W.I.; Song, Y.-S.; Jung, J.; Choe, A.; Ko, H.; Byun, M. Spontaneous Capillary Breakup of Suspended Gradient Polymer Stripes into Spatially Ordered Dot Arrays. Appl. Surf. Sci. 2019, 475, 1003–1009. [Google Scholar] [CrossRef]
- Park, W.I.; Kim, D.-H.; Jung, J.; Hong, S.W.; Lin, Z.; Byun, M. Spatially Ordered Poly(3-hexylthiophene) Fibril Nanostructures via Controlled Evaporative Self-Assembly. Adv. Mater. Technol. 2019, 4, 1800554. [Google Scholar] [CrossRef]
- Kim, B.H.; Shin, D.O.; Jeong, S.J.; Koo, C.M.; Jeon, S.C.; Hwang, W.J.; Lee, S.; Lee, M.G.; Kim, S.O. Hierarchical Self-Assembly of Block Copolymers for Lithography-Free Nanopatterning. Adv. Mater. 2008, 20, 2303–2307. [Google Scholar] [CrossRef]
- Han, W.; He, M.; Byun, M.; Li, B.; Lin, Z. Large-Scale Hierarchically Structured Conjugated Polymer Assemblies with Enhanced Electrical Conductivity. Angew. Chem. Int. Ed. 2013, 52, 2564–2568. [Google Scholar] [CrossRef]
- Kim, H.S.; Lee, C.H.; Sudeep, P.K.; Emrick, T.; Crosby, A.J. Nanoparticle Stripes, Grids, and Ribbons Produced by Flow Coating. Adv. Mater. 2010, 22, 4600–4604. [Google Scholar] [CrossRef]
- Li, B.; Zhang, C.; Jiang, B.; Han, W.; Lin, Z. Flow-Enabled Self-Assembly of Large-Scale Aligned Nanowires. Angew. Chem. Int. Ed. 2015, 54, 4250–4254. [Google Scholar] [CrossRef]
- Kang, S.H.; Hwang, W.S.; Lin, Z.; Kwon, S.H.; Hong, S.W. A Robust Highly Aligned DNA Nanowire Array Enabled Lithography for Graphene Nanoribbons Transistors. Nano Lett. 2015, 15, 7913–7920. [Google Scholar] [CrossRef]
- Li, B.; Han, W.; Jiang, B.; Lin, Z. Crafting Threads of Diblock Copolymer Micelles via Flow-Enabled Self-Assembly. ACS Nano 2014, 8, 2936–2942. [Google Scholar] [CrossRef]
- He, M.; Li, B.; Cui, X.; Jiang, B.; He, Y.; Chen, Y.; O’Neil, D.; Szymanski, P.; EI-Sayed, M.A.; Huang, J.; et al. Meniscus-Assisted Solution Printing of Large-Grained Perovskite Films for High-Efficiency Solar Cells. Nat. Commun. 2017, 8, 16045. [Google Scholar] [CrossRef]
- Abkarian, M.; Nunes, J.; Stone, H.A. Colloidal Crystallization and Bending in a Cylindrical Geometry. J. Am. Chem. Soc. 2004, 126, 5978–5979. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; He, R.; Yang, J.; Zhao, W.; Zhou, C. Stripe-Like Clay Nanotubes Patterns in Glass Capillary Tubes for Capture of Tumor Cells. ACS Appl. Mater. Interfaces 2016, 8, 7709–7719. [Google Scholar] [CrossRef] [PubMed]
- Kong, Y.L.; Boulogne, F.; Kim, H.; Nunes, J.; Feng, J.; Stone, H.A. Deposition of Quantum Dots in a Capillary Tube. Langmuir 2015, 31, 12560–12566. [Google Scholar] [CrossRef]
- Shin, J.I.; Cho, S.J.; Jeon, J.; Lee, K.H.; Wie, J.J. Three-Dimensional Micropatterning of Semiconducting Polymers via Capillary Force-Assisted Evaporative Self-Assembly. Soft Matter 2019, 15, 3854–3863. [Google Scholar] [CrossRef]
- Hawker, C.J.; Russell, T.P. Block Copolymer Lithography: Merging “Bottom-Up” with “Top-Down” Processes. MRS Bull. 2005, 30, 952–966. [Google Scholar] [CrossRef]
- Thurn-Albrecht, T.; Schotter, J.; Kastle, C.A.; Emley, N.; Shibauchi, T.; Krusin-Elbaum, L.; Guarini, K.; Black, C.T.; Tuominen, M.T.; Russell, T.P. Ultrahigh-Density Nanowire Arrays Grown in Self-Assembled Diblock Copolymer Templates. Science 2000, 290, 2126–2129. [Google Scholar] [CrossRef]
- Park, W.I.; Kim, Y.J.; Jeong, J.W.; Kim, K.; Yoo, J.-K.; Hur, Y.H.; Kim, J.M.; Thomas, E.L.; Alexander-Katz, A.; Jung, Y.S. Host-Guest Self-Assembly in Block Copolymer Blends. Sci. Rep. 2013, 3, 3190. [Google Scholar] [CrossRef]
- Crossland, E.J.W.; Nedelcu, M.; Ducati, C.; Ludwigs, S.; Hillmyer, M.A.; Steiner, U.; Snaith, H.J. Block Copolymer Morphologies in Dye-Sensitized Solar Cells: Probing the Photovoltaic Structure-Function Relation. Nano Lett. 2009, 9, 2813–2819. [Google Scholar] [CrossRef]
- Yoo, H.; Byun, M.; Jeong, C.K.; Lee, K. Performance Enhancement of Electronic and Energy Devices via Block Copolymer Self-Assembly. Adv. Mater. 2015, 27, 3982–3998. [Google Scholar] [CrossRef]
- Angelescu, D.E.; Waller, J.H.; Adamson, D.H.; Deshpande, P.; Chou, S.Y.; Register, R.A.; Chaikin, P.M. Macroscopic Orientation of Block Copolymer Cylinders in Single Layer Films by Shearing. Adv. Mater. 2004, 16, 1736–1740. [Google Scholar] [CrossRef]
- Thurn-Albrecht, T.; DeRouchey, J.; Russell, T.P.; Jaeger, H.M. Overcoming Interfacial Interactions with Electric Fields. Macromolecules 2000, 33, 3250–3253. [Google Scholar] [CrossRef]
- Bodycomb, J.; Funaki, Y.; Kimishima, K.; Hashimoto, T. Single-Grain Lamellar Microdomain from a Diblock Copolymer. Macromolecules 1999, 32, 2075–2077. [Google Scholar] [CrossRef]
- Kim, S.H.; Misner, M.J.; Xu, T.; Kimura, M.; Russell, T.P. Highly Oriented and Ordered Arrays from Block Copolymers via Solvent Evaporation. Adv. Mater. 2004, 16, 226–231. [Google Scholar] [CrossRef]
- Ludwigs, S.; BOker, A.; Voronov, A.; Rehse, N.; Magerle, R.; Krausch, G. Self-Assembly of Functional Nanostructures from ABC Triblock Copolymers. Nat. Mater. 2003, 2, 744–747. [Google Scholar] [CrossRef]
- Mansky, P.; Liu, Y.; Huang, E.; Russell, T.P.; Hawker, C.J. Controlling Polymer-Surface Interactions with Random Copolymer Brushes. Science 1997, 275, 1458–1460. [Google Scholar] [CrossRef]
- Bita, I.; Yang, J.K.W.; Jung, Y.S.; Ross, C.A.; Thomas, E.L.; Berggren, K.K. Graphoepitaxy of Self-Assembled Block Copolymers on Two-Dimensional Periodic Patterned Templates. Science 2008, 321, 939–943. [Google Scholar] [CrossRef]
- Segalman, R.A.; Yokoyama, H.; Kramer, E.J. Graphoepitaxy of Spherical Domain Block Copolymer Films. Adv. Mater. 2001, 13, 1152–1155. [Google Scholar] [CrossRef]
- Kim, S.O.; Solak, H.H.; Stoykovich, M.P.; Ferrier, N.J.; de Pablo, J.J.; Nealey, P.F. Epitaxial Self-Assembly of Block Copolymers on Lithographically Defined Nanopatterned Substrates. Nature 2003, 424, 411–414. [Google Scholar] [CrossRef]
- Rockford, L.; Liu, Y.; Mansky, P.; Russell, T.P.; Yoon, M.; Mochrie, G.J. Polymers on Nanoperiodic, Heterogeneous Surfaces. Phys. Rev. Lett. 1999, 82, 2602–2605. [Google Scholar] [CrossRef]
- Jin, H.M.; Park, D.Y.; Jeong, S.J.; Lee, G.Y.; Kim, J.Y.; Mun, J.H.; Cha, S.K.; Lim, J.; Lim, J.S.; Kim, K.H.; et al. Flash Light Millisecond Self-Assembly of High χ Block Copolymers for Wafer-Scale Sub-10 nm Nanopatterning. Adv. Mater. 2017, 29, 1700595. [Google Scholar] [CrossRef]
- Kim, J.H.; Jin, H.M.; Yang, G.G.; Han, K.H.; Yun, T.; Shin, J.Y.; Jeong, S.J.; Kim, S.O. Smart Nanostructured Materials Based on Self-Assembly of Block Copolymers. Adv. Funct. Mater. 2019. [Google Scholar] [CrossRef]
- Park, W.I.; Kim, K.; Jang, H.-I.; Jeong, J.W.; Kim, J.M.; Choi, J.; Park, J.H.; Jung, Y.S. Directed Self-Assembly with Sub-100 Degrees Celcius Processing Temperature, Sub-10 Nanometer Resolution, and Sub-1 Minute Assembly Time. Small 2012, 8, 3762–3768. [Google Scholar] [CrossRef] [PubMed]
- Yim, S.; Sim, D.M.; Park, W.I.; Choi, M.-C.; Choi, J.; Jeon, J.; Kim, K.H.; Jung, Y.S. Surface-Shielding Nanostructures Derived from Self-Assembled Block Copolymers Enable Reliable Plasma Doping for Few-Layer Transition Metal Dichalcogenides. Adv. Funct. Mater. 2016, 26, 5631–5640. [Google Scholar] [CrossRef]
- Hur, Y.H.; Song, S.W.; Kim, J.M.; Park, W.I.; Kim, K.H.; Kim, Y.; Jung, Y.S. Thermodynamic and Kinetic Tuning of Block Copolymer Based on Random Copolymerization for High-Quality Sub-6 nm Pattern Formation. Adv. Funct. Mater. 2018, 28, 1800765. [Google Scholar] [CrossRef]
- Xu, J.; Xia, J.F.; Hong, S.W.; Lin, Z.; Qiu, F.; Yang, Y.L. Self-Assembly of Gradient Concentric Rings via Solvent Evaporation from a Capillary Bridge. Phys. Rev. Lett. 2006, 96, 066104. [Google Scholar] [CrossRef]
- Watts, J.F.; Leadley, S.R.; Castle, J.E.; Blomfield, C.J. Adsorption of PMMA on Oxidized Al and Si Substrates: An Investigation by High-Resolution X-ray Photoelectron Spectroscopy. Langmuir 2000, 16, 2292–2300. [Google Scholar] [CrossRef]
- Bernard, B.; Brown, H.R.; Hawker, C.J.; Kellock, A.J.; Russell, T.P. Adhesion of Polymer Interfaces Reinforced with Random and Diblock Copolymers as a Function of Geometry. Macromolecules 1999, 32, 6254–6260. [Google Scholar] [CrossRef]
- Jung, Y.S.; Ross, C.A. Solvent-Vapor-Induced Tunability of Self-Assembled Block Copolymer Patterns. Adv. Mater. 2009, 21, 2540–2545. [Google Scholar] [CrossRef]
- Jung, Y.S.; Ross, C.A. Orientation-Controlled Self-Assembled Nanolithography Using a Polystyrene-Polydimethylsiloxane Block Copolymer. Nano Lett. 2007, 7, 2046–2050. [Google Scholar] [CrossRef]
- Baralia, G.G.; Filiatre, C.; Nysten, B.; Jonas, A.M. Nanodecoding by Dewetting. Adv. Mater. 2007, 19, 4453–4459. [Google Scholar] [CrossRef]
- Mark, J.E. Physical Properties of Polymers Handbook, 2nd ed.; Springer: New York, NY, USA, 2007; Volume 16, pp. 289–303. [Google Scholar] [CrossRef]
- David, M.O.; Reiter, G.; Sitthai, T.; Schultz, J. Deformation of a Glassy Polymer Film by Long-Range Intermolecular Forces. Langmuir 1998, 14, 5667–5672. [Google Scholar] [CrossRef]
- Israelachivili, J.N. Intermolecular and Surface Forces, 3rd ed.; Academic Press: London, UK, 2011; pp. 183–200. [Google Scholar]
- de Gennes, P.G. Wetting: Statics and Dynamics. Rev. Mod. Phys. 1985, 57, 827–863. [Google Scholar] [CrossRef]
- Yoo, P.J.; Suh, K.Y.; Lee, H.H. Short- and Long-Range Interactions in Thin Films of Polymer Blends in Microchannels. Macromolecules 2002, 35, 3205–3212. [Google Scholar] [CrossRef]
- Reiter, G.; Sharma, A.; Casoli, A.; David, M.; Khanna, R.; Auroy, P. Thin Film Instability Induced by Long-Range Forces. Langmuir 1999, 15, 2551–2558. [Google Scholar] [CrossRef]
- Barton, A.F.M. CRC Handbook of Polymer-Liquid Interaction Parameters and Solubility Parameters, 1st ed.; CRC Press: Boca Raton, FL, USA, 1990; pp. 259–297. [Google Scholar]
- Jung, D.S.; Bang, J.W.; Park, T.W.; Lee, S.H.; Jung, Y.K.; Byun, M.; Cho, Y.-R.; Kim, K.H.; Seong, G.H.; Park, W.I. Pattern Formation of Metal-Oxide Hybrid Nanostructures via the Self-Assembly of di-Block Copolymer Blends. Nanoscale 2019, 11, 18559–18567. [Google Scholar] [CrossRef]
- Kim, H.J.; Chaudhury, M.K.; Owen, M.J. Hydrphobicity Loss and Recovery of Silicone HV Insulation. IEEE Trans. Dielectr. Electr. Insul. 1999, 6, 695–702. [Google Scholar] [CrossRef]
- Olah, A.; Hillborg, H.; Vansco, G.J. Hydrophobic Recovery of UV/ozone Treated Poly (dimethylsiloxane): Adhesion Studies by Contact Mechanics and Mechanism of Surface Modification. Appl. Surf. Sci. 2005, 239, 410–423. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, H.R.; Choe, A.; Park, W.I.; Ko, H.; Byun, M. Lithography-Free Route to Hierarchical Structuring of High-χ Block Copolymers on a Gradient Patterned Surface. Materials 2020, 13, 304. https://doi.org/10.3390/ma13020304
Cho HR, Choe A, Park WI, Ko H, Byun M. Lithography-Free Route to Hierarchical Structuring of High-χ Block Copolymers on a Gradient Patterned Surface. Materials. 2020; 13(2):304. https://doi.org/10.3390/ma13020304
Chicago/Turabian StyleCho, Ha Ryeong, Ayoung Choe, Woon Ik Park, Hyunhyub Ko, and Myunghwan Byun. 2020. "Lithography-Free Route to Hierarchical Structuring of High-χ Block Copolymers on a Gradient Patterned Surface" Materials 13, no. 2: 304. https://doi.org/10.3390/ma13020304
APA StyleCho, H. R., Choe, A., Park, W. I., Ko, H., & Byun, M. (2020). Lithography-Free Route to Hierarchical Structuring of High-χ Block Copolymers on a Gradient Patterned Surface. Materials, 13(2), 304. https://doi.org/10.3390/ma13020304




