Analysis of Strain Field Heterogeneity at the Microstructure Level and Inverse Identification of Composite Constituents by Means of Digital Image Correlation
Abstract
1. Introduction
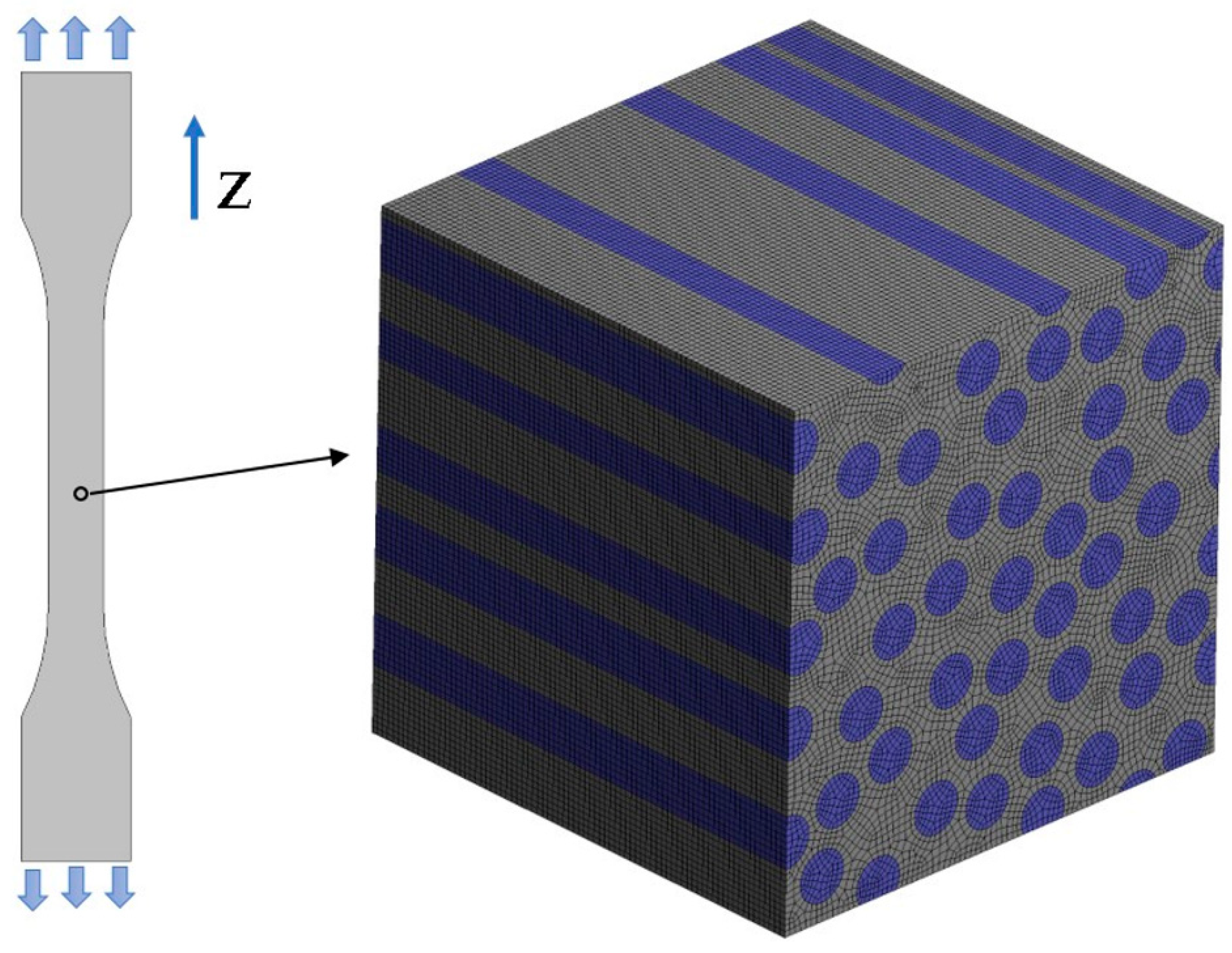
2. Materials and Methods
2.1. Artificial Speckle Patterns
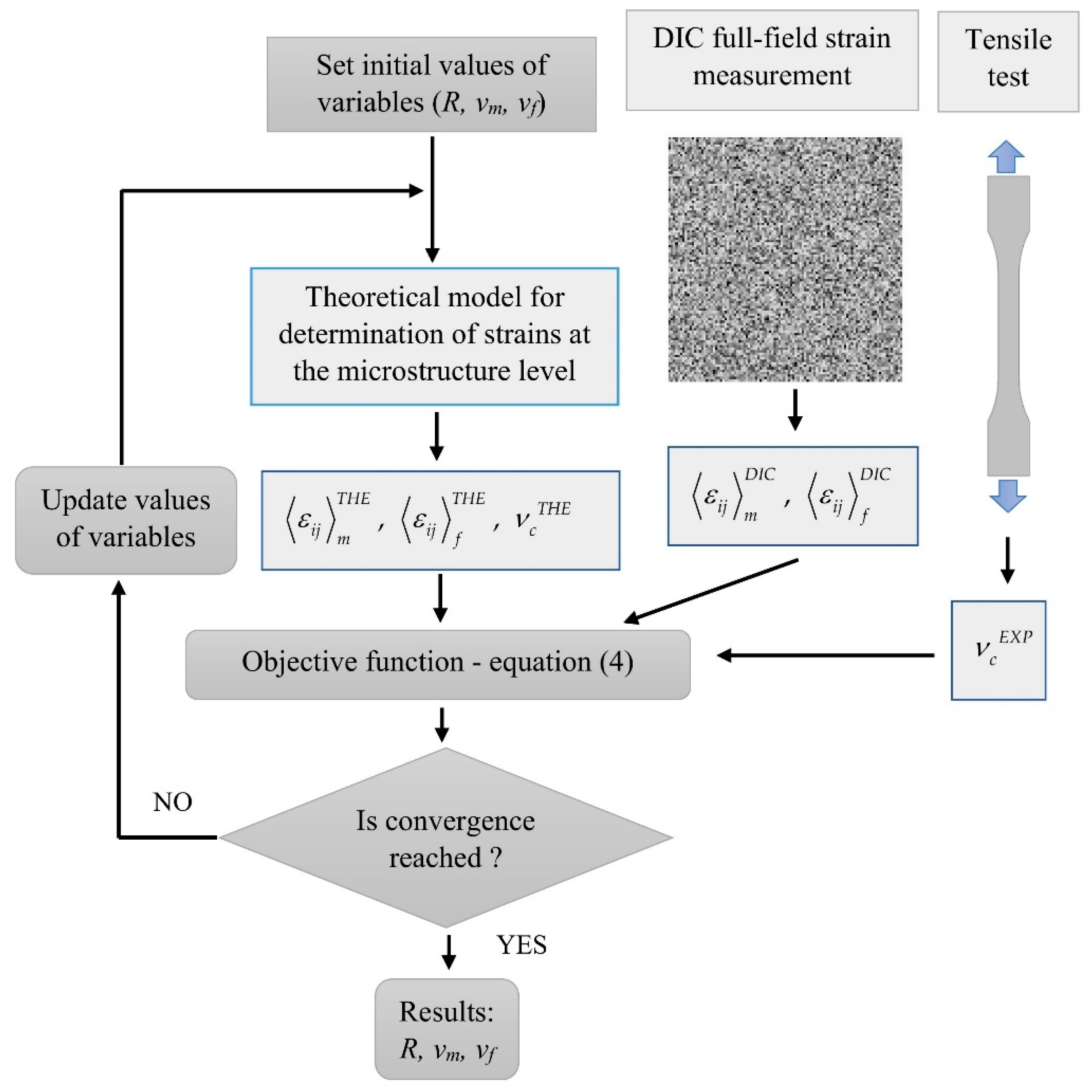
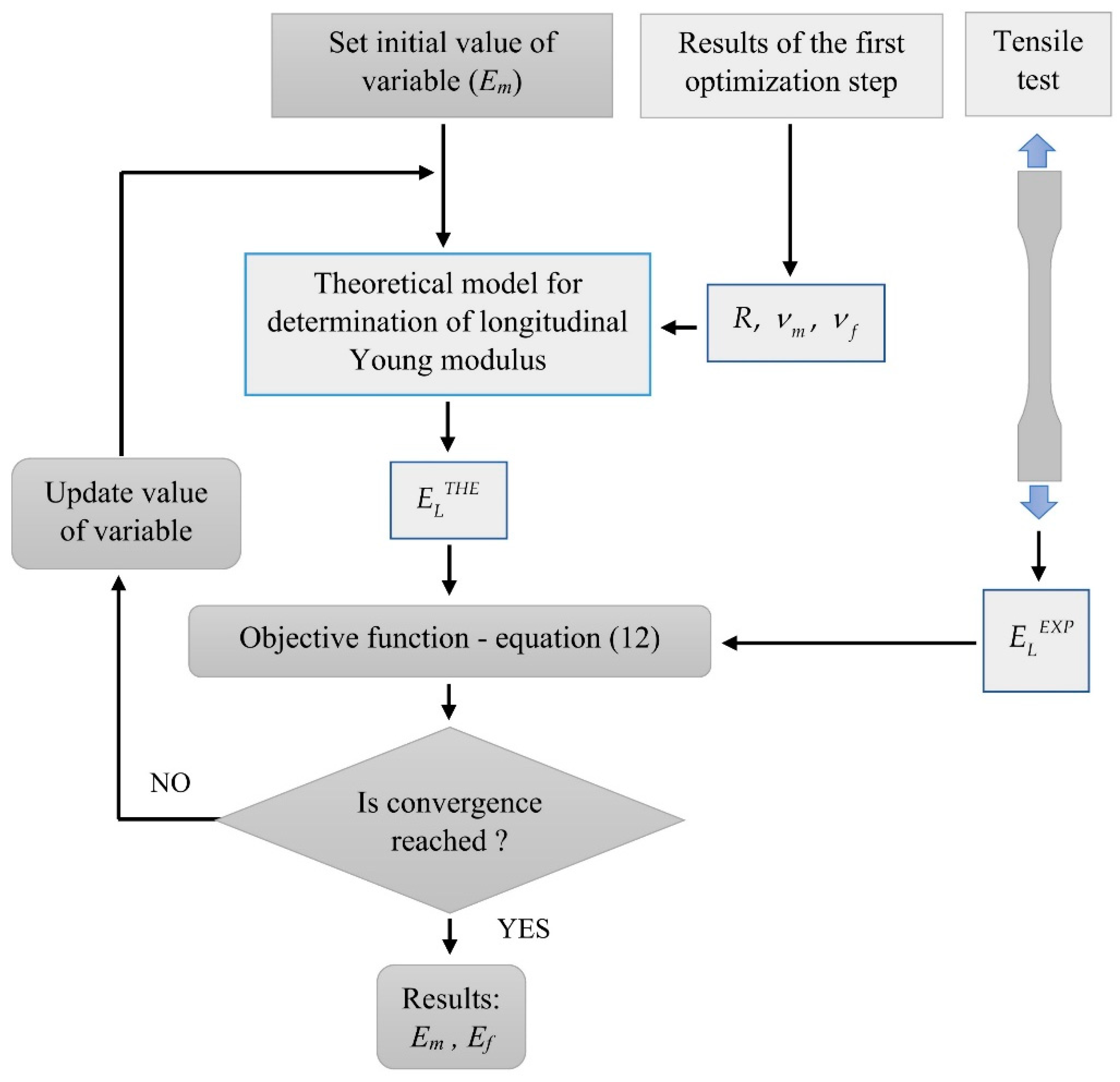
2.2. Inverse Identification Problem
3. Results and Discussion
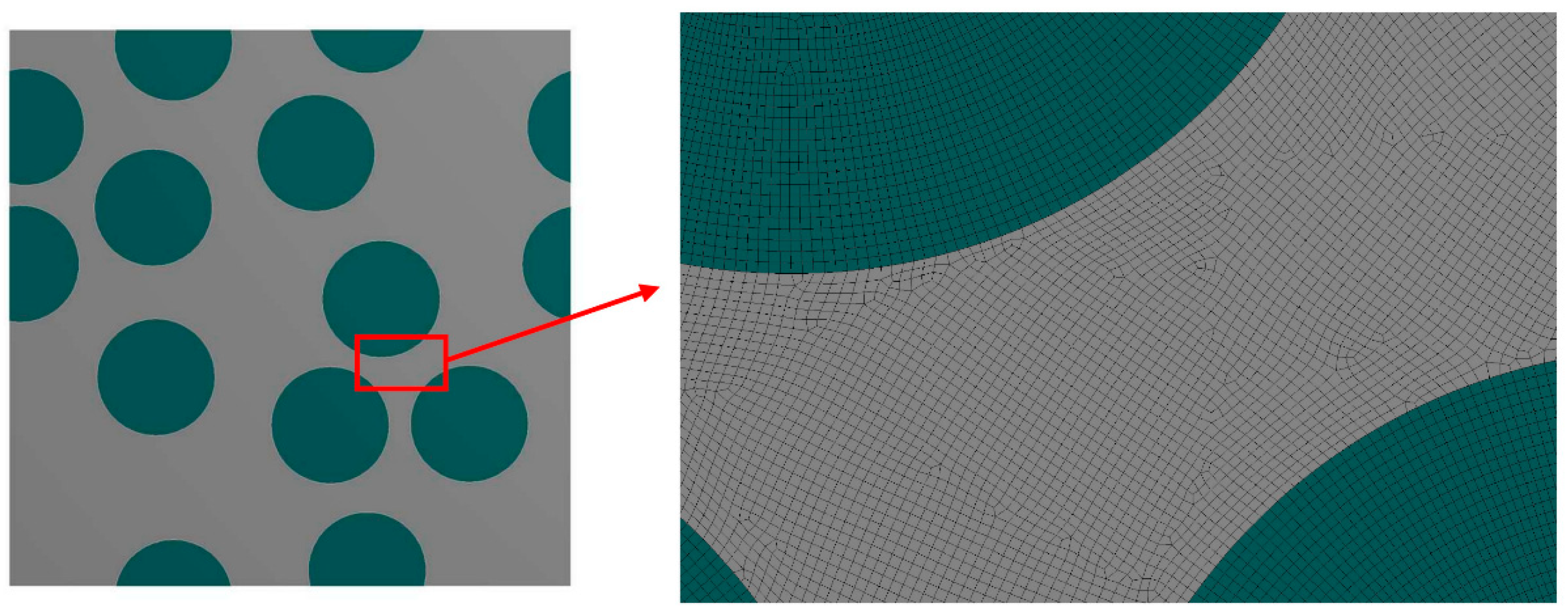
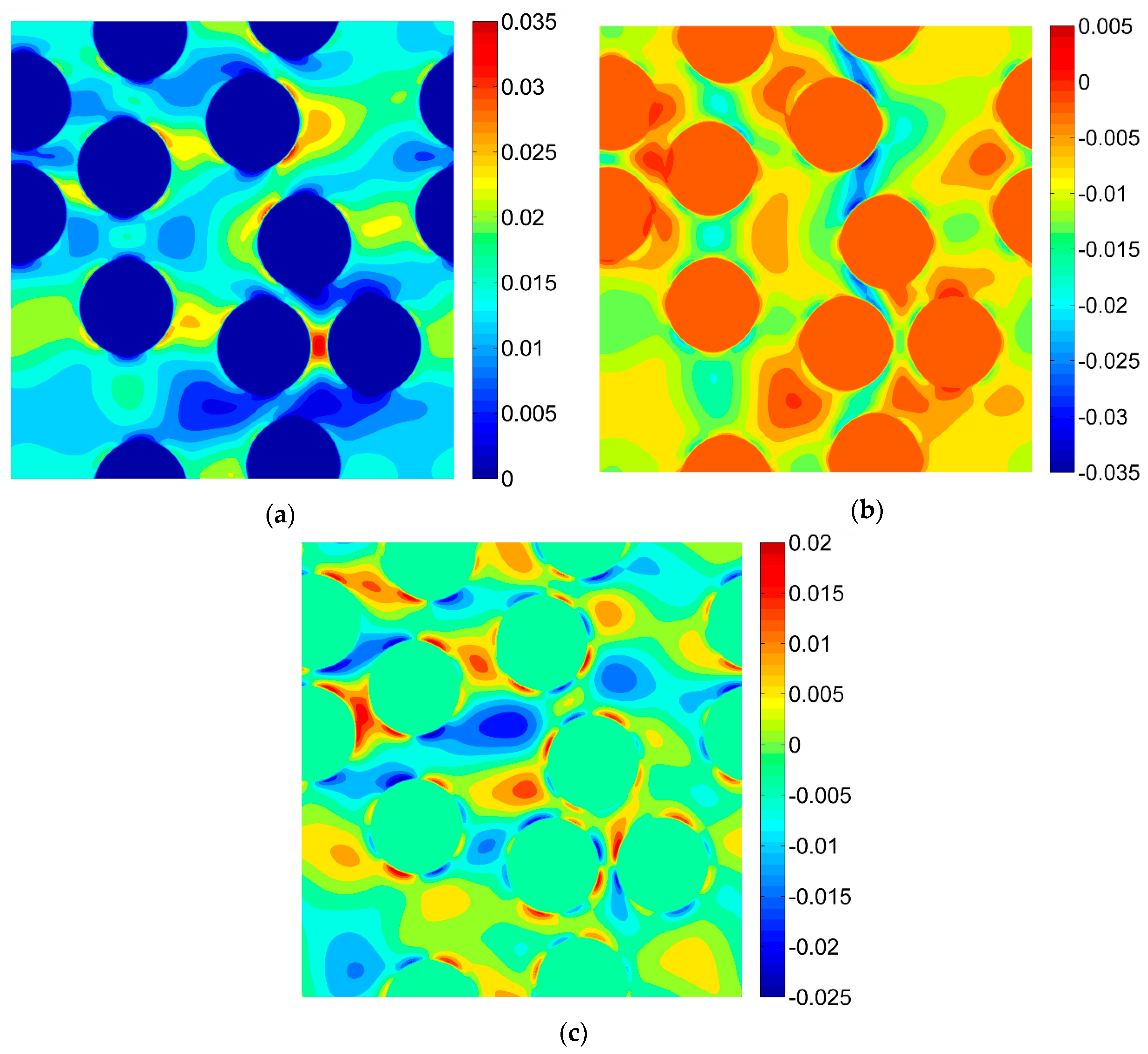
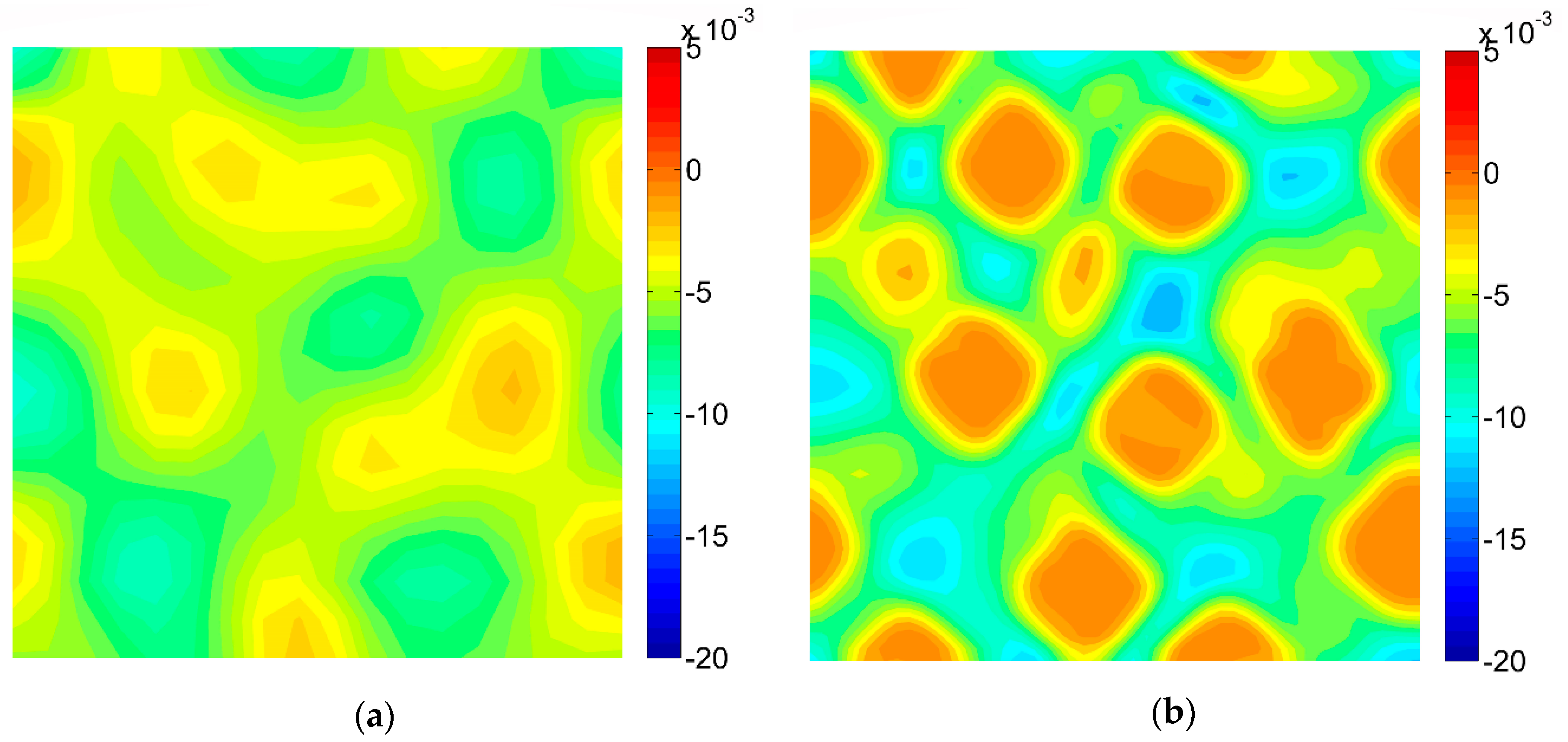
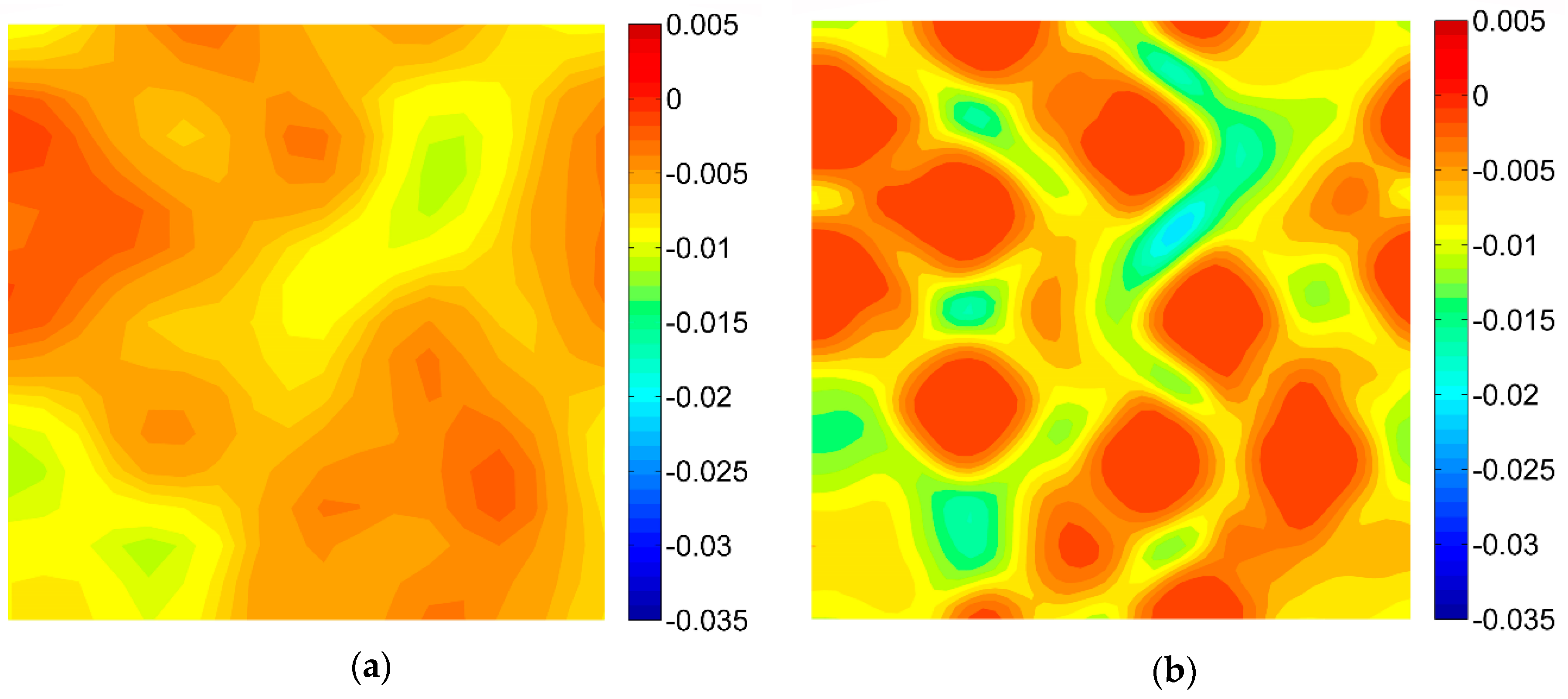
3.1. Numerical Modeling of the Deformation Behavior
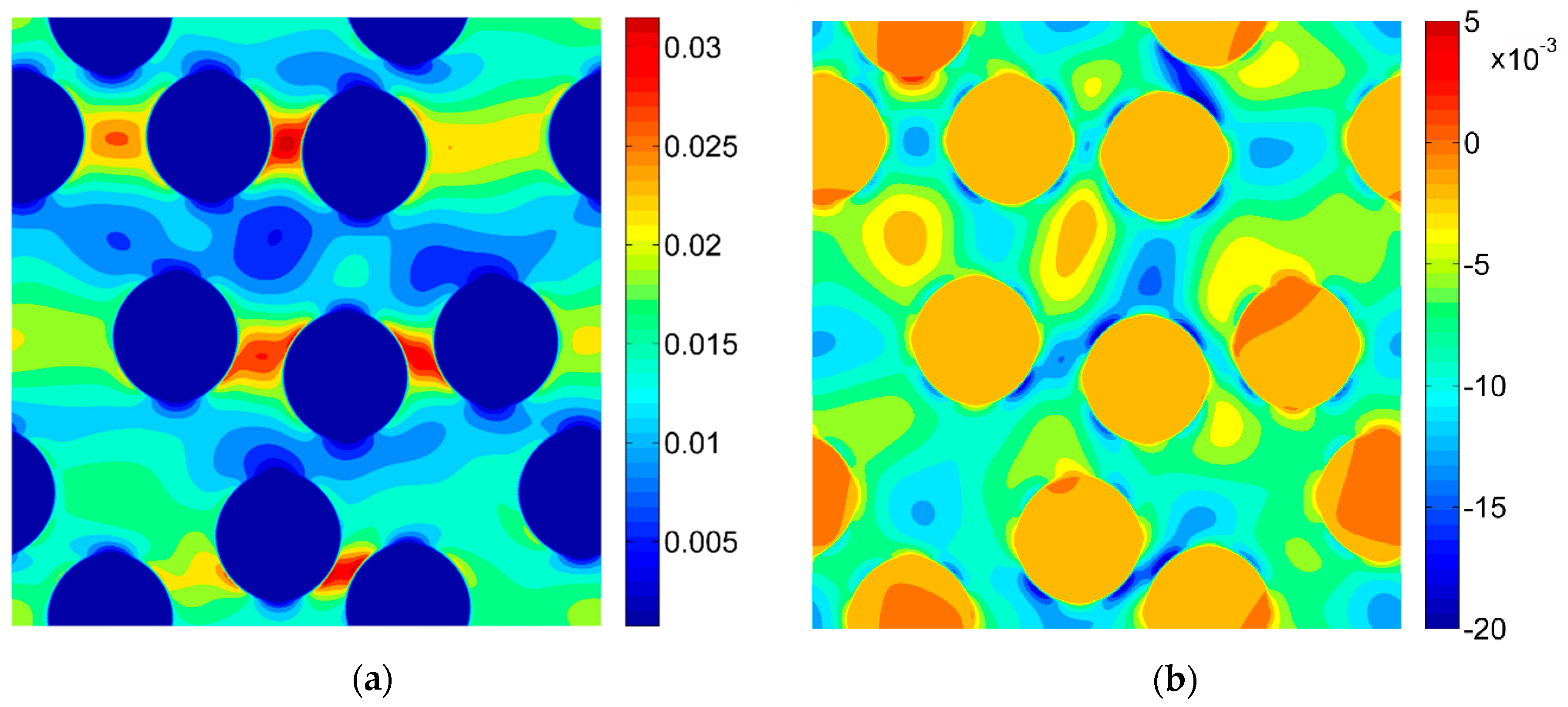
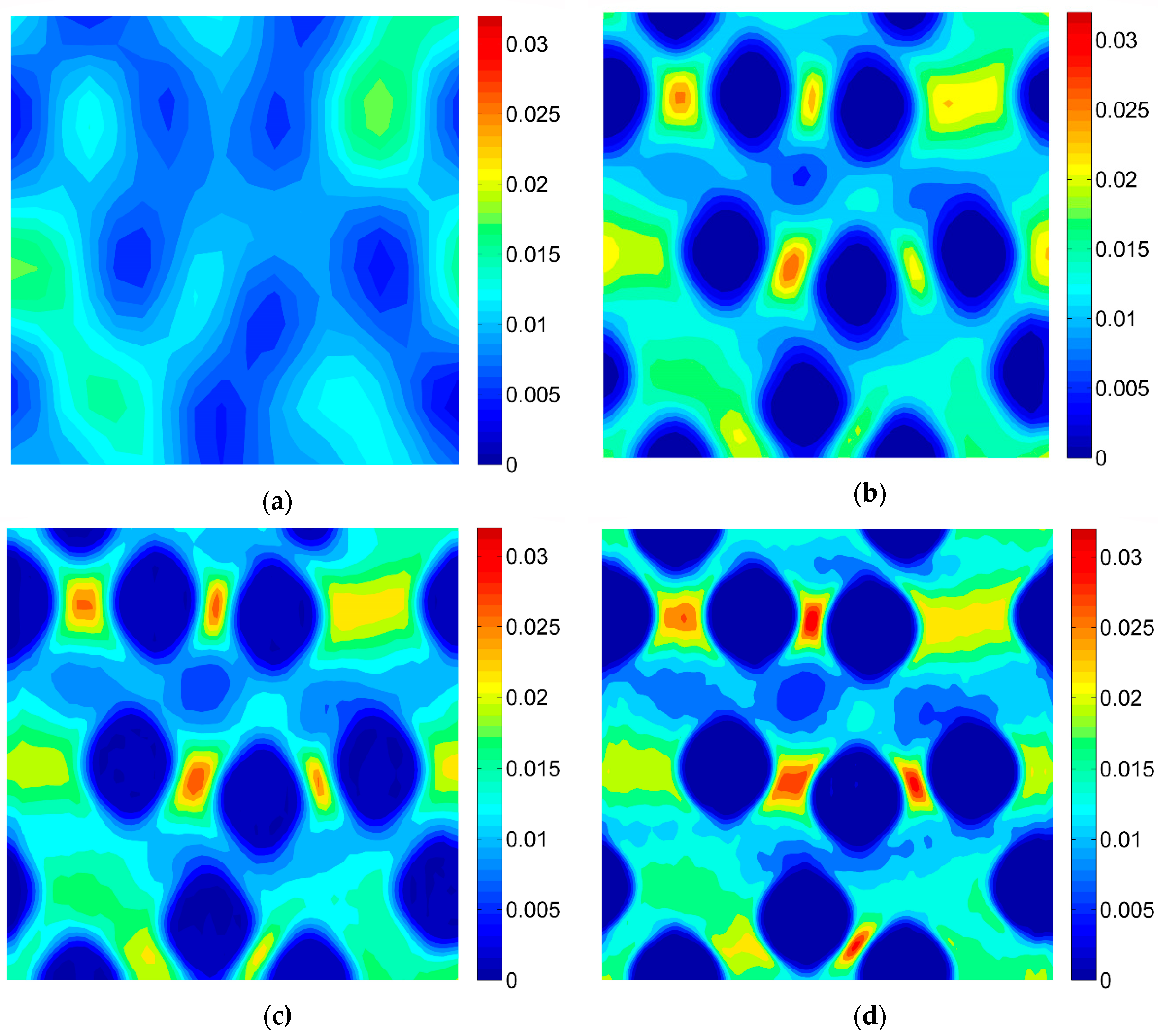
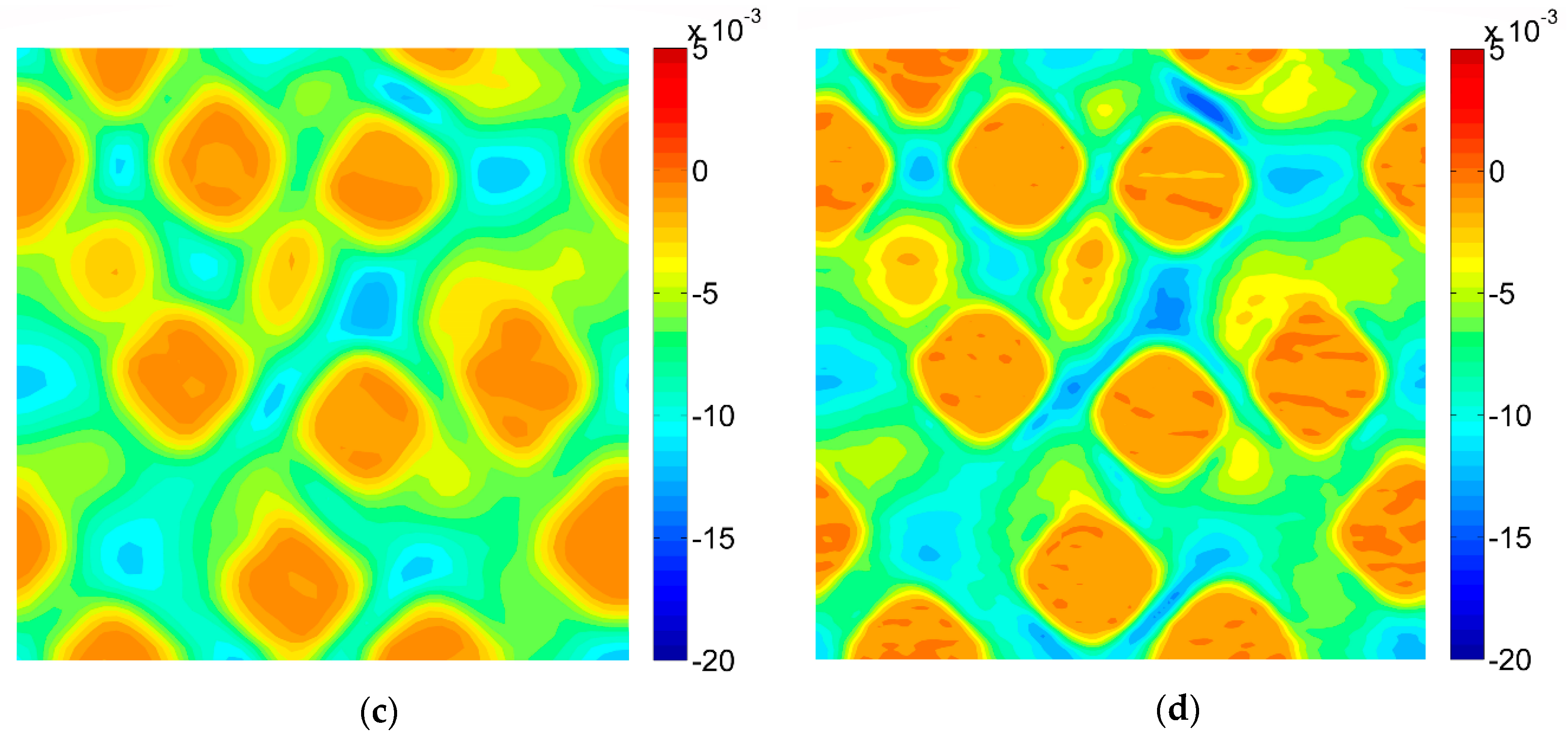
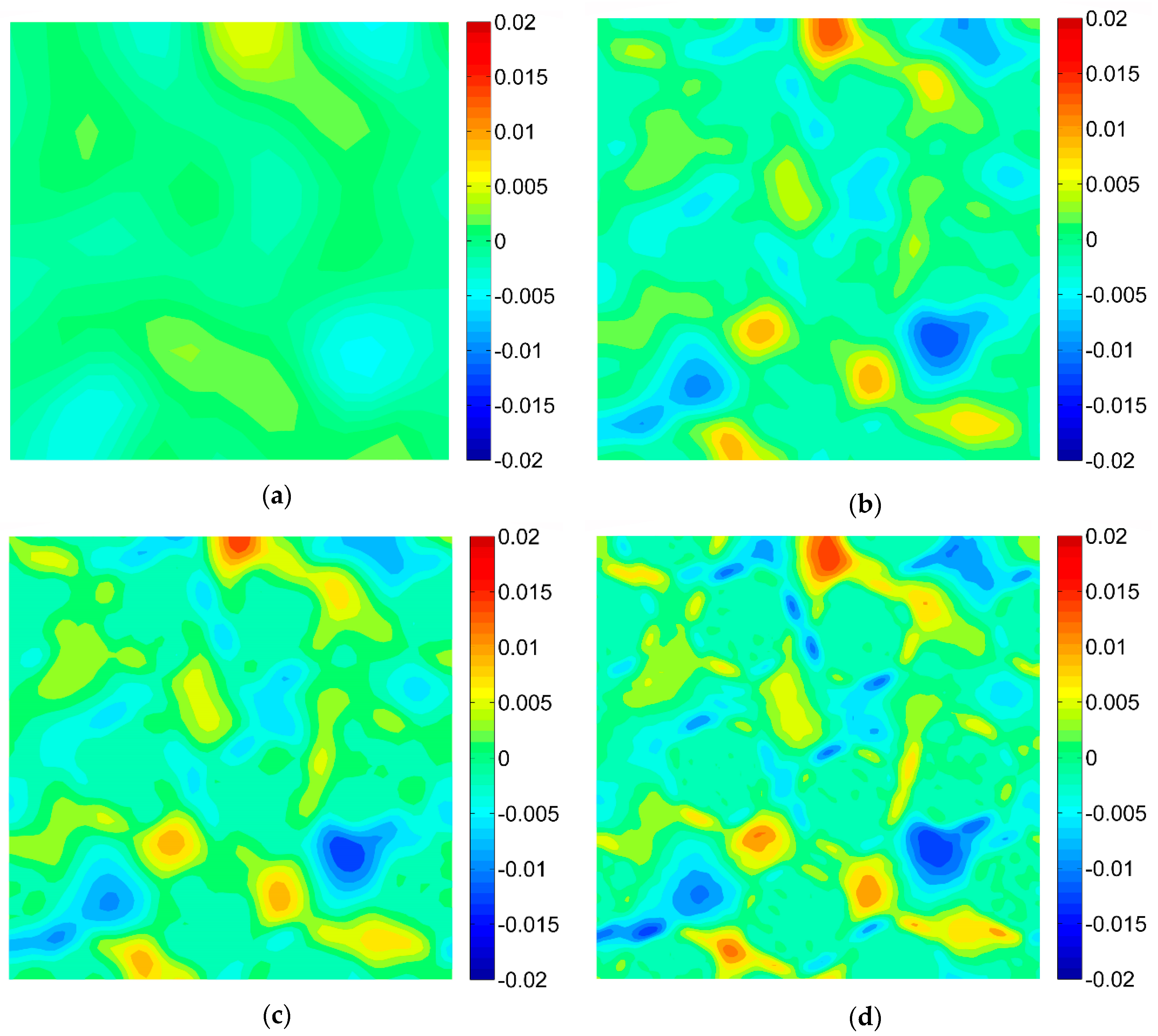
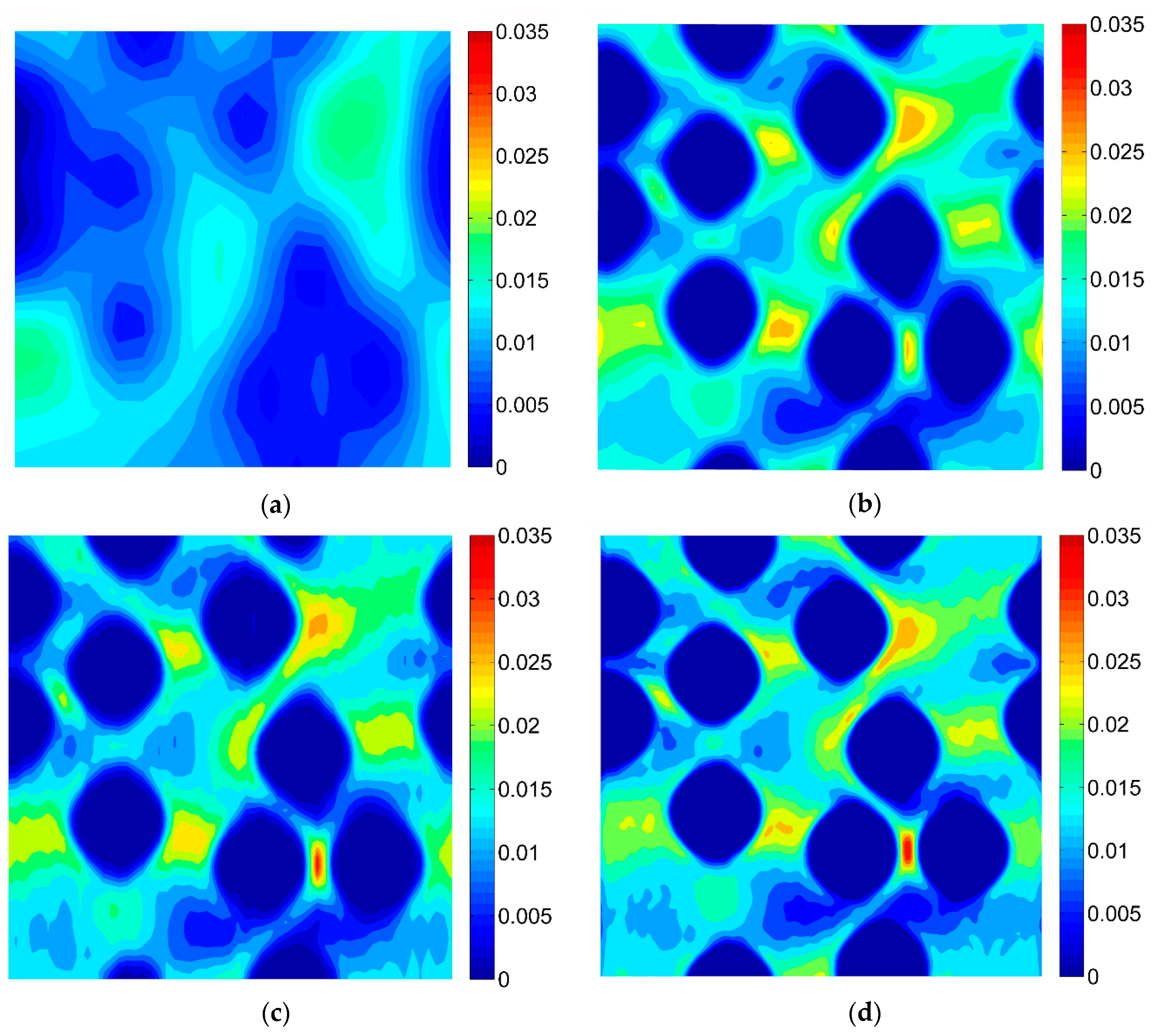
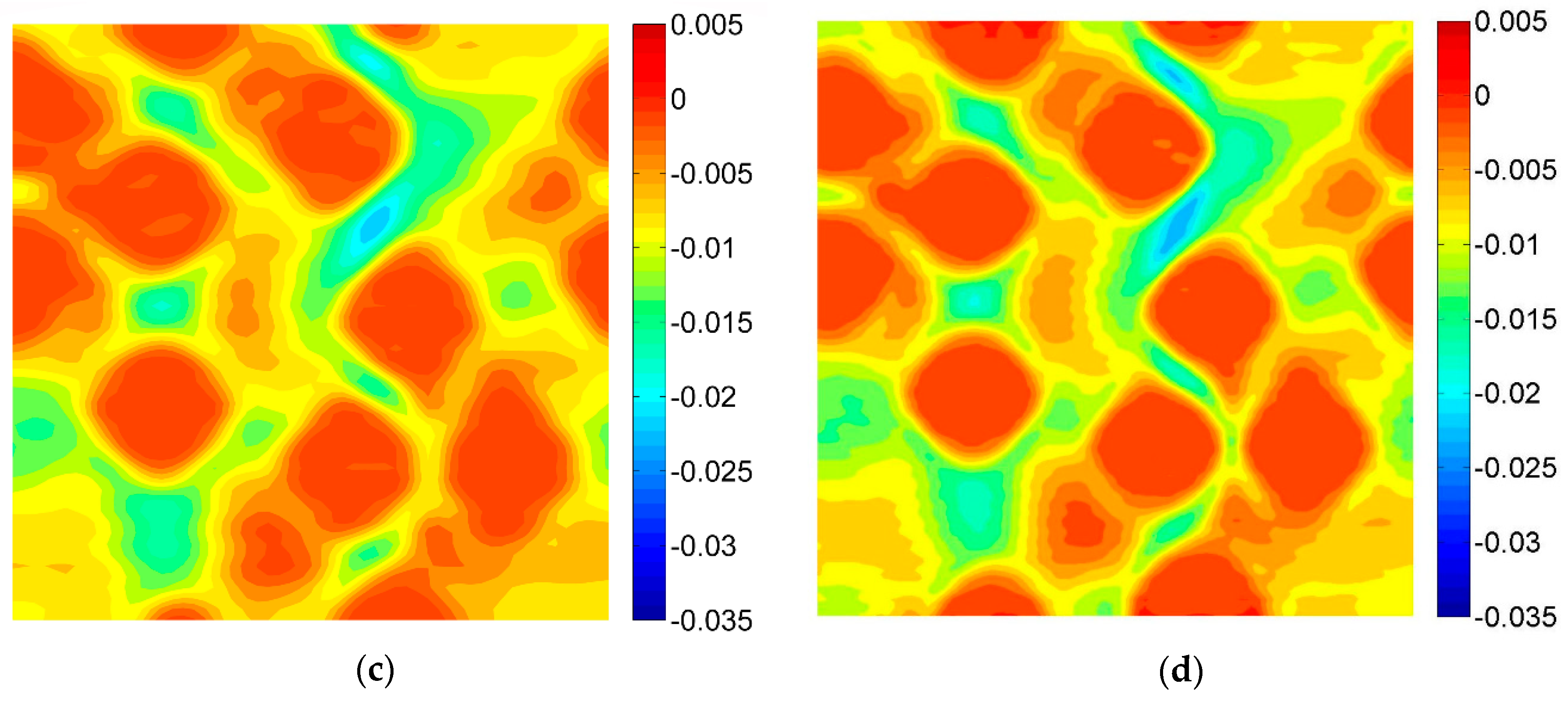
3.2. Results of the Digital Image Correlation
3.3. Results of Inverse Identification
4. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 1957, 241, 376–396. [Google Scholar]
- Benveniste, Y. A new approach to the application of Mori-Tanaka’s theory in composite materials. Mech. Mater. 1987, 6, 147–157. [Google Scholar] [CrossRef]
- Mori, K.; Tanaka, T. Average stress in matrix and average elastic energy of materials with misfitting inclusions Title. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Benveniste, Y. Revisiting the generalized self-consistent scheme in composites: Clarification of some aspects and a new formulation. J. Mech. Phys. Solids 2008, 56, 2984–3002. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Hori, M. Micromechanics: Overall Properties of Heterogeneous Materials, 2nd ed.; Elsevier Science Publishers: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Kouznetsova, V.; Brekelmans, W.A.M.; Baaijens, F.P.T. Approach to micro-macro modeling of heterogeneous materials. Comput. Mech. 2001, 27, 37–48. [Google Scholar] [CrossRef]
- Segurado, J.; Llorca, J. A numerical approximation to the elastic properties of sphere-reinforced composites. J. Mech. Phys. Solids 2002, 50, 2107–2121. [Google Scholar] [CrossRef]
- Ganesh, V.V.; Chawla, N. Effect of particle orientation anisotropy on the tensile behavior of metal matrix composites: Experiments and microstructure-based simulation. Mater. Sci. Eng. A 2005, 391, 342–353. [Google Scholar] [CrossRef]
- Ogierman, W.; Kokot, G. Generation of representative volume elements of heterogeneous materials with distributed orientations of inclusions. Compos. Struct. 2018, 201, 636–646. [Google Scholar] [CrossRef]
- Kamiński, M. Boundary element method homogenization of the periodic linear elastic fiber composites. Eng. Anal. Bound. Elem. 1999, 23, 815–823. [Google Scholar] [CrossRef]
- Fedeliński, P.; Górski, G.; Czyż, T.; Dziatkiewicz, G.; Ptaszny, J. Analysis of effective properties of materials by using the boundary element method. Arch. Mech. 2014, 66, 19–35. [Google Scholar]
- Rodrigues, D.E.S.; Belinha, J.; Pires, F.M.A.; Dinis, L.M.J.S.; Jorge, R.M.N. Material homogenization technique for composites: A meshless formulation. Sci. Technol. Mater. 2018, 30, 50–59. [Google Scholar] [CrossRef]
- Ahmadi, I.; Aghdam, M.M. Micromechanics of fibrous composites subjected to combined shear and thermal loading using a truly meshless method. Comput. Mech. 2010, 46, 387–398. [Google Scholar] [CrossRef]
- Berfield, T.A.; Patel, J.K.; Shimmin, R.G.; Braun, P.V.; Lambros, J.; Sottos, N.R. Micro-and nanoscale deformation measurement of surface and internal planes via digital image correlation. Exp. Mech. 2007, 47, 51–62. [Google Scholar] [CrossRef]
- Grédiac, M.; Hild, F.; Pineau, A. Full-Field Measurements and Identification in Solid Mechanics; John Wiley and Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Barile, C.; Casavola, C.; Pappalettera, G. Digital image correlation comparison of damaged and undamaged aeronautical CFRPs during compression tests. Materials 2019, 12, 249. [Google Scholar] [CrossRef] [PubMed]
- Kokot, G.; Skalski, K.; Makuch, A.; Ogierman, W. Digital image correlation and nanoindentation in evaluation of material parameters of cancellous bone microstructure. Arch. Mater. Sci. Eng. 2017, 83, 10–16. [Google Scholar] [CrossRef]
- Chu, T.C.; Ranson, W.F.; Sutton, M.A. Applications of digital-image-correlation techniques to experimental mechanics. Exp. Mech. 1985, 25, 232–244. [Google Scholar] [CrossRef]
- Schreier, H.; Braasch, J.; Sutton, M. Systematic errors in digital image correlation caused by intensity interpolation. Opt. Eng. 2000, 39, 2915–2921. [Google Scholar] [CrossRef]
- Technical Note, T-Q-400-Accuracy-3DCORR-003-EN. In Error Estimations of 3D Digital Image Correlation Measurements; Dantec Dynamics GmBH: Ulm, Germany, 2006.
- Ghadbeigi, H.; Pinna, C.; Celotto, S.; Yates, J.R. Local plastic strain evolution in a high strength dual-phase steel. Mater. Sci. Eng. A 2010, 527, 5026–5032. [Google Scholar] [CrossRef]
- Ghadbeigi, H.; Pinna, C.; Celotto, S. Quantitative Strain Analysis of the Large Deformation at the Scale of Microstructure: Comparison between Digital Image Correlation and Microgrid Techniques. Exp. Mech. 2012, 52, 1483–1492. [Google Scholar] [CrossRef]
- Anzelotti, G.; Nicoletto, G.; Riva, E. Mesomechanic strain analysis of twill-weave composite lamina under unidirectional in-plane tension. Compos. Part A Appl. Sci. Manuf. 2008, 39, 1294–1301. [Google Scholar] [CrossRef]
- Canal, L.P.; González, C.; Molina-Aldareguía, J.M.; Segurado, J.; Llorca, J. Application of digital image correlation at the microscale in fiber-reinforced composites. Compos. Part A Appl. Sci. Manuf. 2012, 43, 1630–1638. [Google Scholar] [CrossRef]
- Mehdikhani, M.; Aravand, M.; Sabuncuoglu, B.; Callens, M.G.; Lomov, S.V.; Gorbatikh, L. Full-field strain measurements at the micro-scale in fiber-reinforced composites using digital image correlation. Compos. Struct. 2016, 140, 192–201. [Google Scholar] [CrossRef]
- Joo, S.H.; Lee, J.K.; Koo, J.M.; Lee, S.; Suh, D.W.; Kim, H.S. Method for measuring nanoscale local strain in a dual phase steel using digital image correlation with nanodot patterns. Scr. Mater. 2013, 68, 245–248. [Google Scholar] [CrossRef]
- Genovese, K.; Lamberti, L.; Pappalettere, C. A new hybrid technique for in-plane characterization of orthotropic materials. Exp. Mech. 2004, 44, 584–592. [Google Scholar] [CrossRef]
- Conceição António, C.; Rasheed, S. A displacement field approach based on FEM-ANN and experiments for identification of elastic properties of composites. Int. J. Adv. Manuf. Technol. 2018, 95, 4279–4291. [Google Scholar] [CrossRef]
- Lauwagie, T.; Sol, H.; Roebben, G.; Heylen, W.; Shi, Y.; Van der Biest, O. Mixed numerical-experimental identification of elastic properties of orthotropic metal plates. NDT E Int. 2003, 36, 487–495. [Google Scholar] [CrossRef]
- Avril, S.; Bonnet, M.; Bretelle, A.S.; Grédiac, M.; Hild, F.; Ienny, P.; Latourte, F.; Lemosse, D.; Pagano, S.; Pagnacco, E.; et al. Overview of identification methods of mechanical parameters based on full-field measurements. Exp. Mech. 2008, 48, 381–402. [Google Scholar] [CrossRef]
- Barile, C.; Casavola, C.; Pappalettera, G.; Pappalettere, C. Innovative mechanical characterization of materials by combining ESPI and numerical modelling. Int. J. Mech. 2016, 10, 115–123. [Google Scholar]
- Rahmani, B.; Mortazavi, F.; Villemure, I.; Levesque, M. A new approach to inverse identification of mechanical properties of composite materials: Regularized model updating. Compos. Struct. 2013, 105, 116–125. [Google Scholar] [CrossRef]
- Carlsson, L.; Adams, D.; Pipes, B. Experimental Characterization of Advanced Composite Materials, 4th ed.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Pritchard, R.; Lava, P.; Debruyne, D.; Terentjev, E. Precise determination of the Poisson ratio in soft materials with 2D digital image correlation. Soft Matter 2013, 9, 6037. [Google Scholar] [CrossRef]
- Kokot, G.; Orantek, P. The Topology Optimization Using Evolutionary Algorithms. In IUTAM Symposium on Evolutionary Methods in Mechanics; Burczyński, T., Osyczka, A., Eds.; Springer: Dordrecht, The Netherlands, 2004; pp. 173–186. [Google Scholar]
- Ogierman, W. Inverse Identification of Elastic Properties of Constituents of Discontinuously Reinforced Composites. Materials 2018, 11, 2332. [Google Scholar] [CrossRef] [PubMed]
- Kuś, W.; Burczyński, T. Bioinspired Algorithms in Multiscale Optimization. In Computer Methods in Mechanics. Advanced Structured Materials; Kuczma, M., Wilmanski, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Makowski, P.; Kuś, W. Optimization of bone scaffold structures using experimental and numerical data. Acta Mech. 2016, 227, 139–149. [Google Scholar] [CrossRef]
- Beluch, W.; Długosz, A. Multiobjective and multiscale optimization of composite materials by means of evolutionary computations. J. Theor. Appl. Mech. 2016, 54, 397–409. [Google Scholar] [CrossRef]
- Tucker, I.C.; Liang, E. Stiffness predictions for unidirectional short-fibre composites: Review and evaluation. Compos. Sci. Technol. 1999, 59, 655–671. [Google Scholar] [CrossRef]
- Liu, L.; Huang, Z. A Note on mori-tanaka’s method. Acta Mech. Solida Sin. 2014, 27, 234–244. [Google Scholar] [CrossRef]
- Schjødt-Thomsen, J.; Pyrz, R. The Mori-Tanaka stiffness tensor: Diagonal symmetry, complex fibre orientations and non-dilute volume fractions. Mech. Mater. 2001, 33, 531–544. [Google Scholar] [CrossRef]
- Böhm, H. (Ed.) Mechanics of Microstructured Materials; Springer: Vienna, Austria, 2004. [Google Scholar]
- Perdahcioǧlu, E.S.; Geijselaers, H.J.M. Constitutive modeling of two phase materials using the mean field method for homogenization. Int. J. Mater. Form. 2011, 4, 93–102. [Google Scholar] [CrossRef]
- Mura, T. Micromechanics of Defects in Solids; Martinus Nijhoff Publishers: Dordrecht, The Netherlands, 1987. [Google Scholar]
- Liu, H.; Zeng, D.; Li, Y.; Jiang, L. Development of RVE-embedded solid elements model for predicting effective elastic constants of discontinuous fiber reinforced composites. Mech. Mater. 2016, 93, 109–123. [Google Scholar] [CrossRef]
- Omairey, S.L.; Dunning, P.D.; Sriramula, S. Development of an ABAQUS plugin tool for periodic RVE homogenisation. Eng. Comput. 2019, 35, 567–577. [Google Scholar] [CrossRef]





| Em, MPa | Ei, MPa | υm | υi | |
|---|---|---|---|---|
| Material 1 | 3500 | 72,000 | 0.35 | 0.20 |
| Material 2 | 2600 | 115,000 | 0.39 | 0.28 |
| υc | Ec, MPa | |
|---|---|---|
| Material 1 | 0.2881 | 27,734.2 |
| Material 2 | 0.3458 | 42,335.2 |
| <ε11>m | <ε11>f | <ε22>m | <ε22>f | |
|---|---|---|---|---|
| FEM (Finite Element Method), reference Solution | 0.01471 | 0.00124 | −0.00727 | −0.00040 |
| DIC, grid 400 × 400 | 0.01419 | 0.00121 | −0.00697 | −0.00046 |
| - | 3.7% | 6.0% | 4.3% | 16.1% |
| DIC, grid 200 × 200 | 0.01393 | 0.00133 | −0.00682 | −0.00056 |
| - | 5.3% | 6.9% | 6.3% | 41.9% |
| DIC, grid 100 × 100 | 0.01348 | 0.00139 | −0.00654 | −0.00052 |
| - | 8.4% | 12.1% | 10.0% | 30.7% |
| DIC, grid 50 × 50 | 0.01169 | 0.00319 | −0.00577 | −0.00174 |
| - | 20.6% | 156.3% | 20.6% | 340.7% |
| <ε11>m | <ε11>f | <ε22>m | <ε22>f | |
|---|---|---|---|---|
| FEM, reference solution | 0.01505 | 0.00063 | −0.00839 | −0.00033 |
| DIC, grid 400 × 400 | 0.01442 | 0.00061 | −0.00796 | −0.00031 |
| - | 4.2% | 2.5% | 5.1% | 5.9% |
| DIC, grid 200 × 200 | 0.01377 | 0.00060 | −0.00762 | −0.00037 |
| - | 8.5% | 4.1% | 9.2% | 13.7% |
| DIC, grid 100 × 100 | 0.01343 | 0.00059 | −0.00740 | −0.00037 |
| - | 10.8% | 5.8% | 11.7% | 13.6% |
| DIC, grid 50 × 50 | 0.01155 | 0.00178 | −0.00650 | −0.00180 |
| - | 23.2% | 183.2% | 22.5% | 454.4% |
| υm | υf | R | Em, MPa | Ef, MPa | |
|---|---|---|---|---|---|
| FEM-reference solution | 0.3500 | 0.2000 | 20.6 | 3500.0 | 72,000.0 |
| FEM-as input | 0.3593 | 0.1823 | 21.8 | 3345.6 | 72,936.8 |
| - | 2.7% | 8.8% | 6.0% | 4.4% | 1.3% |
| DIC, grid 400 × 400 | 0.3523 | 0.1935 | 18.4 | 3902.6 | 71,908.1 |
| - | 0.7% | 3.3% | 10.4% | 11.5% | 0.1% |
| DIC, grid 200 × 200 | 0.3509 | 0.1949 | 15.8 | 4493.4 | 70,801.7 |
| - | 0.3% | 2.5% | 23.4% | 28.4% | 1.7% |
| DIC, grid 100 × 100 | 0.3449 | 0.2045 | 13.5 | 5162.7 | 69,565.6 |
| - | 1.5% | 2.3% | 34.5% | 47.5% | 3.4% |
| υm | υf | R | Em, MPa | Ef, MPa | |
|---|---|---|---|---|---|
| FEM-reference solution | 0.3900 | 0.2800 | 44.2 | 2600.0 | 115,000.0 |
| FEM-as input | 0.3828 | 0.2897 | 50.5 | 2312.1 | 116,646.7 |
| - | 1.9% | 3.5% | 14.1% | 11.1% | 1.4% |
| DIC, grid 400 × 400 | 0.3748 | 0.3027 | 35.1 | 3270.6 | 114,869.3 |
| - | 3.9% | 8.1% | 20.6% | 25.8% | 0.1% |
| DIC, grid 200 × 200 | 0.3692 | 0.3107 | 25.9 | 4354.8 | 112,857.5 |
| - | 5.3% | 11.0% | 41.4% | 67.5% | 1.9% |
| DIC, grid 100 × 100 | 0.3650 | 0.3175 | 22.9 | 4886.8 | 111,872.9 |
| - | 6.4% | 13.4% | 48.2% | 88.0% | 2.7% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ogierman, W.; Kokot, G. Analysis of Strain Field Heterogeneity at the Microstructure Level and Inverse Identification of Composite Constituents by Means of Digital Image Correlation. Materials 2020, 13, 287. https://doi.org/10.3390/ma13020287
Ogierman W, Kokot G. Analysis of Strain Field Heterogeneity at the Microstructure Level and Inverse Identification of Composite Constituents by Means of Digital Image Correlation. Materials. 2020; 13(2):287. https://doi.org/10.3390/ma13020287
Chicago/Turabian StyleOgierman, Witold, and Grzegorz Kokot. 2020. "Analysis of Strain Field Heterogeneity at the Microstructure Level and Inverse Identification of Composite Constituents by Means of Digital Image Correlation" Materials 13, no. 2: 287. https://doi.org/10.3390/ma13020287
APA StyleOgierman, W., & Kokot, G. (2020). Analysis of Strain Field Heterogeneity at the Microstructure Level and Inverse Identification of Composite Constituents by Means of Digital Image Correlation. Materials, 13(2), 287. https://doi.org/10.3390/ma13020287





