Measurement Modulus of Elasticity Related to the Atomic Density of Planes in Unit Cell of Crystal Lattices
Abstract
1. Introduction
2. Materials and Experiments
3. Methods
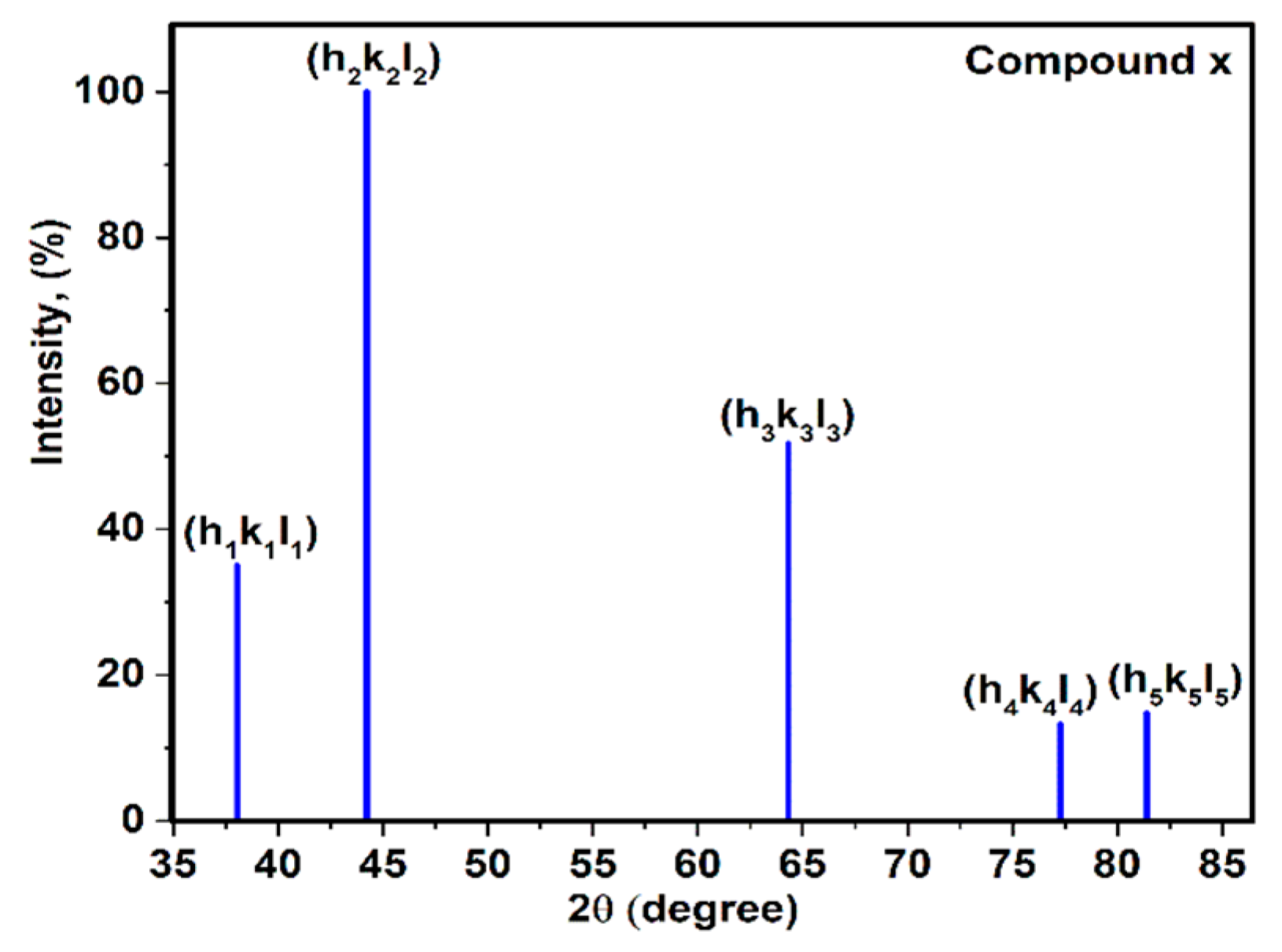
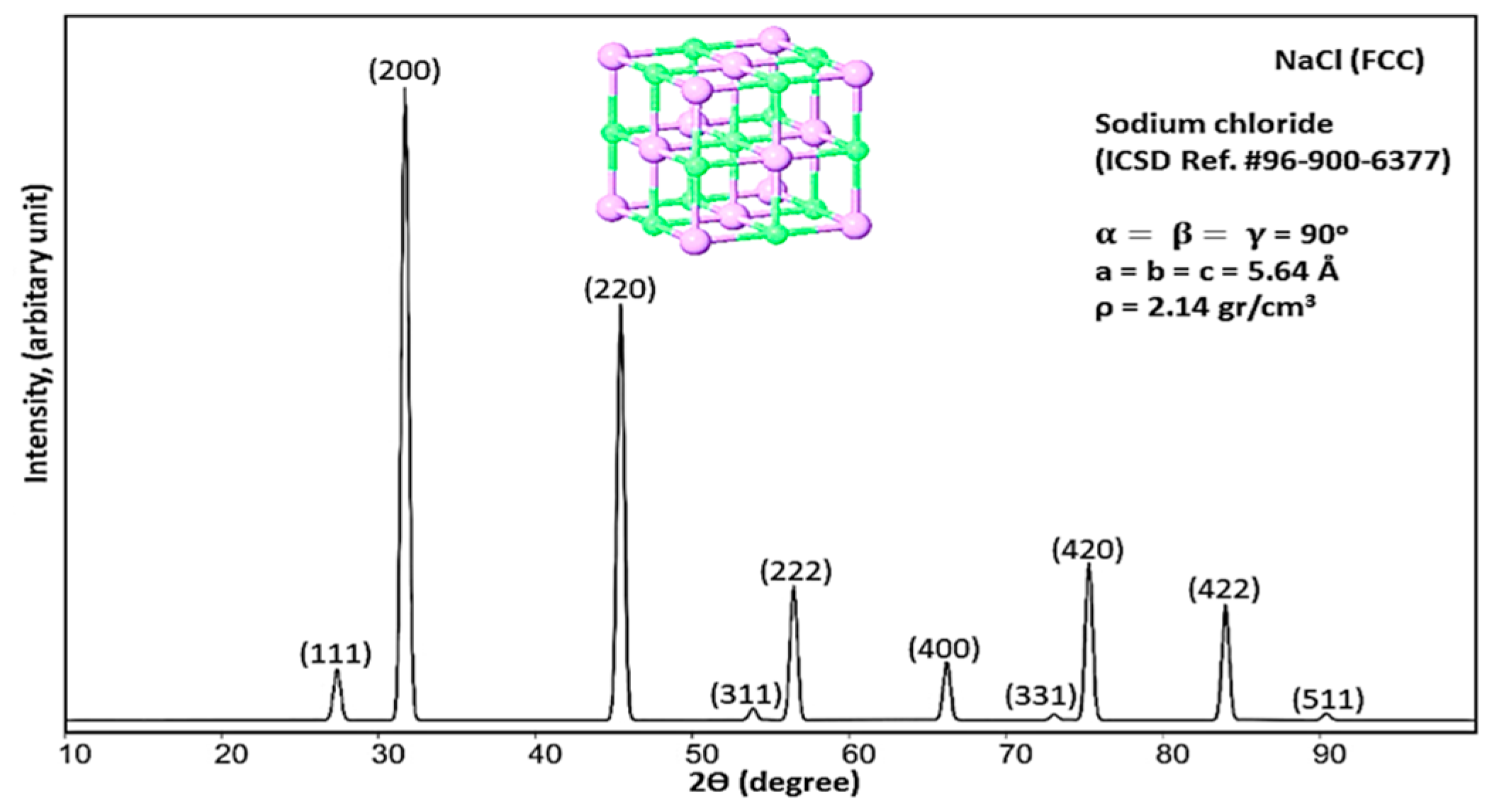
3.1. X-Ray Diffraction of Compound X
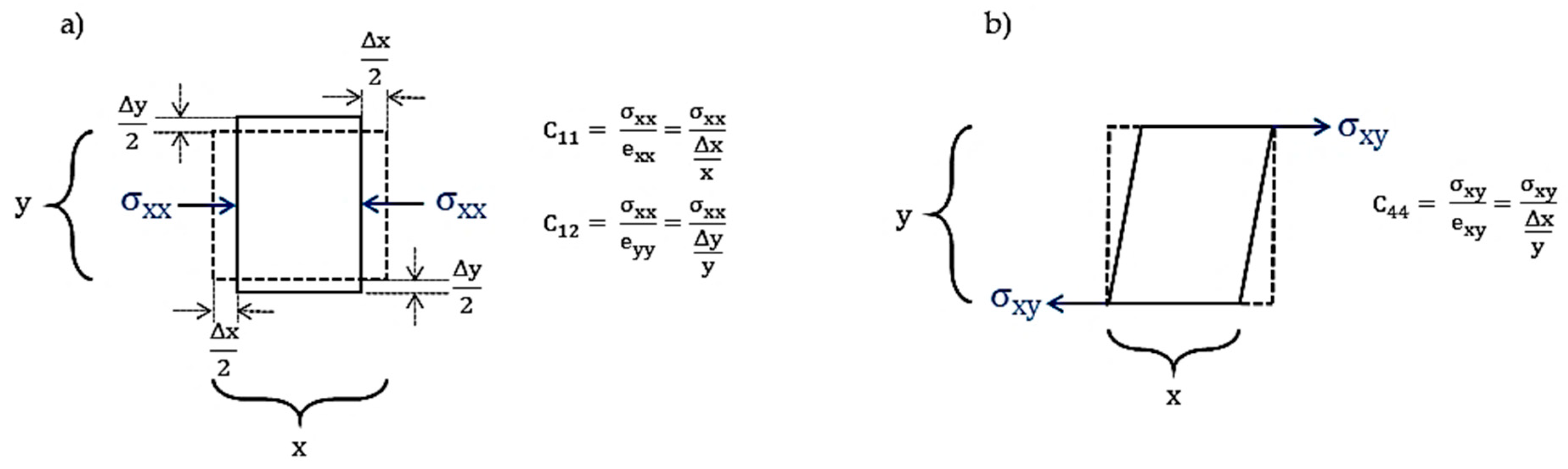
3.2. Elastic Stiffness Constant and Elastic Compliance
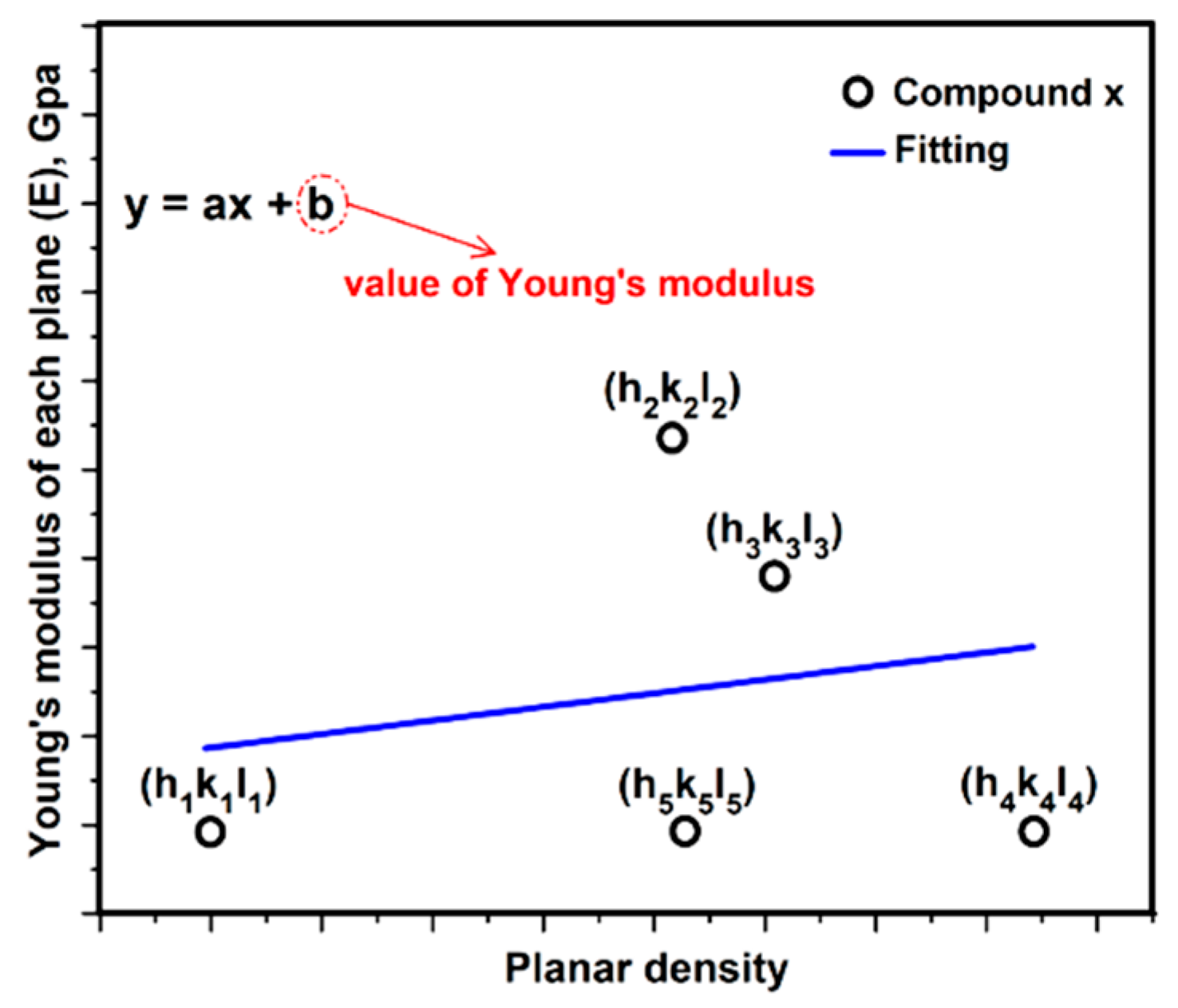
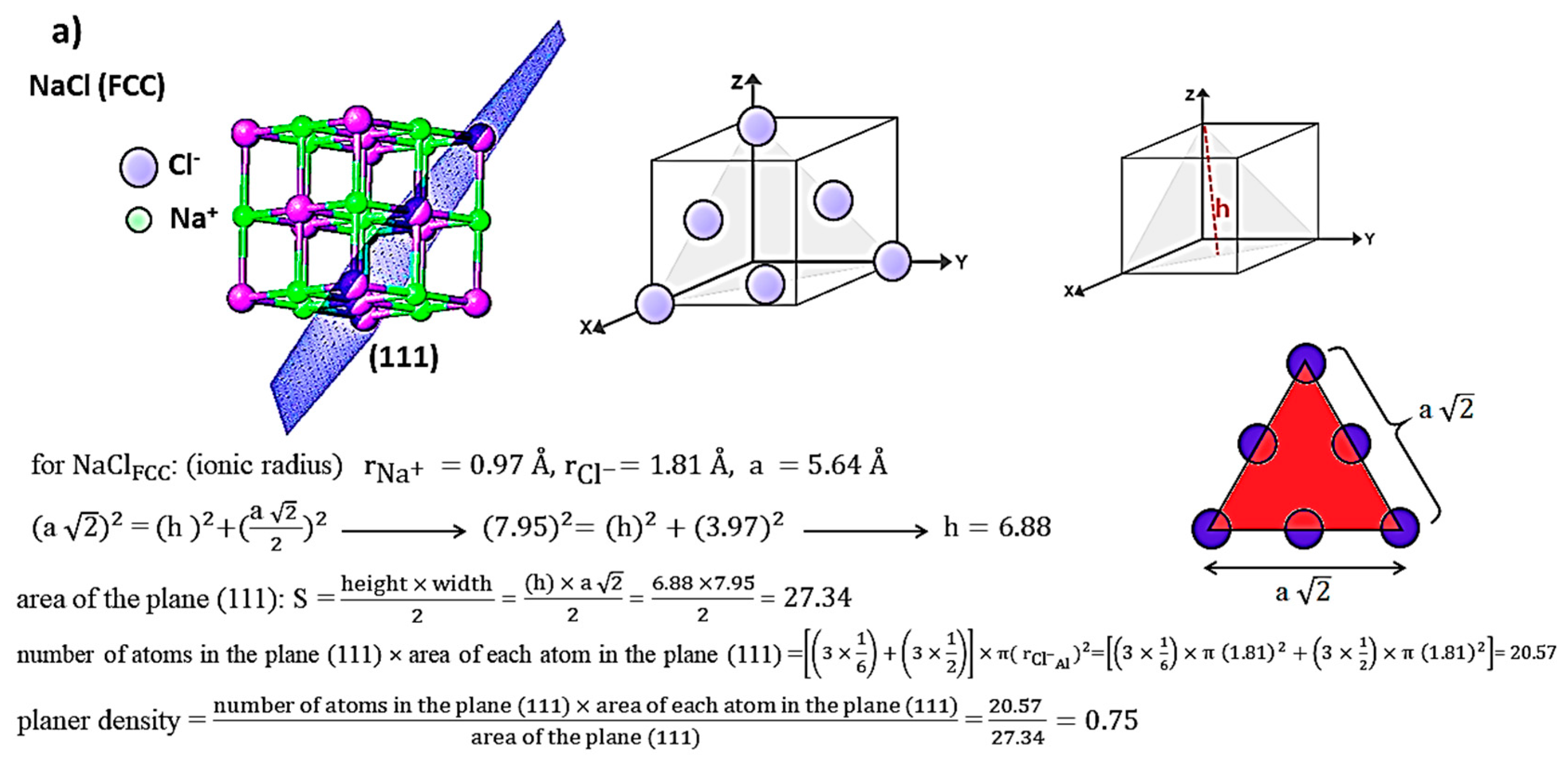
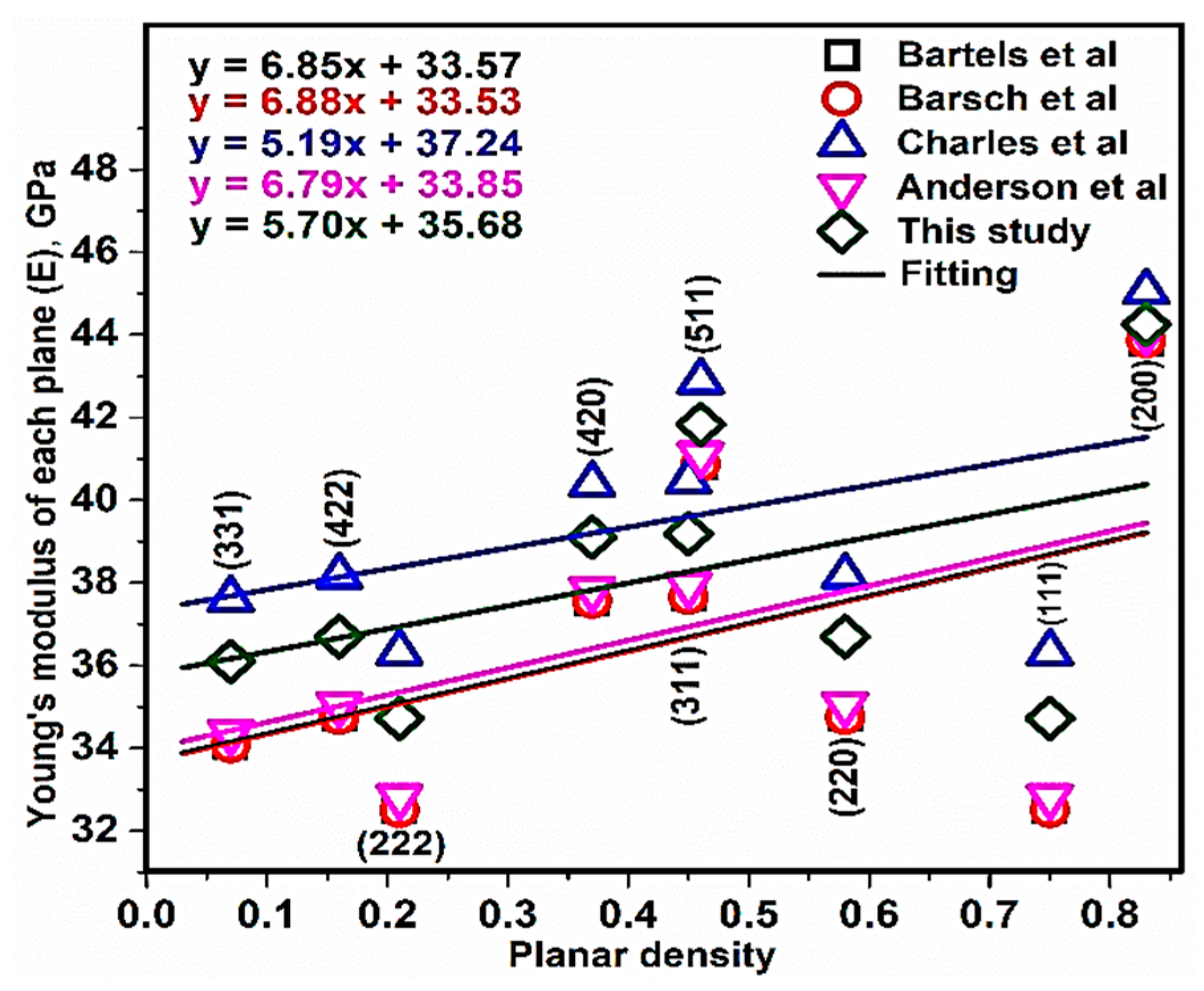
3.3. Relationship between Young’s Modulus Ehkl and Planar Density of Each Diffracted Plane through X-Ray Diffraction
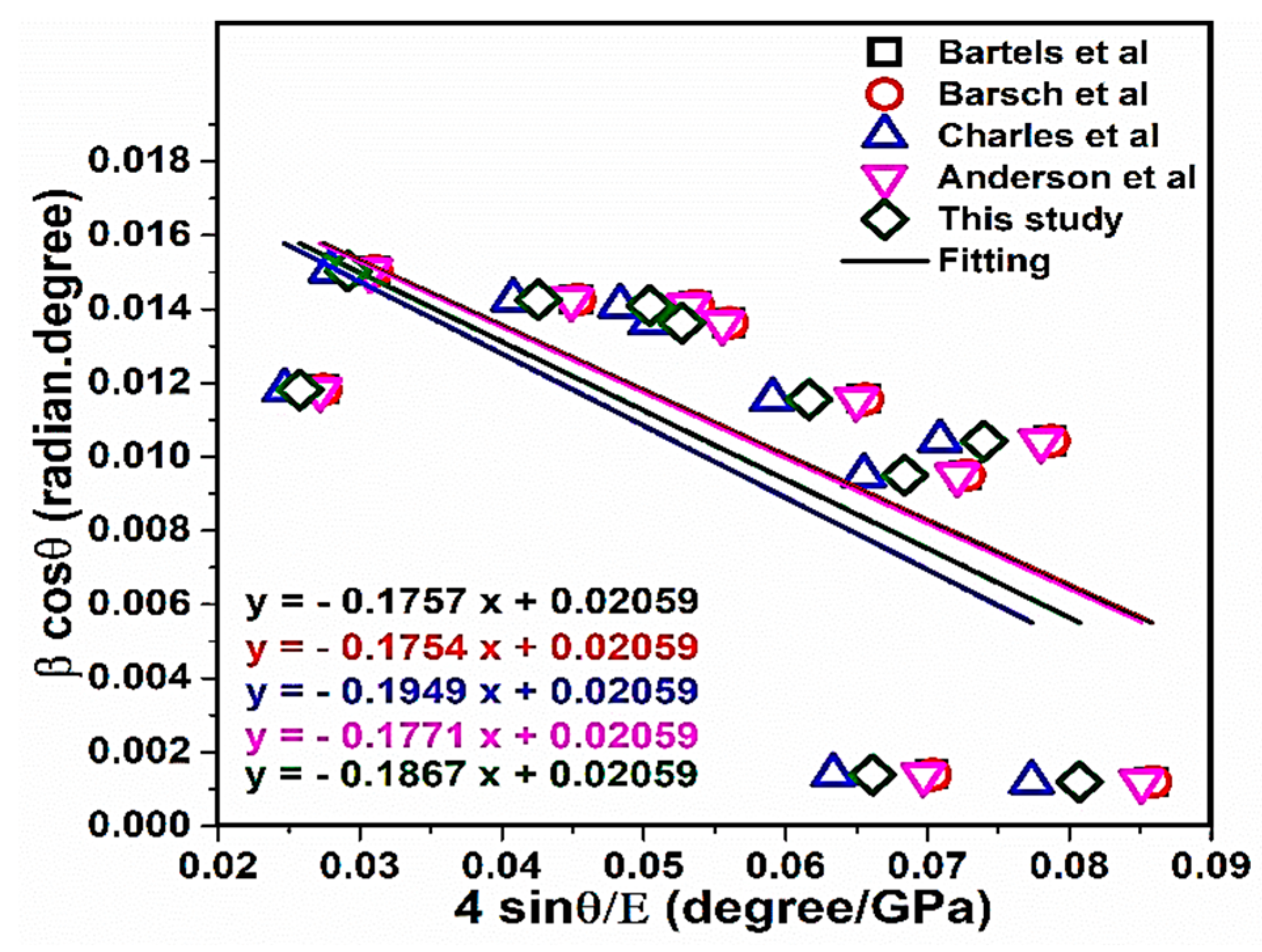
3.4. Modified W–H (USDM Model)
3.5. Modified Williamson–Hall Method (USDM) for NaCl
4. Conclusions
- A new method for measuring the accurate value of the modulus of elasticity of crystalline materials is successfully presented.
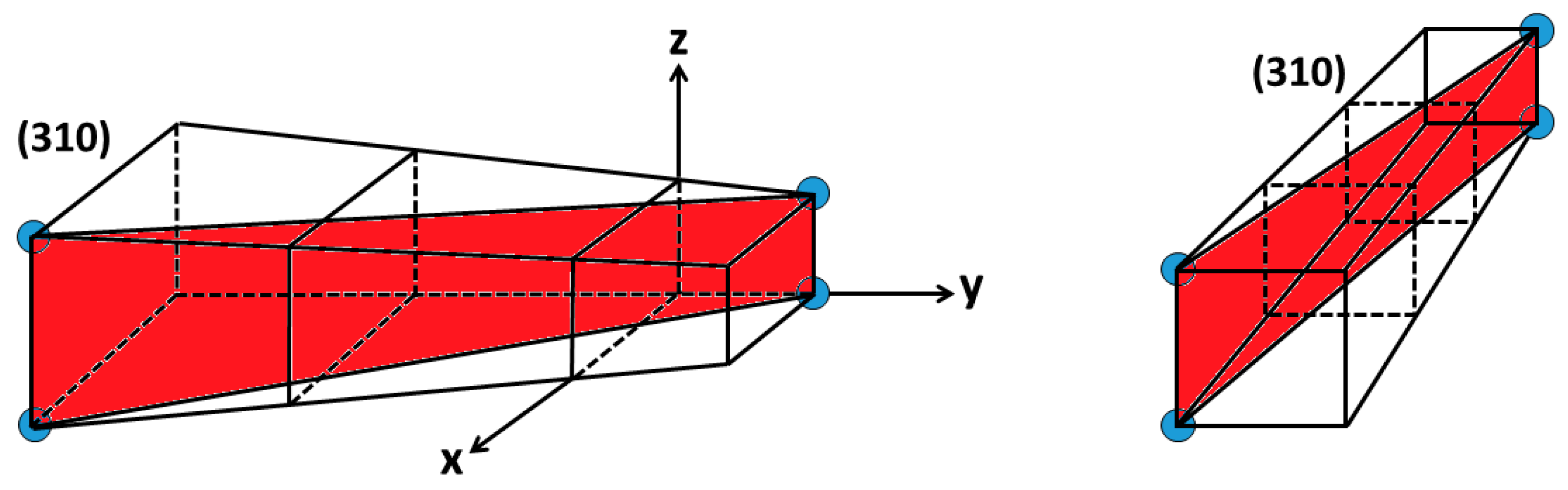
- Planar density for the area of total atoms/ions in the plane divided by the plane area is responsible for the modulus of elasticity of that plane.
- Modulus of elasticity of each plane (y axis) is plotted against the planar density of that plane (x axis), by the least squares method, to give the Young’s modulus of the materials at the intercept.
- Case study of NaCl proved the accuracy of the new method in this study, in good agreement with the ultrasonic technique.
- The Williamson–Hall method, especially in the uniform stress deformation model (USDM), can be used in this method to minimize errors in the least squares method and yield a proper modulus of elasticity, much more accurate than the average value.
- The restriction is that XRD data for planar density calculations are applicable in the uniform distribution of atoms in the crystal lattice with a unit cell, so the method cannot be used for amorphous materials.
- This method can be applied for research as well as industrial applications.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Ma, Y.Z.; Sobernheim, D.; Grazon, J.R. Glossary for Unconventional Oil and Gas Resource Evaluation and Development. In Unconventional Oil and Gas Resources Handbook; Elsevier: Amsterdam, The Netherlands, 2016; Chapter 19; pp. 513–526. [Google Scholar] [CrossRef]
- Ravindran, P.; Fast, L.; Korzhavyi, P.A.; Johansson, B. Density functional theory for calculation of elastic properties of orthorhombic crystals: Application to TiSi2. Appl. Phys. 1998, 84, 4891. [Google Scholar] [CrossRef]
- Fine, M.E.; Brown, L.D.; Marcus, H.L. Elastic constants versus melting temperature in metals. Scr. Metall. 1984, 18, 951–956. [Google Scholar] [CrossRef]
- Nakamura, M. Elastic constants some transition metal-disilicide-single crystals. Met. Mater. Trans. A 1994, 25, 331–340. [Google Scholar] [CrossRef]
- Brich, F. Finite Elastic Strain of Cubic Crystals. Phys. Rev. 1947, 71, 809. [Google Scholar] [CrossRef]
- Leibfried, G.; Ludwig, W. Theory of Anharmonic Effects in Crystals. Solid State Phys. 1961, 12, 275–444. [Google Scholar] [CrossRef]
- Argaman, U.; Makov, G. First-principle study of the temperature dependence of the elastic constants of hcp titanium. Comput. Mater. Sci. 2020, 184, 109917. [Google Scholar] [CrossRef]
- Lubarda, V.A. Apparent elastic constants of cubic Cryst. and their pressure derivatives. Int. J. Non-Linear Mech. 1999, 34, 5–11. [Google Scholar] [CrossRef]
- Yu, F.; Liu, Y. First-Principles Calculations of Structural, Mechanical, and Electronic Properties of the B2-Phase NiTi Shape-Memory Alloy Under High Pressure. Computation 2019, 7, 57. [Google Scholar] [CrossRef]
- Holec, D.; Friák, M.; Neugebauer, J.; Mayrhofer, P.H. Trends in the elastic response of binary early transition metal nitrides. Phys. Rev. B 2012, 85, 064101. [Google Scholar] [CrossRef]
- Knowles, K.M.; Howie, P.R. The Directional Dependence of Elastic Stiffness and Compliance Shear Coefficients and Shear Moduli in Cubic Materials. J. Elast. 2015, 120, 87–108. [Google Scholar] [CrossRef]
- Fan, Q. A new method of calculating planar density: The position-duplication-number method. J. Appl. Cryst. 2016, 49, 1454–1458. [Google Scholar] [CrossRef]
- Abdullah, B.; Tahir, D. Quantitative analysis of X-Ray diffraction spectra for determine structural properties and deformation energy of Al, Cu and Si. J. Phys. Conf. Ser. 2019, 1317, 012052. [Google Scholar] [CrossRef]
- Badawi, F.; Villain, P. Stress and elastic-constant analysis by X-ray diffraction in thin films. J. Appl. Cryst. 2003, 36, 869–879. [Google Scholar] [CrossRef]
- Graham, R.C. X-ray diffraction and the identification and analysis of clay minerals. Soil Sci. 1999, 164, 72–73. [Google Scholar] [CrossRef]
- Hanabusa, T.; Fukura, J.; Fujiwara, H. X-Ray Stress Measurement on the Cementite Phase in Steels. Bull. JSME 1969, 12, 931–939. [Google Scholar] [CrossRef]
- Prabhu, Y.T.; Rao, K.V.; Kumar, V.S.S.; Kumari, B.S. X-Ray Analysis by Williamson-Hall and Size-Strain Plot Methods of ZnO Nanoparticles with Fuel Variation. World J. Nano Sci. Eng. 2014, 4, 21–28. [Google Scholar] [CrossRef]
- Levy, M. Introduction to fundamentals of elastic constants. Exp. Methods Phys. Sci. 2001, 39, 1–35. [Google Scholar] [CrossRef]
- Rajabi, K.; Hosseini-Hashemi, S. Application of the generalized Hooke’s law for viscoelastic materials (GHVMs) in nanoscale mass sensing applications of viscoelastic nanoplates: A theoretical study. Eur. J. Mech. A/Solids 2018, 67, 71–83. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2009, 102, 039902. [Google Scholar] [CrossRef]
- Landau, L.D.; Bell, J.S.; Kearsley, M.J.; Pitaevskii, L.P.; Lifshitz, E.M.; Sykes, J.B. Electrodynamics of Continuous Media; Elsevier: Amsterdam, The Netherlands, 1970; Volume 8, ISBN 9781483293752. [Google Scholar]
- Shafiq, M.; Arif, S.; Ahmad, I.; Jalali Asadabadi, S.; Maqbool, M.; Aliabad, H.A.R. Elastic and mechanical properties of lanthanide monoxides. J. Alloys Compd. 2015, 618, 292–298. [Google Scholar] [CrossRef]
- Li, Y. Relations between elastic constants Cij and texture parameters for hexagonal Materials. J. Appl. Phys. 1990, 67, 2663. [Google Scholar] [CrossRef]
- Papaconstantopoulos, D.A.; Mehl, M.J. Tight-Binding Method in Electronic Structure. Reference Module in Materials Science and Materials Engineering in Encyclopedia of Condensed Matter Physics; Elsevier: Amsterdam, The Netherlands, 2005; pp. 194–206. [Google Scholar] [CrossRef]
- Huntington, H.B. The Elastic Constants of Crystals. Solid State Phys. 1958, 7, 213–351. [Google Scholar] [CrossRef]
- Zhang, J.M.; Zhang, Y.; Xu, K.W.; Ji, V. Young’s modulus surface and Poisson’s ratio curve for cubic metals. J. Phys. Chem. Solids 2007, 68, 503–510. [Google Scholar] [CrossRef]
- Zhang, J.M.; Zhang, Y.; Xu, K.W.; Ji, V. Anisotropic elasticity in hexagonal crystals. Thin Solid Film. 2007, 515, 7020–7024. [Google Scholar] [CrossRef]
- Rabiei, M.; Palevičius, A.; Monshi, A.; Nasiri, S.; Vilkauskas, A.; Janušas, G. Comparing methods for calculating nano crystal size of natural hydroxyapatite using X-Ray diffraction. Nanomaterials 2020, 10, 1627. [Google Scholar] [CrossRef]
- Hertzberg, R.; Vinci, R.; Hertzberg, J.L. Deformation and Fracture Mechanics of Engineering Materials; Wiley: Hoboken, NJ, USA, 1976; Chapter 1: Elastic response of solids. [Google Scholar]
- Berdichevsky, V. Energy of dislocation networks. Int. J. Eng. Sci. 2016, 103, 35–44. [Google Scholar] [CrossRef]
- Abbaschian, R.; Abbaschian, L.; Reed-Hill, R.E. Physical Metallurgy Principles; Boston PWS publishing company: Boston, MA, USA, 2009; ISBN 978-0-495-08254-5. [Google Scholar]
- Shackelford, J.F. Introduction to Materials Science for Engineers, 8th ed.; Pearson: London, UK, 2015; ISBN 9780133826654. [Google Scholar]
- Callister, W.D.; Rethwisch, D.G. Materials Science and Engineering, 9th ed.; Wiley: Hoboken, NJ, USA, 2010; ISBN 978-1-118-32457-8. [Google Scholar]
- Jones, I.P.; Hutchinson, W.B. Stress-state dependence of slip in Titanium-6Al-4V and other H.C.P. metals. Acta Metall. 1981, 29, 951–968. [Google Scholar] [CrossRef]
- Miller, M.P.; Park, J.S.; Dawson, P.R.; Han, T.S. Measuring and modeling distributions of stress state in deforming polycrystals. Acta Mater. 2008, 56, 3927–3939. [Google Scholar] [CrossRef]
- Ungar, T.; Ribarik, G.; Balogh, L.; Salem, A.; Semiatin, S.L.; Vaughan, G.B.M. Burgers vector population, dislocation types and dislocation densities in single grains extracted from a polycrystalline commercial-purity Ti specimen by X-ray line-profile analysis. Scr. Mater. 2010, 63, 69–72. [Google Scholar] [CrossRef]
- Goettler, E. Dislocation structure and work-hardening of copper sinqle crystals with [100] axis orientation I. Dislocation arrangement and cell structure of crystals deformed in tension. Struct. Prop. Condens. Matter 1973, 28, 1057–1076. [Google Scholar] [CrossRef]
- Elliott, S. The Physics and Chemistry of Solids; Wiley: Hoboken, NJ, USA, 1998; ISBN 978-0-471-98195-4. [Google Scholar]
- Bohm, H.J. Introduction to crystal plasticity theory. In Mechanics of Microstructured Materials; Springer: Vienna, Austria, 2004; pp. 125–171. [Google Scholar] [CrossRef]
- Pandech, N.; Sarasamak, K.; Limpijumnong, S. Elastic properties of provskite ATiO3 (A=Be, Mg, Ca, Sr, and Ba) and PbBO3 (B = Ti, Zr, and Hf): First principles calculations. J. Appl. Phys. 2015, 117, 174108. [Google Scholar] [CrossRef]
- Suryanarayana, C.; Norton, M.G. Practical Aspects of X-Ray Diffraction. In X-Ray Diffractio-n; Springer: Boston, MA, USA, 1998; pp. 63–94. [Google Scholar] [CrossRef]
- Nath, D.; Singh, F.; Das, R. X-ray diffraction analysis by Williamson-Hall, Halder-Wagner and size-strain plot methods of CdSe nanoparticles a comparative study. Mater. Chem. Phys. 2020, 239, 122021. [Google Scholar] [CrossRef]
- Deligoz, E.; Colakoglu, Y.; Ciftci, Y. Elastic, electronic, and lattice dynamical properties of CdS, CdSe, and CdTe. Phys. B Condens. Matter 2006, 373, 124–130. [Google Scholar] [CrossRef]
- Kishore, N.; Nagarajan, V.; Chandiramouli, R. Mechanical properties and band structure of CdSe and CdTe nanostructures at high pressure—A first-principles study. Process. Appl. Ceram. 2019, 13, 124–131. [Google Scholar] [CrossRef]
- Bateman, T.B. Elastic Moduli of Single-Crystal Zinc Oxide. J. Appl. Phys. 1962, 33, 3309. [Google Scholar] [CrossRef]
- Bhatia, D.; Sharma, H.; Meena, R.S.; Palkar, V.R. A novel ZnO piezoelectric microcantilever energy scavenger: Fabrication and characterization. Sens. Bio-Sens. Res. 2016, 9, 45–52. [Google Scholar] [CrossRef]
- Emil, E.; Gurmen, S. Estimation of yttrium oxide microstructural parameters using the Williamson–Hall analysis. Mater. Sci. Technol. 2018, 34, 1549–1557. [Google Scholar] [CrossRef]
- Yeheskel, O.; Tevet, O. Elastic Moduli of Transparent Yttria. Am. Ceram. Soc. 1999, 82, 136–144. [Google Scholar] [CrossRef]
- Badehian, H.A.; Salehi, H.; Ghoohestani, M. First-Principles Study of Elastic, Structural, Electronic, Tehrmody-namical, and Optical Properties of Yttria (Y2O3) Ceramic in Cubic Phase. Am. Ceram. Soc. 2013, 96, 1832–1840. [Google Scholar] [CrossRef]
- Migliori, A.; Sarrao, J. Resonant Ultrasound Spectroscopy: Applications to Physics, Materials Measurements, and Nondestructive Evaluation; Wiley: New York, NY, USA, 1997; ISBN 978-0471123606. [Google Scholar]
- Ledbetter, H. Elastic constants of body-centered-cubic titanium monocrystals. Appl. Phys. 2004, 95, 4642. [Google Scholar] [CrossRef]
- Bartels, R.A.; Schuele, D.E. Pressure derivatives of the elastic constants of NaCl and KCl at 295°K and 195°K. J. Phys. Chem. Solids 1965, 26, 537–549. [Google Scholar] [CrossRef]
- Barsch, G.R.; Chang, Z.P. Adiabatic, Isothermal, and Intermediate Pressure Derivatives of the Elastic Constants for Cubic Symmetry. II. Numerical Results for 25 Materials. Basic Solid States Phys. 1967, 19, 139–151. [Google Scholar] [CrossRef]
- Charles, H. Determination of the Elastic Constants of NaCl to 40 Kilobars by Brillouin Scattering. Master’s Thesis, The Institute of Optics the University of Rochester Rochester, New York, NY, USA, 1975. 14627. [Google Scholar]
- Anderson, O.L.; Masuda, K.; Isaak, D.G. A new thermodynamic approach for high-pressure physics. Phys. Earth Planet. Inter. 1995, 91, 3–16. [Google Scholar] [CrossRef]
- Abdou, S.M.; Moharam, H. Characterization of table salt samples from different origins and ESR detection of the induced effects due to gamma irradiation. J. Phys. Conf. Ser. 2019, 1253, 012036. [Google Scholar] [CrossRef]
- Jury, S.H.; Ernst, R.C. The First Approximate Conditions for the Formation of Liquid Crystals in Solution. J. Phys. Colloid Chem. 1949, 53, 609–624. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Prendiville, P.L.; McDonnell, P.; Chang, V.W. An ultrasonic technique for the measurement of the elastic moduli of human cornea. J. Biomech. 1996, 29, 1633–1636. [Google Scholar] [CrossRef]
- Bray, D.E.; Stanley, R.K. Nondestructive Evaluation: A Tool in Design, Manufacturing and Service; Taylor group: Boca Raton, FL, USA, 1997. [Google Scholar] [CrossRef]
- Figliola, R.S.; Beasley, D.E. Theory and Design for Mechanical Measurements; Wiley: Hoboken, NJ, USA, 2011; ISBN 978-1-119-47565-1. [Google Scholar]
- Adachi, S. Handbook on Physical Properties of Semiconductors; Springer: New York, NY, USA, 2004; ISBN 1402077475. [Google Scholar]
- Bodke, M.; Gawai, U.; Patil, A.; Dole, B. Estimation of accurate size, lattice strain using Williamson-Hall models, SSP and TEM of Al doped ZnO nanocrystals. J. Matériaux Tech. 2018, 106, 602. [Google Scholar] [CrossRef]
- Norris, A.N. Poisson’s ratio in cubic materials. Proc. R. Soc. 2006, 462, 3385–3405. [Google Scholar] [CrossRef]
- Wua, L.X.Z.; Feng, H.F.; Wu, S. High-pressure effect on elastic constants, stacking fault energy and correlation with dislocation properties in MgO and CaO. Eur. Phys. J. B 2012, 85, 226. [Google Scholar] [CrossRef]
- Khan, F.S.; Allen, P.B. Temperature Dependence of the Elastic Constants of p+ Silicon. Phys. Status Solidi 1985, 128, 31–38. [Google Scholar] [CrossRef]
- Güler, E.; Güler, M. Elastic and Mechanical Properties of Cubic Diamond under Pressure. Chin. J. Phys. 2015, 53, 040807-11. [Google Scholar] [CrossRef]


| Elastic Constant (C), (Gpa) | Expt. from Ref (Bartels et al.) [53] | Expt. from Ref (Barsch et al.) [54] | Expt. from Ref (Charles et al.) [55] | Theory. from Ref (Anderson et al.) [56] | This Study |
|---|---|---|---|---|---|
| C11 | 48.99 | 49.00 | 50.00 | 49.50 | 49.11 |
| C12 | 12.57 | 12.60 | 12.70 | 13.20 | 12.26 |
| C44 | 12.72 | 12.70 | 14.40 | 12.79 | 13.73 |
| Elastic Compliances (S), (Gpa) | Expt. by (Bartels et al.) | Expt. by (Barsch et al.) | Expt. by (Charles et al.) | Theory. by (Anderson et al.) | This Study |
|---|---|---|---|---|---|
| S11 | 0.0228 | 0.0228 | 0.0222 | 0.0227 | 0.0226 |
| S12 | −0.0046 | −0.0046 | −0.0045 | −0.0047 | −0.0045 |
| S44 | 0.0786 | 0.0787 | 0.0694 | 0.0781 | 0.0728 |
| NaCl | |||||
|---|---|---|---|---|---|
| Crystal System | a ( ) | c ( | Cell Volume | Crystal Density (g/cm3) | Space Group |
| FCC | 5.640 | 5.640 | 181.511 | 2.141 | Fm-3m |
| Study | Young Modulus (E), (Gpa) in This Method (Intercept Value) |
|---|---|
| Expt. by (Bartels et al.) | 33.57 |
| Expt. by (Barsch et al.) | 33.53 |
| Expt. by (Charles et al.) | 37.24 |
| Theory. by (Anderson et al.) | 33.85 |
| This study | 35.68 |
| NaCl | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2θ (Degree) | Β = FWHM (Degree) | θ (Degree) | cosθ (Degree) | 1/cosθ (Degree) | Ln(1/cosθ) (Degree) | Β = FWHM (Radian) | Ln β (Radian) | 4 sinθ (Degree) | β(Radian).cosθ (Degree) | hkl |
| 27.01 | 0.70 | 13.50 | 0.97 | 1.03093 | 0.03046 | 0.01218 | −4.40796 | 0.92 | 0.01181 | 111 |
| 30.91 | 0.90 | 15.45 | 0.96 | 1.04167 | 0.04082 | 0.01566 | −4.15665 | 1.04 | 0.01503 | 200 |
| 45.08 | 0.89 | 22.54 | 0.92 | 1.08696 | 0.08338 | 0.01549 | −4.16782 | 1.52 | 0.01425 | 220 |
| 53.70 | 0.91 | 26.85 | 0.89 | 1.1236 | 0.11653 | 0.01583 | −4.1456 | 1.80 | 0.01409 | 311 |
| 56.79 | 0.90 | 28.39 | 0.87 | 1.14943 | 0.13926 | 0.01566 | −4.15665 | 1.88 | 0.01362 | 222 |
| 66.98 | 0.80 | 33.49 | 0.83 | 1.20482 | 0.18633 | 0.01392 | −4.27443 | 2.20 | 0.01155 | 400 |
| 72.99 | 0.10 | 36.49 | 0.80 | 1.25 | 0.22314 | 0.00174 | −6.35387 | 2.36 | 0.00139 | 331 |
| 76.05 | 0.70 | 38.02 | 0.78 | 1.28205 | 0.24846 | 0.01218 | −4.40796 | 2.44 | 0.0095 | 420 |
| 83.93 | 0.81 | 41.96 | 0.74 | 1.35135 | 0.30111 | 0.01409 | −4.26201 | 2.64 | 0.01043 | 422 |
| 92.60 | 0.10 | 46.30 | 0.69 | 1.44928 | 0.37106 | 0.00174 | −6.35387 | 2.88 | 0.0012 | 511 |
| Mechanical Properties | |||||
|---|---|---|---|---|---|
| Study | (GPa) | µ a (GPa) | b | B c (GPa) | |
| Expt. by (Bartels et al.) | −0.1757 | −0.00523 | 14.91 | 0.24 | 24.71 |
| Expt. by (Barsch et al.) | −0.1754 | −0.00523 | 14.90 | 0.24 | 24.73 |
| Expt. by (Charles et al.) | −0.1949 | −0.00523 | 16.10 | 0.23 | 25.13 |
| Theory. by (Anderson et al.) | −0.1771 | −0.00523 | 14.93 | 0.25 | 25.30 |
| This study | −0.1867 | −0.00523 | 15.60 | 0.23 | 24.54 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rabiei, M.; Palevicius, A.; Dashti, A.; Nasiri, S.; Monshi, A.; Vilkauskas, A.; Janusas, G. Measurement Modulus of Elasticity Related to the Atomic Density of Planes in Unit Cell of Crystal Lattices. Materials 2020, 13, 4380. https://doi.org/10.3390/ma13194380
Rabiei M, Palevicius A, Dashti A, Nasiri S, Monshi A, Vilkauskas A, Janusas G. Measurement Modulus of Elasticity Related to the Atomic Density of Planes in Unit Cell of Crystal Lattices. Materials. 2020; 13(19):4380. https://doi.org/10.3390/ma13194380
Chicago/Turabian StyleRabiei, Marzieh, Arvydas Palevicius, Amir Dashti, Sohrab Nasiri, Ahmad Monshi, Andrius Vilkauskas, and Giedrius Janusas. 2020. "Measurement Modulus of Elasticity Related to the Atomic Density of Planes in Unit Cell of Crystal Lattices" Materials 13, no. 19: 4380. https://doi.org/10.3390/ma13194380
APA StyleRabiei, M., Palevicius, A., Dashti, A., Nasiri, S., Monshi, A., Vilkauskas, A., & Janusas, G. (2020). Measurement Modulus of Elasticity Related to the Atomic Density of Planes in Unit Cell of Crystal Lattices. Materials, 13(19), 4380. https://doi.org/10.3390/ma13194380







