Procedure for Determining the Uncertainties in the Modeling of Surface Roughness in the Turning of NiTi Alloys Using the Monte Carlo Method
Abstract
:1. Introduction
2. General Assumptions
3. Results of the Measurements and Associated Uncertainties Obtained Experimentally
4. Modeling of Surface Roughness
4.1. Calculations Based on the Mathematical Models
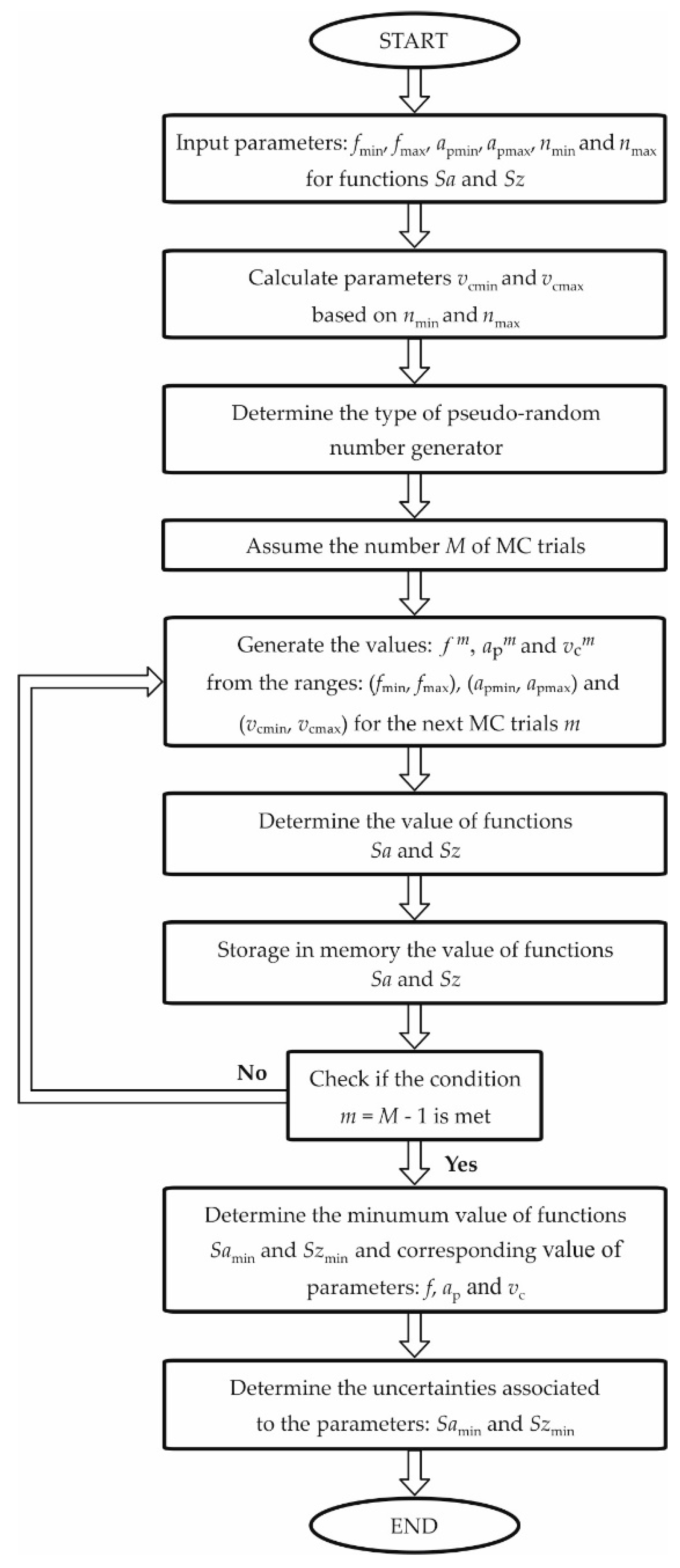
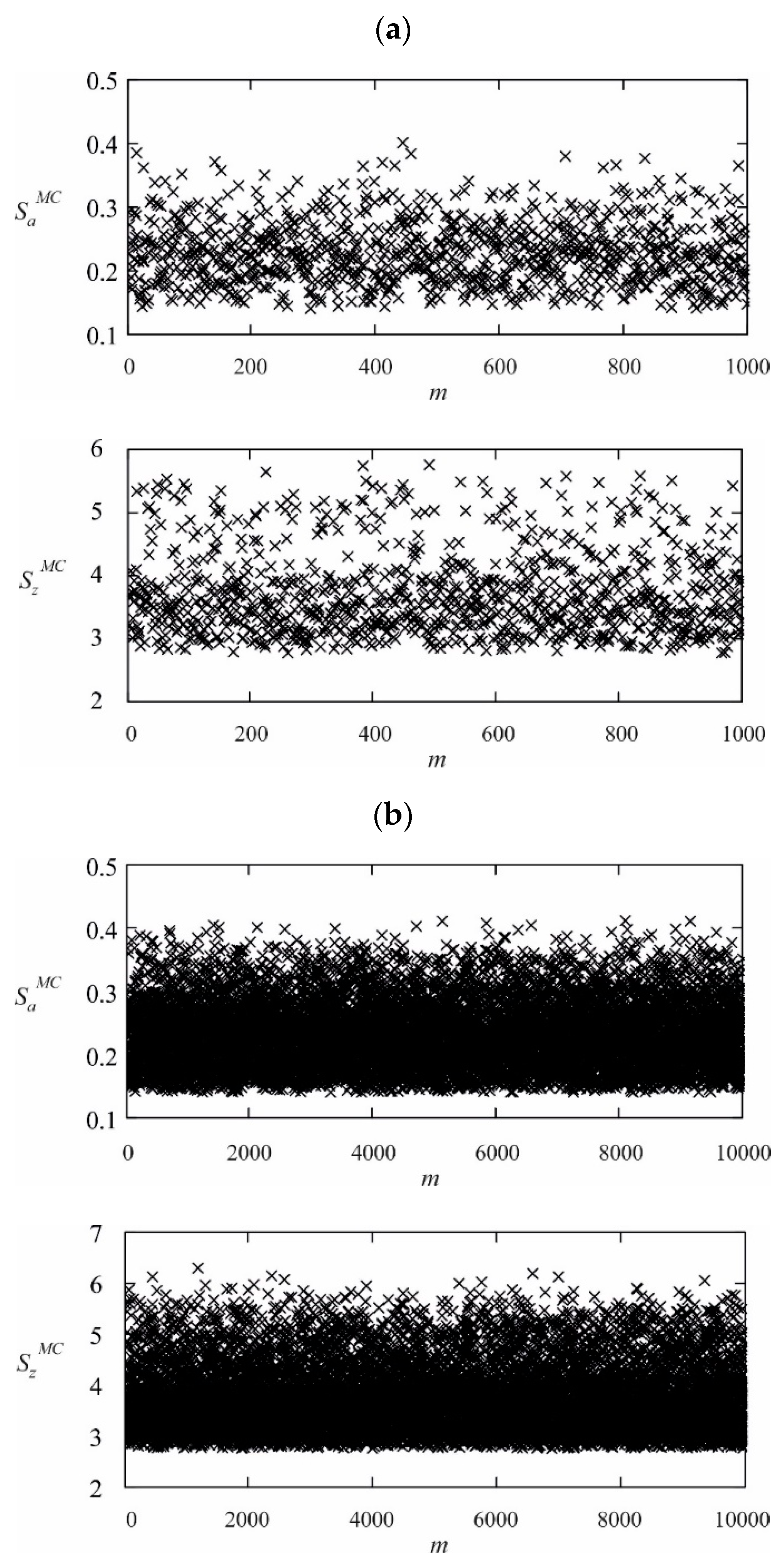
4.2. Modeling Based on the Monte Carlo Method
- Create four vectors that include the integer numbers:where 247,483,123.
- Set the four-element initial vector W from the range of 0 to
- Calculate:where , and denote the particular elements of the vectors , and W, while the functions and denote the modulo from and the largest integer digit no greater than respectively.
- If replace with
- Calculate:
- Finally, return:
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Abbas, A.T.; Sharma, N.; Anwar, S.; Hashmi, F.H.; Jamil, M.; Hegab, H. Towards Optimization of Surface Roughness and Productivity Aspects during High-Speed Machining of Ti–6Al–4V. Materials 2019, 12, 3749. [Google Scholar] [CrossRef] [Green Version]
- Alajmi, M.S.; Almeshal, A.M. Prediction and Optimization of Surface Roughness in a Turning Process Using the ANFIS-QPSO Method. Materials 2020, 13, 2986. [Google Scholar] [CrossRef]
- Benardos, P.G.; Vosniakos, G.C. Predicting Surface Roughness in Machining: A Review. Int. J. Mach. Tools Manuf. 2003, 43, 833–844. [Google Scholar] [CrossRef]
- Romanska-Zapala, A.; Bomberg, M.; Yarbrough, D.W. Buildings with Environmental Quality Management: Part 4: A path to the future NZEB. J. Build. Phys. 2019, 43, 3–21. [Google Scholar] [CrossRef]
- Yarbrough, D.W.; Bomberg, M.; Romanska-Zapala, A. On the Next Generation of Low Energy Buildings. Adv. Build. Energy Res. 2019, 1–8. [Google Scholar] [CrossRef]
- Kowalczyk, M. Application of Taguchi Method to Optimization of Surface Roughness during Precise Turning of NiTi Shape Memory Alloy. Proc. SPIE 2017, 104455, 104455G-1–104455G-10. [Google Scholar]
- Kowalczyk, M. Application of the Monte Carlo Method for the Optimization of Surface Roughness during Precise Turning of NiTi Shape Memory Alloy. Proc. SPIE 2018, 10808, 108084P-1–108084P-9. [Google Scholar]
- Lin, H.C.; Lin, K.M.; Chen, Y.C. A Study on the Machining Characteristics of TiNi Shape Memory Alloys. J. Mater. Process. Technol. 2000, 105, 327–332. [Google Scholar] [CrossRef]
- Matras, A. Research and Optimization of Surface Roughness in Milling of SLM Semi-Finished Parts Manufactured by Using the Different Laser Scanning Speed. Materials 2020, 13, 9. [Google Scholar] [CrossRef] [Green Version]
- Karkalos, N.E.; Galanis, N.I.; Markopoulos, A.P. Surface Roughness Prediction for the Milling of Ti–6Al–4V ELI Alloy with the use of Statistical and Soft Computing Techniques. Measurement 2016, 90, 25–35. [Google Scholar] [CrossRef]
- Chaudhari, R.; Vora, J.J.; Patel, V.; Lacalle, L.N.L.; Parikh, D.M. Surface Analysis of Wire-Electrical-Discharge-Machining-Processed Shape-Memory Alloys. Materials 2020, 13, 530. [Google Scholar] [CrossRef] [Green Version]
- Elahinia, M.H.; Hashemi, M.; Tabesh, M.; Bhaduri, S.B. Manufacturing and Processing of NiTi Implants: A Review. Prog. Mater. Sci. 2012, 57, 911–946. [Google Scholar] [CrossRef]
- Guo, Y.; Klink, A.; Fu, C.; Snyder, J. Machinability and Surface Integrity of Nitinol Shape Memory Alloy. CIRP Ann. Manuf. Technol. 2013, 62, 83–86. [Google Scholar] [CrossRef]
- Kaynak, Y.; Robertson, S.W.; Karacac, H.E.; Jawahir, I.S. Progressive Tool-Wear in Machining of Room-Temperature Austenitic NiTi Alloys: The Influence of Cooling/Lubricating, Melting, and Heat Treatment Conditions. J. Mater. Process. Technol. 2015, 215, 95–104. [Google Scholar] [CrossRef]
- Piquard, R.; Acunto, A.D.; Laheurte, P.; Dudzinski, D. Micro-End Milling of NiTi Biomedical Alloys, Burr Formation and Phase Transformation. Prec. Eng. 2014, 38, 356–364. [Google Scholar] [CrossRef] [Green Version]
- Biermann, D.; Kahleyss, F.; Krebs, E.; Upmeier, T. A Study on Micro-Machining Technology for the Machining of NiTi: Five-Axis Micro-Milling and Micro Deep-Hole Drilling. JMEPEG 2011, 20, 745–751. [Google Scholar] [CrossRef]
- Dash, B.; Das, M.; Mahapatra, T.R.; Mishra, D.A. Concise Review on Machinability of NiTi Shape Memory Alloys. Mat. Tod. Proc. 2019, 18, 5141–5150. [Google Scholar] [CrossRef]
- Kaynak, Y.; Karacac, H.E.; Jawahir, I.S. Surface Integrity Characteristics of NiTi Shape Memory Alloys Resulting from Dry and Cryogenic Machining. Procedia CIRP 2014, 13, 393–398. [Google Scholar] [CrossRef] [Green Version]
- Kaynak, Y.; Karaca, H.E.; Noebe, R.D.; Jawahir, I.S. Tool Wear Analysis in Cryogenic Machining of NiTi Shape Memory Alloys: A Comparison of Tool Wear Performance with Dry and MQL Machining. Wear 2013, 306, 51–63. [Google Scholar] [CrossRef]
- Weinert, K.; Petzoldt, V.; Kotter, D. Turning and Drilling of NiTi Shape Memory Alloys. CIRP Ann. Manuf. Technol. 2004, 53, 65–68. [Google Scholar] [CrossRef]
- Weinert, K.; Petzoldt, V. Machining of NiTi based Shape Memory Alloys. Mater. Sci. Eng. 2004, 378, 180–184. [Google Scholar] [CrossRef]
- Weinert, K.; Petzoldt, V. Machining NiTi Micro-Parts by Micro-Milling. Mater. Sci. Eng. 2008, 481–482, 672–675. [Google Scholar] [CrossRef]
- Wu, S.K.; Lin, H.C.; Chen, C.C. A Study on the Machinability of a Ti 49,6 Ni 50,4 Shape Memory Alloy. Mater. Lett. 1999, 40, 27–32. [Google Scholar] [CrossRef]
- Madić, M.; Radovanović, M. Possibility of using the Monte Carlo Method for Solving Machining Optimization Problems. Mech. Eng. 2014, 12, 27–36. [Google Scholar]
- Nguyen, H.T.; Hsu, Q.C. Surface Roughness Analysis in the Hard Milling of JIS SKD61 Alloy Steel. Appl. Sci. 2016, 6, 172. [Google Scholar] [CrossRef] [Green Version]
- Zagorski, I.; Kłonica, M.; Kulisz, M.; Łoza, K. Effect of the AWJM Method on the Machined Surface Layer of AZ91D Magnesium Alloy and Simulation of Roughness Parameters Using Neural Networks. Materials 2018, 11, 2111. [Google Scholar] [CrossRef] [Green Version]
- Aver’yanova, I.O.; Bogomolov, D.Y.; Poroshin, V.V. ISO 25178 Standard for Three-Dimensional Parametric Assessment of Surface Texture. Russ. Eng. Res. 2017, 37, 513–516. [Google Scholar] [CrossRef]
- Kolahan, F.; Manoochehri, M.; Hosseini, A. Application of Taguchi Method and ANOVA Analysis for Simultaneous Optimization of Machining Parameters and Tool Geometry in Turning. Eng. Tech. 2011, 74, 82–85. [Google Scholar]
- Mia, M.; Dhar, N.R. Prediction of Surface Roughness in Hard Turning Under High Pressure Coolant using Artificial Neural Network. Measurement 2016, 92, 464–474. [Google Scholar] [CrossRef]
- Nalbant, M.; Gokkaya, H.; Toktas, I.; Sur, G. The Experimental Investigation of the Effects of Uncoated, PVD and CVD-Coated Cemented Carbide Inserts and Cutting Parameters on Surface Roughness in CNC Turning and its Prediction using Artificial Neural Networks. Rob. Comp. Integ. Manuf. 2009, 25, 211–223. [Google Scholar] [CrossRef]
- Shankar, N.V.S.; Shankar, H.R.; Kumar, N.P.; Saichandu, K. Process Parameter Optimization for Minimizing Vibrations and Surface Roughness During Turning EN19 Steel Using Coated Carbide Tool. Mater. Today Proc. 2020, 24, 788–797. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, H.; Jia, Z.; Feng, Y.; Liang, S.Y. Floor surface roughness model considering tool vibration in the process of micro-milling. Int. J. Adv. Manuf. Technol. 2018, 94, 4415–4425. [Google Scholar] [CrossRef]
- Feng, Y.; Hsu, F.-C.; Lu, Y.-T.; Lin, Y.-F.; Lin, C.-T.; Lin, C.-F.; Lu, Y.-C.; Lu, X.; Liang, S.Y. Surface roughness prediction in ultrasonic vibration-assisted milling. J. Adv. Mech. Des. Syst. Manuf. 2020, 14, 1–11. [Google Scholar] [CrossRef]
- Feng, Y.; Hung, T.-P.; Lu, Y.-T.; Lin, Y.-F.; Hsu, F.-C.; Lin, C.-F.; Lu, Y.-C.; Lu, X.; Liang, S.Y. Surface roughness modeling in Laser-assisted End Milling of Inconel 718. Mach. Sci. Tech. 2019, 23, 650–668. [Google Scholar] [CrossRef]
- Feng, Y.; Hung, T.-P.; Lu, Y.-T.; Lin, Y.-F.; Hsu, F.-C.; Lin, C.-F.; Lu, Y.-C.; Lu, X.; Liang, S.Y. Inverse Analysis of Inconel 718 Laser-Assisted Milling to Achieve Machined Surface Roughness. Int. J. Prec. Eng. Manuf. 2018, 19, 1611–1618. [Google Scholar] [CrossRef]
- Bhuyan, R.K.; Mohanty, S.; Routara, B.C. RSM and Fuzzy Logic Approaches for Predicting the Surface Roughness during EDM of Al-SiCp MMC. Mater. Today Proc. 2017, 4, 1947–1956. [Google Scholar] [CrossRef]
- Öztürk, S.; Kahraman, M.F. Modeling and Optimization of Machining Parameters during Grinding of Flat Glass using Response Surface Methodology and Probabilistic Uncertainty Analysis based on Monte Carlo Simulation. Measurement 2019, 145, 274–291. [Google Scholar] [CrossRef]
- Prasath, K.M.; Pradheep, T.; Suresh, S. Application of Taguchi and Response Surface Methodology (RSM) in Steel Turning Process to Improve Surface Roughness and Material Removal Rate. Mater. Today Proc. 2018, 5, 24622–24631. [Google Scholar] [CrossRef]
- Chomsamutr, K.; Jongprasithporn, S. Optimization Parameters of Tool Life Model using the Taguchi Approach and Response Surface Methodology. Int. J. Comput. Inf. Sci. 2012, 9, 120–125. [Google Scholar]
- Motorcu, A.R. The Optimization of Machining Parameters Using the Taguchi Method for Surface Roughness of AISI 8660 Hardened Alloy Steel. J. Mech. Eng. Sci. 2010, 56, 391–401. [Google Scholar]
- Kuram, E.; Simsek, B.T.; Ozcelik, B.; Demirbas, E.; Askin, S. Optimization of the Cutting Fluids and Parameters Using Taguchi and ANOVA in Milling. In Proceedings of the World Congress on Engineering, London, UK, 30 June–2 July 2010; pp. 1–5. [Google Scholar]
- Rama, R.S.; Padmanabhan, G. Application of Taguchi Methods and ANOVA in Optimization of Process Parameters for Metal Removal Rate in Electrochemical Machining of Al/5%SiC composites. Int. J. Eng. Res. Appl. 2012, 2, 192–197. [Google Scholar]
- Kahraman, M.F.; Öztürk, S. Experimental Study of Newly Structural Design Grinding Wheel Considering Response Surface Optimization and Monte Carlo Simulation. Measurement 2019, 147, 36–48. [Google Scholar] [CrossRef]
- Lu, X.; Wang, F.; Xue, L.; Feng, Y.; Liang, S.Y. Investigation of material removal rate and surface roughness using multi-objective optimization for micro-milling of inconel 718. Ind. Lub. Tribo. 2019, 71, 787–794. [Google Scholar] [CrossRef]
- Lu, X.; Wang, X.; Sun, J.; Zhang, H.; Feng, Y. The Influence Factors and Prediction of Curve Surface Roughness in Micro-Milling Nickel-Based Superalloy. In Proceedings of the ASME 2018 13th International Manufacturing Science and Engineering Conference, College Station, TX, USA, 18–22 June 2018. [Google Scholar]
- Kubisa, S.; Moskowicz, S. A Study on Transitivity of Monte Carlo based Evaluation of the Confidence Interval for a Measurement Result. Pomiary Kontrola Autom. 2007, 53, 7–10. [Google Scholar]
- BIPM; IEC; IFCC; ILAC; ISO; IUPAC; IUPAP; OIML. Evaluation of Measurement Data—Supplement 1 to the ‘Guide to the Expression of Uncertainty in Measurement’—Propagation of Distributions Using a Monte Carlo Method; Organisation for Standardization: Geneva, Switzerland, 2008. [Google Scholar]
- Tomczyk, K. Influence of Monte Carlo Generations Applied for Modelling of Measuring Instruments on Maximum Distance Error. Trans. Inst. Meas. Control 2019, 41, 74–84. [Google Scholar] [CrossRef]
- Tomczyk, K. Monte Carlo-based Procedure for Determining the Maximum Energy at the Output of Accelerometers. Energies 2020, 13, 1552. [Google Scholar] [CrossRef] [Green Version]
- Palenčár, R.; Sopkuliak, P.; Palenčár, J.; Ďuriš, S.; Suroviak, E.; Halaj, M. Application of Monte Carlo Method for Evaluation of Uncertainties of ITS-90 by Standard Platinum Resistance Thermometer. Meas. Sci. Rev. 2017, 17, 108–116. [Google Scholar] [CrossRef] [Green Version]
- Guimarães Couto, P.R.; Carreteiro Damasceno, J.; Pinheiro de Oliveira, S. Monte Carlo Simulations applied to Uncertainty in Measurement. In Theory and Applications of Monte Carlo Simulations; Chan, V.W.K., Ed.; Intech Open: London, UK, 2013; pp. 27–51. [Google Scholar]
- Harris, P.M.; Cox, M.G. On a Monte Carlo Method for Measurement Uncertainty Evaluation and its Implementation. Metrologia 2014, 51, 176–182. [Google Scholar] [CrossRef]
- Sanjeevi, R.; Nagaraja, R.; Krishnan, B.R. Vision-based Surface Roughness Accuracy Prediction in the CNC Milling Process (Al6061) using ANN. Mater. Today Proc. 2020, in press. [Google Scholar] [CrossRef]
- Singh, N.K.; Singh, Y.; Kumar, S.; Sharma, A. Predictive Analysis of Surface Roughness in EDM using Semi-Empirical, ANN and ANFIS Techniques: A Comparative Study. Mater. Today Proc. 2020, 25, 735–741. [Google Scholar] [CrossRef]
- Dudzik, M.; Mielnik, R.; Wrobel, Z. Preliminary Analysis of the Effectiveness of the use of Artificial Neural Networks for Modelling Time-Voltage and Time-Current Signals of the Combination Wave Generator. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion (Speedam), Amalfi, Italy, 20–22 June 2018; pp. 1095–1100. [Google Scholar]
- Dudzik, M.; Stręk, A.M. ANN Architecture Specifications for Modelling of Open-Cell Aluminum under Compression. Math. Probl. Eng. 2020, 2020, 2834317. [Google Scholar] [CrossRef] [Green Version]
- Gopan, V.; Wins, L.D.; Surendran, A. Integrated ANN-GA Approach for Predictive Modeling And Optimization of Grinding Parameters With Surface Roughness As the Response. Mater. Today Proc. 2018, 5, 12133–12141. [Google Scholar] [CrossRef]
- Barzani, M.M.; Zalnezhad, E.; Sarhan, A.A.D.; Farahany, S.; Ramesh, S. Fuzzy Logic based Model for Predicting Surface Roughness of Machined Al–Si–Cu–Fe die Casting Alloy using Different Additives-turning. Measurement 2015, 61, 150–161. [Google Scholar] [CrossRef]
- Naresh, C.; Bose, P.S.C.; Rao, C.S.P. ANFIS based Predictive Model for Wire EDM Responses involving Material Removal Rate and Surface Roughness of Nitinol Alloy. Mater. Today Proc. 2020. [Google Scholar] [CrossRef]
- Tseng, T.L.B.; Konada, U.; Kwon, Y.J. A Novel Approach to Predict Surface Roughness in Machining Operations using Fuzzy Set Theory. J. Comp. Design. Eng. 2016, 3, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Zuperl, U.; Cus, F. Surface Roughness Fuzzy Inference System within the Control Simulation of end Milling. Prec. Eng. 2016, 43, 530–543. [Google Scholar] [CrossRef]
- Barrios, J.M.; Romero, P.E. Decision Tree Methods for Predicting Surface Roughness in Fused Deposition Modeling Parts. Materials 2019, 12, 2574. [Google Scholar] [CrossRef] [Green Version]
- BIPM; IEC; IFCC; ILAC; ISO; IUPAC; IUPAP; OIML. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement; Working Group 1 of the Joint Committee for Guides in Metrology (JCGM/WG 1): Paris, France, 2008. [Google Scholar]
- Wichmann, B.A.; Hill, I.D. Generating Good Pseudo-Random Numbers. Comput. Stat. Data Anal. 2006, 51, 1614–1622. [Google Scholar] [CrossRef]
| no. | n [rev/min] | |||
|---|---|---|---|---|
| 1 | 0.038 | 0.030 | 20 | 1498 |
| 2 | 0.080 | 30 | 1997 | |
| 3 | 0.130 | 50 | 2496 | |
| 4 | 0.058 | 0.030 | 20 | 1997 |
| 5 | 0.080 | 30 | 2496 | |
| 6 | 0.130 | 50 | 1498 | |
| 7 | 0.077 | 0.030 | 20 | 2496 |
| 8 | 0.080 | 30 | 1498 | |
| 9 | 0.130 | 50 | 1997 |
| Ms | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| n | ||||||||||
| Factor Sa [μm] | ||||||||||
| 1 | 0.454 | 0.179 | 0.288 | 0.244 | 0.333 | 0.427 | 0.261 | 0.430 | 0.407 | |
| 2 | 0.404 | 0.159 | 0.278 | 0.194 | 0.363 | 0.377 | 0.351 | 0.380 | 0.387 | |
| 3 | 0.304 | 0.039 | 0.148 | 0.094 | 0.383 | 0.277 | 0.231 | 0.280 | 0.287 | |
| 4 | 0.284 | 0.049 | 0.128 | 0.074 | 0.223 | 0.257 | 0.231 | 0.260 | 0.307 | |
| 5 | 0.424 | 0.169 | 0.288 | 0.214 | 0.323 | 0.397 | 0.351 | 0.400 | 0.407 | |
| 6 | 0.414 | 0.159 | 0.258 | 0.204 | 0.313 | 0.387 | 0.361 | 0.390 | 0.387 | |
| 7 | 0.344 | 0.089 | 0.188 | 0.134 | 0.293 | 0.317 | 0.271 | 0.320 | 0.307 | |
| 8 | 0.444 | 0.189 | 0.288 | 0.234 | 0.313 | 0.417 | 0.371 | 0.420 | 0.427 | |
| 9 | 0.314 | 0.059 | 0.138 | 0.104 | 0.273 | 0.287 | 0.261 | 0.290 | 0.317 | |
| 10 | 0.354 | 0.099 | 0.178 | 0.144 | 0.213 | 0.327 | 0.321 | 0.330 | 0.337 | |
| 0.374 | 0.119 | 0.218 | 0.164 | 0.303 | 0.347 | 0.301 | 0.350 | 0.357 | ||
| Factor Sz [μm] | ||||||||||
| 1 | 6.921 | 3.390 | 4.267 | 3.183 | 4.390 | 5.338 | 4.940 | 5.203 | 4.087 | |
| 2 | 6.845 | 3.312 | 4.186 | 3.105 | 4.341 | 5.197 | 4.861 | 5.081 | 4.005 | |
| 3 | 6.950 | 3.419 | 4.313 | 3.212 | 4.432 | 5.296 | 4.979 | 5.261 | 4.119 | |
| 4 | 6.864 | 3.346 | 4.214 | 3.129 | 4.327 | 5.219 | 4.882 | 5.140 | 4.036 | |
| 5 | 6.936 | 3.371 | 4.276 | 3.197 | 4.301 | 5.321 | 5.021 | 5.212 | 4.105 | |
| 6 | 6.831 | 3.340 | 4.209 | 3.083 | 4.305 | 5.181 | 4.856 | 5.114 | 4.004 | |
| 7 | 6.915 | 3.387 | 4.261 | 3.171 | 4.360 | 5.348 | 4.937 | 5.223 | 4.042 | |
| 8 | 6.963 | 3.392 | 4.312 | 3.226 | 4.412 | 5.189 | 4.867 | 5.243 | 4.137 | |
| 9 | 6.970 | 3.402 | 4.321 | 3.225 | 4.392 | 5.317 | 5.005 | 5.260 | 4.148 | |
| 10 | 6.833 | 3.275 | 4.184 | 3.112 | 4.261 | 5.158 | 4.894 | 5.081 | 4.024 | |
| 6.903 | 3.363 | 4.254 | 3.164 | 4.352 | 5.256 | 4.924 | 5.179 | 4.071 | ||
| no. | Mean | Uncertainties Based on the Measurement Data | ||
|---|---|---|---|---|
| 1 | 0.374 | 6.903 | 0.008 | 0.006 |
| 2 | 0.119 | 3.363 | 0.006 | 0.004 |
| 3 | 0.218 | 4.254 | 0.010 | 0.006 |
| 4 | 0.164 | 3.164 | 0.008 | 0.006 |
| 5 | 0.303 | 4.352 | 0.006 | 0.006 |
| 6 | 0.347 | 5.256 | 0.008 | 0.012 |
| 7 | 0.301 | 4.924 | 0.008 | 0.008 |
| 8 | 0.350 | 5.179 | 0.008 | 0.012 |
| 9 | 0.357 | 4.071 | 0.006 | 0.006 |
| no. | Values of the Functions | Uncertainties Based on the Mathematical Models | ||||
|---|---|---|---|---|---|---|
| [μm] | ||||||
| 1 | 0.311 | 6.381 | 0.018 | 0.036 | 0.239 | 0.478 |
| 2 | 0.145 | 3.446 | 0.003 | 0.006 | 0.074 | 0.148 |
| 3 | 0.257 | 4.660 | 0.017 | 0.034 | 0.150 | 0.300 |
| 4 | 0.202 | 3.558 | 0.012 | 0.024 | 0.232 | 0.464 |
| 5 | 0.241 | 3.848 | 0.004 | 0.008 | 0.051 | 0.102 |
| 6 | 0.373 | 5.326 | 0.018 | 0.036 | 0.139 | 0.278 |
| 7 | 0.328 | 5.04 | 0.013 | 0.026 | 0.238 | 0.476 |
| 8 | 0.387 | 5.568 | 0.005 | 0.010 | 0.072 | 0.144 |
| 9 | 0.294 | 3.557 | 0.018 | 0.036 | 0.147 | 0.294 |
| no. | Parameters/Factors | Results | |||
|---|---|---|---|---|---|
| 1 | [no.] | ||||
| 2 | 0.141 | 0.141 | 0.140 | 0.140 | |
| 3 | [no.] | 294 | 8144 | 60915 | 692749 |
| 4 | 0.039 | 0.039 | 0.038 | 0.038 | |
| 5 | 0.070 | 0.075 | 0.071 | 0.070 | |
| 6 | n | 2063 | 2123 | 2102 | 2101 |
| 7 | 0.230 | 0.230 | 0.230 | 0.230 | |
| 8 | 0.002 | 0.003 | 0.003 | 0.003 | |
| 9 | 2.780 | 2.777 | 2.770 | 2.770 | |
| 10 | [no.] | 966 | 6276 | 87578 | 179181 |
| 11 | 0.057 | 0.060 | 0.059 | 0.059 | |
| 12 | 0.092 | 0.092 | 0.092 | 0.093 | |
| 13 | n | 2061 | 2065 | 2098 | 2095 |
| 14 | 3.712 | 3.725 | 3.733 | 3.730 | |
| 15 | 0.425 | 0.417 | 0.425 | 0.426 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kowalczyk, M.; Tomczyk, K. Procedure for Determining the Uncertainties in the Modeling of Surface Roughness in the Turning of NiTi Alloys Using the Monte Carlo Method. Materials 2020, 13, 4338. https://doi.org/10.3390/ma13194338
Kowalczyk M, Tomczyk K. Procedure for Determining the Uncertainties in the Modeling of Surface Roughness in the Turning of NiTi Alloys Using the Monte Carlo Method. Materials. 2020; 13(19):4338. https://doi.org/10.3390/ma13194338
Chicago/Turabian StyleKowalczyk, Małgorzata, and Krzysztof Tomczyk. 2020. "Procedure for Determining the Uncertainties in the Modeling of Surface Roughness in the Turning of NiTi Alloys Using the Monte Carlo Method" Materials 13, no. 19: 4338. https://doi.org/10.3390/ma13194338
APA StyleKowalczyk, M., & Tomczyk, K. (2020). Procedure for Determining the Uncertainties in the Modeling of Surface Roughness in the Turning of NiTi Alloys Using the Monte Carlo Method. Materials, 13(19), 4338. https://doi.org/10.3390/ma13194338






