Conditions of the Presence of Bimodal Amplitude Distribution of Two-Process Surfaces
Abstract
1. Introduction
2. Theoretical Considerations
3. The Analysis of Generated Surfaces
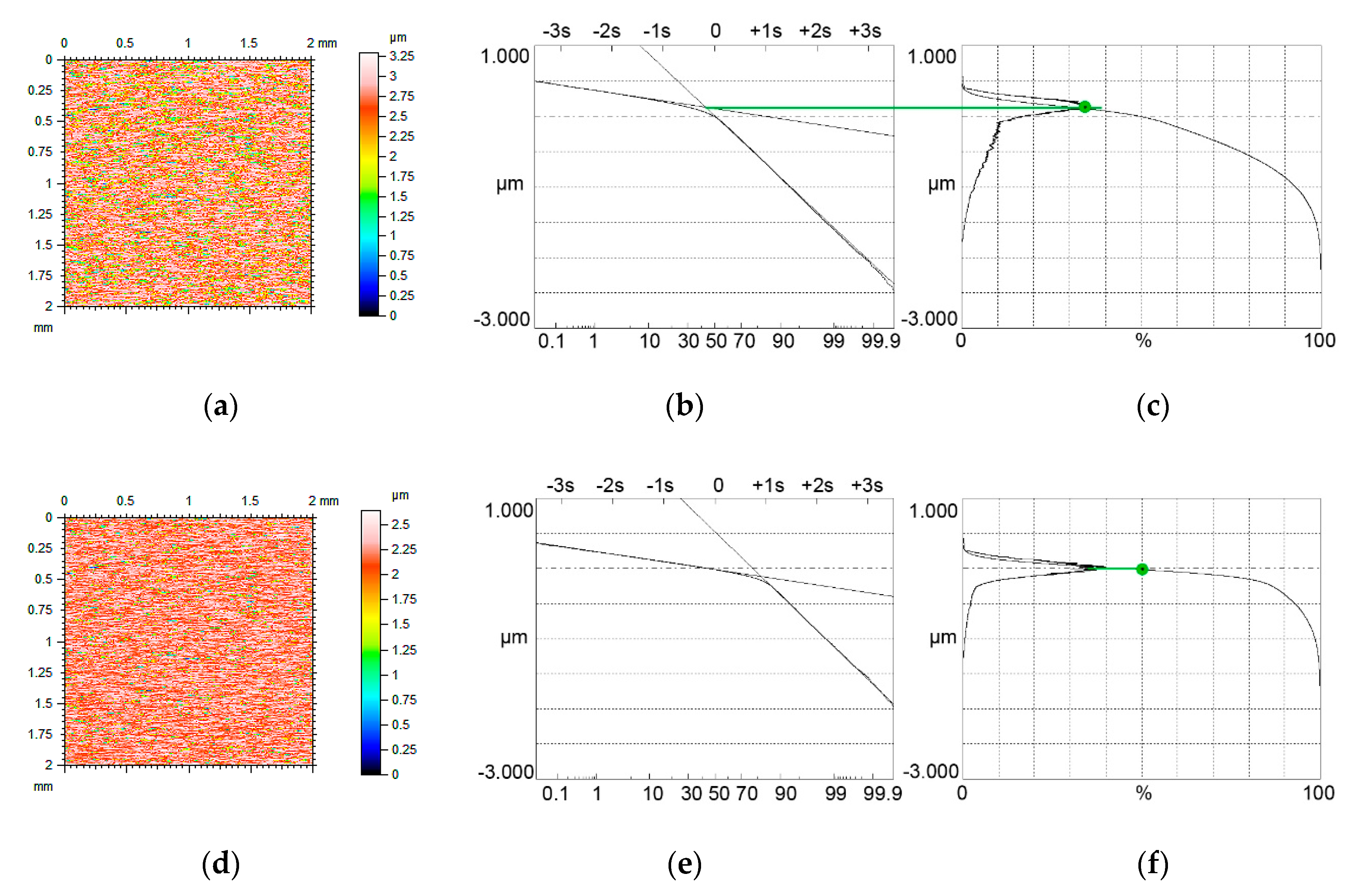
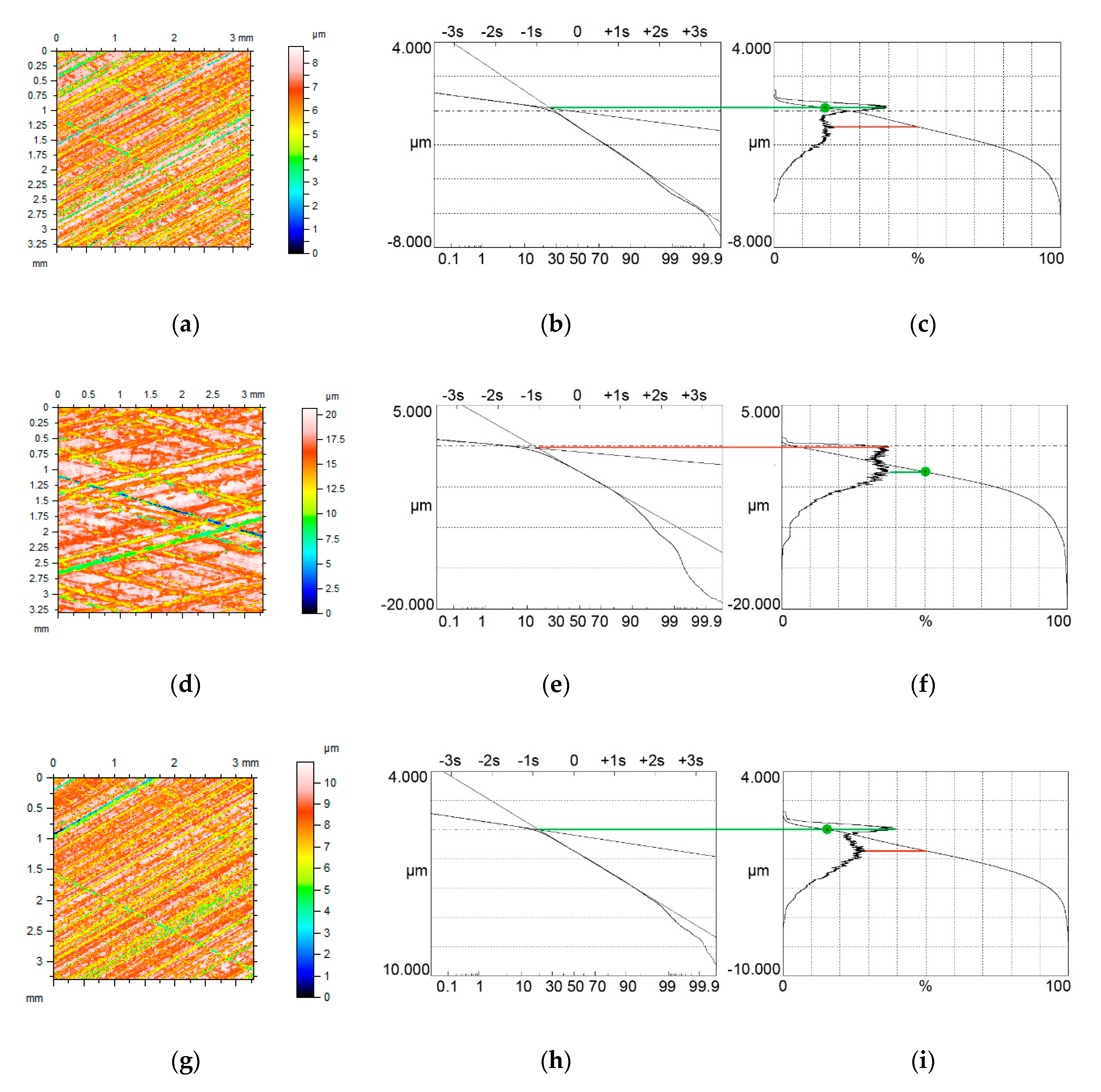
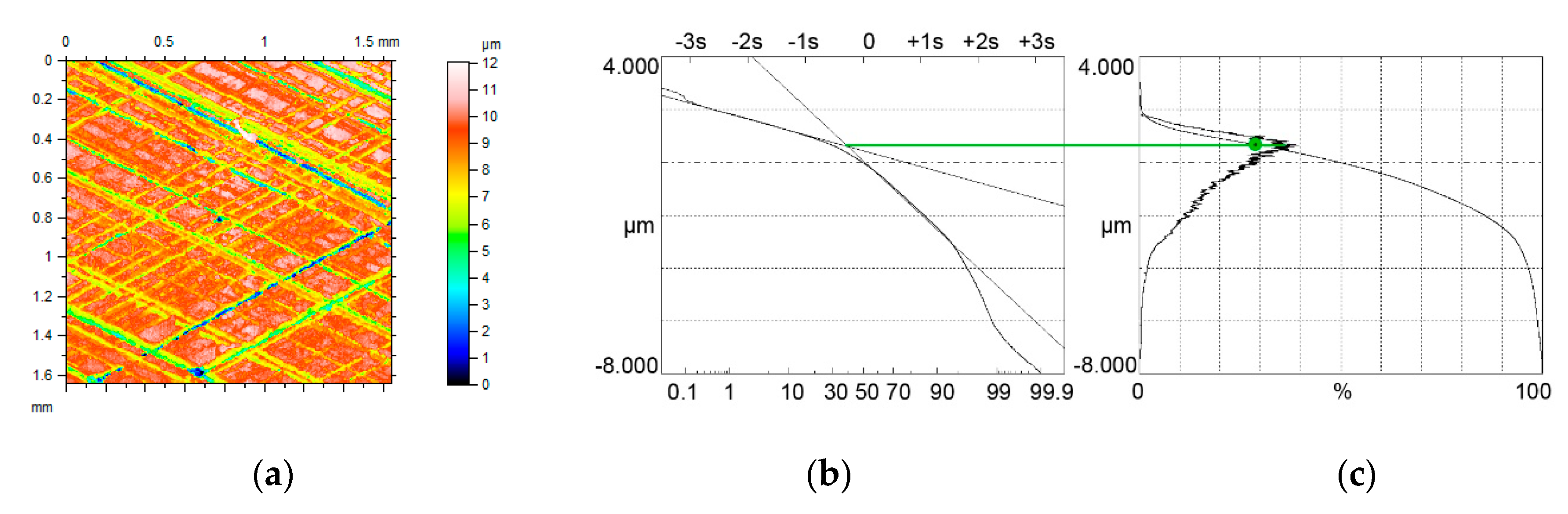
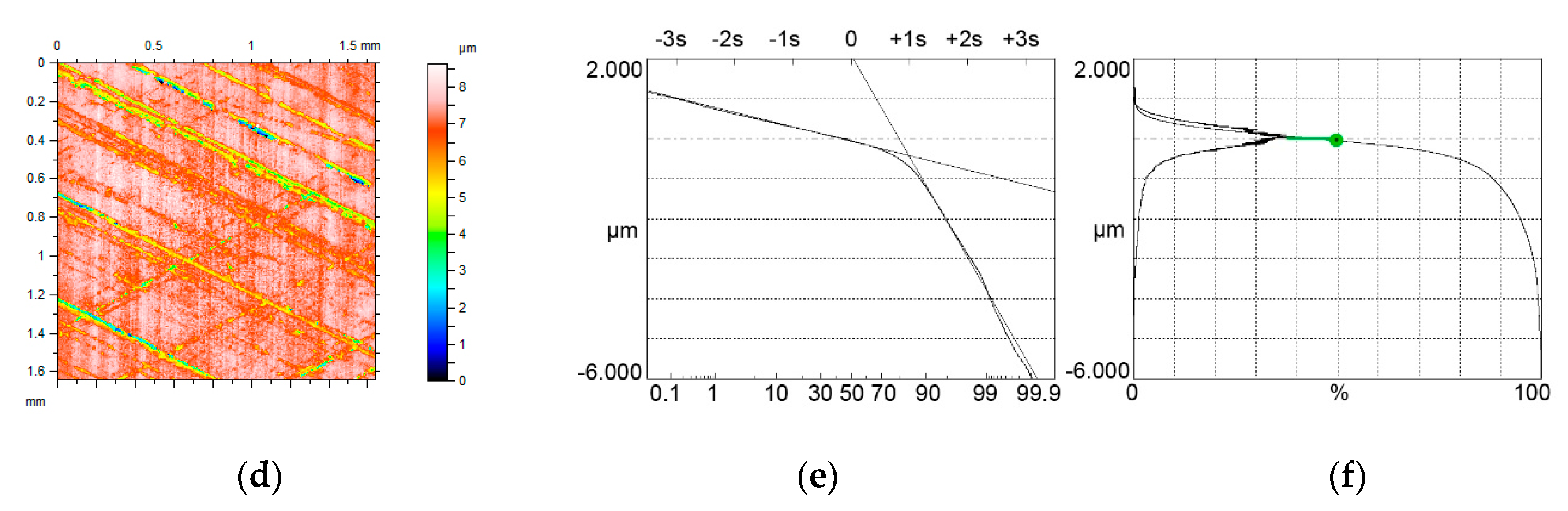
4. The Analysis of Measured Surfaces
5. Conclusions
- Limiting conditions of bimodal height distribution of two-process surface topography were developed. They depend on the ratio of the standard deviations of the valley and plateau parts Svq/Spq and on the material ratio at the transition between plateau and valley portions Smq. Based on these conditions, bimodal and unimodal height probability distributions were correctly discriminated for modeled and measured surfaces.
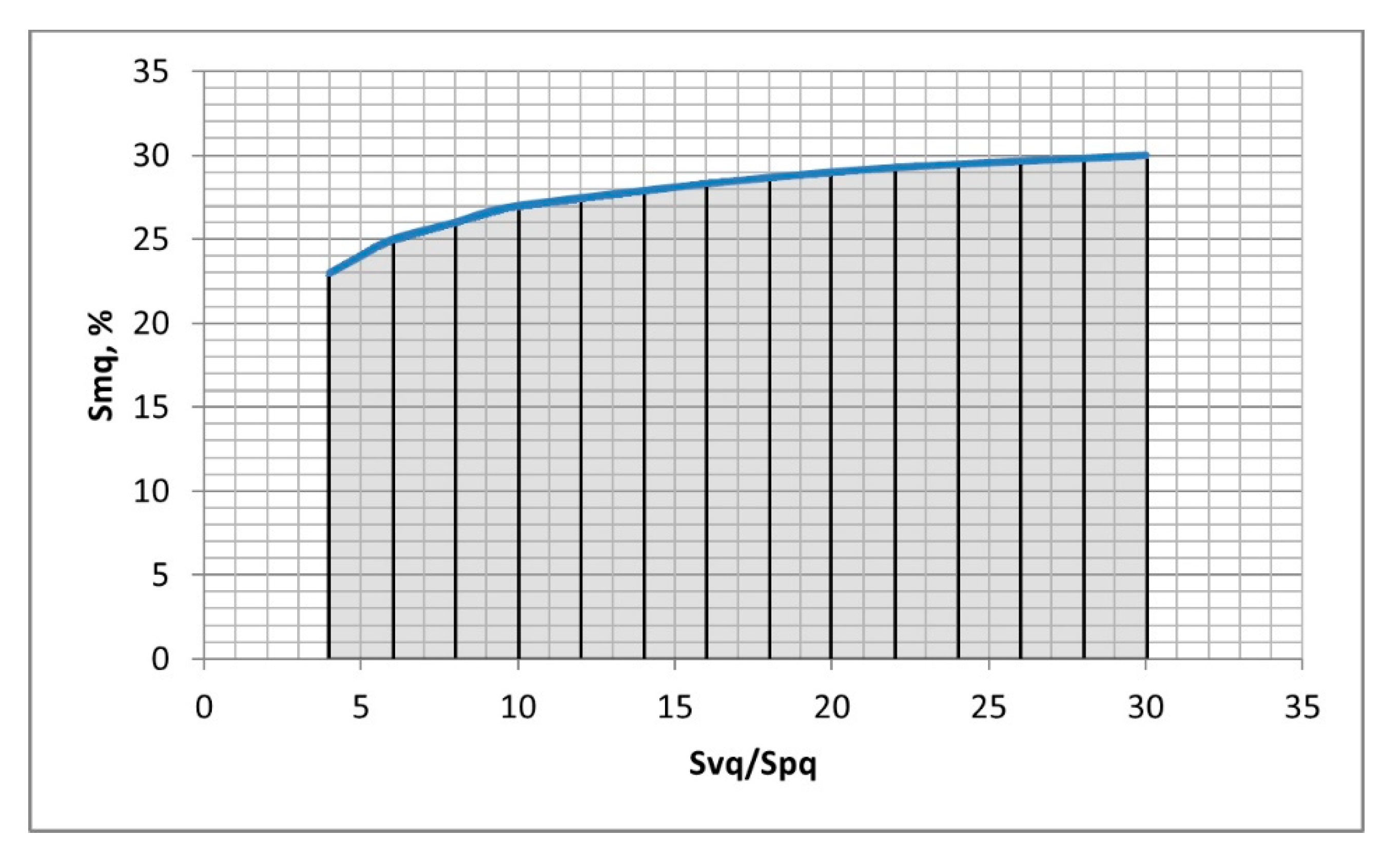
- The bimodal ratio increased when the Svq/Spq ratio increased. Typically, the upper peak is the major mode. However, for low values of the Smq parameter and for low Svq/Spq ratio, the lower peak, which corresponds to the material ratio of 50%, can be the major mode.
- When the Smq parameter is not lower than 50%, unimodal amplitude distribution exists. The mode and the smallest slope of the material ratio curve appear at the material ratio of 50%.
- For unimodal height distribution and the value of the Spq parameter smaller than 50%, the mode corresponds to the Smq material ratio.
- The results are functionally important because of the high tribological significance of the material ratio curve. In particular, the position of its smallest slope deserves attention.
Author Contributions
Funding
Conflicts of Interest
References
- Whitehouse, D.J. Handbook of Surface Metrology; Institute of Physics Publishing: Bristol, UK; Philadelphia, PA, USA, 1994. [Google Scholar]
- Thomas, T.R. Computer simulation of wear. Wear 1972, 22, 84–90. [Google Scholar] [CrossRef]
- Stout, K.J.; Spedding, T.A. The characterization of the combustion engine bore. Wear 1982, 83, 311–326. [Google Scholar] [CrossRef]
- Stout, K.J.; Davis, E.J. Surface topography of cylinder bores—The relationship between manufacture, characterization and function. Wear 1984, 95, 111–125. [Google Scholar] [CrossRef]
- Stout, K.J.; Davis, E.J.; Sullivan, P.J. Atlas of Machined Surfaces; Chapman & Hall: London, UK, 1990. [Google Scholar]
- Thomas, T.R. Rough Surfaces; Imperial College Press: London, UK, 1999. [Google Scholar]
- Grabon, W.; Pawlus, P.; Wos, S.; Koszela, W.; Wieczorowski, M. Evolutions of cylinder liner surface texture and tribological performance of piston ring-liner assembly. Tribol. Int. 2018, 127, 545–556. [Google Scholar] [CrossRef]
- Campbell, J.C. Cylinder bore surface roughness in internal combustion engines: Its appreciation and control. Wear 1972, 19, 163–168. [Google Scholar] [CrossRef]
- Jeng, Y.R. Impact of plateaued surfaces on tribological performance. Tribol. Trans. 1996, 39, 354–361. [Google Scholar] [CrossRef]
- Dzierwa, A.; Pawlus, P.; Zelasko, W.; Reizer, R. The study of the tribological properties of one-process and two-process textures after vapour blasting and lapping using pin-on disc tests. Key Eng. Mater. 2013, 527, 217–222. [Google Scholar] [CrossRef]
- Buj Corral, I.; Calvet, J.V.; Salcedo, M.C. Use of roughness probability parameters to quantify the material removed in plateau-honing. Int. J. Mach. Tools Manuf. 2010, 50, 621–629. [Google Scholar] [CrossRef]
- Rosen, B.G.; Anderberg, C.; Ohlsson, R. Parameter correlation study of cylinder liner roughness for production and quality control. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2008, 222, 1475–1487. [Google Scholar] [CrossRef]
- Hu, S.; Huang, W.; Brunetiere, N.; Song, Z.; Liu, X.; Wang, Y. Stratified effect of continuous bi-Gaussian rough surface on lubrication and asperity contact. Tribol. Int. 2016, 104, 328–341. [Google Scholar] [CrossRef]
- Hu, S.; Huang, W.; Shi, X.; Peng, Z.; Liu, X.; Wang, Y. Bi-Gaussian stratified effect of rough surfaces on acoustic emission under a dry sliding friction. Tribol. Int. 2018, 119, 308–315. [Google Scholar] [CrossRef]
- Hu, S.; Huang, W.; Shi, X.; Peng, Z.; Liu, X. Mechanism of bi-Gaussian surface topographies on generating acoustic emissions under a sliding friction. Tribol. Int. 2019, 131, 64–72. [Google Scholar] [CrossRef]
- Pawlus, P.; Zelasko, W.; Reizer, R.; Wieczorowski, M. Calculation of plasticity index of two-process surfaces. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2017, 231, 572–582. [Google Scholar] [CrossRef]
- Pawlus, P.; Zelasko, W.; Dzierwa, A. The effect of isotropic one-process and two-process surface textures on contact of flat surfaces. Materials 2019, 12, 4092. [Google Scholar] [CrossRef]
- Pawlus, P.; Reizer, R.; Wieczorowski, M.; Zelasko, W. The effect of sampling interval on the predictions of an asperity contact model of two-process surfaces. Bull. Pol. Acad. Sci. Tech. Sci. 2017, 65, 391–398. [Google Scholar] [CrossRef]
- Pawlus, P.; Reizer, R.; Wieczorowski, M. Characterization of the shape of height distribution of two-process profile. Measurement 2020, 153, 107387. [Google Scholar] [CrossRef]
- Bohm, H.J. Parameters for evaluating the wearing behaviour of surfaces. Int. J. Mach. Tools Manuf. 1992, 32, 109–113. [Google Scholar] [CrossRef]
- Mummery, L. Surface Texture Analysis—The Handbook; Hommelwerke GmbH: Muehlhausen, Germany, 1990. [Google Scholar]
- Schneider, U.; Steckroth, A.; Rau, N.; Hubner, G. An approach to the evaluation of surface profiles by separating them into functionally different parts. Surf. Topogr. 1988, 1, 343–355. [Google Scholar]
- Nielsen, H.S. New approaches to surface roughness evaluation of special surfaces. Precis. Eng. 1988, 10, 209–213. [Google Scholar] [CrossRef]
- Malburg, M.C.; Raja, J.; Whitehouse, D.J. Characterization of surface texture generated by plateau–honing process. CIRP Ann. 1993, 42, 637–640. [Google Scholar] [CrossRef]
- Sannareddy, H.; Raja, J.; Chen, K. Characterization of surface texture generated by multi–process manufacture. In Proceedings of the 7th International Conference On Metrology and Properties of Engineering Surfaces, Gothenburg, Sweden, 26–29 June 1998; pp. 111–117. [Google Scholar]
- Whitehouse, D.J. Assessment of surface finish profiles produced by multiprocess manufacture. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 1985, 199, 263–270. [Google Scholar] [CrossRef]
- Zipin, R.B. Analysis of the Rk surface roughness parameter proposals. Precis. Eng. 1990, 12, 106–108. [Google Scholar] [CrossRef]
- Pawlus, P.; Reizer, R.; Wieczorowski, M.; Krolczyk, G. Material ratio curve as information on the state of surface topography—A review. Precis. Eng. 2020, in press. [Google Scholar] [CrossRef]
- Pawlus, P. Simulation of stratified surface topography. Wear 2008, 264, 457–463. [Google Scholar] [CrossRef]
- Peng, W.; Bhushan, B. Modelling of surfaces with a bimodal roughness distribution. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2000, 214, 459–470. [Google Scholar] [CrossRef]
- Hu, S.; Brunetiere, N.; Huang, W.; Liu, X.; Wang, Y. Bi-Gaussian surface identification and reconstruction with revised autocorrelation functions. Tribol. Int. 2017, 110, 185–194. [Google Scholar] [CrossRef]
- Hu, S.; Brunetiere, N.; Huang, W.; Liu, X.; Wang, Y. Continuous separating method for characterizing and reconstructing bi-Gaussian stratified surfaces. Tribol. Int. 2016, 102, 454–462. [Google Scholar] [CrossRef]
- Perez-Rafols, F.; Almqvist, A. Generating randomly rough surfaces with given height probability distribution and power spectrum. Tribol. Int. 2019, 131, 591–604. [Google Scholar] [CrossRef]
- Wu, J.J. Simulation of rough surfaces with FFT. Tribol. Int. 2000, 33, 47–58. [Google Scholar] [CrossRef]
- Zhang, C.; Mapes, B.E.; Soden, B.J. Bimodality in tropical water vapour. Q. J. R. Meteorol. Soc. 2003, 129, 2847–2866. [Google Scholar] [CrossRef]
- Schilling, M.F.; Watkins, A.E.; Watkins, W. Is Human Height Bimodal? Am. Stat. 2002, 56, 223–229. [Google Scholar] [CrossRef]
- Eisenberger, I. Genesis of Bimodal Distributions. Technometrics 1964, 6, 357–363. [Google Scholar] [CrossRef]
- Holzmann, H.; Vollmer, S. A likelihood ratio test for bimodality in two-component mixtures with application to regional income distribution in the EU. AStA Adv. Stat. Anal. 2008, 92, 57–69. [Google Scholar] [CrossRef]
- Sitek, G. The modes of a mixture of two normal distributions. Silesian J. Pure Appl. Math. 2016, 6, 59–67. [Google Scholar]
- Behboodian, J. On the modes of a mixture of two normal distributions. Technometrics 1970, 12, 131–139. [Google Scholar] [CrossRef]
- Grabon, W.; Pawlus, P.; Wos, S.; Koszela, W.; Wieczorowski, M. Effects of honed cylinder liner surface texture on tribological properties of piston ring-liner assembly in short time tests. Tribol. Int. 2017, 113, 137–148. [Google Scholar] [CrossRef]
- Grabon, W.; Pawlus, P.; Wos, S.; Koszela, W.; Wieczorowski, M. Effects of cylinder liner surface topography on friction and wear of liner-ring system at low temperature. Tribol. Int. 2018, 121, 148–160. [Google Scholar] [CrossRef]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pawlus, P.; Reizer, R.; Wieczorowski, M. Conditions of the Presence of Bimodal Amplitude Distribution of Two-Process Surfaces. Materials 2020, 13, 4037. https://doi.org/10.3390/ma13184037
Pawlus P, Reizer R, Wieczorowski M. Conditions of the Presence of Bimodal Amplitude Distribution of Two-Process Surfaces. Materials. 2020; 13(18):4037. https://doi.org/10.3390/ma13184037
Chicago/Turabian StylePawlus, Pawel, Rafal Reizer, and Michal Wieczorowski. 2020. "Conditions of the Presence of Bimodal Amplitude Distribution of Two-Process Surfaces" Materials 13, no. 18: 4037. https://doi.org/10.3390/ma13184037
APA StylePawlus, P., Reizer, R., & Wieczorowski, M. (2020). Conditions of the Presence of Bimodal Amplitude Distribution of Two-Process Surfaces. Materials, 13(18), 4037. https://doi.org/10.3390/ma13184037






