Abstract
The blast resistance of a sandwich-walled cylinder/ring comprising two metal face-sheets and a graded metal foam core, subjected to internal air blast loading, is investigated. Analytical models are developed for the deformation of the sandwich cylinder with positive and negative gradient cores under internal blast loading. The deformation process is divided into three distinct phases, namely the fluid–structure interaction phase, core-crushing phase, and outer face-sheet deformation phase. Finite element modeling is performed using the Voronoi material model. The proposed analytical models are verified through finite element analysis, and reasonable agreement is observed between the analytical predictions and finite element results. The sandwich structures with high energy absorption capacity or low maximum radial deflection are satisfied for the protecting purpose of impact/blast resistance requirements. Typical deformation processes are classified and analyzed; the effects of explosive charge, face-sheet thickness, and core gradient on the structural response are also examined. The results indicate that both the deformation modes and the structural response of the cylinders are sensitive to the blast charge and core configuration. It is concluded that energy absorption capacity and maximum radial deflection are two conflicting goals for achieving high impact/blast resistance capability. An in-depth understanding of the behavior in sandwich-walled cylinders under blast impulse and the influence of the core configuration helps realize the advantages and disadvantages of using graded foam materials in sandwich structures and can provide a guideline for structural design.
1. Introduction
Sandwich structures generally consist of two metal face-sheets and a foam core [1,2]. In the past three decades, sandwich structures were widely used in aerospace, marine, and other novel impact/blast resistant structures because of their excellent performance of ultra-light, high stiffness and strength to weight ratios, and effective energy absorption (EA) capacity under impact loading [3,4,5]. Dynamic responses of such composite sandwich structures subjected to impact/blast loading have been extensively studied [6,7,8]. Recently, graded cellular materials, in which the mechanical properties vary gradually or layer-by-layer, were always utilized as cores in sandwich composites [9,10,11]. Sandwich structures with graded core configurations have elicited increasing attention recently because they possess better blast resistance than sandwich structures with monolithic cores [12,13,14]. A graded foam core in a sandwich structure shows great potential to be effective for structural design to improve the overall impact/blast resistance. Graded foam has been receiving increasing attention recently because of its remarkable blast resistance, and its properties can be easily designed and controlled [15,16,17]. Shen et al. [18] found that only one densification wave front appears in cellular materials with a positive gradient, whereas two densification wave fronts appear in cellular materials with a negative gradient. Liu et al. [19] developed theoretical solutions for cellular materials with different density distributions, such as linear, quadratic, and square root. Zhang et al. [20] analyzed the dynamic response of layered cellular materials under impulse loading by using the Voronoi material model. Liang et al. [21,22] investigated the blast behaviors of 1D foam materials with different distributions and developed corresponding theoretical models.
Taking into consideration the damages produced by blasts, blast protection devices need to be improved, because traditional blast-resistant devices shows low efficiency and high cost [23]. Composite sandwich structures have been developed for high blast resistance performance because of their potential for foam core absorbing energy and limited force transfer to protected objects compared with equivalent monolithic counterparts [24]. Sandwich-walled tubes have been proposed as a novel container for temporary storage or transportation of explosive substances [25]. However, investigations on the dynamic response of sandwich-walled cylinders under internal blast loading are precious limited due to the complicated loading behavior caused by fluid–structure interaction and multiple reflections of blast pressure [26]. Shen et al. [27] reported the dynamic behaviors of short sandwich-wall cylinders under internal blast loading and found that the composite structures offer better blast resistance compared with traditional tubes. Karagiozova et al. [28] developed a theoretical solution for the deformation of sandwich-walled cylinders to investigate core densification and face-sheet behavior. Recently, Liang et al. [29] conducted internal blast experiments and simulations on sandwich tubes. Results confirmed that the maximum deformation of sandwich cylinders is sensitive to core, internal face-sheet, and charge mass.
Although several investigations on the dynamic behaviors of sandwich cylinders/rings were reported in the literature, no appropriate analytical model for the deformation of sandwich cylinders/rings with graded cores subjected to internal blast loading has been proposed [30]. A more in-depth understanding of the dynamic response of sandwich cylinders/rings together with the influence of core gradient would assist designers in using graded foam materials in sandwich structures. This paper presents the results of an investigation on the blast response of metal sandwich cylinders/rings with typical double-layered foam cores under internal blast loading. Theoretical and numerical studies were performed to obtain insight into the factors governing the face-sheet deformation and core crushing. In addition, the Voronoi material model is used to simulate the dynamic behaviors of sandwich-walled cylinders under blast loading. The theoretical predictions are compared with finite element (FE) results, and validation of the analytical model of sandwich-walled cylinders is demonstrated. The blast responses of sandwich-walled cylinders are investigated to clarify the effects of core gradient, face-sheet thickness, and charge loading.
2. Analytical Model
A theoretical analysis is conducted to provide an estimate of the dynamic response and EA of sandwich cylinders/rings under internal air blast. Such an estimate is expected to provide further insights into the design of graded foam-cored sandwich-walled rings with better blast resistance than monolithic foam-cored rings. Typically, in double-layered cores, the gradient is positive when the soft core is placed inside [31]. In Figure 1, the structure of the cross-section of a cylinder is presented.
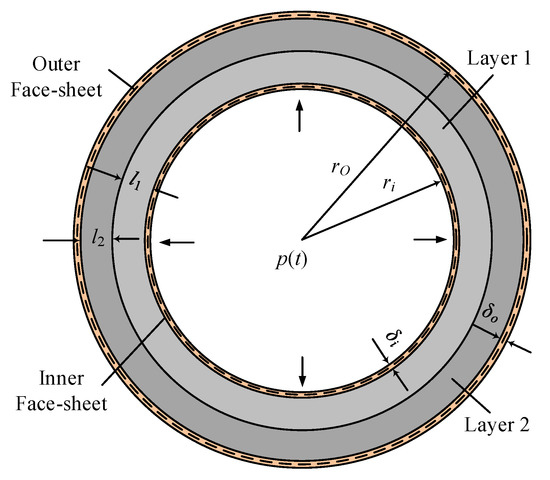
Figure 1.
Schematic of the cross-section of a sandwich cylinder/ring.
The inner and outer face-sheets are made of metal shells with a thickness of ti and to and radius of ri and ro. The face-sheets are assumed a rigid–ideally plastic material with a yield strength of σY and density of ρf. The core is made of double-layer foam with a thickness of l1 and l2. The densities and corresponding plateau stresses of layers 1 and 2 are ρ1 and ρ2, and σ1 and σ2, respectively. The core gradient is positive when ρ1 < ρ2. Cores with positive and negative gradients (ρ1 < ρ2 and ρ1 > ρ2) are considered in this study.
Dynamic crushing of the foam core has been proposed in the literature based on 1D “shock wave” theory. Shock wave is considered a shock-like densification wave with a fast-propagating thin crushing layer called wave front, which separates the compacted and undeformed regions. Reid and Peng [32] studied shock wave theory to doctrinaire the densification enhancement of a wood material, and they proposed the simplified rigid–perfectly plastic–locking (R-PP-L) material model. The crushing stress σd of the shock front is considered a function of propagation velocity v through the conservation of mass and momentum at the shock front and by idealizing a cellular material as the R-PP-L model [33]:
where σ0 and εd are the plateau stress and densification of the foam material, respectively.
The size of the foam cell is smaller than its core thickness. Similar to what has been conducted in previous studies, the foam core is considered as a homogeneous material with a strictly concave stress–strain curve in this study, and the topology of foam materials is disregarded. The R-PP-L material model and the shock wave theory are used to analyze blast resistance situations of foam core crushing. The core displays constant compressive stress in the transverse direction of the face-sheet with no lateral expansion up to a particular densification strain. Neither the axial nor longitudinal tensile strengths of the foam core are regarded. In general, impact loading slightly influences the densification strain of the core [34]. However, the densification strain could be approximately regarded as a constant value because blast loading is extremely high [31]. Face-sheet thickness is also assumed a constant value in the expansion process because its thickness is lower than that of the core.
The dynamic response of face-sheets and the process of compaction wave that propagates through the foam core are combined to propose analytical solutions. The blast response of a sandwich-walled ring is modeled as a three-phase analysis frame (Figure 2). First, in the fluid–structure interaction (FSI) phase, the blast impulse accelerates the inner face-sheet to an initial velocity of v0. In the core-crushing phase, the inner face-sheet with the initial velocity impacts the core. In the outer face-sheet deformation phase, the outer face-sheet begins to deform after the core compacts fully.
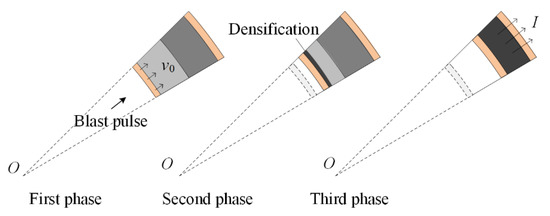
Figure 2.
Three response phases for the blast response of a sandwich-walled cylinder.
2.1. First Phase: FSI
The actual loading on this face-sheet due to an air blast is the reflected over-pressure because FSI affects the air blast and the inner face-sheet. The over-pressure of this incident blast wave, pi(t), impinges on the structure, leading to a reflected over-pressure p(t). The pressure of the air blast decays exponentially. Generally, it can be approximated as an equivalent triangular pressure pulse, and the pressure could be expressed as
where p0 is the peak reflected over-pressure of the air blast loading, τ0 is the air blast loading duration, and t is the time.
The initial velocity of the inner face-sheet can be obtained on the basis of the conservation of momentum as the following:
where p(t) is the pressure history of the loading, and ρf and δi are the density and thickness of the inner face-sheet, respectively. The initial velocity of core crushing is obtained by ignoring the slight crushing process of the core in the first phase and combining Equations (2) and (3) as follows:
2.2. Second Phase: Core Crushing
The governing equations of the positive- and negative-gradient double-layer foam core-crushing processes of the foam-cored ring are deduced. Different from the dynamic behavior of the homogeneous foam-cored sandwich-walled ring, the deformation process of the double-layer foam-cored sandwich-walled ring is related to the core gradient.
2.2.1. Positive Gradient Core Situation
For a positive foam core, a low-density layer is placed inside (ρ1 < ρ2 and σ1 < σ2). The reaction stress at the interface between two layers is the plateau stress of the low-density foam core, σ1. As the reaction stress is still below the plateau stress of layer 2, the hard layer remains undeformed during the time before layer 1 is completely crushed. Consequently, a densification wave initially occurs in layer 1. Then, the compaction wave propagates to the outer layer after layer 1 compacts completely. As shown in Figure 3, the response process is divided into two stages when the core is a positive gradient.
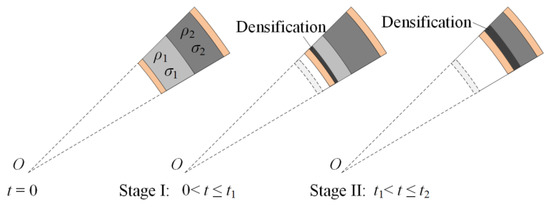
Figure 3.
Response process of a cylinder with a positive-gradient core.
In stage I, the compaction wave prorogates until the front of the crushing wave arrives at the interface. The displacements of the inner faces of the two layers in stages I and II are and and and , respectively. The velocities of the inner faces of the two layers in stages I and II are and and and , respectively. The superscript and subscript refer to stage and layer numbers, respectively. Face-sheets are perfectly rigid–plastic, and maintain a constant flow stress value of σY. Figure 4 shows that the circumferential stress causes radial stress in the inner face-sheet as follows:
where ri is the radius of the inner face-sheet.
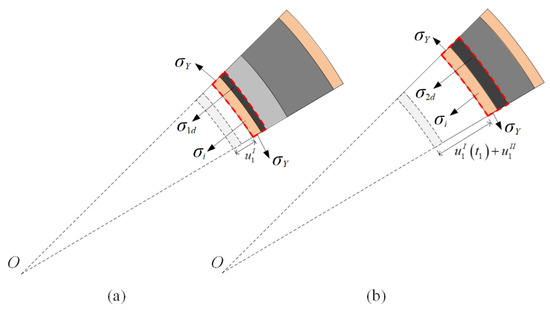
Figure 4.
Stress analysis for a cylinder with a positive-gradient core. (a) Stage I, and (b) stage II.
Figure 4a shows that the velocity of the crushed part is equal to the inner face-sheet in stage I. The motion of the inner face-sheet is given as
where σ1d is the crushing stress on the wave front in layer 1, and ε1d is the densification strain of layer 1. By combining Equations (1), (5), and (6), the velocity of the inner face-sheet and compacted part in stage I, , is given as
where ρ1 is the foam density of layer 1.
The initial conditions are
Assume that layer 1 does not deform further in stage II. The compaction part and inner face-sheet are considered rigid bodies to compress layer 2. In Figure 4b, the equations of motion in stage II are given as follows:
where σ2d is the crushing stress on the wave front in layer 2, and ε2d is the densification strain of layer 2. Moreover, the initial conditions could be given as
2.2.2. Negative-Gradient Core Situation
For a negative core, the low-density layer is placed outside (ρ1 > ρ2 and σ1 > σ2). The reaction stress at the interface is equal to the plateau stress of the inner layer, σ1, which exceeds the plateau stress of the soft layer, σ2. Young’s modulus approaches infinity when the core is regarded as the R-PP-L material model. Therefore, the critical velocity of the foam material is approximate to zero. Thus, the face near the blast end crushes first. Subsequently, a new densification wave begins at layer 2 when the stress wave reaches the interface between the two layers. Two compaction waves propagate from the two inner faces of the two layers to their outer faces in the same direction. As shown in Figure 5, the crushing process could be divided into two stages.
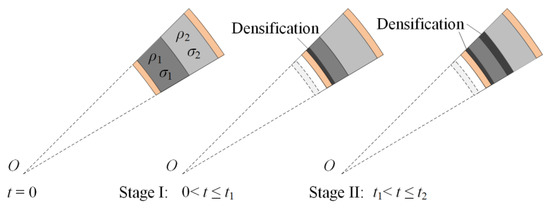
Figure 5.
Response process of the core with a negative gradient.
In stage I, double compaction waves simultaneously occur in layers 1 and 2 in the same direction when 0 < t ≤ t1. The densification part masses and in stage I are derived as
where ρ2 is the foam density of layer 2.
As shown in Figure 6a, the momentum conservation of the undeformed part of layer 1 and the compaction part of layer 2 gives
where is the compaction wave velocity of layer 2 in stage I.
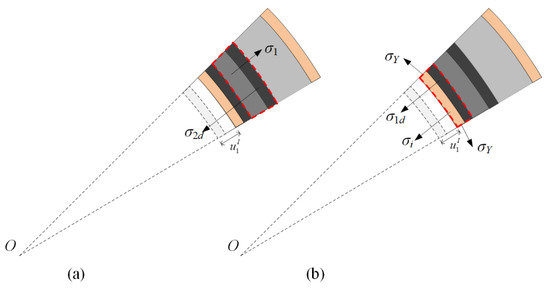
Figure 6.
Stress analysis for a cylinder with a negative-gradient core in stage I. (a) The undeformed part of layer 1 and the compaction part of layer 2, and (b) the compacted part of layer 1.
Substituting Equations (1), (14), and (15) into Equation (16) yields
The initial conditions are
The compaction wave velocity in layer 1 relative to that in layer 2 is . According to the stress analysis in Figure 6b, the velocity of the inner face-sheet relative to that of the compacted part in stage I, , is given as the motion equation as follows:
The initial conditions are
Stage II starts at t = t1 when either layer entirely compacts, and finishes at t = t2 when the other layer complete crushes. It is indicated that this stage exists in two scenarios.
Scenario 1: Layer 1 is fully compacted earlier than layer 2. The compaction part mass of layer 2, , in stage I is derived as
Figure 7a shows that the conservation of momentum with respect to the inner face-sheet, the compaction part of layer 1, and the compaction part of layer 2 leads to
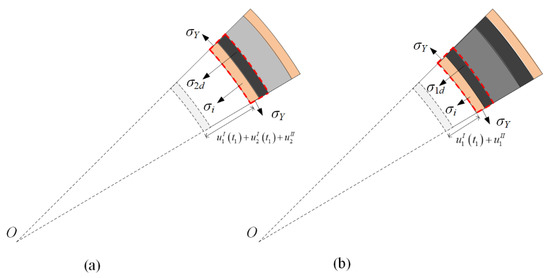
Figure 7.
Stress analysis for a cylinder with a negative-gradient core in stage II. (a) Scenario 1, and (b) Scenario 2.
The initial conditions are
Scenario 2: Layer 2 absolutely densifies firstly. The densification part mass of layer 1, , in stage I is derived as
Figure 7b shows that the momentum conservation of the inner face-sheet and the compacted part of layer 1 leads to
The initial conditions are
2.3. Third Phase: Outer Face-Sheet Deformation
As the core compacts fully, the outer face-sheet starts to deform. Figure 8 shows that the deformation process can be divided into two stages. The velocity of the outer face-sheet initially increases due to the compression of the inner face-sheet and the core. Then, the inner face-sheet separates from the core when the velocities of the inner and outer face-sheets are equal. The velocity of the outer face-sheet begins to decrease.
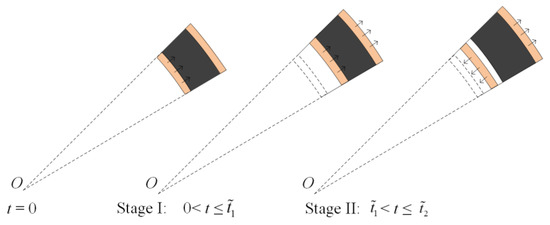
Figure 8.
Deformation process of the third phase.
In stage I, the core, together with the inner face-sheet, compresses the outer face-sheet. Figure 9a shows the stress analysis for the inner face-sheet and the core. The equation of motion for the inner face-sheet is given as follows:
where is the stress between the core and outer face-sheet. The velocities of the inner face-sheet in stages I and II are and , respectively. The displacements of the inner face-sheet in stages I and II are and , respectively.
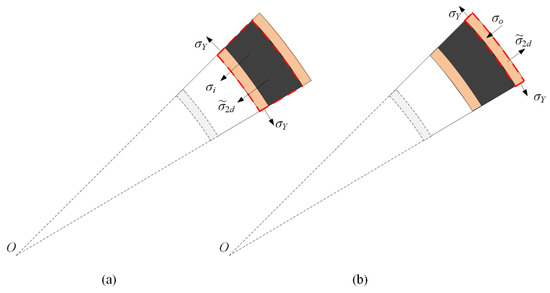
Figure 9.
Stress analysis for the sandwich-walled ring in stage I. (a) The inner face-sheet and the core, and (b) the outer face-sheet.
The initial conditions are
Figure 9b shows the stress analysis for the outer face-sheet. The equations of motion for the outer face-sheet are
where the velocities of the inner face-sheet in stages I and II are and , respectively. The displacements of the outer face-sheet in stages I and II are and , respectively.
The initial conditions are
In stage II, the velocity of the outer face-sheet reaches the maximum and then begins to decrease. The inner face-sheet separates from the core, and the outer face-sheet and the core move together. Figure 10a depicts the stress analysis for the inner face-sheet in stage II. The equations of motion for the inner face-sheet are given as follows:
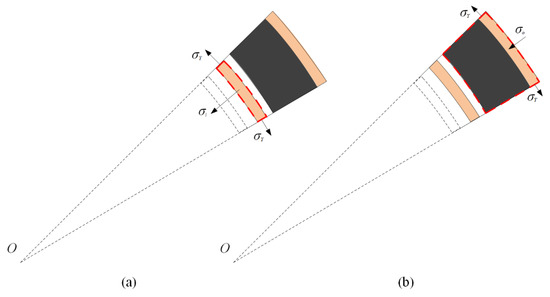
Figure 10.
Stress analysis for the sandwich-walled ring in stage II. (a) The inner face-sheet, and (b) the outer face-sheet.
The initial conditions are
Figure 10b shows the stress analysis for the outer face-sheet in stage II. The equations of motion for the outer face-sheet are
The initial conditions are
3. FE Model
3.1. Foam Core Modeling
An analytical model cannot account for natural variations in microstructure that are typical in most foam materials. FE simulations are conducted to verify and provide a detailed description of the blast response of foam-cored sandwich-wall rings. The Voronoi technique is a smart tool used to simulate the deformation process and dynamic behavior of foam materials and sandwich structures. In this study, the foam core is generated using the Voronoi algorithm by the MATLAB 2015a software. Numerical simulation is performed using the ABAQUS/Explicit software. The cells nucleate simultaneously in a given area A and grow at an isotropic rate. The irregular degree of foam cell is given as follows:
where δmin and δ0 are the minimum distance between any two nuclei and between adjacent nuclei, respectively. The process of cell generation can be divided into four stages (Figure 11). First, N nuclei, which are constrained to be larger than δmin, are randomly generated in a given area A. The distance between adjacent nuclei is given as
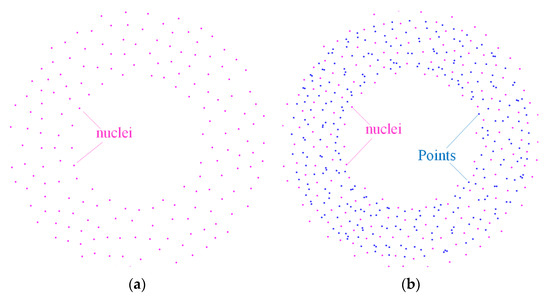
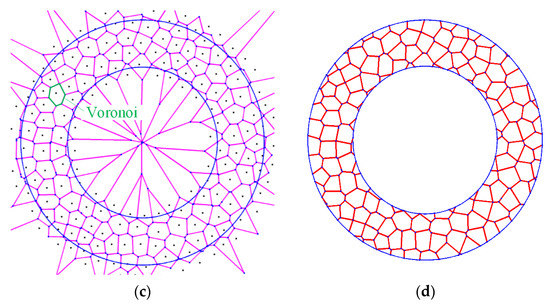
Figure 11.
Generated nuclei and constructed Voronoi structure. (a) nuclei in given spaces; (b) Delaunaytriangulation and Voronoi diagram; (c) Voronoi structure. (d) foam core achieved.
Second, points are generated by copying the nuclei to the surrounding region. Then, points close to the nucleus are interconnected, and Delaunay triangulation and Voronoi diagrams are generated. Finally, the Voronoi part is achieved when the area out of the area A is deleted. The top and bottom edges in the normal direction of crushing direction were free. The displacement boundary was mainly used in problems related to plastic deformation. The corresponding nodes on the opposite edge of the mesh have the same expansion in the normal direction. Self-contact was defined for all the cell surfaces.
3.2. Material Model
The detonation products of charges are described by the Jones–Wilkins–Lee (JWL) model. In the model, the pressure distribution is relative with relative volume and internal energy:
where p is the product pressure, V is the relative volume, A, B, R1, R2, and ω are charge constants; and E0 is the initial internal energy. The JWL constants of the charge are listed in Table 1. The FE model of the core is constructed by the Voronoi technique. The base material is aluminum. The cell wall of the core is assumed an elastic–perfectly plastic model. The base material parameters are listed in Table 2.

Table 1.
JWL model parameters of the charge [30].

Table 2.
Base material parameters [35].
3.3. Numerical Model
Numerical simulations are performed with the ABAQUS 6.9/Explicit software. Two typical FE models of sandwich-walled rings are shown in Figure 12. A double-layer core with a positive or negative gradient is sandwiched between face-sheets. The core and face-sheets are modeled using the S4R shell element type. Self-contact is also specified between the face-sheets that may contact other cell faces during crushing. General contact is used for parts. The friction coefficient between the core and face-sheets is 0.02 [36]. A good agreement was achieved between the results of the FE model and corresponding experiments [29].
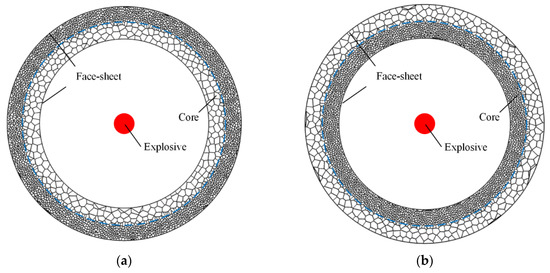
Figure 12.
Finite element (FE) models [29]. (a) Positive gradient core, and (b) negative gradient core.
4. Comparisons of Theoretical and Numerical Results
Comparisons of the FE results for the deformation of the maximum radial deflection (MRD) and analytical predictions based on axisymmetric deformation of a sandwich ring are performed to verify the theoretical solutions. The deformation processes of rings with positive and negative cores are presented in Figure 13 and Figure 14. When the gradient is positive, only one shock wave propagates from the inside to the outside during the complete crushing process. The phenomenon coincides with the analytical prediction. When the gradient is negative, double shock fronts propagate outside in the same direction. However, this phenomenon is different from the continuous-density foam that has double shock fronts with opposite directions [37].
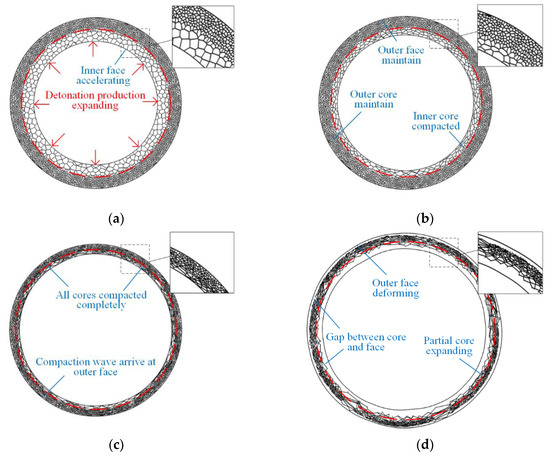
Figure 13.
FE results of sandwich rings with positive gradient core. (a) First phase, (b) second phase compaction wave, (c) second phase outer core compacted, and (d) third phase.
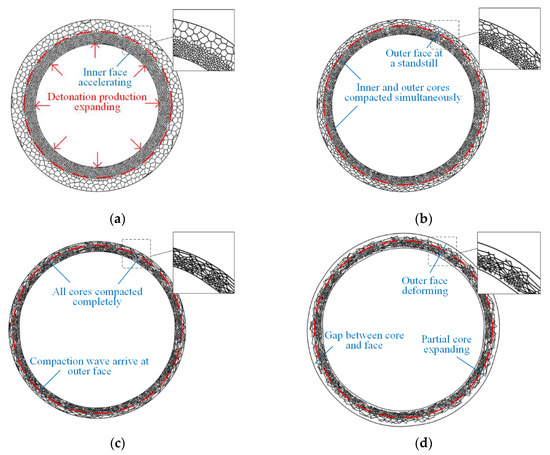
Figure 14.
FE results of sandwich rings with negative gradient core. (a) First phase, (b) second phase, (c) end of second phase, and (d) third phase.
The velocity histories of face-sheets are shown in Figure 15. The theoretical solution results in a larger MRD than the FE results. The theoretical predictions can generally describe the essential features of the three phases obtained by the numerical results. A difference is observed between the numerical simulation and theoretical prediction for the inner face-sheet during the first phase because the interaction between the inner face-sheet and core is neglected in this phase. As shown in Figure 16, reasonable agreement is observed between the theoretical predictions and simulation results for the face-sheets. The theoretical predictions can give a good prediction for the FE results, however, the sudden change between phases in the theoretical model does not coincide with the gradual transitions in the FE results. This deviation is also related to the R-PP-L model used in the theoretical model. The reflected over-pressure history at the location where a possible maximum reflected over-pressure history p(t) occurs can be measured because the air blast does not have a uniform distribution along the axial direction of the ring. The theoretical results are obtained by using the maximum reflected over-pressure history p(t). Using theoretical results as a criterion for the design of a structure with limited MRD is conservative.
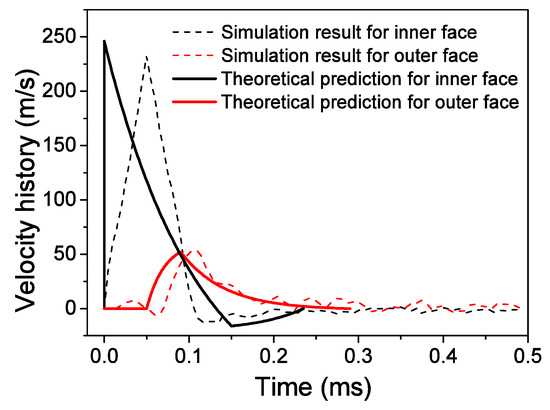
Figure 15.
Comparison of face-sheet velocities between theoretical predictions and FE results.
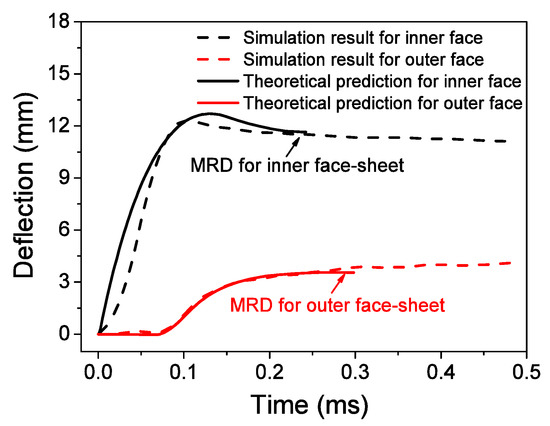
Figure 16.
Comparison of maximum radial deflections (MRDs) of face-sheets between theoretical predictions and FE results.
5. Discussion
Determining the plastic dissipation of the core and the MRD of face-sheets for sandwich-walled rings is of practical interest. The sandwich-walled ring with high EA and low MRD is a good choice to maximize the blast resistance of the sandwich-walled ring at a given mass subjected to internal blast loading.
Given that the elastic deformation energy of the core is negligible in comparison with the plastic deformation energy, the plastic dissipation of the layered foam under a quasi-static state can be calculated as follows:
The plastic dissipation under blast loading can be obtained as
where ξ is the Lagrangian coordinate of the shock front.
By substituting Equations (1) and (47) into Equation (48), the above equation can be rewritten as
Based on Equations (31) and (38), the MRD of the inner face-sheet is given as
Based on Equations (35) and (41), the MRD of the outer face-sheet is given as
As shown in Figure 17a, the EA capacity of the sandwich-walled ring with a double-layer core increases with the internal explosive mass. The relationship between EA and explosive mass can be explained as follows. According to Equation (3), a high internal explosive mass leads to a high initial velocity in Phase I, which leads to high crushing stress based on Equation (1). Considering Equation (49), the EA capacity increases with velocity-dependent dynamic enhancement and increasing crushed displacement. Figure 17b shows the effect of explosive mass on the MRDs of the inner and outer face-sheets. The MRDs are small for the sandwich-walled rings under low explosive loading due to the low impulse for face-sheets. This phenomenon coincides with our previous investigation [30]. In addition, the EA of the core increases by 182% as the internal pressure increases 22%. It is indicated that the increase in explosive charge would seriously increase the burden of blast-protection structures, whether in terms of MRD or EA.
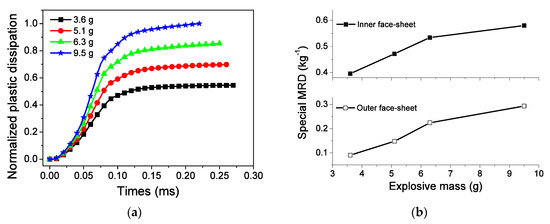
Figure 17.
Influence of explosive mass on energy absorption (EA) and MRD. (a) EA, and (b) MRD.
For a given blast loading and core configuration, the sandwich-walled rings with thin face-sheets absorb much energy and deform seriously, as shown in Figure 18. The increase in face-sheet thickness leads to a rise in the mass and stiffness of sandwich-walled rings because of the decrease in energy dissipation. The thin face-sheet can improve the EA capability. However, this phenomenon easily leads to large deformation of the face-sheet, resulting in weak blast resistance. Different from Ref. [29], the thickness of face-sheets varies in a certain range. This leads to a significant increase in blast resistance performance, but the total mass of the structure increases.
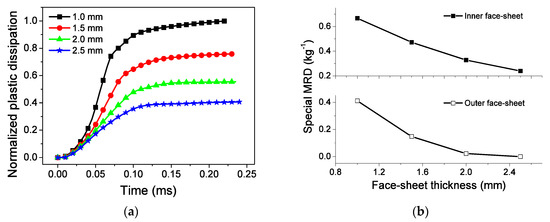
Figure 18.
Influence of face-sheet thickness on EA and MRD. (a) EA, and (b) MRD.
The core gradient is defined as
where r1 and r2 are the thicknesses of layers 1 and 2, respectively. The core gradient is positive when the low-density layer is located inside. Figure 19 depicts the gradient influence on the EA and MRD of the sandwich-walled ring. For a given geometrical sandwich-walled ring subjected to identical blast loading, the dissipated energy increases as the core gradient increases. The ring with a graded core displays better EA capability compared with the ring with a uniform core. However, the decrease in gradient is attributed to the reduction in the MRDs of face-sheets Figure 19b. EA and MRD are two conflicting objectives to evaluate blast resistance for explosive mass, face-sheet thickness, and core gradient. Karagiozova [28] found that although the core causes a reduction in the maximum velocity, the use of high-density foam is not a way to reduce the displacements. This conclusion is consistent with the phenomenon in Figure 19b.
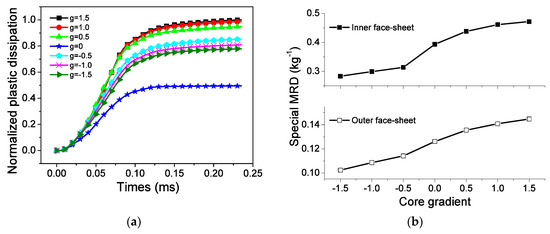
Figure 19.
Influence of core gradient on EA and MRD. (a) EA, and (b) MRD.
6. Conclusions
Theoretical analysis of the blast protection of graded metal foam-cored sandwich cylinders/rings is performed in this study. The mechanism of deformation is studied for a graded foam-cored sandwich cylinder/ring employing numerical and analytical methods. Several conclusions can be made with respect to the deformation process of graded metal foam-cored sandwich cylinders/rings resulting from an internal blast loading.
The deformation process can be modeled as three phases: FSI phase, core-crushing phase, and outer face-sheet deformation phase. For the core crushing, only one shock wave propagates from the inner layer to the outer layer for a positive-gradient core. Two compaction waves emerging at two internal faces of two layers simultaneously propagate outward in the same direction for a negative-gradient core.
The dynamic responses and EA of sandwich-walled rings with graded foam cores are compared with those of ungraded ones. When graded sandwich-walled rings and ungraded rings are subjected to an identical air blast, the MRD of the former is smaller than that of the latter, whereas the EA of the former is stronger than that of the latter. It is concluded that EA and MRD are two conflicting goals for achieving high impact/blast resistance capability for explosive mass, face-sheet thickness, and core gradient.
Author Contributions
Formal analysis, X.L. and K.Z.; investigation, M.L.; methodology, F.L.; project administration, M.L.; software, K.Z.; validation, F.L.; visualization, X.L.; writing—original draft, M.L. and Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China (11802337).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alqwasmi, N.; Tarlochan, F.; Alkhatib, S.E. Study of mild steel sandwich structure energy absorption performance subjected to localized impulsive loading. Materials 2020, 13, 670. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Li, X.; Wang, Z.; Wu, G.; Lu, G.; Zhao, L. Sandwich panels with layered graded aluminum honeycomb cores under blast loading. Compos. Struct. 2017, 173, 242–254. [Google Scholar] [CrossRef]
- Zhou, T.; Zhang, P.; Xiao, W.; Liu, J.; Cheng, Y. Experimental investigation on the performance of pvc foam core sandwich panels under air blast loading. Compos. Struct. 2019, 226, 111081. [Google Scholar] [CrossRef]
- Sun, Y.; Guo, L.-C.; Wang, T.-S.; Yao, L.-J.; Sun, X.-Y. Bending strength and failure of single-layer and double-layer sandwich structure with graded truss core. Compos. Struct. 2019, 226, 111204. [Google Scholar] [CrossRef]
- Amaro, A.M.; Neto, M.A.; Cirne, J.S.; Reis, P.N.B. Mechanical characterization of different aluminium foams at high strain rates. Materials 2019, 12, 1428. [Google Scholar] [CrossRef]
- Qu, J.; Ju, D.; Gao, S.; Chen, J. Research on the dynamic mechanical properties of polymethacrylimide foam sandwich structure. Compos. Struct. 2018, 204, 22–30. [Google Scholar] [CrossRef]
- Chen, Y.; Ye, L.; Escobedo-Diaz, J.P.; Zhang, Y.-X.; Fu, K. Quasi-static and dynamic progressive crushing of cf/ep composite sandwich panels under in-plane localised compressive loads. Compos. Struct. 2019, 222, 110839. [Google Scholar] [CrossRef]
- Sun, Y.; Li, Q.M. Dynamic compressive behaviour of cellular materials: A review of phenomenon, mechanism and modelling. Int. J. Impact Eng. 2018, 112, 74–115. [Google Scholar] [CrossRef]
- Davids, S.A.; Langdon, G.S.; Nurick, G.N. The influence of charge geometry on the response of partially confined right circular stainless steel cylinders subjected to blast loading. Int. J. Impact Eng. 2017, 108, 252–262. [Google Scholar] [CrossRef]
- Baba, B.O. Curved sandwich composites with layer-wise graded cores under impact loads. Compos. Struct. 2017, 159, 1–11. [Google Scholar] [CrossRef]
- Chang, B.; Zheng, Z.; Zhang, Y.; Zhao, K.; He, S.; Yu, J. Crashworthiness design of graded cellular materials: An asymptotic solution considering loading rate sensitivity. Int. J. Impact Eng. 2020, 143, 103611. [Google Scholar] [CrossRef]
- Jing, L.; Su, X.; Chen, D.; Yang, F.; Zhao, L. Experimental and numerical study of sandwich beams with layered-gradient foam cores under low-velocity impact. Thin-Walled Struct. 2019, 135, 227–244. [Google Scholar] [CrossRef]
- Sun, G.; Zhang, J.; Li, S.; Fang, J.; Wang, E.; Li, Q. Dynamic response of sandwich panel with hierarchical honeycomb cores subject to blast loading. Thin-Walled Struct. 2019, 142, 499–515. [Google Scholar] [CrossRef]
- Jin, X.; Wang, Z.; Ning, J.; Xiao, G.; Liu, E.; Shu, X. Dynamic response of sandwich structures with graded auxetic honeycomb cores under blast loading. Compos. Part B Eng. 2016, 106, 206–217. [Google Scholar] [CrossRef]
- Liang, M.Z.; Li, X.Y.; Lin, Y.L.; Zhang, K.F.; Lu, F.Y. Dynamic compressive behaviors of two-layer graded aluminum foams under blast loading. Materials 2019, 12, 1445. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, S.; Zhao, K.; Zheng, Z.; Yang, L.; Yu, J. Blast alleviation of cellular sacrificial cladding: A nonlinear plastic shock model. Int. J. Appl. Mech. 2016, 8, 1650057. [Google Scholar] [CrossRef]
- Chen, G.; Cheng, Y.; Zhang, P.; Liu, J.; Chen, C.; Cai, S. Design and modelling of auxetic double arrowhead honeycomb core sandwich panels for performance improvement under air blast loading. J. Sandwich Struct. Mater. 2020, 1099636220935563. [Google Scholar] [CrossRef]
- Shen, C.J.; Lu, G.; Yu, T.X. Investigation into the behavior of a graded cellular rod under impact. Int. J. Impact Eng. 2014, 74, 92–106. [Google Scholar] [CrossRef]
- Liu, J.; Hou, B.; Lu, F.; Zhao, H. A theoretical study of shock front propagation in the density graded cellular rods. Int. J. Impact Eng. 2015, 80, 133–142. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Zhao, L. Dynamic response of functionally graded cellular materials based on the voronoi model. Compos. Part B Eng. 2016, 85, 176–187. [Google Scholar] [CrossRef]
- Liang, M.; Lu, F.; Zhang, G.; Li, X. Design of stepwise foam claddings subjected to air-blast based on voronoi model. Steel Compos. Struct. 2017, 23, 107–114. [Google Scholar] [CrossRef]
- Liang, M.; Li, Z.; Lu, F.; Li, X. Theoretical and numerical investigation of blast responses of continuous-density graded cellular materials. Compos. Struct. 2017, 164, 170–179. [Google Scholar] [CrossRef]
- Eloy, F.D.S.; Gomes, G.F.; Ancelotti, J.A.C.; da Cunha, J.S.S.; Faria Bombard, A.J.; Junqueira, D.M. Experimental dynamic analysis of composite sandwich beams with magnetorheological honeycomb core. Eng. Struct. 2018, 176, 231–242. [Google Scholar] [CrossRef]
- Birman, V.; Kardomateas, G.A. Review of current trends in research and applications of sandwich structures. Compos. Part B Eng. 2018, 142, 221–240. [Google Scholar] [CrossRef]
- Liu, X.; Tian, X.; Lu, T.J.; Zhou, D.; Liang, B. Blast resistance of sandwich-walled hollow cylinders with graded metallic foam cores. Compos. Struct. 2012, 94, 2485–2493. [Google Scholar] [CrossRef]
- Zhu, W.; Huang, G.-Y.; Liu, C.-M.; Feng, S.-S. Experimental and numerical investigation of a hollow cylindrical water barrier against internal blast loading. Eng. Struct. 2018, 172, 789–806. [Google Scholar] [CrossRef]
- Shen, J.; Lu, G.; Zhao, L.; Zhang, Q. Short sandwich tubes subjected to internal explosive loading. Eng. Struct. 2013, 55, 56–65. [Google Scholar] [CrossRef]
- Karagiozova, D.; Langdon, G.S.; Nurick, G.N.; Niven, T. The influence of a low density foam sandwich core on the response of a partially confined steel cylinder to internal air-blast. Int. J. Impact Eng. 2016, 92, 32–49. [Google Scholar] [CrossRef]
- Liang, M.; Lu, F.; Zhang, G.; Li, X. Experimental and numerical study of aluminum foam-cored sandwich tubes subjected to internal air blast. Compos. Part B Eng. 2017, 125, 134–143. [Google Scholar] [CrossRef]
- Liang, M.; Zhang, G.; Lu, F.; Li, X. Blast resistance and design of sandwich cylinder with graded foam cores based on the voronoi algorithm. Thin-Walled Struct. 2017, 112, 98–106. [Google Scholar] [CrossRef]
- Liang, M.Z.; Li, X.Y.; Lin, Y.L.; Lu, F.Y. Compaction wave propagation in layered cellular materials under air-blast. Int. J. Appl. Mech. 2019, 11, 1950003. [Google Scholar] [CrossRef]
- Reid, S.R.; Peng, C. Dynamic uniaxial crushing of wood. Int. J. Impact Eng. 1997, 19, 531–570. [Google Scholar] [CrossRef]
- Tan, P.J.; Reid, S.R.; Harrigan, J.J.; Zou, Z.; Li, S. Dynamic compressive strength properties of aluminium foams. Part II—‘shock’ theory and comparison with experimental data and numerical models. J. Mech. Phys. Solids 2005, 53, 2206–2230. [Google Scholar] [CrossRef]
- Jing, L.; Zhao, L.M. Blast resistance and energy absorption of sandwich panels with layered gradient metallic foam cores. J. Sandw. Struct. Mater. 2019, 21, 464–482. [Google Scholar] [CrossRef]
- Liang, M.; Li, X.; Lin, Y.; Zhang, K.; Lu, F. Influence of multi-layer core on the blast response of composite sandwich cylinders. Int. J. Appl. Mech. 2020, 12, 2050018. [Google Scholar] [CrossRef]
- Zheng, Z.; Wang, C.; Yu, J.; Reid, S.R.; Harrigan, J.J. Dynamic stress-strain states for metal foams using a 3d cellular model. J. Mech. Phys. Solids 2014, 72, 93–114. [Google Scholar] [CrossRef]
- Shen, C.J.; Yu, T.X.; Lu, G. Double shock mode in graded cellular rod under impact. Int. J. Solids Struct. 2013, 50, 217–233. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).