Detection of Micro-Cracks in Metals Using Modulation of PZT-Induced Lamb Waves
Abstract
1. Introduction
2. Materials and Methods
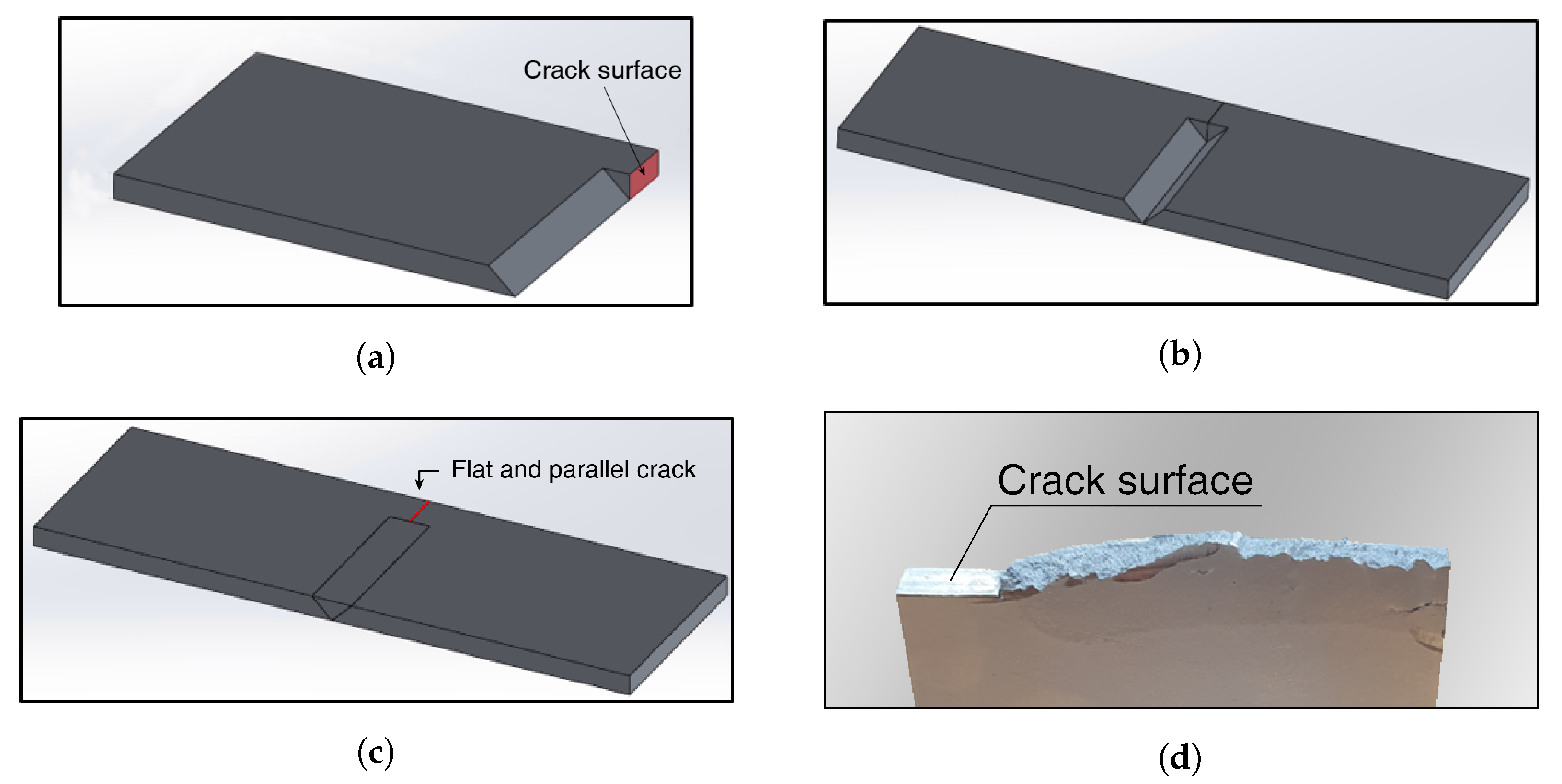
2.1. Generation of Two Types of Crack Specimen
2.2. Excitation and Sensing Equipment
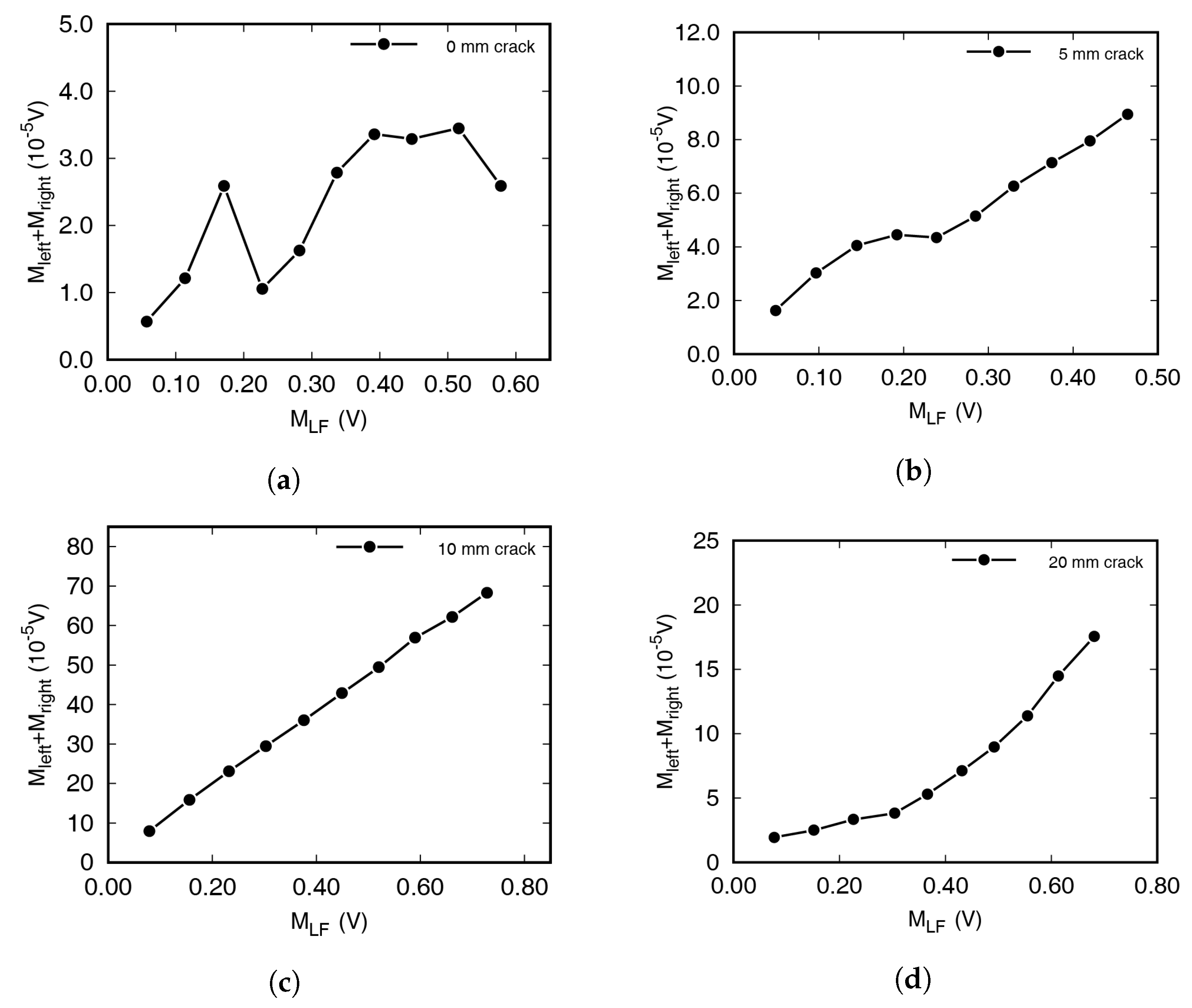
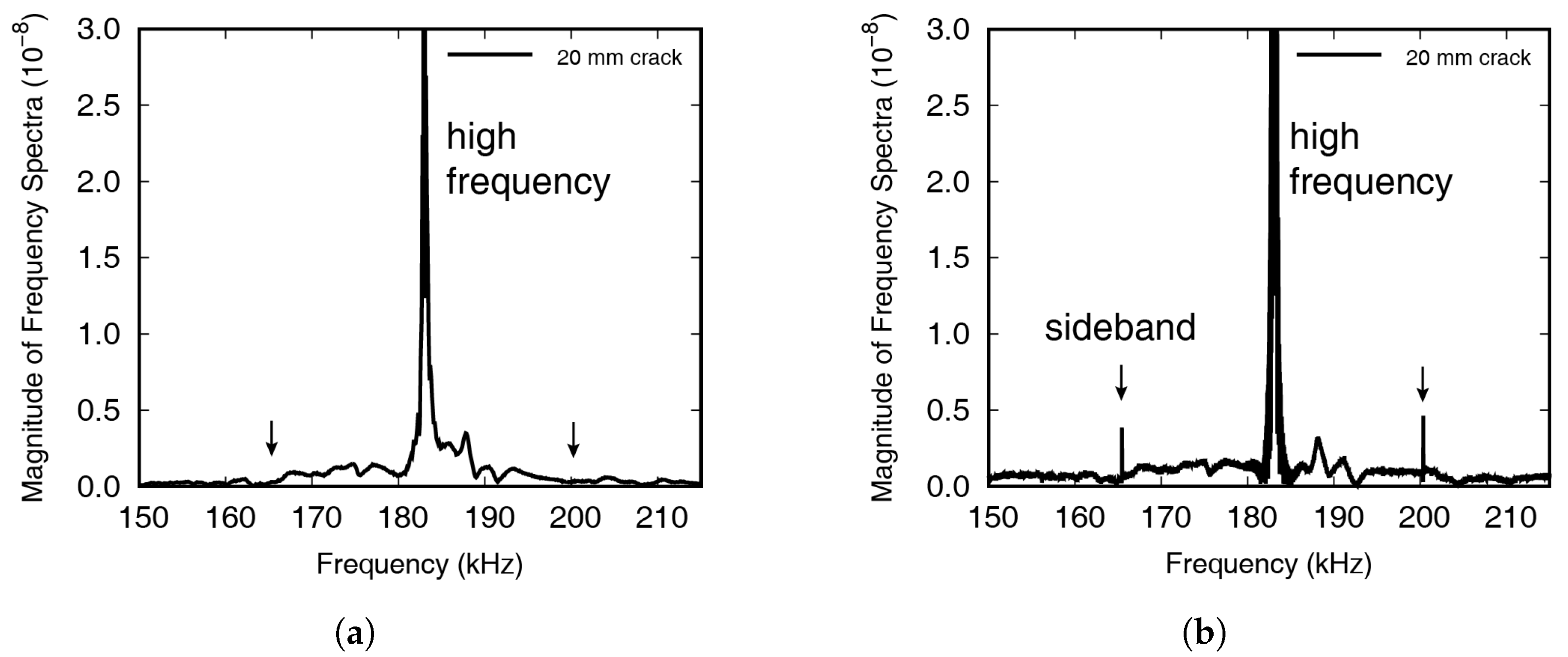
3. Quantitative Analysis of Wave Modulation with Seam Crack
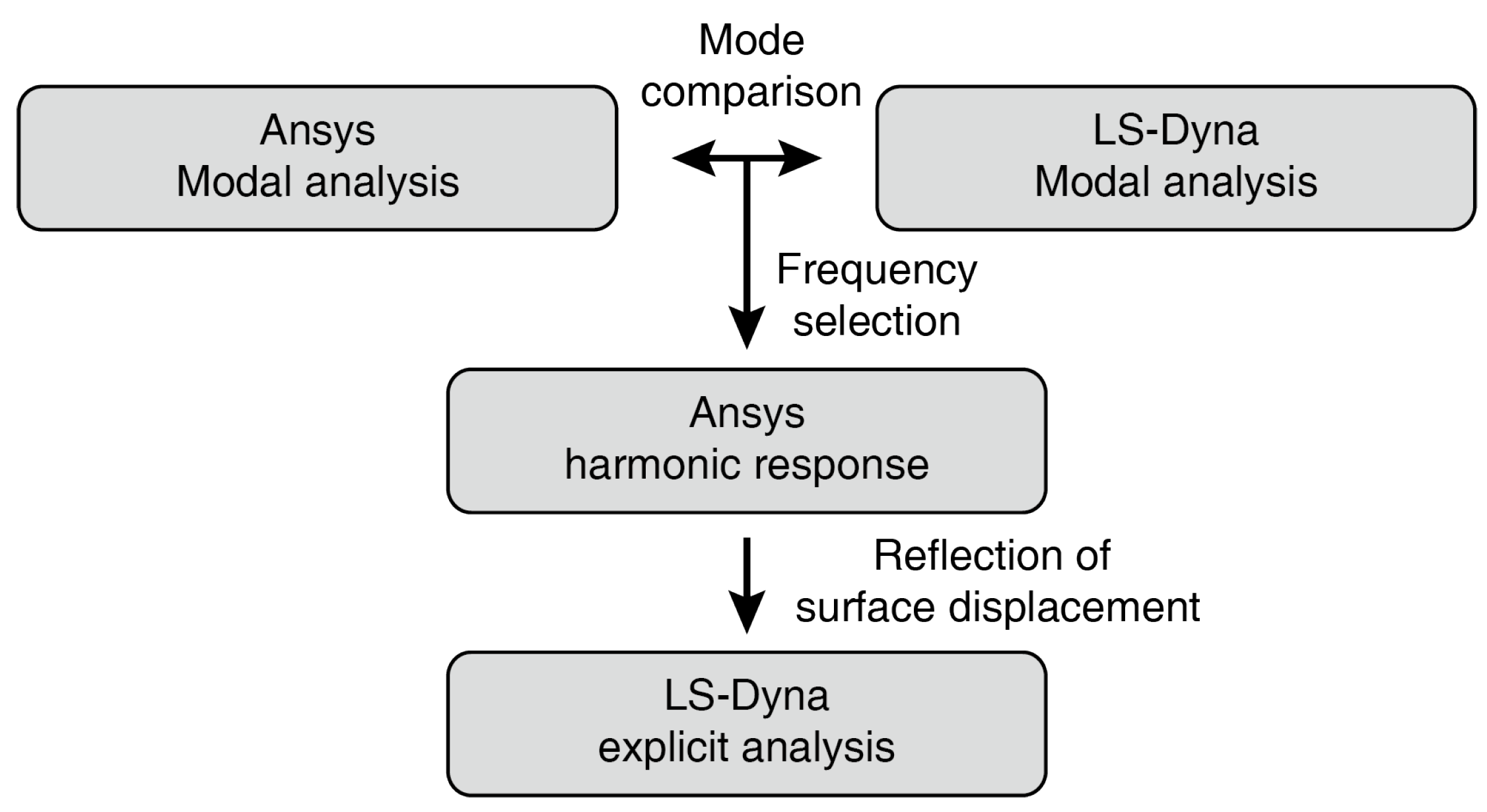
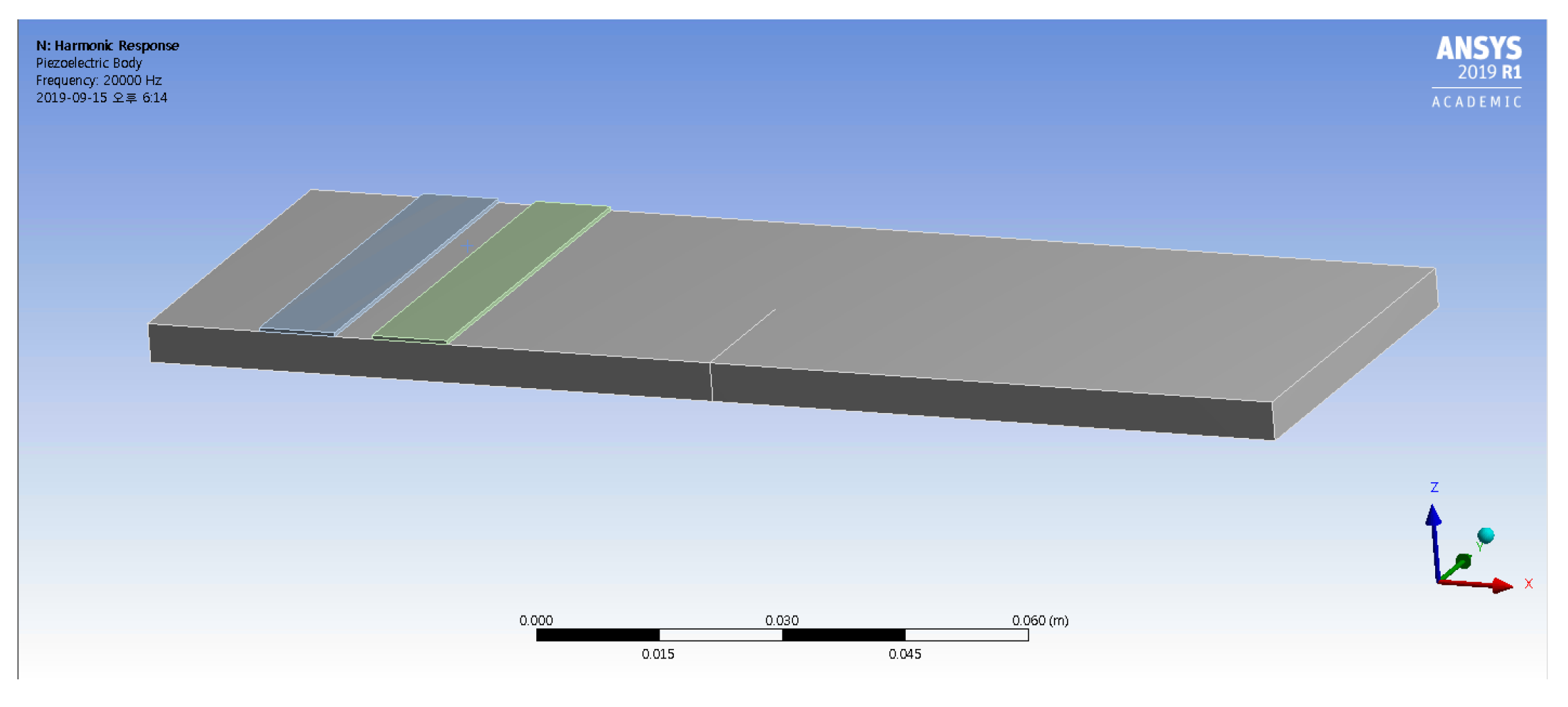
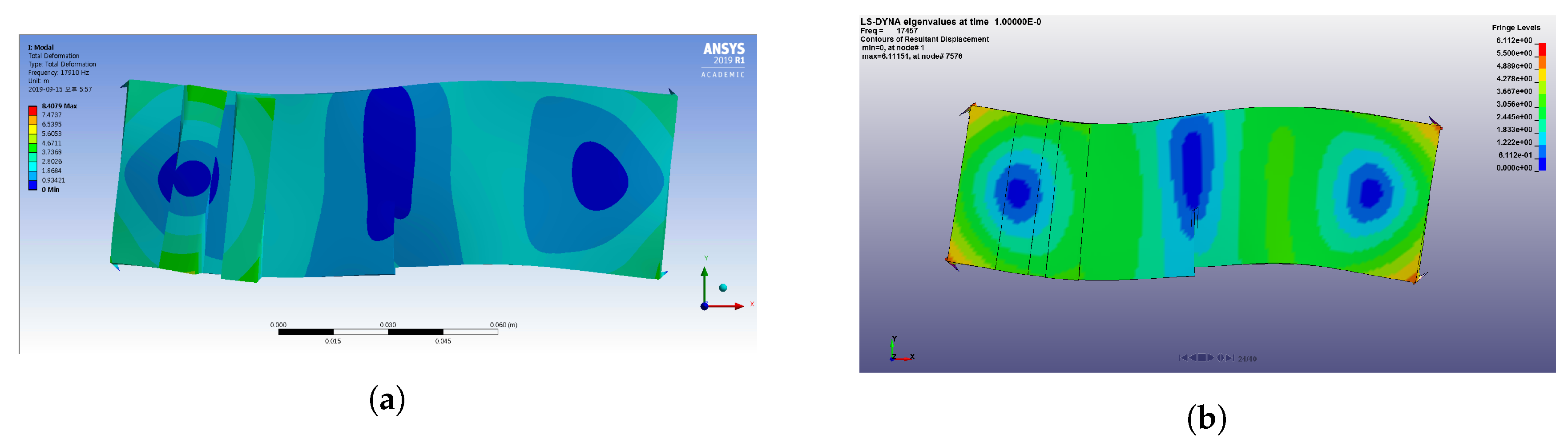
4. Numerical Simulations
5. Crack Detection Algorithm
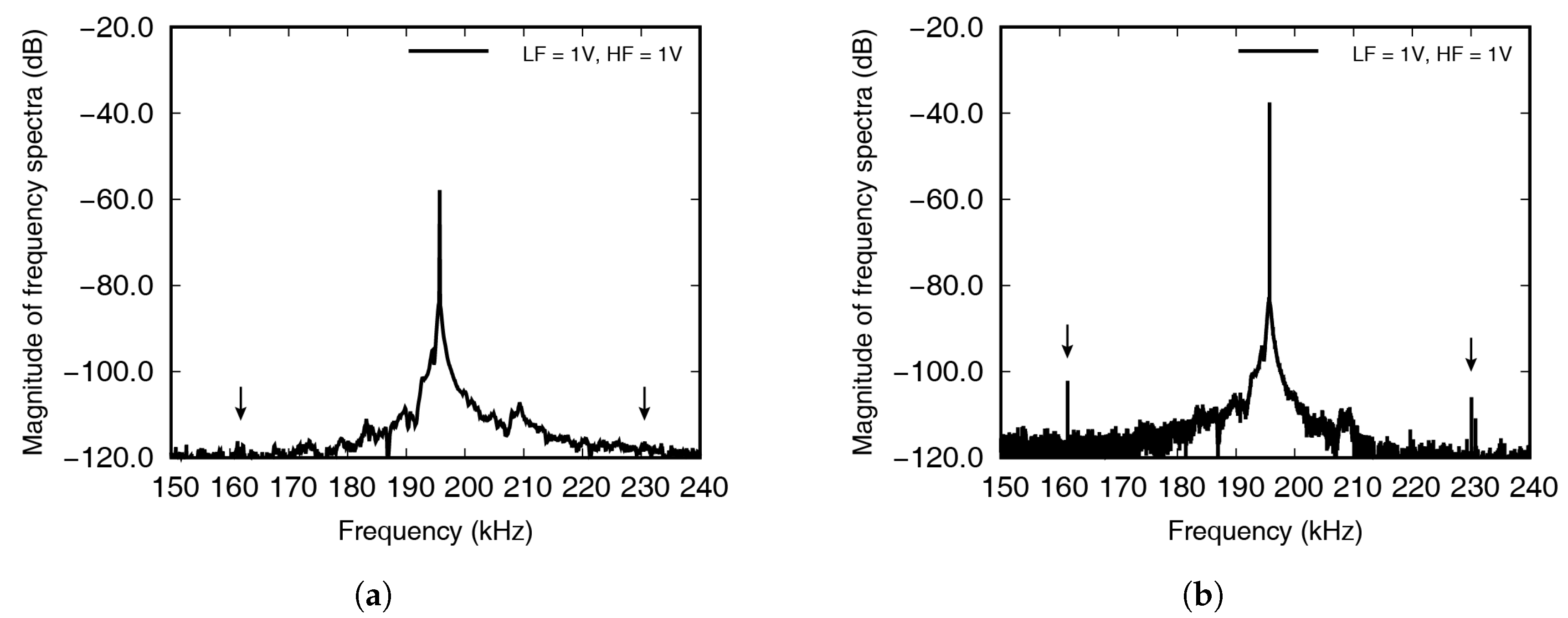
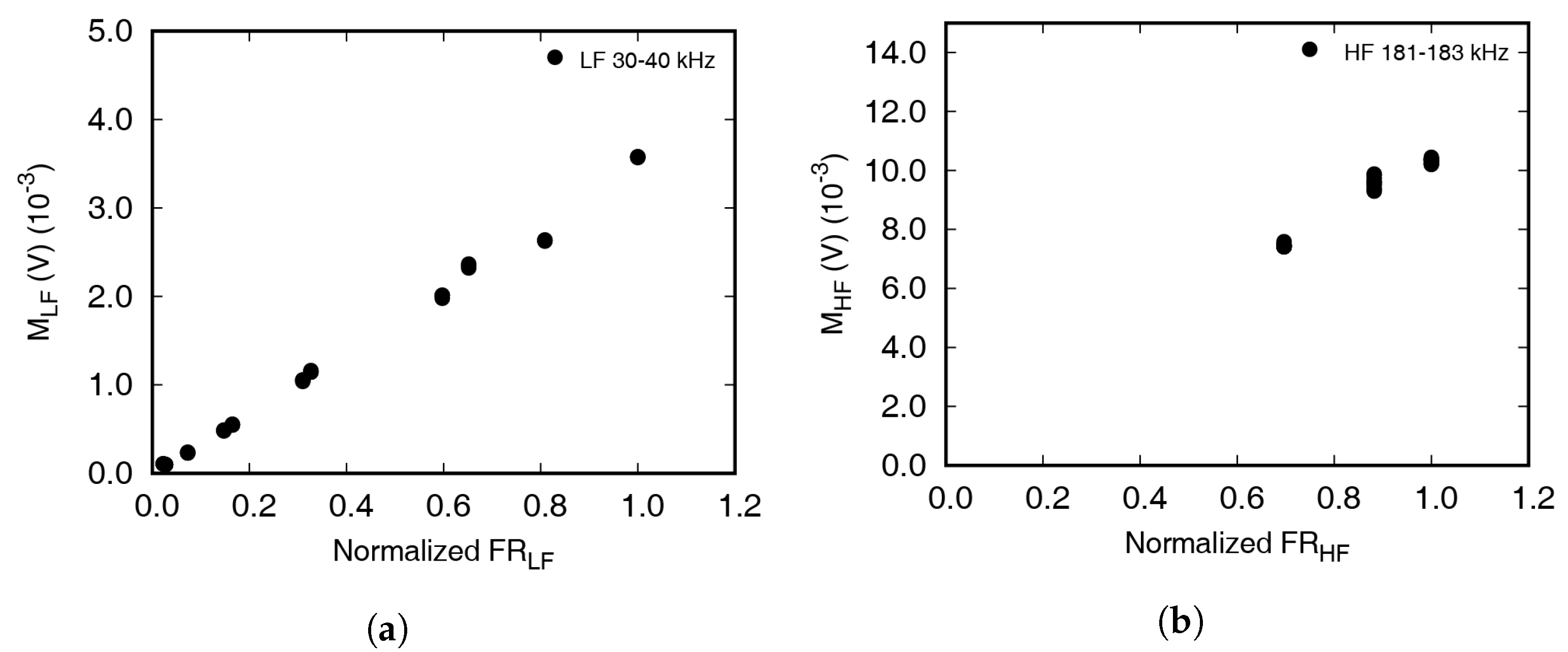
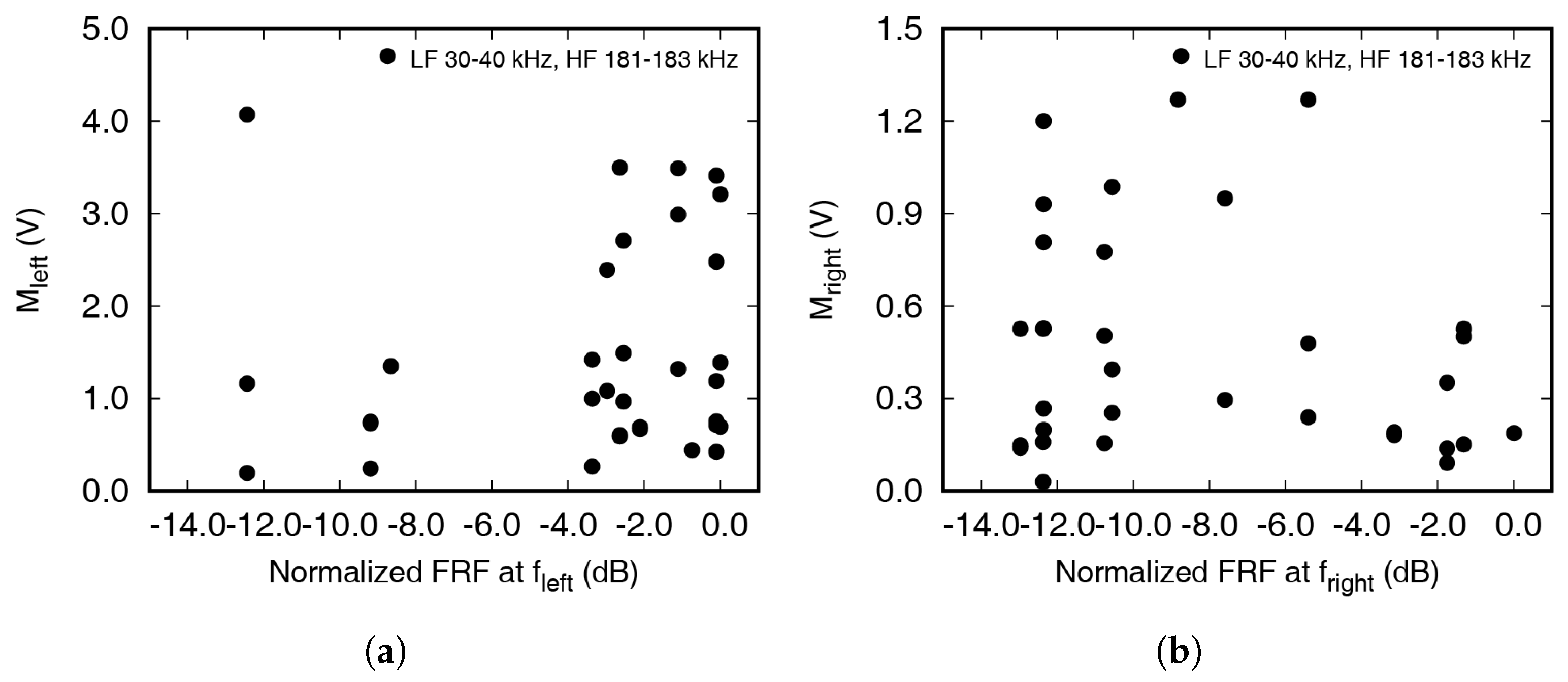
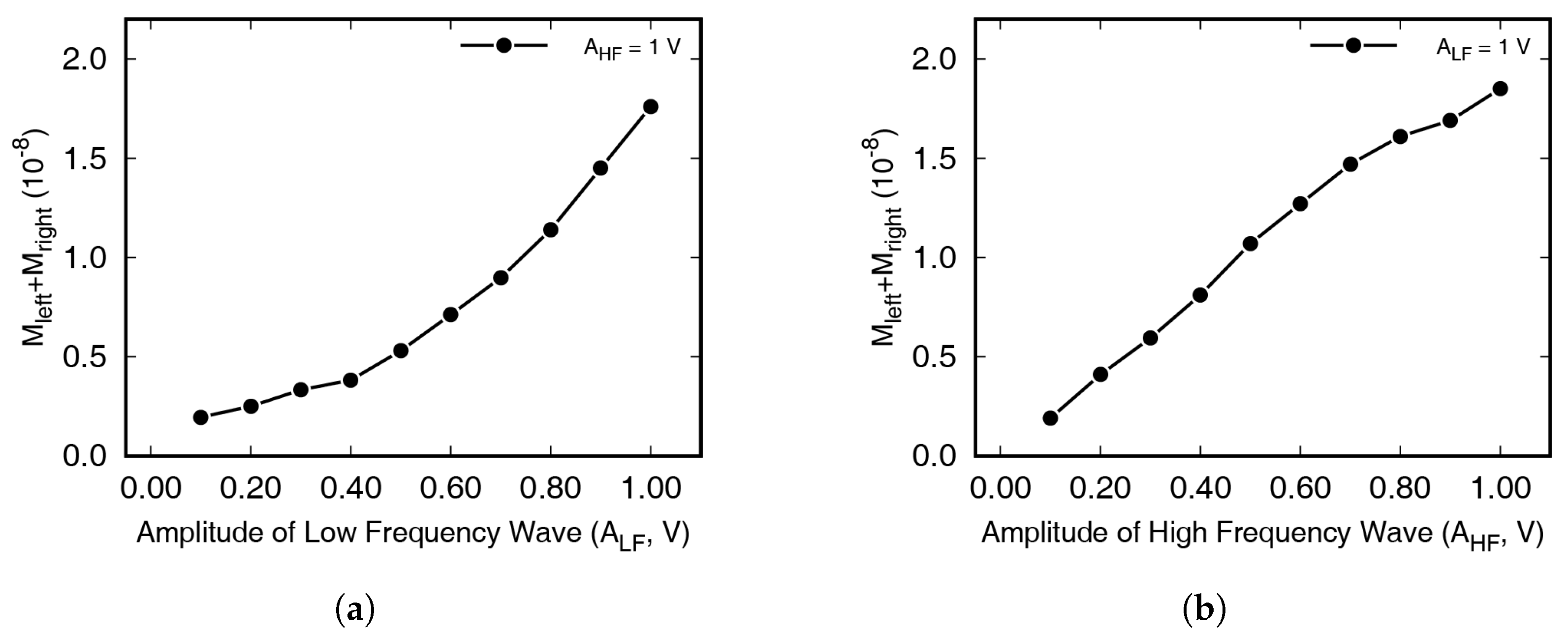
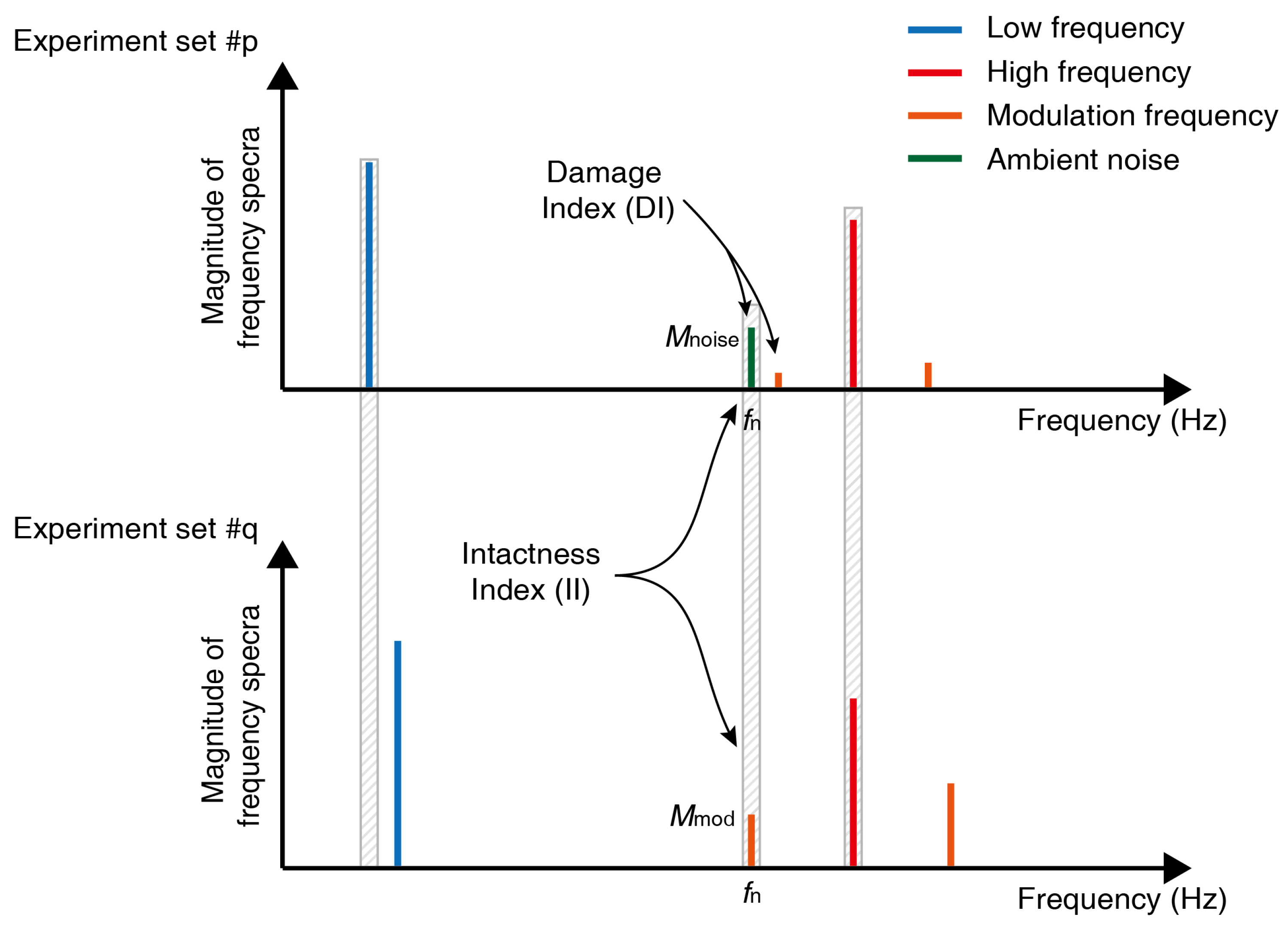
5.1. Nonlinear Indexes
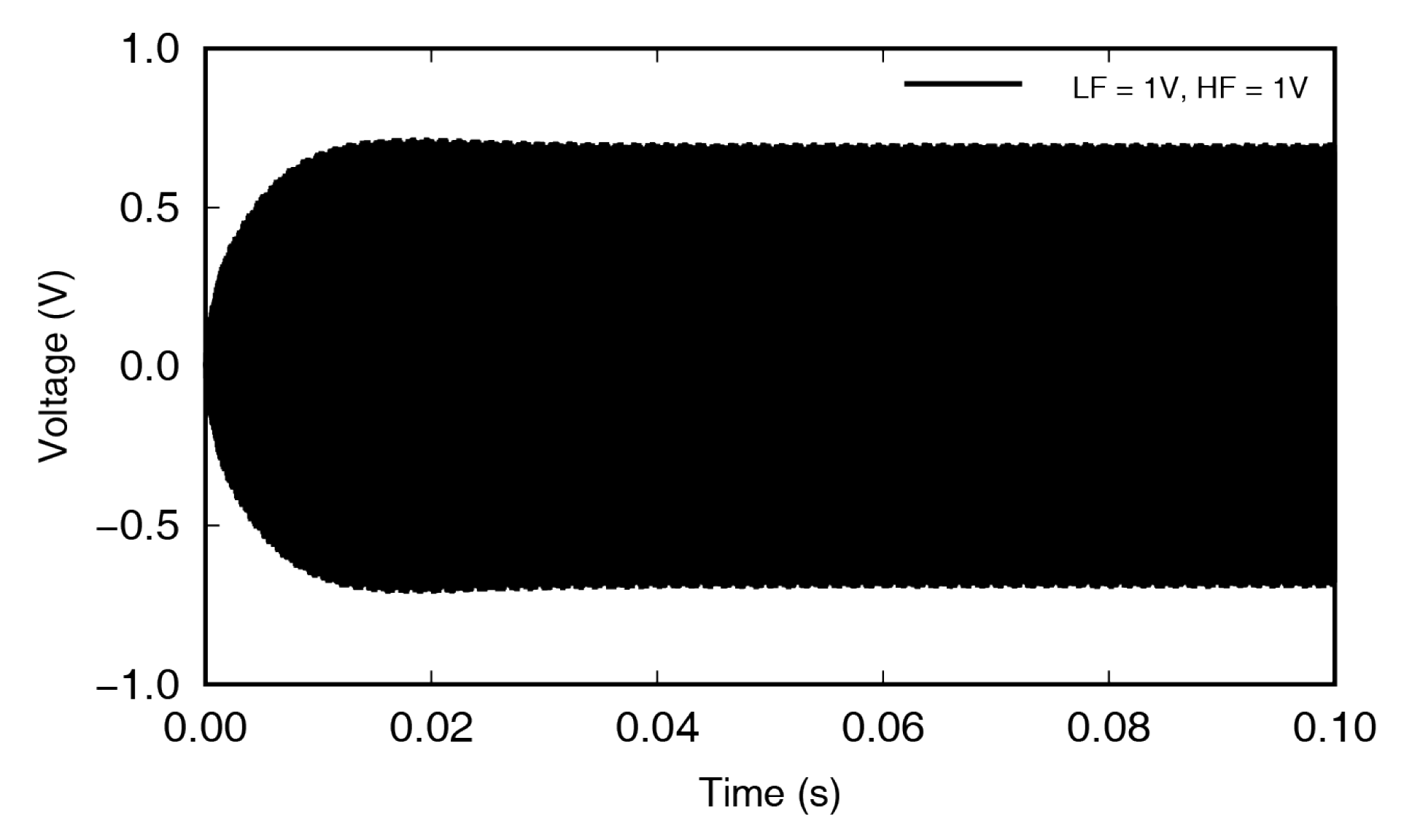
5.2. Excitation Conditions
5.3. Damage Determination Criteria
5.4. Application to Fatigue Crack
6. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Campbell, F.C. Elements of Metallurgy and Engineering Alloys; ASM International: Materials Park, OH, USA, 2008. [Google Scholar]
- Pons, A.J.; Karma, A. Helical crack-front instability in mixed-mode fracture. Nature 2010, 464, 85. [Google Scholar] [CrossRef]
- Gholizadeh, S. A review of non-destructive testing methods of composite materials. Procedia Struct. Integr. 2016, 1, 50–57. [Google Scholar] [CrossRef]
- Rens, K.L.; Wipf, T.J.; Klaiber, F.W. Review of nondestructive evaluation techniques of civil infrastructure. J. Perform. Constr. Facil. 1997, 11, 152–160. [Google Scholar] [CrossRef]
- Cawley, P. Non-destructive testing—Current capabilities and future directions. Proc. Inst. Mech. Eng. Part J. Mater. Des. Appl. 2001, 215, 213–223. [Google Scholar]
- Adams, D. Health Monitoring of Structural Materials and Componenets: Methods with Applications; John Wiley & Sons: New York, NY, USA, 2007. [Google Scholar]
- Kazakov, V.V.; Sutin, A.; Johnson, P.A. Sensitive imaging of an elastic nonlinear wave-scattering source in a solid. Appl. Phys. Lett. 2002, 81, 646–648. [Google Scholar] [CrossRef]
- Walker, J.S. Fast Fourier Transforms; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Jhang, K.Y. Nonlinear ultrasonic techniques for nondestructive assessment of micro damage in material: A review. Int. J. Precis. Eng. Manuf. 2009, 10, 123–135. [Google Scholar] [CrossRef]
- Nazarov, V.E.; Sutin, A.M. Nonlinear elastic constants of solids with cracks. J. Acoust. Soc. Am. 1997, 102, 3349–3354. [Google Scholar] [CrossRef]
- Cantrell, J.H.; Yost, W.T. Nonlinear ultrasonic characterization of fatigue microstructures. Int. J. Fatigue 2001, 23, 487. [Google Scholar] [CrossRef]
- Lee, S.E.; Jin, S.; Hong, J.W. Periodic nonlinear waves resulting from the contact interaction of a crack. J. Appl. Phys. 2017, 122, 124303. [Google Scholar] [CrossRef]
- Croxford, A.J.; Wilcox, P.D.; Drinkwater, B.W.; Nagy, P.B. The use of non-collinear mixing for nonlinear ultrasonic detection of plasticity and fatigue. J. Acoust. Soc. Am. 2009, 126, EL117. [Google Scholar] [CrossRef]
- Klepka, A.; Staszewski, W.J.; Jenal, R.; Szwedo, M.; Iwaniec, J.; Uhl, T. Nonlinear acoustics for fatigue crack detection–experimental investigations of vibro-acoustic wave modulations. Struct. Health Monit. 2012, 11, 197–211. [Google Scholar] [CrossRef]
- Sessler, J.G.; Weiss, V. Crack Detection Apparatus and Method; Technical Report; Department of the Navy: Washington, DC, USA, 1975.
- Didenkulov, I.; Sutin, A.; Ekimov, A.; Kazakov, V. Interaction of Sound and Vibrations in Concrete with Cracks. AIP Conf. Proc. 2000, 524, 279. [Google Scholar]
- Duffour, P.; Morbidini, M.; Cawley, P. A study of the vibro-acoustic modulation technique for the detection of cracks in metals. J. Acoust. Soc. Am. 2006, 119, 1463–1475. [Google Scholar] [CrossRef]
- Sohn, H.; Lim, H.J.; DeSimio, M.P.; Brown, K.; Derriso, M. Nonlinear ultrasonic wave modulation for online fatigue crack detection. J. Sound Vib. 2014, 333, 1473–1484. [Google Scholar] [CrossRef]
- Sohn, H.; Lim, H.J.; Yang, S. A fatigue crack detection methodology. In Smart Sensors for Health and Environment Monitoring; Springer: Berlin/Heidelberg, Germany, 2015; pp. 233–253. [Google Scholar]
- Kawashima, K.; Ryuji, O.; Toshihiro, I.; Fujita, H.; Shima, T. Nonlinear acoustic response through minute surface cracks: FEM simulation and experimentation. Ultrasonics 2002, 40, 611. [Google Scholar] [CrossRef]
- Solodov, I.; Krohn, N.; Busse, G. Nonlinear ultrasonic NDT for early defect recognition and imaging. In European Conf. on NDT (ECNDT), Moscow; Citeseer: Forest Grove, OR, USA, 2010. [Google Scholar]
- Sutin, A.; Johnson, P. Nonlinear elastic wave nde ii. nonlinear wave modulation spectroscopy and nonlinear time reversed acoustics. AIP Conf. Proc. 2005, 760, 385. [Google Scholar]
- Zaitsev, V.; Sas, P. Nonlinear response of a weakly damaged metal sample: A dissipative modulation mechanism of vibro-acoustic interaction. J. Vib. Control. 2000, 6, 803–822. [Google Scholar] [CrossRef]
- Lim, H.J.; Sohn, H.; DeSimio, M.P.; Brown, K. Reference-free fatigue crack detection using nonlinear ultrasonic modulation under various temperature and loading conditions. Mech. Syst. Signal Process. 2014, 45, 468–478. [Google Scholar] [CrossRef]
- Lim, H.J.; Kim, Y.; Koo, G.; Yang, S.; Sohn, H.; Bae, I.h.; Jang, J.H. Development and field application of a nonlinear ultrasonic modulation technique for fatigue crack detection without reference data from an intact condition. Smart Mater. Struct. 2016, 25, 095055. [Google Scholar] [CrossRef]
- Li, W.; Hu, S.; Deng, M. Combination of Phase Matching and Phase-Reversal Approaches for Thermal Damage Assessment by Second Harmonic Lamb Waves. Materials 2018, 11, 1961. [Google Scholar] [CrossRef]
- Rucka, M. Monitoring Steel Bolted Joints during a Monotonic Tensile Test Using Linear and Nonlinear Lamb Wave Methods: A Feasibility Study. Metals 2018, 8, 683. [Google Scholar] [CrossRef]
- Lim, H.U.; Hong, J.W. Thermo-mechanical simulation of guided waves in pipes excited by laser pulses. In Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2013; International Society for Optics and Photonics: San Diego, CA, USA, 2013; Volume 8692, p. 86921S. [Google Scholar]
- Liu, W.; Hong, J.W. Three-dimensional Lamb wave propagation excited by a phased piezoelectric array. Smart Mater. Struct. 2010, 19, 085002. [Google Scholar] [CrossRef]
- Liu, W.; Hong, J.W. Modeling of three-dimensional Lamb wave propagation excited by laser pulses. Ultrasonics 2015, 55, 113–122. [Google Scholar] [CrossRef]
- Guan, L.; Zou, M.; Wan, X.; Li, Y. Nonlinear Lamb Wave Micro-Crack Direction Identification in Plates with Mixed-Frequency Technique. Appl. Sci. 2020, 10, 2135. [Google Scholar] [CrossRef]
- Li, X.; Shui, G.; Zhao, Y.; Wang, Y.S. Propagation of Non-Linear Lamb Waves in Adhesive Joint with Micro-Cracks Distributing Randomly. Appl. Sci. 2020, 10, 741. [Google Scholar] [CrossRef]
- Totten, G. Fatigue Crack Propagation. Adv. Mater. Process. 2008, 166, 39–44. [Google Scholar]
- Sadler, J.; Maev, R.G. Experimental and theoretical basis of Lamb waves and their applications in material sciences. Can. J. Phys. 2007, 85, 707–731. [Google Scholar] [CrossRef]
- Stratoudaki, T.; Edwards, C.; Dixon, S.; Palmer, S.B. Laser-based ultrasound measurements of optical absorption depth in epoxy resins. In Lasers in Material Processing and Manufacturing; International Society for Optics and Photonics: San Diego, CA, USA, 2002; Volume 4915, pp. 298–304. [Google Scholar]
- Jang, T.; Lee, J.; Lee, S. An Effective Generation of Lamb Waves in a Thin Plate Using Laser Line Array Illumination and Their Propagation Characteristics. In AIP Conference Proceedings; American Institute of Physics: New York, NY, USA, 2003; Volume 657, pp. 311–318. [Google Scholar]
- Dutta, D.; Sohn, H.; Harries, K.A.; Rizzo, P. A nonlinear acoustic technique for crack detection in metallic structures. Struct. Health Monit. 2009, 8, 251. [Google Scholar] [CrossRef]
- Mecchi, A.C.L.; Nader, G.; Silva, E.C.N.; Adamowski, J.C. ABCM Symposium Series in Mechatronics; ABCM—Brazilian Society of Mechanical Sciences and Engineering: Rio de Janeiro, Brazil, 2004; Volume 1, p. 653. [Google Scholar]
- Fierro, G.P.M.; Meo, M. Residual fatigue life estimation using a nonlinear ultrasound modulation method. Smart Mater. Struct. 2015, 24, 025040. [Google Scholar] [CrossRef]
- Kim, Y.; Lim, H.J.; Sohn, H. Nonlinear ultrasonic modulation based failure warning for aluminum plates subject to fatigue loading. Int. J. Fatigue 2018, 114, 130–137. [Google Scholar] [CrossRef]
- Altair. HyperWorks for LS-DYNA; Altair Engineering Inc.: Troy, MI, USA, 2011. [Google Scholar]
- Lee, S.E.; Lim, H.J.; Jin, S.; Sohn, H.; Hong, J.W. Micro-crack detection with nonlinear wave modulation technique and its application to loaded cracks. NDT E Int. 2019, 107, 102132. [Google Scholar] [CrossRef]
- Yoder, N.C.; Adams, D.E. Vibro-acoustic modulation utilizing a swept probing signal for robust crack detection. Struct. Health Monit. 2010, 9, 257–267. [Google Scholar] [CrossRef]




| Property | Symbol | Value |
|---|---|---|
| Electromechanical coupling factor | 0.63 | |
| 0.72 | ||
| 0.36 | ||
| 0.68 | ||
| Piezoelectric charge constant (10 m/V) | 400 | |
| 590 | ||
| Poisson’s ratio | 0.35 | |
| Density () | 7700 | |
| Elastic constant ( ) | 12.1 | |
| 7.54 | ||
| 7.52 | ||
| 11.1 | ||
| 2.11 | ||
| 2.26 |
| Crack Length (mm) | LF (kHz) | HF (kHz) |
|---|---|---|
| 0 | 33.94 | 196.35 |
| 5 | 34.42 | 195.56 |
| 10 | 34.52 | 195.86 |
| 20 | 34.35 | 195.70 |
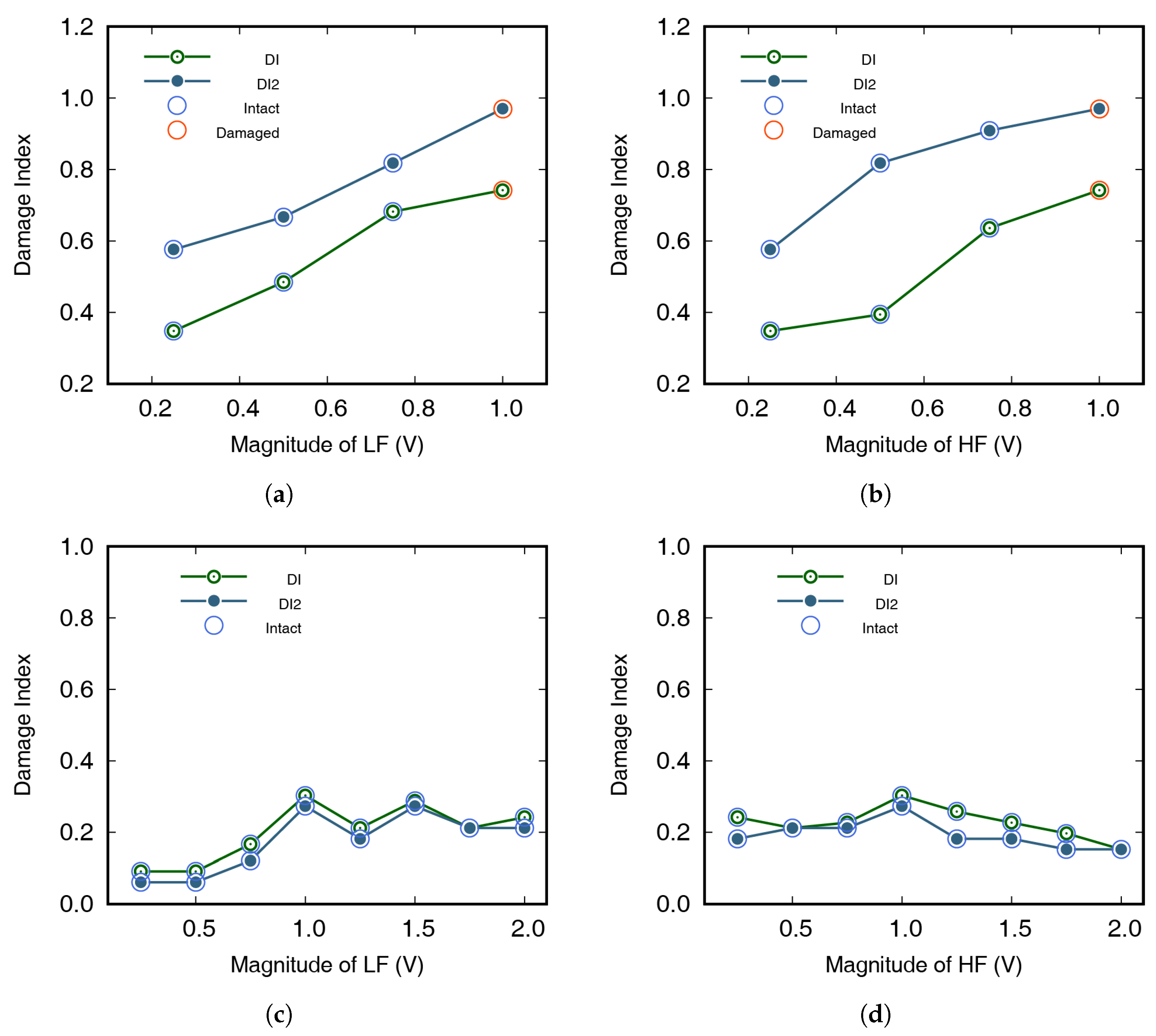
| LF (V) | HF (V) | DI | DI2 | II | II2 | Test Result |
|---|---|---|---|---|---|---|
| 0.25 | 1.0 | 0.348 | 0.576 | 0.394 | 0.212 | Intact |
| 0.5 | 1.0 | 0.485 | 0.667 | 0.318 | 0.182 | Intact |
| 0.75 | 1.0 | 0.682 | 0.818 | 0.121 | 0.030 | Intact |
| 1.0 | 1.0 | 0.742 | 0.970 | 0.015 | 0.0 | Damaged |
| 1.0 | 0.25 | 0.348 | 0.576 | 0.394 | 0.212 | Intact |
| 1.0 | 0.5 | 0.394 | 0.818 | 0.273 | 0.030 | Intact |
| 1.0 | 0.75 | 0.636 | 0.909 | 0.136 | 0.0 | Intact |
| 1.0 | 1.0 | 0.742 | 0.970 | 0.015 | 0.0 | Damaged |
| LF (V) | HF (V) | DI | DI2 | II | II2 | Test Result |
|---|---|---|---|---|---|---|
| 0.25 | 1.0 | 0.091 | 0.061 | 0.576 | 0.818 | Intact |
| 0.5 | 1.0 | 0.091 | 0.061 | 0.561 | 0.848 | Intact |
| 0.75 | 1.0 | 0.167 | 0.121 | 0.485 | 0.485 | Intact |
| 1.0 | 1.0 | 0.303 | 0.273 | 0.182 | 0.303 | Intact |
| 1.25 | 1.0 | 0.212 | 0.182 | 0.288 | 0.364 | Intact |
| 1.5 | 1.0 | 0.288 | 0.273 | 0.303 | 0.485 | Intact |
| 1.75 | 1.0 | 0.212 | 0.212 | 0.242 | 0.242 | Intact |
| 2.0 | 1.0 | 0.242 | 0.212 | 0.242 | 0.364 | Intact |
| 1.0 | 0.25 | 0.242 | 0.182 | 0.379 | 0.606 | Intact |
| 1.0 | 0.5 | 0.212 | 0.212 | 0.348 | 0.576 | Intact |
| 1.0 | 0.75 | 0.227 | 0.212 | 0.470 | 0.636 | Intact |
| 1.0 | 1.0 | 0.303 | 0.273 | 0.182 | 0.303 | Intact |
| 1.0 | 1.25 | 0.258 | 0.182 | 0.182 | 0.273 | Intact |
| 1.0 | 1.5 | 0.227 | 0.182 | 0.303 | 0.273 | Intact |
| 1.0 | 1.75 | 0.197 | 0.152 | 0.394 | 0.636 | Intact |
| 1.0 | 2.0 | 0.152 | 0.152 | 0.424 | 0.515 | Intact |
| Condition | Intactness Index | Damage Index | Test Result | |
|---|---|---|---|---|
| Specimen #1 | Intact | 0.455, 0.515 | 0.348, 0.182 | Intact |
| Damaged | 0 | 1 | Crack | |
| Specimen #2 | Intact | 0.061, 0.152 | 0.45, 0.242 | Intact |
| Damaged | 0 | 0.97 | Crack | |
| Specimen #3 | Intact | 0.106, 0.060 | 0.621, 0.379 | Intact |
| Damaged | 0 | 1 | Crack |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.E.; Hong, J.-W. Detection of Micro-Cracks in Metals Using Modulation of PZT-Induced Lamb Waves. Materials 2020, 13, 3823. https://doi.org/10.3390/ma13173823
Lee SE, Hong J-W. Detection of Micro-Cracks in Metals Using Modulation of PZT-Induced Lamb Waves. Materials. 2020; 13(17):3823. https://doi.org/10.3390/ma13173823
Chicago/Turabian StyleLee, Sang Eon, and Jung-Wuk Hong. 2020. "Detection of Micro-Cracks in Metals Using Modulation of PZT-Induced Lamb Waves" Materials 13, no. 17: 3823. https://doi.org/10.3390/ma13173823
APA StyleLee, S. E., & Hong, J.-W. (2020). Detection of Micro-Cracks in Metals Using Modulation of PZT-Induced Lamb Waves. Materials, 13(17), 3823. https://doi.org/10.3390/ma13173823




