Analytical Solutions Based on Fourier Cosine Series for the Free Vibrations of Functionally Graded Material Rectangular Mindlin Plates
Abstract
1. Introduction
2. Methodology
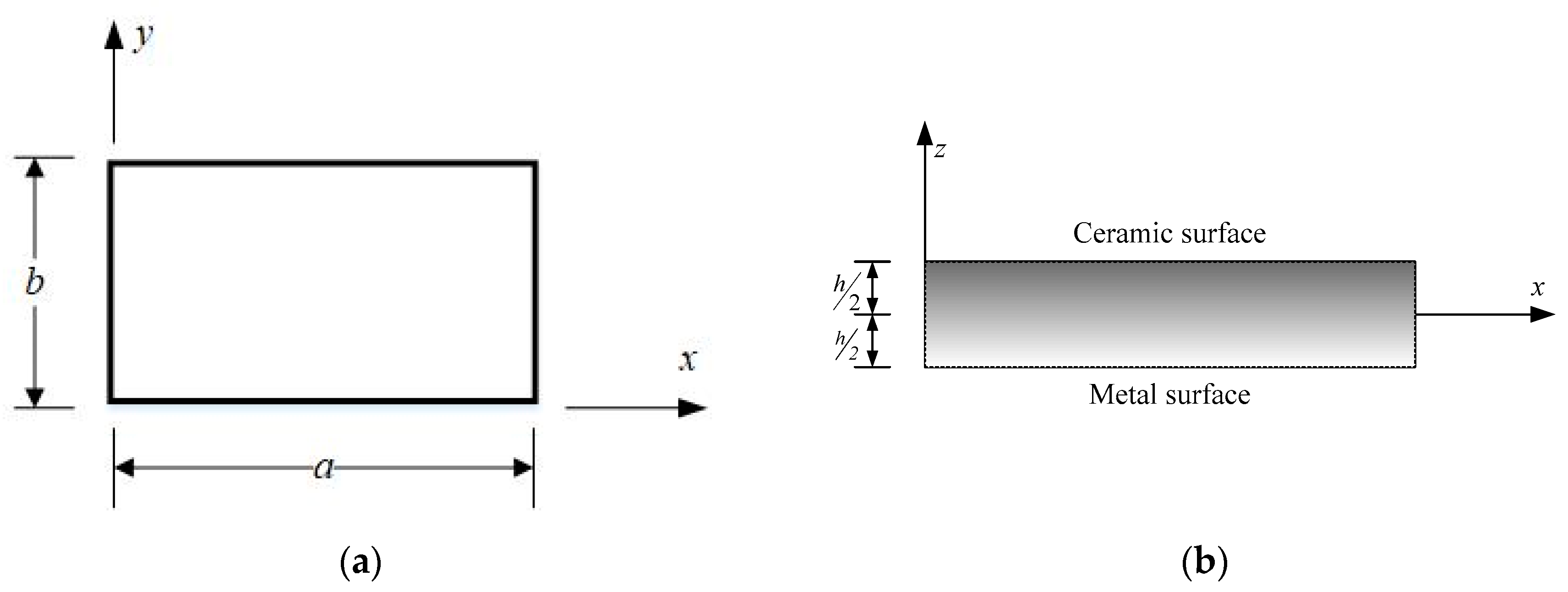
2.1. Material Models
2.2. Governing Equations and Boundary Conditions
- Simply supported: ;
- Clamped: = = = = = 0, and
- Free: .
2.3. Series Solutions
3. Convergence Studies and Comparisons
4. Numerical Results
- The constraint increases when a free boundary condition changes to a simply supported boundary condition. The constraint further increases in a clamped boundary condition. Higher constraint results in higher plate stiffness and larger natural frequencies. Therefore, > > > and > > > > > (where the subscripts indicate the boundary conditions) if the first six rigid body modes with zero frequencies are considered for plates with FFFF boundary conditions.
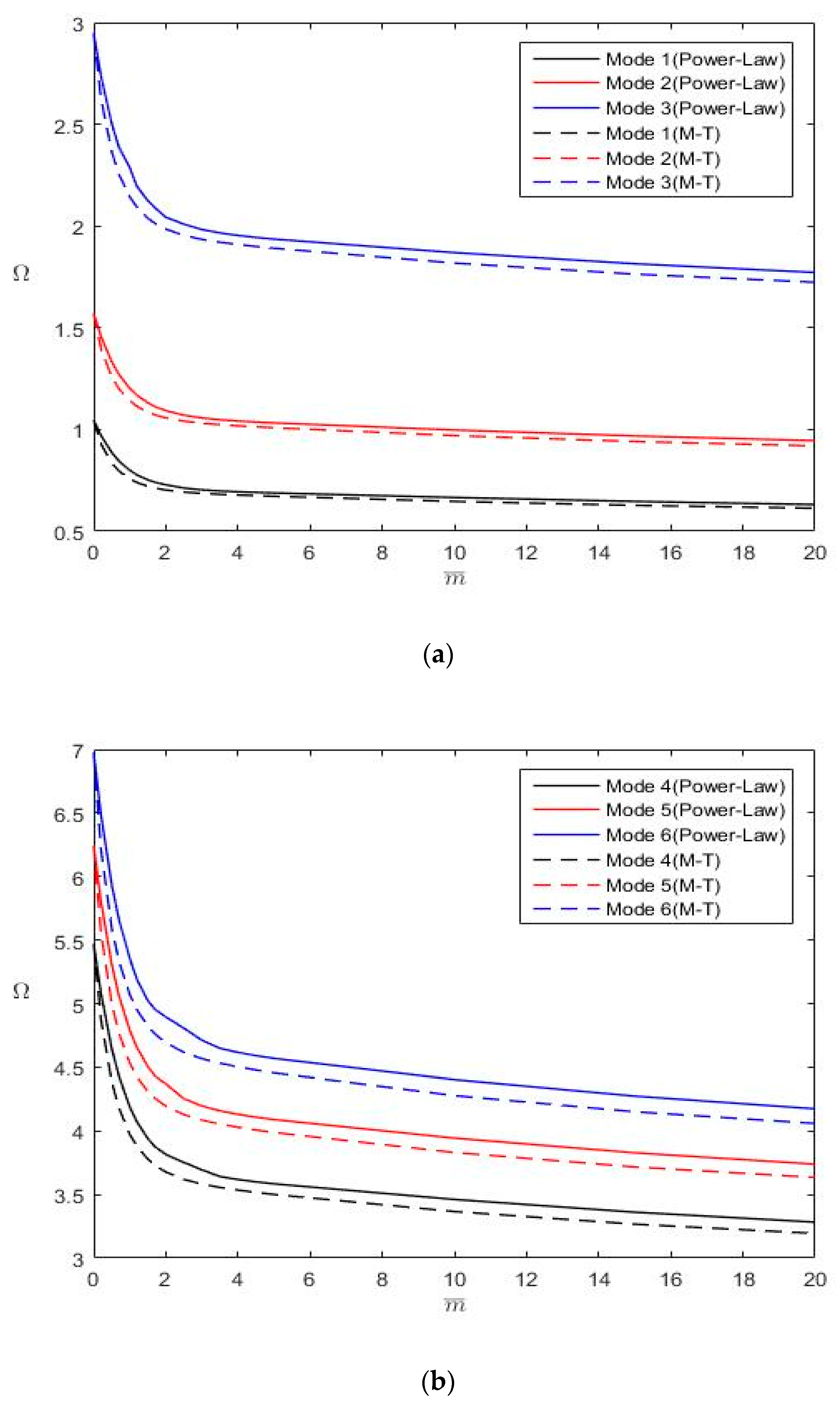
- The Mori–Tanaka material model provides a larger Young’s modulus than the power-law material model does; however, both models yield the same density distribution (Figure 2). Consequently, FGM plates following the Mori-Tanaka material model have larger natural frequencies than those following the power-law material model.
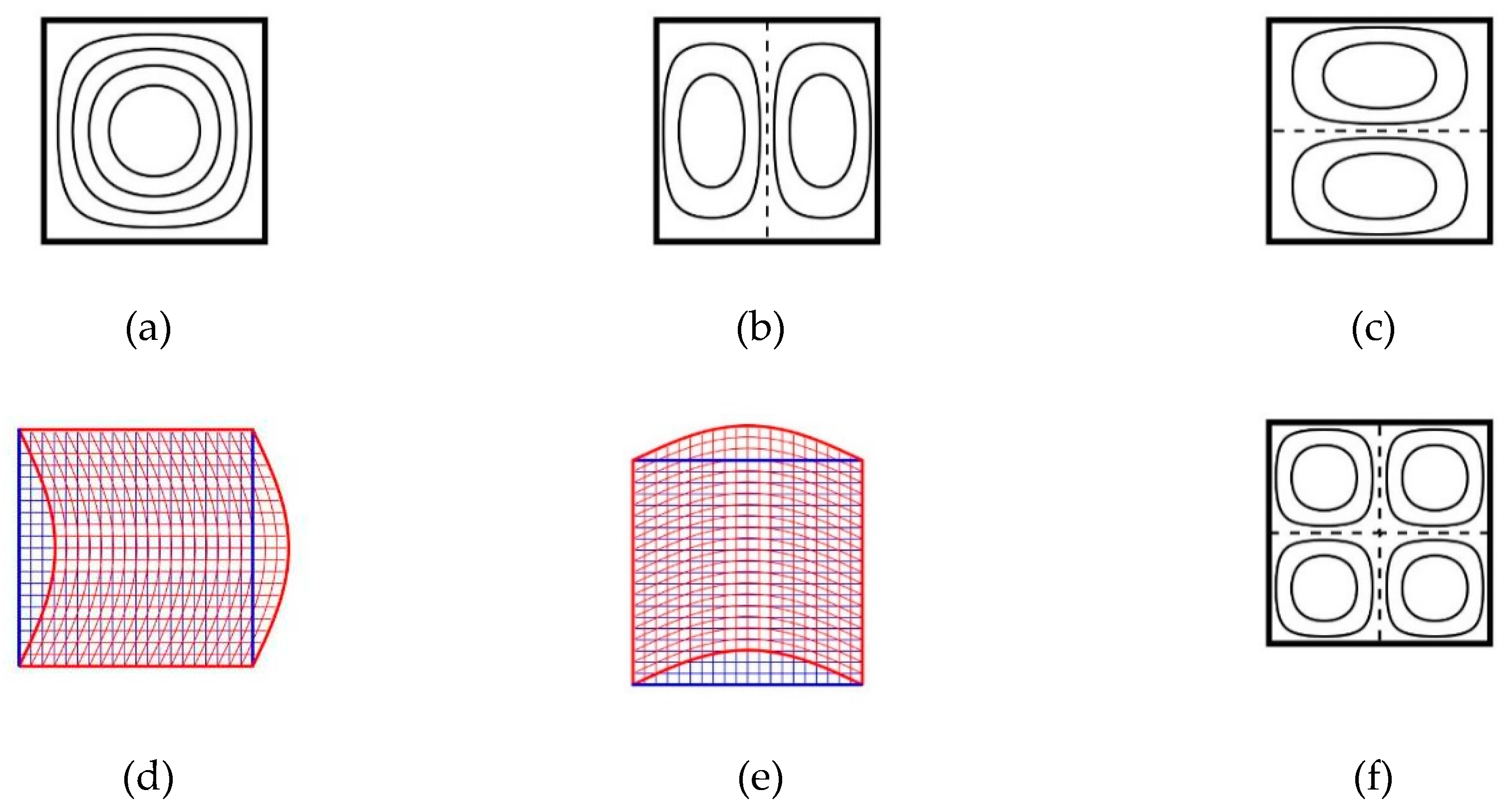
- No in-plane displacement-dominated mode exists in the first six modes for thin square plates with h/a = 0.02; however, such a mode may exist for moderately thick plates with h/a = 0.1.
- The nondimensional frequencies () of plates with h/a = 0.1 are less than those of plates with h/a = 0.02 because h/a is involved in the definition of . When converting to , one finds that the trend is opposite for because the plate rigidity increases with h/a.
5. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Niino, M.; Maeda, S. Recent development status of functionally gradient materials. ISIJ Int. 1990, 30, 699–703. [Google Scholar] [CrossRef]
- Jha, D.K.; Kant, T.; Singh, R.K. A critical review of recent research on functionally graded plates. Compos. Struct. 2013, 96, 833–849. [Google Scholar] [CrossRef]
- Gupta, A.; Talha, M. Recent development in modeling and analysis of functionally graded materials and structures. Prog. Aerosp. Sci. 2015, 79, 1–14. [Google Scholar] [CrossRef]
- Swaminathan, K.; Naveenkumar, D.T.; Zenkour, A.M.; Carrera, E. Stress, vibration and buckling analyses of FGM plates—A state-of-the-art review. Compos. Struct. 2015, 120, 10–31. [Google Scholar] [CrossRef]
- Zhang, N.; Khan, T.; Guo, H.; Shi, S.; Zhong, W.; Zhang, W. Functionally graded materials: An overview of stability, buckling, and free vibration analysis. Adv. Mater. Sci. Eng. 2019, 2019, 1–18. [Google Scholar] [CrossRef]
- Liew, K.M.; Pan, Z.; Zhang, L.W. The recent progress of functionally graded CNT reinforced composites and structures. Sci. China Phys. Mech. Astron. 2020, 63, 234601. [Google Scholar] [CrossRef]
- Abrate, S. Functionally graded plates behave like homogeneous plates. Compos. Part B Eng. 2008, 39, 151–158. [Google Scholar] [CrossRef]
- Zhang, D.G.; Zhou, Y.H. A theoretical analysis of FGM thin plates based on physical neutral surface. Comput. Mater. Sci. 2008, 44, 716–720. [Google Scholar] [CrossRef]
- Yang, Y.; Shen, H.S. Dynamic response of initially stressed functional graded rectangular thin plates. Compos. Struct. 2001, 54, 497–508. [Google Scholar] [CrossRef]
- Zhao, X.; Lee, Y.Y.; Liew, K.M. Free vibration analysis of functionally graded plates using the element-free kp-Ritz method. J. Sound Vib. 2009, 319, 918–939. [Google Scholar] [CrossRef]
- Fu, Y.; Yao, J.; Wan, Z.; Zhao, G. Free vibration analysis of moderately thick orthotropic functionally graded plates with general boundary conditions. Materials 2018, 11, 273–292. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, A.J.M.; Batra, R.C.; Roque, C.M.C.; Qian, L.F.; Jorge, R.M.N. Natural frequencies of functionally graded plates by a meshless method. Compos. Struct. 2006, 75, 593–600. [Google Scholar] [CrossRef]
- Huang, C.S.; McGee, O.G.; Chang, M.J. Vibrations of cracked rectangular FGM thick plates. Compos. Struct. 2011, 93, 1747–1764. [Google Scholar] [CrossRef]
- Hong, C.C. GDQ computation for thermal vibration of thick FGM plates by using fully homogeneous equation and TSDT. Thin-Walled Struct. 2019, 135, 78–88. [Google Scholar] [CrossRef]
- Qian, L.F.; Batra, R.C.; Chen, L.M. Static and dynamic deformations of thick functionally graded elastic plates by using higher-order shear and normal deformable plate theory and meshless local Petrov-Galerkin method. Compos. Part B 2004, 35, 685–697. [Google Scholar] [CrossRef]
- Roque, C.M.C.; Ferreira, A.J.M.; Jorge, R.M.N. A radial basis function approach for the free vibration analysis of functionally graded plates using a refined theory. J. Sound Vib. 2007, 300, 1048–1070. [Google Scholar] [CrossRef]
- Uymaz, B.; Aydogdu, M. Three-dimensional vibration analysis of functionally graded plates under various boundary conditions. J. Reinf. Plast. Compos. 2007, 26, 1847–1863. [Google Scholar] [CrossRef]
- Cui, J.; Zhou, T.R.; Ye, R.C.; Gaidai, O.; Li, Z.C.; Tao, S.H. Three-dimensional vibration analysis of a functionally graded sandwich rectangular plate resting on an elastic foundation using a semi-analytical method. Materials 2019, 12, 3401. [Google Scholar] [CrossRef]
- Huang, C.S.; Yang, P.J.; Chang, M.J. Three-dimensional vibrations of functionally graded material cracked rectangular plates with through internal cracks. Compos. Struct. 2012, 94, 2764–2776. [Google Scholar] [CrossRef]
- Huang, C.S.; McGee, O.G.; Wang, K.P. Three-dimensional vibrations of cracked rectangular parallelepipeds of functionally graded material. Int. J. Mech. Sci. 2013, 70, 1–25. [Google Scholar] [CrossRef]
- Burlayenko, V.N.; Sadowski, T.; Dimitrova, S. Three-dimensional free vibration analysis of thermally loaded FGM sandwich plates. Materials 2019, 12, 2377. [Google Scholar] [CrossRef] [PubMed]
- Hosseini-Hashemi, S.; Rokni Damavandi Taher, H.; Akhavan, H.; Omidi, M. Free vibration of functionally graded rectangular plates using first-order shear deformation plate theory. Appl. Math. Modeling 2009, 34, 1276–1291. [Google Scholar] [CrossRef]
- Hosseini-Hashemi, S.; Fadaee, M.; Atashipour, S.R. A new exact analytical approach for free vibration of Reissner–Mindlin functionally graded rectangular plates. Int. J. Mech. Sci. 2011, 53, 11–22. [Google Scholar] [CrossRef]
- Ghashochi-Bargh, H.; Razavi, S. A simple analytical model for free vibration of orthotropic and functionally graded rectangular plates. Alex. Eng. J. 2018, 57, 595–607. [Google Scholar] [CrossRef]
- Hosseini-Hashemi, S.; Fadaee, M.; Atashipour, S.R. Study on the free vibration of thick functionally graded rectangular plates according to a new exact closed-form procedure. Compos. Struct. 2011, 93, 722–735. [Google Scholar] [CrossRef]
- Matsunaga, H. Free vibration and stability of functionally graded plates according to a 2-D higher-order deformation theory. Compos. Struct. 2008, 82, 499–512. [Google Scholar] [CrossRef]
- Sekkal, M.; Fahsi, B.; Tounsi, A.; Mahmoud, S.R. A novel and simple higher order shear deformation theory for stability and vibration of functionally graded sandwich plate. Steel Compos. Struct. 2017, 25, 389–401. [Google Scholar]
- Vel, S.S.; Batra, R.C. Three-dimensional exact solution for the vibration of functionally graded rectangular plates. J. Sound Vib. 2004, 272, 703–730. [Google Scholar] [CrossRef]
- Reddy, J.N.; Cheng, Z.Q. Frequency of functionally graded plates with three-dimensional asymptotic approach. J. Eng. Mech. ASCE 2003, 129, 896–900. [Google Scholar] [CrossRef]
- Huo, R.L.; Liu, W.Q.; Wu, P.; Zhou, D. Analytical solutions for sandwich plates considering permeation effect by 3-D elasticity theory. Steel Compos. Struct. 2017, 25, 127–139. [Google Scholar]
- Tolstov, G.P. Fourier Series; Prentice-Hall: Englewood Cli’s, NJ, USA, 1965. [Google Scholar]
- Mindlin, R.D. Influence of rotary inertia and shear on flexural motions of isotropic, elastic plates. J. Appl. Mech. ASME 1951, 18, 31–38. [Google Scholar]
- Li, W.L. Free vibrations of beams with general boundary conditions. J. Sound Vib. 2000, 237, 709–725. [Google Scholar] [CrossRef]
- Li, W.L.; Zhang, X.; Du, J.; Liu, Z. An exact series solution for the transverse vibration of rectangular plates with general elastic boundary supports. J. Sound Vib. 2009, 321, 254–269. [Google Scholar] [CrossRef]
- Liew, K.M.; Xiang, Y.; Kitipornchai, S. Transverse vibration of thick rectangular plates-I. Comprehensive sets of boundary conditions. Comput. Struct. 1993, 49, 1–29. [Google Scholar] [CrossRef]
- Du, J.; Li, W.L.; Jin, G.; Yang, T.; Liu, Z. An analytical method for the in-plane vibration analysis of rectangular plates with elastically restrained edges. J. Sound Vib. 2007, 306, 908–927. [Google Scholar] [CrossRef]


| Material | Properties | ||
|---|---|---|---|
| E (GPa) | Poisson’s Ratio (ν) | (kg/m3) | |
| Aluminum (Al) | 70.0 | 0.3 | 2702 |
| Alumina (Al2O3) | 380 | 0.3 | 3800 |
| Zirconia (ZrO2) | 200 | 0.3 | 5700 |
| Material Model | Material Ingredient | Mode | Exact Closed-Form Sol. | Published | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 15 | 25 | 30 | 35 | |||||
| Power-Law | Al/Al2O3 | 1 | 4.510 | 4.433 | 4.422 | 4.419 | 4.418 | 4.418 | 4.419 (1,1) | <4.420> (4.347) |
| 2 | 11.03 | 10.63 | 10.60 | 10.60 | 10.58 | 10.58 | 10.59 (1,2) | <10.59> (10.42) | ||
| 3 | 11.03 | 10.63 | 10.60 | 10.56 | 10.58 | 10.58 | 10.59 (2,1) | </> (10.42) | ||
| 4 * | 16.22 | 16.20 | 16.20 | 16.20 | 16.20 | 16.20 | 16.20 (1,0) | <×> (15.94) | ||
| 5 * | 16.22 | 16.20 | 16.20 | 16.20 | 16.20 | 16.20 | 16.20 (0,1) | <×> (/) | ||
| 6 | 16.90 | 16.34 | 16.31 | 16.30 | 16.30 | 16.30 | 16.31 (2,2) | <16.31> (/) | ||
| M-T | Al/ZrO2 | 1 | 5.288 | 5.205 | 5.193 | 5.190 | 5.190 | 5.190 | 5.192 (1,1) | {5.096} |
| 2 | 12.90 | 12.45 | 12.42 | 12.41 | 12.41 | 12.41 | 12.41 (1,2) | {12.30} | ||
| 3 | 12.90 | 12.45 | 12.42 | 12.41 | 12.41 | 12.41 | 12.41 (2,1) | {12.30} | ||
| 4 * | 18.10 | 18.09 | 18.08 | 18.08 | 18.08 | 18.08 | 18.08 (1,0) | {17.49} | ||
| 5 * | 18.10 | 18.09 | 18.08 | 18.08 | 18.08 | 18.08 | 18.08 (0,1) | {17.49} | ||
| 6 | 19.74 | 19.12 | 19.08 | 19.07 | 19.06 | 19.06 | 19.09 (2,2) | {18.87} | ||
| Mode | Published | |||||||
|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 15 | 25 | 30 | 35 | |||
| 0 | 1 | 8.183 | 8.079 | 8.073 | 8.071 | 8.071 | 8.070 | {8.070} <8.070> |
| 2 | 15.37 | 14.91 | 14.88 | 14.87 | 14.86 | 14.86 | {14.86} <14.86> | |
| 3 | 18.25 | 17.95 | 17.93 | 17.92 | 17.92 | 17.92 | {17.92} <17.92> | |
| 4 * | 19.50 | 19.49 | 19.48 | 19.48 | 19.48 | 19.48 | [19.48] < × > | |
| 5 | 24.49 | 23.91 | 23.87 | 23.85 | 23.85 | 23.85 | {23.85} <23.85> | |
| 6 | 27.72 | 26.44 | 26.32 | 26.29 | 26.29 | 26.28 | {26.28} </> | |
| 1 | 1 | 6.320 | 6.228 | 6.223 | 6.221 | 6.221 | 6.221 | <6.220> |
| 2 | 11.89 | 11.51 | 11.48 | 11.47 | 11.47 | 11.47 | <11.47> | |
| 3 | 14.17 | 13.94 | 13.92 | 13.91 | 13.91 | 13.91 | <13.92> | |
| 4 * | 16.22 | 16.20 | 16.20 | 16.20 | 16.20 | 16.20 | <×> | |
| 5 | 19.05 | 18.57 | 18.54 | 18.53 | 18.53 | 18.53 | <18.54> | |
| 6 | 21.62 | 20.48 | 20.38 | 20.35 | 20.35 | 20.35 | </> | |
| Mode | Published | |||||||
|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 15 | 25 | 30 | 35 | |||
| 0 | 1 | 1.039 | 1.038 | 1.038 | 1.038 | 1.038 | 1.038 | {1.038} (1.030) |
| 2 | 2.399 | 2.428 | 2.435 | 2.438 | 2.439 | 2.439 | {2.440} (2.391) | |
| 3 | 6.134 | 6.082 | 6.079 | 6.079 | 6.079 | 6.079 | {6.080} (6.005) | |
| 4 * | 6.548 | 6.576 | 6.578 | 6.580 | 6.581 | 6.581 | {/} (7.636) | |
| 5 | 7.742 | 7.702 | 7.712 | 7.715 | 7.716 | 7.716 | {7.716} (/) | |
| 6 | 8.417 | 8.518 | 8.533 | 8.544 | 8.545 | 8.546 | {8.548} (/) | |
| 5 | 1 | 0.6833 | 0.6826 | 0.6827 | 0.6828 | 0.6828 | 0.6828 | (0.6768) |
| 2 | 1.575 | 1.594 | 1.599 | 1.601 | 1.601 | 1.601 | (1.568) | |
| 3 | 4.017 | 3.983 | 3.981 | 3.981 | 3.981 | 3.981 | (3.927) | |
| 4 * | 4.253 | 4.272 | 4.273 | 4.274 | 4.274 | 4.275 | (4.263) | |
| 5 | 5.065 | 5.039 | 5.045 | 5.047 | 5.047 | 5.047 | (/) | |
| 6 | 5.510 | 5.577 | 5.586 | 5.593 | 5.594 | 5.594 | (/) | |
| Mode | Published | |||||||
|---|---|---|---|---|---|---|---|---|
| 5 | 15 | 25 | 35 | 40 | 45 | |||
| 0 | 1 | 3.823 | 3.842 | 3.846 | 3.847 | 3.849 | 3.849 | {3.849} |
| 2 | 6.921 | 5.794 | 5.745 | 5.737 | 5.736 | 5.736 | {5.733} | |
| 3 | 7.821 | 7.091 | 7.064 | 7.059 | 7.060 | 7.060 | {7.058} | |
| 4 | 10.08 | 9.665 | 9.656 | 9.655 | 9.660 | 9.660 | {9.660} | |
| 5 | 10.08 | 9.665 | 9.656 | 9.655 | 9.660 | 9.660 | {9.660} | |
| 6 | 16.93 | 16.76 | 16.74 | 16.74 | 16.75 | 16.75 | {16.75} | |
| 5 | 1 | 2.508 | 2.521 | 2.523 | 2.524 | 2.524 | 2.524 | (2.512) |
| 2 | 4.516 | 3.790 | 3.759 | 3.753 | 3.752 | 3.752 | (3.746) | |
| 3 | 5.111 | 4.640 | 4.623 | 4.620 | 4.620 | 4.619 | (4.608) | |
| 4 | 6.579 | 6.314 | 6.309 | 6.308 | 6.308 | 6.308 | (6.270) | |
| 5 | 6.579 | 6.314 | 6.309 | 6.308 | 6.308 | 6.308 | (6.270) | |
| 6 | 11.03 | 10.92 | 10.91 | 10.91 | 10.91 | 10.91 | (/) | |
| Case | SFSF | SSSF | SCSF | SCSS | SFFF | SSFF | CSFF | CSSF |
| Ave. Differences (%) | 0.080 | 0.045 | 0.040 | 0.054 | 0.088 | 0.045 | 0.056 | 0.030 |
| Case | CFSF | CFCF | CSCF | CCFF | CCSF | CCSS | CCCF | CCCS |
| Ave. Differences (%) | 0.056 | 0.044 | 0.020 | 0.055 | 0.028 | 0.045 | 0.024 | 0.049 |
| b/a | h/a | Mode | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |||
| 1 | 0.02 | 0 | 10.84 | 22.03 | 22.03 | 32.36 | 39.29 | 39.49 |
| 0.5 | 9.184 | 18.67 | 18.67 | 27.44 | 33.32 | 33.48 | ||
| 2 | 7.527 | 15.30 | 15.30 | 22.49 | 27.30 | 27.44 | ||
| 5 | 7.133 | 14.49 | 14.49 | 21.29 | 25.84 | 25.97 | ||
| 0.1 | 0 | 9.842 | 18.77 | 18.77 | 26.31 | 31.00 | 31.30 | |
| 0.5 | 8.409 | 16.11 | 16.11 | 22.64 | 26.73 | 26.98 | ||
| 2 | 6.902 | 13.23 | 13.23 | 18.58 | 21.94 | 22.15 | ||
| 5 | 6.451 | 12.27 | 12.27 | 17.15 | 20.18 | 20.38 | ||
| 2 | 0.02 | 0 | 7.413 | 9.593 | 13.48 | 19.05 | 19.23 | 21.34 |
| 0.5 | 6.281 | 8.128 | 11.43 | 16.14 | 16.29 | 18.09 | ||
| 2 | 5.148 | 6.662 | 9.363 | 13.23 | 13.35 | 14.83 | ||
| 5 | 4.879 | 6.313 | 8.872 | 12.53 | 12.65 | 14.04 | ||
| 0.1 | 0 | 6.897 | 8.815 | 12.16 | 16.64 | 16.75 | 18.30 | |
| 0.5 | 5.882 | 7.523 | 10.39 | 14.27 | 14.33 | 15.70 | ||
| 2 | 4.827 | 6.173 | 8.521 | 11.71 | 11.75 | 12.88 | ||
| 5 | 4.526 | 5.779 | 7.960 | 10.88 | 10.95 | 11.95 | ||
| b/a | h/a | Mode | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |||
| 1 | 0.02 | 0 | 4.038 | 5.976 | 7.361 | 10.44 | 10.44 | 18.41 |
| 0.5 | 3.421 | 5.067 | 6.238 | 8.849 | 8.849 | 15.59 | ||
| 2 | 2.804 | 4.153 | 5.112 | 7.252 | 7.252 | 12.78 | ||
| 5 | 2.657 | 3.932 | 4.843 | 6.869 | 6.869 | 12.11 | ||
| 0.1 | 0 | 3.849 | 5.735 | 7.060 | 9.660 | 9.660 | 16.75 | |
| 0.5 | 3.269 | 4.861 | 5.988 | 8.213 | 8.213 | 14.25 | ||
| 2 | 2.677 | 3.969 | 4.893 | 6.711 | 6.711 | 11.63 | ||
| 5 | 2.525 | 3.752 | 4.621 | 6.312 | 6.312 | 10.91 | ||
| 2 | 0.02 | 0 | 1.656 | 1.997 | 4.389 | 4.511 | 6.690 | 7.604 |
| 0.5 | 1.405 | 1.693 | 3.719 | 3.821 | 5.670 | 6.442 | ||
| 2 | 1.152 | 1.387 | 3.048 | 3.132 | 4.647 | 5.280 | ||
| 5 | 1.090 | 1.315 | 2.888 | 2.969 | 4.401 | 5.004 | ||
| 0.1 | 0 | 1.610 | 1.927 | 4.196 | 4.382 | 6.419 | 7.176 | |
| 0.5 | 1.364 | 1.636 | 3.563 | 3.717 | 5.443 | 6.099 | ||
| 2 | 1.117 | 1.341 | 2.918 | 3.042 | 4.446 | 4.991 | ||
| 5 | 1.058 | 1.267 | 2.753 | 2.875 | 4.201 | 4.700 | ||
| BC | h/a | Material Model | Mode | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||||
| CFFF | 0.02 | 0 | Power-Law | 1.049 | 2.552 | 6.418 | 8.180 | 9.273 | 16.17 |
| 0.5 | 0.8888 | 2.162 | 5.437 | 6.930 | 7.857 | 13.70 | |||
| 2 | 0.7284 | 1.772 | 4.456 | 5.678 | 6.439 | 11.23 | |||
| 5 | 0.6907 | 1.680 | 4.224 | 5.383 | 6.102 | 10.63 | |||
| 0.1 | 0 | Power-Law or M-T | 1.038 | 2.439 | 6.079 | 6.581 * | 7.716 | 8.546 | |
| 0.5 | Power-Law | 0.8000 | 2.072 | 5.168 | 5.907 * | 6.555 | 7.280 | ||
| M-T | 0.8089 | 1.960 | 4.879 | 5.606 * | 6.186 | 6.877 | |||
| 2 | Power-Law | 0.7211 | 1.698 | 4.230 | 4.946 * | 5.359 | 5.962 | ||
| M-T | 0.6973 | 1.643 | 4.087 | 4.650 * | 5.176 | 5.759 | |||
| 5 | Power-Law | 0.6828 | 1.601 | 3.981 | 4.275 * | 5.047 | 5.594 | ||
| M-T | 0.6666 | 1.564 | 3.886 | 4.073 * | 4.926 | 5.457 | |||
| CFSF | 0.02 | 0 | Power-Law | 4.591 | 6.191 | 11.91 | 14.90 | 16.90 | 23.15 |
| 0.5 | 3.664 | 4.950 | 9.511 | 11.89 | 13.50 | 18.48 | |||
| 2 | 3.084 | 4.162 | 8.000 | 10.00 | 11.36 | 15.55 | |||
| 5 | 2.950 | 3.981 | 7.652 | 9.569 | 10.86 | 14.87 | |||
| 0.1 | 0 | 4.401 | 5.820 | 10.89 | 13.45 | 15.05 | 15.57 * | ||
| 0.5 | 3.526 | 4.678 | 8.742 | 10.83 | 12.14 | 13.27 * | |||
| 2 | 2.963 | 3.922 | 7.316 | 9.071 | 10.16 | 10.99 * | |||
| 5 | 2.818 | 3.724 | 6.935 | 8.563 | 9.569 | 9.641 * | |||
| BC | Mode | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| SSFF | 0 | 0.9943 | 5.011 | 5.600 | 10.63 | 12.16 * | 14.10 |
| 0.5 | 0.8432 | 4.254 | 4.754 | 9.044 | 10.92 * | 12.00 | |
| 2 | 0.6910 | 3.481 | 3.891 | 7.398 | 9.134 * | 9.806 | |
| 5 | 0.6538 | 3.286 | 3.672 | 6.951 | 7.896 * | 9.204 | |
| CSFF | 0 | 1.571 | 5.472 | 6.977 | 8.176 * | 11.71 | 14.51 |
| 0.5 | 1.333 | 4.648 | 5.936 | 7.340 | 9.984 | 12.35 | |
| 2 | 1.093 | 3.804 | 4.860 | 6.148 * | 8.171 | 10.10 | |
| 5 | 1.033 | 3.585 | 4.569 | 5.313 * | 7.653 | 9.470 | |
| CSSF | 0 | 4.837 | 8.710 | 13.92 | 16.36 * | 17.23 | 17.83 |
| 0.5 | 4.113 | 7.416 | 11.89 | 14.63 * | 14.74 | 15.25 | |
| 2 | 3.372 | 6.072 | 9.747 | 11.98 | 12.31 * | 12.49 | |
| 5 | 3.175 | 5.703 | 9.106 | 10.60 * | 11.23 | 11.64 | |
| CCFF | 0 | 2.019 | 6.700 | 7.481 | 12.71 | 15.41 * | 16.62 |
| 0.5 | 1.714 | 5.703 | 6.369 | 10.85 | 13.80 * | 14.22 | |
| 2 | 1.405 | 4.668 | 5.217 | 8.883 | 11.42 * | 11.78 | |
| 5 | 1.327 | 4.385 | 4.900 | 8.300 | 9.983 * | 10.87 | |
| CCCF | 0 | 6.685 | 10.78 | 16.41 | 19.75 | 20.31 | 23.79 * |
| 0.5 | 5.701 | 9.207 | 14.01 | 16.90 | 17.43 | 21.36 * | |
| 2 | 4.678 | 7.546 | 11.55 | 13.83 | 14.29 | 17.88 * | |
| 5 | 4.385 | 7.050 | 10.72 | 12.85 | 13.25 | 15.46 * | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, C.-S.; Huang, S.H. Analytical Solutions Based on Fourier Cosine Series for the Free Vibrations of Functionally Graded Material Rectangular Mindlin Plates. Materials 2020, 13, 3820. https://doi.org/10.3390/ma13173820
Huang C-S, Huang SH. Analytical Solutions Based on Fourier Cosine Series for the Free Vibrations of Functionally Graded Material Rectangular Mindlin Plates. Materials. 2020; 13(17):3820. https://doi.org/10.3390/ma13173820
Chicago/Turabian StyleHuang, Chiung-Shiann, and S. H. Huang. 2020. "Analytical Solutions Based on Fourier Cosine Series for the Free Vibrations of Functionally Graded Material Rectangular Mindlin Plates" Materials 13, no. 17: 3820. https://doi.org/10.3390/ma13173820
APA StyleHuang, C.-S., & Huang, S. H. (2020). Analytical Solutions Based on Fourier Cosine Series for the Free Vibrations of Functionally Graded Material Rectangular Mindlin Plates. Materials, 13(17), 3820. https://doi.org/10.3390/ma13173820




