Fused Filament Fabricated Polypropylene Composite Reinforced by Aligned Glass Fibers
Abstract
1. Introduction
2. Materials and Methods
2.1. Test Material and Specimen Fabrication
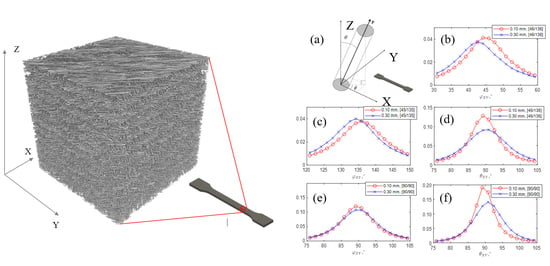
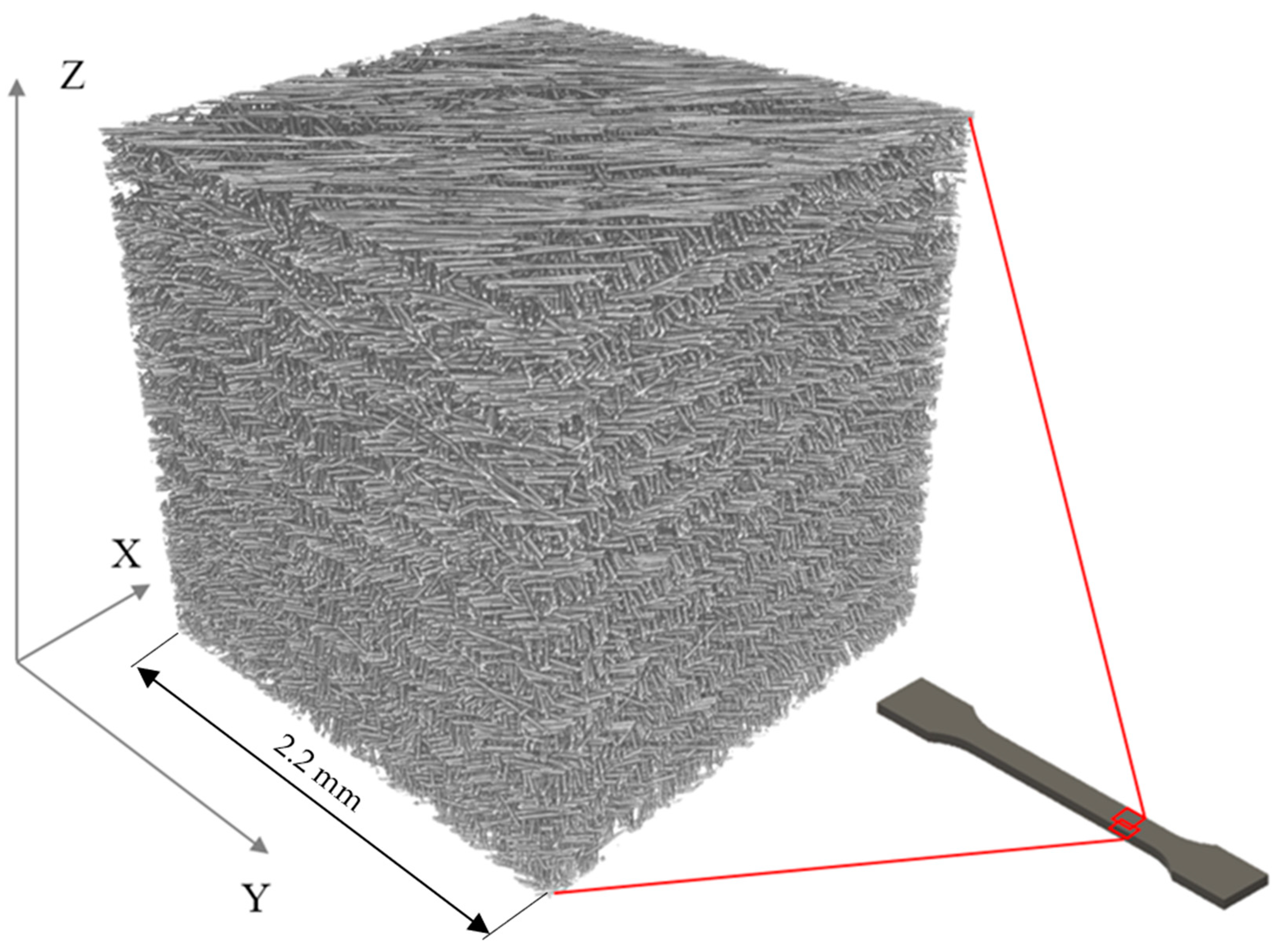
2.2. X-ray Micro-Computed Tomography
2.3. Mechanical Testing
3. Results and Discussion
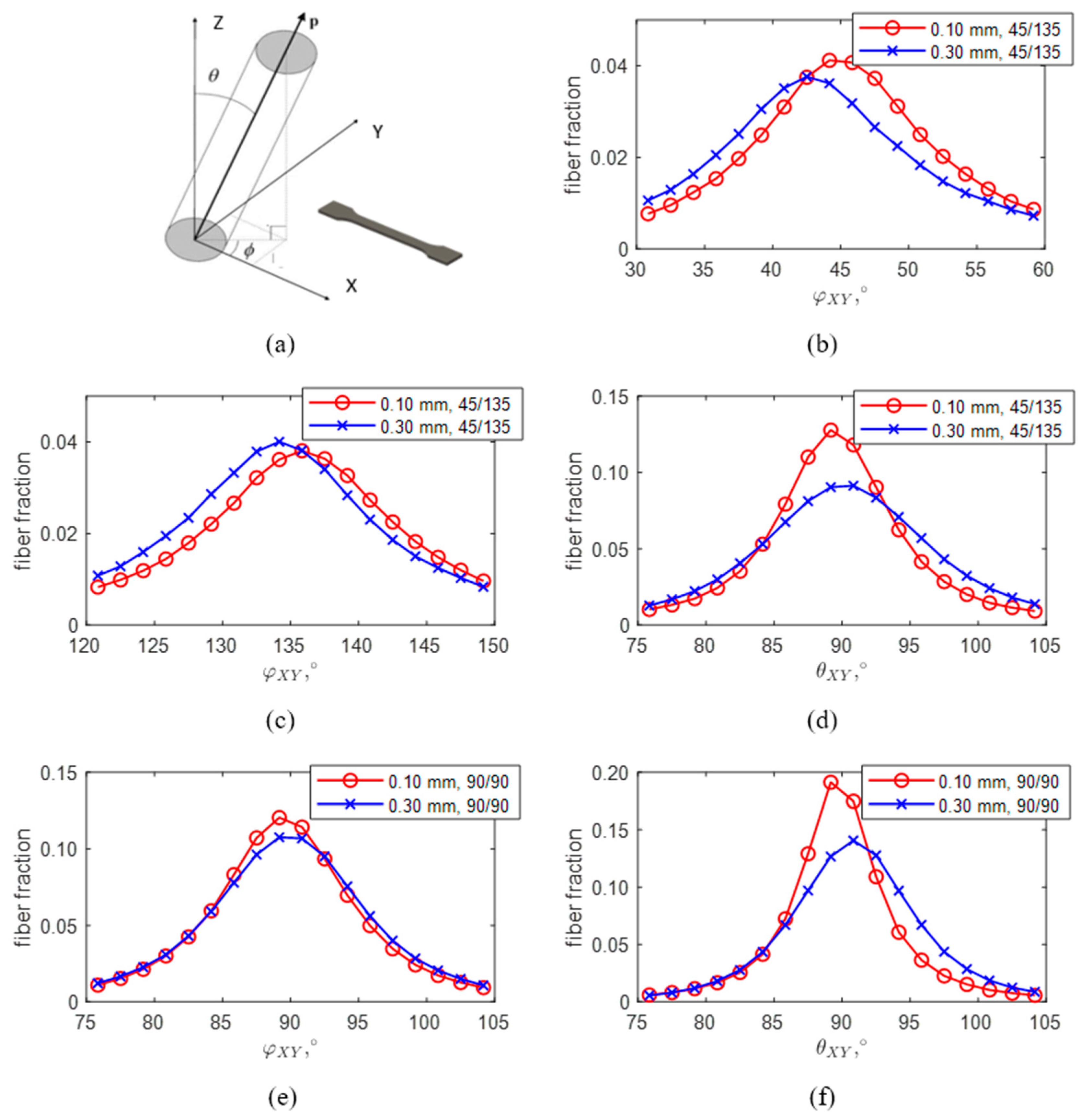
3.1. Fibers Orientation
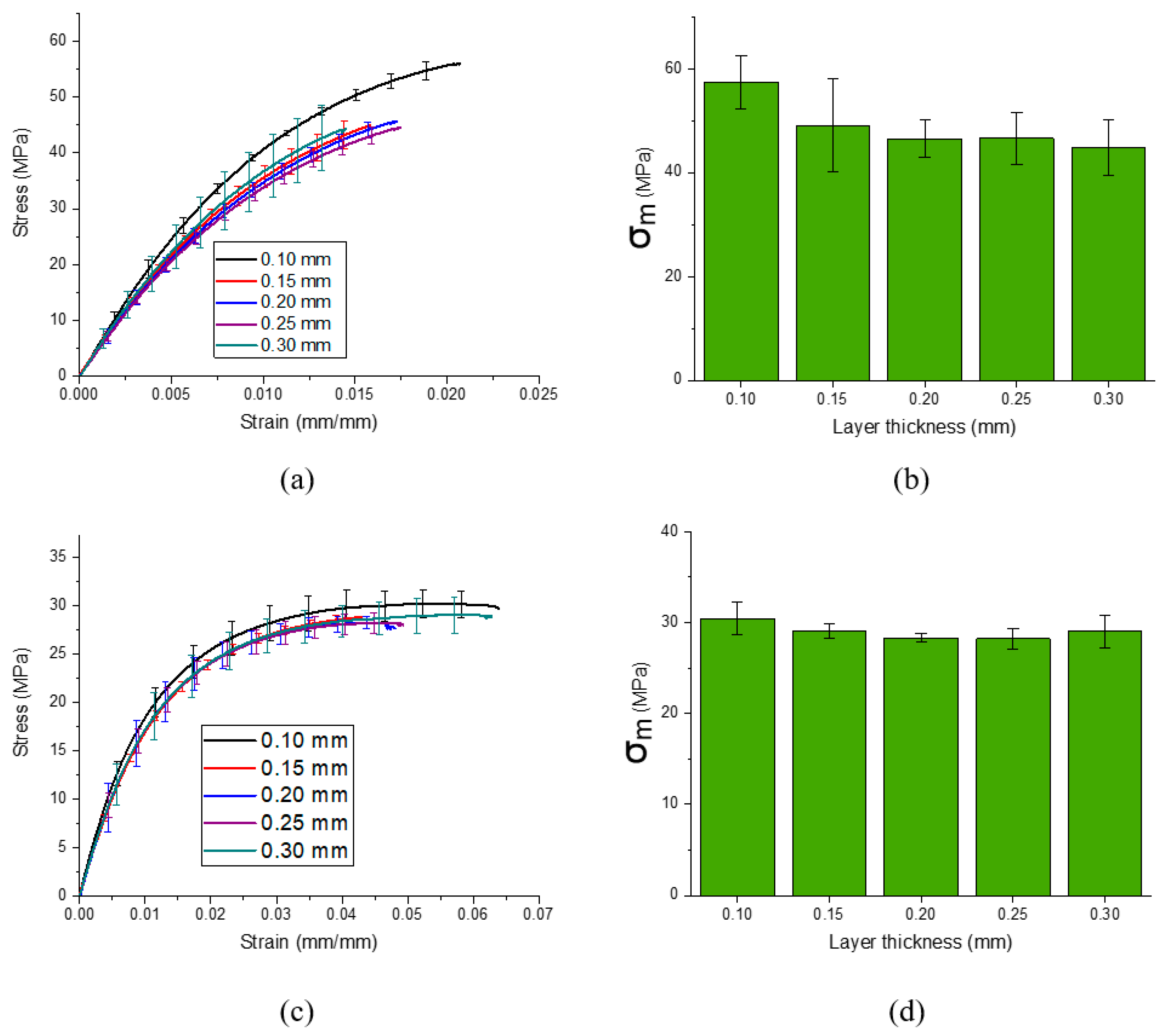
3.2. Mechanical Properties
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Murr, L.E. Frontiers of 3D Printing / Additive Manufacturing: From Human Organs to Aircraft Fabrication. J. Mater. Sci. Technol. 2016, 32, 987–995. [Google Scholar] [CrossRef]
- Ning, F.; Cong, W.; Hu, Y.; Wang, H. Additive manufacturing of carbon fiber-reinforced plastic composites using fused deposition modeling: Effects of process parameters on tensile properties, J. Compos. Mater. 2016, 1–12. [Google Scholar] [CrossRef]
- Blok, L.G.; Longana, M.L.; Yu, H.; Woods, B.K.S. An investigation into 3D printing of fi bre reinforced thermoplastic composites. Addit. Manuf. 2018, 22, 176–186. [Google Scholar] [CrossRef]
- Thiago, R.; Ferreira, L.; Cardoso, I.; Assis, T.; Bürger, D. Experimental characterization and micrography of 3D printed PLA and PLA reinforced with short carbon fibers. Compos. Part B 2017, 124, 88–100. [Google Scholar] [CrossRef]
- Shofner, M.L.; Lozano, K.; Rodrı, F.J. Nanofiber-Reinforced Polymers Prepared by Fused Deposition Modeling. J. Appl. Polym. Sci. 2002, 89, 3081–3090. [Google Scholar] [CrossRef]
- Melenka, G.W.; Cheung, B.K.O.; Schofield, J.S.; Dawson, M.R.; Carey, J.P. Evaluation and prediction of the tensile properties of continuous fiber-reinforced 3D printed structures. Compos. Struct. 2016, 153, 866–875. [Google Scholar] [CrossRef]
- Vaneker, T.H.J. Material Extrusion of Continuous Fiber Reinforced Plastics Using Commingled Yarn. Procedia CIRP 2017, 66, 317–322. [Google Scholar] [CrossRef]
- Brenken, B.; Barocio, E.; Favaloro, A.; Kunc, V.; Pipes, R.B. Fused filament fabrication of fiber-reinforced polymers: A review. Addit. Manuf. 2018, 21, 1–16. [Google Scholar] [CrossRef]
- Fu, S.; Lauke, B. Effects of Fiber Length and Fiber Orientation distributions on the tensile strength of short-fiber-reinforced polymers. Compos. Sci. Technol. 1996, 56, 1179–1190. [Google Scholar] [CrossRef]
- Zhong, W.; Li, F.; Zhang, Z.; Song, L.; Li, Z. Short fiber reinforced composites for fused deposition modeling. Mater. Sci. Eng. A 2001, 301, 125–130. [Google Scholar] [CrossRef]
- Ning, F.; Cong, W.; Wei, J.; Wang, S.; Zhang, M. Additive Manufacturing of CFRP Composites Using Fused Deposition Modeling: Effects of Carbon Fiber Content and Length. In Proceedings of the ASME 2015 International Manufacturing Science and Engineering Conference, Charlotte, NC, USA, 8–12 June 2015. [Google Scholar] [CrossRef]
- Tekinalp, H.L.; Kunc, V.; Velez-Garcia, G.M.; Duty, C.E.; Love, L.J.; Naskar, A.K.; Blue, C.A.; Ozcan, S. Highly oriented carbon fiber-polymer composites via additive manufacturing, Compos. Sci. Technol. 2014, 105, 144–150. [Google Scholar] [CrossRef]
- Ziemian, C.; Sharma, M.; Ziemi, S. Anisotropic Mechanical Properties of ABS Parts Fabricated by Fused Deposition Modelling. Mech. Eng. 2012. [Google Scholar] [CrossRef]
- Goh, G.D.; Yap, Y.L.; Tan, H.K.J.; Sing, S.L.; Goh, G.L.; Yeong, W.Y.; Yap, Y.L.; Tan, H.K.J.; Sing, S.L.; Goh, G.L.; et al. Process–Structure–Properties in Polymer Additive Manufacturing via Material Extrusion: A Review. Crit. Rev. Solid State Mater. Sci. 2019, 113–133. [Google Scholar] [CrossRef]
- Onwubolu, G.C.; Rayegani, F. Characterization and Optimization of Mechanical Properties of ABS Parts Manufactured by the Fused Deposition Modelling Process. Int. J. Manuf. Eng. 2014, 1–13. [Google Scholar] [CrossRef]
- Huang, B.; Singamneni, S. Raster angle mechanics in fused deposition modelling, J. Compos. Mater. 2015. [Google Scholar] [CrossRef]
- Hertle, S.; Drexler, M.; Drummer, D. Additive Manufacturing of Poly (propylene) by Means of Melt Extrusion. Macromol. Mater. Eng. 2016, 1–12. [Google Scholar] [CrossRef]
- Spoerk, M.; Gonzalez-Gutierrez, J.; Lichal, C.; Cajner, H.; Berger, G.R.; Schuschnigg, S.; Cardon, L.; Holzer, C. Optimisation of the Adhesion of Polypropylene-Based Materials during Extrusion-Based Additive Manufacturing. Polymers 2018, 10, 490. [Google Scholar] [CrossRef]
- Silva, A.F.; Carneiro, O.S.; Gomes, R. 3D Printing of Polypropylene Using the Fused Filament Fabrication Technique. AIP Conf. Proc. 2017, 1896, 1–5. [Google Scholar] [CrossRef]
- Sodeifian, G.; Ghaseminejad, S.; Yousefid, A.A. Physics Preparation of polypropylene / short glass fiber composite as Fused Deposition Modeling (FDM) filament. Results Phys. 2019, 12, 205–222. [Google Scholar] [CrossRef]
- Garcea, S.C.; Wang, Y.; Withers, P.J. X-ray computed tomography of polymer composites. Compos. Sci. Technol. 2018, 156, 305–319. [Google Scholar] [CrossRef]
- Straumit, I.; Lomov, S.V.; Wevers, M. Quantification of the internal structure and automatic generation of voxel models of textile composites from X-ray computed tomography data. Compos. Part A Appl. Sci. Manuf. 2015, 69, 150–158. [Google Scholar] [CrossRef]
- Karamov, R.; Martulli, L.M.; Kerschbaum, M.; Sergeichev, I.; Swolfs, Y.; Lomov, S.V. Micro-CT based structure tensor analysis of fibre orientation in random fibre composites versus high-fidelity fibre identification methods. Compos. Struct. 2019, 111818. [Google Scholar] [CrossRef]
- Jerabek, M.; Major, Z.; Lang, R.W. Strain determination of polymeric materials using digital image correlation. Polym. Test. 2010, 29, 407–416. [Google Scholar] [CrossRef]
- Krenchel, H. Fibre Reinforcement: Theoretical and Practical Investigations of the Elasticity and Strength of Fibre-reinforced Materials; Akademisk Forlag: Copenhagen, Denmark, 1964. [Google Scholar]
- Cordin, M.; Bechtold, T.; Pham, T. Effect of fibre orientation on the mechanical properties of polypropylene–lyocell composites. Cellulose 2018, 25, 7197–7210. [Google Scholar] [CrossRef]


| Properties | Values | Unit |
|---|---|---|
| Specific gravity | 1.07 | g/cm3 |
| Melting temperature | 145 | °C |
| Glass fiber length | 100–300 | µm |
| Glass fiber diameter | 15–20 | µm |
| Glass fiber average mass fraction | 25 | % |
| Diameter tolerance | ±0.05 | mm |
| Layer Thickness (mm) | Raster Angle | Modulus (MPa) | Strength (MPa) | Stress at Break (MPa) | Strain at Break (mm/mm) |
|---|---|---|---|---|---|
| 0.10 | (45, 135) | 2470 ± 127 | 30.4 ± 1.8 | 26.8 ± 4.7 | 0.073 ± 0.021 |
| 0.15 | 2080 ± 125 | 29.1 ± 0.8 | 26.6 ± 1.2 | 0.067 ± 0.031 | |
| 0.20 | 2250 ± 668 | 28.3 ± 0.5 | 26.0 ± 4.6 | 0.055 ± 0.022 | |
| 0.25 | 2230 ± 298 | 28.2 ± 1.1 | 25.1 ± 2.4 | 0.053 ± 0.037 | |
| 0.30 | 2190 ± 453 | 29.0 ± 1.8 | 25.7 ± 3.9 | 0.074 ± 0.072 | |
| 0.10 | (90, 90) | 5280 ± 345 | 57.4 ± 5.1 | 54.5 ± 8.1 | 0.025 ± 0.011 |
| 0.15 | 4610 ± 291 | 49.1 ± 8.9 | 46.2 ± 7.6 | 0.022 ± 0.011 | |
| 0.20 | 4510 ± 415 | 46.5 ± 3.6 | 43.1 ± 1.6 | 0.018 ± 0.003 | |
| 0.25 | 4440 ± 198 | 46.6 ± 5.0 | 42.6 ± 7.0 | 0.021 ± 0.007 | |
| 0.30 | 4830 ± 708 | 44.8 ± 5.4 | 42.1 ± 8.9 | 0.015 ± 0.002 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shulga, E.; Karamov, R.; S. Sergeichev, I.; D. Konev, S.; I. Shurygina, L.; S. Akhatov, I.; D. Shandakov, S.; G. Nasibulin, A. Fused Filament Fabricated Polypropylene Composite Reinforced by Aligned Glass Fibers. Materials 2020, 13, 3442. https://doi.org/10.3390/ma13163442
Shulga E, Karamov R, S. Sergeichev I, D. Konev S, I. Shurygina L, S. Akhatov I, D. Shandakov S, G. Nasibulin A. Fused Filament Fabricated Polypropylene Composite Reinforced by Aligned Glass Fibers. Materials. 2020; 13(16):3442. https://doi.org/10.3390/ma13163442
Chicago/Turabian StyleShulga, Eugene, Radmir Karamov, Ivan S. Sergeichev, Stepan D. Konev, Liliya I. Shurygina, Iskander S. Akhatov, Sergey D. Shandakov, and Albert G. Nasibulin. 2020. "Fused Filament Fabricated Polypropylene Composite Reinforced by Aligned Glass Fibers" Materials 13, no. 16: 3442. https://doi.org/10.3390/ma13163442
APA StyleShulga, E., Karamov, R., S. Sergeichev, I., D. Konev, S., I. Shurygina, L., S. Akhatov, I., D. Shandakov, S., & G. Nasibulin, A. (2020). Fused Filament Fabricated Polypropylene Composite Reinforced by Aligned Glass Fibers. Materials, 13(16), 3442. https://doi.org/10.3390/ma13163442