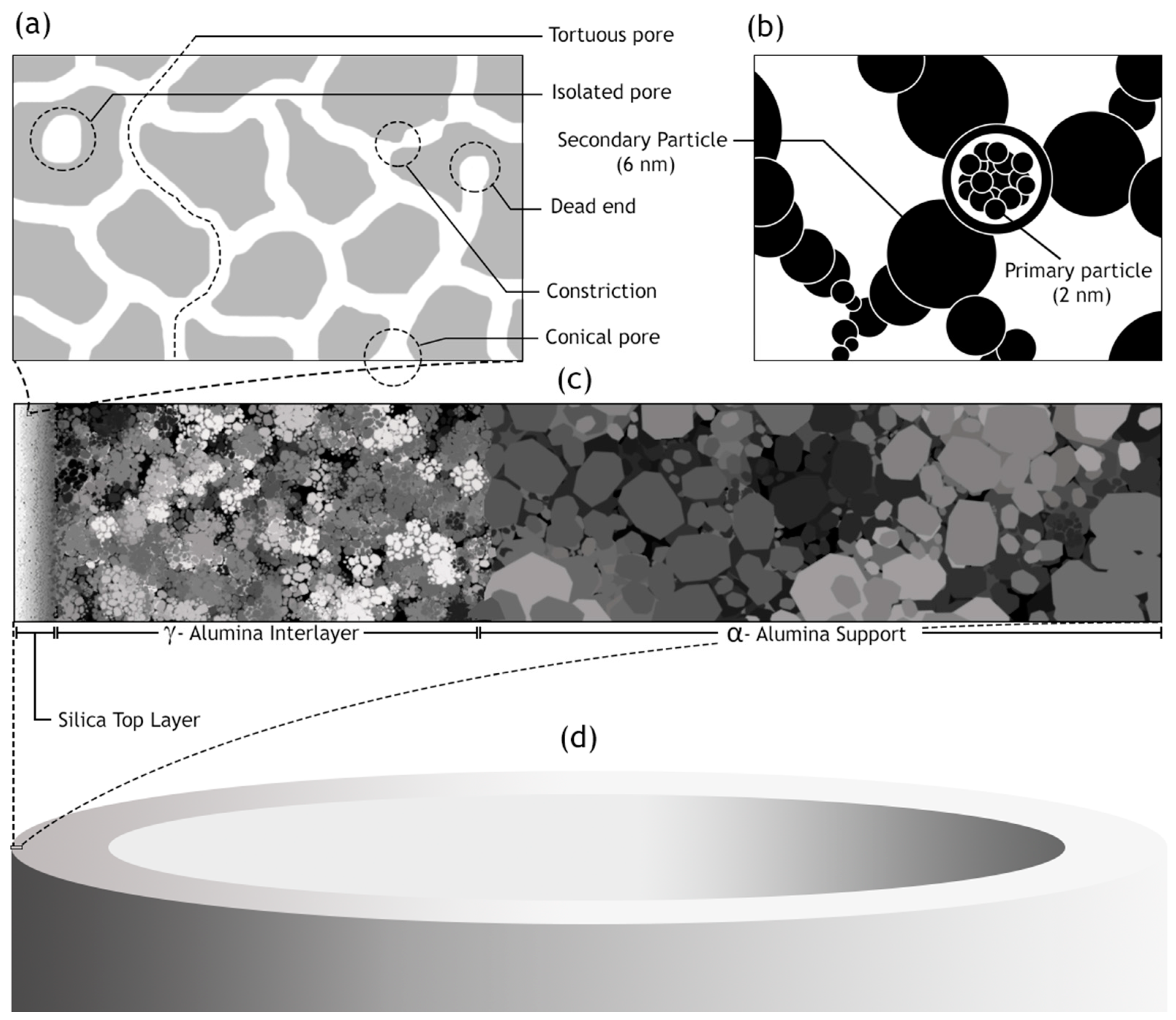
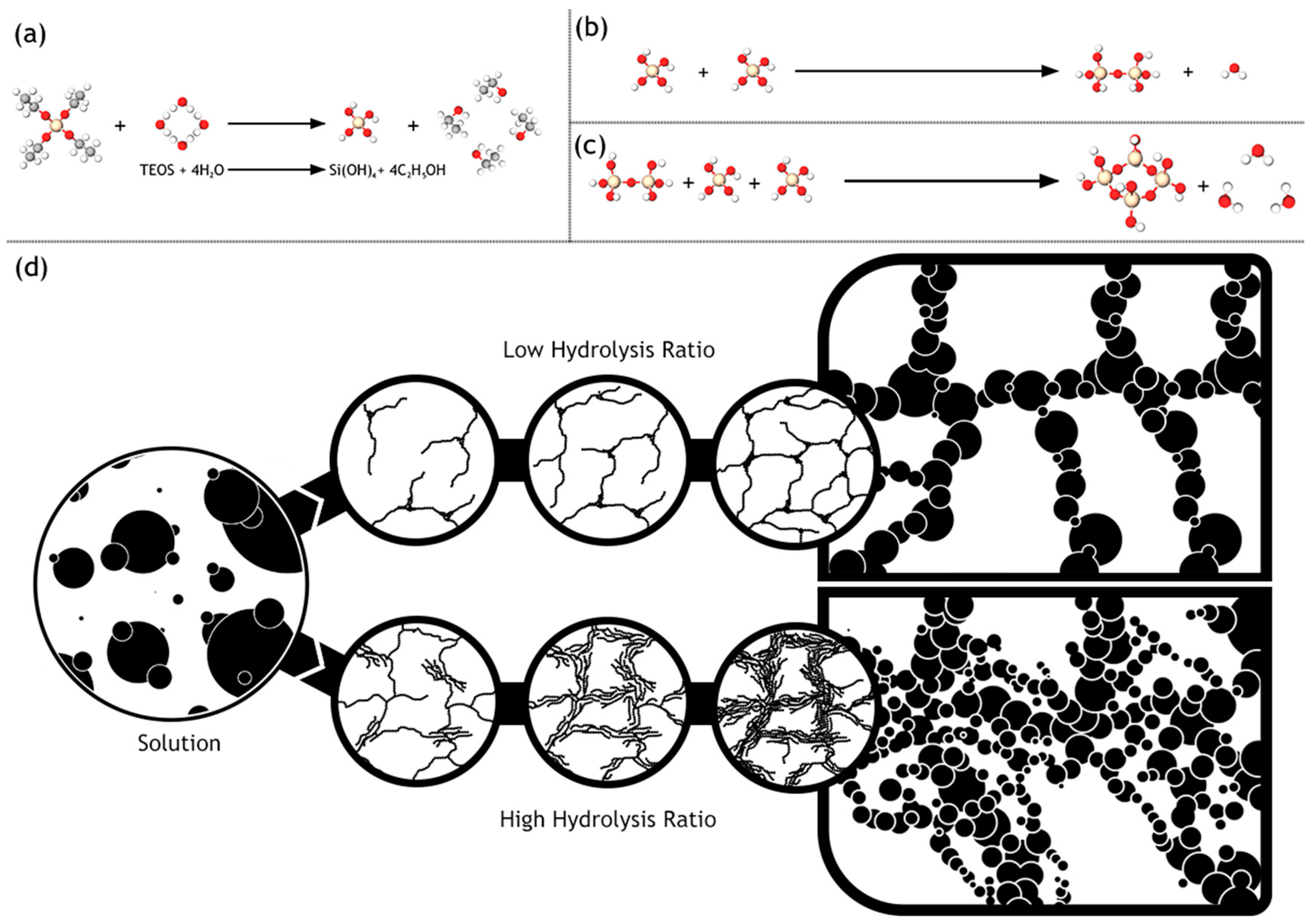
5.1. Advent of Sol–Gel Synthesized Silica Membranes
The synthesis of a selective layer for the purpose of pervaporation is itself a complex process. Hence, obtaining a membrane layer devoid of defects, with suitable thickness and porosity was very important. As a result, early studies (
Table 1) were quite successful in the synthesis aspect and subsequently laid the foundation for future investigation and modifications. However, the membrane viability requiring verification by undergoing pervaporation could not be covered. In one such study on manufacturing silica membranes by Klein et al. [
6], the efficacy and superiority of the sol–gel method was highlighted. The study also emphasizes the high temperature stability and chemical resistance, making them advantageous over the organic membranes. A solution was prepared with tetraethyl orthosilicate (TEOS), water and ethanol. Subsequently 1 M aqueous nitric acid solution was added to initiate hydrolysis. Further treatment with reagents, as well as, ensuing chemical processes; 0.1 mm thick sheets were formed. The amount of water was varied to study the effects on the microstructure. Two moles of water yield the most suitable membrane morphology. The reflected light micrograph of this sample, however, shows connectivity between pinholes on the bottom surface to the large pores present on the top surface. The performance and stability of these membranes were not quantified. This limitation might be largely due to the nascency of the manufacturing process for the fabrication of silica membranes. Pervaporation performance for silica membranes displaying acid resistance was demonstrated by Kitao et al. [
46]. The repeated dipping of the porous substrate in silica polymer and calcination resulted in sufficiently small pores (1 µm). The membrane employed a tubular α-alumina substrate as a support. Acetic acid/water pervaporation studies showed favorable fluxes and separation factor in addition to the membrane stability. The membranes synthesized by Kitao et al. corroborate the favorable features of inorganic membranes over their organic counterparts. The study by Brinker et al. [
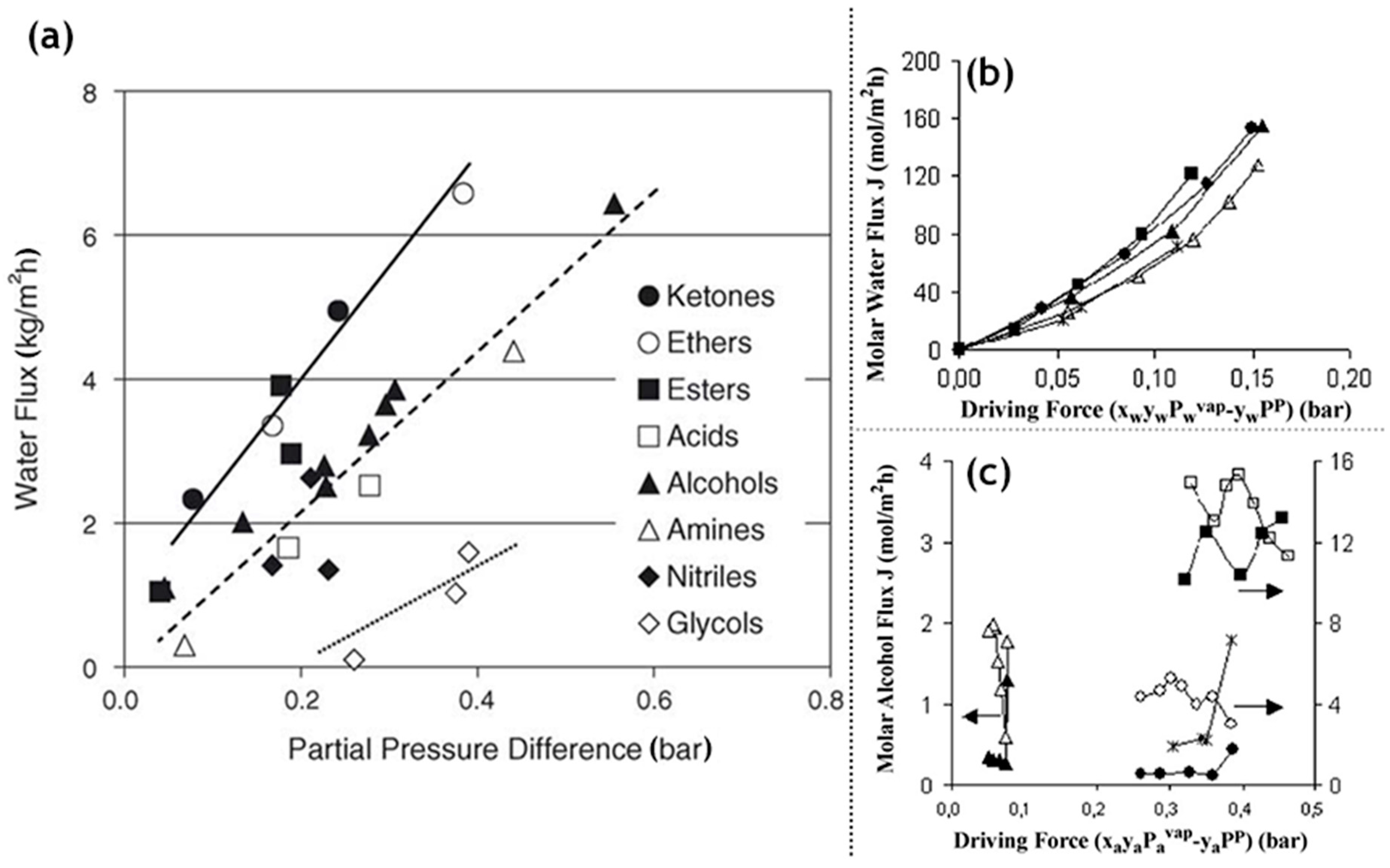
47] demonstrates a major step towards the characterization of membrane parameters. The ultramicroporous membrane synthesized by Brinker et al. has a thickness in the range of 20–120 nm. Alumina supported selective layer facilitates high fluxes. Unprecedented pore sizes, smaller than 10 Å, have the capability of promoting size dependent trans-membrane mass transport at high temperatures resulting in enhanced selectivity (
Figure 4). It was also highlighted in this study that particulate sols offer better control to obtain narrow particle size distributions with the porosity being unaffected at 33% for any arrangement, they do suffer many limitations in comparison to the polymeric sols. Particulate sols may crack as the particle size is decreased, tendency for phase transition or grain growth leading to coarse microstructures as well as their intrinsic instability on account of their solubility in liquid phases as the particle size decreases. Polymeric sols do not suffer from these limitations. However, inorganic membranes made using polymeric sols should be thin in order to curb against low volume fraction porosity with a corollary decrease in flux. Three α-alumina layers with anγ-inner layer were used with the pore size ranging from 10 µm to 4.0 nm. It was found that thickness of the selective top layer was dependent on sol aging time, solvent dilution and casting/dipping time.Permeability characterizations using He, N
2, O
2 and CO
2 displayed selectivities in the lower range of Knudsen dominated diffusion regime thereby indicating that the molecular sieving effect was not the major mode of mass transport. This study, however, presented the role of aging and the role of capillary pressure in the drying phase encountered in dip coating. Zeolitic membranes offer profound control over pore sizes ranging between 2 and 10 nm. However, the major hurdle to their adoption as a viable alternative is because of their prevalence existing in a powder-form. Mesoporous silica membranes on the other hand offer controllability over their microstructure. Ryoo et al. [
48] successfully fabricated 0.5 mm thick membranes, spanning uptoa few centimeters in size. The membranes were strengthened by repeated adsorption and evacuation of TEOS enhancing strength before calcinations. Cetylpyridinium chloride was chosen as a surfactant for generating mesostructures via S
+I
− type ionic mechanism. Synthesizing ordered mesoporous silica, which was crack resistant during calcination by exposure to tetraethyl orthosilicate vapor at 423 K was a key finding of this study.
As the confidence in the sol–gel technique for synthesis of pervaporation-friendly suitable membranes was established, pervaporation measurements were performed to quantify their performance. Subsequent studies, venturing more into the performance aspects, were also incorporating newer methods of characterizations to ascertain the quality of the membrane. Commercial nanofiltration membranes at that time were polymeric in nature and hence failure at high operating temperatures and instability towards chemicals have limited their usability. Tsuru et al. [
56] reported the development of a sol–gel synthesized ceramic membrane made of silica-zirconia composite oxide. The molecular weight cutoff gives an idea of pore size distribution and refers to the ability of a membrane to retain an excess of 90% of a solute in Daltons. The molecular weight cutoff was manipulated by controlling the diameter of the sol used in the final coating stage. As such, this has resulted in four sols with colloidal diameters as 42, 16, 13 and 11 nm. Three membranes were prepared by using the sol with the largest diameters in conjunction with other sols used in the final stage. Characterization using the humid air permeation method yielded pore diameters of 2.9, 1.6 and 1.0 nm in the same order of colloidal diameters of the latter three sols. The addition of zirconia increased the stability of these membranes. The membrane with the smallest pore size showed the permeate volume flux as being dependent on the type of solute, while the others did not show the same dependency. The molecular sieving effect was evidenced based on the filtration performance. Solute-membrane interactions also seem to be in effect due to the difference between the fluxes of sugars, glycols and alcohols. This was later investigated in a study by Tsuru et al. Since the pore sizes were not characteristic of the viscous flow regime, which was demonstrated by the product of permeability and viscosity. Activation energies were found to be a function of the pore size and kinetic diameter of the permeating alcohol. A novel method of preparing mesoporous silica in powder as well as film forms was proposed in the study by Roh et al. [
57]. The solvent evaporation method utilizes an acidic environment, constructively influencing the condensation of cationic inorganic species. Powder form was reportedly developed within 10 min, whereas mesoporous films in a matter of seconds. This method avoids extreme synthesis conditions and offers the advantage of recovering the solvent used in the synthesis. However, pore size and stability studies were not characterized for the film-type.
The studies covered in this section by various groups laid the foundation for fabricating silica membranes for the purpose of pervaporation. They also signaled towards the adoption of the solution–gelation route as the most suitable method for manufacturing these membranes. These studies were also monumental as they highlighted the advantages and novel features of the silica-based membranes at a time when the industry and academic research were dominated by the polymeric membranes. The use of silica membranes for pervaporation-based recovery of solvents in contrast to polymeric membranes or distillation was gaining acceptance.
5.2. Pervaporation Applications of Commercial Silica Membranes
Inorganic silica membranes have the immense potential to completely change the industrial processes dependent on distillation. In the late 1990s and the early 2000s, several commercial membranes were being manufactured. These membranes needed to undergo many tests centered on their efficiency, selectivity, flux output and their versatility in dealing with a few possible solvent mixtures. Various alternatives were appearing for silica membrane-based pervaporation [
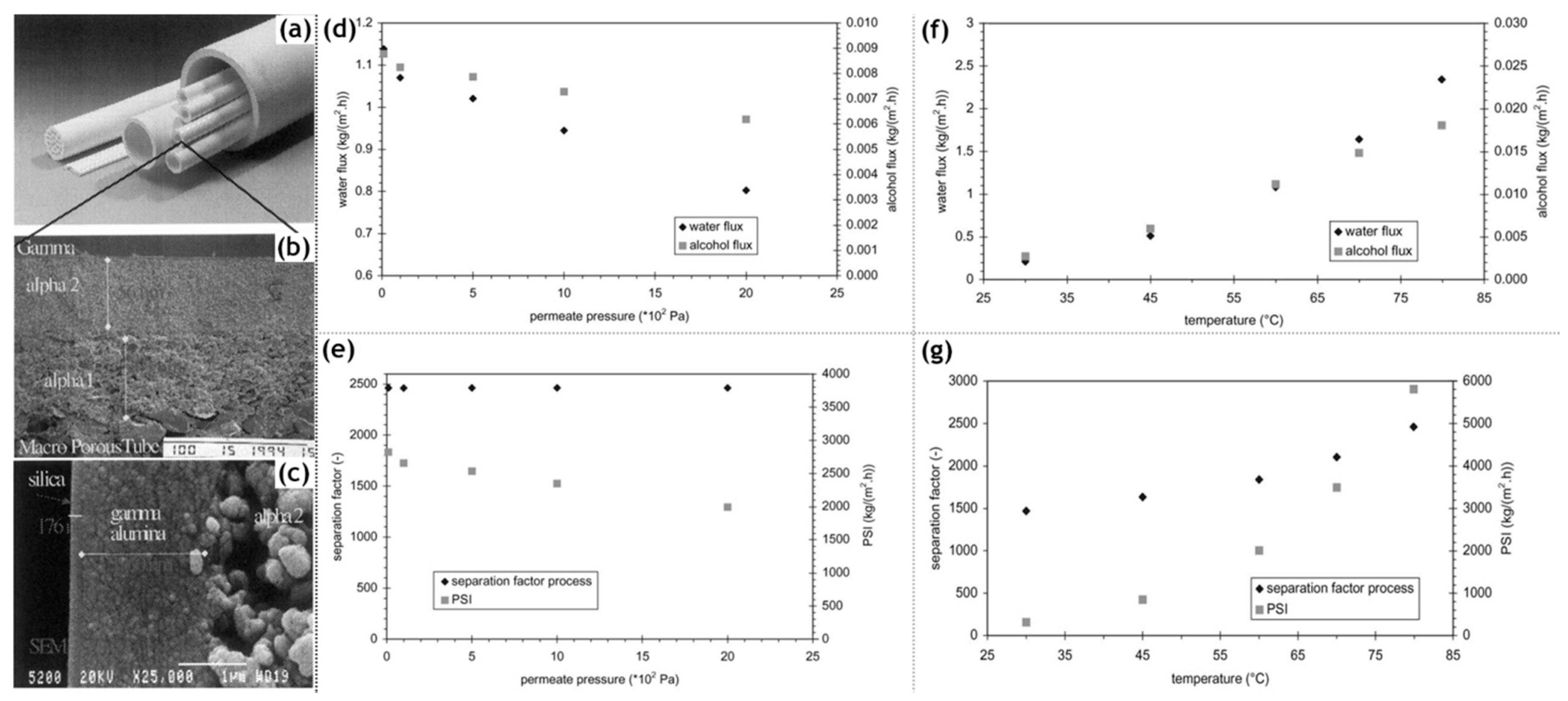
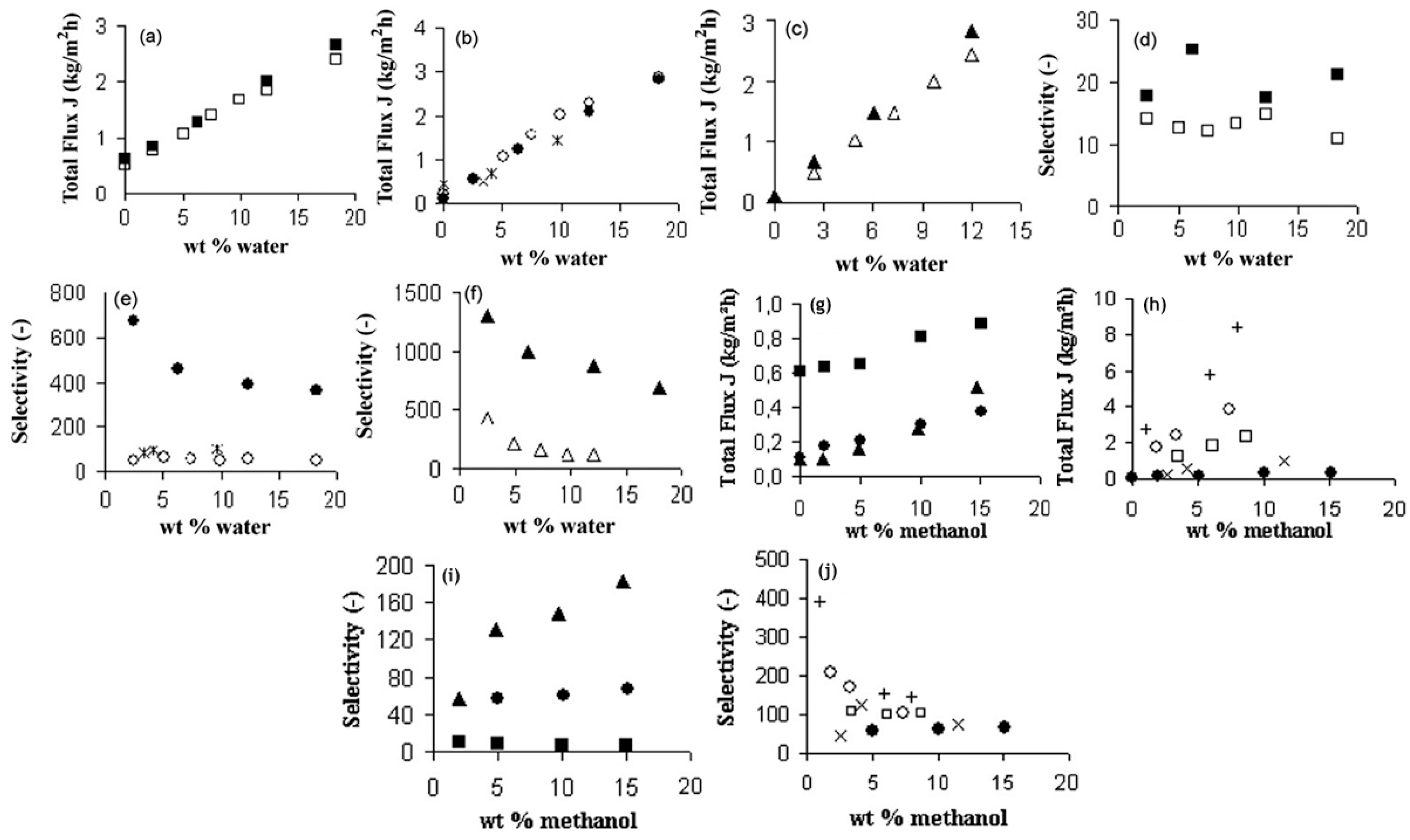
58]. Pervap Silica Membrane System (SMS) was developed by Sulzer Chemtech GmbH (Linden, Germany) in 2000 and is an appropriate example of ceramic membrane suited for industrial pervaporation. Even though, Zeolite A membranes come in the same category, they are highly susceptible to even mild acidic environments and thereby making them unsuitable for effluent streams of esterification reactions as an instance. Other alternatives, offering better mechanical strength as well as stability against extreme pH environments are the various microporous silica membranes fabricated by Netherlands Energy Research Center (ECN) (Petten, The Netherlands). The arrangement of membranes to offer better performances than free standing units is known as a module. The Pervap SMS module has annular passages arranged in series that create turbulence and isothermal operation is ensured. A tubular membrane was developed by ECN, and its pervaporation performance was heavily scrutinized in the study by Veen et al. [
59]. The geometry of the membrane was tubular with lengths achievable up to a meter and pores with a 0.4 nm diameter (
Figure 5a–c). Extremely high selectivity was ensured as the water flux grew exponentially in contrast to the small organic flux at a temperature ranging from 100–300 °C. Operations at high temperatures require less area, hence balancing the cost of fabrication. The support consists of 2 γ-alumina layers and an α-alumina layer. This was done to ensure a defect-free selective layer of the sol–gel synthesized silica top layer. The feed composition was constituted by 4.5 wt% water, 95.5 wt% isopropyl alcohol and some heavy hydrocarbons. The proposed membranes had better chemical stability than the zeolite A membranes. Pervaporation performances for other aqueous organic mixtures such as acetone, dimethylformamide (DMF), tetrahydrofuran (THF), methylethyl ketone and other common organic compounds were reported (
Figure 5d–g). However, the water concentration studied was small enough to avoid stability related complication, due to the inherent hydrophilicity of silica membranes.
Based on the pervaporation of isopropyl alcohol in water using the Netherlands Energy Research Center (ECN) membrane, characterization of the transport mechanism was carried out by Verkerk et al. [
60] Maxwell–Stefan modeling considers the interactions between the two components of a binary mixture. These interactions are especially significant for common lower alcohols such as ethanol and isopropyl alcohol (
Table 2). Quite simply put, a driving force is envisaged to cause permeation across the microporous ceramic membrane and opposing interactions are thought to arise via friction by the membrane as well as the presence of the other component in the binary system. From the work of Wolf et al. [
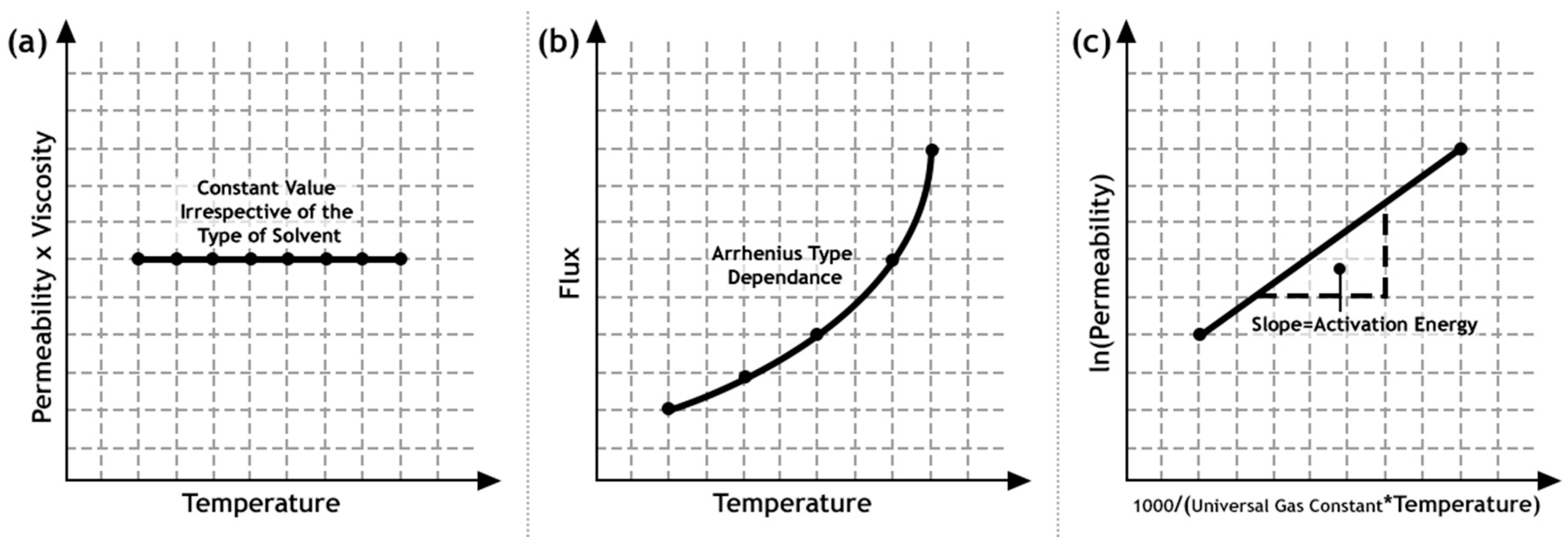
61], it was found that adsorption does not differentiate between isopropyl alcohol and water. Water flux is caused by its own driving force, whereas the alcohol flux occurs due its driving force as well as the drag force by water. Water flux increased by a large difference, in contrast to the alcohol flux; leading to an increase in the separation factor pervaporation separation index; defined as the product of the total flux and the separation factor. Based on pervaporation experiments, water flux was affected by its own driving force. The presence of isopropanol does seem to cause some disparity between the diffusion coefficient for pure water and water present in a binary system. The flux of alcohol was agreed to the theoretical modeling, however the contribution from the drag effect by water was found to be constant up to 50 wt% water and then increased for dilute solutions.
The study conducted by Constantino et al. [
62] demonstrates that the pervaporation process is not limited to only separation based applications. During butyl acetate synthesis, azeotropic mixtures are encountered, which is also a heat sensitive reaction. Both features make it amenable to pervaporation rather than distillation. The commercial tubular silica membrane was utilized based on its effectiveness towards a plethora of organic–water as well as organic–organic systems based on numerous studies. A numerical model was employed using the commercial software gPROMS (general process modeling system). Several binary mixtures comprising of n-butanol and water differing in concentration were studied. Since an increase in temperature increases the driving force for water, the permeate flux experienced an increment. Ternary as well as quaternary mixtures comprising of varying concentrations of n-butanol, acrylic acid, butyl acetate and water were also studied. For multicomponent mixtures, increases in the feed water composition as well as temperature led to an increase in the total permeate flux. It was also observed that the presence of acrylic acid and butyl acetate molecules introduced resistance to the mass transfer process. The applicability of membranes assisted pervaporation towards the esterification reaction was analyzed. A fixed bed reactor was used in congruence with a membrane. This fixed bed membrane reactor resulted in a 66% increase than the reactor for not utilizing membrane assisted pervaporation.
The commercial silica membranes were heavily scrutinized as apparent from their subjection to various aqueous organic mixtures. This was essential in ensuring their suitability for industrial operations. Theses membranes showed promising pervaporation performance as observed by their acceptable selectivity and flux magnitudes. Their inherent structural, thermal and chemical stabilities were displayed in addition to their performance. However, to ascertain their competitiveness from other alternatives such as their polymeric or zeolitic counterparts, comparative studies were required.
5.3. Comparative Studies on Commercial Silica Membranes
Many studies aimed at comparing the various commercial alternatives encompassing silica-based membranes, zeolites as well as polymeric membranes (
Figure 6). These membranes were assessed based on their pervaporation performance against a wide matrix of feed compositions differing from each other on the basis of organic components as well as concentrations. These studies aimed at critically assessing the prospect of considering silica membranes as a suitable candidate for affecting membrane based pervaporative solvent recovery and/or dehydration.
The lower energy consumption and almost negligible carbon footprint characteristic of membrane based solvent recovery and dehydration in comparison to conventional distillation are accompanied by the advantage of economic feasibility. Aqueous solutions of 34 different alcohols, glycols, carboxylic acids, esters, ethers, ketones, amines, nitriles and halogenated hydrocarbons were tested on the silica membranes developed by ECN (Petten, The Netherlands) and Sulzer Chemtech GmbH (Linden, Germany) [
66]. For the same driving force, fluxes of ketones and ethers were highly satisfactory, whereas glycols ranked the lowest with the rest of the organic families in between (
Table 3). The importance of the membrane architecture was realized in this study and forced flows with baffles than an annular duct was found to be a better module design. For the widely applicable case of the isopropyl alcohol and water binary mixture, there was a 40% reduction in cost and 85% energy was saved by switching from distillation to a membrane-based pervaporation unit. Commercially available microporous silica membranes (PERVAP SMS, Sulzer Chemtech GmbH) have been compared with polymeric (PERVAP 2202, PERVAP 2510, Sulzer Chemtech GmbH) and zeolite (NaA type, SMART Cemocal Company Ltd. (Essex, UK)) membranes on the basis of their overall pervaporation performance by Gallego-Lizon et al. [
67]. Water and t-BuOH mixtures were chosen with feed concentrations ranging upto 20 wt% water and temperatures in the 60–100 °C range. In the polymeric PVA class of membranes, PERVAP 2510 yielded better flux and displayed greater stability then the other alternatives. Water flux was highly sensitive to temperature variation, especially for dilute mixtures. The separation factor however experienced reduction due to swelling of the membrane. For the silica membrane, the effect of decreasing water concentration on the feed side resulted in enhanced total fluxes and better separation factors. An increase in the temperature increased the flux. Highest fluxes were obtained by the silica membranes followed by the zeolite and then the polymer membranes. The separation factor however was the largest for zeolite, then polymeric and least for the silica membrane. This trade-off needs to be considered for any particular application. Urtiaga et al. [
68] sought to compare the pervaporation performances of two commercial silica membranes against the acetone–water mixture (30 wt% water) and other compounds as impurities. Pervap SMS (Sulzer Chemtech, Linden, Germany) and Pervatech BV (Rijssen, The Netherlands) were under investigation. The separation factor for both membranes increased for low water concentrations with an increase in operating temperature, however, SMS membranes were found to be more selective. Templated silica mesoporous membranes offer high porosity, narrow pore size distributions accompanied with low tortuosities [
69]. Based on the concentration of the structure directing template as well as the synthetic route, hexagonal (MCM-41), cubic (MCM-48) or lamellar symmetry (MCM-50) pore geometries were reported. Hexagonal MCM-41 type mesoporous silica membranes are not practical as the permeation pathways are oriented perpendicular to the desired direction of mass flow. MCM-48 due to their robustly interconnected porous channels offer minimal tortuosity in every direction, combined with a fabrication strategy to obtain thin membranes, makes them a favorable alternative for pervaporation applications. Commercially available inorganic silica membranes offer more advantages than the polymeric alternatives; however, the correlation of the design parameters with the pervaporation performance parameters is still poorly understood. Further studies are required to completely understand the governing transport phenomenon empirically. The commercial silica membrane known as PVP (Pervatech BV, Rijssen, The Netherlands) was assessed for pervaporation of custom water–isopropanol mixture and a commercial mixture containing the requisite concentrations of the two components [
70]. A relation between a flux with a chemical potential gradientis established and verified with experimental results. γ-alumina supported Pervatech PVP and α-alumina supported amorphous silica membrane Pervap SMS were used for the mixtures. It was observed that the water flux increased with increasing temperature and decreasing membrane thickness. The PVP membrane provided a larger water flux than Pervap SMS, however, the mass transfer parameter capturing the influence of adsorption of the permeating species remained constant for both membranes. The importance of process flow adopted in a particular pervaporation process has been highlighted by Schleger et al. [
63] Each module is reminiscent of isothermal modules, Pervap silica membranes from Sulzer Chemtech, Linden, Germany, which are constituted of tubes within a tube arrangement with a heat flux entering from the outer surface and pervaporation occurring on the inside. Membranes can undergo series or parallel pathways to suit the needs of the application. The need for finding the best arrangement is governed by the price of the inorganic membranes. An arrangement with less membrane area and higher operating costs is favorable.
Table 4 summarizes the performance of Pervap SMS (Sulzer Chemtech, Linden, Germany).
Pervaporative dehydration performance of tubular-type zeolite membranes (Mitsui Engineering and Shipbuilding, Japan) and tubular amorphous silica membranes (ECN, the Netherlands) were compared [
64]. These membranes were installed in a bench-scale seven membrane shell and tube design module with baffles perpendicular to the axial stream flow. The feed solution comprised of isopropyl alcohol and water (10 wt%) at 80 °C. The study aimed to examine the impact on pervaporation performance in response to the variation of parameters such as feed composition, operating temperature, driving pressure and state of feed vapor. It was found that with an increase in temperature, both fluxes as well as selectivity were improved. An increase of the water concentration in the feed mixture increased the total flux, and followed the trend opposite to increasing molecular weights for methanol, ethanol and n-butanol in the case of the A-type zeolite membrane. Methanol permeation was found to depend on pore-blocking, which is due to capillary condensation and the adsorption of water molecules on the surface. Amorphous silica membrane yielded a higher water flux for all the three alcohols, but selectivity was slower in comparison to the zeolite membrane. The impact of permeate pressure or the driving force showed different behavior for the two membranes. The water flux was reduced, whereas the selectivity remained the same for the zeolite membrane. Both the water flux and selectivity were reduced with a decrease in the driving force. It is widely acknowledged that these two membranes are better alternatives than polymeric membranes such as PVA/PAN-membranes. Amorphous silica membrane can be described as an excellent flux, medium selectivity membrane, whereas the A-type zeolite membrane can be described as a high flux and high selectivity membrane. The major difference in these characteristics lies in the thickness between the membranes with the forms being 50 times thinner than the latter. The mechanism also differs substantially with silica membrane operating on adsorption and diffusion interactions, whereas molecular sieve effects governing the permeation in the zeolite membrane. Hence, silica membranes are more suitable for separating large amounts of water at the cost of purity. Superheated feed vapor is found to positively influence the performance. Both membranes displayed prolonged stability and ease of manufacturing. Another more extensive comparison of zeolite membranes vis-à-vis silica ceramic membranes was attempted by Sommer et al. [
65]. Commercial tubular A-, T- and Y-type zeolites manufactured by Mitsui and microporous silica membranes by ECN and Pervatech were compared, based on their pervaporation performance for more than 30 different mixtures. These encompassed alcohols, glycols, carboxylic acids, esters, ethers, ketones, amines, nitriles and halogenated hydrocarbons as the organic component. Based on these investigations, the selectivity followed the order, zeolite A > zeoliteT > Pervatech silica > ECN silica. The flux, however, follows the order, ECN silica > Pervatech silica > zeolite A > zeolite T. These trends can be explained based on the thicknesses of the two classes of membranes and the ordered structure of the zeolite membranes. All the membranes showed remarkable stability towards aprotic solvents. A-type zeolite is susceptible to acidic compositions, whereas the other zeolite type can tolerate acidity to a certain limit. Silica membranes can remain unaffected to a pH value as low as 3.
An in-depth understanding of the transport mechanism facilitating pervaporation is required to aid in synthesizing membranes properties well suited for the particular application. Various mechanisms through which permeation can proceed have been suggested in the literature; however, the exact mode remains indiscernible. The study by Bettens et al. [
71] on commercial tubular microporous silica membrane manufactured by Pervatech (Rijssen, The Netherlands) on pure components such as water, methanol, ethanol, 2-propanol and n-propanol aims to elucidate the transport phenomenon and encounter explicit dependencies of various control and structural parameters on the overall performance. The transport of a pure component has been modeled using the pore flow model as well as the adsorption–diffusion model. The former method assumes convective transport with a phase change from liquid to vapor as the component encounter smaller pores. The latter approach assumes the membrane to be dense so that diffusion and no convection is present. It simplifies the transport to three different regimes such as sorption of the pure component to the membrane surface, followed by diffusion across it and finally desorption on the permeate side to constitute the permeate stream. Pervaporation results indicate significant temperature dependence as evidenced with a water flux being affected the most with temperature variation. This points towards the adsorption–diffusion description of the process. Activation energy of diffusion for water was greater than those of the alcohols. It was found that the strength of adsorption as well as the activation energy increased with the number of carbon atoms for the alcohols. Size parameters such as molecular weight, kinetic diameter and effective diameter had no relation with the flux indicating that sorption was dominant over diffusion and can be the rate determining step for the process. It was found that hydrogen bond interactions affected the sorption majorly and the flux had a strong dependence on polarity. Surface tension and contact angle measurements for alcohols indicate the interplay of poorly understood sublayer interactions. It was concluded that the Fickian analysis for pure component diffusion was apt; however, multicomponent mixtures give rise to many other interactions, which may not fall under its purview. Polymeric membranes possess preferential water selectivity but at the cost of the flux as well as thermal, mechanical and chemical stabilities. On the other hand, inorganic membranes consist of hydrothermally fabricated zeolite membranes and sol–gel synthesized silica membranes. Zeolite membranes are a promising alternative; however, their industrial adaption has been hindered by their high cost of manufacturing. Silica membranes, on the other hand, are a promising alternative as evidenced in their application to water-n-butanol pervaporation as recovery of N-butanol from the extract and raffinite streams in the production of 1,1-dibutoxyethane green fuel. Boutikos et al. [
72] investigated the performance of the commercially available silica Pervatech membrane for the above-mentioned application. It was observed that for feed flow rates above 23 L/h, mass transfer resistance due to the presence of the concentration gradient that reduces the flux of the required component was insignificant. The increase in the permeate pressure decreased the flux due to a smaller driving force and marginally decreased the separation factor. An increase in the temperature increased the diffusion coefficient and an increase in the feed water concentration increased the vapor pressure, i.e., the driving force; these work constructively to increase the total permeation flux. The drag effect experienced by the n-butanol molecules as well as their interaction with the water molecules led to an increase in their permeation with increasing water concentration. However, this was accompanied by a decrease in the separation factor. Selectivity did not possess a dependence on temperature. A semiempirical expression was developed for the permeance of water and n-butanol.
Numerous studies on the commercial silica membranes pointed towards them offering acceptable partial component fluxes and selectivities that justified their substitution for the polymeric membranes. Zeolitic membranes cannot be out ruled in comparison to the silica membranes, they do however, face a stiff competition. Commercial silica membranes have displayed impressive chemical resistance against a wide matrix of organic–water mixtures. These membranes are not susceptible to swelling and hence the characterization of the mode of mass transport can be performed without ambiguity. These investigations that sought to compare and quantify the pervaporation performance of silica membranes provided a firm ground for their adoption by industry to achieve solvent recovery (
Table 5).
5.4. Modified Silica Membranes
Based on the numerous applications presented in the previous sections, the versatility of the silica membranes can be gauged. The inherent material properties provide the synthesized membranes with superior mechanical, thermal and chemical stabilities. The commercial modules have been found to outperform the polymer based membranes. These commercial silica membranes, however, do suffer from several disadvantages stemming out from the same material properties. In addition to this, the commercial silica membranes have fixed membrane structure and hence cause stagnation in the steady growth of silica membrane technology. There exists a large room for improvements to overcome the various limitations of silica membranes. These modifications (
Table 6) werecovered in this section as these lay the groundwork for the future scope of this mature and extensively investigated field of research.
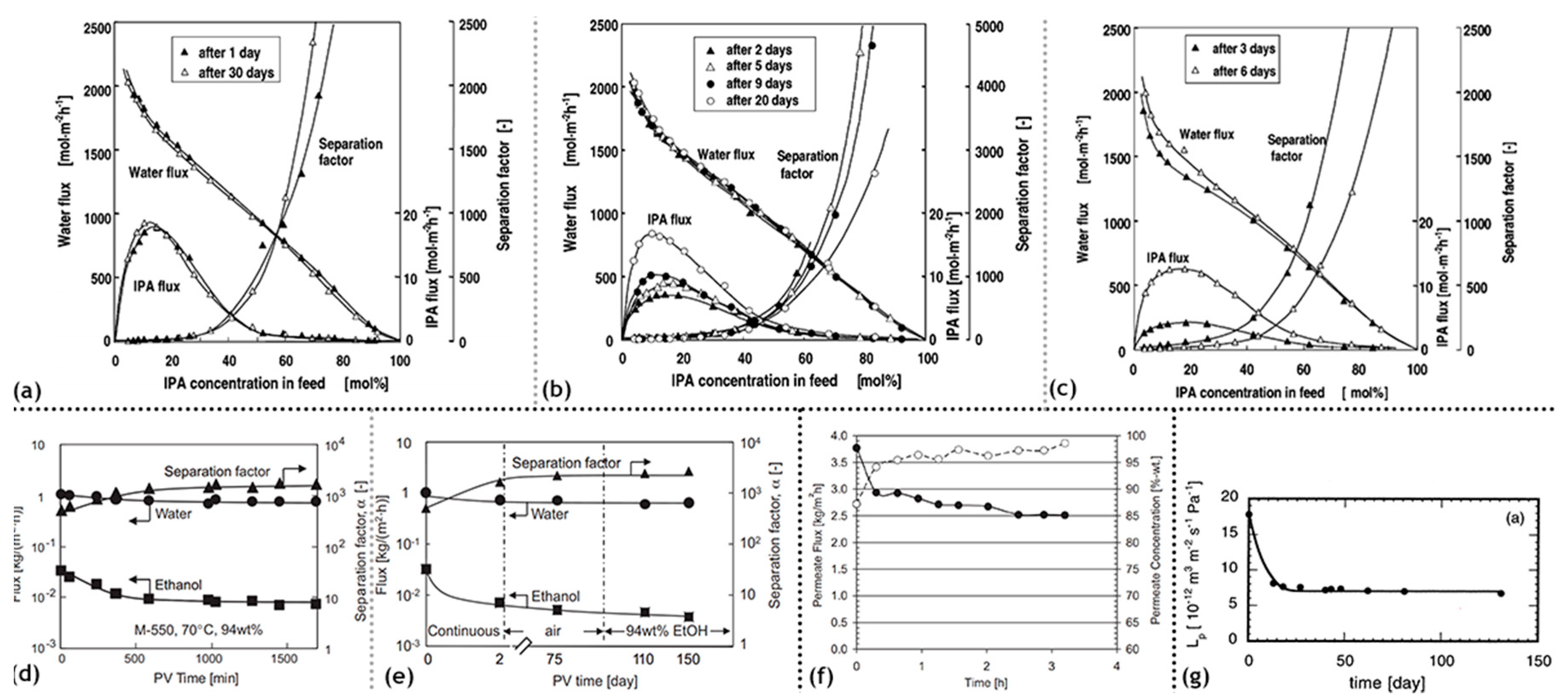
It wasobserved that silica membranes didsuffer from their inherent hydrophilic properties. Stability against water is one of the essential features in determining the viability of a particular membrane for its utilization in pervaporation. Silica membranes offer high porosity and flux but however are very susceptible to swelling and degradation on exposure to water whereas crystalline zirconia and titania, although water resistant have poor porosity and size distribution, with pores mainly present on grain boundaries. A hybrid of silica and zirconia or titania can however offer a suitable alternative. The work conducted by Asaeda et al. [
2] focuses on analyzing the effect of zirconia concentration and calcination temperature on the stability of the membrane for pervaporation applications. Homogeneity of silica-zirconia composites can be obtained with alkoxide hydrolysis and condensation reactions and subsequent calcination. The sol–gel method entailed using two diverse routes: the conventional partial hydrolysis and condensation reaction or simultaneous hydrolysis and condensation reaction. Hot-coating methods were employed where α-alumina porous cylindrical tubes were used as support, smoothed by α-alumina particles to obtain pore sizes below 1 nm. This was followed by washing in boiling water for guarding against silica rich phases. The SiO
2-ZrO
2 (ZrO
2:50%) membrane was subjected to four consecutive runs against various IPA/water concentrations and it was observed that for each run the water flux drastically decreased monotonically with increasing IPA concentrations. The IPA flux increased and reached a peak at around 20 mol% IPA concentration and then decreased due to a change in the effective pore size brought on the reaction of IPA molecules with hydroxyl groups. It was found that for each subsequent run, preceded by a 12 h submergence in dilute aqueous IPA mixture (4 mol%), the IPA flux increased accompanied with a marginal increase in water flux. This indicated an inherent instability of the membrane hypothesized to be mainly borne out of either intrinsic material properties of the composite membrane or silica rich phases present due to the in-homogeneity resulting from the synthesis route. The former warrants a further investigation into other materials, whereas the latter was taken into account by employing the hot-coating method along with washing in boiling water to remove silica rich phases. Lower heating temperatures yielded high porosity membranes, which has resulted in better performance due to the corollary increase in water flux. Stability against was water improved with an increase in the zirconia content. This delayed the onset of surface hydroxyl groups. Quick drying was favored over slow drying as it ensured well dispersion of the phases. Based on the pervaporation studies conducted on IPA/water and THF/water mixtures, it was concluded that the water flux displayed a dependence on partial water vapor on the feed side rather than vapor pressure difference across the feed and permeate side. A comparative study was conducted by Asaeda et al. [
3] between silica, silica-zirconia and silica-titania membranes based on their pervaporative performance against aqueous acetic and propionic acid solutions. The sol–gel synthesis route in conjunction with hot coating methods on a smoothed α-alumina cylindrical tube support were employed for enhanced stability for each of the membrane materials. The sols used were tetra-ethoxysilane, zirconium tetra n-butoxide (ZrTB) and titanium tetra isopropoxide (TiTP). Solubility of silica, zirconia and titania gel powders in deionized water, acetic acid and its aqueous mixture showed marked solubility in silica in water, which decreased significantly with increasing acetic acid concentration. Zirconia solubility increased with increasing acetic acid concentration, whereas titania largely remained insoluble for the entire concentration range. Silica membranes were observed to be quite stable for higher acid concentrations, however, succumbed in the lower concentration range. Silica-zirconia membranes faced degradation, whereas silica-titania membranes maintained structural integrity, but at the cost of low water flux. Silica membranes present a better alternative based on water flux but remained operable for acetic acid concentrations higher than 20 mol%. Simulation results based on the simple pore model were in good agreement with the experimentally obtained results. The inherent instability of silica membranes towards water is a well-known disadvantage. However, this limitation can be overcome by enriching the silica membrane with suitable components or modifications. Brinkman et al. [
78] focus on the degradation affected by the hydrolysis of the Si-O-Si siloxane bonds by a substitution with silicon-carbon bonds. This led to a subsequent decrease in the typical pore size due to the smaller bond lengths, thereby making the membrane viable for molecular sieving. This modification also led to a remarkable improvement in its hydrothermal stability. This novel organic–inorganic membrane offers a suitable option for pervaporation applications by constructively combining the positive features of membranes from different classes of materials, which otherwise are not able to fulfill all the desired features on their own. Membrane material selection for a particular application is itself a contentious issue and this is further complicated by a limited understanding of the transport mechanism affecting the required component to diffuse through, ensuring a commercially viable flux level as well as reliable selectivity. In the study by Bettens et al. [
74] the simplified Maxwell–Stefan model was vindicated by performing pervaporation of water–alcohol and methanol–alcohol binary mixtures across methylated silica membranes. It was assumed that the diffusion in the bulk of the feed side can be neglected in the cases of turbulence, and only the resistance from the selective layer out of the various supporting interlayers is the rate determining step. Subsequent desorption from the support layer and vapor boundary layer diffusion occur rapidly on the application of low permeate pressure. The generalized Maxwell–Stefan model considers a particular species in a multicomponent system to be acted upon by driving forces and simultaneously encounter friction due to its interaction with other species. Pervaporation of alcohol–water and alcohol–methanol mixtures across an ECN methylated silica membrane at 60 °C and turbulent flow displayed good agreement between the experimentally obtained results and the Maxwell–Stefan single-file diffusion model (
Table 7). However, for aqueous mixtures, the dragging of alcohol molecules by the water flux could not be quantified and requires other models such as the extended Langmuir model for complete description.
The phenyl functionalized silica membranes developed by Araki et al. [
1] utilizing the sol–gel route of synthesis displayed a prominent hydrophobic nature. The absence of silanol groups compounded the stability of these membranes against dilute aqueous organic feed concentration range. The γ-alumina interlayer in conjunction with α-alumina support provided better control on pore size as well as guarded against defects in the active top-layer. Cetyltrimethyl ammonium bromide (CTAB) was used togenerate pores of desirable size exploiting its molecular template function. The cross-sectional FE-SEM image indicated a 0.1 µm thick silica layer and its remarkable adhesion to the γ-alumina interlayer along with a largely defect-free surface. Intensity of bands in FT-IR spectrum corresponding to the phenyl group was increased with increasing phenyltriethoxysilane (PhTES) concentration. Contact angle measurements corroborated the hypothesis that the hydrophobic character increased with increasing PhTES concentration. This was furthermore accompanied with a decrease in single gas permeances for He, H
2, CO
2, N
2 and CH
4. Pervaporation studies with ethyl acetate (EA) indicated 0.32 mol/l CTAB concentration as optimum since higher concentrations could not be obtained. EA flux increased with the CTAB concentration, whereas water flux stagnated due to the pore blocking action of EA molecules. EA diffusion was increased with increasing PhTES concentration along with a significant decrease in water flux and 80 mol% PhTES concentration offered the highest separation factor. The separation factor was decreased, whereas the fluxes for both the components increased as a function of EA feed concentration. The temperature of the feed was varied, and it was observed to increase the fluxes of both EA and water, which however led to a decrease in the separation factor due to a larger increment in the latter. The water flux was unaffected by the presence of the functional group and the pore blocking effect was sustained even at elevated temperatures. The partition coefficients for EA, methylethyl ketone (MEK) and isopropyl alcohol (IPA) showed that the flux of the organic component increased in accordance with its hydrophobic character. It was also concluded that a large kinetic diameter required fewer number of molecules to achieve the desired level of pore blocking.
The pervaporation performance is a multifunctionally dependent complex process. As such, there are many parameters to be controlled and multiple trade-offs to balance. The hydrodynamic conditions on the feed side also have a bearing on the permeation transport as evidenced in the study that was conducted by Cuperus et al. [
80] on tubular silica membranes. The Reynolds number as a function of the linear flow velocity of the feed and inner diameter of the membrane as the characteristic length was used to find an optimum between the increased water flux and the costs of sustaining high operating feed flow rates. A Reynolds number of 3500 was proposed as a suitable compromise between the two factors. The major limitation to the versatility for handling various mixtures for pervaporation as well as their limited penetration into the industry are because of the instability induced by extreme pH environments. Modifications to the support and selective layer by doping were investigated in the study conducted by Sekulic et al. [
81]. It was observed that the addition of alumina negatively impacts the chemical stability, whereas the addition of titania and zirconia in controlled amounts, enhances the range of stable operation. However, high dopant levels come at a cost of poor structural strength due to the degradation of the polymeric matrix.
Pervaporation studies by Chowdhury et al. [
69] on these membranes and their comparison with α-alumina supported mesoporous γ-alumina membranes show their versatility as being a possible option for industrial nanofiltration processes. Investigation into permeability was conducted by passing water, ethanol, 1-propanol, 2-butanol, toluene and hexane through both the membranes. In the case of the α-alumina support layer, pressure difference and liquid viscosity are the two main parameters influencing the flux, lying in the domain of viscous flow model, which is typical of macroporous membranes. γ-alumina layers, on the other hand, have the capability of differentiation based on the hydrophobic or hydrophilic nature. Permeation of hydrophilic liquids is favored because of the constructive hydrogen bond interactions. These have a marked impact on the effective pore size available for each of the testing species. The existence of a threshold pressure to affect non-zero flux exclusively for toluene and hexane could not be explained. In contrast to the γ-alumina membrane, Mobil Composition of Matter No. 48(MCM-48) membranes displayed different fluxes for each of the alcohols, with alkoxylation possibly hindering the flow of higher alcohols. MCM-48 membranes were found to be superior primarily because of their lesser thickness and contributions from high porosity and high tortuosity. The effect of mesoporous layer on the overall pervaporation performance and membrane stability was studied by Sekulic et al. [
84]. Two membranes differing only in the material constituting the interlayer were examined. In one case was the widely used γ-alumina interlayer, which restricted the operation of the membrane to a pH range of 4–10, whereas in other case was crystalline mesoporous titania. The support was α-alumina with a microporous silica selective top-layer in both the cases. Pervaporation experiments were conducted using 2-butanol, 2-propanol or ethanol and water mixtures. Size based molecular sieving caused a 2-butanol/water mixture to have the lowest flux and highest selectivity with the ethanol/water mixture on the opposite end of the spectrum for both the membranes. Increase in the flux and decrease in the separation factor were demonstrated for dilute aqueous mixtures attributed mainly to the dragging effect by the water molecules. Enhanced temperature operation provided better overall pervaporation performance. There was a marked decrease in the separation factors in the case of mesoporous titania. Single gas permeation results indicated the absence of defects for both the membranes. The main reason for this difference was hypothesized to be due to the trivalent nature of the aluminum cation, introducing acidic sites, making the membrane hydrophilic, whereas the oxidation state of titania being the same as silica does not affect any changes in the otherwise pre-existing membrane. The presence of these hydrophilic sites on and at the vicinity of the pore walls can increase the driving force causing preferential permeation of water.
The substitution of the reactive OH groups on the surface with methyl groups, improve the stability and hence the life-cycle of the silica membranes. This was observed in the study conducted by Campaniello et al. [
15]. The stability and long period analysis of membranes still require further studies to be able to assess them for industrial applications. Mesoporous γ-alumina support was employed and a single step as well as two step acid catalyzed hydrolysis methods for sol preparation was performed. The two-step route yielded a narrower particle size distribution in contrast to pure silica and one step route methylated silica membranes. Pure silica membranes showed a marked decrease in the water flux when in operation for few weeks. This affect can be attributed to the pore blocking by the water molecules with more prominent hydrogen bridge or chemisorptions in comparison to physisorption. The methylated silica membranes decrease the water flux due to their hydrophobic nature, however the membranes remain significantly more stable than the pure counterpart. However, even with methylation, operating temperatures above 95 °C has led to degradation of the selective top layer.
The mechanism of mass transport is a function of pore sizes as mentioned in a variety of literature sources; it however is also heavily dependent on the nature of the species being permeated through the membrane. Pervaporation experiments were carried out on water–organic component mixtures by Johan et al. [
73]. The organic components used in the study are methanol,
N,
N-dimethylformamide and 1,4-dioxane. Each of the components were investigated based on the response of their flux and separation factor to changes in temperature and feed composition. It was observed that because of its large kinetic diameter and small dipole moment, 1,4-dioxane yielded large separation factors. However, the opposite was true, for methanol, which with its quite similar diameter to water and low dipole moment, was able to penetrate the membrane along with water. DMF, on the other hand, has a large diameter and significant dipole moment, which cause it to be adhered to the pore walls resulting in delayed diffusion. As the silica pore size is lesser than the molecular diameter of water, surface diffusion rather than gas diffusion was the governing mechanism explaining water transport. The fluxes for methanol could not be explained by the standard Maxwell–Stefan diffusion theory, as the driving force was found to be constituted of partial pressure gradient as well as the coupling effect of being dragged along with the considerably higher water flux. It was observed that 1,4-dioxane diffusion occurs via the mode of viscous flow through pathways such as mesopores and small defects. DMF is also thought to undergo the same mode of transport although its micropore permeation is also contested. This is because it demonstrated a pore blocking effect, restricted to the microporous domain. The mechanism of pervaporation separation achieved with hydrophobic mesoporous silica membrane has been disseminated from the study conducted by Jin et al. [
75]. The silica membrane was prepared by dip-coating on commercial porous alumina tubes. The hydrophobicity was attributed to the membrane by subsequent surface modification using 1,1,1,3,3,3-hexamethyldisilazane (
Figure 7). XRD patterns showed that the α-alumina support had been adequately covered by the silica selective layer. Successive dip-coating ensured minimal penetration of the silica sol into the pores of the alumina support. The surface modification resulted in the appearance of trimethylsilyl functional groups, which has rendered both the increased surface hydrophobicity and the surface potential. Pervaporation studies were conducted with binary mixtures of ethanol and acetone with water as well as ternary mixtures comprising of ethanol or acetone with water and acetic acid for mimicking the actual industrial effluent streams. In contrast to zeolites, separation factor was less, however, the corresponding flux was large. The membrane was performed satisfactorily for ternary mixtures as well. The adsorption diffusion model adequately explains the transport model in the study.
Yamashita et al. [
85] in their work have tried to overcome the problem of the orientation of microscale channels perpendicular to the direction of intended permeation flow. Porous anodic alumina in conjunction with the silica-surfactant nanochannel assembly membrane was utilized to separate phenol, benzene sulfonate and benzene disulfonate from a water–ethanol solution. The pore sizes in the anodic alumina ranged from 10 to 100 nm, which upon treating with a solution of cetyltrimethylammonium bromide surfactant and tetraethyl orthosilicate formed pores of size 3.4 nm along with the preexisting channels. The removal of surfactant was refrained as this promotes hydrophobic interactions between the channel walls and the organic molecules. Molecular sieving effects can be overlooked due to similar molecular diameters. The three molecules differ in terms of charges, with phenol being neutral, single anionic charge carried by benzene sulfonate and a dianionic charge carried by benzene disulfonate. The flux of the organic molecules followed the trend of decreasing charge due to the anion-exchange adsorption mechanism. A decrease in the ethanol concentration decreased the flux of phenol, whereas it was increased for the other two. This shows the interplay of dipole interactions, solvation and anion-exchange efficiencies and the ability to control the flux by simple variation in ethanol–water composition. The conventional methods of synthesis for silica membranes are mainly sol–gel routes and chemical vapor deposition. Although extensive studies on silica membranes derived from these manufacturing techniques have been conducted, there remain many limitations intrinsic to the nature of each of these processes. A novel method of synthesizing silica microspheres using microfluidic hydrodynamic flow has been proposed by Carroll et al. [
86]. This can eliminate the wide pore size distributions and offer opportunities for assembly into two- and three-dimensional arrays with hierarchical porosity. The microspheres were prevented from coalescing by constant stirring. Utilizing this technique, monodispersity of size was ensured. At most 5 µm sized particle can be generated by using channel widths of the order of 10 µm fabricated using soft lithography. Smaller droplets require more meticulous fabrication techniques and/or rigorous flow rates. The orientation and the corresponding tortuosity of the pores are essential in controlling the amount of resistance that a preferred component endures to form the permeate. In this regard, a study by Wooten et al. [
87] overcame the parallel orientation of the hexagonal pore structures rendering them highly useful for pervaporation analyses (
Figure 8). This required the use of surface modification, surface patterning and control over other parameters. Successful orientation of the hexagonal pores was characterized by transmission electron microscopy of the silicon thin film after the dissolution of the strongly bonded anodic aluminum oxide support, pore visibility in scanning electron microscopy and solvent flux data obtained during pervaporation measurements (
Figure 8). The templating was done using sandwiching between neutral copolymer barrier layers or air-curing.
Tsuru et al. [
88] aimed to differentiate organic–organic mixtures. The mixtures studied were comprised of hexanol, octanol or decanol in ethanol or hexane, decane or tetradecane in ethanol. Reverse osmosis was employed for their separation from the ethanol medium. A silica-zirconia membrane was employed for this task with pore sizes ranging between 0.8 and 2 nm and a molecular weight cutoff of 200 Da. An increase in pressure has increased the expulsion of all the alcohols and alkanes. Temperature did not affect the alkanes, whereas alcohols showed a decrease with an increasing trend. The application of the bilayer model showed a good agreement between reverse osmosis and diffusion.
Distillation is more suited for scaled up industrial applications but proves to be expensive or impractical in dealing with azeotropes. Membrane technology requires less energy consumption and can differentiate azeotropes, and close boiling point mixtures, but scalability has always been an issue. A combination or a hybrid of these two technologies used in conjunction can offer many viable process flows. These possibilities were explored by Sommer et al. [
89]. High temperature operation is always desired and hence membranes can replace distillation columns in spray drying, dimethyl carbonate and methyl-tert-butyl-ether production and many other applications. Four main configurations were proposed, which are as follows: (1) azeotrope splitting by membrane followed by distillation, (2) pervaporation by membrane of top or bottom stream of the distillation, (3) membrane between two distillation columns and (4) membrane combined with column via side stream processing. Configuration 1 was suited for highly volatile acetonitrile and methyl ethyl ketone. Configuration 3 offered a 20% reduction in cost in contrast to the conventional route. Configuration 4 requires a lesser number of trays and reduces the reflux ratio of the accompanying column when the membrane is in proximity to the pinch point. A 40% reduction in the cost of investment and operation as well as 85% savings of energy could be achieved. The incorporation of inorganic membranes rather than polymeric ones offered 11% lower separation costs. A combination of membrane-based vapor permeation and distillation proved to be superior to isothermal and adiabatic permeation based on the overall performance.
γ-alumina interlayers were supported on ceramic hollow fiber membrane supports in the study by Peters et al. [
82]. The organic solvents used in pervaporation dehydration were n-butanol and dimethylformamide. Single gas permeation studies showed selectivity towards helium with low permeation for nitrogen, characteristic of microporous silica membranes. The interaction of n-butanol with the surface silanol groups as well as the alumina layers may promote densification leading to a decrease in the performance of the membrane with the passage of time. The selectivity, however, is improved on prolonged exposure due to the pore blocking by alcohol. As dimethylformamide has an inherently large dipole moment, the same kind of results is expected for its prolonged interaction to the silica membrane. The molecular diameter is large and thereby making its permeation highly susceptible to pore sizes. In contrast to the tubular supports, ceramic hollow fibers were found to be economical and possessing large surface area/volume.
Although the hydrothermal stability of silica membranes has posed a marked limitation in their adoption as a versatile tool for industrial applications, the different solutions in mitigating this feature have spurred several membranes. In one such study conducted by ten Hove et al. [
90] silica, hybrid silica as well as zirconium doped silica membranes were analyzed on the basis of gar permeance. The latter two have been derived using 1,2-bis(triethoxysilyl)ethane as a precursor. Hydrothermal tests were conducted, which involved placing the membranes just above the meniscus of boiling water while ensuring no direct contact. It was noticed that the membranes showed the same permeance and selectivity as that of the α-alumina layer and thereby indicating the deterioration of the selective top layer. A hydrothermal test performed at 100 °C, resulted in silica membrane losing its selectivity with the other two variants experiencing no change. Subsequently membranes were exposed to conditions akin to the water gas shift reaction. Once again hybrid silica membranes did not display any major changes until a temperature limit of 300 °C. However, exposures to conditions around 400 °C show the indications of degradation of the hybrid and zirconium doped silica membranes. Another peculiar observation was the measurable drop in the carbon dioxide permeance at 200 °C and 300 °C for the zirconium doped variety. This was ascribed to the Bronsted-acidic property of zirconium/silica oxides. The effects of introducing alkali metal cations in the pure silica mordenite framework inverted type zeolite membranes have seldom been studied. The study conducted by Xu et al. [
91] aims to investigate the role that this addition may have towards the pervaporation performance of the membrane. Varying amounts of sodium chloride was added and it was observed that this aided in the nucleation process and hence leading to denser and more stable hydrophobic membranes. However, increased amounts of this dopant repelled the agglomeration of nucleation sites thereby leading to a weaker diffused gel structure. The potassium ions displayed a similar trend, whereas cesium ions had a negative effect on the pervaporation performance of the membrane. A 5 wt % ethanol–water mixture was tested at 60 °C. To impart a hydrophobic character to silica membranes, which are inherently hydrophilic by nature, the surface silanol groups need to be removed or shielded to eliminate their interaction with water molecules. Vinyl-functionalized silica membranes have been synthesized and tested for their pervaporation performance in the study conducted by Araki et al. [
92]. The membrane architecture comprised of an α-alumina base layer and γ-alumina interlayer and the selective top layer was prepared via the sol–gel route with vinyltrimethoxysilane as the precursor. The vinyl layer degrades at temperatures higher than 453 K. The role of the support layer on the pervaporation performance was also investigated. Two different supports, the first one being the α-alumina tubular support and the other one being alumina hollow fiber. Ethanol-, methyl acetate- and methyl ethyl ketone-water binary systems were subjected to the pervaporation process. The hollow fiber alumina support typically yielded three times the fluxes of the conventional tubular support. The elimination of surface silanol groups to combat the hydrophilic character that leads to structural degradation has been a topic of intense research in the domain of silica based pervaporation membranes. In the study by Kanezashi et al. [
93] the silanol groups have been substituted by fluorine. The membrane was synthesized via the sol–gel route, using NH
4F for introducing the dopant in the silica gel network and bis(triethoxysilyl)methane as the silica precursor. Fluorine manifested itself by forming covalent bonds with carbon and silica atoms. Increased helium and hydrogen permeances indicated a small enlargement of the pore size. The water permeation flux as well as the selectivity remained somewhat unchanged however, the newly synthesized membrane showed a substantial decrease in the hydrophilic character. However, pervaporation for long term operating time intervals need to be performed to ascertain any direct contribution to membrane stability. Another study conducted by Wu et al. [
94] presents a solution to a recurring theme in silica based membrane separation. For silica membranes to offer a viable alternative to conventional separation processes in the industry, stability or long-term stable operation is a prerequisite. Pure silica mordenite framework inverted type zeolite or silicalite-1 has uniform pore size distribution and high characteristic selectivity and flux. Immersion in the dopamine solution generated a thin indiscernible poly-dopamine layer. This layer did not impart any measurable thickness as well as any change in the static contact angle. The typical deterioration of pervaporation performance as observed in unmodified silicalite-1 membranes was slowed down for the modified membranes. It was also observed that prolonging the duration of immersion did not yield positive results and hence an optimum time of 24 h was finalized. This study presents a useful modification to silicalite-1 membranes, particularly for ethanol dehydration to produce bioethanol. In the study by Zhang et al. [
95] lanthanum and yttrium doped mesoporous silica membranes were assessed for their pervaporation performance in desalination applications. The doping with these rare earth elements can potentially change the hydrothermal stability by establishing strong silicon oxygen and a rare earth element covalent bond. The associated hydrophilicity aided for efficient water transport across the membrane yielding successful desalination at significantly lower operating temperature than the normal boiling point of water. The finer microstructure as well as lower mass transfer resistance also led to the efficacy of the desalination process. The successful up scaling of this method can address the problem of growing shortage of freshwater in the world.
The study by Klinov et al. [
96] explores on the validity of the solution-diffusion model and its use for determining the optimum operating conditions as well as the best suited selective layer thickness for pervaporation of ethanol–water and isopropanol–water mixtures. The membrane used pertains to the class of organic–inorganic hybrid silica membranes. The organic component imparting enhanced hydrothermal stability and viscosity to guard against structural failures due to nanocracks. The inorganic component imparts hydrophilicity as well as structural strength. These types of membranes were developed by Pervatech BV, Rijssen, The Netherlands. When the organic component flux was compared for both the binary mixtures, the ethanol system was greater by an order of magnitude from the isopropanol system, the difference being attributed to the kinetic diameter of the molecules as well as the relative volatility of water. The selectivity shows a non-monotonic trend and hence a maximum for a particular water concentration and hence this factor needs to be addressed to ensure smooth operation. The optimum thickness of the selective layer was proposed to be approximately 50 nm. The predictions of the solution-diffusion model are in good agreement with the experimental results.
Modified silica membranes and their proposed applications have now begun to surpass the domain of separation based on membrane assisted pervaporation process. Novel and interesting solutions to a plethora of problems plaguing the conventional technologies are coming up in recent years. Acetone and methyl ethyl ketone are valuable solvents, especially in the pharmaceutical industry. Their successful isolation from binary or multicomponent mixtures provides an invaluable route, bypassing the limitation and high costs associated with distillation and other conventional technologies in use. The study by La Rocca et al. [
97] deals with this problem using two variants of zirconium doped hybrid silica membranes. These variants defer in the precursor used, which are bis(triethoxysilyl)methane and bis(triethoxysilyl)ethane. The doping positively affected the selectivity and influenced flux. An increase in the number of undesirable components in multicomponent feed mixtures inadvertently reduced the flux. A drop in the pervaporation performance was observed especially in the cases of toluene and dichloromethane. This was hypothesized to arise out of unaccounted coupling effects. The control of microstructure by the variation in synthesis conditions has a profound impact on the pervaporation performance of a particular membrane. In the study by Lan et al. [
98] this aspect of membrane based pervaporation has been explored. However, to establish an unequivocal link between these two parameters, the number of characterizations such as single component gas permeation, water contact angle measurement, scanning electron microscopy, X-ray diffraction as well as energy dispersive X-ray need to be performed as evident in this study. Tetrabutylammonium ion in modest amounts leads to a dense and hydrophobic membrane, which leads to good pervaporation performance and stability. However, higher amounts tended to impede and disrupt the crystallization process, leading to weaker and compromised gel networks. The effect of other tetraalkylammonium ions was also investigated; however, the same constructive effects were not encountered.
Novel methods to establish a circular economy in the ambit of membrane based pervaporation technology are gaining ground in recent years. Due to the abundance and non-toxicity of silica, waste products can act as silica source rather than on the sole reliance on costly precursors. In the study conducted by da Silva et al. [
99] rice husk was subjected to acid leaching treatment to isolate silica. The high purity silica was then applied in an organic membrane to improve the pervaporation performance. The importance of pervaporation in industries based on solvents is quite evident. However, the study by Wang et al. [
100] brings forth the applications centered on purification and removal of toxic chemicals from the environment. Methyl tert-butyl ether is a toxic compound requiring efficient removal to mitigate the risks posed to the ecosystem as well as counter any exposure to the general populace. Mesoporous silica membranes employing α-alumina support synthesized via the sol–gel route and dip-coating technique was further enhanced for its effectiveness. Silylation of the membranes was done using 1H,1H,2H,2H-perfluorooctyltriethoxysilane, trifluoropropyltriethoxysilane, octyltriethoxysilane and propyltriethoxysilane. There was an increase in the hydrophobicity of the silylated membranes as evidenced by the contact angle measurements. This improved the separation factor for methyl tert-butyl ether/water systems. 1H,1H,2H,2H-perfluorooctyltriethoxysilane silylated membrane yielded highest selectivity, whereas propyltriethoxysilanesilylated membrane yielded the highest flux. The membrane silylated with the former provided a suitable tradeoff between selectivity and flux. Pure silica mordenite framework inverted type zeolite also known as silicalite-1 was synthesized in the study conducted by Ueno et al. [
101]. The support used was tubular silica and no other silica source, for instance, synthesis gel, was employed. The source of seeding of the selective layer was the support itself. The membrane displayed a good pervaporation performance for ethanol–water system. A selectivity of 66 and high fluxes were achieved. The selective layer thickness was obtained to be around 7 µm. The negligible use of reagents and the comparatively simplistic fabrication procedure makes it amenable to adoption for industrial applications. In the study by Raza et al. [
102] two routes of membrane synthesis and their subsequent impact on the pervaporation performance were investigated. Hybrid membranes were fabricated using bis(triethoxysilyl)ethane with and without hydrochloric acid treatment via the sol–gel route. The subsequent treatment with the acid promoted densification leading to higher separation factors, however, a lesser flux in comparison to the untreated one. However, the drop in the total flux was not significant, when applied to pervaporation of acetic acid-water binary systems. The stability was found to be improved in the long run.
Modified membranes have the potential of overcoming the limitations posed by the α-alumina supported traditional mesoporous silica tubular membrane. Studies aimed at improving the hydrophobic character and the overall stability of the membrane has been the recurring theme in recent times when compared to the long history of this mature field. It is imperative to acknowledge the saturation of information surrounding the commercial membranes. It is imminent that modified silica membranes tailored according to very specific set of conditions offer enormous strides for this ever-growing and dynamic field.