Characterization of Microcrack Orientation Using the Directivity of Secondary Sound Source Induced by an Incident Ultrasonic Transverse Wave
Abstract
1. Introduction
2. Theoretical Fundamentals
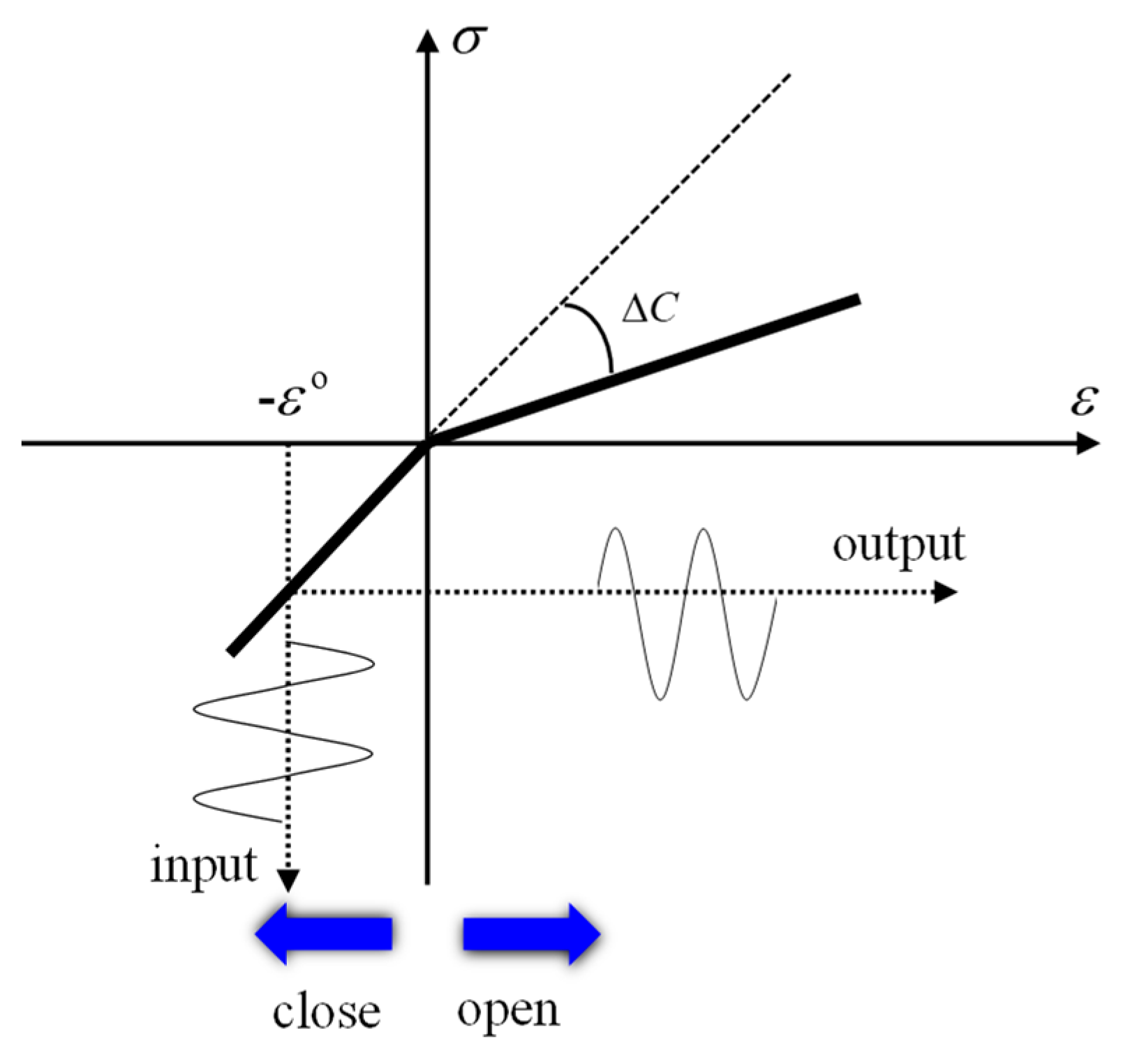
2.1. Bilinear Stress–Strain Model
2.2. Nonlinear Interaction between the UTW and the Microcrack
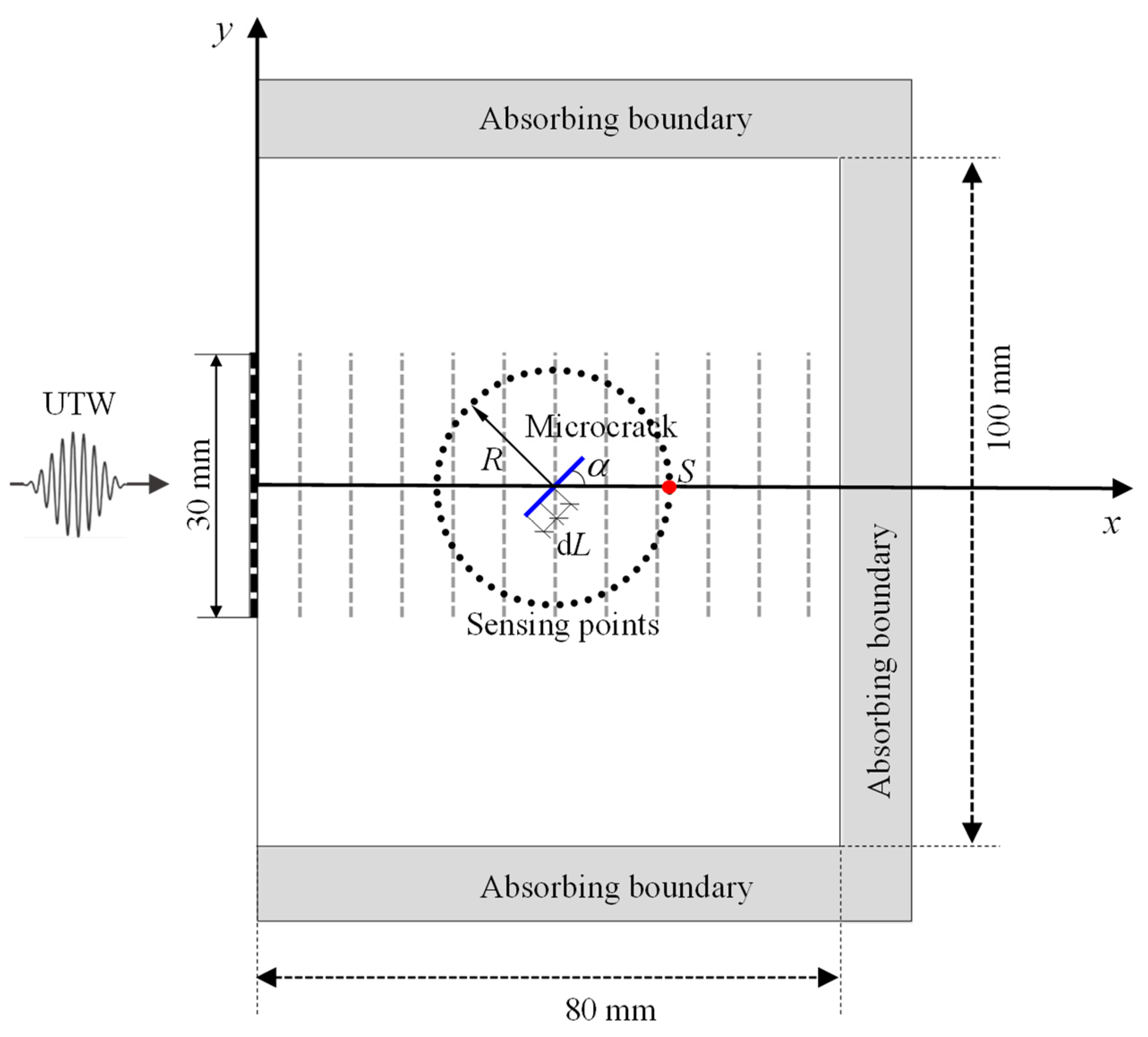
2.3. Simulation Modeling
3. Simulation Results and Discussions
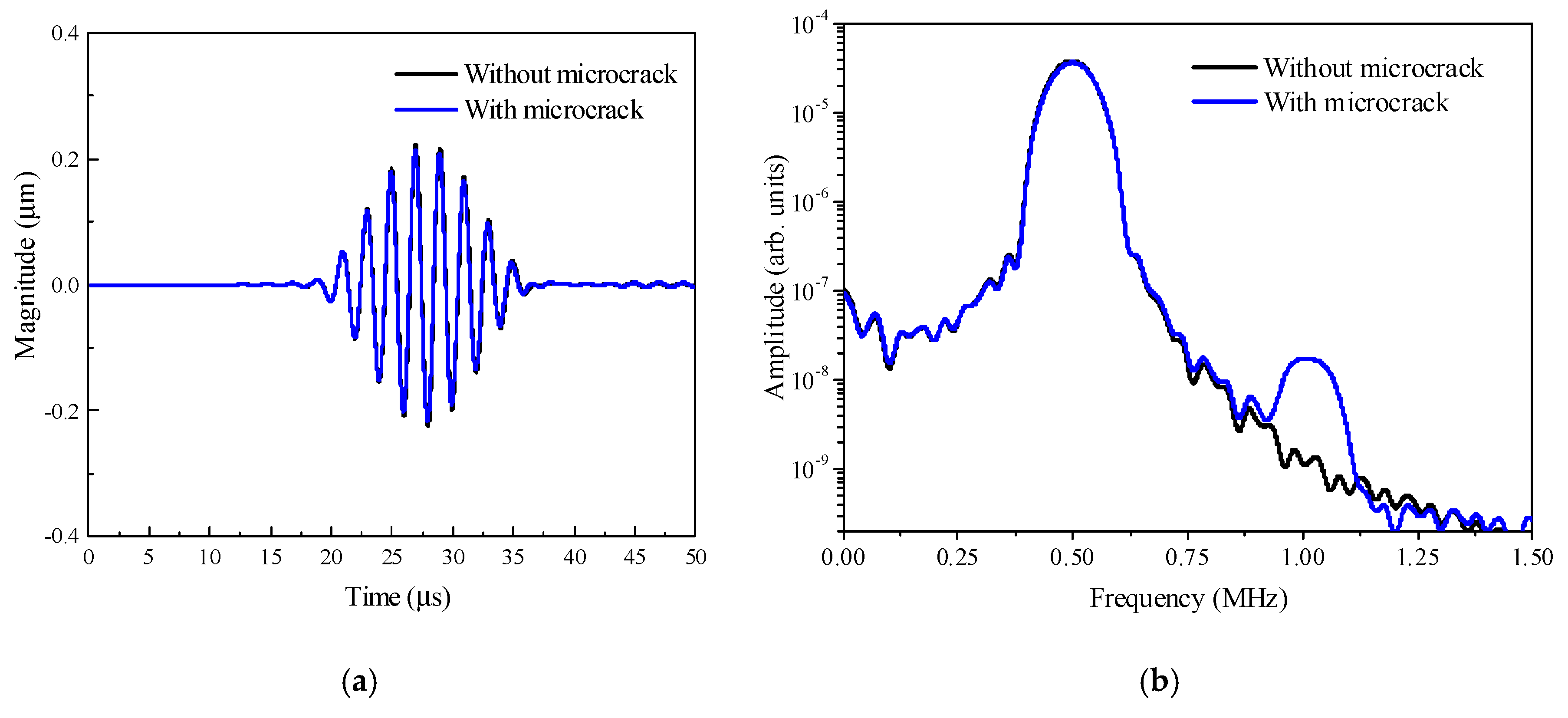
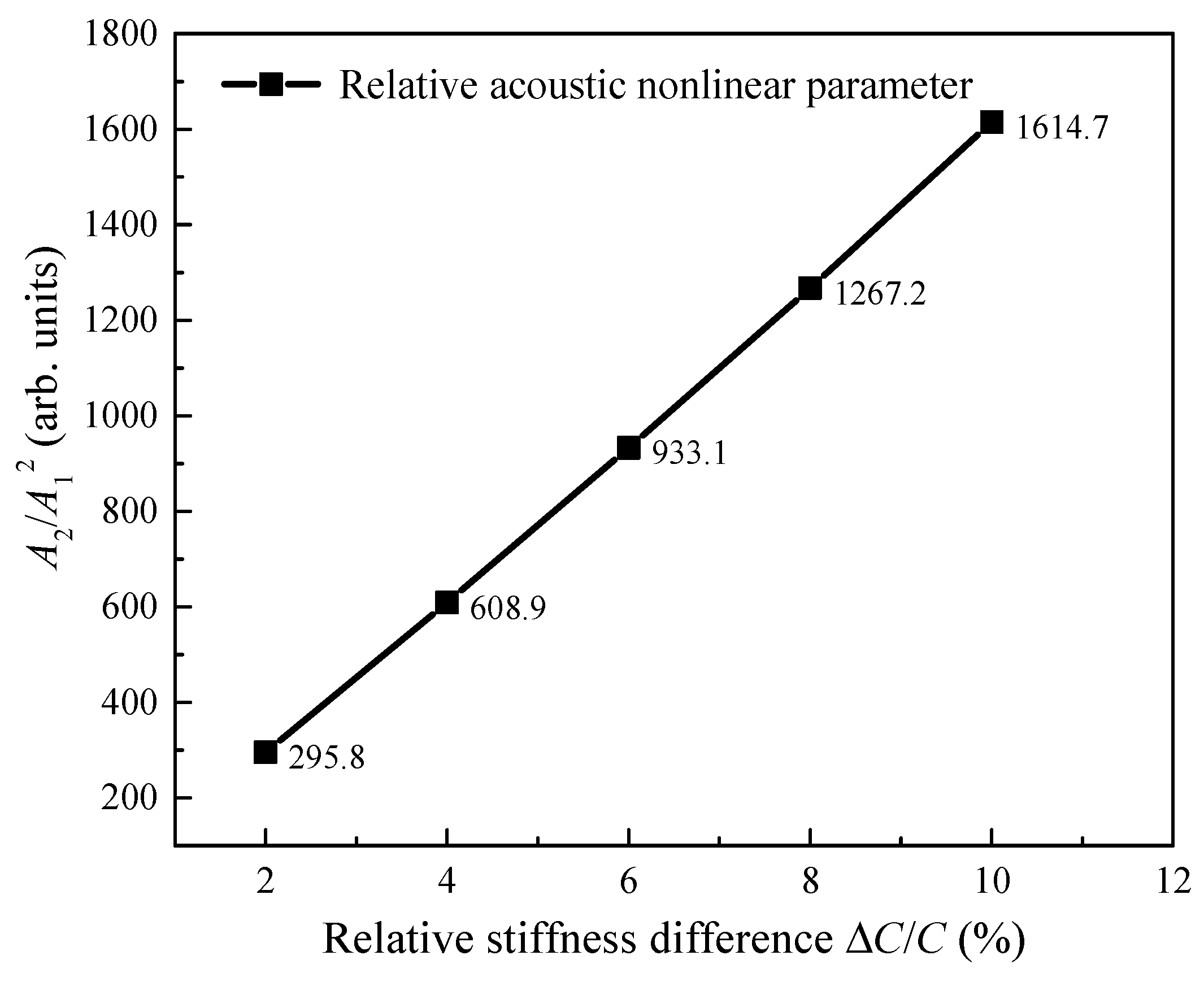
3.1. Analysis of the Second Harmonic Radiated by the SSS
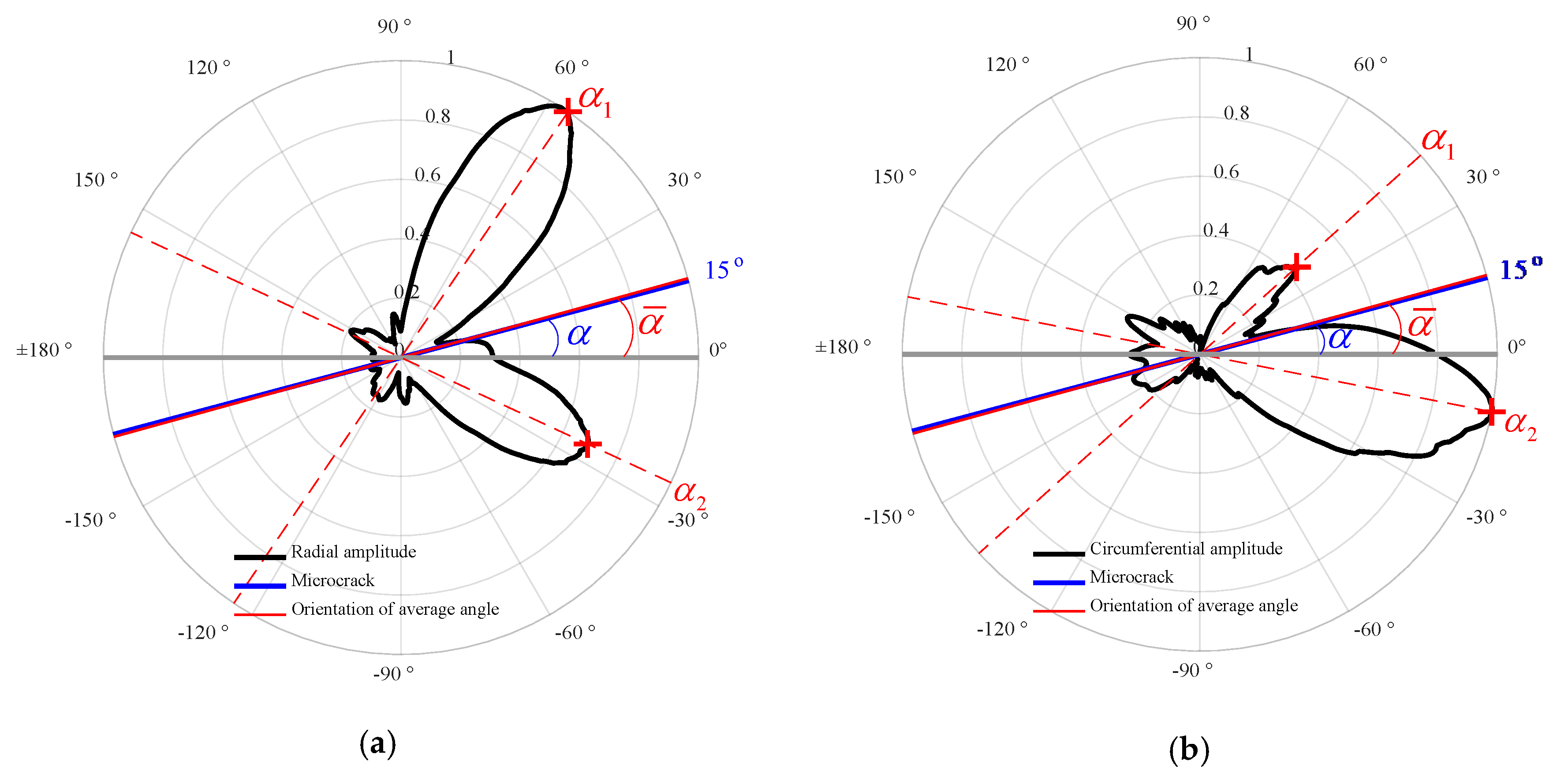
3.2. Directivity Analysis of the SSS
- Step 1: Preprocess the time-domain signals acquired at the sensing circle shown in Figure 2 with Hanning-window modulation;
- Step 2: Calculate the amplitude–frequency curves of the time-domain signals preprocessed;
- Step 3: Extract the peak values of the second harmonic desired, and normalize them by the maximum peak value of the second harmonic acquired at the sensing circle;
- Step 4: Transform the normalized peak values of second harmonics from the Cartesian coordinate system into the polar coordinate system;
- Step 5: Plot the normalized peak values in the polar coordinate system and then obtain the directivity of the SSS.
3.2.1. Effects of the Microcrack Orientation on the Directivity of the SSS
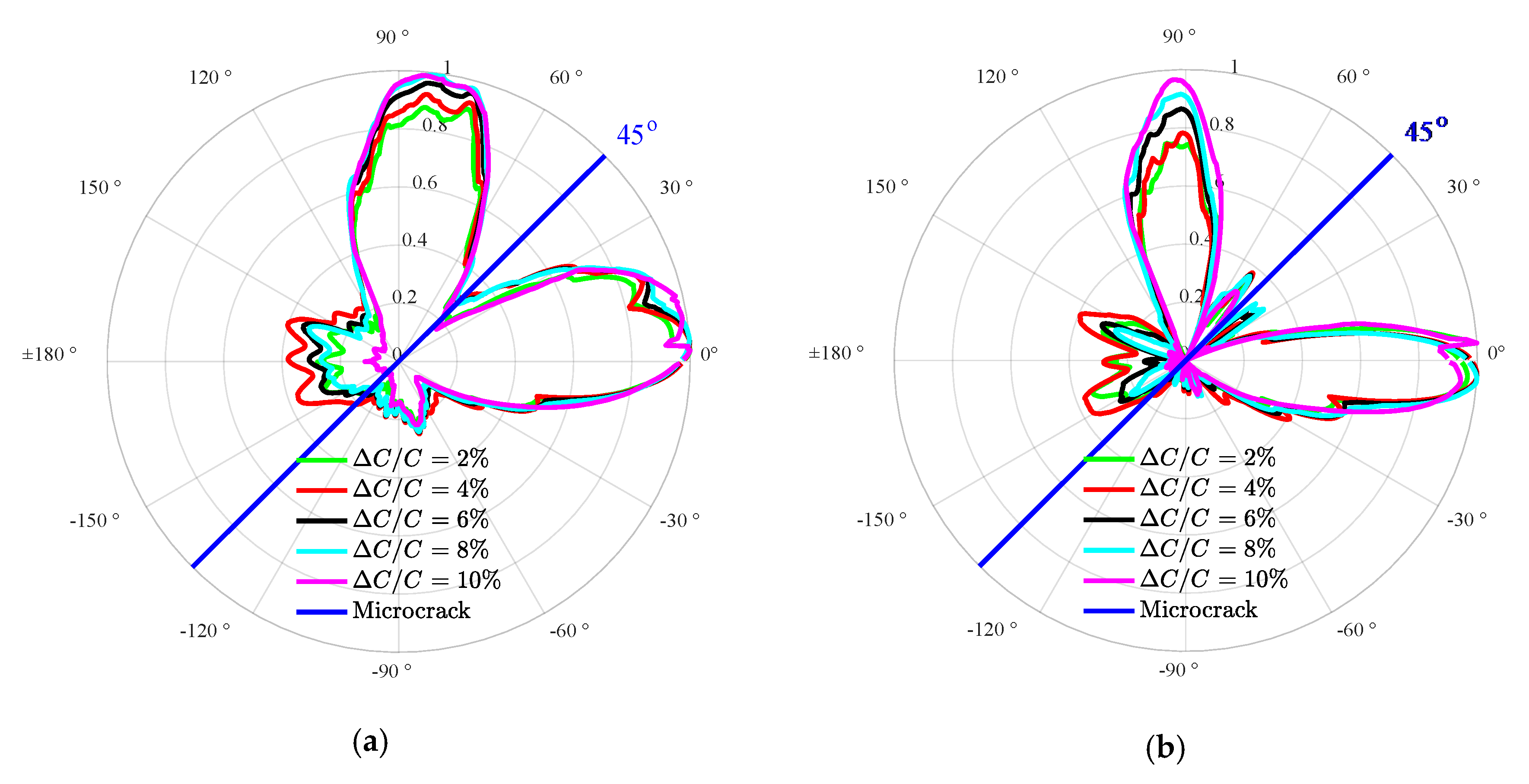
3.2.2. Effects of the Stiffness Difference on the Directivity of the SSS
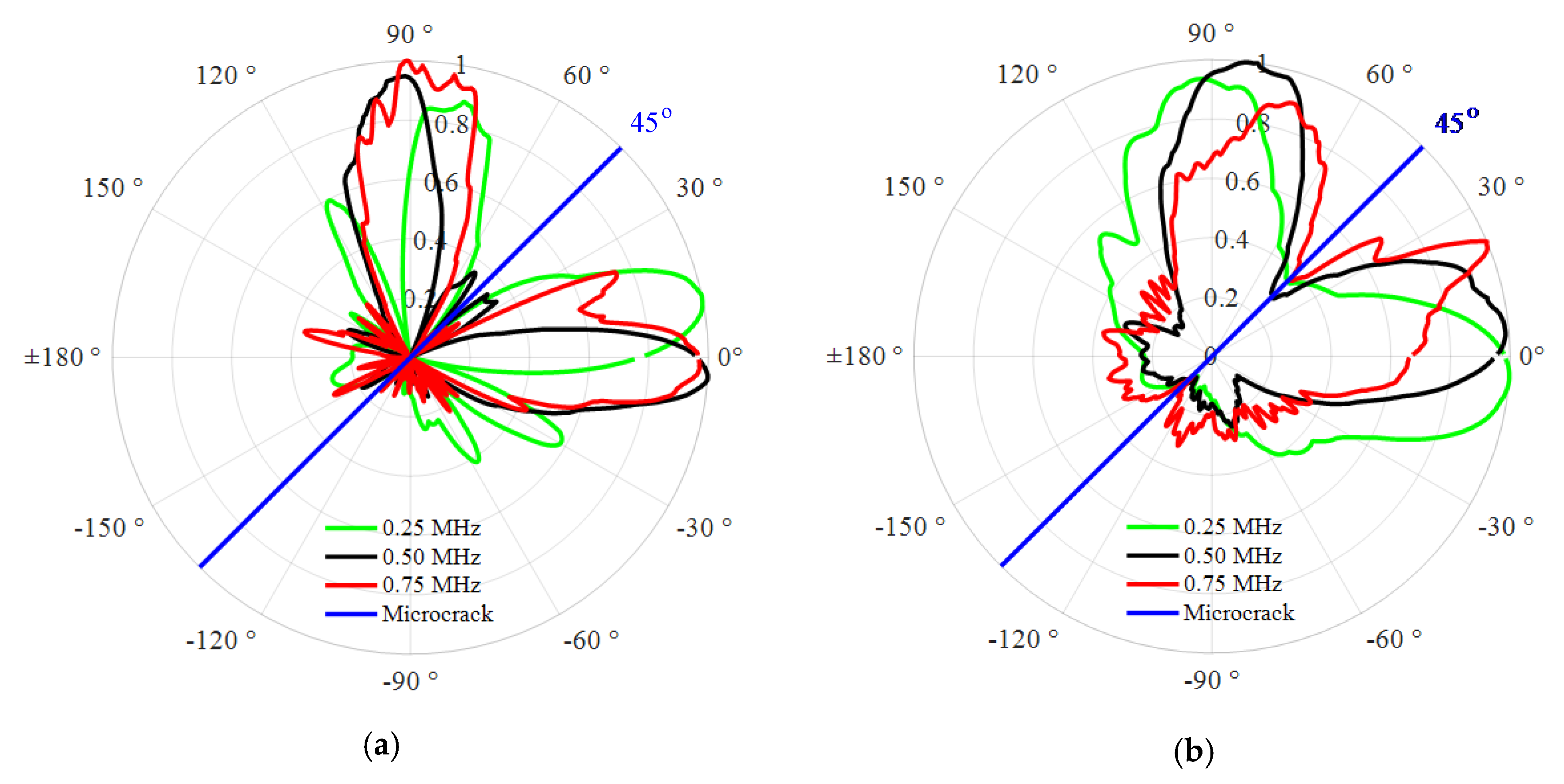
3.2.3. Effects of the UTW Driving Frequency on the Directivity of the SSS
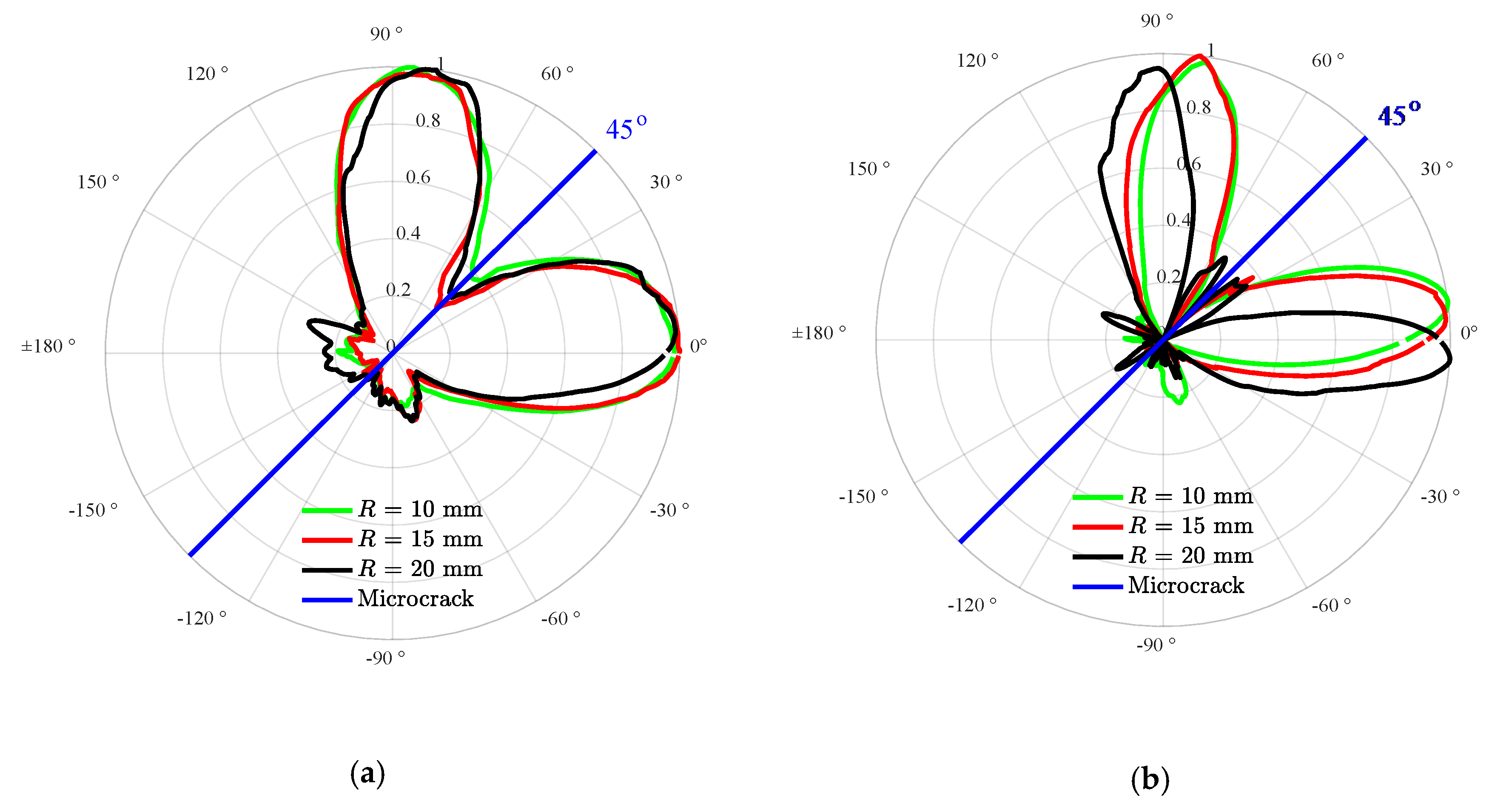
3.2.4. Effects of the Radius of the Sensing Circle on the Directivity of the SSS
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zakar, F.; Mueller, E. Investigation of a Columbus, Ohio train derailment caused by fractured rail. Case Stud. Eng. Fail. Anal. 2016, 7, 41–49. [Google Scholar] [CrossRef][Green Version]
- Ringsberg, J.W. Life prediction of rolling contact fatigue crack initiation. Int. J. Fatigue 2001, 23, 575–586. [Google Scholar] [CrossRef]
- Xu, C.; Yang, Z.; Qiao, B. Traveling distance estimation for dispersive Lamb waves through sparse Bayesian learning strategy. Smart Mater. Struct. 2019, 28, 85008. [Google Scholar] [CrossRef]
- Zhou, C.; Su, Z.; Cheng, L. Quantitative evaluation of orientation-specific damage using elastic waves and probability-based diagnostic imaging. Mech. Syst. Signal Process. 2011, 25, 2135–2156. [Google Scholar] [CrossRef]
- Hisao, O. Reflection of elastic waves by an infinitely long ribbon crack. Jpn. J. Appl. Phys. 1982, 21, 120–122. [Google Scholar]
- Chillara, V.K.; Lissenden, C.J. On some aspects of material behavior relating microstructure and ultrasonic higher harmonic generation. Int. J. Eng. Sci. 2015, 94, 59–70. [Google Scholar] [CrossRef]
- Lv, H.; Jiao, J.; Meng, X.; He, C.; Wu, B. Characterization of nonlinear ultrasonic effects using the dynamic wavelet fingerprint technique. J. Sound Vib. 2017, 389, 364–379. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Niu, D.; Hu, X. Application of nonlinear ultrasonic technique to characterize the creep damage in ASME T92 steel welded joints. NDT E Int. 2018, 98, 8–16. [Google Scholar] [CrossRef]
- Torello, D.; Selby, N.; Kim, J.Y.; Qu, J.; Jacobs, L.J. Determination of absolute material nonlinearity with air-coupled ultrasonic receivers. Ultrasonics 2017, 81, 107–117. [Google Scholar] [CrossRef]
- Pau, A.; Vestroni, F. The role of material and geometric nonlinearities in acoustoelasticity. Wave Motion 2019, 86, 79–90. [Google Scholar] [CrossRef]
- Solodov, I.Y.; Krohn, N.; Busse, G. CAN: An example of nonclassical acoustic nonlinearity in solids. Ultrasonics 2002, 40, 621–625. [Google Scholar] [CrossRef]
- Zhang, C.; He, L.; Liu, S.; Yang, Q. A new vibro-acoustic modulation technique for closed crack detection based on electromagnetic loading. Appl. Acoust. 2019, 157, 107004. [Google Scholar] [CrossRef]
- Den, A.; Johnson, P. Nonlinear Elastic Wave Spectroscopy (NEWS) Techniques to Discern Material Damage, Part I: Nonlinear Wave Modulation Spectroscopy (NWMS). Res. Nondestruct. Eval. 2000, 12, 17–30. [Google Scholar]
- Ogam, G.; Groby, J.P.; Ogam, E. A non-linear vibration spectroscopy model for structures with closed cracks. Int. J. Non-Linear Mech. 2014, 59, 60–68. [Google Scholar] [CrossRef]
- Maier, S.; Kim, J.Y.; Forstenhäusler, M.; James, J.; Laurence, J. Noncontact nonlinear resonance ultrasound spectroscopy (NRUS) for small metallic specimens. NDT E Int. 2018, 98, 37–44. [Google Scholar] [CrossRef]
- Deng, M.; Pei, J. Assessment of accumulated fatigue damage in solid plates using nonlinear Lamb wave approach. Appl. Phys. Lett. 2007, 90, 121902. [Google Scholar] [CrossRef]
- Li, F.; Zhao, Y.; Cao, P. Mixing of ultrasonic Lamb waves in thin plates with quadratic nonlinearity. Ultrasonics 2018, 87, 33–43. [Google Scholar] [CrossRef]
- Ding, X.; Zhao, Y.; Deng, M.; Shui, G.; Hu, N. One-way Lamb mixing method in thin plates with randomly distributed microcracks. Int. J. Mech. Sci. 2019, 171, 105371. [Google Scholar] [CrossRef]
- Zhu, W.; Deng, M.; Xiang, Y. Second harmonic generation of Lamb wave in numerical perspective. Chin. Phys. Lett. 2016, 33, 104301. [Google Scholar] [CrossRef]
- Li, W.; Jiang, C.; Deng, M. Thermal damage assessment of metallic plates using a nonlinear electromagnetic acoustic resonance technique. NDT E Int. 2019, 108, 102172. [Google Scholar] [CrossRef]
- Shui, G.; Wang, Y.; Gong, F. Evaluation of plastic damage for metallic materials under tensile load using nonlinear transverse waves. NDT E Int. 2013, 55, 1–8. [Google Scholar] [CrossRef]
- Matlack, K.H.; Kim, J.Y.; Jacobs, L.J.; Qu, J. Review of second harmonic generation measurement techniques for material state determination in metals. J. Nondestruct. Eval. 2015, 34, 273. [Google Scholar] [CrossRef]
- Metya, A.; Ghosh, M.; Parida, N.; Sagar, S.P. Higher harmonic analysis of ultrasonic signal for ageing behaviour study of C-250 grade maraging steel. NDT E Int. 2008, 41, 484–489. [Google Scholar] [CrossRef]
- Matlack, K.; Wall, J.; Kim, J.Y.; Qu, J.; Jacobs, L.; Viehrig, H.W. Evaluation of radiation damage using nonlinear ultrasound. J. Appl. Phys. 2012, 111, 054911. [Google Scholar] [CrossRef]
- Broda, D.; Staszewski, W.; Martowicz, A.; Uhl, T.; Silberschmidt, V. Modelling of nonlinear crack–wave interactions for damage detection based on ultrasound—A review. J. Sound. Vib. 2014, 333, 1097–1118. [Google Scholar] [CrossRef]
- Friswell, M.I.; Penny, J.E.T. Crack modeling for structural health monitoring. Struct. Health Monit. 2002, 1, 139–148. [Google Scholar] [CrossRef]
- Wang, K.; Fan, Z.; Su, Z. Orienting fatigue cracks using contact acoustic nonlinearity in scattered plate waves. Smart Mater. Struct. 2018, 27, 09LT01. [Google Scholar] [CrossRef]
- Wang, K.; Liu, M.; Su, Z.; Yuan, S.; Fan, Z. Analytical insight into “breathing” crack-induced acoustic nonlinearity with an application to quantitative evaluation of contact cracks. Ultrasonics 2018, 88, 157–167. [Google Scholar] [CrossRef]
- Wang, K.; Li, Y.; Su, Z.; Guan, R.; Lu, Y.; Yuan, S. Nonlinear aspects of “breathing” crack-disturbed plate waves: 3-D analytical modeling with experimental validation. Int. J. Mech. Sci. 2019, 159, 140–150. [Google Scholar] [CrossRef]
- Settimi, V.; Trovalusci, P.; Rega, G. Dynamical properties of a composite microcracked bar based on a generalized continuum formulation. Continu. Mech. Therm. 2019, 31, 1627–1644. [Google Scholar] [CrossRef]
- Lv, H.; Jiao, J.; Wu, B. Evaluation of fatigue crack orientation using non-collinear shear wave mixing method. J. Nondestruct. Eval. 2018, 37, 74. [Google Scholar] [CrossRef]
- Blanloeuil, P.; Meziane, A.; Norris, A.N. Analytical extension of finite element solution for computing the nonlinear far field of ultrasonic waves scattered by a closed crack. Wave Motion 2016, 66, 132–146. [Google Scholar] [CrossRef][Green Version]
- Zhang, J.; Drinkwater, B.W.; Wilcox, P.D. Defect characterization using an ultrasonic array to measure the scattering coefficient matrix. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2008, 55, 2254–2265. [Google Scholar] [CrossRef] [PubMed]
- Blanloeuil, P.; Meziane, A.; Bacon, C. Numerical study of nonlinear interaction between a crack and elastic waves under an oblique incidence. Wave Motion 2014, 51, 425–437. [Google Scholar] [CrossRef]
- Wang, J.; Liu, L.; Hu, N.; Deng, M. Characterization of microcrack’s orientation using secondary acoustic source directivity induced by an incident ultrasonic longitudinal wave. J. Shanxi Norm. Univ. (Nat. Sci. Ed.) 2019, 47, 59–64. [Google Scholar]
- Norris, A.N. Symmetry conditions for third order elastic moduli and implications in nonlinear wave theory. J. Elast. 1991, 25, 247–257. [Google Scholar] [CrossRef]
- Zheng, Y.; Maev, R.G.; Solodov, I.Y. Nonlinear acoustic applications for material characterization: A review. Can. J. Phys. 1999, 77, 927–967. [Google Scholar] [CrossRef]
- Pruell, C.; Kim, J.; Qu, J.; Jacobs, L.J. Evaluation of fatigue damage using nonlinear guided waves. Smart Mater. Struct. 2009, 18, 035003. [Google Scholar] [CrossRef]
- Zhou, C.; Hong, M.; Su, Z.; Wang, Q.; Cheng, L. Evaluation of fatigue cracks using nonlinearities of acousto-ultrasonic waves acquired by an active sensor network. Smart Mater. Struct. 2013, 22, 015018. [Google Scholar] [CrossRef]
- Liu, X.; Bo, L.; Yang, K.; Liu, Y.; Zhao, Y.; Zhang, J.; Hu, N.; Deng, M. Locating and imaging contact delamination based on chaotic detection of nonlinear Lamb waves. Mech. Syst. Signal Process. 2018, 109, 58–73. [Google Scholar] [CrossRef]
- Hong, M.; Su, Z.; Lu, Y.; Sohn, H.; Qing, X. Locating fatigue damage using temporal signal features of nonlinear Lamb waves. Mech. Syst. Signal Process. 2015, 60–61, 182–197. [Google Scholar] [CrossRef]
- Shen, Y.; Giurgiutiu, V. Predictive modeling of nonlinear wave propagation for structural health monitoring with piezoelectric wafer active sensors. J. Intel. Mat. Syst. Struct. 2013, 25, 506–520. [Google Scholar] [CrossRef]
- Biwa, S.; Hiraiwa, S.; Matsumoto, E. Stiffness evaluation of contacting surfaces by bulk and interface waves. Ultrasonics 2007, 47, 123–129. [Google Scholar] [CrossRef] [PubMed]


| Density |
Elasticity Modulus |
Poisson’s Ratio | Velocity of Longitudinal Wave | Velocity of Transverse Wave |
|---|---|---|---|---|
| 2700 kg/m3 | 69 GPa | 0.33 | 6158 m/s | 3103 m/s |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Xu, C.; Zhao, Y.; Hu, N.; Deng, M. Characterization of Microcrack Orientation Using the Directivity of Secondary Sound Source Induced by an Incident Ultrasonic Transverse Wave. Materials 2020, 13, 3318. https://doi.org/10.3390/ma13153318
Wang J, Xu C, Zhao Y, Hu N, Deng M. Characterization of Microcrack Orientation Using the Directivity of Secondary Sound Source Induced by an Incident Ultrasonic Transverse Wave. Materials. 2020; 13(15):3318. https://doi.org/10.3390/ma13153318
Chicago/Turabian StyleWang, Jishuo, Caibin Xu, Youxuan Zhao, Ning Hu, and Mingxi Deng. 2020. "Characterization of Microcrack Orientation Using the Directivity of Secondary Sound Source Induced by an Incident Ultrasonic Transverse Wave" Materials 13, no. 15: 3318. https://doi.org/10.3390/ma13153318
APA StyleWang, J., Xu, C., Zhao, Y., Hu, N., & Deng, M. (2020). Characterization of Microcrack Orientation Using the Directivity of Secondary Sound Source Induced by an Incident Ultrasonic Transverse Wave. Materials, 13(15), 3318. https://doi.org/10.3390/ma13153318






