A Review of Experimentally Informed Micromechanical Modeling of Nanoporous Metals: From Structural Descriptors to Predictive Structure–Property Relationships
Abstract
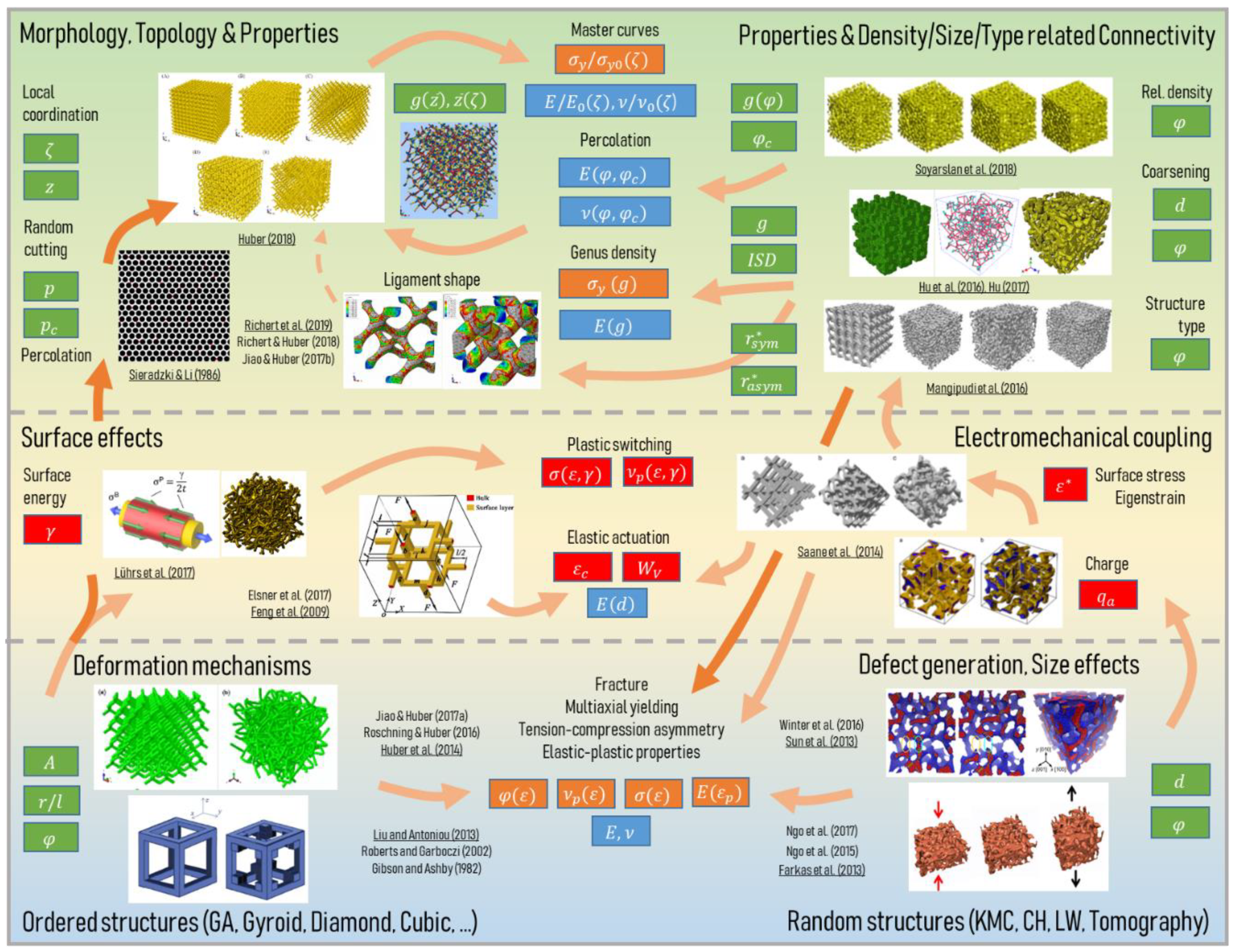
1. Introduction
2. Morphological Descriptors
2.1. Pioneering Work
2.2. Imaging Techniques
2.3. Image Processing
2.3.1. Segmentation and Surface Extraction
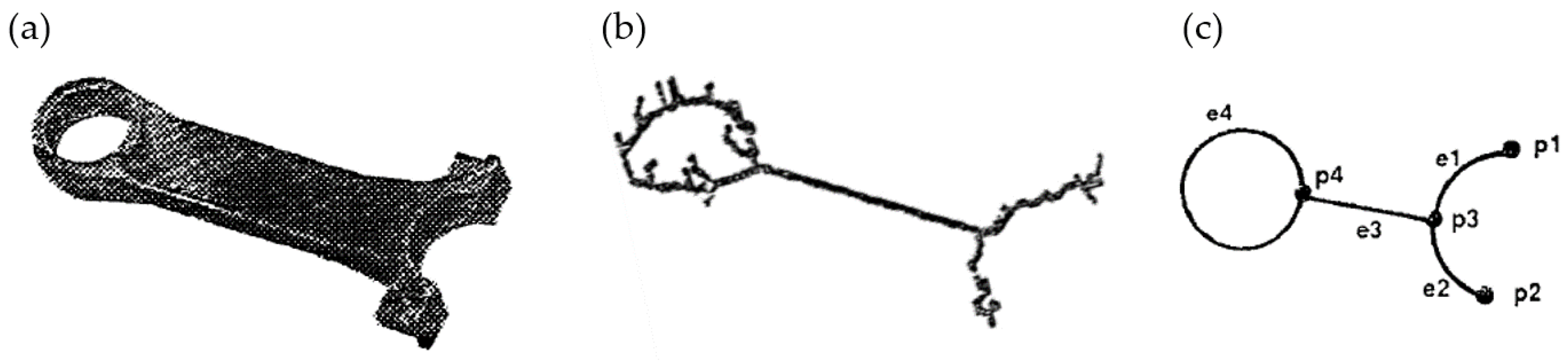
2.3.2. Skeletonization
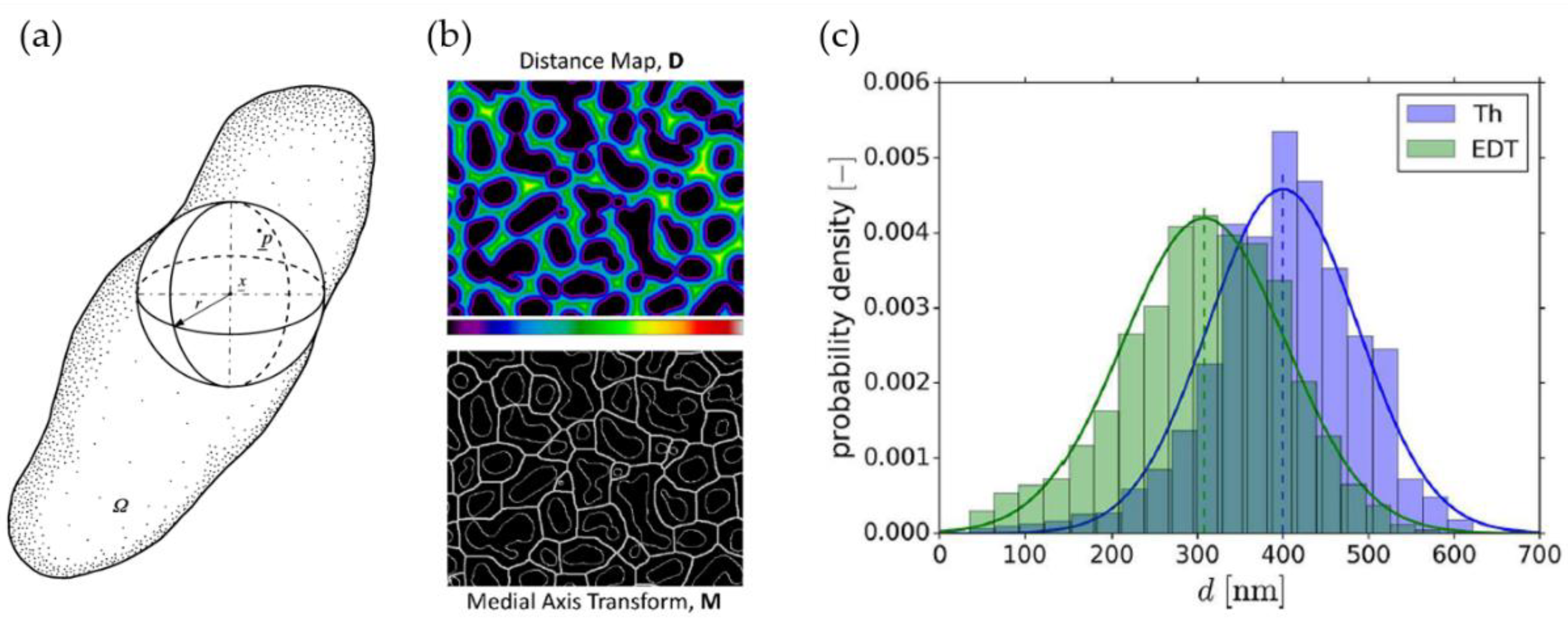
2.3.3. Thickness Computation
2.4. Morphological Analysis and Descriptors
2.4.1. Characteristic Feature Size and Length Scale
- surface area per volume, [17]
- specific area calculated as the ratio of solid (gold) surface to solid volume, [33]
- inverse of the interfacial area per unit volume, [74]
- reciprocal of interfacial area per volume, [75]
- specific surface area, , defined as the surface area per unit volume of the phase (solidAu) [34]
- surface area per unit volume of gold phase used as the characteristic length scale of the structure, , [18], p. 120
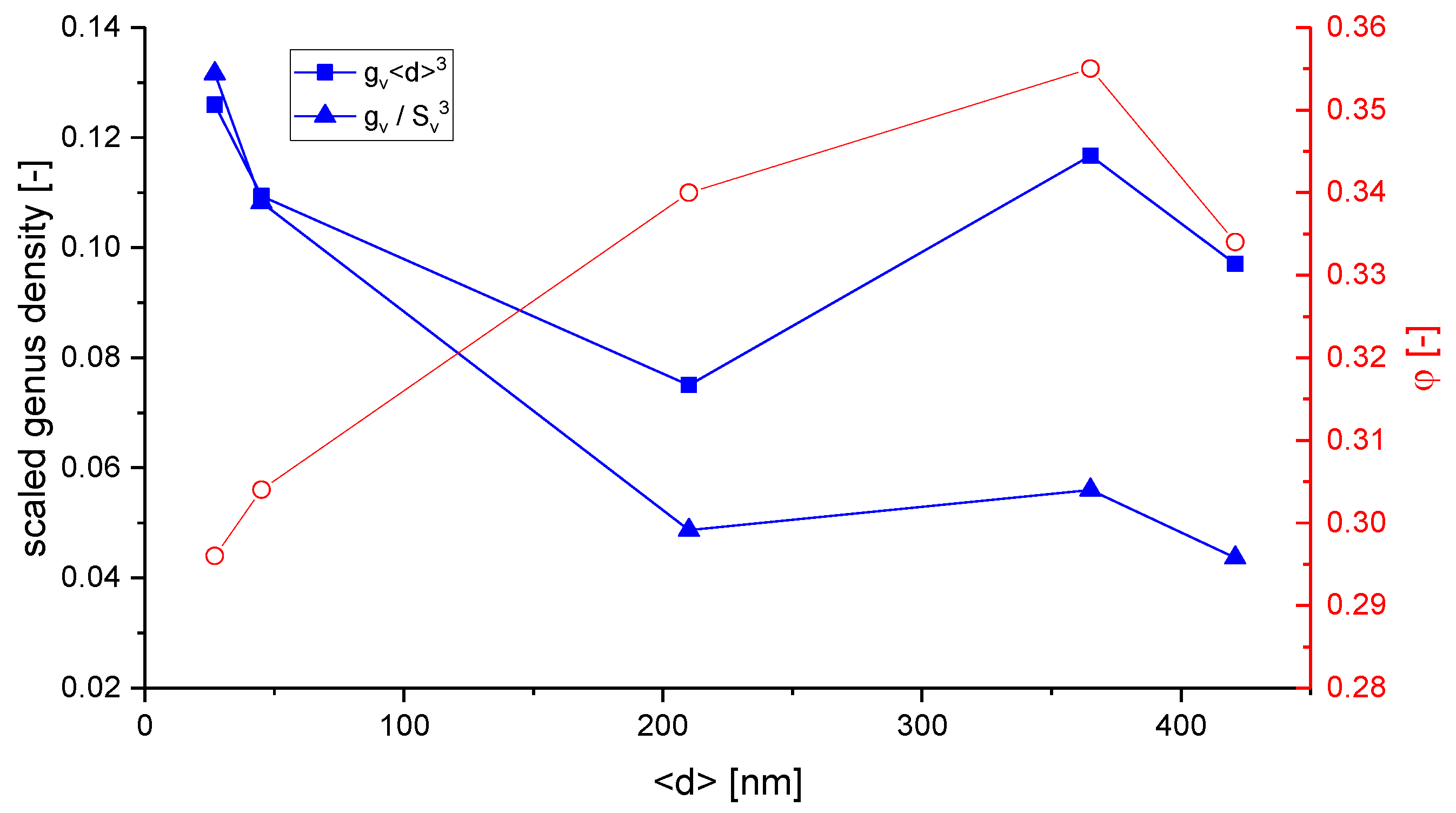
- surface area per unit foam volume used for scaling the genus density, [18], p. 121
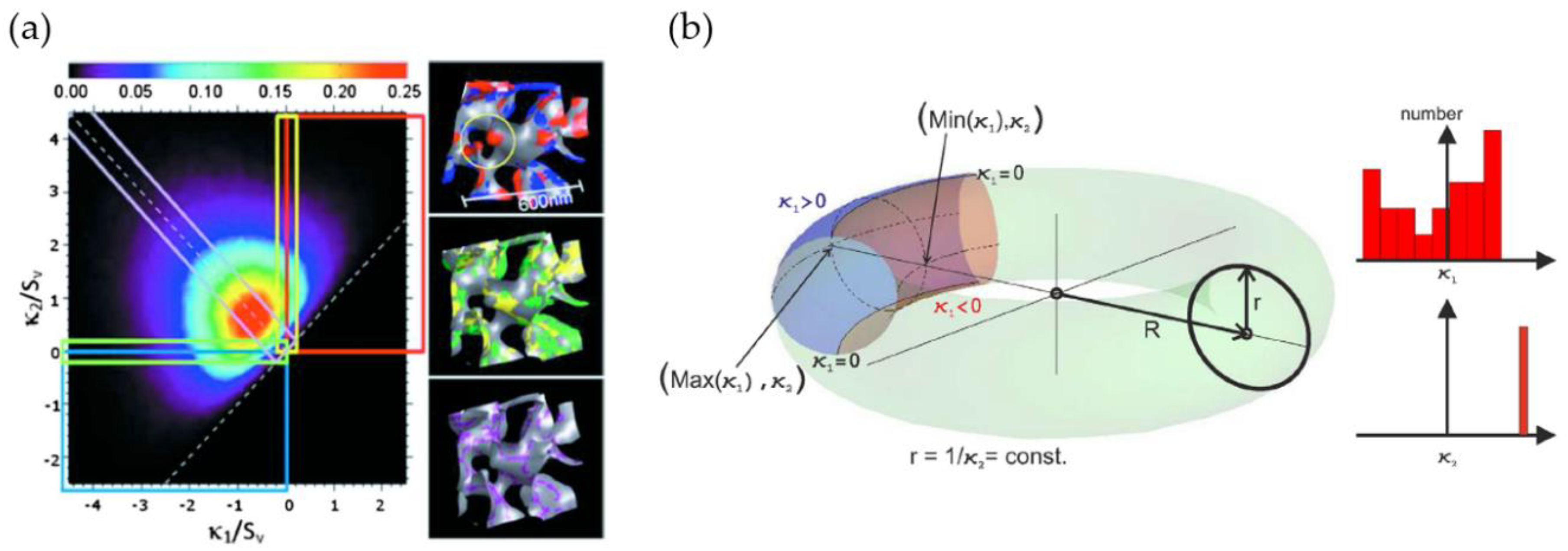
2.4.2. Interfacial Surface Curvatures
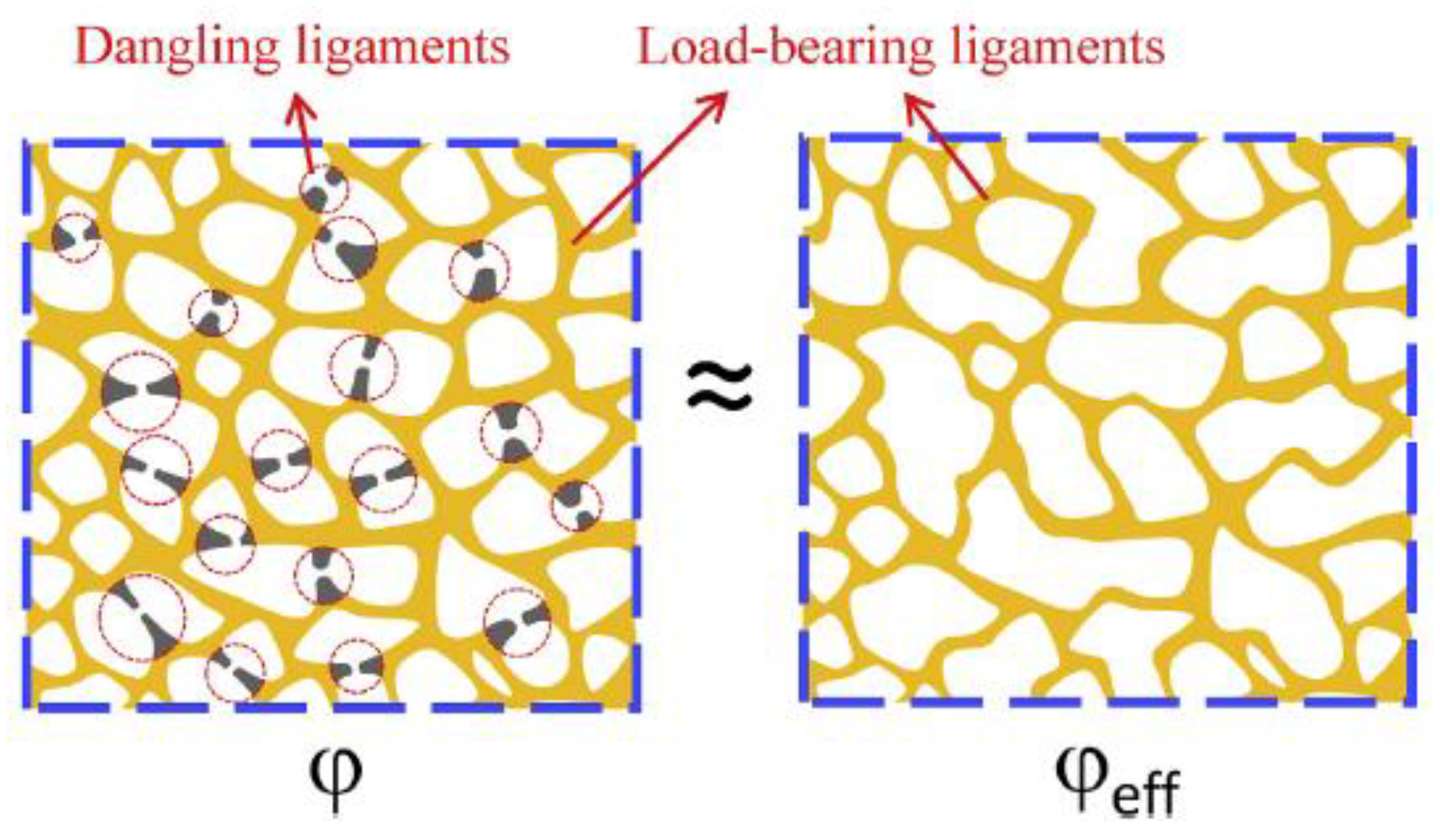
2.4.3. Effective Load-Bearing Structure
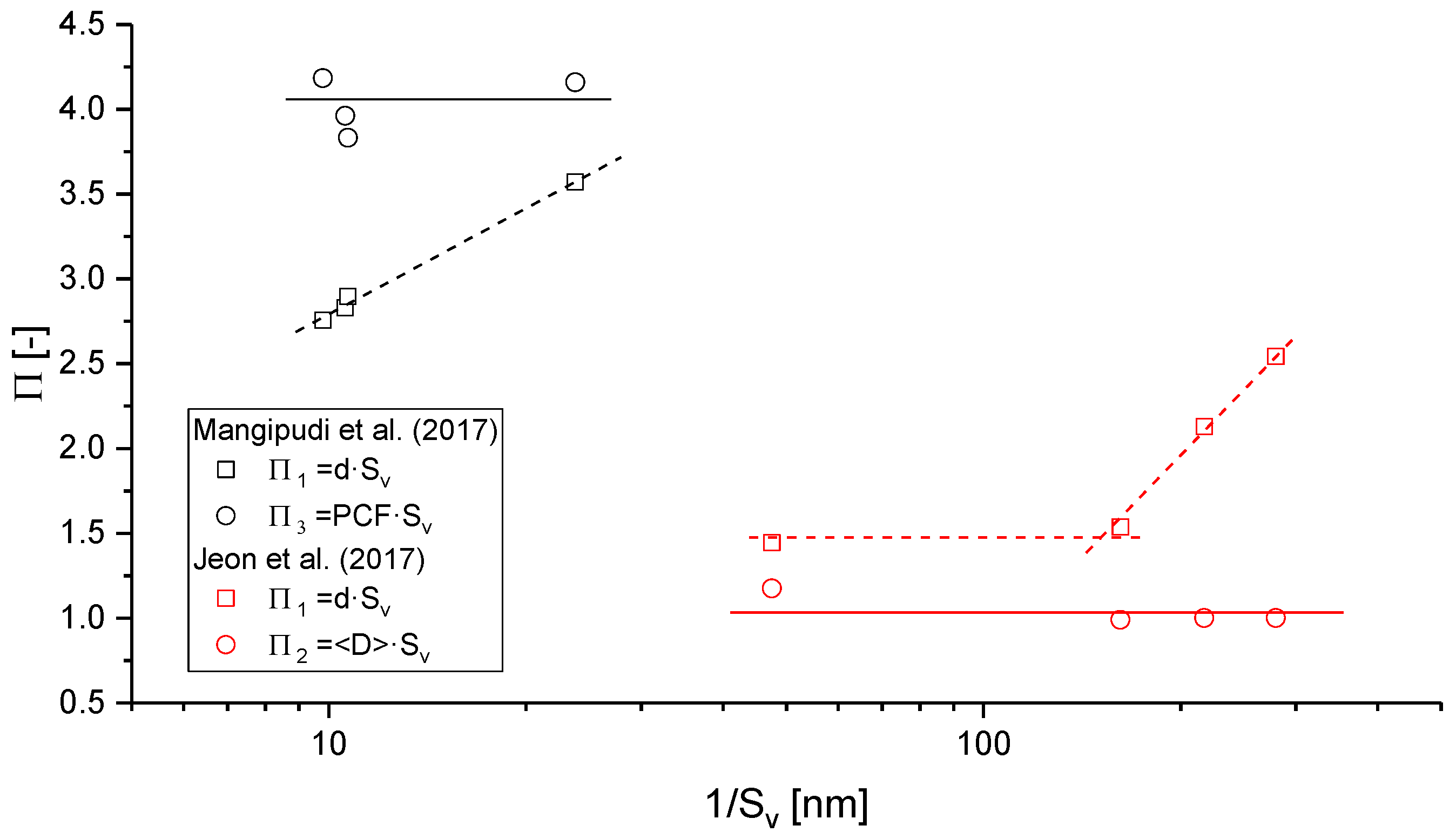
2.4.4. Connectivity and Genus
2.4.5. Ligament Diameter Distribution
2.4.6. Ligament Length Distribution
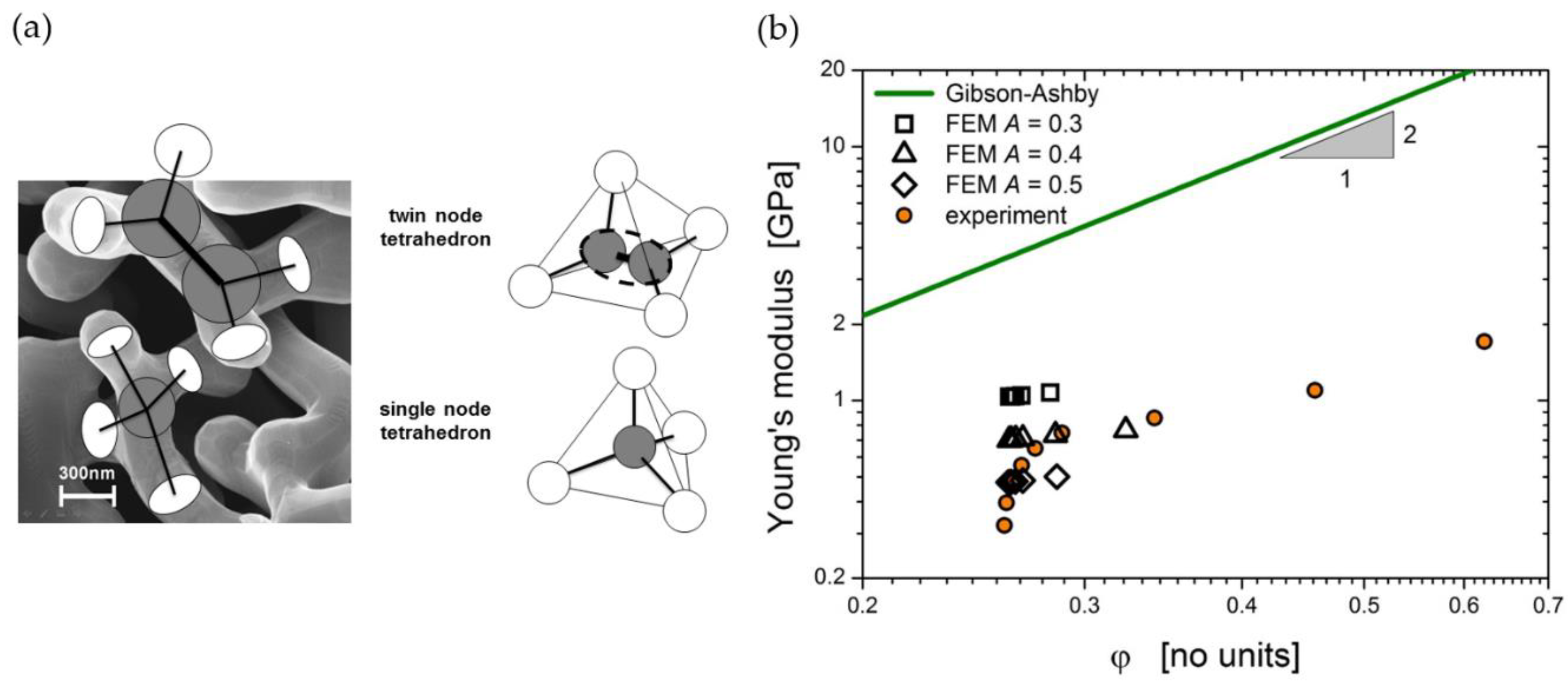
2.4.7. Ligament Shape Distribution
2.5. Concluding Remarks on Structural Characterization
3. Micromechanical Modeling
3.1. Elastic–Plastic Deformation Behavior
3.1.1. Tension/Compression
3.1.2. Macroscopic Compression
3.1.3. Macroscopic Tension until Fracture
3.1.4. Multiaxial Yielding
3.2. Surface Effects
3.2.1. Surface Elasticity
3.2.2. Surface Energy
3.3. Topology
3.3.1. Scaled Genus/Connectivity Density
3.3.2. Percolation
3.3.3. Evolution of Network Connectivity during Coarsening
3.4. Concluding Remarks on Micromechanical Modeling
4. Summary and Future Prospects
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Note
Abbreviations
| BS | biggest-sphere |
| DART | discrete algebraic reconstruction |
| DFT | density functional theory |
| ECD | electrochemical dealloying |
| EDT | Euclidean distance transform |
| ET | electron tomography |
| FE | finite element |
| FEM | finite element method |
| FIB | focused ion beam |
| GA | Gibson–Ashby |
| IND | interfacial normal distributions |
| ISD | interfacial shape distribution |
| KMC | kinetic Monte Carlo |
| LMD | liquid metal dealloying |
| MAT | medial axis transform |
| MD | molecular dynamics |
| NPG | nanoporous gold |
| OSS | open-source software |
| PCF | pair correlation function |
| PXCT | ptychographic X-ray computed tomography |
| ROI | Region of Interest |
| RVE | representative volume element |
| SANS | small-angle neutron scattering |
| SEM | scanning electron microscopy |
| STL | standard triangulation language |
| TEM | transmission electron microscopy |
| Th | Thickness (biggest-sphere) |
| TVM | total variation minimization |
| TXM | transmission X-ray microscopy |
| VOI | Volume of Interest |
| WBPJ | weighted back-projection |
Symbols
| average of | |
| surface energy | |
| strain | |
| cut fraction | |
| percolation threshold (cut fraction) | |
| total cut fraction | |
| principle curvatures | |
| macroscopic Poisson’s ratio | |
| plastic Poisson’s ratio | |
| stress | |
| ultimate tensile strength | |
| macroscopic yield stress | |
| yield stress of the solid phase | |
| solid fraction | |
| percolation threshold (solid fraction) | |
| effective solid fraction | |
| parabolic function constant (ligament shape) | |
| randomization of beam network | |
| concavity parameter (ligament shape) | |
| size of the nodal mass | |
| leading constant GA (bending) | |
| leading constant GA (elastic) | |
| leading constant GA (tension) | |
| leading constant GA (yield) | |
| scaled connectivity density | |
| ligament diameter (thickness) | |
| macroscopic Young’s modulus | |
| work hardening rate | |
| Young’s modulus of the solid phase | |
| surface elastic modulus | |
| percolation exponent | |
| residual surface stress | |
| genus | |
| scaled genus | |
| hardness | |
| fracture toughness | |
| ligament length | |
| characteristic length scale (feature) | |
| characteristic spacing | |
| RVE edge length | |
| exponent coarsening power law | |
| exponent GA equation (elastic) | |
| exponent GA equation (yield) | |
| porosity | |
| percolation threshold (porosity) | |
| charge density | |
| ligament radius | |
| ligament shape parameter (symmetry) | |
| ligament shape parameter (asymmetry) | |
| ligament aspect ratio | |
| surface area per volume | |
| inverse specific surface area | |
| coarsening time | |
| volume | |
| volume-to-surface ratio | |
| coordination number (local) | |
| average coordination number |
References
- Weissmüller, J.; Sieradzki, K. Dealloyed nanoporous materials with interface-controlled behavior. MRS Bull. 2018, 43, 14–19. [Google Scholar] [CrossRef]
- Chen, Q.; Ding, Y.; Chen, M. Nanoporous metal by dealloying for electrochemical energy conversion and storage. MRS Bull. 2018, 43, 43–48. [Google Scholar] [CrossRef]
- Şeker, E.; Shih, W.-C.; Stine, K.J. Nanoporous metals by alloy corrosion: Bioanalytical and biomedical applications. MRS Bull. 2018, 43, 49–56. [Google Scholar] [CrossRef]
- McCue, I.; Karma, A.; Erlebacher, J. Pattern formation during electrochemical and liquid metal dealloying. MRS Bull. 2018, 43, 27–34. [Google Scholar] [CrossRef]
- Lilleodden, E.T.; Voorhees, P.W. On the topological, morphological, and microstructural characterization of nanoporous metals. MRS Bull. 2018, 43, 20–26. [Google Scholar] [CrossRef]
- Jin, H.-J.; Weissmüller, J.; Farkas, D. Mechanical response of nanoporous metals: A story of size, surface stress, and severed struts. MRS Bull. 2018, 43, 35–42. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids. Structure & Properties, 1st ed.; Pergamon Press: Oxford, UK, 1988; ISBN 0-08-036607-4. [Google Scholar]
- Ashby, M.F.; Bréchet, Y.J.M. Designing hybrid materials. Acta Mater. 2003, 51, 5801–5821. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. The mechanics of three-dimensional cellular materials. Proc. R. Soc. Lond. A 1982, 382, 43–59. [Google Scholar] [CrossRef]
- Biener, J.; Hodge, A.M.; Hamza, A.V.; Hsiung, L.M.; Satcher, J.H. Nanoporous Au: A high yield strength material. J. Appl. Phys. 2005, 97, 24301. [Google Scholar] [CrossRef]
- Jin, H.-J.; Kurmanaeva, L.; Schmauch, J.; Rösner, H.; Ivanisenko, Y.; Weissmüller, J. Deforming nanoporous metal: Role of lattice coherency. Acta Mater. 2009, 57, 2665–2672. [Google Scholar] [CrossRef]
- Volkert, C.A.; Lilleodden, E.T.; Kramer, D.; Weissmüller, J. Approaching the theoretical strength in nanoporous Au. Appl. Phys. Lett. 2006, 89, 61920. [Google Scholar] [CrossRef]
- Weissmüller, J.; Newman, R.C.; Jin, H.-J.; Hodge, A.M.; Kysar, J.W. Nanoporous Metals by Alloy Corrosion: Formation and Mechanical Properties. MRS Bull. 2009, 34, 577–586. [Google Scholar] [CrossRef]
- Xiang, Y.-H.; Liu, L.-Z.; Shao, J.-C.; Jin, H.-J. A universal scaling relationship between the strength and Young’s modulus of dealloyed porous Fe0.80Cr0.20. Acta Mater. 2020, 186, 105–115. [Google Scholar] [CrossRef]
- Saane, S.S.R.; Mangipudi, K.R.; Loos, K.U.; de Hosson, J.T.M.; Onck, P.R. Multiscale modeling of charge-induced deformation of nanoporous gold structures. J. Mech. Phys. Solids 2014, 66, 1–15. [Google Scholar] [CrossRef]
- Rösner, H.; Parida, S.; Kramer, D.; Volkert, C.A.; Weissmüller, J. Reconstructing a Nanoporous Metal in Three Dimensions: An Electron Tomography Study of Dealloyed Gold Leaf. Adv. Eng. Mater. 2007, 9, 535–541. [Google Scholar] [CrossRef]
- Chen, Y.-c.K.; Chu, Y.S.; Yi, J.; McNulty, I.; Shen, Q.; Voorhees, P.W.; Dunand, D.C. Morphological and topological analysis of coarsened nanoporous gold by x-ray nanotomography. Appl. Phys. Lett. 2010, 96, 43122. [Google Scholar] [CrossRef][Green Version]
- Mangipudi, K.R.; Epler, E.; Volkert, C.A. Topology-dependent scaling laws for the stiffness and strength of nanoporous gold. Acta Mater. 2016, 119, 115–122. [Google Scholar] [CrossRef]
- Hu, K.; Ziehmer, M.; Wang, K.; Lilleodden, E.T. Nanoporous gold: 3D structural analyses of representative volumes and their implications on scaling relations of mechanical behaviour. Philos. Mag. 2016, 96, 3322–3335. [Google Scholar] [CrossRef]
- Roberts, A.P.; Garboczi, E.J. Elastic properties of model random three-dimensional open-cell solids. J. Mech. Phys. Solids 2002, 50, 33–55. [Google Scholar] [CrossRef]
- Xia, R.; Wu, R.N.; Liu, Y.L.; Sun, X.Y. The Role of Computer Simulation in Nanoporous Metals-A Review. Materials 2015, 8, 5060–5083. [Google Scholar] [CrossRef]
- Gong, L.; Kyriakides, S.; Jang, W.-Y. Compressive response of open-cell foams. Part I: Morphology and elastic properties. Int. J. Solids Struct. 2005, 42, 1355–1379. [Google Scholar] [CrossRef]
- Kanaun, S.; Tkachenko, O. Representative volume element and effective elastic properties of open cell foam materials with random microstructures. JOMMS 2007, 2, 1607–1628. [Google Scholar] [CrossRef][Green Version]
- Jang, W.-Y.; Kraynik, A.M.; Kyriakides, S. On the microstructure of open-cell foams and its effect on elastic properties. Int. J. Solids Struct. 2008, 45, 1845–1875. [Google Scholar] [CrossRef]
- Li, R.; Sieradzki, K. Ductile-brittle transition in random porous Au. Phys. Rev. Lett. 1992, 68, 1168–1171. [Google Scholar] [CrossRef] [PubMed]
- Fujita, T.; Qian, L.-H.; Inoke, K.; Erlebacher, J.; Chen, M.-W. Three-dimensional morphology of nanoporous gold. Appl. Phys. Lett. 2008, 92, 251902. [Google Scholar] [CrossRef]
- Ma, Z.-D.; Kikuchi, N.; Hagiwara, I. Structural topology and shape optimization for a frequency response problem. Comput. Mech. 1993, 13, 157–174. [Google Scholar] [CrossRef]
- Viergever, M.A.; Serra, J.; Soille, P. Mathematical Morphology and Its Applications to Image Processing; Springer Netherlands: Dordrecht, The Netherlands, 1994; ISBN 978-94-010-4453-0. [Google Scholar]
- Rosenfeld, A. Three-dimensional digital topology. Inf. Control 1981, 50, 119–127. [Google Scholar] [CrossRef]
- Corcoran, S.G.; Wiesler, D.; Barker, J.; Sieradzki, K. An in Situ Small Angle Neutron Scattering Investigation of Ag O. 7 Au 0. 3 Dealloying. MRS Proc. 1994, 376. [Google Scholar] [CrossRef]
- Corcoran, S.G.; Wiesler, D.G.; Sieradzki, K. An in Situ Small Angle Neutron Scattering Investigation of Ag 0.7 Au 0.3 Dealloying Under Potential Control. MRS Proc. 1996, 451. [Google Scholar] [CrossRef]
- Berk, N.F. Scattering properties of the leveled-wave model of random morphologies. Phys. Rev. A 1991, 44, 5069–5079. [Google Scholar] [CrossRef]
- Chen-Wiegart, Y.-c.K.; Wang, S.; Chu, Y.S.; Liu, W.; McNulty, I.; Voorhees, P.W.; Dunand, D.C. Structural evolution of nanoporous gold during thermal coarsening. Acta Mater. 2012, 60, 4972–4981. [Google Scholar] [CrossRef]
- Mangipudi, K.R.; Radisch, V.; Holzer, L.; Volkert, C.A. A FIB-nanotomography method for accurate 3D reconstruction of open nanoporous structures. Ultramicroscopy 2016, 163, 38–47. [Google Scholar] [CrossRef] [PubMed]
- Zabihzadeh, S.; van Petegem, S.; Holler, M.; Diaz, A.; Duarte, L.I.; van Swygenhoven, H. Deformation behavior of nanoporous polycrystalline silver. Part I: Microstructure and mechanical properties. Acta Mater. 2017, 131, 467–474. [Google Scholar] [CrossRef]
- Hu, K. Micromechanical and Three-Dimensional Microstructural Characterization of Nanoporous Gold-Epoxy Composites. Ph.D. Thesis, Hamburg University of Technology, Hamburg, Germany, 2017. [Google Scholar]
- Hart, R.G. Electron microscopy of unstained biological material: The polytropic montage. Science 1968, 159, 1464–1467. [Google Scholar] [CrossRef]
- Koster, A.J.; Grimm, R.; Typke, D.; Hegerl, R.; Stoschek, A.; Walz, J.; Baumeister, W. Perspectives of molecular and cellular electron tomography. J. Struct. Biol. 1997, 120, 276–308. [Google Scholar] [CrossRef]
- Penczek, P.; Radermacher, M.; Frank, J. Three-dimensional reconstruction of single particles embedded in ice. Ultramicroscopy 1992, 40, 33–53. [Google Scholar] [CrossRef]
- Chen, D.; Goris, B.; Bleichrodt, F.; Mezerji, H.H.; Bals, S.; Batenburg, K.J.; de With, G.; Friedrich, H. The properties of SIRT, TVM, and DART for 3D imaging of tubular domains in nanocomposite thin-films and sections. Ultramicroscopy 2014, 147, 137–148. [Google Scholar] [CrossRef]
- Wang, G.; Ye, J.C.; Mueller, K.; Fessler, J.A. Image Reconstruction is a New Frontier of Machine Learning. IEEE Trans. Med. Imaging 2018, 37, 1289–1296. [Google Scholar] [CrossRef]
- Ziehmer, M.; Hu, K.; Wang, K.; Lilleodden, E.T. A principle curvatures analysis of the isothermal evolution of nanoporous gold: Quantifying the characteristic length-scales. Acta Mater. 2016, 120, 24–31. [Google Scholar] [CrossRef]
- Jeon, H.; Kang, N.-R.; Gwak, E.-J.; Jang, J.-i.; Han, H.N.; Hwang, J.Y.; Lee, S.; Kim, J.-Y. Self-similarity in the structure of coarsened nanoporous gold. Scr. Mater. 2017, 137, 46–49. [Google Scholar] [CrossRef]
- Stuckner, J.; Frei, K.; McCue, I.; Demkowicz, M.J.; Murayama, M. AQUAMI: An open source Python package and GUI for the automatic quantitative analysis of morphologically complex multiphase materials. Comput. Mater. Sci. 2017, 139, 320–329. [Google Scholar] [CrossRef]
- McCue, I.; Stuckner, J.; Murayama, M.; Demkowicz, M.J. Gaining new insights into nanoporous gold by mining and analysis of published images. Sci. Rep. 2018, 8, 6761. [Google Scholar] [CrossRef] [PubMed]
- Mischaikow, K.; Kokubu, H.; Mrozek, M.; Pilarczyk, P.; Gedeon, T.; Lessard, J.-P.; Gameiro, M. CHomp: Computational Homology Project. Available online: http://chomp.rutgers.edu/ (accessed on 10 June 2020).
- Li, Y.; Dinh Ngô, B.-N.; Markmann, J.; Weissmüller, J. Topology evolution during coarsening of nanoscale metal network structures. Phys. Rev. Mater. 2019, 3. [Google Scholar] [CrossRef]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef] [PubMed]
- Badwe, N.; Chen, X.; Sieradzki, K. Mechanical properties of nanoporous gold in tension. Acta Mater. 2017, 129, 251–258. [Google Scholar] [CrossRef]
- Richert, C.; Huber, N. Skeletonization, Geometrical Analysis, and Finite Element Modeling of Nanoporous Gold Based on 3D Tomography Data. Metals 2018, 8, 282. [Google Scholar] [CrossRef]
- Fang, Q.; Boas, D.A. Tetrahedral mesh generation from volumetric binary and gray-scale images. In Proceedings of the IEEE International Symposium on Biomedical Imaging, Boston, MA, USA, 28 June–1 July 2009; pp. 1142–1145. [Google Scholar]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 15012. [Google Scholar] [CrossRef]
- Richert, C.; Odermatt, A.; Huber, N. Computation of Thickness and Mechanical Properties of Interconnected Structures: Accuracy, Deviations, and Approaches for Correction. Front. Mater. 2019, 6, 352. [Google Scholar] [CrossRef]
- Brun, F.; Mancini, L.; Kasae, P.; Favretto, S.; Dreossi, D.; Tromba, G. Pore3D: A software library for quantitative analysis of porous media. Nuclear Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2010, 615, 326–332. [Google Scholar] [CrossRef]
- Larsson, E.; Gürsoy, D.; de Carlo, F.; Lilleodden, E.; Storm, M.; Wilde, F.; Hu, K.; Müller, M.; Greving, I. Nanoporous gold: A hierarchical and multiscale 3D test pattern for characterizing X-ray nano-tomography systems. J. Synchrotron Radiat. 2019, 26, 194–204. [Google Scholar] [CrossRef]
- Seker, E.; Reed, M.; Begley, M. Nanoporous Gold: Fabrication, Characterization, and Applications. Materials 2009, 2, 2188–2215. [Google Scholar] [CrossRef]
- Parida, S.; Kramer, D.; Volkert, C.A.; Rösner, H.; Erlebacher, J.; Weissmüller, J. Volume change during the formation of nanoporous gold by dealloying. Phys. Rev. Lett. 2006, 97, 35504. [Google Scholar] [CrossRef] [PubMed]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Serra, J. Image Analysis and Mathematical Morphology [1]; Academic Press: London, UK, 1982; ISBN 0-12-637240-3. [Google Scholar]
- Lee, T.C.; Kashyap, R.L.; Chu, C.N. Building Skeleton Models via 3-D Medial Surface Axis Thinning Algorithms. CVGIP: Graphical Models Image Process. 1994, 56, 462–478. [Google Scholar] [CrossRef]
- Jain, A.K. Fundamentals of Digital Image Processing; Prentice-Hall: Englewood Cliffs, NJ, USA, 1989; ISBN 0133361659. [Google Scholar]
- Arganda-Carreras, I.; Fernández-González, R.; Muñoz-Barrutia, A.; Ortiz-De-Solorzano, C. 3D reconstruction of histological sections: Application to mammary gland tissue. Microsc. Res. Tech. 2010, 73, 1019–1029. [Google Scholar] [CrossRef] [PubMed]
- Hildebrand, T.; Rüegsegger, P. A new method for the model-independent assessment of thickness in three-dimensional images. J. Microsc. 1997, 185, 67–75. [Google Scholar] [CrossRef]
- Doube, M.; Kłosowski, M.M.; Arganda-Carreras, I.; Cordelières, F.P.; Dougherty, R.P.; Jackson, J.S.; Schmid, B.; Hutchinson, J.R.; Shefelbine, S.J. BoneJ: Free and extensible bone image analysis in ImageJ. Bone 2010, 47, 1076–1079. [Google Scholar] [CrossRef]
- Soyarslan, C.; Bargmann, S.; Pradas, M.; Weissmüller, J. 3D stochastic bicontinuous microstructures: Generation, topology and elasticity. Acta Mater. 2018, 149, 326–340. [Google Scholar] [CrossRef]
- Ollion, J.; Cochennec, J.; Loll, F.; Escudé, C.; Boudier, T. TANGO: A generic tool for high-throughput 3D image analysis for studying nuclear organization. Bioinformatics 2013, 29, 1840–1841. [Google Scholar] [CrossRef]
- Liu, Y.; Jin, D.; Li, C.; Janz, K.F.; Burns, T.L.; Torner, J.C.; Levy, S.M.; Saha, P.K. A robust algorithm for thickness computation at low resolution and its application to in vivo trabecular bone CT imaging. IEEE Trans. Biomed. Eng. 2014, 61, 2057–2069. [Google Scholar] [CrossRef]
- Jin, D.; Guo, J.; Dougherty, T.M.; Iyer, K.S.; Hoffman, E.A.; Saha, P.K. A semi-automatic framework of measuring pulmonary arterial metrics at anatomic airway locations using CT imaging. Proc. SPIE Int. Soc. Opt. Eng. 2016, 9788. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, X.; Guo, J.; Jin, D.; Letuchy, E.M.; Burns, T.L.; Levy, S.M.; Hoffman, E.A.; Saha, P.K. Quantitative imaging of peripheral trabecular bone microarchitecture using MDCT. Med. Phys. 2018, 45, 236–249. [Google Scholar] [CrossRef] [PubMed]
- Guha, I.; Nadeem, S.A.; You, C.; Zhang, X.; Levy, S.M.; Wang, G.; Torner, J.C.; Saha, P.K. Deep Learning Based High-Resolution Reconstruction of Trabecular Bone Microstructures from Low-Resolution CT Scans using GAN-CIRCLE. Proc. SPIE Int. Soc. Opt. Eng. 2020, 11317. [Google Scholar] [CrossRef]
- McCue, I.; Benn, E.; Gaskey, B.; Erlebacher, J. Dealloying and Dealloyed Materials. Annu. Rev. Mater. Res. 2016, 46, 263–286. [Google Scholar] [CrossRef]
- Gnegel, S.; Li, J.; Mameka, N.; Huber, N.; Düster, A. Numerical Investigation of Polymer Coated Nanoporous Gold. Materials 2019, 12, 2178. [Google Scholar] [CrossRef]
- Kril, C.E.; Birringer, R. Estimating grain-size distributions in nanocrystalline materials from X-ray diffraction profile analysis. Philos. Mag. A 1998, 77, 621–640. [Google Scholar] [CrossRef]
- Kwon, Y.; Thornton, K.; Voorhees, P.W. The topology and morphology of bicontinuous interfaces during coarsening. Europhys. Lett. 2009, 86, 46005. [Google Scholar] [CrossRef]
- Kwon, Y.; Thornton, K.; Voorhees, P.W. Morphology and topology in coarsening of domains via non-conserved and conserved dynamics. Philos. Mag. 2010, 90, 317–335. [Google Scholar] [CrossRef]
- Chen-Wiegart, Y.-c.K.; Wada, T.; Butakov, N.; Xiao, X.; de Carlo, F.; Kato, H.; Wang, J.; Dunand, D.C.; Maire, E. 3D morphological evolution of porous titanium by x-ray micro- and nano-tomography. J. Mater. Res. 2013, 28, 2444–2452. [Google Scholar] [CrossRef]
- Zhao, C.; Wada, T.; de Andrade, V.; Williams, G.J.; Gelb, J.; Li, L.; Thieme, J.; Kato, H.; Chen-Wiegart, Y.-c.K. Three-Dimensional Morphological and Chemical Evolution of Nanoporous Stainless Steel by Liquid Metal Dealloying. ACS Appl. Mater. Interfaces 2017, 9, 34172–34184. [Google Scholar] [CrossRef]
- Liu, L.-Z.; Ye, X.-L.; Jin, H.-J. Interpreting anomalous low-strength and low-stiffness of nanoporous gold: Quantification of network connectivity. Acta Mater. 2016, 118, 77–87. [Google Scholar] [CrossRef]
- Mameka, N.; Wang, K.; Markmann, J.; Lilleodden, E.T.; Weissmüller, J. Nanoporous Gold—Testing Macro-scale Samples to Probe Small-scale Mechanical Behavior. Mater. Res. Lett. 2016, 4, 27–36. [Google Scholar] [CrossRef]
- Huber, N. Connections Between Topology and Macroscopic Mechanical Properties of Three-Dimensional Open-Pore Materials. Front. Mater. 2018, 5, 5801. [Google Scholar] [CrossRef]
- Munkres, J.R. Algebraic Topology; Addison-Wesley: Redwood City, CA, USA, 1984; ISBN 9780201045864. [Google Scholar]
- Euler, L. Elementa doctrinae solidorum. In Euler Archive—All Works; University of the Pacific: Stockton, CA, USA, 1758; p. 230. [Google Scholar]
- Odgaard, A.; Gundersen, H.J.G. Quantification of connectivity in cancellous bone, with special emphasis on 3-D reconstructions. Bone 1993, 14, 173–182. [Google Scholar] [CrossRef]
- Pressley, A. Elementary Differential Geometry, 2nd ed.; Academic Press: Cambridge, MA, USA, 2006; ISBN 978-1-84882-890-2. [Google Scholar]
- Liu, L.-Z.; Jin, H.-J. Scaling equation for the elastic modulus of nanoporous gold with “fixed” network connectivity. Appl. Phys. Lett. 2017, 110, 211902. [Google Scholar] [CrossRef]
- Tse, A.Y.; Karasz, E.K.; Sieradzki, K. Dealloying and morphology evolution of ordered and disordered Cu3Au. Scr. Mater. 2020, 176, 112–116. [Google Scholar] [CrossRef]
- Stuckner, J.; Frei, K.; Corcoran, S.G.; Reynolds, W.T.; Murayama, M. Assessing the influence of processing parameters and external loading on the nanoporous structure and morphology of nanoporous gold toward catalytic applications. J. Phys. Chem. Solids 2020, 136, 109139. [Google Scholar] [CrossRef]
- Mangipudi, K.R.; Epler, E.; Volkert, C.A. Morphological similarity and structure-dependent scaling laws of nanoporous gold from different synthesis methods. Acta Mater. 2017, 140, 337–343. [Google Scholar] [CrossRef]
- Huber, N.; Viswanath, R.N.; Mameka, N.; Markmann, J.; Weißmüller, J. Scaling laws of nanoporous metals under uniaxial compression. Acta Mater. 2014, 67, 252–265. [Google Scholar] [CrossRef]
- Stuckner, J.; Murayama, M. Mechanical properties of nanoporous gold subjected to tensile stresses in real-time, sub-microscopic scale. J. Mater. Sci. 2019, 54, 12106–12115. [Google Scholar] [CrossRef]
- Pia, G.; Delogu, F. Nanoporous Au: Statistical analysis of morphological features and evaluation of their influence on the elastic deformation behavior by phenomenological modeling. Acta Mater. 2015, 85, 250–260. [Google Scholar] [CrossRef]
- Roschning, B.; Huber, N. Scaling laws of nanoporous gold under uniaxial compression: Effects of structural disorder on the solid fraction, elastic Poisson’s ratio, Young’s modulus and yield strength. J. Mech. Phys. Solids 2016, 92, 55–71. [Google Scholar] [CrossRef]
- Liu, R.; Antoniou, A. A relationship between the geometrical structure of a nanoporous metal foam and its modulus. Acta Mater. 2013, 61, 2390–2402. [Google Scholar] [CrossRef]
- Kertis, F.; Snyder, J.; Govada, L.; Khurshid, S.; Chayen, N.; Erlebacher, J. Structure/processing relationships in the fabrication of nanoporous gold. JOM 2010, 62, 50–56. [Google Scholar] [CrossRef]
- Erlebacher, J.; McCue, I. Geometric characterization of nanoporous metals. Acta Mater. 2012, 60, 6164–6174. [Google Scholar] [CrossRef]
- Luxner, M.H.; Stampfl, J.; Pettermann, H.E. Finite element modeling concepts and linear analyses of 3D regular open cell structures. J. Mater. Sci. 2005, 40, 5859–5866. [Google Scholar] [CrossRef]
- Luxner, M.H.; Stampfl, J.; Pettermann, H.E. Numerical simulations of 3D open cell structures – influence of structural irregularities on elasto-plasticity and deformation localization. Int. J. Solids Struct. 2007, 44, 2990–3003. [Google Scholar] [CrossRef]
- Nachtrab, S.; Kapfer, S.C.; Arns, C.H.; Madadi, M.; Mecke, K.; Schröder-Turk, G.E. Morphology and linear-elastic moduli of random network solids. Adv. Mater. Weinheim. 2011, 23, 2633–2637. [Google Scholar] [CrossRef]
- Gan, Y.X.; Chen, C.; Shen, Y.P. Three-dimensional modeling of the mechanical property of linearly elastic open cell foams. Int. J. Solids Struct. 2005, 42, 6628–6642. [Google Scholar] [CrossRef]
- Jang, W.-Y.; Kyriakides, S.; Kraynik, A.M. On the compressive strength of open-cell metal foams with Kelvin and random cell structures. Int. J. Solids Struct. 2010, 47, 2872–2883. [Google Scholar] [CrossRef]
- Harb, R.; Taciroglu, E.; Ghoniem, N. Partitioning of elastic energy in open-cell foams under finite deformations. Acta Mater. 2013, 61, 1454–1468. [Google Scholar] [CrossRef]
- Jiao, J.; Huber, N. Deformation mechanisms in nanoporous metals: Effect of ligament shape and disorder. Comput. Mater. Sci. 2017, 127, 194–203. [Google Scholar] [CrossRef][Green Version]
- Griffiths, E.; Bargmann, S.; Reddy, B.D. Elastic behaviour at the nanoscale of innovative composites of nanoporous gold and polymer. Extreme Mech. Lett. 2017, 17, 16–23. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free Energy of a Nonuniform System. I. Interfacial Free Energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Erlebacher, J. Mechanism of coarsening and bubble formation in high-genus nanoporous metals. Phys. Rev. Lett. 2011, 106, 225504. [Google Scholar] [CrossRef]
- Roberts, A.P.; Garboczi, E.J. Elastic properties of a tungsten–silver composite by reconstruction and computation. J Mech. Phys. Solids 1999, 47, 2029–2055. [Google Scholar] [CrossRef][Green Version]
- Antman, S.S.; Sirovich, L.; Marsden, J.E.; Wiggins, S.; Torquato, S. Random Heterogeneous Materials; Springer New York: New York, NY, USA, 2002; ISBN 978-1-4757-6357-7. [Google Scholar]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Foiles, S.M.; Baskes, M.I.; Daw, M.S. Embedded-atom-method functions for the fcc metals Cu, Ag, Au, Ni, Pd, Pt, and their alloys. Phys. Rev. B Condens. Matter 1986, 33, 7983–7991. [Google Scholar] [CrossRef]
- Crowson, D.; Farkas, D.; Corcoran, S.G. Geometric relaxation of nanoporous metals: The role of surface relaxation. Scr. Mater. 2007, 56, 919–922. [Google Scholar] [CrossRef]
- Crowson, D.A.; Farkas, D.; Corcoran, S.G. Mechanical stability of nanoporous metals with small ligament sizes. Scr. Mater. 2009, 61, 497–499. [Google Scholar] [CrossRef]
- Farkas, D.; Caro, A.; Bringa, E.; Crowson, D. Mechanical response of nanoporous gold. Acta Mater. 2013, 61, 3249–3256. [Google Scholar] [CrossRef]
- Jiao, J.; Huber, N. Effect of nodal mass on macroscopic mechanical properties of nanoporous metals. Int. J. Mech. Sci. 2017, 134, 234–243. [Google Scholar] [CrossRef]
- Odermatt, A.; Richert, C.; Huber, N. Prediction of elastic-plastic deformation of nanoporous metals by FEM beam modeling: A bottom-up approach from ligaments to real microstructures. Mater. Sci. Eng. A 2020, 791, 139700. [Google Scholar] [CrossRef]
- Ngô, B.-N.D.; Stukowski, A.; Mameka, N.; Markmann, J.; Albe, K.; Weissmüller, J. Anomalous compliance and early yielding of nanoporous gold. Acta Mater. 2015, 93, 144–155. [Google Scholar] [CrossRef]
- Ngô, B.-N.D.; Roschning, B.; Albe, K.; Weissmüller, J.; Markmann, J. On the origin of the anomalous compliance of dealloying-derived nanoporous gold. Scr. Mater. 2017, 130, 74–77. [Google Scholar] [CrossRef]
- Sun, X.-Y.; Xu, G.-K.; Li, X.; Feng, X.-Q.; Gao, H. Mechanical properties and scaling laws of nanoporous gold. J. Appl. Phys. 2013, 113, 23505. [Google Scholar] [CrossRef]
- Winter, N.; Becton, M.; Zhang, L.; Wang, X. Failure Mechanisms and Scaling Laws of Nanoporous Aluminum: A Computational Study. Adv. Eng. Mater. 2016, 18, 632–642. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids. Structure and Properties, 2nd ed.; 1. paperback ed. (with corr.), transferred to digital printing; Cambridge University Press: Cambridge, UK, 2001; ISBN 0521495601. [Google Scholar]
- Briot, N.J.; Kennerknecht, T.; Eberl, C.; Balk, T.J. Mechanical properties of bulk single crystalline nanoporous gold investigated by millimetre-scale tension and compression testing. Philos. Mag. 2014, 94, 847–866. [Google Scholar] [CrossRef]
- Sun, Y.; Ye, J.; Minor, A.M.; Balk, T.J. In situ indentation of nanoporous gold thin films in the transmission electron microscope. Microsc. Res. Tech. 2009, 72, 232–241. [Google Scholar] [CrossRef]
- Lührs, L.; Soyarslan, C.; Markmann, J.; Bargmann, S.; Weissmüller, J. Elastic and plastic Poisson’s ratios of nanoporous gold. Scr. Mater. 2016, 110, 65–69. [Google Scholar] [CrossRef]
- Mangipudi, K.R.; Epler, E.; Volkert, C.A. On the multiaxial yielding and hardness to yield stress relation of nanoporous gold. Scr. Mater. 2018, 146, 150–153. [Google Scholar] [CrossRef]
- Shaw, M.C.; Sata, T. The plastic behavior of cellular materials. Int. J. Mech. Sci. 1966, 8, 469–478. [Google Scholar] [CrossRef]
- Kramer, D.; Viswanath, R.N.; Weissmüller, J. Surface-Stress Induced Macroscopic Bending of Nanoporous Gold Cantilevers. Nano Lett. 2004, 4, 793–796. [Google Scholar] [CrossRef]
- Jin, H.-J.; Weissmüller, J. Bulk Nanoporous Metal for Actuation. Adv. Eng. Mater. 2010, 12, 714–723. [Google Scholar] [CrossRef]
- Jin, H.-J.; Weissmüller, J. A material with electrically tunable strength and flow stress. Science 2011, 332, 1179–1182. [Google Scholar] [CrossRef] [PubMed]
- Mameka, N.; Markmann, J.; Weissmüller, J. On the impact of capillarity for strength at the nanoscale. Nat. Commun. 2017, 8, 1976. [Google Scholar] [CrossRef]
- Feng, X.-Q.; Xia, R.; Li, X.; Li, B. Surface effects on the elastic modulus of nanoporous materials. Appl. Phys. Lett. 2009, 94, 11916. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Weissmüller, J.; Larché, F. A general theory of curved deformable interfaces in solids at equilibrium. Philos. Mag. A 1998, 78, 1093–1109. [Google Scholar] [CrossRef]
- Miller, R.E.; Shenoy, V.B. Size-dependent elastic properties of nanosized structural elements. Nanotechnology 2000, 11, 139–147. [Google Scholar] [CrossRef]
- Shenoy, V.B. Atomistic calculations of elastic properties of metallic fcc crystal surfaces. Phys. Rev. B 2005, 71. [Google Scholar] [CrossRef]
- Elsner, B.A.M.; Müller, S.; Bargmann, S.; Weissmüller, J. Surface excess elasticity of gold: Ab initio coefficients and impact on the effective elastic response of nanowires. Acta Mater. 2017, 124, 468–477. [Google Scholar] [CrossRef]
- Michl, A.; Weissmüller, J.; Müller, S. Electrocapillary Coupling at Metal Surfaces from First Principles: On the Impact of Excess Charge on Surface Stress and Relaxation. Langmuir 2018, 34, 4920–4928. [Google Scholar] [CrossRef] [PubMed]
- Lührs, L.; Zandersons, B.; Huber, N.; Weissmüller, J. Plastic Poisson’s Ratio of Nanoporous Metals: A Macroscopic Signature of Tension-Compression Asymmetry at the Nanoscale. Nano Lett. 2017, 17, 6258–6266. [Google Scholar] [CrossRef] [PubMed]
- Sahimi, M. Applications of Percolation Theory; Taylor & Francis: London, UK, 1994; ISBN 0748400761. [Google Scholar]
- Kováčik, J. Correlation between Young’s modulus and porosity in porous materials. J. Mater. Sci. Lett. 1999, 18, 1007–1010. [Google Scholar] [CrossRef]
- Geslin, P.-A.; Buchet, M.; Wada, T.; Kato, H. Phase-field investigation of the coarsening of porous structures by surface diffusion. Phys. Rev. Mater. 2019, 3. [Google Scholar] [CrossRef]
- Sieradzki, K.; Li, R. Fracture Behavior of a Solid with Random Porosity. Phys. Rev. Lett. 1986, 2509–2512. [Google Scholar] [CrossRef]
- Huber, N.; Tsakmakis, C. Determination of constitutive properties from spherical indentation data using neural networks. Part I: The case of pure kinematic hardening in plasticity laws. J. Mech. Phys. Solids 1999, 47, 1569–1588. [Google Scholar] [CrossRef]
- Huber, N.; Tsakmakis, C. Determination of constitutive properties from spherical indentation data using neural networks. Part II: Plasticity with nonlinear isotropic and kinematic hardening. J. Mech. Phys. Solids 1999, 47, 1589–1607. [Google Scholar] [CrossRef]
- Huber, N.; Tyulyukovskiy, E. A new loading history for identification of viscoplastic properties by spherical indentation. J. Mater. Res. 2004, 19, 101–113. [Google Scholar] [CrossRef]
- Cornec, A.; Kabir, M.R.; Huber, N. Use of spherical indentation technique for measurement of property variations of γTiAl. J. Mater. Res. 2012, 27, 378–388. [Google Scholar] [CrossRef]
- Wang, K.; Hartig, C.; Blankenburg, M.; Müller, M.; Günther, R.; Weissmüller, J. Local flow stresses in interpenetrating-phase composites based on nanoporous gold—In situ diffraction. Scr. Mater. 2017, 127, 151–155. [Google Scholar] [CrossRef]
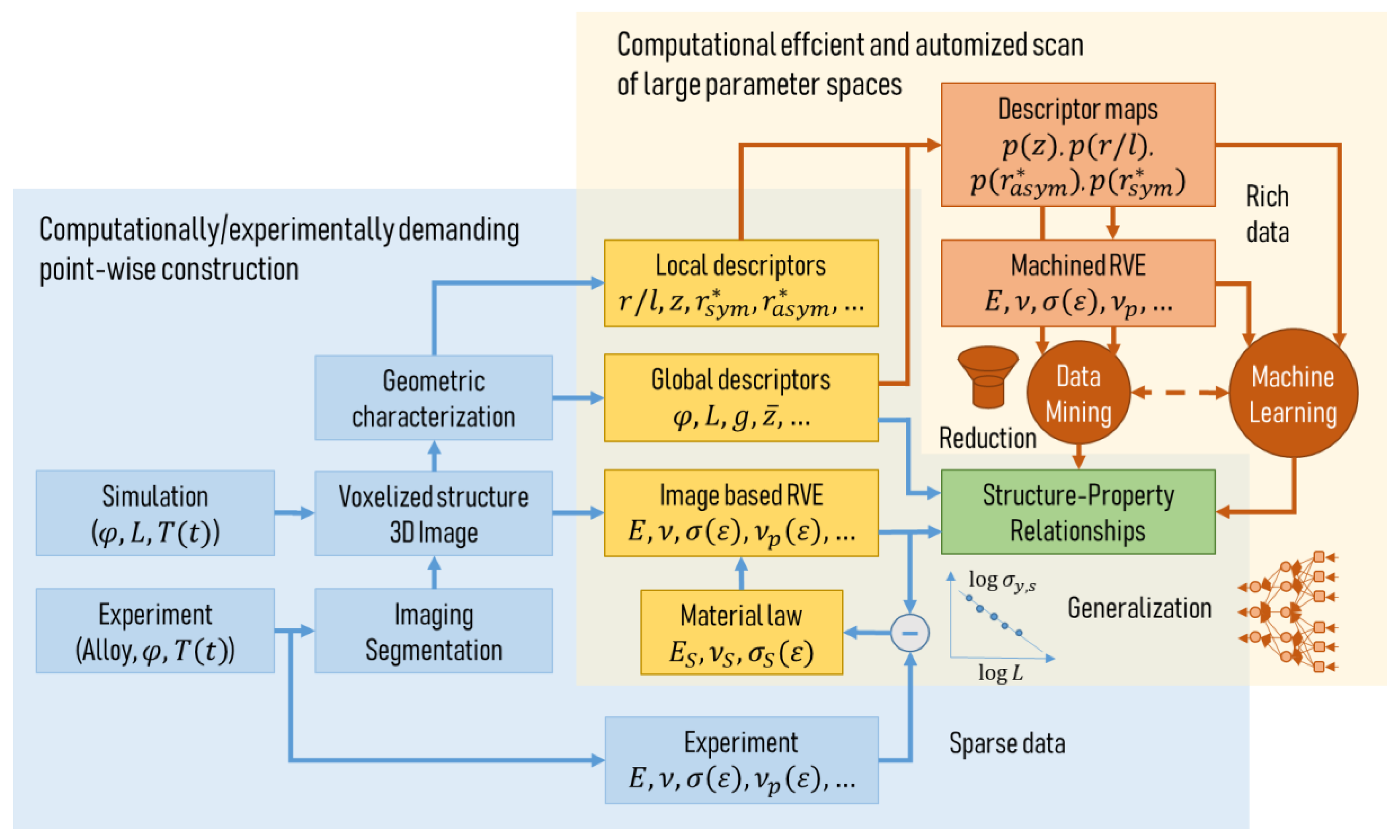
- Bock, F.E.; Aydin, R.C.; Cyron, C.J.; Huber, N.; Kalidindi, S.R.; Klusemann, B. A Review of the Application of Machine Learning and Data Mining Approaches in Continuum Materials Mechanics. Front. Mater. 2019, 6, 443. [Google Scholar] [CrossRef]
- Huber, N.; Kalidindi, S.R.; Klusemann, B.; Cyron, C.J. Machine Learning and Data Mining in Materials Science; Frontiers Media SA: Lausanne, Switzerland, 2020; ISBN 9782889636518. [Google Scholar]





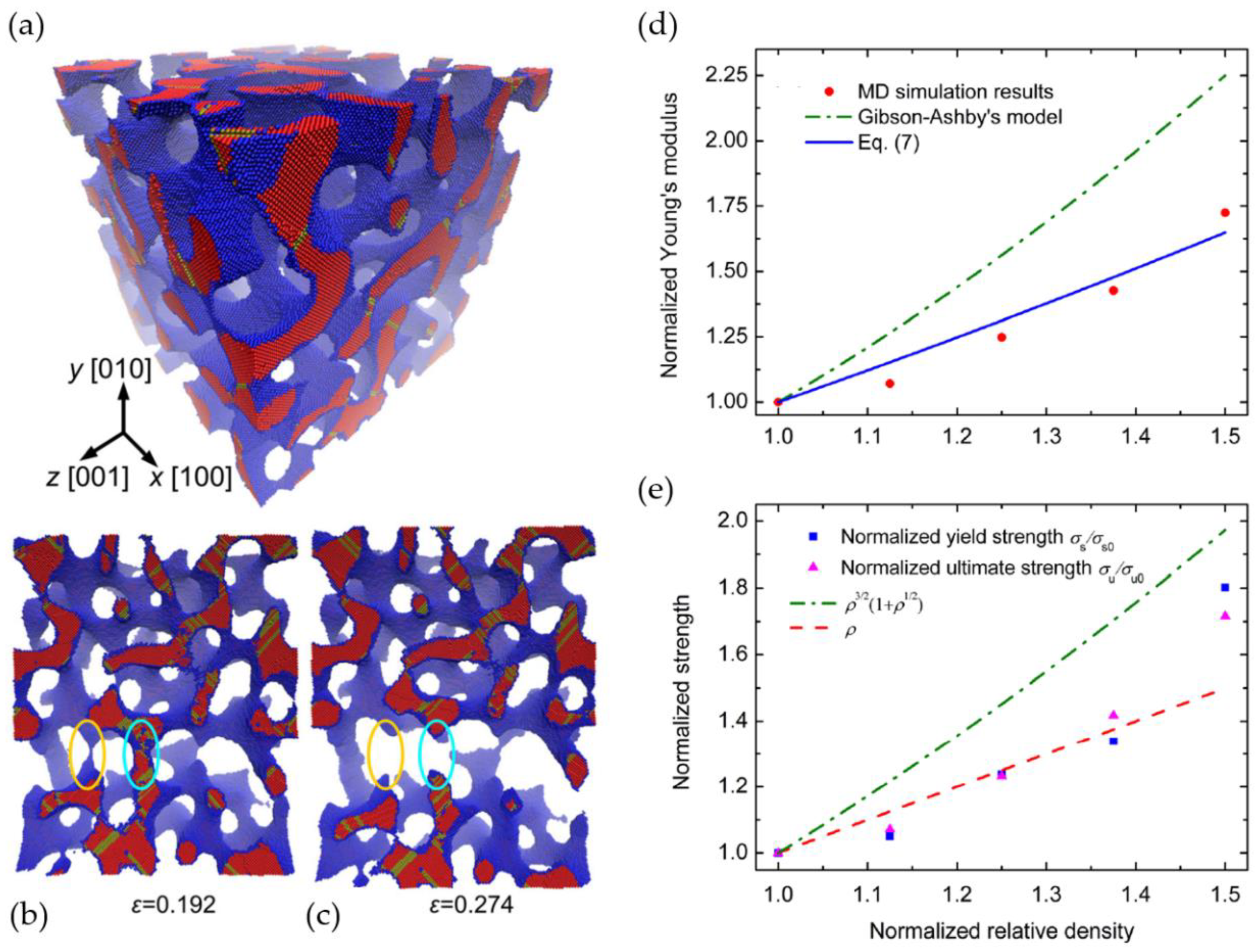
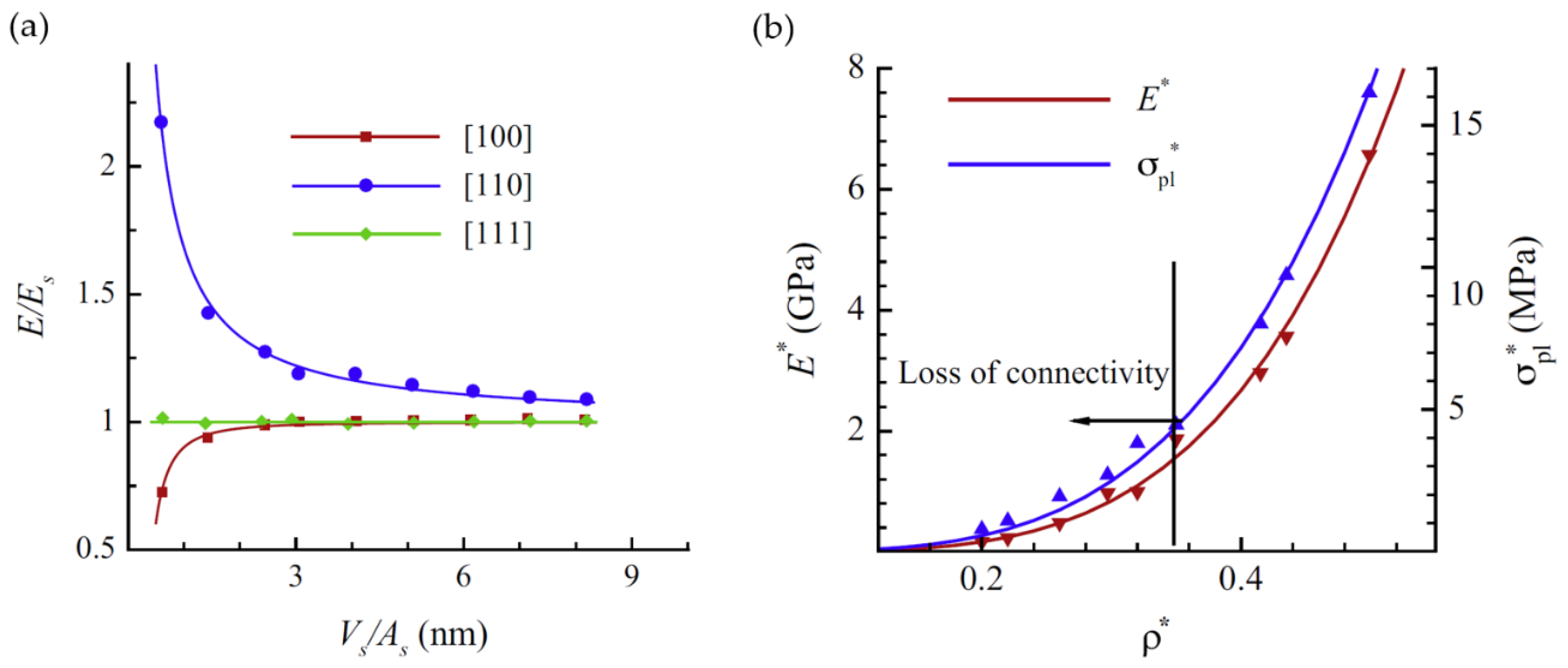


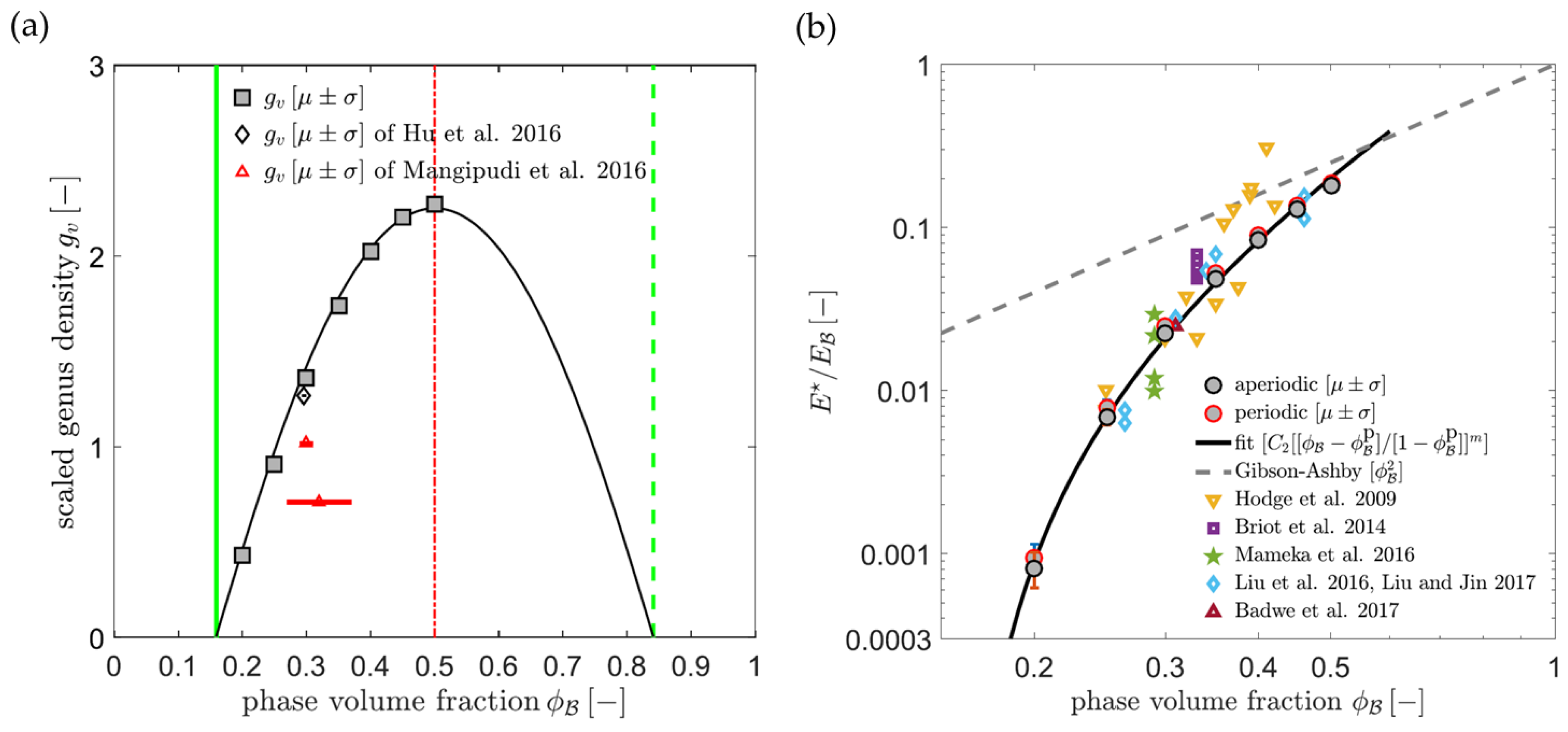

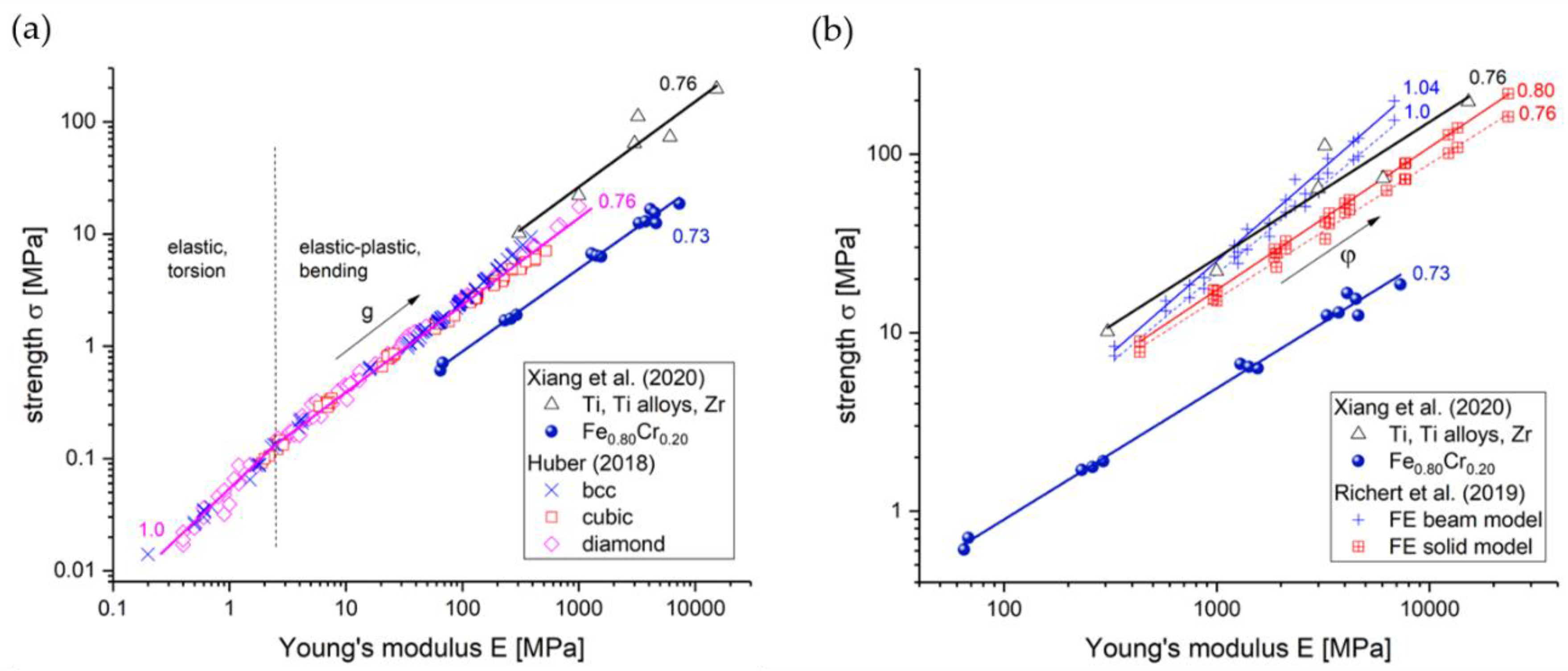
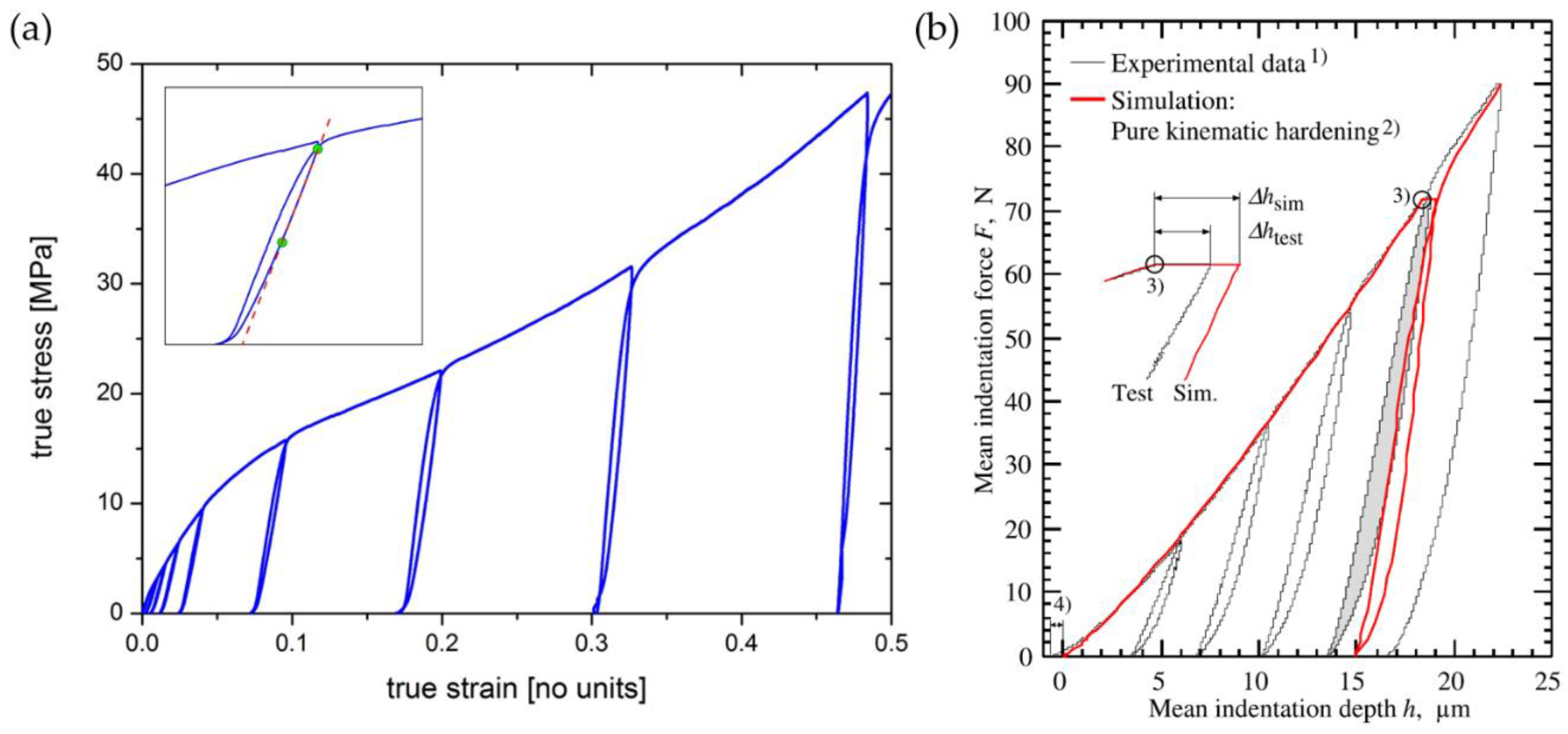
| Software | OSS | Reference | VS | SC | FT | MA | Applied by |
|---|---|---|---|---|---|---|---|
| Amira-Avizo | no | ThermoFisher Scientific | X | X | X | X | [35,42,43] |
| Aquami | yes | [44] | X | X | X | X | [45] |
| CHomP | yes | [46] | – | – | – | X | [47] |
| Fiji/ImageJ | yes | [48] | X | X | X | X | [19,42,44,49,50] |
| iso2meshtoolbox | yes | [51] | X | – | – | – | [18] |
| Mathematica | no | Wolfram Research | X | X | X | X | [42] |
| MATLAB | no | MathWorks | X | X | X | X | [34] |
| MAVI | no | Fraunhofer ITWM | X | X | X | X | [16] |
| OVITO | yes | [52] | X | – | – | – | [53] |
| Pore3D | yes | [54] | – | X | X | – | [55] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Richert, C.; Huber, N. A Review of Experimentally Informed Micromechanical Modeling of Nanoporous Metals: From Structural Descriptors to Predictive Structure–Property Relationships. Materials 2020, 13, 3307. https://doi.org/10.3390/ma13153307
Richert C, Huber N. A Review of Experimentally Informed Micromechanical Modeling of Nanoporous Metals: From Structural Descriptors to Predictive Structure–Property Relationships. Materials. 2020; 13(15):3307. https://doi.org/10.3390/ma13153307
Chicago/Turabian StyleRichert, Claudia, and Norbert Huber. 2020. "A Review of Experimentally Informed Micromechanical Modeling of Nanoporous Metals: From Structural Descriptors to Predictive Structure–Property Relationships" Materials 13, no. 15: 3307. https://doi.org/10.3390/ma13153307
APA StyleRichert, C., & Huber, N. (2020). A Review of Experimentally Informed Micromechanical Modeling of Nanoporous Metals: From Structural Descriptors to Predictive Structure–Property Relationships. Materials, 13(15), 3307. https://doi.org/10.3390/ma13153307






