Phase Field Simulation of Laminated Glass Beam
Abstract
:1. Introduction
2. Laminated Glass Beam Mechanical Response
2.1. Physical Problem
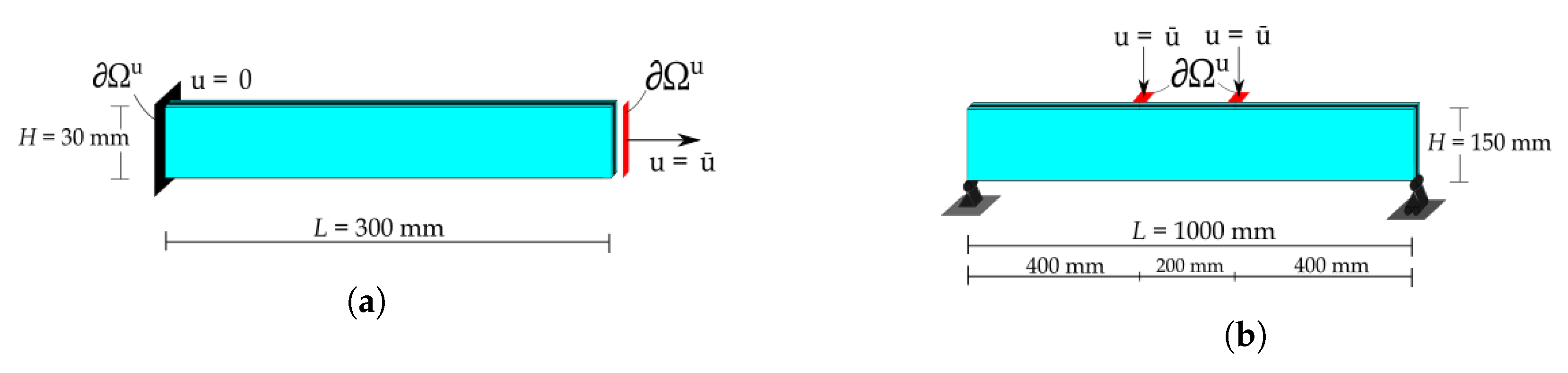
- Unidirectional traction test (UD test): We consider the case in which the element is uniaxially loaded orthogonally to the direction of the dominant cracks that may appear within the element. Cracks parallel to the direction of loading are characterised by null or negative opening stress so that they do not alter the tensile response. Therefore, one can only consider the effects of the cracks orthogonal to the tensile stress that can be efficiently modelled in a unidirectional traction test. This simple but representative set-up is optimal to analyse the influence of the material parameters on the mechanical response of the laminated glass element. The traction test has been modelled as the tensile set-up presented in [8] where compression forces on the specimen ends, which might lead to local failure, are avoided by gluing both ends of the specimen to steel angles where bolted plates apply the traction force. The set-up is reported in Figure 2a. The representative element is fixed on the left extremity, whereas a horizontal displacement is applied on the right side. To provide a sufficient redundancy to the laminated glass beam [9], a tempered glass is considered as high strain glass, thus permitting to investigate a wider variety of interface behaviours thanks to its higher loading capacity.
2.2. Problem Formulation: Phase Field Approach
- strain energy densitywhich represents the quadratic strain energy density of a damageable material with being the fourth-order elastic tensor of the material and being the symmetric part of the displacement gradient.
- fracture energy densitywhere the constant represents the fracture energy of each layer, whereas is a length parameter that defines the width of the transition zone between the damaged and the undamaged zone in the i-th layer. A parameter representative of the material strength is defined as .
3. Materials and Methods
4. Results
4.1. Unidirectional Traction Tests
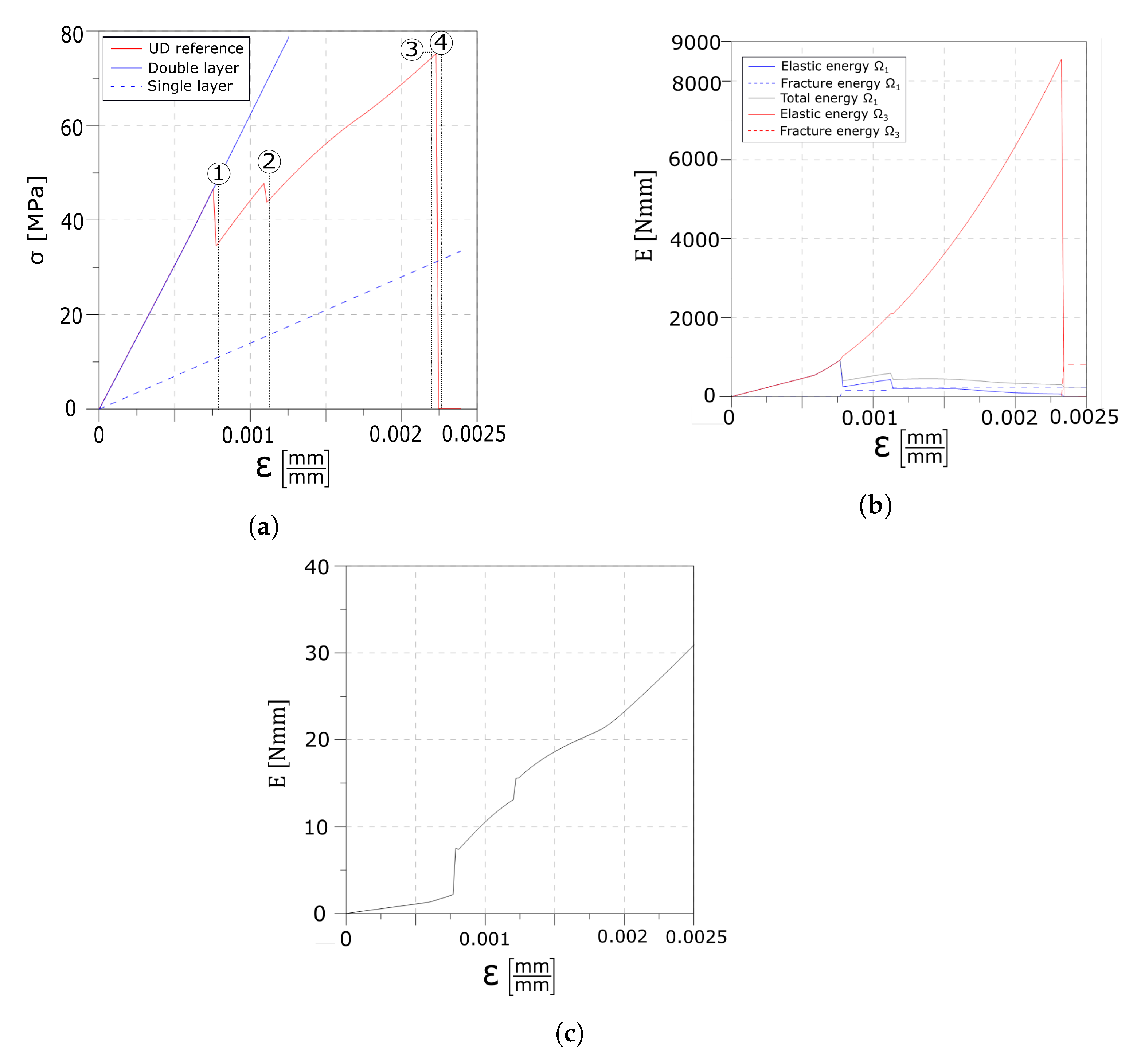
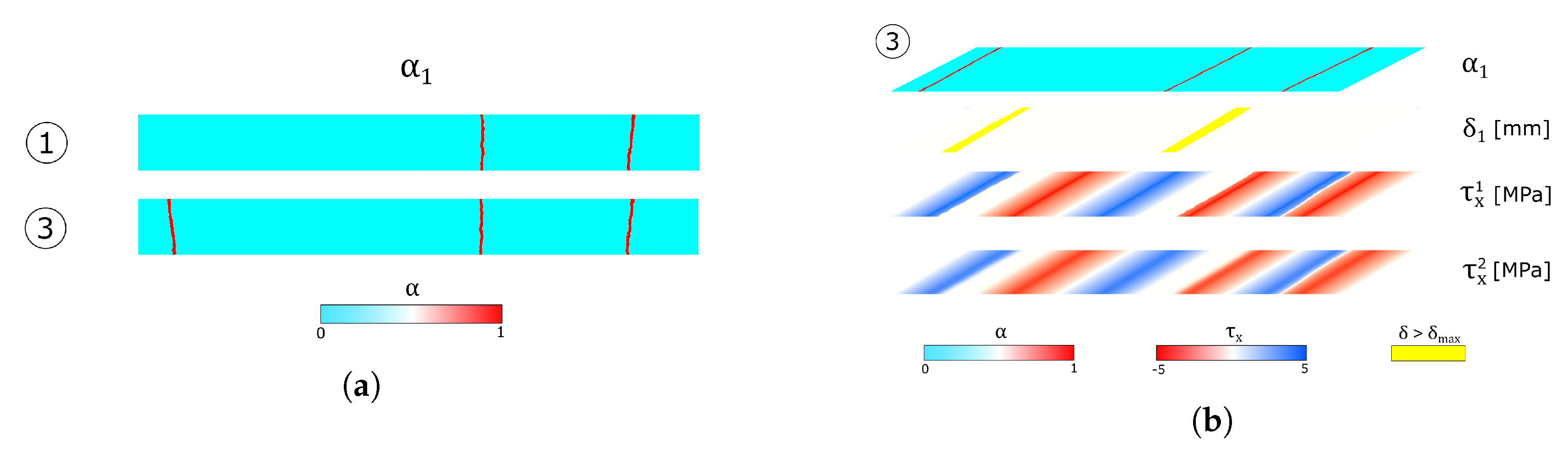
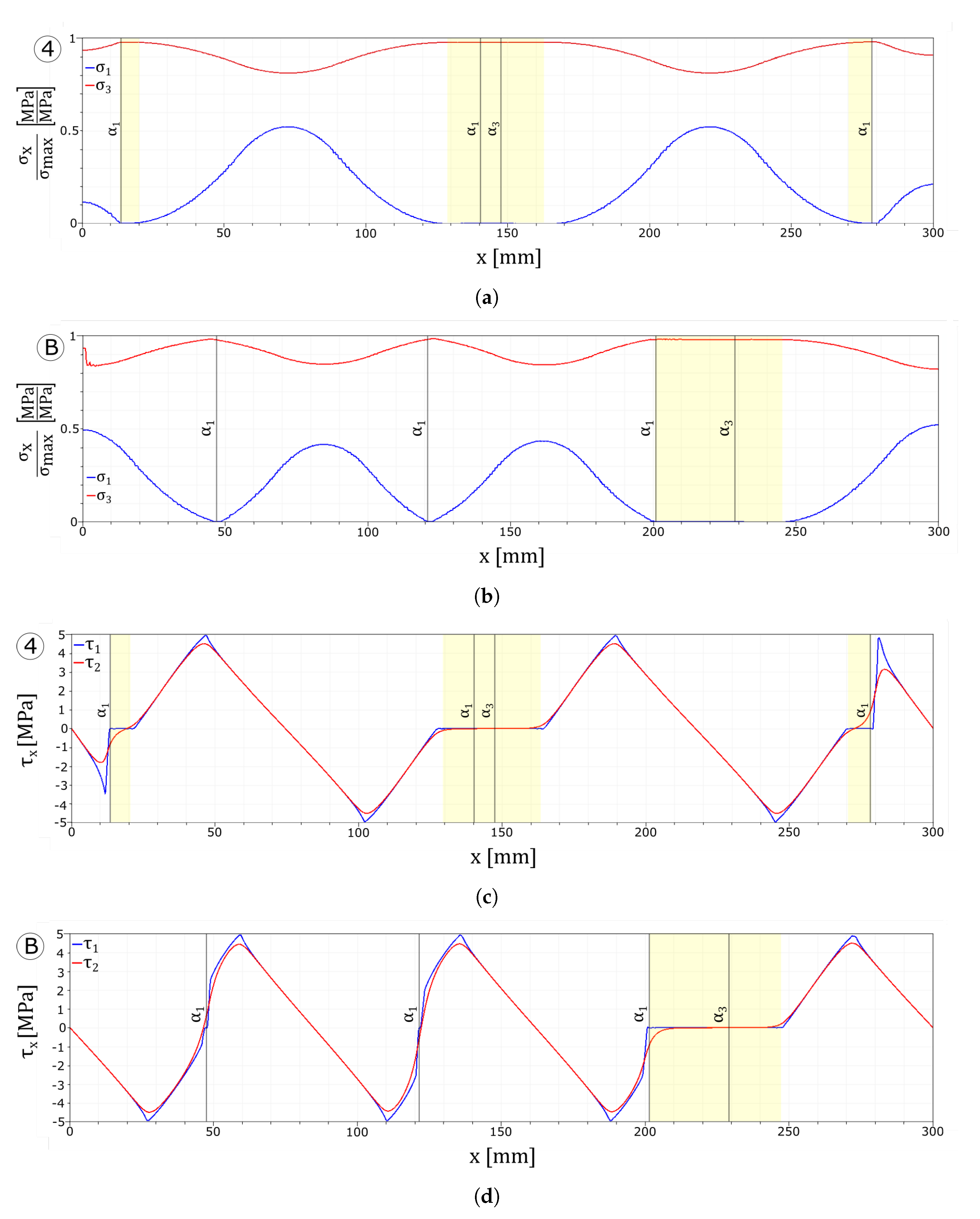
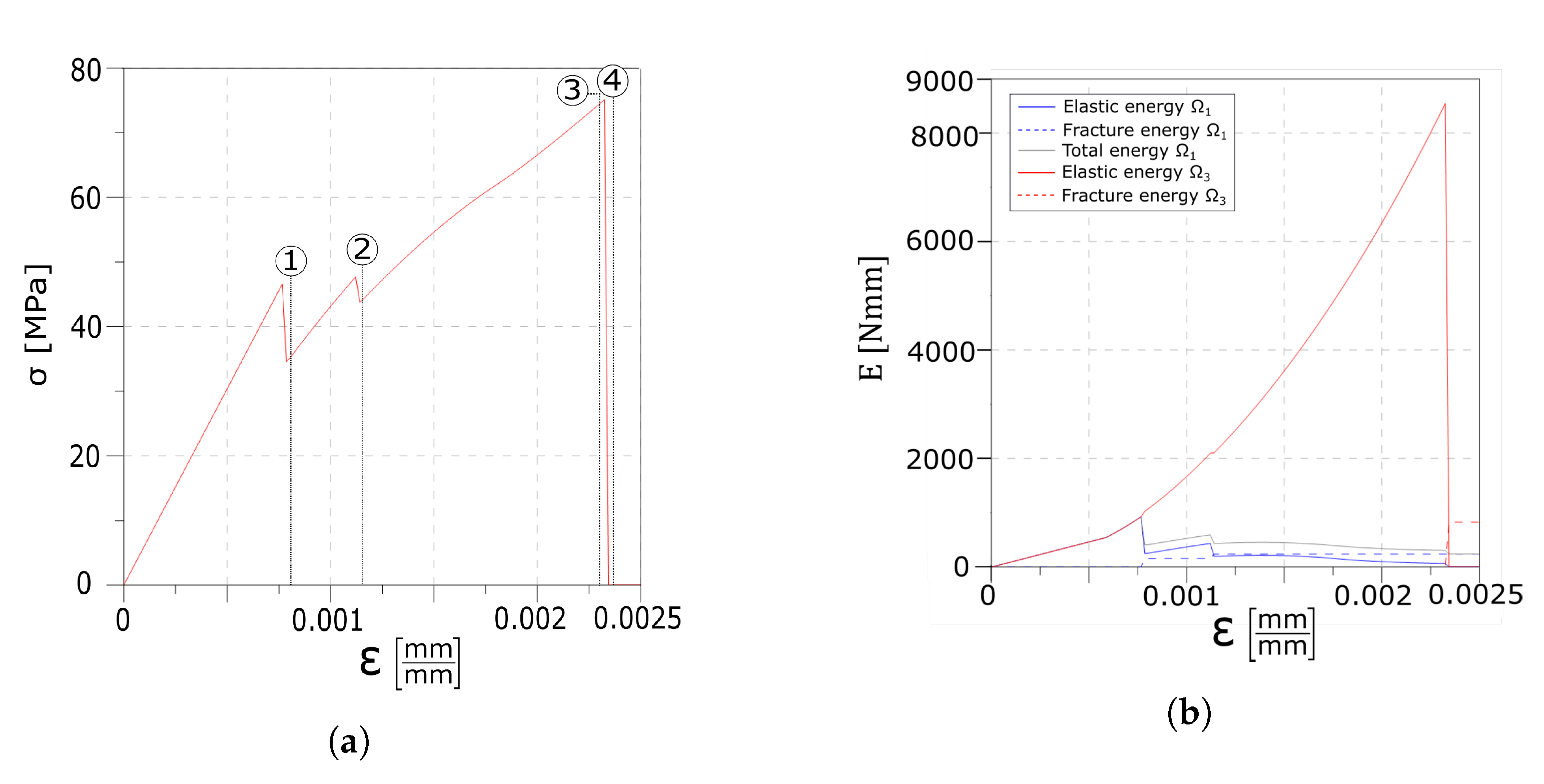
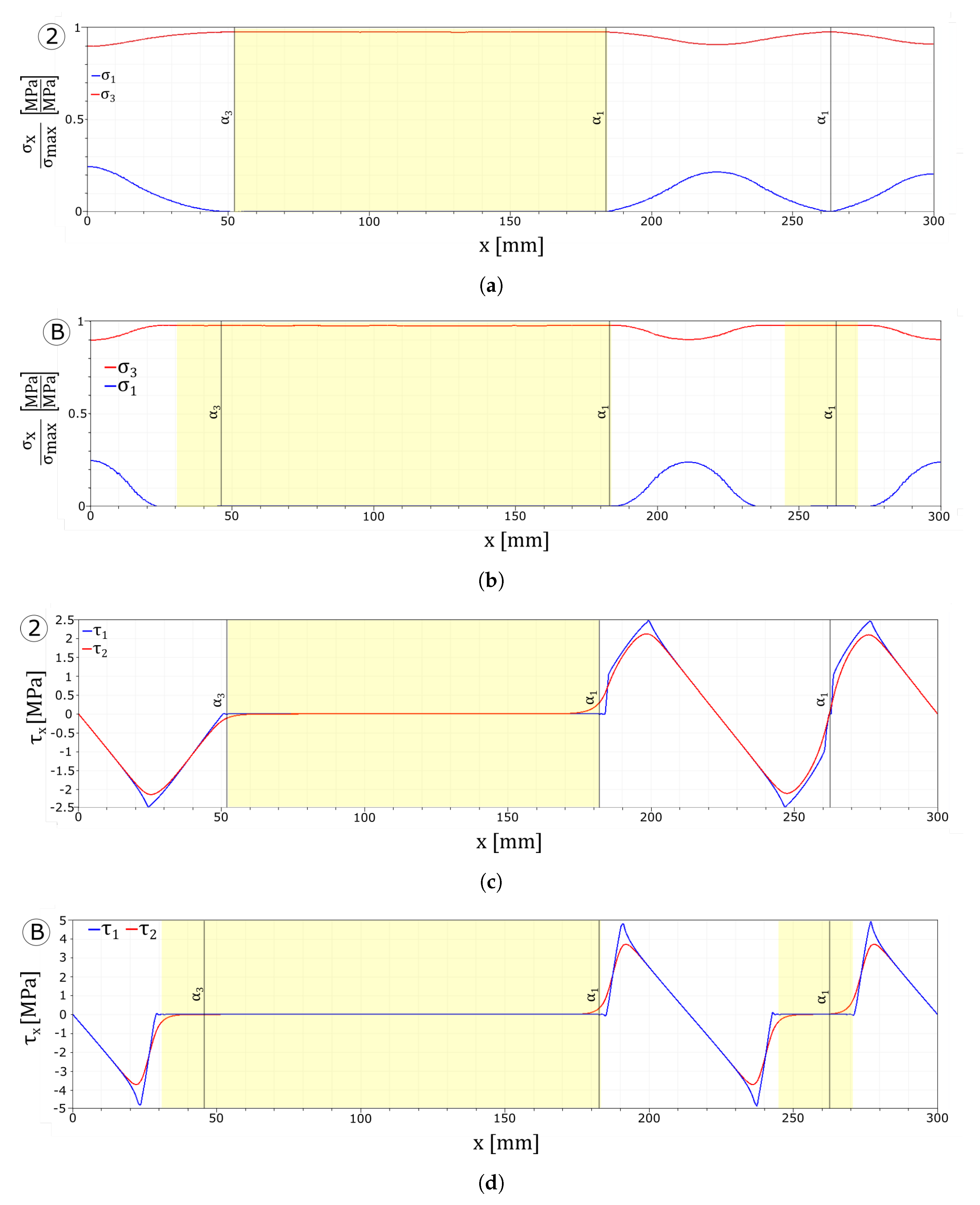
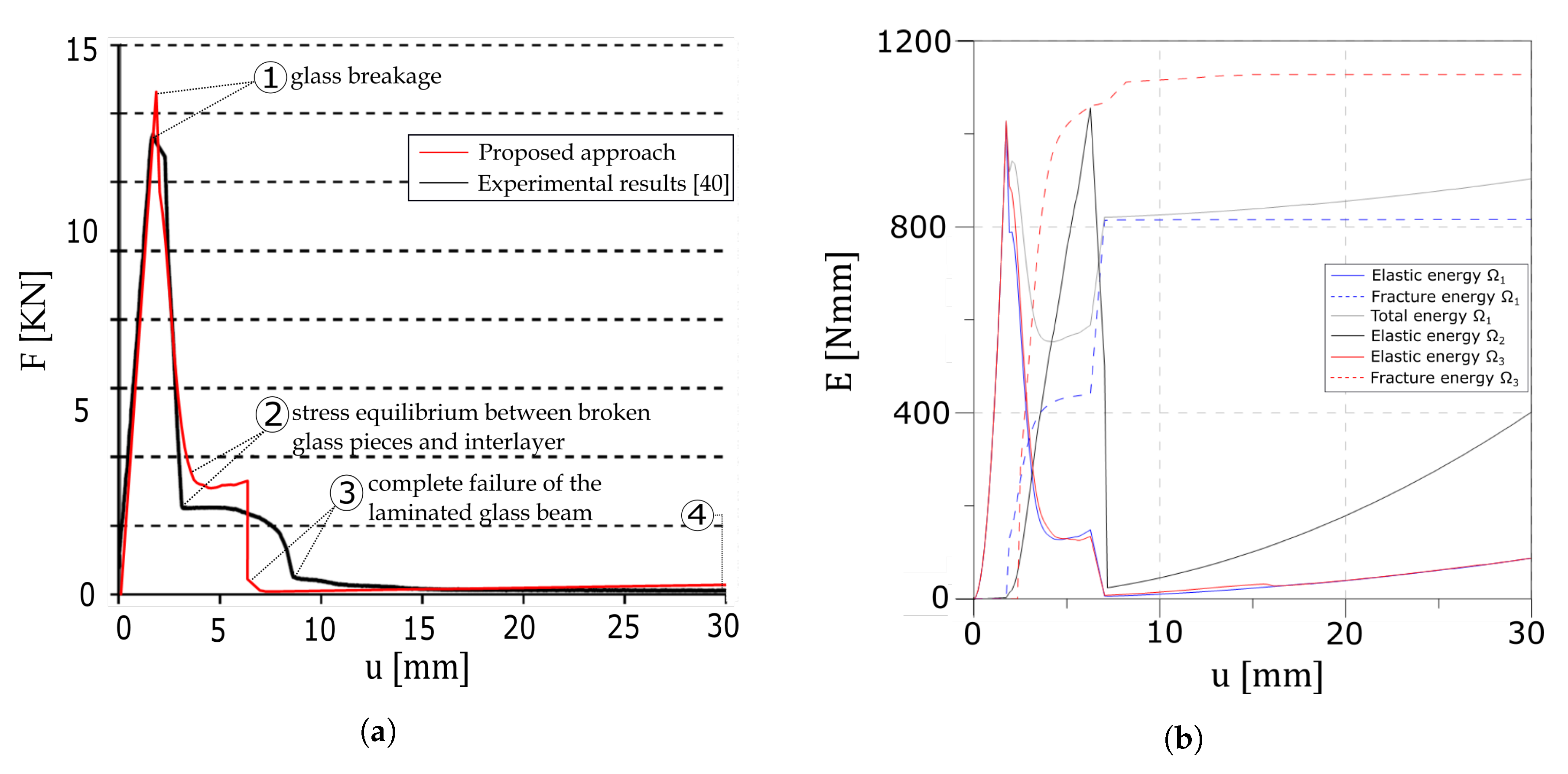
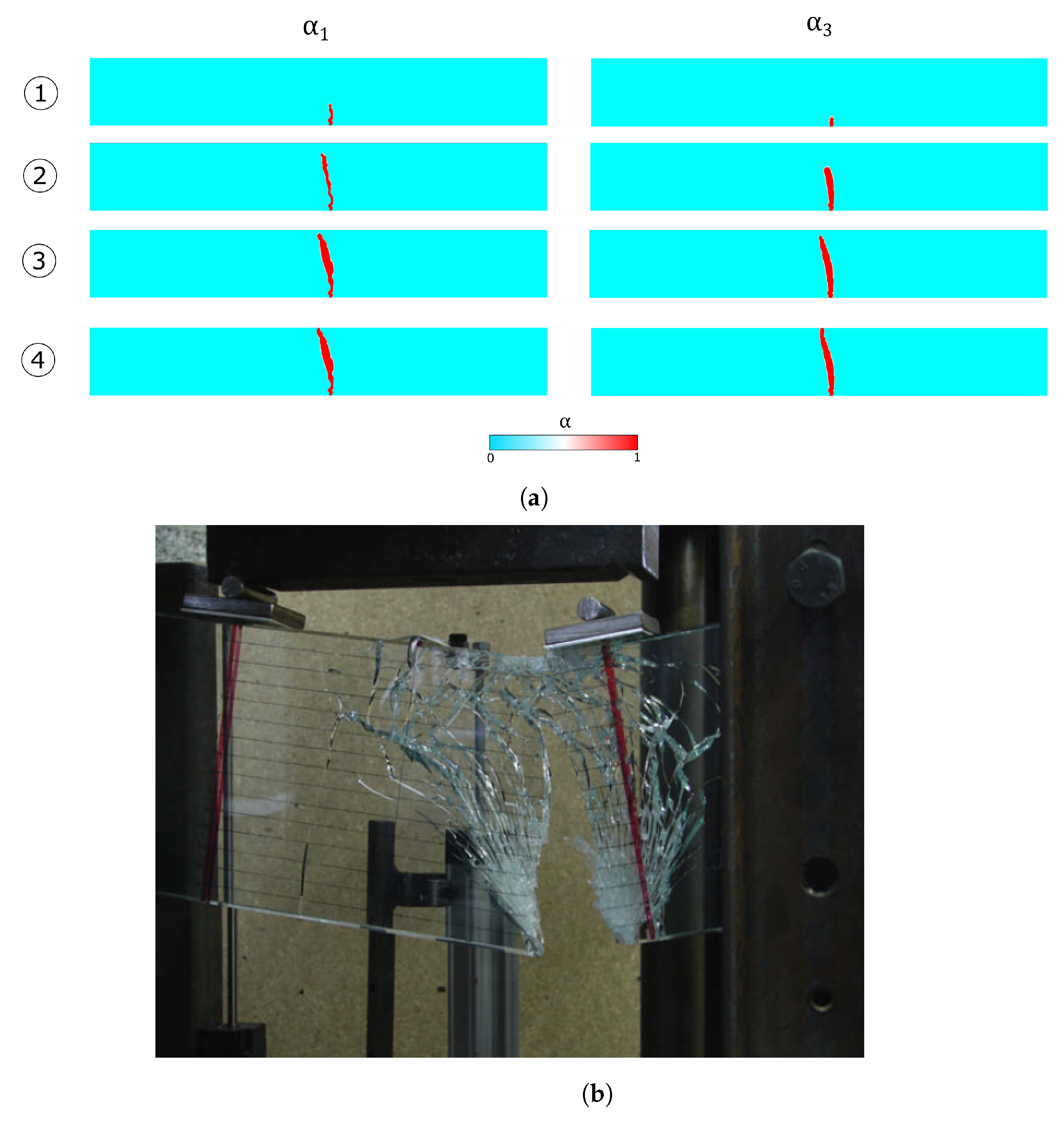
4.1.1. Reference Test
4.1.2. Weibull’s Module Tests
4.1.3. Interlayer Stiffness Test
4.1.4. Weak Interface Tests
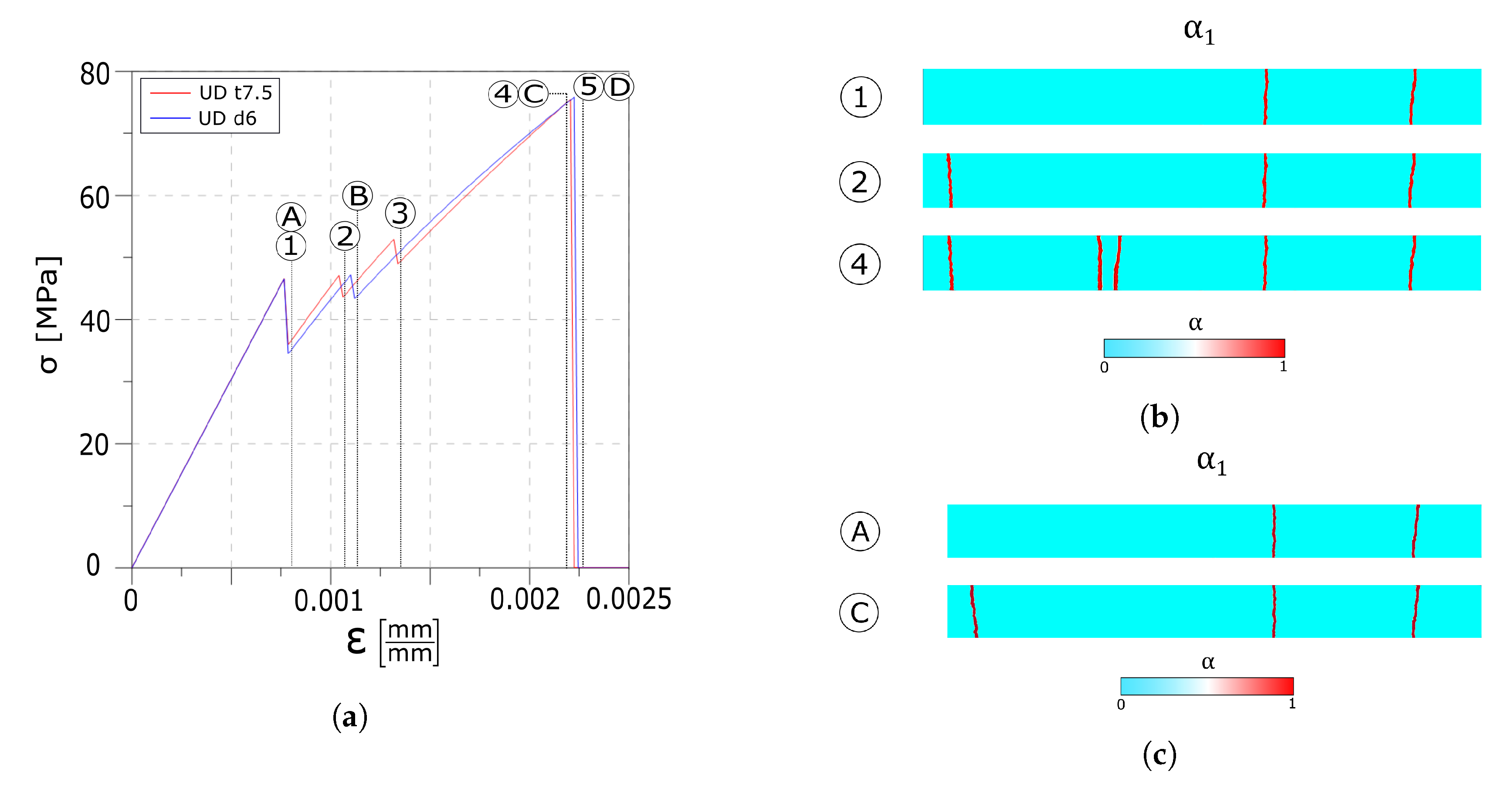
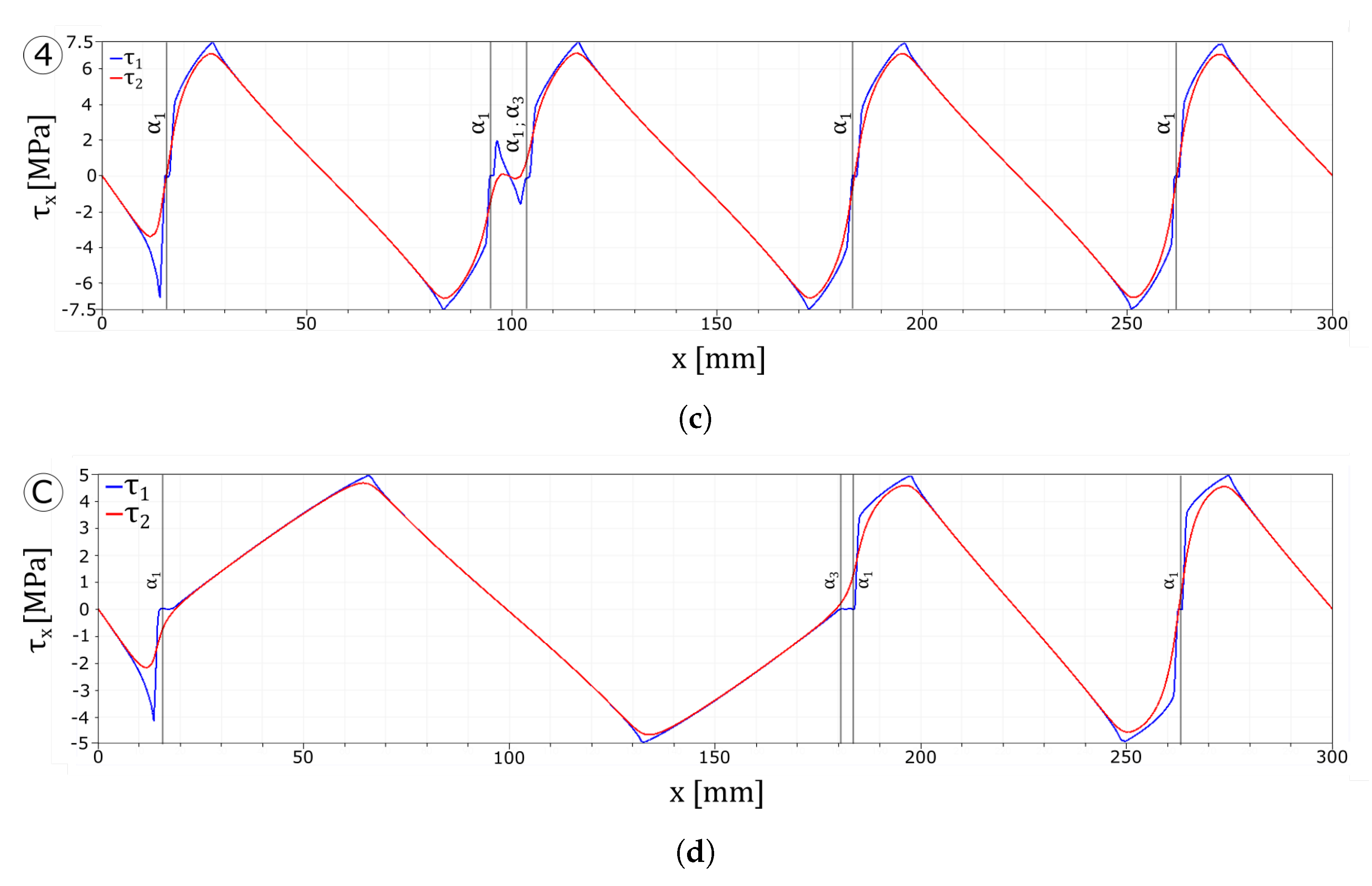
4.1.5. Strong Interface Tests
4.2. Four-Point Bending Tests
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| PBV | Polyvinyl butyral |
| UD | Unidirectional (traction) |
| FPB | Four point bending |
| s.r.f. | Stress reduction factor |
References
- Ivanov, I.V. Analysis, modelling, and optimization of laminated glasses as plane beam. Int. J. Solids Struct. 2006, 43, 6887–6907. [Google Scholar] [CrossRef] [Green Version]
- Foraboschi, P. Analytical model for laminated-glass plate. Compos. Part Eng. 2012, 43, 2094–2106. [Google Scholar] [CrossRef]
- Santo, D.; Mattei, S.; Bedon, C. Elastic Critical Moment for the Lateral–Torsional Buckling (LTB) Analysis of Structural Glass Beams with Discrete Mechanical Lateral Restraints. Materials 2020, 13, 2492. [Google Scholar] [CrossRef]
- Xu, J.; Li, Y.; Liu, B.; Zhu, M.; Ge, D. Experimental study on mechanical behavior of PVB laminated glass under quasi-static and dynamic loadings. Compos. Part Eng. 2011, 42, 302–308. [Google Scholar] [CrossRef]
- Centelles, X.; Castro, J.R.; Cabeza, L.F. Experimental results of mechanical, adhesive, and laminated connections for laminated glass elements—A review. Eng. Struct. 2019, 180, 192–204. [Google Scholar] [CrossRef]
- Samieian, M.A.; Cormie, D.; Smith, D.; Wholey, W.; Blackman, B.R.; Dear, J.P.; Hooper, P.A. On the bonding between glass and PVB in laminated glass. Eng. Fract. Mech. 2019, 214, 504–519. [Google Scholar] [CrossRef]
- Biolzi, L.; Cattaneo, S.; Orlando, M.; Piscitelli, L.R.; Spinelli, P. Post-failure Behaviour of Laminated Glass Beams Using Different Interlayers. Compos. Struct. 2018, 202, 578–589. [Google Scholar] [CrossRef]
- Biolzi, L.; Orlando, M.; Piscitelli, L.R.; Spinelli, P. Static and dynamic response of progressively damaged ionoplast laminated glass beams. Compos. Struct. 2016, 157, 337–347. [Google Scholar] [CrossRef]
- Biolzi, L.; Cattaneo, S.; Rosati, G. Progressive damage and fracture of laminated glass beams. Constr. Build. Mater. 2010, 24, 577–584. [Google Scholar] [CrossRef]
- Galuppi, L.; Royer-Carfagni, G. A homogenized analysis ’a la Hashin for cracked lamnates undes equi-biaxial stress. Applications to laminated glass. Compos. Part B Eng. 2017, 179, 332–347. [Google Scholar] [CrossRef]
- Duser, A.V.; Jagota, A.; Bennison, S. Analysis of glass/Polyvinyl butyral laminates subjected to uniform pressure. J. Eng. Mech. 1999, 124, 435–442. [Google Scholar] [CrossRef]
- Biolzi, L.; Bonati, A.; Cattaneo, S. Laminated Glass Cantilever Plates under Static and Impact Loading. Adv. Civ. Eng. 2018, 2018. [Google Scholar] [CrossRef]
- Linz, P.D.; Hooper, P.A.; Arora, H.; Wang, Y.; Smith, D.; Blackman, B.R.K.; Dear, J.P. Delamination properties of laminated glass windows subject to blast loading. Int. J. Impact Eng. 2017, 105, 39–53. [Google Scholar] [CrossRef] [Green Version]
- Wei, J.; Dharani, L. Fracture mechanics of laminated glass subjected to blast loading. Theor. Appl. Fract. Mech. 2005, 44, 157–167. [Google Scholar] [CrossRef]
- Vedrtnam, A.; Pawar, S. Experimental and simulation studies on fracture and adhesion test of laminated glass. Eng. Fract. Mech. 2018, 190, 461–470. [Google Scholar] [CrossRef]
- Teotia, M.; Soni, R. Applications of finite element modelling in failure anaysis of laminated glass composites: A review. Eng. Fail. Anal. 2018, 94, 412–437. [Google Scholar] [CrossRef]
- León Baldelli, A.A.; Babadjian, J.F.; Bourdin, B.; Henao, D.; Maurini, C. A variational model for fracture and debonding of thin films under in-plane loadings. J. Mech. Phys. Solids 2014, 70, 320–348. [Google Scholar] [CrossRef] [Green Version]
- Alessi, R.; Freddi, F. Phase-field modelling of failure in hybrid laminates. Compos. Struct. 2017, 181, 9–25. [Google Scholar] [CrossRef]
- Alessi, R.; Freddi, F. Failure and complex crack patterns in hybrid laminates: A phase-field approach. Compos. Part. B Eng. 2019, 179, 107256. [Google Scholar] [CrossRef]
- Jalalvand, M.; Czél, G.; Fuller, J.D.; Winsom, M.R.; Canal, L.P.; Gonzáles, C.D.; LLorca, J. Energy dissipation during delamination in composite materials—An experimental assessment of the cohesive law and the stress-strain field ahead of a crack tip. Compos. Sci. Technol. 2016, 134, 115–124. [Google Scholar] [CrossRef] [Green Version]
- Bourdin, B.; Francfort, G.A.; Marigo, J.J. Numerical experiments in revisited brittle fracture. J. Mech. Phys. Solids 2000, 48, 797–826. [Google Scholar] [CrossRef]
- Ambrosio, L.; Tortorelli, V.M. Approximation of functionals depending on jumps by elliptic functionals via Γ-convergence. Comm. Pure Appl. Math. 1990, 43, 999–1036. [Google Scholar] [CrossRef]
- Ambrosio, L.; Tortorelli, V.M. On the approximation of free discontinuity problems. Boll. Un. Mat. Ital. B (7) 1992, 6, 105–123. [Google Scholar]
- Francfort, G.; Marigo, J.J. Revisiting brittle fracture as an energy minimization problem. J. Mech. Phys. Solids 1998, 46, 1319–1342. [Google Scholar] [CrossRef]
- Amor, H.; Marigo, J.J.; Maurini, C. Regularized formulation of the variational brittle fracture with unilateral contact: Numerical experiments. J. Mech. Phys. Solids 2009, 57, 1209–1229. [Google Scholar] [CrossRef]
- Freddi, F.; Royer-Carfagni, G. Regularized variational theories of fracture: A unified approach. J. Mech. Phys. Solids 2010, 58, 1154–1174. [Google Scholar] [CrossRef]
- Freddi, F.; Royer-Carfagni, G. Variational fracture mechanics to model compressive splitting of masonry-like materials. Ann. Solid Struct. Mech. 2011, 2, 57–67. [Google Scholar] [CrossRef]
- Lancioni, G.; Royer-Carfagni, G. The Variational Approach to Fracture Mechanics. A Practical Application to the French Panthéon in Paris. J. Elast. 2009, 95, 1–30. [Google Scholar] [CrossRef]
- Alessi, R.; Marigo, J.J.; Vidoli, S. Gradient Damage Models Coupled with Plasticity and Nucleation of Cohesive Cracks. Arch. Ration. Mech. Anal. 2014, 214, 575–615. [Google Scholar] [CrossRef]
- Alessi, R.; Marigo, J.J.; Vidoli, S. Gradient damage models coupled with plasticity: Variational formulation and main properties. Mech. Mater. 2015, 80, 351–367. [Google Scholar] [CrossRef]
- Alessi, R.; Marigo, J.J.; Maurini, C.; Vidoli, S. Coupling damage and plasticity for a phase-field regularisation of brittle, cohesive and ductile fracture: One-dimensional examples. Int. J. Mech. Sci. 2017, 149, 559–576. [Google Scholar] [CrossRef] [Green Version]
- Freddi, F.; Royer-Carfagni, G. Plastic Flow as an Energy Minimization Problem. Numerical Experiments. J. Elast. 2014, 116, 53–74. [Google Scholar] [CrossRef]
- Freddi, F.; Royer-Carfagni, G. Phase-field slip-line theory of plasticity. J. Mech. Phys. Solids 2016, 94, 257–272. [Google Scholar] [CrossRef]
- Miehe, C.; Teichtmeister, S.; Aldakheel, F. Phase-field modelling of ductile fracture: A variational gradient-extended plasticity-damage theory and its micromorphic regularization. Phylosophical Trans. Ser. Math. Phys. Eng. Sci. 2016, 374. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Freddi, F.; Iurlano, F. Numerical insight of a variational smeared approach to cohesive fracture. J. Mech. Phys. Solids 2017, 98, 156–171. [Google Scholar] [CrossRef] [Green Version]
- Bourdin, B.; Larsen, C.J.; Richardson, C.L. A time-discrete model for dynamic fracture based on crack regularization. Int. J. Fract. 2011, 168, 133–143. [Google Scholar] [CrossRef]
- Li, T.; Marigo, J.J. Crack Tip Equation of Motion in Dynamic Gradient Damage Models. J. Elast. 2017, 127, 25–57. [Google Scholar] [CrossRef]
- Wu, J.Y.; Nguyen, V.P.; Nguyen, C.T.; Sutula, D.; Sinaie, S.; Bordas, S. Phase-field modelling of fracture. Adv. Appl. Mech. 2019. [Google Scholar] [CrossRef]
- D’Ambrosio, G.; Galuppi, L.; Royer-Carfagni, G. A simple model for the post-breakage response of laminated glass under in-plane loading. Compos. Struct. 2019, 230, 111426. [Google Scholar] [CrossRef]
- Belis, J.; Depauw, J.; Callewaert, D.; Delincé, D.; Van Impe, R. Failure mechanisms and residual capacity of annealed glass/SGP laminated beams at room temperature. Eng. Fail. Anal. 2009, 16, 1866–1875. [Google Scholar] [CrossRef] [Green Version]
- CNR Advisory Commitee. Guide for the Design, Construction and Control of Buildings with Structural Glass Elements. DT 210, 2013. [Google Scholar]
- Logg, A.; Mardal, K.A.; Wells, G.N. Automated Solution of Differential Equations by the Finite Element Metho; Springer: Berlin, Germany, 2012. [Google Scholar]
- Utkarsh, A. The ParaView Guide: A Parallel Visualization Application; Kitware: Clifton Park, NY, USA, 2015. [Google Scholar]
- Corradi, M.; Speranzini, E. Post-Cracking Capacity of Glass Beams Reinforced with Steel Fibers. Materials 2019, 12, 231. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, D.; Wei, D. Rate-Dependent Cohesive Zone Model for Fracture Simulation of Soda-Lime Glass Plate. Materials 2020, 13, 749. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.; Wang, Q.; Chen, H.; Sun, J.; He, L. Comparative Study on Crack Initiation and Propagation of Glass under Thermal Loading. Materials 2016, 9, 794. [Google Scholar] [CrossRef] [PubMed] [Green Version]






| Layer | h [mm] | E [MPa] | ℓ [mm] | [MPa] | m | |
|---|---|---|---|---|---|---|
| 1—Float glass UD | 5 | 70,000 | 0.2 | 6 | 56.12 (w = 0.045) | 25 |
| 2—PVB interlayer | 1.52 | 500 | 0.45 | / | / | / |
| 3—High strain glass UD | 5 | 70,000 | 0.2 | 6 | 177.48 (w = 0.45) | 25 |
| 4—Float glass FPB | 6 | 70,000 | 0.2 | 20 | 30.91 (w = 0.013) | 25 |
| 5—SGP interlayer | 1.52 | 580 | 0.45 | / | / | / |
| [MPa] | [mm] | [mm] | [N/mm] |
|---|---|---|---|
| 5 | 0.03 | 0.3 |
| m | s.r.f. min | s.r.f. max | [MPa] | [MPa] |
|---|---|---|---|---|
| 9 | 0.20 | 1.62 | 31.24 | 67.58 |
| 25 | 0.62 | 1.16 | 44.19 | 60.45 |
| 52 | 0.80 | 1.075 | 50.20 | 58.19 |
| Test n | Changed Parameter | Value |
|---|---|---|
| 1—UD reference | / | Reference value |
| 2—UD m9 | m | 9 |
| 3—UD m52 | m | 52 |
| 4—UD E1500 | 1500 MPa | |
| 5—UD tau2.5 | 2.5 MPa | |
| 6—UD tau7.5 | 7.5 MPa | |
| 7—UD d2 | ||
| 8—UD d6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Freddi, F.; Mingazzi, L. Phase Field Simulation of Laminated Glass Beam. Materials 2020, 13, 3218. https://doi.org/10.3390/ma13143218
Freddi F, Mingazzi L. Phase Field Simulation of Laminated Glass Beam. Materials. 2020; 13(14):3218. https://doi.org/10.3390/ma13143218
Chicago/Turabian StyleFreddi, Francesco, and Lorenzo Mingazzi. 2020. "Phase Field Simulation of Laminated Glass Beam" Materials 13, no. 14: 3218. https://doi.org/10.3390/ma13143218
APA StyleFreddi, F., & Mingazzi, L. (2020). Phase Field Simulation of Laminated Glass Beam. Materials, 13(14), 3218. https://doi.org/10.3390/ma13143218





