Magnetically Induced Carrier Distribution in a Composite Rod of Piezoelectric Semiconductors and Piezomagnetics
Abstract
1. Introduction
2. Governing Equations
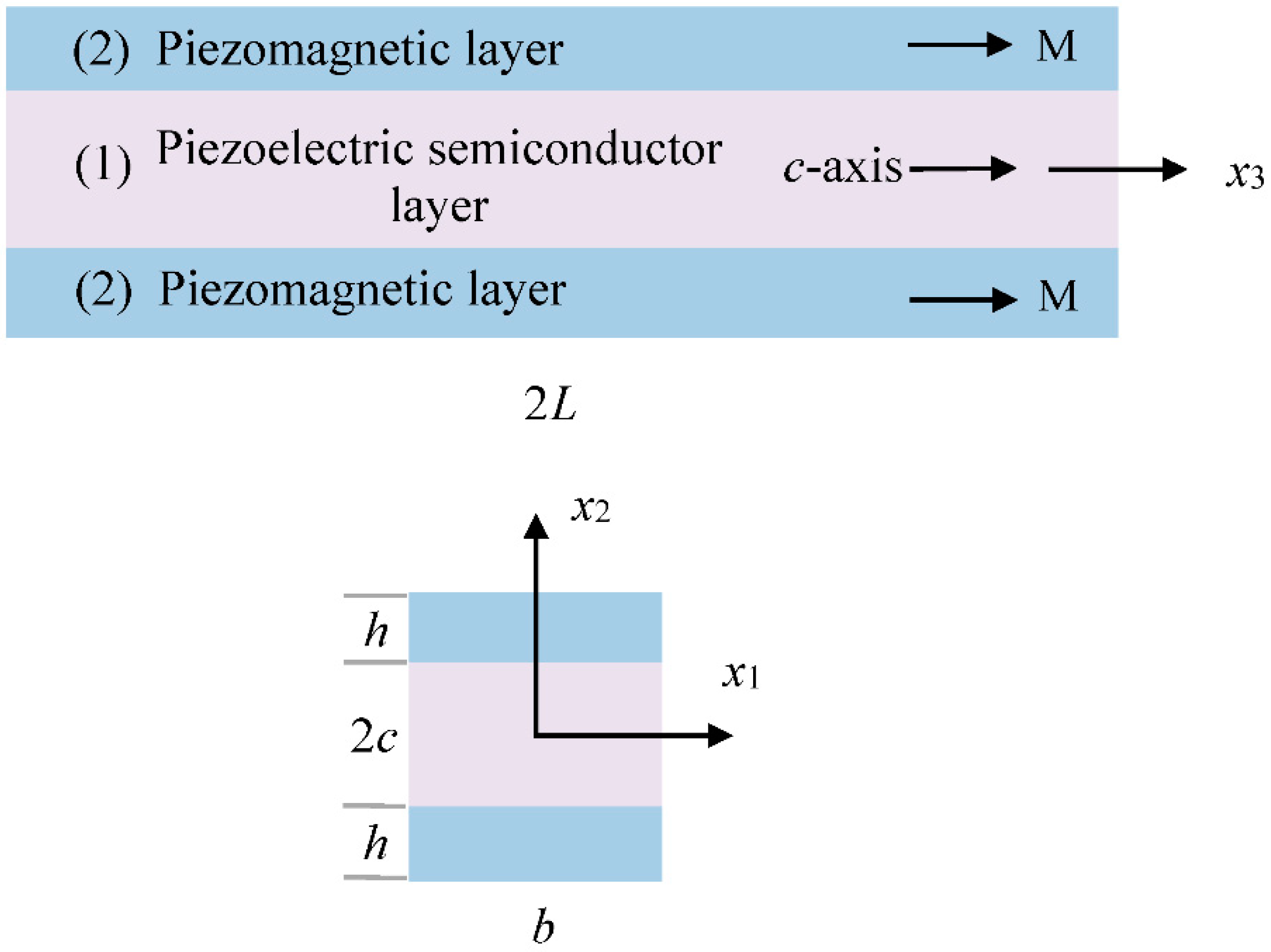
3. One-Dimensional Model for Extension
4. Analytical Solution
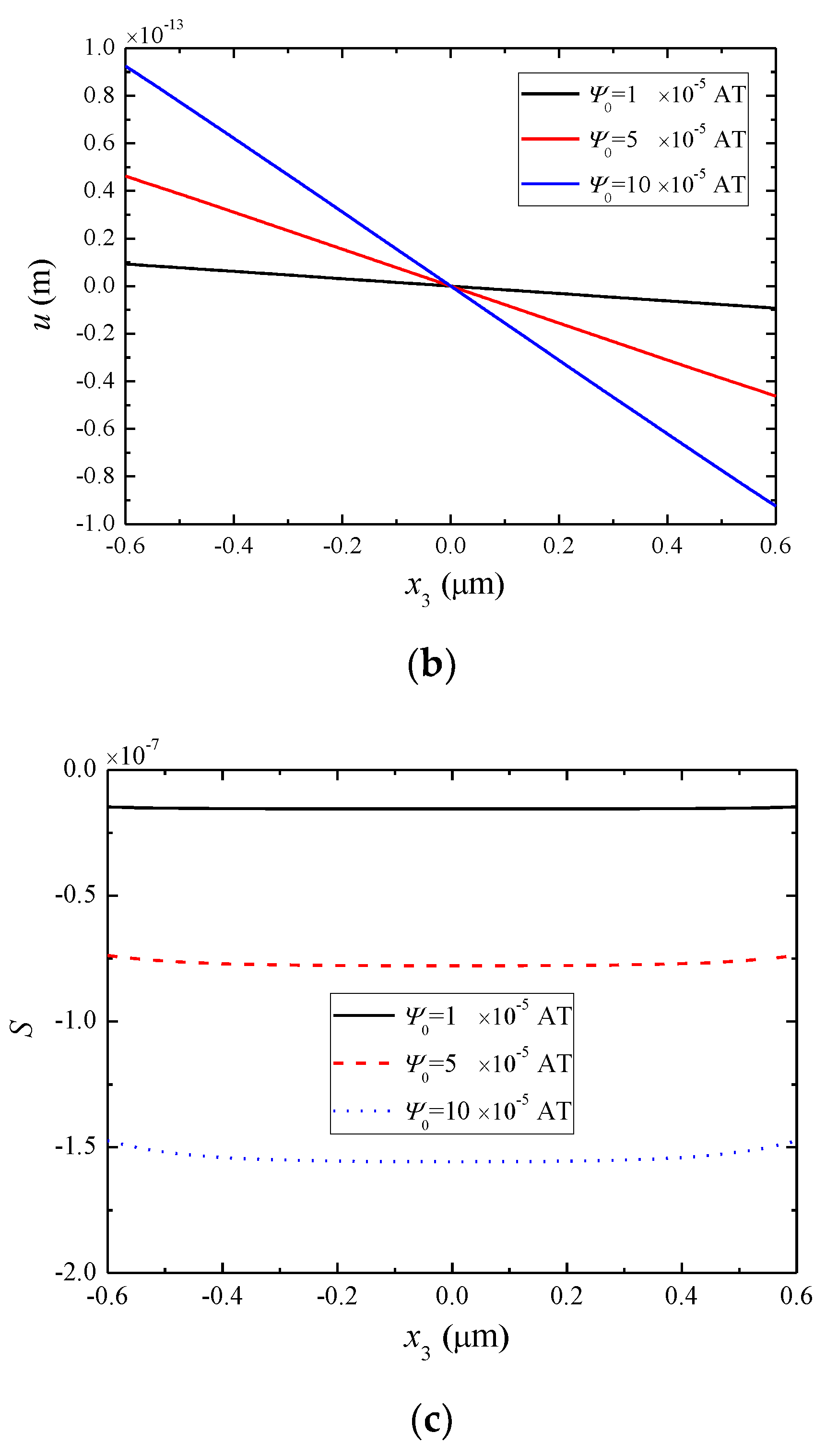
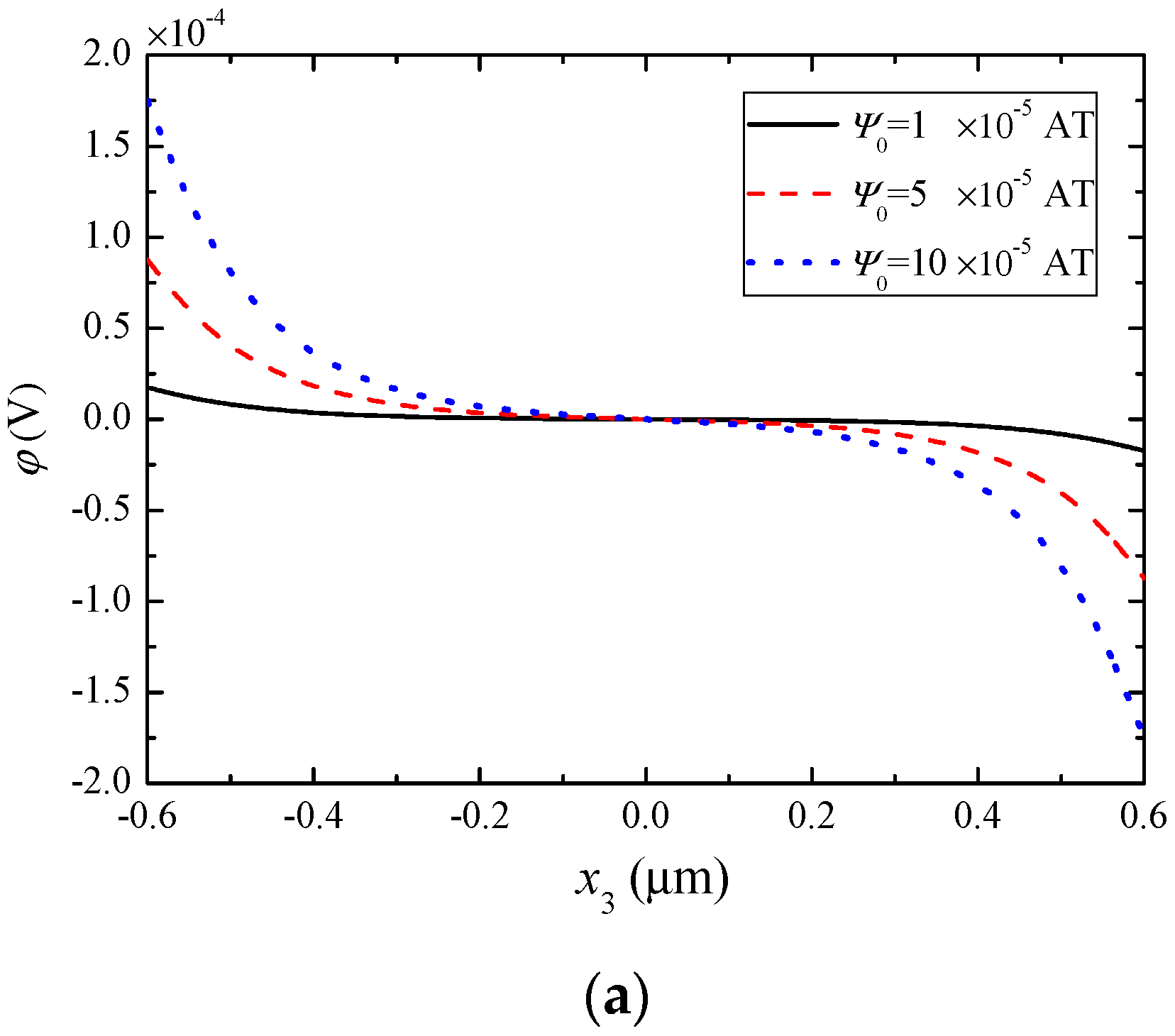
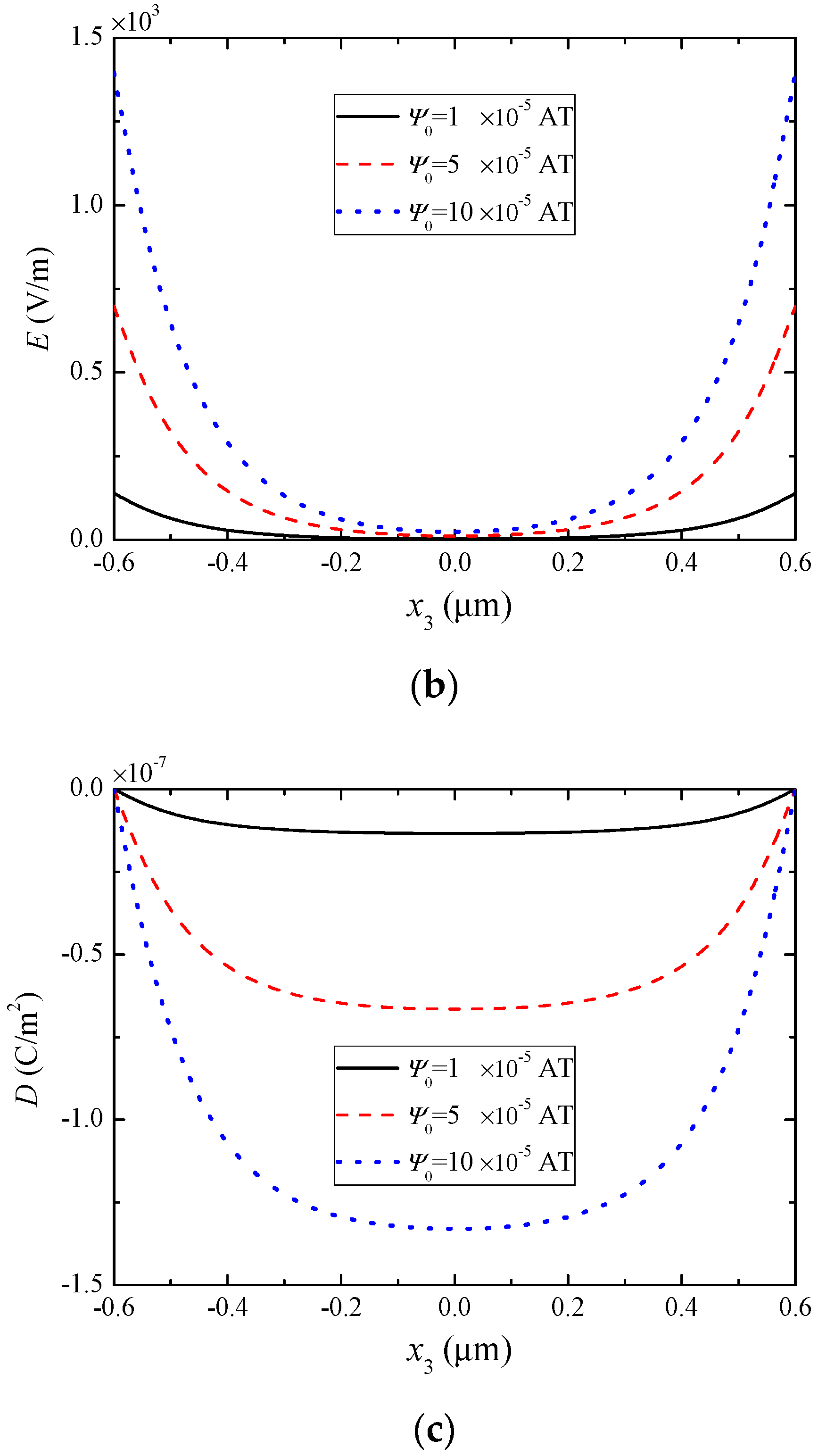
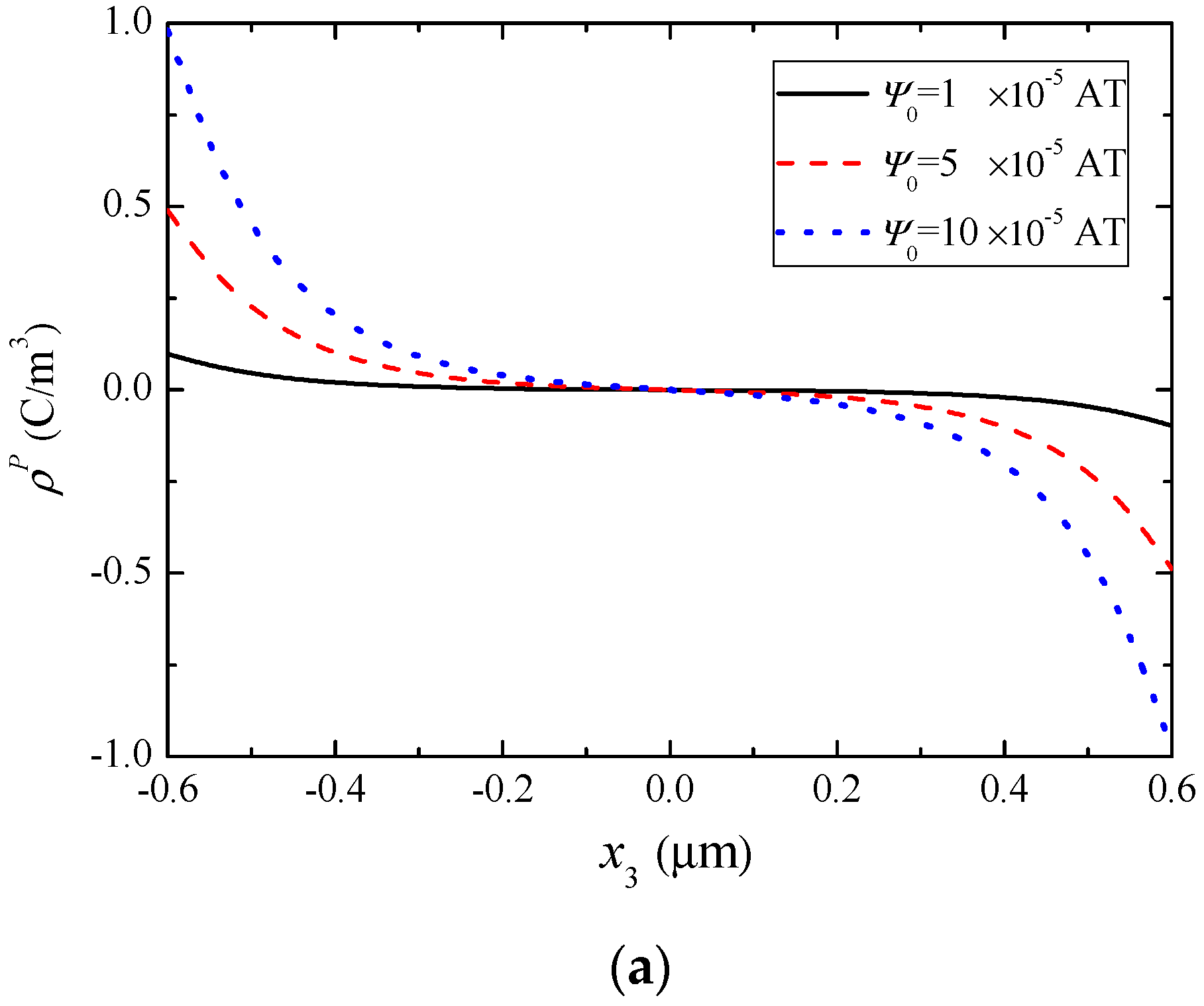
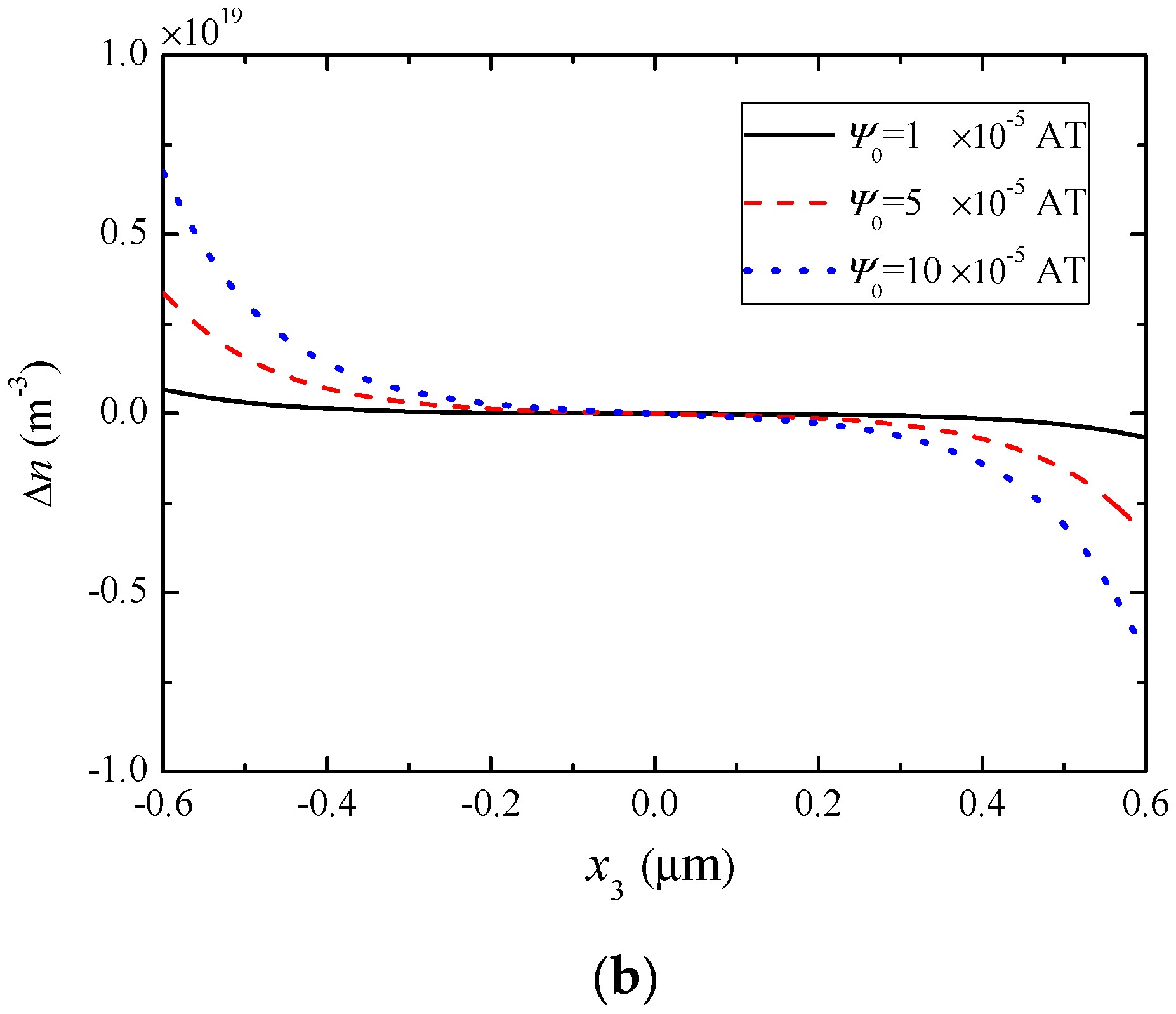
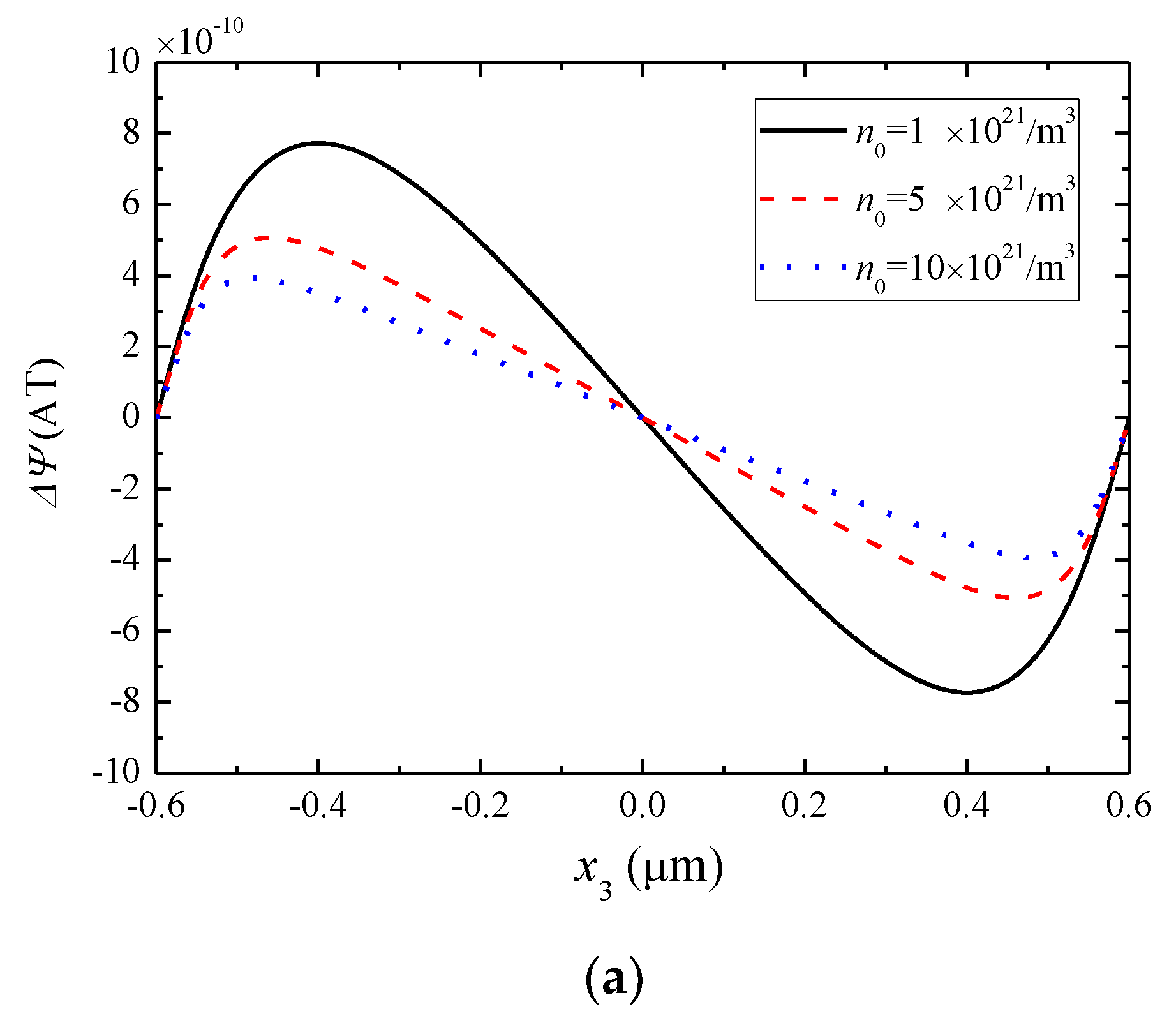
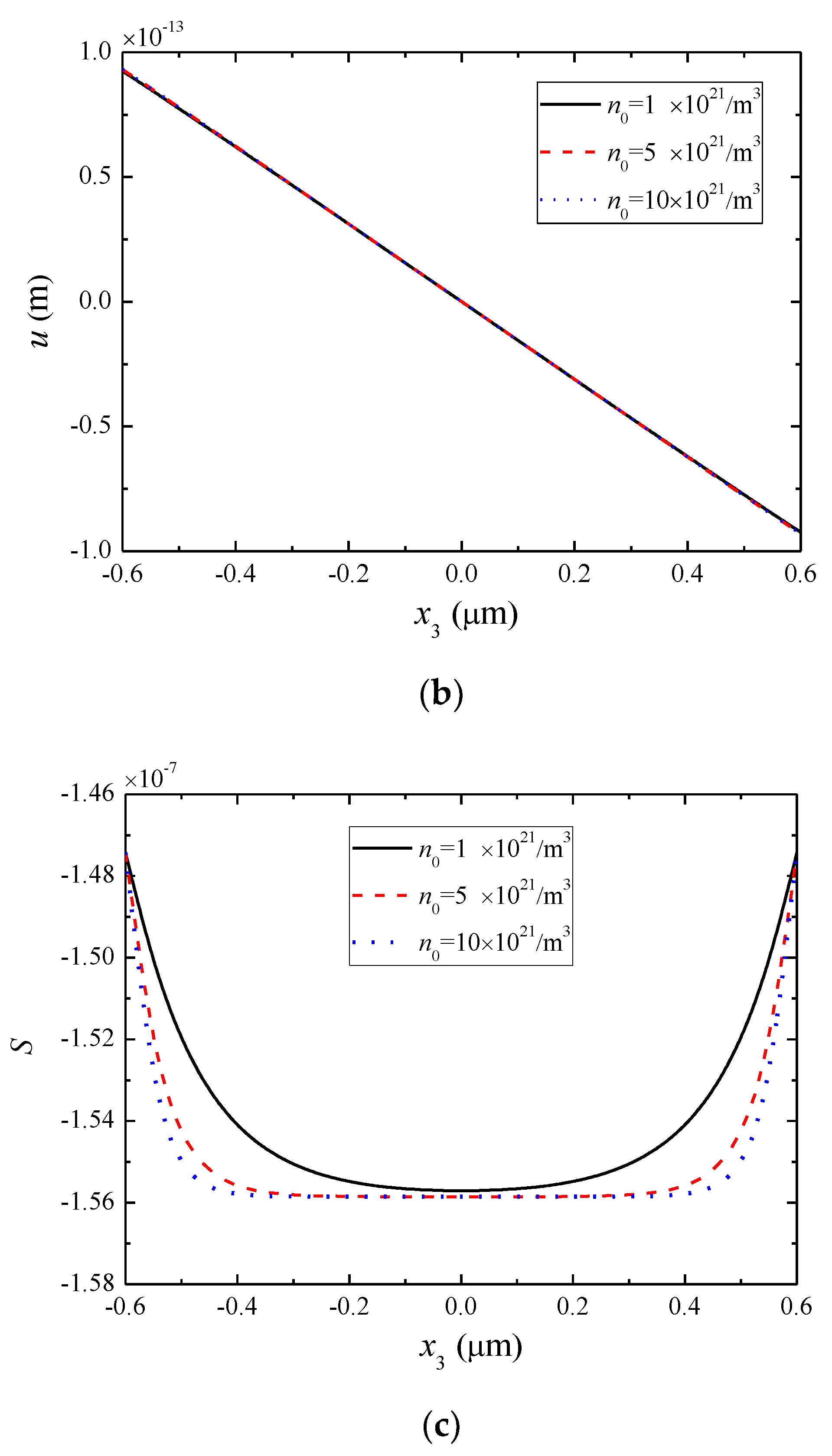
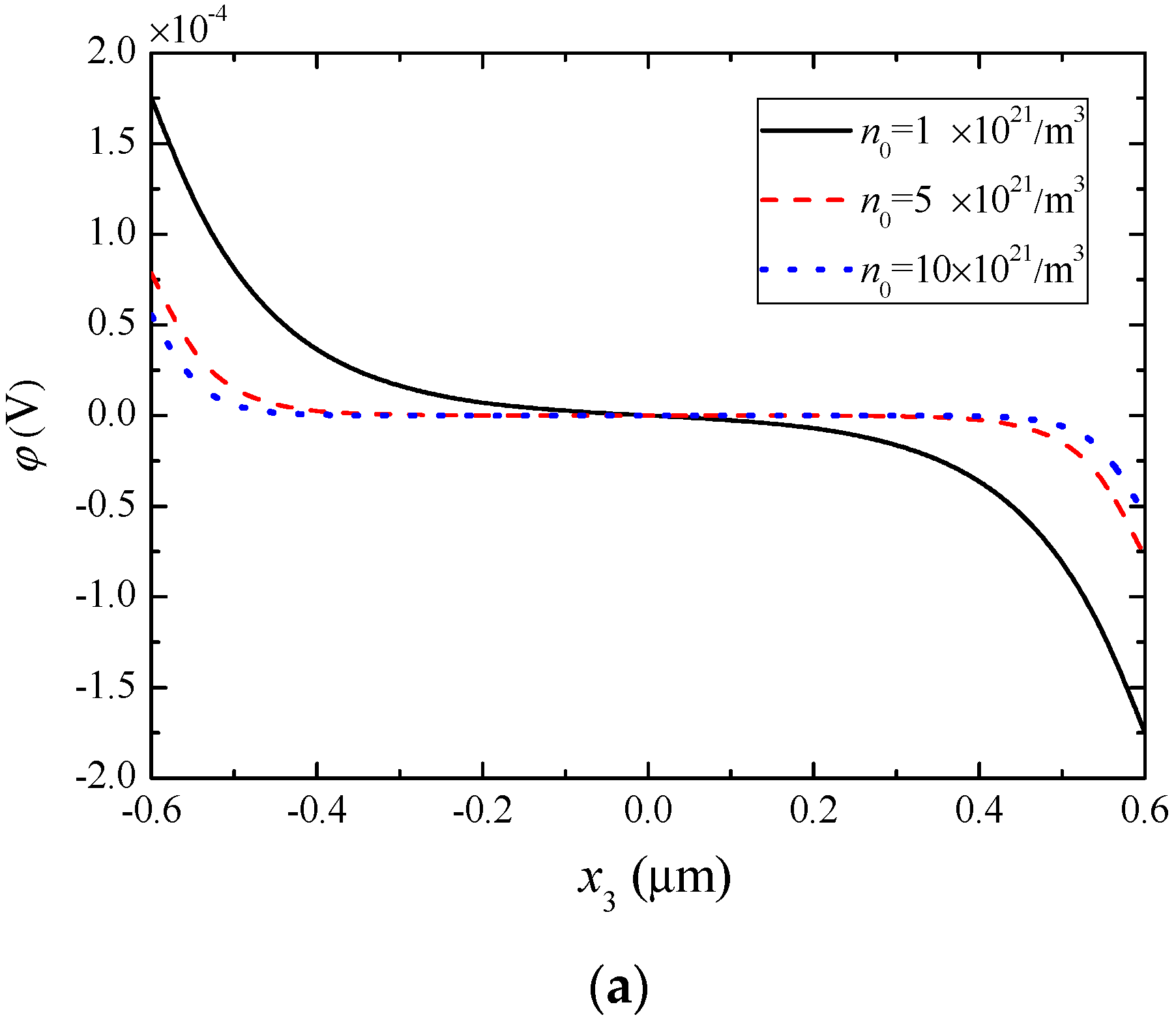
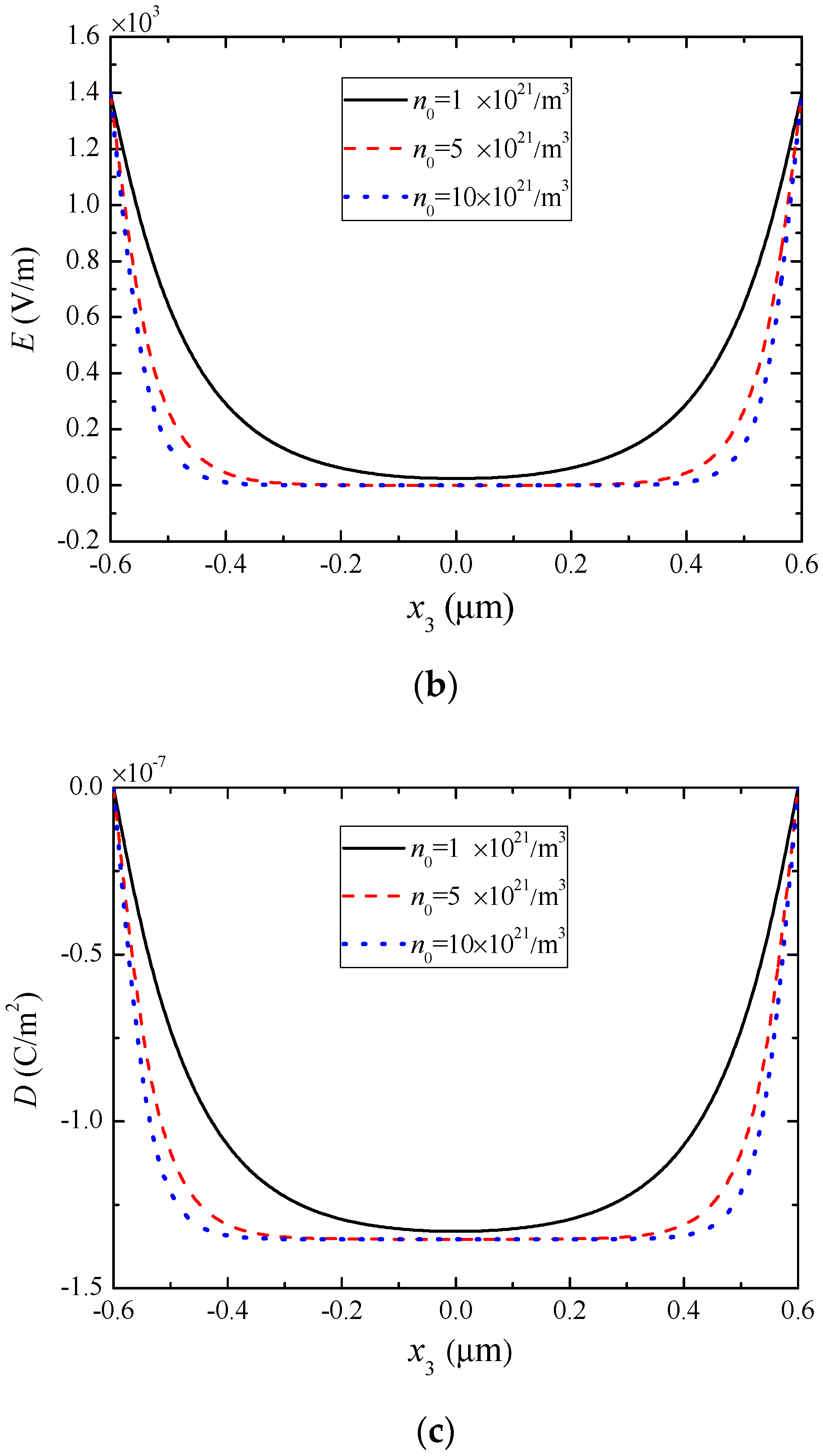
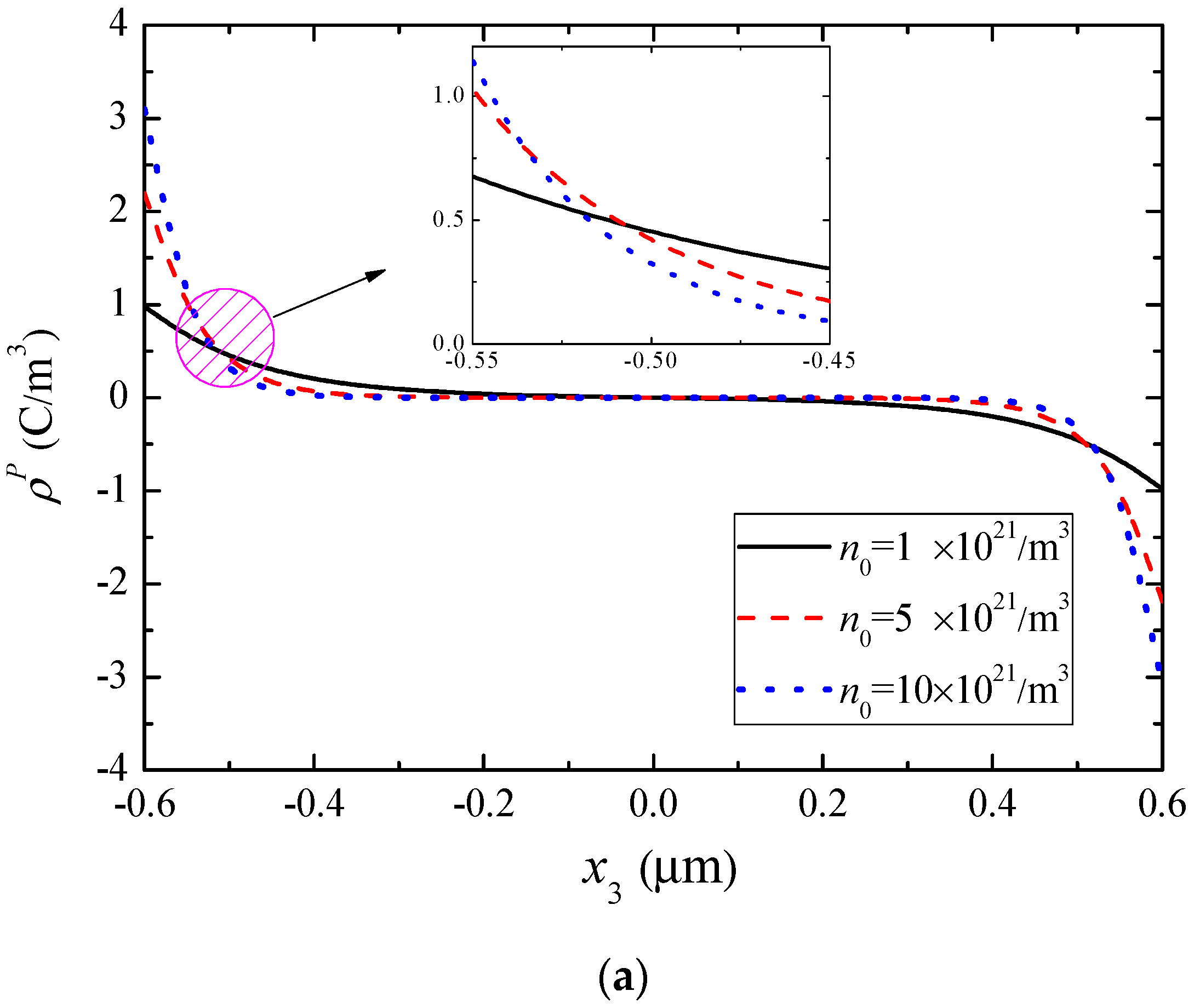
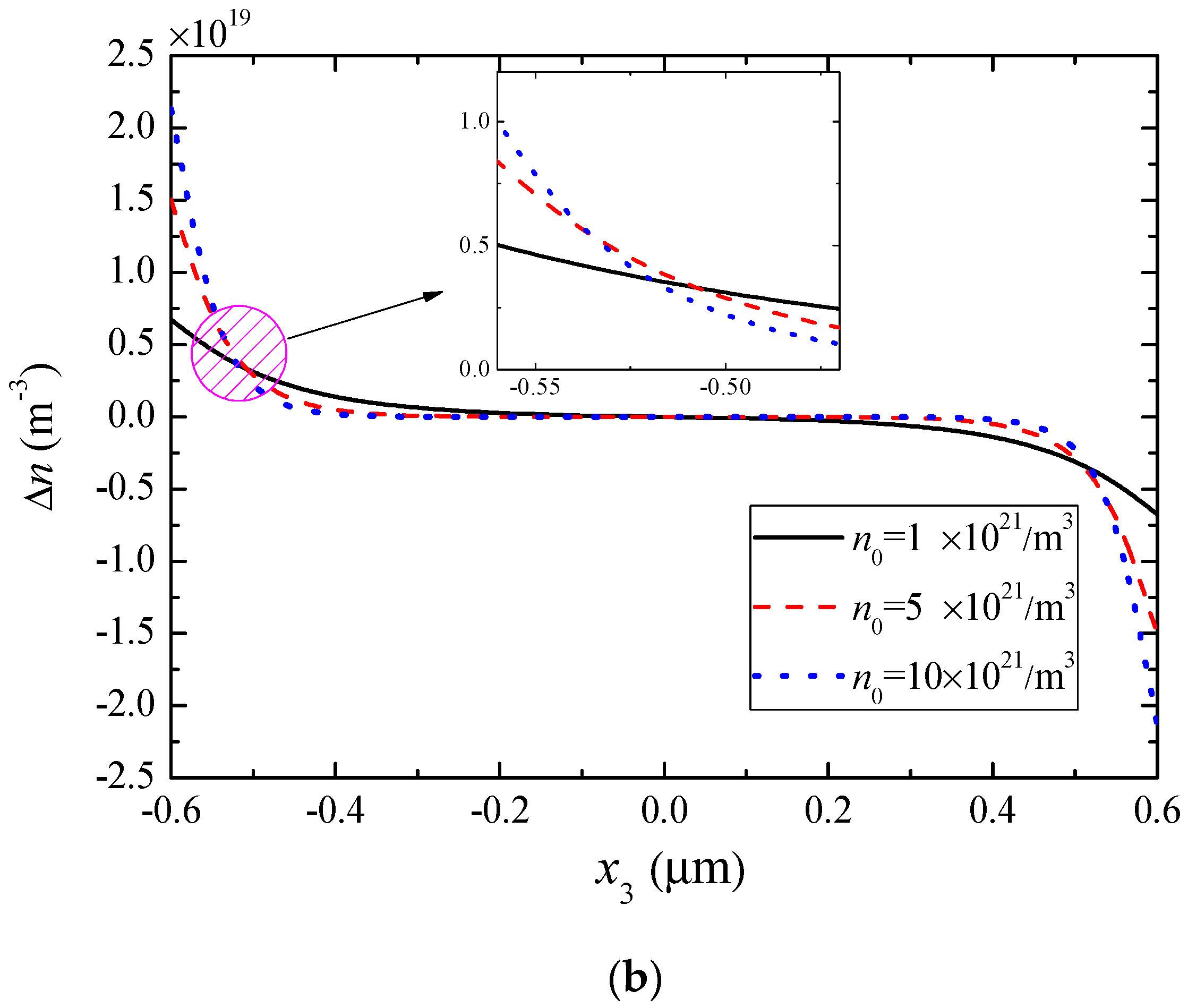
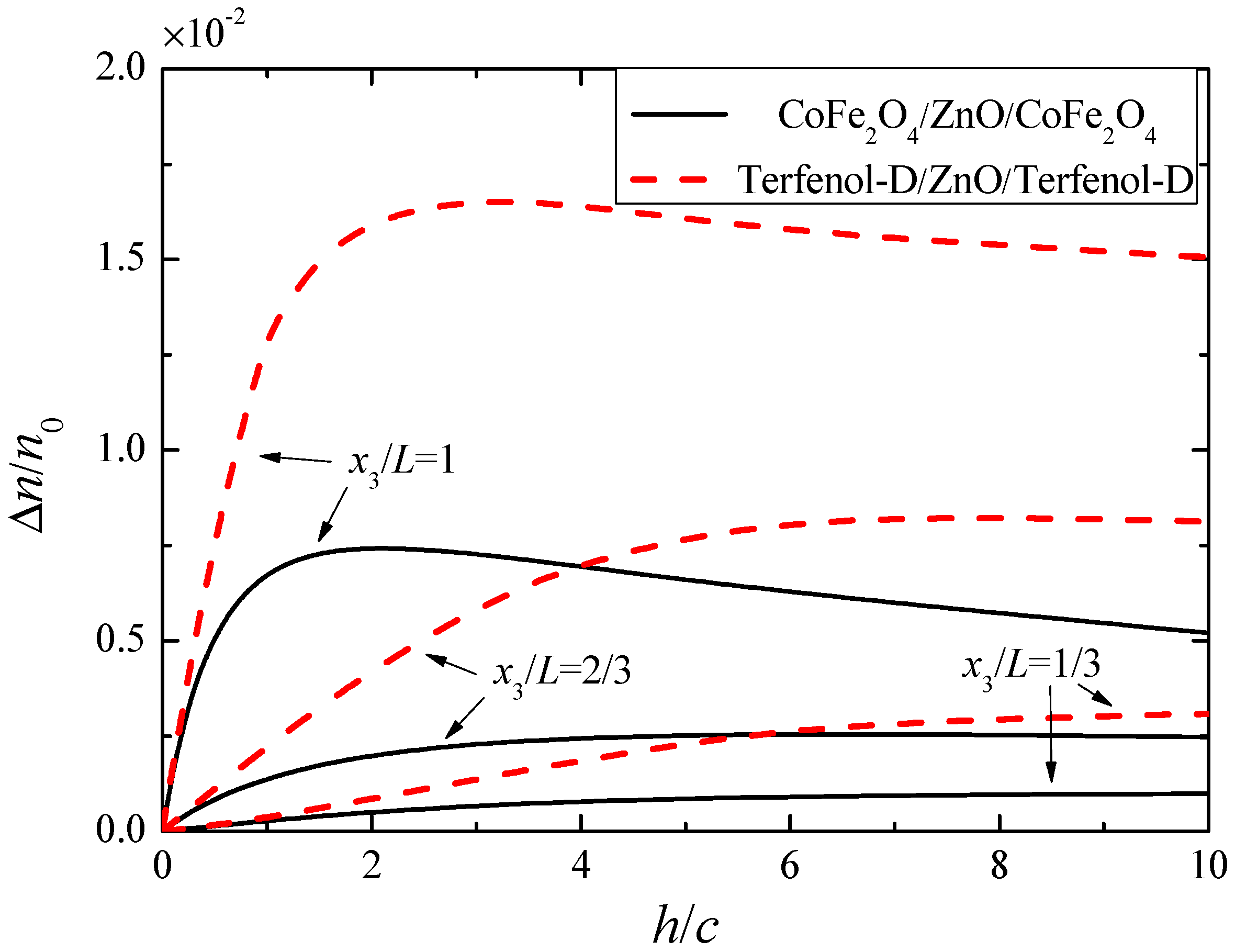
5. Numerical Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hickernell, F.S. The piezoelectric semiconductor and acoustoelectronic device development in the sixties. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 737–745. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.L.; Wu, W.Z.; Falconi, C. Piezotronics and piezo-phototronics with third-generation semiconductors. MRS Bull. 2018, 43, 922–927. [Google Scholar] [CrossRef]
- Zhang, Y.; Leng, Y.S.; Willatzen, M.; Huang, B.L. Theory of piezotronics and piezo-phototronics. MRS Bull. 2018, 43, 928–935. [Google Scholar] [CrossRef]
- Hu, W.G.; Kalantar-Zadeh, K.; Gupta, K.; Liu, C.P. Piezotronic materials and large-scale piezotronics array devices. MRS Bull. 2018, 43, 936–940. [Google Scholar] [CrossRef]
- Fröemling, T.; Yu, R.M.; Mintken, M.; Adelung, R.; Rödel, J. Piezotronic sensors. MRS Bull. 2018, 43, 941–945. [Google Scholar] [CrossRef]
- Wang, X.D.; Rohrer, G.S.; Li, H.X. Piezotronic modulations in electro- and photochemical catalysis. MRS Bull. 2018, 43, 946–951. [Google Scholar] [CrossRef]
- Bao, R.R.; Hu, Y.F.; Yang, Q.; Pan, C.F. Piezophototronic effect on optoelectronic nanodevices. MRS Bull. 2018, 43, 952–958. [Google Scholar] [CrossRef]
- Gao, P.X.; Song, J.H.; Liu, J.; Wang, Z.L. Nanowire piezoelectric nanogenerators on plastic substrates as flexible power sources for nanodevices. Adv. Mater. 2007, 19, 67–72. [Google Scholar] [CrossRef]
- Romano, G.; Mantini, G.; Garlo, A.D.; D’Amico, A.; Falconi, C.; Wang, Z.L. Piezoelectric potential in vertically aligned nanowires for high output nanogenerators. Nanotechnology 2011, 22, 465401. [Google Scholar] [CrossRef]
- Liu, Y.D.; Wahyudin, E.T.N.; He, J.H.; Zhai, J.Y. Piezotronics and piezo-phototronics in two-dimensional materials. MRS Bull. 2018, 43, 959–964. [Google Scholar] [CrossRef]
- Cui, N.Y.; Wu, W.W.; Zhao, Y.; Bai, S.; Meng, L.X.; Qin, Y.; Wang, Z.L. Magnetic force driven nanogenerators as a noncontact energy harvester and sensor. Nano Lett. 2012, 12, 37013705. [Google Scholar] [CrossRef]
- Huang, L.B.; Bai, G.X.; Wong, M.C.; Yang, Z.B.; Wu, W.; Hao, J.H. Magnetic-assisted noncontact triboelectric nanogenerator converting mechanical energy into electricity and light emissions. Adv. Mater. 2016, 28, 2744–2751. [Google Scholar] [CrossRef] [PubMed]
- Wong, M.C.; Chen, L.; Tsang, M.K.; Zhang, Y.; Hao, J.H. Magnetic-induced luminescence from flexible composite laminates by coupling magnetic field to piezophotonic effect. Adv. Mater. 2015, 27, 4488–4495. [Google Scholar] [CrossRef] [PubMed]
- Peng, M.Z.; Zhang, Y.; Liu, Y.D.; Song, M.; Zhai, J.Y.; Wang, Z.L. Magnetic-mechanical-electrical-optical coupling effects in GaN-based led/rare-earth Terfenol-D structures. Adv. Mater. 2014, 26, 6767–6772. [Google Scholar] [CrossRef]
- Liu, Y.D.; Guo, J.M.; Yu, A.F.; Zhang, Y.; Kou, J.Z.; Zhang, K.; Wen, R.M.; Zhang, Y.; Zhai, J.Y.; Wang, Z.L. Magnetic-induced-piezopotential gated MoS2 field-effect transistor at room temperature. Adv. Mater. 2018, 30, 1704524. [Google Scholar] [CrossRef] [PubMed]
- Piotrowski, C.; Bendson, S.A.; Loeding, N.W.; Mularie, W.M. Integrated Magnetostrictive-Piezoelectric-Metal Oxide Semiconductor Magnetic Playback Head. U.S. Patent 4,520,413, 28 May 1985. [Google Scholar]
- Srinivasan, G.; Laletsin, V.M.; Hayes, R.; Puddubnaya, N.; Rasmussen, E.T.; Fekel, D.J. Giant magnetoelectric effects in layered composites of nickel zinc ferrite and lead zirconate titanate. Solid State Commun. 2002, 124, 373–378. [Google Scholar] [CrossRef]
- Bichurin, M.I.; Petrov, V.M.; Srinivasan, G. Theroy of low frequency magnetoelectric effects in ferromagnetic-ferroelectric layered composites. J. Appl. Phys. 2002, 92, 7681–7683. [Google Scholar] [CrossRef]
- Dong, S.X.; Li, J.F.; Viehlan, D. Giant magneto-electric effect in laminate composites. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2003, 50, 1236–1239. [Google Scholar] [CrossRef]
- Soh, A.K.; Liu, J.X. Interfacial shear horizontal waves in a piezoelectric-piezomagnetic bi-material. Phil. Mag. Lett. 2006, 86, 31–35. [Google Scholar] [CrossRef]
- Chen, W.Q.; Lee, K.Y.; Ding, H.J. On free vibration of non-homogeneous transversely isotropic magneto-electro-elastic plates. J. Sound Vib. 2005, 279, 237–251. [Google Scholar] [CrossRef]
- Nan, C.W.; Bichurin, M.I.; Dong, S.X.; Viehland, D.; Srinivasan, G. Multiferroic magnetoelectric composites: Historical perspectives, status, and future directions. J. Appl. Phys. 2008, 103, 031101. [Google Scholar] [CrossRef]
- Auld, B.A. Acoustic Fields and Waves in Solids; John Wiley and Sons: New York, NY, USA, 1973; Volume I. [Google Scholar]
- Pierret, R.F. Semiconductor Device Fundamentals; Pearson: Uttar Pradesh, India, 1996. [Google Scholar]
- Wauer, J.; Suherman, S. Thickness vibrations of a piezo-semiconducting plate layer. Int. J. Eng. Sci. 1997, 35, 1387–1404. [Google Scholar] [CrossRef]
- Li, P.; Jin, F.; Yang, J.S. Effects of semiconduction on electromechanical energy conversion in piezoelectrics. Smart Mater. Struct. 2015, 24, 025021. [Google Scholar] [CrossRef]
- Gu, C.L.; Jin, F. Shear-horizontal surface waves in a half-space of piezoelectric semiconductors. Phil. Mag. Lett. 2015, 95, 92–100. [Google Scholar] [CrossRef]
- Sharma, J.N.; Sharma, K.K.; Kumar, A. Acousto-diffusive waves in a piezoelectric-semiconductor-piezoelectric sandwich structure. World J. Mech. 2011, 1, 247–255. [Google Scholar] [CrossRef]
- Jiao, F.Y.; Wei, P.J.; Zhou, Y.H.; Zhou, X.L. Wave propagation through a piezoelectric semiconductor slab sandwiched by two piezoelectric half-spaces. Eur. J. Mech. A-Solids 2019, 75, 70–81. [Google Scholar] [CrossRef]
- Jiao, F.Y.; Wei, P.J.; Zhou, Y.H.; Zhou, X.L. The dispersion and attenuation of the multi-physical fields coupled waves in a piezoelectric semiconductor. Ultrasonics 2019, 92, 68–78. [Google Scholar] [CrossRef]
- Liang, Y.X.; Hu, Y.T. Effect of interaction among the three time scales on the propagation characteristics of coupled waves in a piezoelectric semiconductor rod. Nano Energy 2019, 68, 104345. [Google Scholar] [CrossRef]
- Tian, R.; Liu, J.X.; Pan, E.; Wang, Y.S.; Soh, A.K. Some characteristics of elastic waves in a piezoelectric semiconductor plate. J. Appl. Phys. 2019, 126, 125701. [Google Scholar] [CrossRef]
- Sladek, J.; Sladek, V.; Pan, E.; Wuensche, M. Fracture analysis in piezoelectric semiconductors under a thermal load. Eng. Fract. Mech. 2014, 126, 27–39. [Google Scholar] [CrossRef]
- Zhao, M.H.; Pan, Y.B.; Fan, C.Y.; Xu, G.T. Extended displacement discontinuity method for analysis of cracks in 2D piezoelectric semiconductors. Int. J. Solids Struct. 2016, 94–95, 50–59. [Google Scholar] [CrossRef]
- Qin, G.S.; Lu, C.S.; Zhang, X.; Zhao, M.H. Electric current dependent fracture in GaN piezoelectric semiconductor ceramics. Materials 2018, 11, 2000. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.L.; Luo, Y.X.; Cheng, R.R.; Wang, X.Y. Electromechanical fields in piezoelectric semiconductor nanofibers under an axial force. MRS Adv. 2017, 2, 3421–3426. [Google Scholar] [CrossRef]
- Afraneo, R.; Lovat, G.; Burghignoli, P.; Falconi, C. Piezo-semiconductive quasi-1D nanodevices with or without anti-symmetry. Adv. Mater. 2012, 24, 4719–4724. [Google Scholar] [CrossRef]
- Zhao, M.H.; Liu, X.; Fan, C.Y.; Lu, C.S.; Wang, B.B. Theoretical analysis on the extension of a piezoelectric semi-conductor nanowire: Effects of flexoelectricity and strain gradient. J. Appl. Phys. 2020, 127, 085707. [Google Scholar] [CrossRef]
- Cheng, R.R.; Zhang, C.L.; Chen, W.Q.; Yang, J.S. Piezotronic effects in the extension of a composite fiber of piezoelectric dielectrics and nonpiezoelectric semiconductors. J. Appl. Phys. 2018, 124, 064506. [Google Scholar] [CrossRef]
- Gao, Y.F.; Wang, Z.L. Electrostatic potential in a bent piezoelectric nanowire. The fundamental theory of nanogenerator and nanopiezotrionics. Nano Lett. 2007, 7, 2499–2505. [Google Scholar] [CrossRef]
- Gao, Y.F.; Wang, Z.L. Equilibrium potential of free charge carriers in a bent piezoelectric semiconductive nanowire. Nano Lett. 2009, 9, 1103–1110. [Google Scholar] [CrossRef]
- Fan, S.Q.; Liang, Y.X.; Xie, J.M.; Hu, Y.T. Exact solutions to the electromechanical quantities inside a statically-bent circular ZnO nanowire by taking into account both the piezoelectric property and the semiconducting performance: Part I-Linearized analysis. Nano Energy 2017, 40, 82–87. [Google Scholar] [CrossRef]
- Liang, Y.X.; Fan, S.Q.; Chen, X.D.; Hu, Y.T. Nonlinear effect of carrier drift on the performance of an n-type ZnO nanowire nanogenerator by coupling piezoelectric effect and semiconduction. Nanotechnology 2018, 9, 1917–1925. [Google Scholar] [CrossRef]
- Dai, X.Y.; Zhu, F.; Qian, Z.H.; Yang, J.S. Electric potential and carrier distribution in a piezoelectric semiconductor nanowire in time-harmonic bending vibration. Nano Energy 2018, 43, 22–28. [Google Scholar] [CrossRef]
- Liang, Y.X.; Hu, Y.T. Influence of doping concentration on the outputs of a bent ZnO nanowire. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2019, 66, 1793–1797. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.X.; Zhang, C.L.; Chen, W.Q.; Yang, J.S. An analysis of PN junctions in piezoelectric semiconductors. J. Appl. Phys. 2017, 122, 204502. [Google Scholar] [CrossRef]
- Yang, G.Y.; Du, J.K.; Wang, J.; Yang, J.S. Electromechanical fields in a nonuniform piezoelectric semiconductor rod. Mech. Mater. Struct. 2018, 13, 103–120. [Google Scholar] [CrossRef]
- Luo, Y.X.; Cheng, R.R.; Zhang, C.L.; Chen, W.Q.; Yang, J.S. Electromechanical fields near a circular PN Junction between two piezoelectric semiconductors. Acta Mech. Solida Sin. 2018, 31, 127–140. [Google Scholar] [CrossRef]
- Guo, M.K.; Li, Y.; Qin, G.S.; Zhao, M.H. Nonlinear solutions of PN junctions of piezoelectric semiconductors. Acta Mech. 2019, 230, 1825–1841. [Google Scholar] [CrossRef]
- Qin, L.F.; Chen, Q.M.; Cheng, H.B.; Chen, Q.; Li, J.F.; Wang, Q.M. Viscosity sensor using ZnO and AlN thin film bulk acoustic resonators with tilted polar c-axis orientations. J. Appl. Phys. 2011, 110, 094511. [Google Scholar] [CrossRef]
- Srinivas, S.; Li, J.Y.; Zhou, Y.C.; Soh, A.K. The effective magnetoelectroelastic moduli of matrix-based multiferroic composites. J. Appl. Phys. 2006, 99, 043905. [Google Scholar] [CrossRef]
- Pan, E.; Chen, W.Q. Green’s Functions in Anisotropic Media; Cambridge University Press: New York, NY, USA, 2015. [Google Scholar]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Liu, J.; Feng, W.; Yang, J. Magnetically Induced Carrier Distribution in a Composite Rod of Piezoelectric Semiconductors and Piezomagnetics. Materials 2020, 13, 3115. https://doi.org/10.3390/ma13143115
Wang G, Liu J, Feng W, Yang J. Magnetically Induced Carrier Distribution in a Composite Rod of Piezoelectric Semiconductors and Piezomagnetics. Materials. 2020; 13(14):3115. https://doi.org/10.3390/ma13143115
Chicago/Turabian StyleWang, Guolin, Jinxi Liu, Wenjie Feng, and Jiashi Yang. 2020. "Magnetically Induced Carrier Distribution in a Composite Rod of Piezoelectric Semiconductors and Piezomagnetics" Materials 13, no. 14: 3115. https://doi.org/10.3390/ma13143115
APA StyleWang, G., Liu, J., Feng, W., & Yang, J. (2020). Magnetically Induced Carrier Distribution in a Composite Rod of Piezoelectric Semiconductors and Piezomagnetics. Materials, 13(14), 3115. https://doi.org/10.3390/ma13143115





