1. Introduction
Miniaturization of metallic components brings advantages such as space savings, lower energy consumption or improved behavior of high-frequency components (transmission, reflection, etc.). Manufacturing of such parts on industrial scale requires the ability to reliably produce micro-scaled structures. That means, that a manufacturing tolerance on the sub-micron level is necessary. Micro-milling is a widely used technology for machining miniaturized parts with high potential. It presents a technological down-scale of the traditional milling methodology. It also shares the advantages of the macro-milling: high material removal rate and great process flexibility. Hence, it is possible to produce complex three-dimensional geometries with acceptable manufacturing times.
One important application of micro-milling is the manufacturing of waveguides for giga- and terahertz applications. With increasing frequency, the wavelength is approaching the lower μm-range and surface quality become increasingly important. The waveguide efficiency is influenced significantly by the surface roughness. As it is shown by Dikemlik et al. surface roughness significantly influences the reflection and affects the signal-noise ratio [
1]. This could be confirmed by Iwai et al. for high-frequency transmission lines along with a method to measure the effect [
2]. Tian et al. demonstrated a successful fabrication of a terahertz waveguide with extremely low transmission loss due to, amongst other things, low surface roughness [
3]. Thus, precise control of the manufacturing process is necessary to ensure the reliable fabrication of these components.
The micro-milling process can be simply scaled down to some degree. However, new challenges arise on the technological and on the material part when a critical grade of miniaturization is reached. Therefore, the influencing factors and their behavior on microscale must be studied in detail. Numerous factors influence surface integrity, such as tool properties, cutting parameters, workpiece properties, and cutting phenomena, which are summarized by Wang et al. [
4]. As has been shown above, surface roughness is especially important for the quality of high-frequency components. Strain-hardening on the other hand can help to improve control over the manufacturing process. For our study, surface roughness and strain hardening are chosen to represent the surface quality.
Various parameters have been shown to influence surface roughness. Yuan et al. reported that the diamond-tool cutting edge radius between 0.3 μm and 0.6 μm has a considerable effect on surface roughness [
5]. An experimental study of copper 101 using tungsten carbide micro-endmills by Filitz et al. indicated that surface roughness increases with feed rate [
6]. Additionally, Aurich et al. showed that the tilt angle of the main spindle significantly changes material removal on the microscale and influences burr formation as well as surface topography [
7]. Gao et al. surveyed different micro-milling parameters of nickel-based single crystal superalloy [
8]. He discovered that feed rate, spindle speed, and milling depth have the most influence on surface roughness. From these sources, it can be concluded that cutting edge radius and feed rate (i.e., single tooth feed) have the most influence on micro-milled surface roughness.
Surface strain-hardening depends on the machined material and is difficult to generalize. In this context, the ploughing effect which significantly increases strain-hardening of the surface and the cutting forces at the micro-level should be mentioned. Klocke et al., for example, found that the cutting regime is dominated by the ploughing effect (alternatively micro-milling size-effect) if the uncut chip thickness in on the same order as the tool edge-radius [
9]. Already in 1996 it was reported by Yuan et al., that diamond tool sharpness has a significant influence on surface strain-hardening [
5]. Lai et al. showed systematically, that the micro-cutter edge radius is the cause for minimum chip thickness
hmin [
10]. For OFHC-Copper, the tool cutting edge radius of 2 μm,
hmin is proposed to be 0.25 times the cutting edge radius. Additionally, they proposed that the micro-milling size-effect is caused by material behavior at the micron level. Additionally, Biermann et al. characterized the influence of
hmin on the burr formation [
11]. In conclusion, it can be stated that the interplay of the undeformed chip thickness and
hmin which is mainly influenced by the cutting edge radius is critical for surface strain-hardening. These factors are supposed to be most relevant to the current study.
The ploughing effect is rarely measured directly from the surface hardness but is rather associated with the increase of cutting forces on the micro-scale. Niu et al. reported that cutting forces increase with increasing tooth feed and cutting edge radius [
12], which is in good agreement with the theory. Furthermore, the mentioned study of Lai et al. presents a model to predict the cutting forces taking into account the size-effect by the strain-gradient plasticity [
10]. However, it is important to measure these effects directly from the machined surfaces to verify the materials response. As demonstrated by Boehme et al. on austenitic stainless steel, nanoindentation is an effective method to directly investigate critical changes in mechanical properties of micro-milled surfaces [
13].
In the present study, the effect of tool geometry (cutting edge radius, cutting edge roughness) and undeformed chip thickness (via single tooth feed) on surface roughness and strain-hardened zone have been investigated. The tool geometry will certainly influence the resulting surface. However, the exact roughness is difficult to predict theoretically. For this reason, surface morphology was studied experimentally.
While the sharper cutting edge will produce less strain-hardening, the depth and hardness of the strain-hardened zone cannot be predicted. Therefore surface strain-hardening by micro-milling has been researched by means of multi-step nanoindentation.
Two different tool geometries with cutting edge radius of 17 nm and 670 nm are compared. Additionally, the undeformed chip thickness is varied via single tooth feed by 3 μm, 8 μm and 14 μm. The roughness of the machined AA6082 aluminum surfaces is examined microscopically. The surface hardness is determined by instrumented indentation with indentation depth from approx. 200 nm to more than 9 μm.
2. Materials and Methods
In the present study, a plate of AA6082 (short for EN AW6082-T651, alloy AlSi1MgMn) was used for the milling experiments. The AA6082-plate was machined with two different tools and different feeds per tooth for each tool. Additional reference samples from the AA6082-plate and 99.999% high purity aluminum were electropolished to represent an undeformed material surface. Indentation analysis was performed for milled and electropolished samples. Roughness was only determined on milled samples. An overview of used materials with respective surface treatments is presented in
Table 1.
2.1. Materials
AA6082 is a medium strength aluminum alloy with an excellent corrosion resistance which is widely used for machining (average hardness 106 HV20, chemical properties in
Table 2). This material is compared to recrystallized 99.999% pure aluminum as a base-line reference (average hardness 12 HV5, chemical properties in
Table 3).
2.2. Tools and Milling Parameters
For comparison, two different commercially available single-tooth micro end-mills were used for micro-milling. These are a solid carbide (SC) end-mill (Sphinx Tools AG, Derendingen, Switzerland) and a monocrystalline diamond (MD) end-mill (Diatec Diamond Technology LLC, Pforzheim, Germany). Both mills are nominally similar with an effective cutter diameter of 500 μm and the cutting length of 1000 μm and 500 μm respectively.
Important surface producing geometrical characteristics of the tools were not available from the datasheets. For this reason, the tools were inspected microscopically. New unused tools were used for the analysis to represent those used to mill the actual surfaces.
Wedge angle
β, and cutting edge radius
r (see
Figure 1) were determined directly from optical and Scanning Electron Microscope (SEM) images. Additionally, flank and rake face morphology were evaluated qualitatively.
For cutting edge roughness analysis three optical images of the cutting edge were taken perpendicularly to the rake face (view field 160 μm). Optical images were used preferably to SEM or confocal images, because of the shallow depth of field which generates better edge contrast. Only the inner 80% of the image width were used for analysis because of unsharpness at image edges. Cutting edge profile was extracted via image recognition software (“Analyze_Stripes” plug-in of the Fiji software [
14]). From the cutting edge profile one-dimensional roughness values, Root Mean Square Roughness
Rq and Maximum peak-to-peak-valley height
Rt, were determined according to the ISO4287-1997.
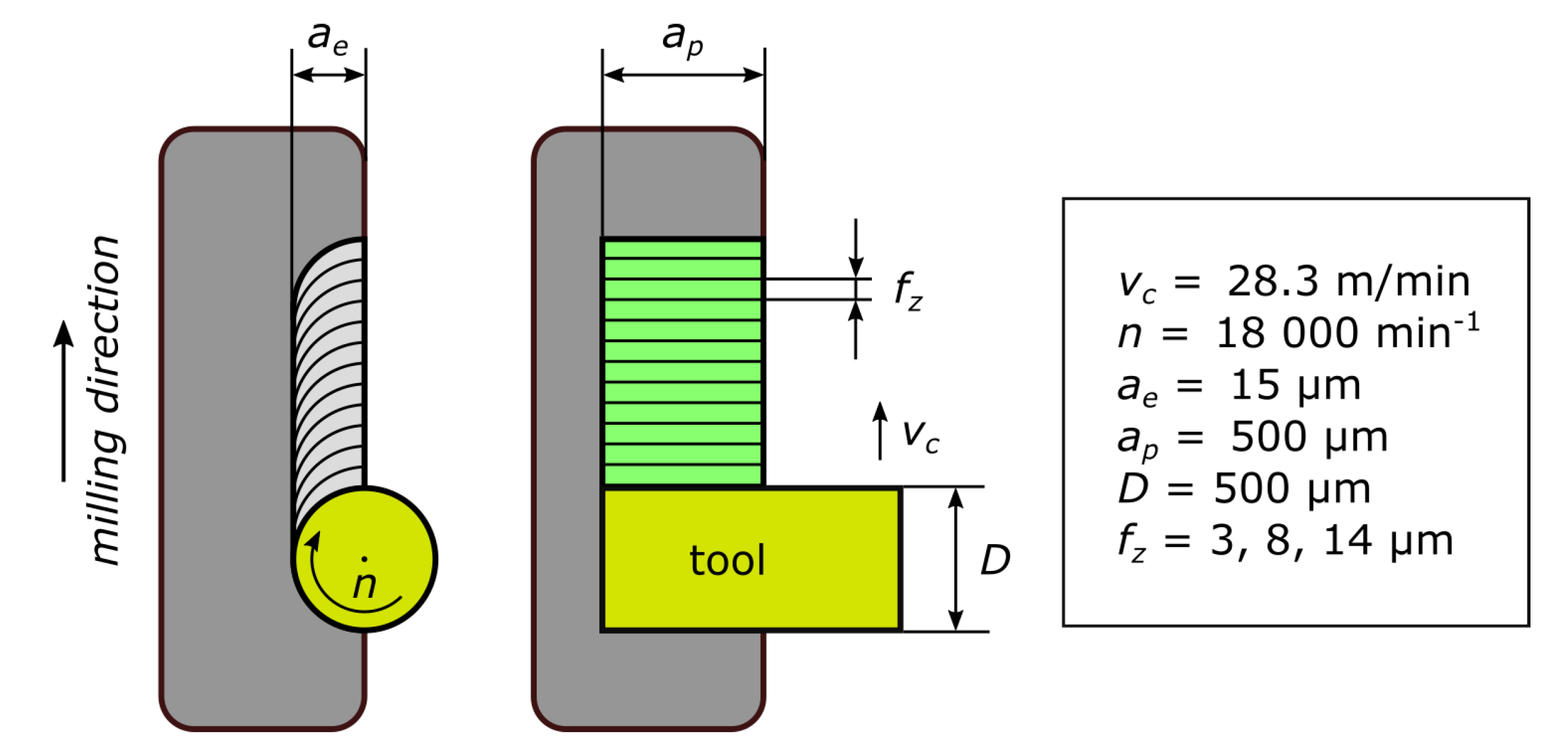
The samples were produced on the “KERN Pyramid Nano” CNC machining center (at Rohde and Schwarz, Teisnach plant, Germany). For all experiments cutting velocity
vc, rotational speed
n, axial cutting depth
ae, radial cutting depth
ap, and tool diameter
D were identical, while the feed per tooth
fz was varied by 3, 8 and 14 μm. The process parameters are shown in
Figure 2. The peripherally milled surface is used for further analysis (highlighted green in
Figure 2).
2.3. Electropolishing
To evaluate the effect of micro-milling on surface hardness undeformed (by machining) reference samples were prepared. For this purpose specimens of AA6082 and Al5N were cold mounted and electropolished. These samples represent a non-strain-hardened surface. It has been shown before, that this sample preparation technique removes the deformation layer produces a very smooth aluminum surface [
15].
2.4. Surface Roughness Analysis
To measure the roughness of the machined surfaces, confocal microscopy images were taken (Leitz Ergoplan confocal microscope, 20× lens). One-dimensional roughness parameters
Rq and
Rt were determined analogously to cutting edge roughness according to ISO4287-1997 with the Gwyddion software. For these measurements, equidistant profiles (distance of 10 μm) perpendicular (horizontal, 6× per image) and parallel to the milling direction (vertical, 8× per image) were extracted (for directions compare
Figure 2).
The analysis of roughness as a result of intermetallic compounds was not the focus of this study. Thus, locations with large intermetallic phases were systematically avoided in roughness measurements. Likewise, locations with imaging artifacts were avoided.
2.5. Instrumented Indentation via Enhanced Stiffness Procedure (ESP)
Instrumented indentation is a method widely used to determine material hardness from micro- to the nanoscale. The material is penetrated with a geometrically well-defined indenter to a certain maximum load. Load and indenter displacement (indentation depth) are recorded continuously. Indentation hardness
HIT is then acquired from the contact mechanical analysis of the achieved load-depth-curve. This is usually done with the well established Oliver–Pharr-Method [
16] (as proposed by the DIN ISO 14577-1).
This principle is often applied to measure the hardness of thin films, as initially proposed by Bückle [
17,
18]. Here, knowledge about film thickness is necessary to ensure, that the indentation depth is less than 1/10 of the film thickness (Bückle-rule). To measure
HIT at different depths multiple indents would be necessary.
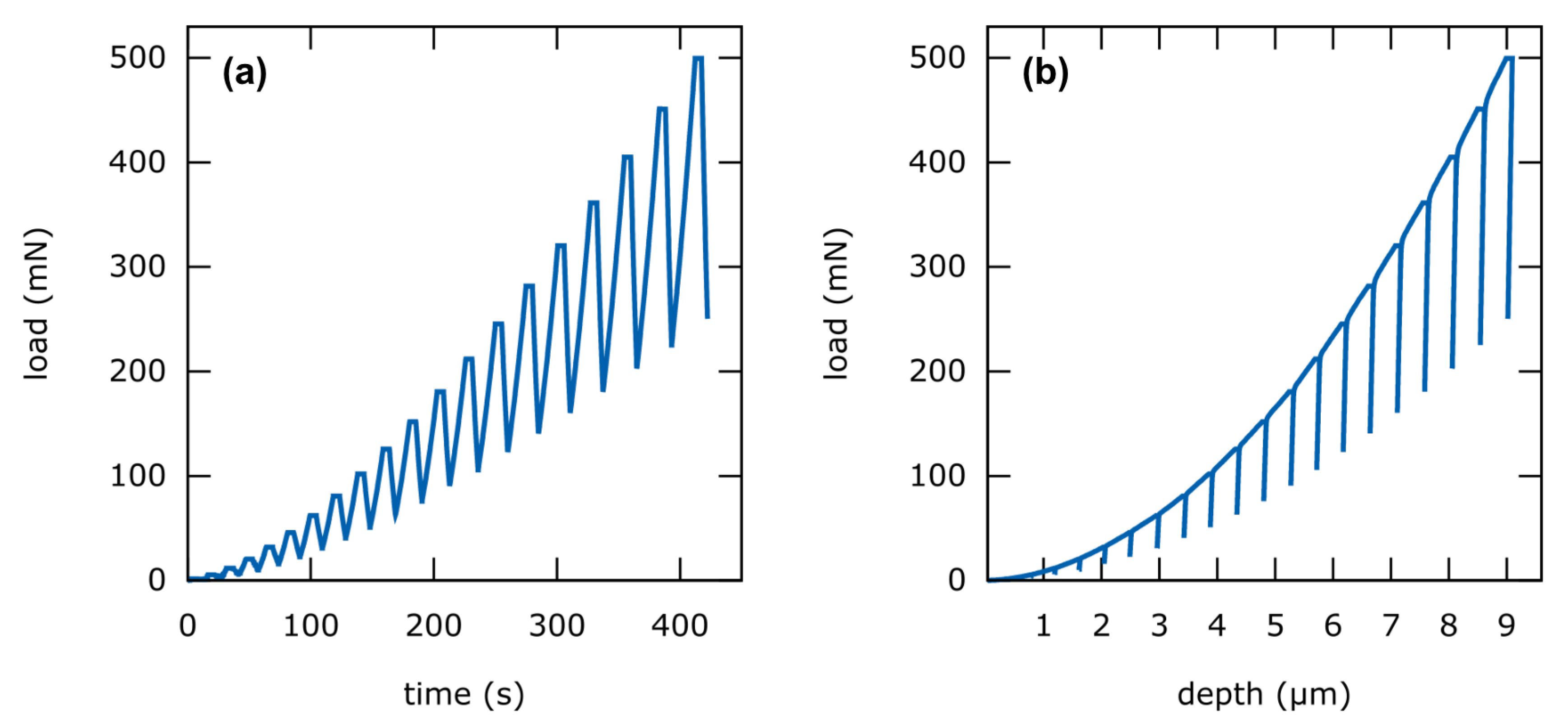
In this work, we used the so-called Enhanced Stiffness Procedure (ESP) implemented in the Picodentor HM500 (Helmut-Fischer GmbH, Sindelfingen, Germany) which is used for indentation. Here the maximum test load is applied in several partial load cycles each one followed by a partial relief cycle. A time-load diagram of the used ESP-procedure is shown in
Figure 3a. The entire measurement is performed at the same location until the maximum test load is reached.
The ESP-load-depth-curve (
Figure 3b) is analyzed with the same data analysis model used for single indentation measurements, i.e., Oliver–Pharr method. However, the partial stress-relief-cycles of the ESP-curve are evaluated as separate indentation curves. As a result,
HIT is obtained at different depths from a single indent.
In this study, the Picodentor HM500 equipped with a Berkovich indenter (tip radius 153 nm) is used for the indentation testing. The ESP-procedure is performed with the same parameters for all samples (
Table 4). The measurement is repeated at least five times per specimen and an average hardness-depth curve is calculated. The curves are evaluated with the Oliver–Pharr method as described above to achieve indentation hardness values.
2.6. Surface Strain-Hardening Analysis
Indentation hardness is an averaged value from a plastically deformed volume below the indenter [
19]. Therefore, hardness measured at a certain depth is not the actual hardness at this depth. To achieve additional information about the strain-hardened layer due to micro-milling (i.e., bulk hardness, the hardness of the strain-hardened layer, layer thickness, etc.) a film-substrate model from Equation (
1) was fitted to the hardness-depth data.
There are many approaches to model composite hardness of a film-substrate system. Broitman or Fischer–Cripps both show a summary of important models [
20,
21]. The approach developed by Korsunky et al. is a film-substrate model based on a volume law of mixtures [
22]. The advantage of the Korsunsky-model lies in its suitability for numerical fits, which i.e., was demonstrated by Tuck et al. [
23,
24]. That makes this model also especially suitable for our study.
The effective hardness
Heff (i.e.,
HIT measured directly by nanoindentation) is described by Korsunsky et al. as the function of film hardness
Hf and substrate hardenss
Hs:
Here, t is the film thickness, h the indentation depth, and α the factor which describes film plasticity. This model assumes constant hardness over depth within the surface layer. In our case it means, that the strain-hardened zone is modeled with constant hardness over depth. Under this prerequisite, the Korsunsky-model was numerically fitted to the averaged hardness depth curves achieved from the ESP-measurements. This was done by the nonlinear least-squares Marquardt–Levenberg algorithm as implemented in the Gnuplot fit module (Gnuplot 5.2: an interactive plotting program).
4. Discussion
4.1. Roughness of the Micro-Milled Surfaces
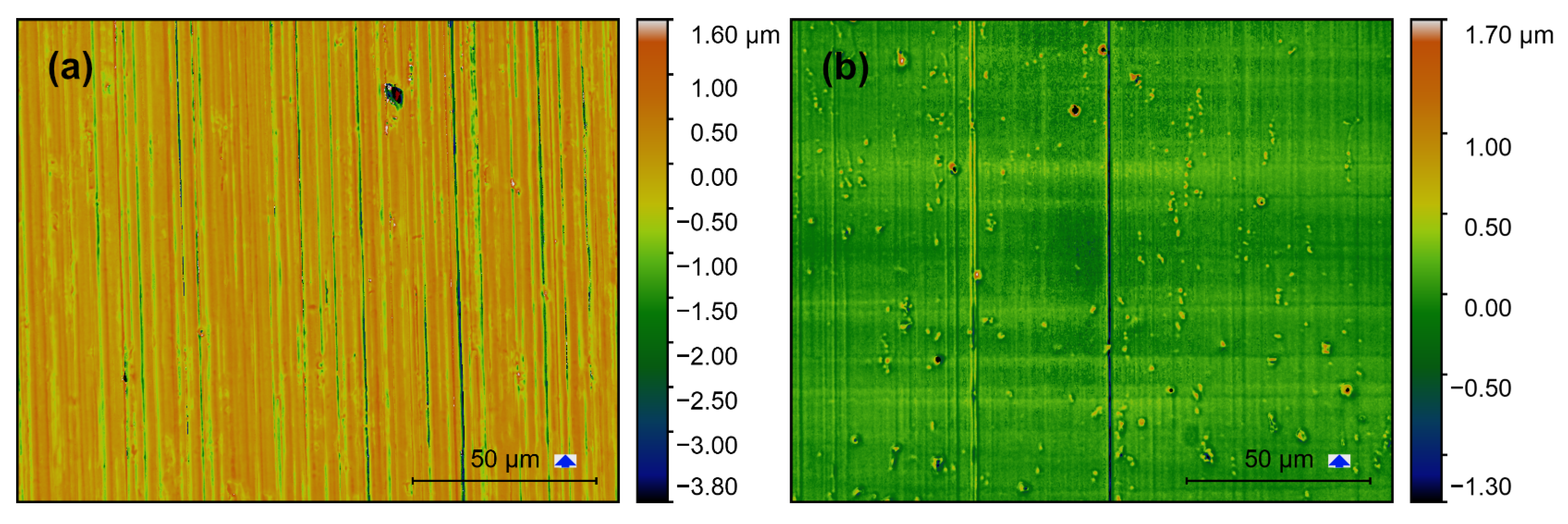
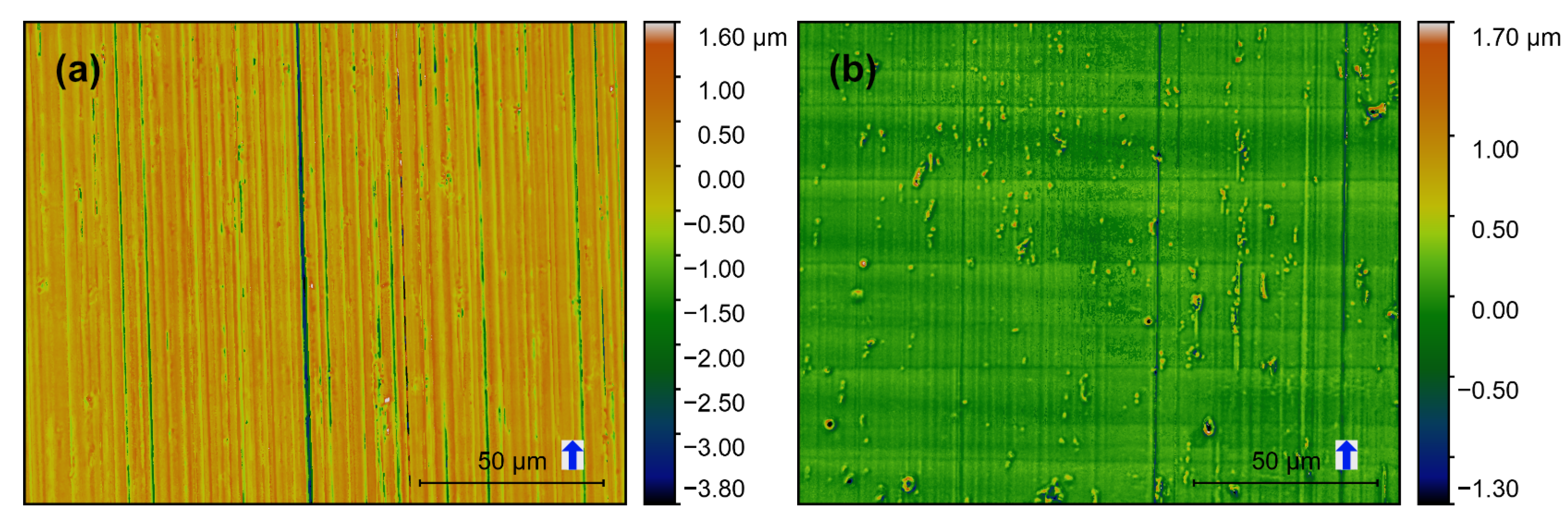
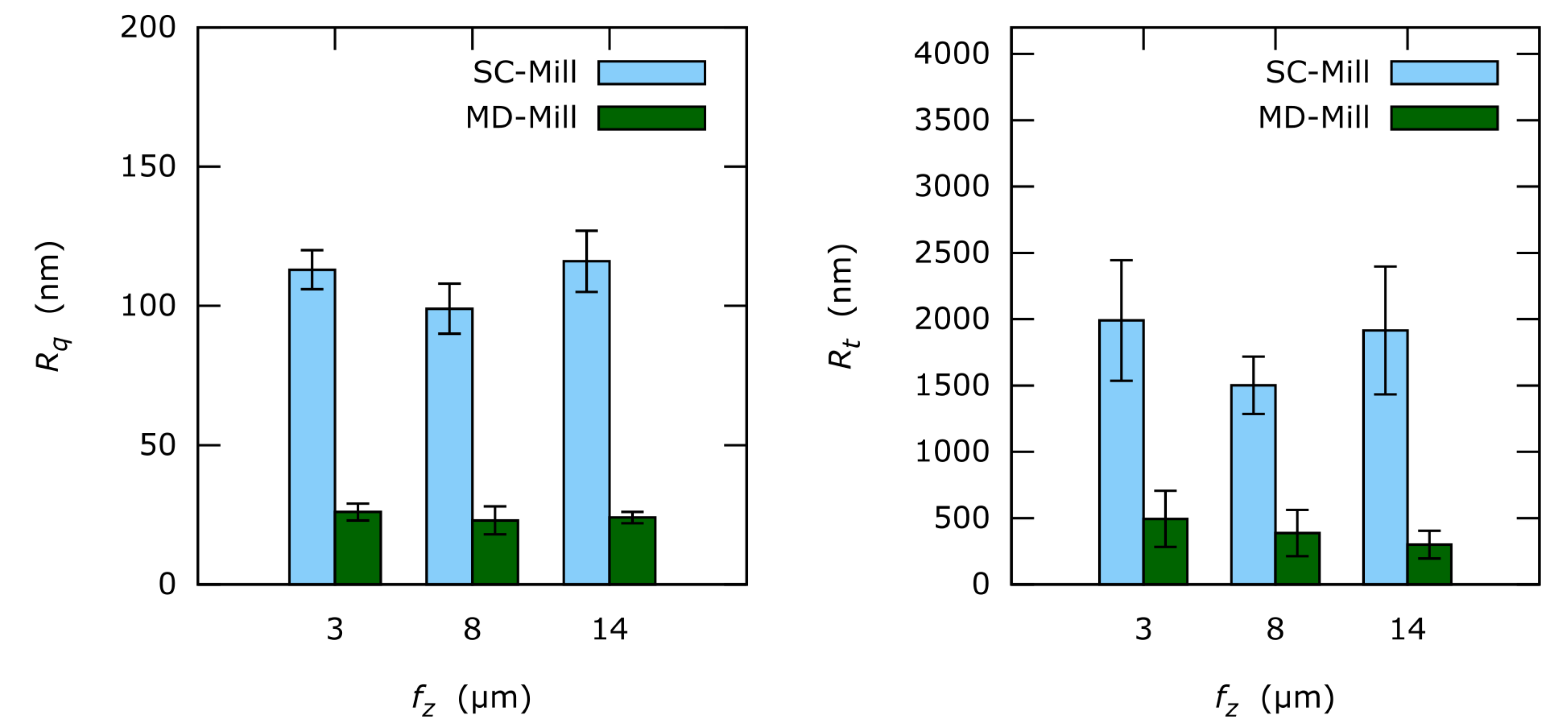
Results demonstrate significant differences for one-dimensional horizontal roughness (perpendicular to the milling direction) of both mills. The surface features are generated by the cutting edge roughness. Cutting edge roughness is replicated on the machined surface, while the original roughness is smoothed out significantly during milling.
In the case of the SC-tool, the cutting edge geometry replicates on the sample surface and produces comparably high roughness with random features (probably due to tungsten carbide particles). Due to this process, the cutting edge Rq is lowered by a factor of 20. Thus, the remaining surface roughness is still remarkable. Here the roughness is mainly influenced by the cutting edge geometry.
On the other hand, the MD-tool produces very smooth surfaces with systematic features. The replication factor of cutting edge roughness is difficult to estimate because the cutting edge roughness of the MD-tool is very low, and could not be determined optically or with SEM. Since the MD-tool cutting edge is extremely smooth, the remaining low surface roughness is mainly causes by two factors: small intermetallic phases (non-directional) and fz (parallel to the milling direction).
Additionally, systematic vertical lines are visible on confocal images of the MD-milled surfaces. These are generated by the few defects of the MD-tool cutting edge. SEM-images (not shown here) confirm, that these features run through the complete milled surface.
Large intermetallic phases produce height differences much higher, than the effect of the mill geometry (Δh > 10 μm). This poses a potential problem during coating of the so produced component. However, this only can be dealt with by exchanging AA6082 by another purer material with less intermetallic phases.
At least, fz, β and flank morphology have no significant influence on surface roughness. In case of fz the reason is probably the chosen parameter range.
4.2. Surface Strain-Hardening
According to Filitz et al. the specific cutting energy increases with decreasing undeformed chip thickness due to micro-milling size effect [
6]. In our terms, this means the that size effect should increase when
fz (corresponding to undeformed chip thickness) converges to
hmin. Kim at al. suggest the
hmin ≈
r/3 [
25].
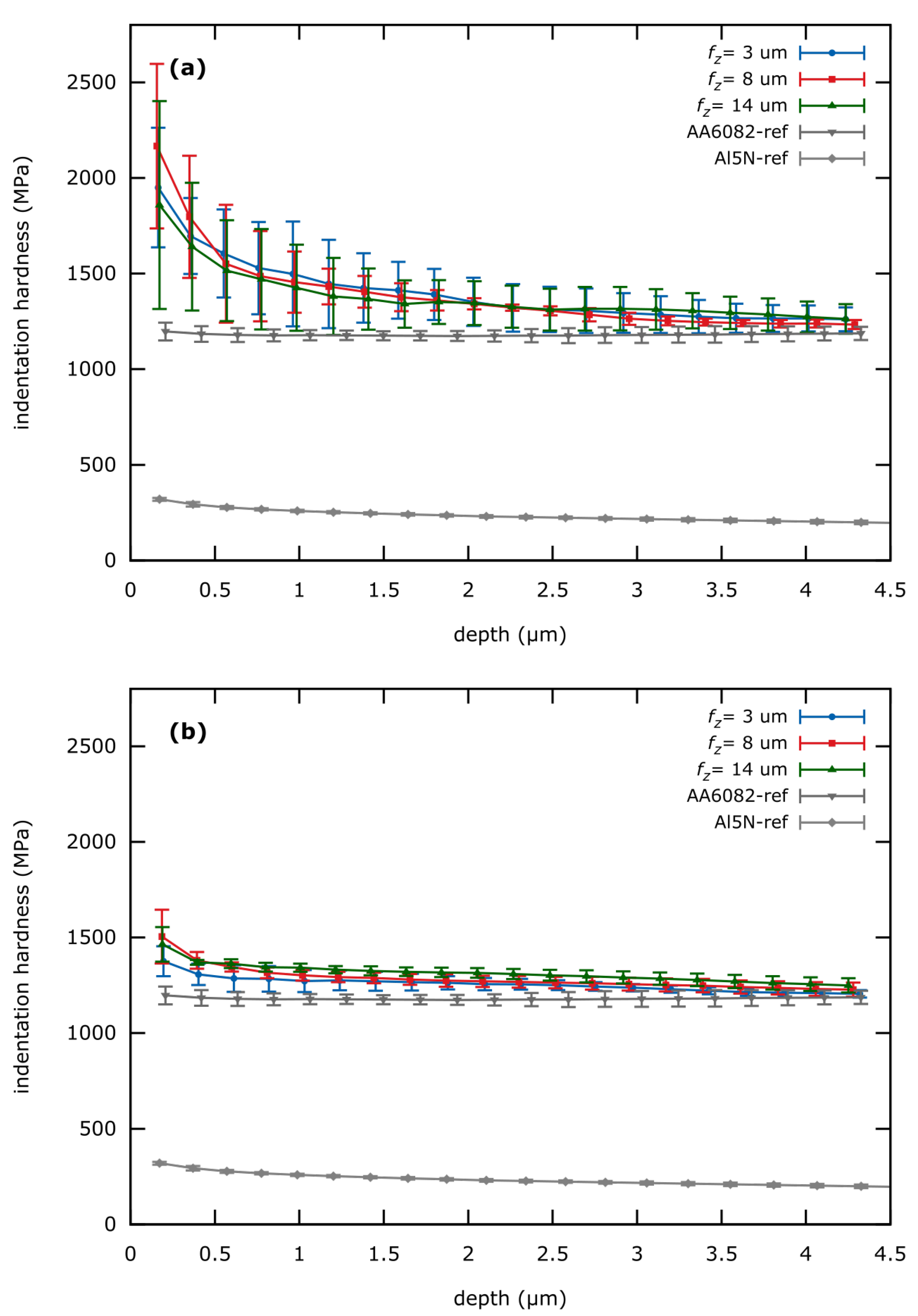
Both mills investigated in this study have different r-values and therefore different hmin. For the MD-tool, fz = 3 μm, which is 500 times greater than the corresponding hmin. This hmin-value is beyond reach (<10 nm), which means, that in case of the MD-tool the milling process is in a pure cutting regime.
This is consistent with the ESP-results where only minimal hardness increase at depths below 500 nm can be observed. This hardness increase can be attributed to surface strain-hardening and not the indentation size effect by the comparison to the electropolished AA6082 reference. Here no significant indentation size effect, i.e., no hardness increase at low depths is observable.
This is however different for the SC-tool. Estimated from the cutting edge radius, the fz = 3 μm here is only 15 time hmin. Therefore, undeformed chip thickness is much closer to hmin and a significant ploughing effect can be anticipated. This is verified by the achieved results, which demonstrate significant strain-hardening (hardness increase) at depth below 1 μm.
The Korsunsky film-substrate model expects hardness at low indentation depth to be dominated by the film only. Therefore, a plateau at low depths is expected, which is also demonstrated by Tuck [
23,
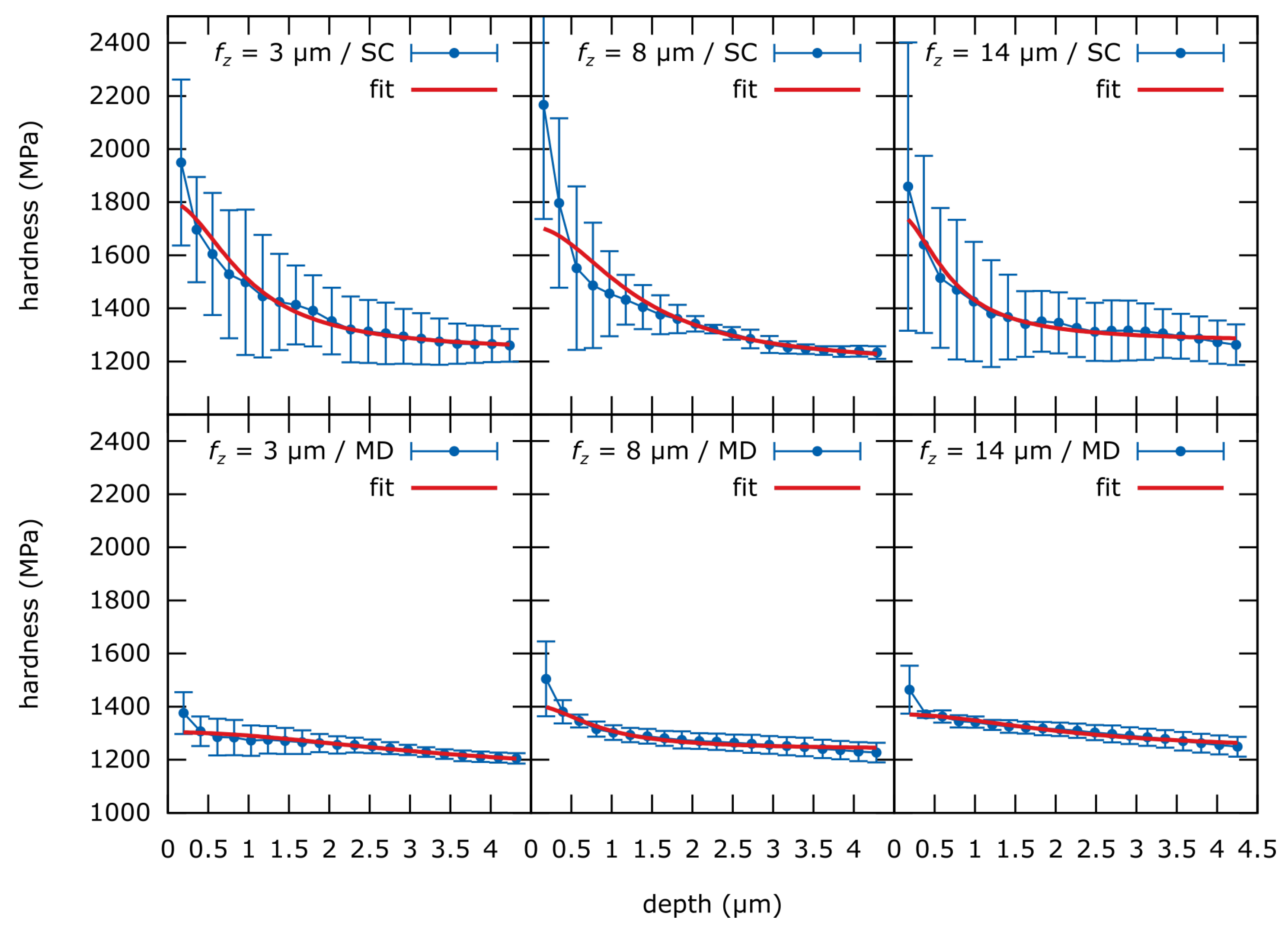
24]. This behavior cannot be observed in the present data set (
Figure 14). Apparently, the hardness increases with decreasing indentation depth, while the maximum (which would be indicated by a plateau) could not be measured.
As it has been mentioned above, indentation hardness is averaged from the plastic zone beneath the indenter [
19]. According to the Bückle–Rule, this zone extends in the indentation direction for least 10 times the indentation depth [
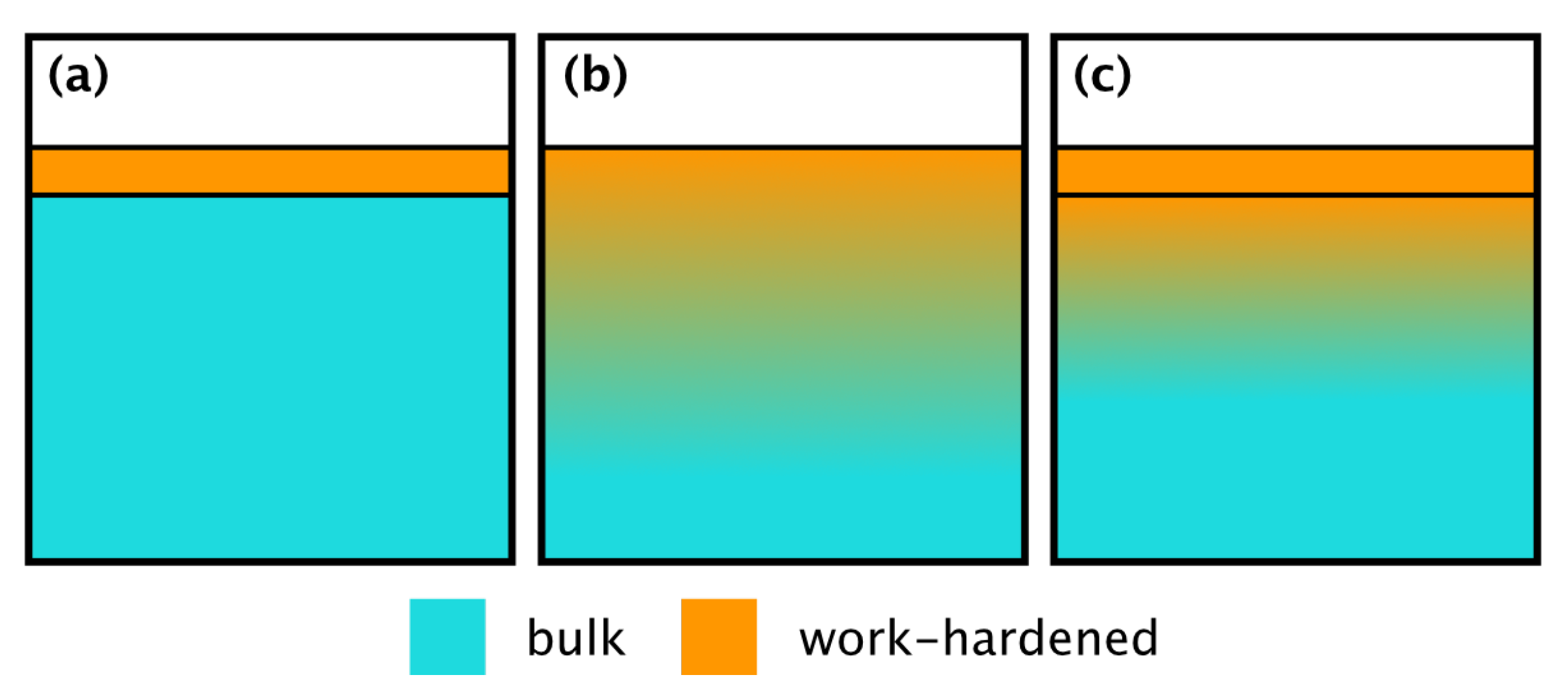
17]. This leads to three options for interpreting the experimental data. The different possibilities are illustrated in
Figure 15, while all options would lead to no observable hardness plateau at low depths.
Figure 15 presents principal possibilities of strain-hardening at the material surface. The simplest model is a uniformly hard surface layer on top of softer bulk material (
Figure 15a). This model also corresponds with the film-substrate-hardness model of Korsunsky [
22]. The next possibility is a gradually hardened surface (
Figure 15b). Here the maximum hardness at the surface decreases continuously towards the bulk. The last is the combination of the first two models which implies a uniformly hard surface layer and gradually decreasing hardness below it (
Figure 15c).
The material stress under the tool has been analyzed for micro-milling by Lai et al. [
10]. They demonstrate by FEM-simulations that stress in the material decreases with depth. Since material stress correlates with strain-hardening, the model of a uniformly harden surface layer (
Figure 15a) can be discarded.
The model of the gradually hardened surface layer (
Figure 15b) corresponds well with the stress-analysis by Lai et al., however, it is lacking the native surface oxide layer. This surface layer could be implemented in the combined model (
Figure 15c). However, according to Evertsson et al. the thickness of such layers usually below 10 nm [
26]. Such a thin layer would be insufficient to significantly increase surface hardness on the observed length scale and can, therefore, be neglected. Consequently, the model (c) could be practically reduced to the model (b).
No suitable data model is available at the moment. Based on the presented Korsunsky-fits and stress data from the literature it can be concluded that the surfaces generated by micro-milling are gradually strain-hardened. It also can be approximated from the 8%-onset of the hardness increase and the Bückle–Rule, that the hardened layer is very thin. For an approximation of the strain-hardened layer thickness, the average height of the 8%-onset can be divided by 10 according to the Bückle–Rule. This results in a layer thickness of less than 200 nm for the SC-tool- and less than 70 nm for the MD-tool -produced surfaces.
The variation of the fz seems to have no effect of strain-hardening. However, it should be noted that the HIT-error is especially high for low depths. The reason is that surface roughness increasingly influences the results at a lower depth. DIN ISO 14577-1 proposes the following relation of the minimum indentation depth and roughness of the analyzed surface: h ≥ 20·Ra. This results in a minimum indentation depth h of 340 nm for the MD-tool and 1380 nm for the SC-tool. Hardness values achieved for depth below these values are beyond the recommendation of the normative and have to be interpreted cautiously. Therefore, a different approach is needed, to determine the hardness values especially of the SC-tool machined surfaces at very low depth.
5. Conclusions and Outlook
Concerning the morphology of micro-machined surfaces, it could be concluded that surface roughness is mainly influenced by the tool geometry and not by the process parameters (in the chosen parameter range). The SC-tool with higher r and rough cutting edge replicates on the micro-milled material. The resulting surfaces show high roughness perpendicular to the milling direction (along cutting edge) with no systematic effects parallel to the milling direction. The MD-tool with an extremely small r and almost featureless cutting edge produce very smooth surfaces. However, the existent features are systematic and originate from intermetallic phases of all sizes, fz, and smaller cutting edge defects. Additionally, a slight correlation of fz to vertical roughness could be observed. These findings are to be taken into account in the selection of materials, tools, and production methods for the manufacture of micro components where surface roughness is critical. This also applies to the production of RF components for use in the terahertz range.
By extracting depth-dependent HIT of the micro-machined surfaces, much could be learned about the mechanical properties of these surfaces. The main factor influencing the surface strain-hardening is r of the used tool. The influence of the process parameters could not be evaluated due to high error at low indentation depths. The Korsunsky model of a uniformly hard film (i.e., strain-hardened layer) is suitable for determining hardness at greater indentation depths. However, for h < 500 nm the fit quality is insufficient. This indicates, that the produced surfaces are probably gradually hardened with max. HIT on the surface.
The hardness gradient and max. HIT depend highly on r and fz (i.e., undeformed chip thickness). The influence of fz on strain-hardening could not be observed in this study, because of the chosen parameter range. For SC-tool machined surfaces with big r the strain-hardened zone is thinner than 200 nm. For MD-milled surfaces with an almost infinitely small r this zone is thinner than 40 nm.
To improve the data analysis of the indentation results a new model has to be developed to incorporate the depth-dependent hardness of the strain-hardened layer at low depth. To study the influence of the process parameters, the experiments should be repeated with different fz-values. Values below, equal or slightly above hmin depending on the used tool’s r are of major interest. Additionally, the effect of the cutting edge wear is still an open point and should be inspected closely.