Reinforcement Efficiency of Cellulose Microfibers for the Tensile Stiffness and Strength of Rigid Low-Density Polyurethane Foams
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Foam Production
2.3. Foam Characterization
3. Model
3.1. Mechanical Reinforcement Efficiency of Foams
3.2. Stiffness and Strength of Foam Struts
3.2.1. Young’s Modulus
3.2.2. Strength
3.2.3. Fiber Orientation Distribution
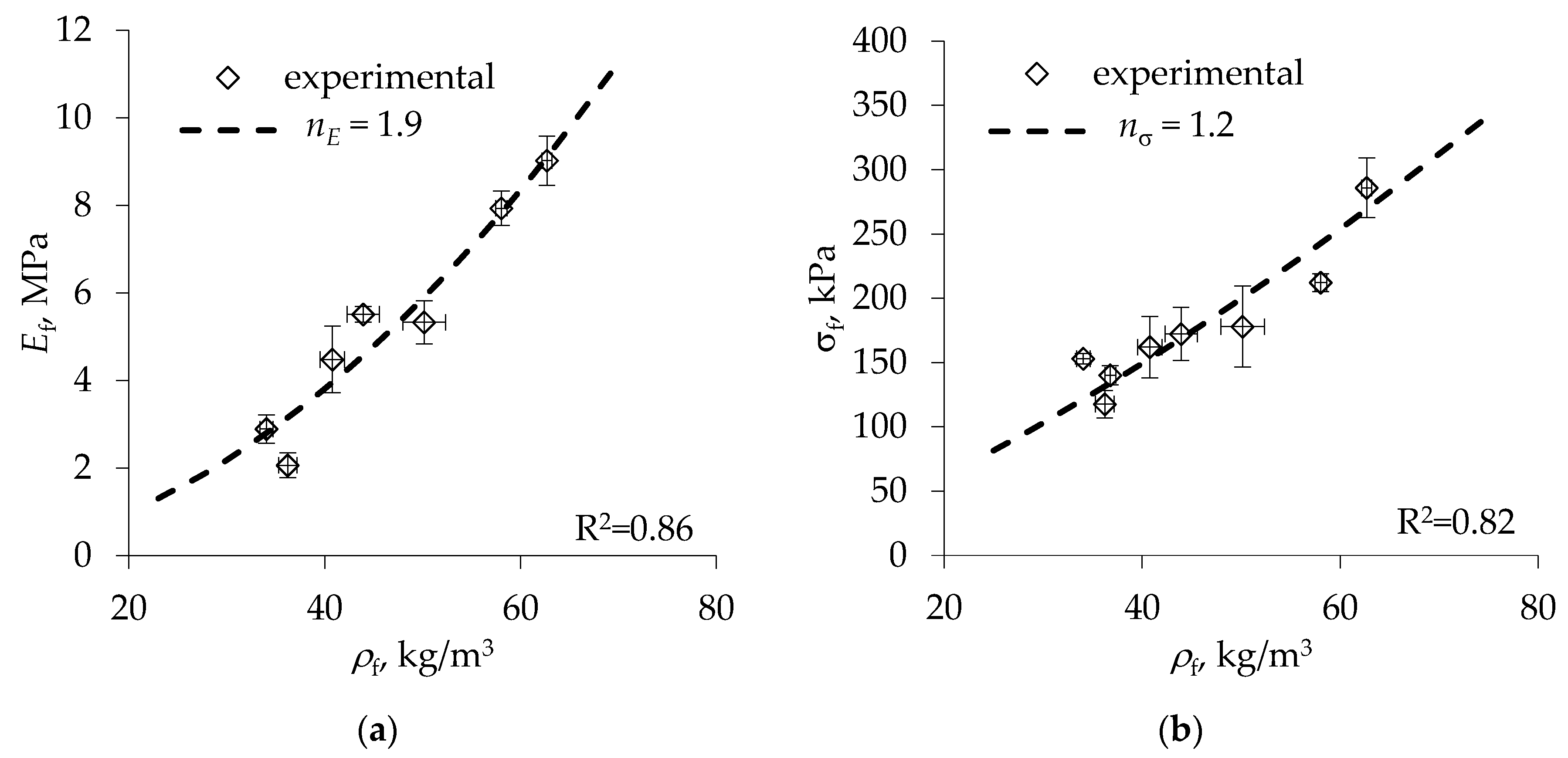
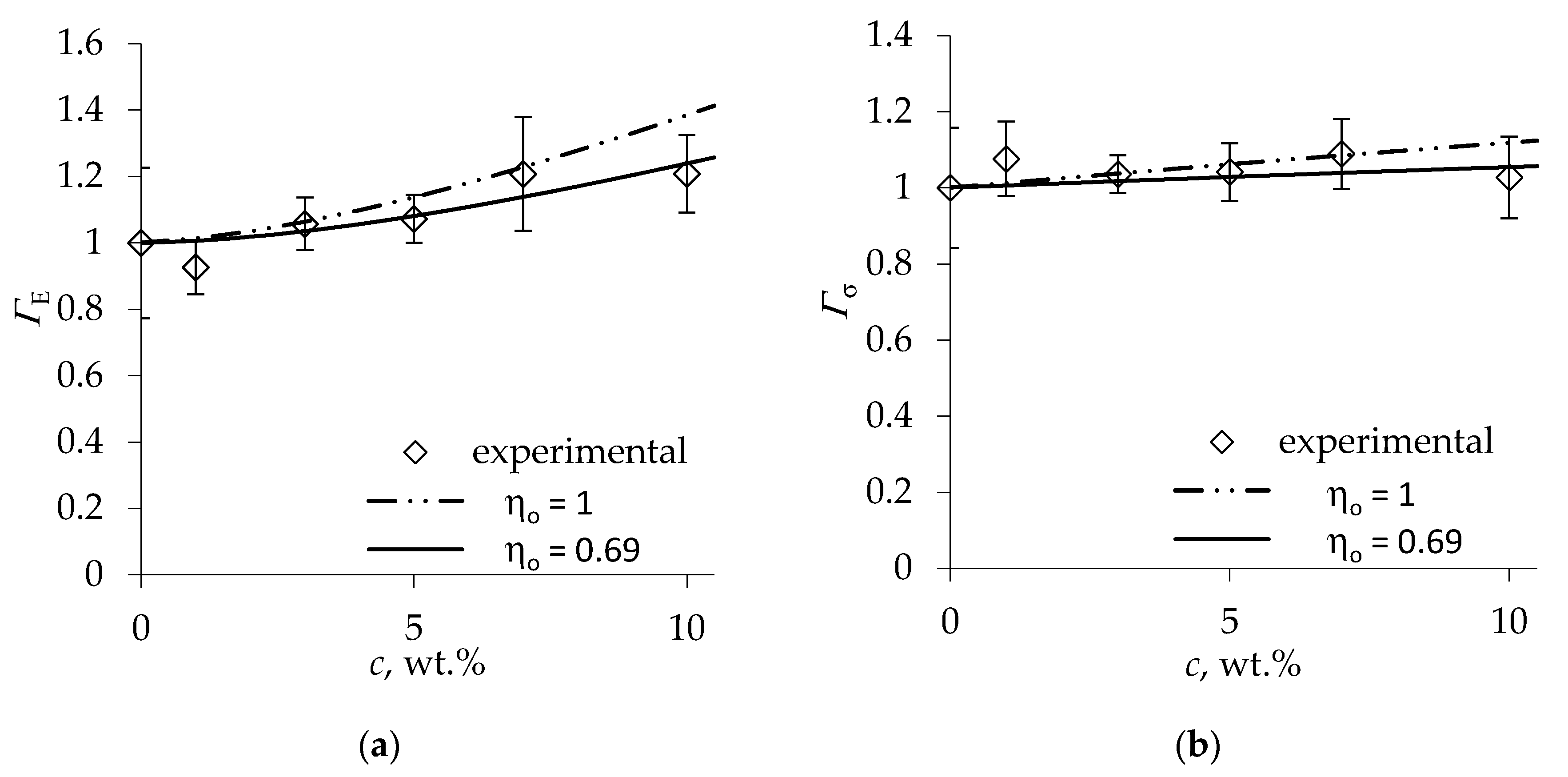
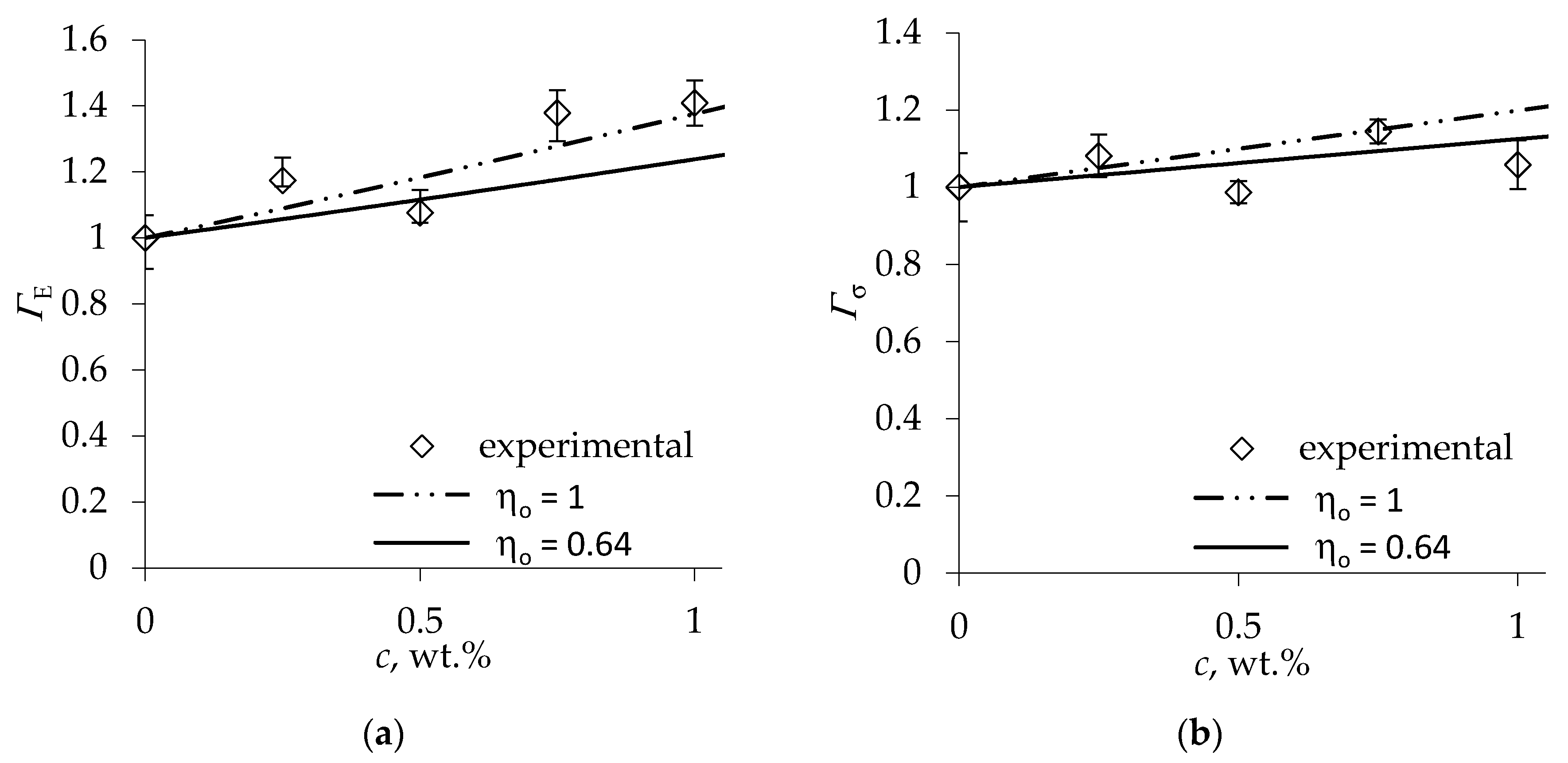
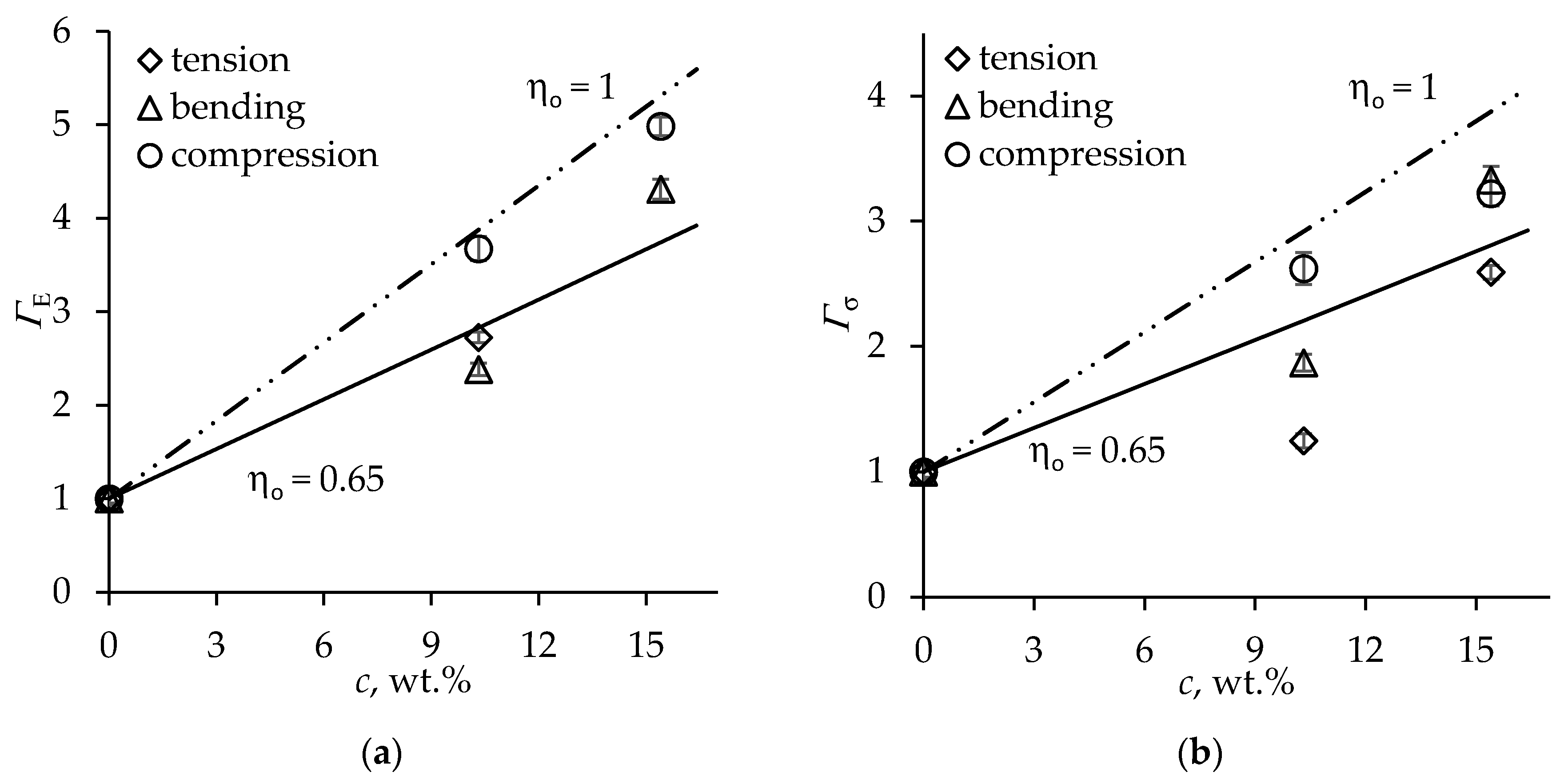
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gama, N.V.; Ferreira, A.; Barros-Timmons, A. Polyurethane Foams: Past, Present, and Future. Materials 2018, 11, 1841. [Google Scholar] [CrossRef] [PubMed]
- Chiacchiarelli, L. Sustainable, nanostructured, and bio-based polyurethanes for energy-efficient sandwich structures applied to the construction industry. In Biomass, Biopolymer-Based Materials, and Bioenergy; Elsevier BV: Amsterdam, The Netherlands, 2019; pp. 135–160. [Google Scholar]
- Joshi, M.; Adak, B.; Butola, B.S. Polyurethane nanocomposite based gas barrier films, membranes and coatings: A review on synthesis, characterization and potential applications. Prog. Mater. Sci. 2018, 97, 230–282. [Google Scholar] [CrossRef]
- Stirna, U.; Beverte, I.; Yakushin, V.; Cabulis, U. Mechanical properties of rigid polyurethane foams at room and cryogenic temperatures. J. Cell. Plast. 2011, 47, 337–355. [Google Scholar] [CrossRef]
- Saha, M.; Kabir, E.; Jeelani, S. Enhancement in thermal and mechanical properties of polyurethane foam infused with nanoparticles. Mater. Sci. Eng. A 2008, 479, 213–222. [Google Scholar] [CrossRef]
- Cabulis, U.; Sevastyanova, I.; Andersons, J.; Beverte, I. Rapeseed oil-based rigid polyisocyanurate foams modified with nanoparticles of various type. Polimery 2014, 59, 207–212. [Google Scholar] [CrossRef]
- Dwan’Isa, J.-P.L.; Mohanty, A.; Misra, M.; Drzal, L.T.; Kazemizadeh, M. Biobased polyurethane and its composite with glass fiber. J. Mater. Sci. 2004, 39, 2081–2087. [Google Scholar] [CrossRef]
- Kim, S.H.; Park, H.C.; Jeong, H.M.; Kim, B.K. Glass fiber reinforced rigid polyurethane foams. J. Mater. Sci. 2010, 45, 2675–2680. [Google Scholar] [CrossRef]
- Yakushin, V.; Stirna, U.; Bel’Kova, L.; Deme, L.; Sevastyanova, I. Properties of rigid polyurethane foams filled with milled carbon fibers. Mech. Compos. Mater. 2011, 46, 679–688. [Google Scholar] [CrossRef]
- Moon, R.J.; Martini, A.; Nairn, J.; Simonsen, J.; Youngblood, J.P. Cellulose nanomaterials review: Structure, properties and nanocomposites. Chem. Soc. Rev. 2011, 40, 3941. [Google Scholar] [CrossRef]
- Berglund, L.A.; Peijs, T. Cellulose Biocomposites—From Bulk Moldings to Nanostructured Systems. MRS Bull. 2010, 35, 201–207. [Google Scholar] [CrossRef]
- Siró, I.; Plackett, D. Microfibrillated cellulose and new nanocomposite materials: A review. Cellulose 2010, 17, 459–494. [Google Scholar] [CrossRef]
- Turk, J.; Oven, P.; Poljanšek, I.; Lešek, A.; Knez, F.; Rebec, K.M. Evaluation of an environmental profile comparison for nanocellulose production and supply chain by applying different life cycle assessment methods. J. Clean. Prod. 2020, 247, 119107. [Google Scholar] [CrossRef]
- Arvidsson, R.; Nguyen, D.; Svanström, M. Life Cycle Assessment of Cellulose Nanofibrils Production by Mechanical Treatment and Two Different Pretreatment Processes. Environ. Sci. Technol. 2015, 49, 6881–6890. [Google Scholar] [CrossRef] [PubMed]
- Hussain, S.; Kortschot, M. Polyurethane foam mechanical reinforcement by low-aspect ratio micro-crystalline cellulose and glass fibres. J. Cell. Plast. 2014, 51, 59–73. [Google Scholar] [CrossRef]
- Mosiewicki, M.A.; Rojek, P.; Michałowski, S.; Aranguren, M.I.; Prociak, A. Rapeseed oil-based polyurethane foams modified with glycerol and cellulose micro/nanocrystals. J. Appl. Polym. Sci. 2014, 132, 41602. [Google Scholar] [CrossRef]
- Kurańska, M.; Prociak, A.; Michalowski, S.; Cabulis, U.; Kirpluks, M. Microcellulose as a natural filler in polyurethane foams based on the biopolyol from rapeseed oil. Polimery 2016, 61, 625–632. [Google Scholar] [CrossRef]
- Shen, J.; Han, X.; Lee, L.J. Nanoscaled Reinforcement of Polystyrene Foams using Carbon Nanofibers. J. Cell. Plast. 2006, 42, 105–126. [Google Scholar] [CrossRef]
- Okamoto, M.; Nam, P.H.; Maiti, P.; Kotaka, T.; Nakayama, T.; Takada, M.; Ohshima, M.; Usuki, A.; Hasegawa, N.; Okamoto, H. Biaxial Flow-Induced Alignment of Silicate Layers in Polypropylene/Clay Nanocomposite Foam. Nano Lett. 2001, 1, 503–505. [Google Scholar] [CrossRef]
- Nam, P.H.; Maiti, P.; Okamoto, M.; Kotaka, T.; Nakayama, T.; Takada, M.; Ohshima, M.; Usuki, A.; Hasegawa, N.; Okamoto, H. Foam processing and cellular structure of polypropylene/clay nanocomposites. Polym. Eng. Sci. 2002, 42, 1907–1918. [Google Scholar] [CrossRef]
- Strauss, W.; D’Souza, N. Supercritical CO2 Processed Polystyrene Nanocomposite Foams. J. Cell. Plast. 2004, 40, 229–241. [Google Scholar] [CrossRef]
- Shaayegan, V.; Ameli, A.; Wang, S.; Park, C.B. Experimental observation and modeling of fiber rotation and translation during foam injection molding of polymer composites. Compos. Part A Appl. Sci. Manuf. 2016, 88, 67–74. [Google Scholar] [CrossRef]
- Wang, S.; Ameli, A.; Shaayegan, V.; Kazemi, Y.; Huang, Y.; Naguib, H.E.; Park, C.B. Modelling of Rod-Like Fillers’ Rotation and Translation near Two Growing Cells in Conductive Polymer Composite Foam Processing. Polymers 2018, 10, 261. [Google Scholar] [CrossRef] [PubMed]
- Gimenez, R.B.; Leonardi, L.; Cerrutti, P.; Amalvy, J.; Chiacchiarelli, L.M. Improved specific thermomechanical properties of polyurethane nanocomposite foams based on castor oil and bacterial nanocellulose. J. Appl. Polym. Sci. 2017, 134, 44982. [Google Scholar] [CrossRef]
- Septevani, A.A.; Evans, D.A.C.; Hosseinmardi, A.; Martin, D.J.; Simonsen, J.; Conley, J.F.; Annamalai, P.K. Atomic Layer Deposition of Metal Oxide on Nanocellulose for Enabling Microscopic Characterization of Polymer Nanocomposites. Small 2018, 14, 1803439. [Google Scholar] [CrossRef] [PubMed]
- Shishkina, O.; Lomov, S.V.; Verpoest, I.; Gorbatikh, L. Modeling of elastic properties of cell-wall material in nanoclay-reinforced foams. J. Cell. Plast. 2015, 52, 107–130. [Google Scholar] [CrossRef]
- Andersons, J.; Kirpluks, M.; Cabulis, U. Modelling the Strength of Cellulose Nanofiber-Filled Rigid Low-Density PU Foams. Key Eng. Mater. 2019, 827, 159–164. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Lobos, J.; Velankar, S.S. How much do nanoparticle fillers improve the modulus and strength of polymer foams? J. Cell. Plast. 2014, 52, 57–88. [Google Scholar] [CrossRef]
- Siegmann, A.; Kenig, S.; Alperstein, D.; Narkis, M. Mechanical behavior of reinforced polyurethane foams. Polym. Compos. 1983, 4, 113–119. [Google Scholar] [CrossRef]
- Hamilton, A.R.; Thomsen, O.T.; Madaleno, L.A.; Jensen, L.R.; Rauhe, J.C.M.; Pyrz, R. Evaluation of the anisotropic mechanical properties of reinforced polyurethane foams. Compos. Sci. Technol. 2013, 87, 210–217. [Google Scholar] [CrossRef]
- Reitz, D.; Schuetz, M.; Glicksman, L. A Basic Study of Aging of Foam Insulation. J. Cell. Plast. 1984, 20, 104–113. [Google Scholar] [CrossRef]
- Ahern, A.; Verbist, G.; Weaire, D.; Phelan, R.; Fleurent, H. The conductivity of foams: A generalisation of the electrical to the thermal case. Colloids Surf. A Physicochem. Eng. Asp. 2005, 263, 275–279. [Google Scholar] [CrossRef]
- Andersons, J.; Kirpluks, M.; Stiebra, L.; Cabulis, U. Anisotropy of the stiffness and strength of rigid low-density closed-cell polyisocyanurate foams. Mater. Des. 2016, 92, 836–845. [Google Scholar] [CrossRef]
- Nairn, J.A. Generalized Shear-Lag Analysis Including Imperfect Interfaces. Adv. Compos. Lett. 2004, 13, 263–274. [Google Scholar] [CrossRef]
- Hine, P.; Parveen, B.; Brands, D.; Caton-Rose, F. Validation of the modified rule of mixtures using a combination of fibre orientation and fibre length measurements. Compos. Part A Appl. Sci. Manuf. 2014, 64, 70–78. [Google Scholar] [CrossRef]
- Fukuda, H.; Chou, T.-W. A probabilistic theory of the strength of short-fibre composites with variable fibre length and orientation. J. Mater. Sci. 1982, 17, 1003–1011. [Google Scholar] [CrossRef]
- Andersons, J.; Spārniņš, E.; Joffe, R. Stiffness and strength of flax fiber/polymer matrix composites. Polym. Compos. 2006, 27, 221–229. [Google Scholar] [CrossRef]
- Dafalias, Y.F. Orientation distribution function in non-affine rotations. J. Mech. Phys. Solids 2001, 49, 2493–2516. [Google Scholar] [CrossRef]
- Eichhorn, S.J.; Young, R.J. The Young’s modulus of a microcrystalline cellulose. Cellulose 2001, 8, 197–207. [Google Scholar] [CrossRef]
- Roberts, R.J.; Rowe, R.C.; York, P. The Poisson’s ratio of microcrystalline cellulose. Int. J. Pharm. 1994, 105, 177–180. [Google Scholar] [CrossRef]
- Li, Y.; Ren, H.; Ragauskas, A.J. Rigid polyurethane foam/cellulose whisker nanocomposites: Preparation, characterization, and properties. J. Nanosci. Nanotechnol. 2011, 11, 6904–6911. [Google Scholar] [CrossRef]
- Luo, X.; Mohanty, A.; Misra, M. Water-Blown Rigid Biofoams from Soy-Based Biopolyurethane and Microcrystalline Cellulose. J. Am. Oil Chem. Soc. 2012, 89, 2057–2065. [Google Scholar] [CrossRef]
- Andersons, J.; Filipova, I.; Kirpluks, M.; Cabulis, U. Evaluation of the Apparent Interfacial Shear Strength of Nanocellulose/PVA Composites. Key Eng. Mater. 2018, 774, 54–59. [Google Scholar] [CrossRef]
- Leng, W.; Pan, B. Thermal Insulating and Mechanical Properties of Cellulose Nanofibrils Modified Polyurethane Foam Composite as Structural Insulated Material. Forests 2019, 10, 200. [Google Scholar] [CrossRef]
- Li, Y.; Ragauskas, A.J. Ethanol organosolv lignin-based rigid polyurethane foam reinforced with cellulose nanowhiskers. RSC Adv. 2012, 2, 3347. [Google Scholar] [CrossRef]
- Chen, P.; Ogawa, Y.; Nishiyama, Y.; Ismail, A.E.; Mazeau, K. Linear, non-linear and plastic bending deformation of cellulose nanocrystals. Phys. Chem. Chem. Phys. 2016, 18, 19880–19887. [Google Scholar] [CrossRef] [PubMed]
- Araki, J.; Wada, M.; Kuga, S.; Okano, T. Flow properties of microcrystalline cellulose suspension prepared by acid treatment of native cellulose. Colloids Surf. A Physicochem. Eng. Asp. 1998, 142, 75–82. [Google Scholar] [CrossRef]
- Zhai, L.; Kim, H.C.; Kim, J.W.; Kang, J.; Kim, J. Elastic moduli of cellulose nanofibers isolated from various cellulose resources by using aqueous counter collision. Cellulose 2018, 25, 4261–4268. [Google Scholar] [CrossRef]
- Saito, T.; Kuramae, R.; Wohlert, J.; Berglund, L.A.; Isogai, A. An Ultrastrong Nanofibrillar Biomaterial: The Strength of Single Cellulose Nanofibrils Revealed via Sonication-Induced Fragmentation. Biomacromolecules 2012, 14, 248–253. [Google Scholar] [CrossRef]

| Fiber Loading, wt % | Cell Length, μm | Cell Width, μm | Shape Anisotropy R |
|---|---|---|---|
| 0 | 745 (130) 1 | 480 (73) | 1.56 (0.18) |
| 1 | 567 (104) | 364 (55) | 1.56 (0.17) |
| 3 | 514 (166) | 345 (90) | 1.48 (0.18) |
| 5 | 565 (130) | 362 (65) | 1.56 (0.18) |
| 7 | 502 (105) | 333 (56) | 1.51 (0.17) |
| 10 | 498 (149) | 337 (82) | 1.47 (0.16) |
| Fiber Loading, wt % | Foam Density, kg/m3 | Young’s Modulus, MPa | Tensile Strength, kPa | Strain at Failure, % |
|---|---|---|---|---|
| 0 | 33.1 (1.3) 1 | 3.36 (0.76) | 127 (20) | 6.6 (0.3) |
| 1 | 33.0 (0.5) | 3.10 (0.27) | 137 (12) | 7.6 (0.6) |
| 3 | 34.3 (0.5) | 3.90 (0.29) | 142 (7) | 6.4 (1.0)) |
| 5 | 33.4 (0.5) | 3.66 (0.25) | 134 (12) | 5.9 (0.4) |
| 7 | 35.6 (0.7) | 4.74 (0.67) | 152 (13) | 5.6 (0.7) |
| 10 | 35.8 (0.5) | 4.86 (0.47) | 148 (16) | 5.0 (0.6) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andersons, J.; Kirpluks, M.; Cabulis, U. Reinforcement Efficiency of Cellulose Microfibers for the Tensile Stiffness and Strength of Rigid Low-Density Polyurethane Foams. Materials 2020, 13, 2725. https://doi.org/10.3390/ma13122725
Andersons J, Kirpluks M, Cabulis U. Reinforcement Efficiency of Cellulose Microfibers for the Tensile Stiffness and Strength of Rigid Low-Density Polyurethane Foams. Materials. 2020; 13(12):2725. https://doi.org/10.3390/ma13122725
Chicago/Turabian StyleAndersons, Jānis, Mikelis Kirpluks, and Ugis Cabulis. 2020. "Reinforcement Efficiency of Cellulose Microfibers for the Tensile Stiffness and Strength of Rigid Low-Density Polyurethane Foams" Materials 13, no. 12: 2725. https://doi.org/10.3390/ma13122725
APA StyleAndersons, J., Kirpluks, M., & Cabulis, U. (2020). Reinforcement Efficiency of Cellulose Microfibers for the Tensile Stiffness and Strength of Rigid Low-Density Polyurethane Foams. Materials, 13(12), 2725. https://doi.org/10.3390/ma13122725






