Magnetic Induction Tomography Spectroscopy for Structural and Functional Characterization in Metallic Materials
Abstract
1. Introduction
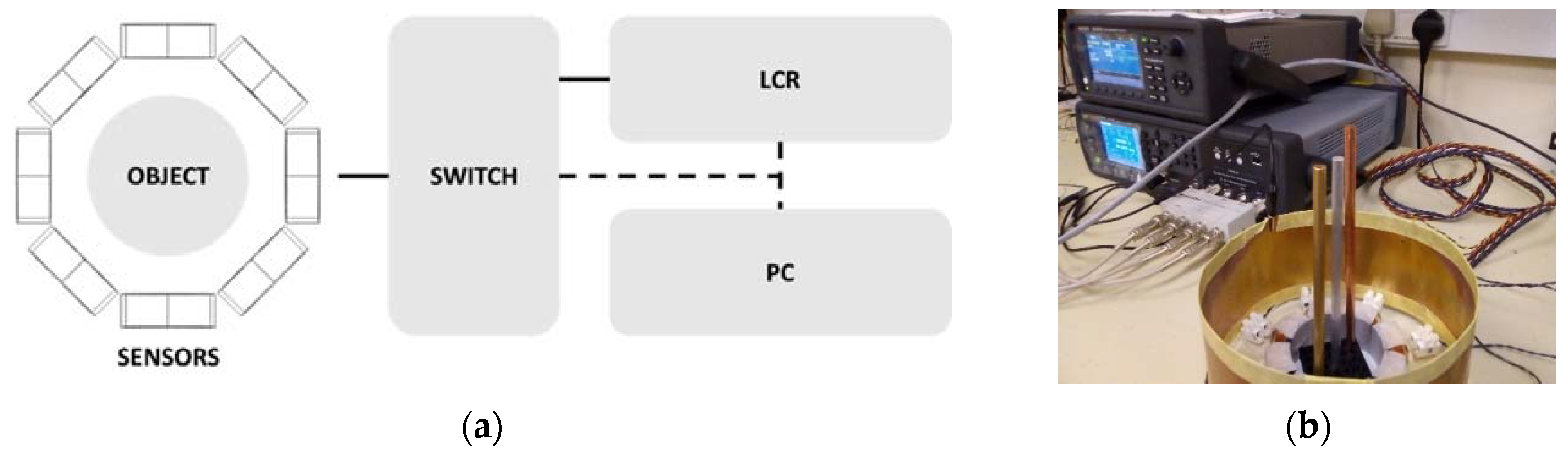
2. Experimental Setup
3. Sensor Modelling
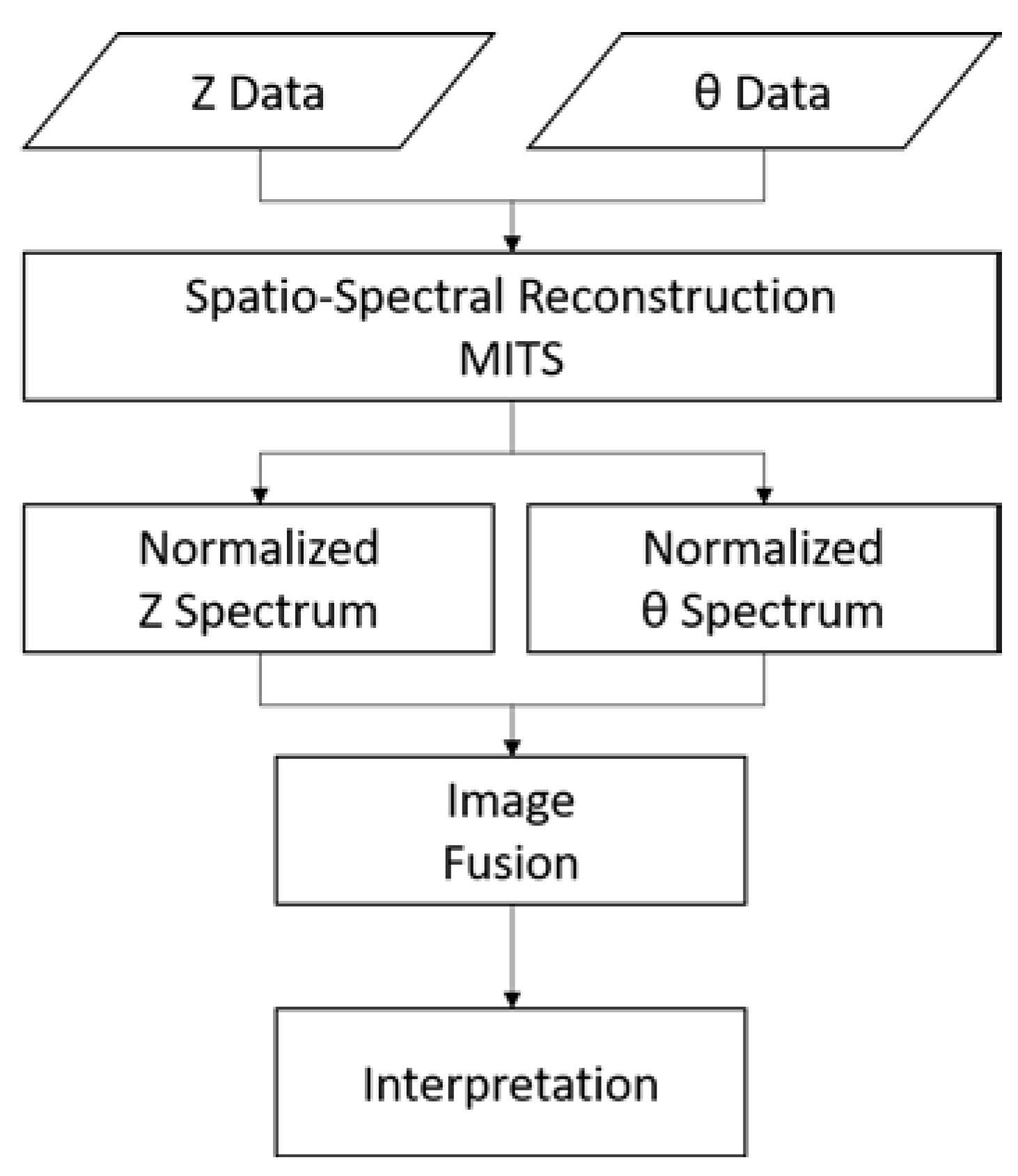
4. Spatio-Spectral Image Reconstruction Algorithm
5. Results and Analysis
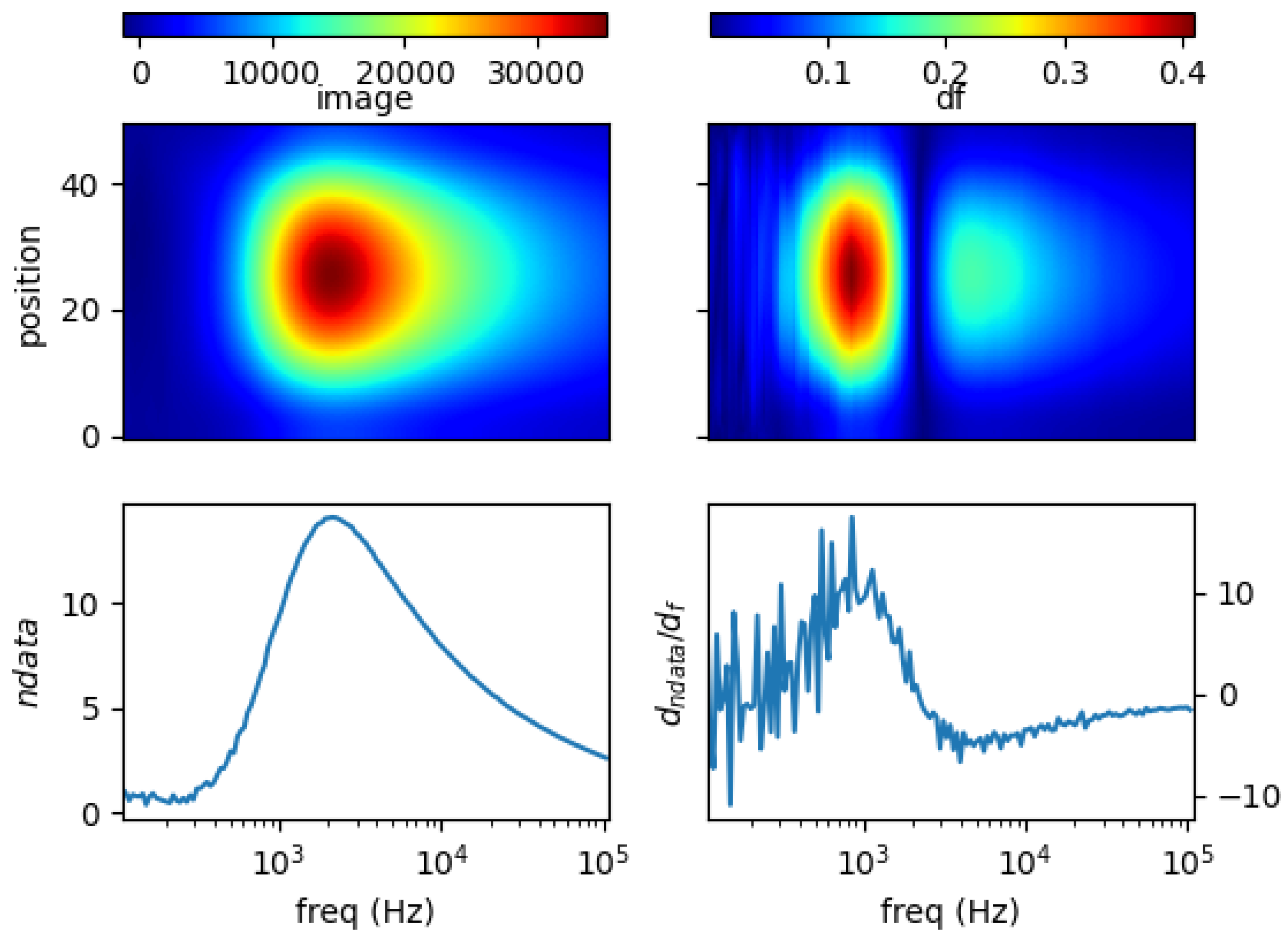
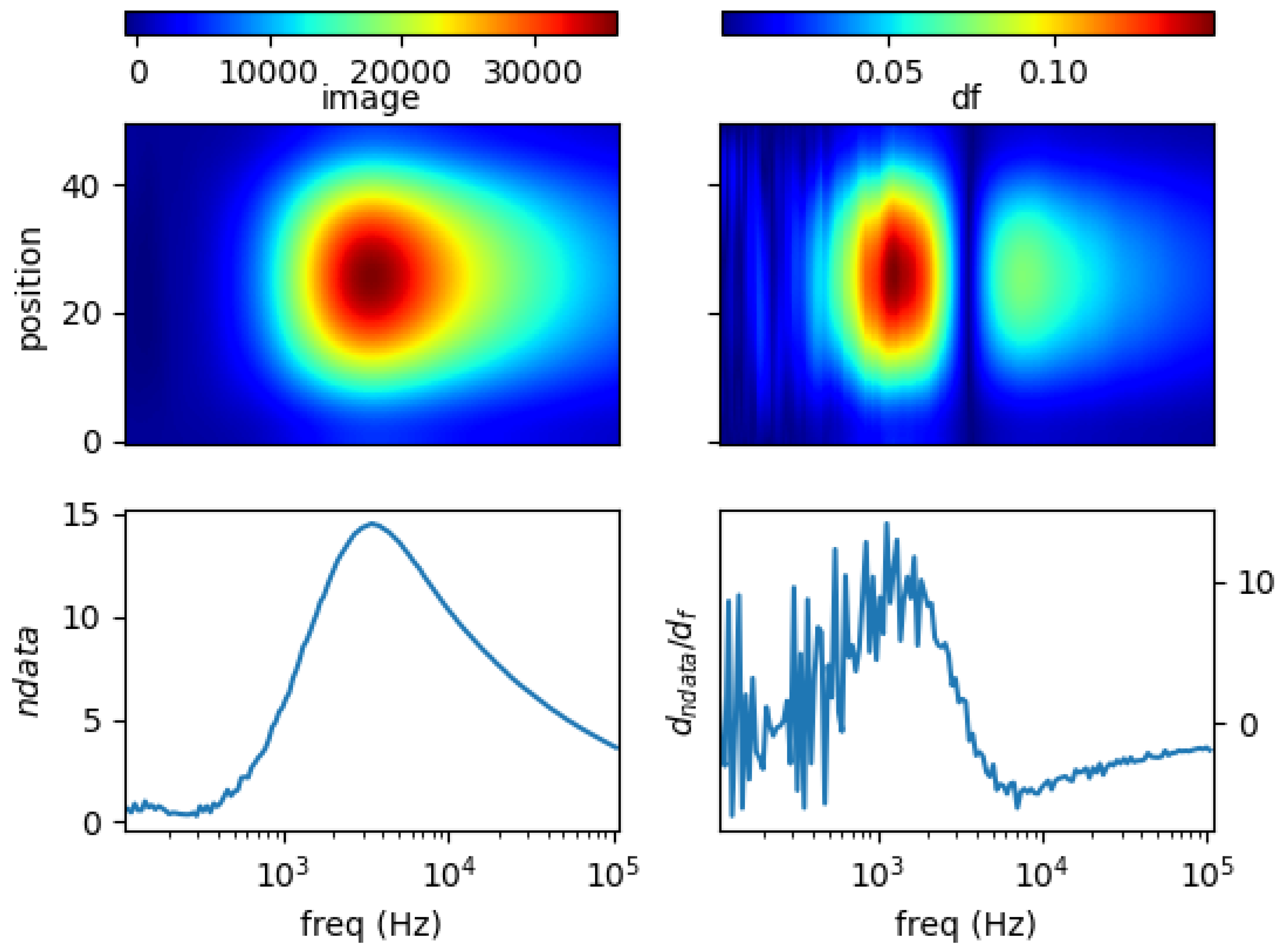
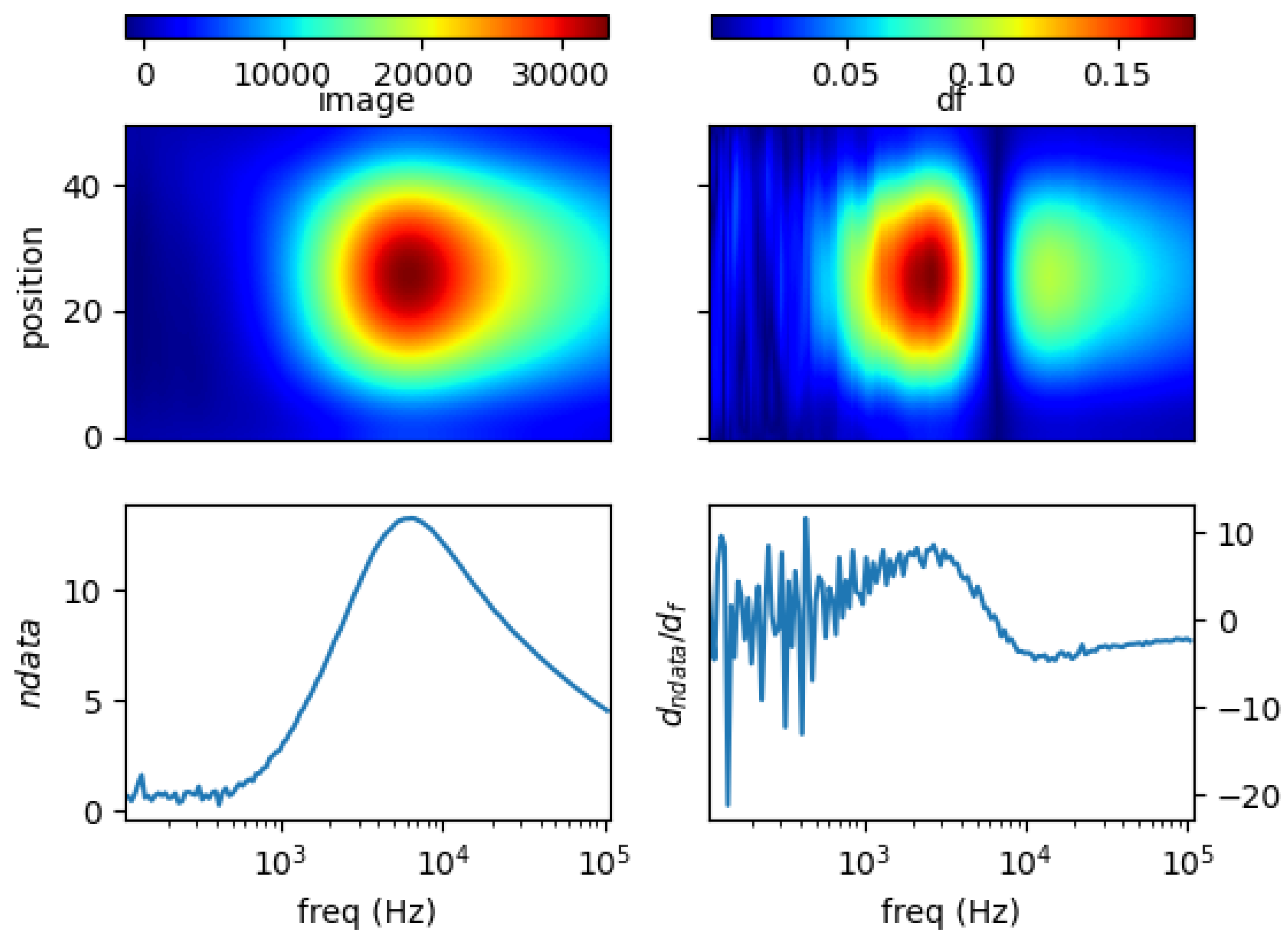
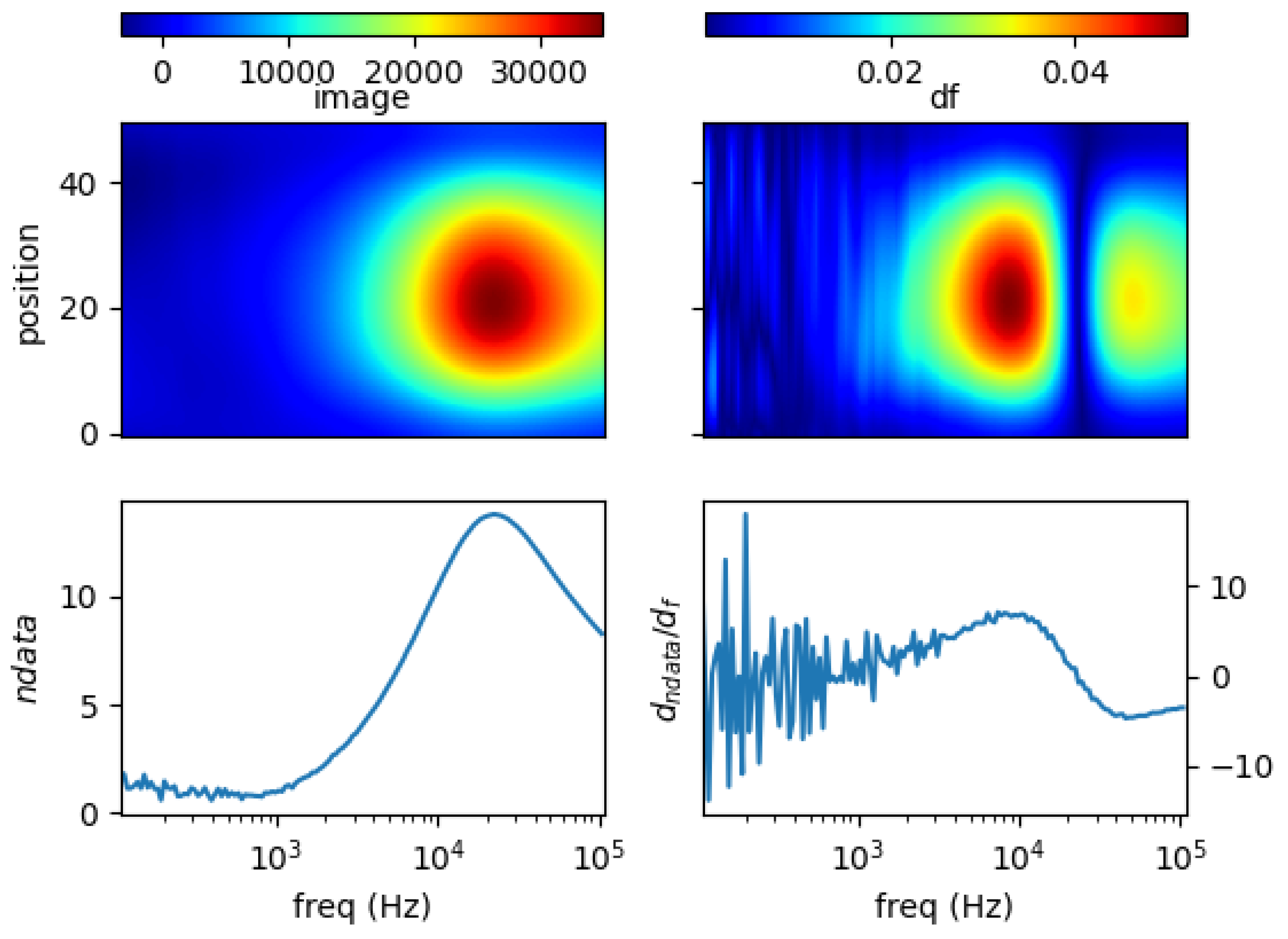
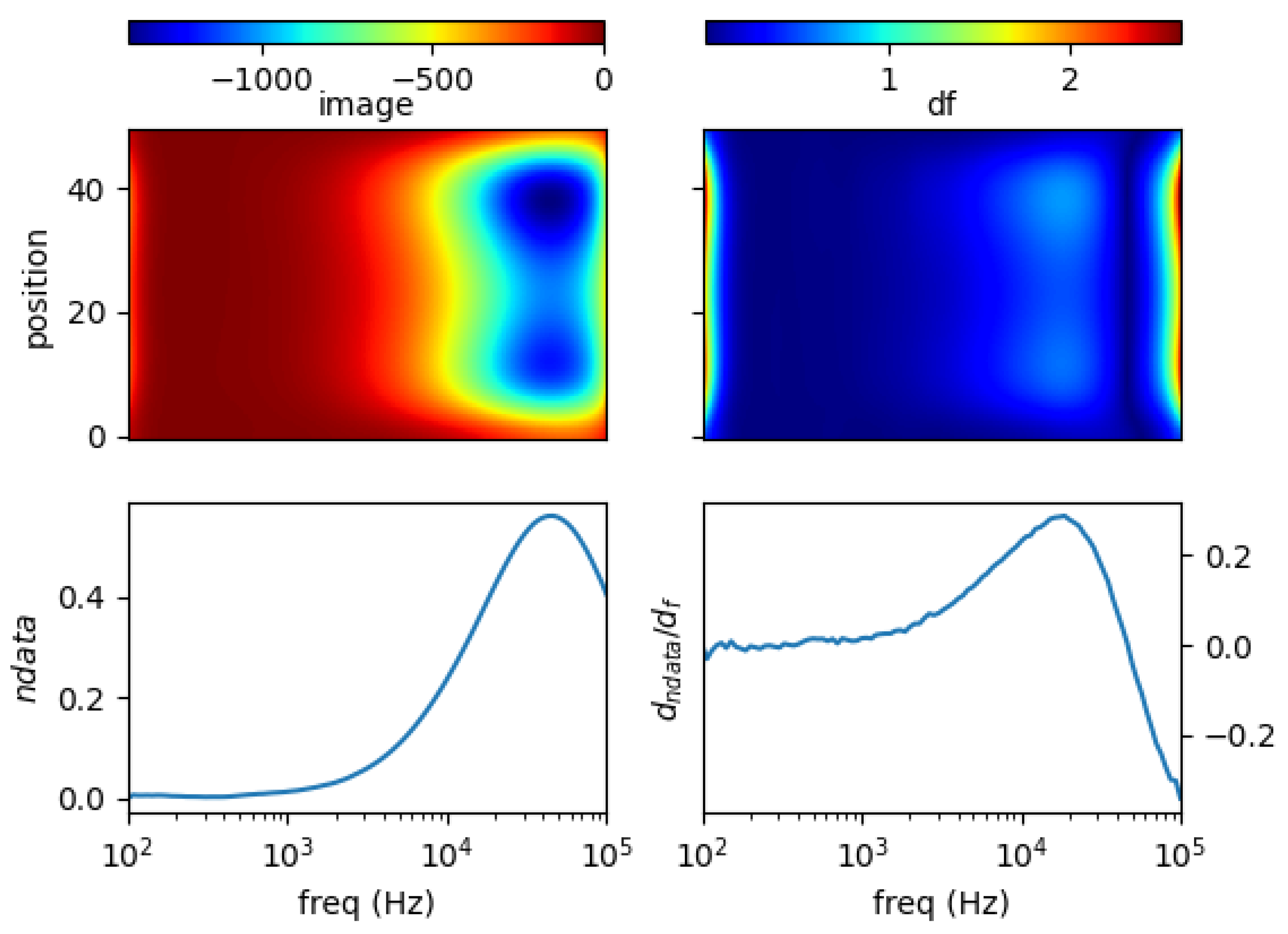
5.1. Single Metal Sample
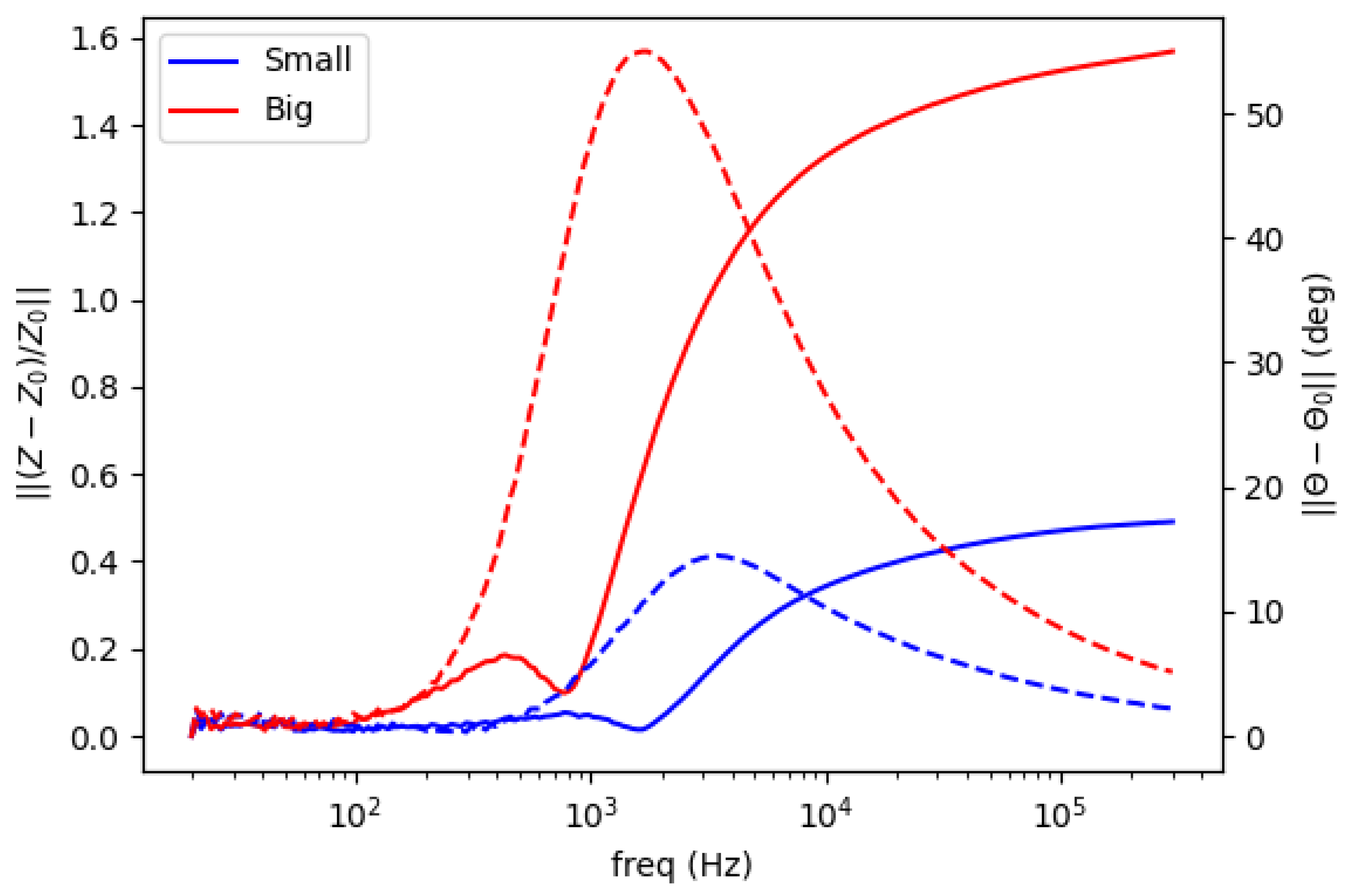
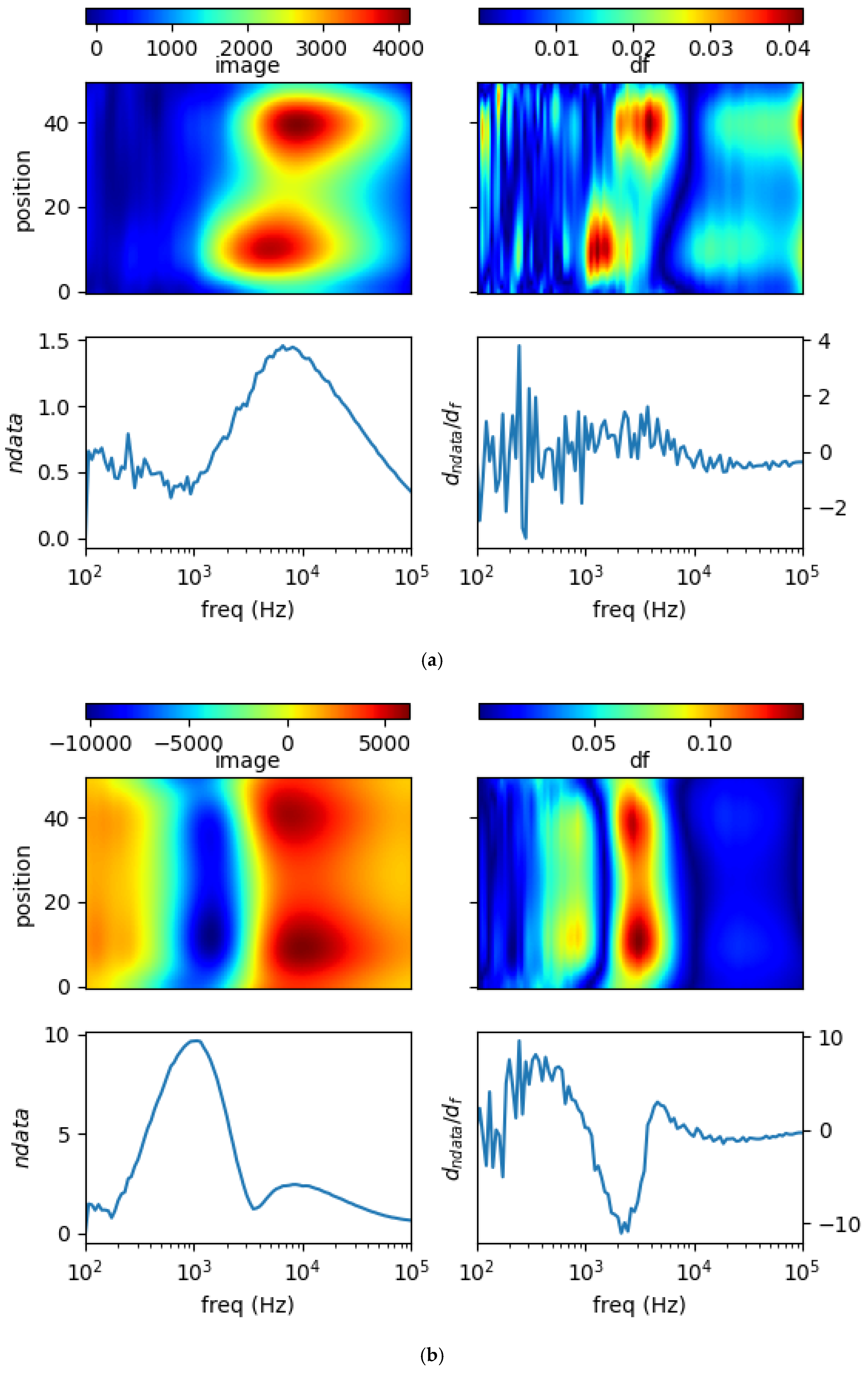
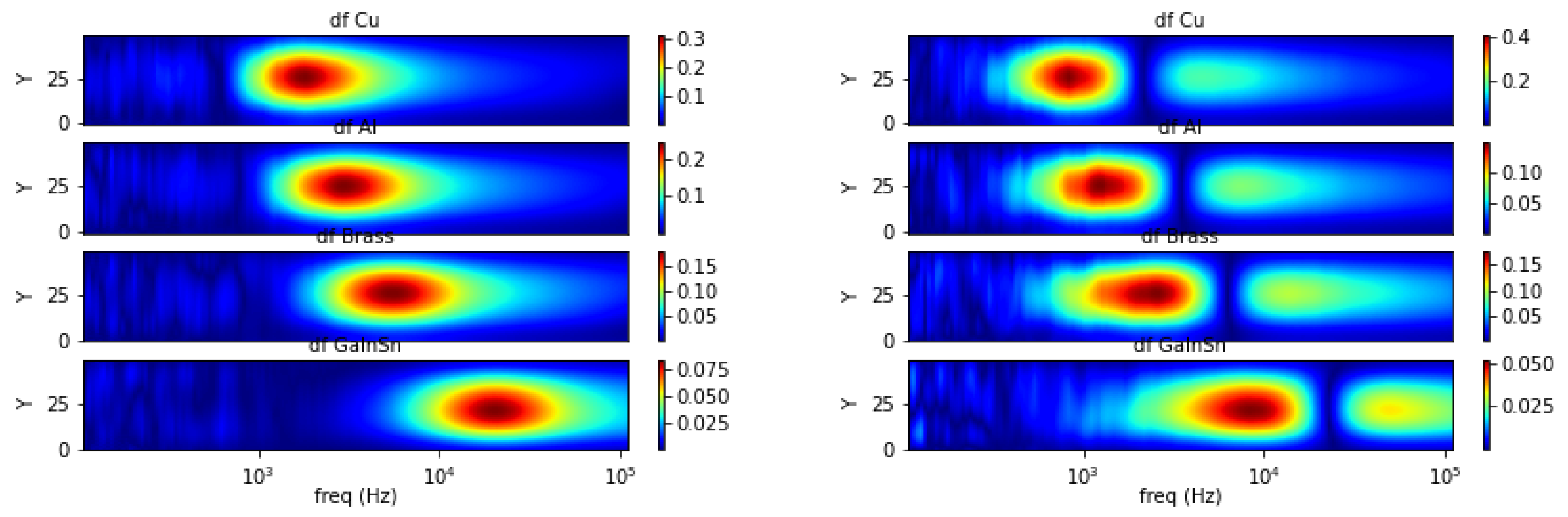
5.2. Different Samples at Different Locations
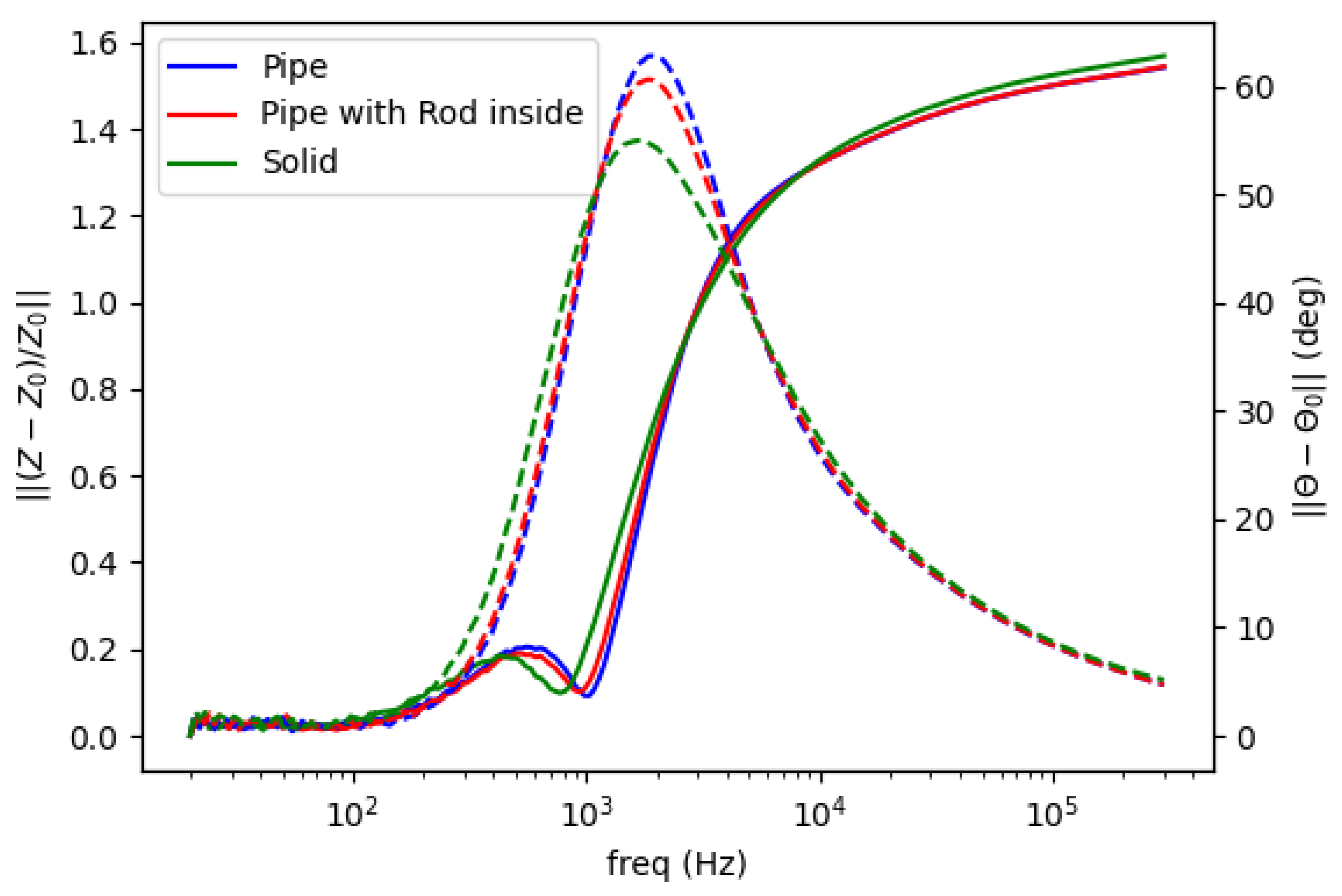
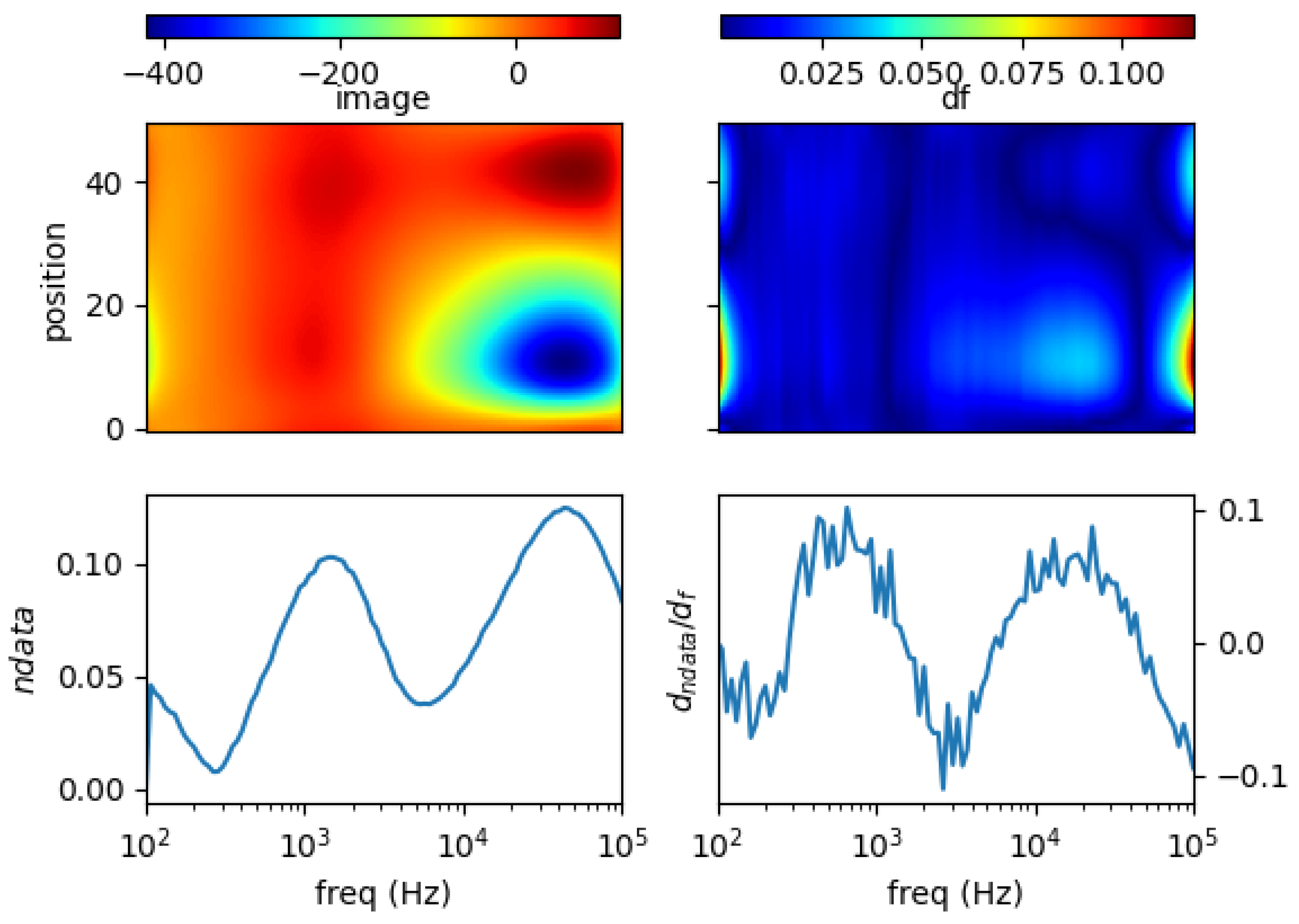
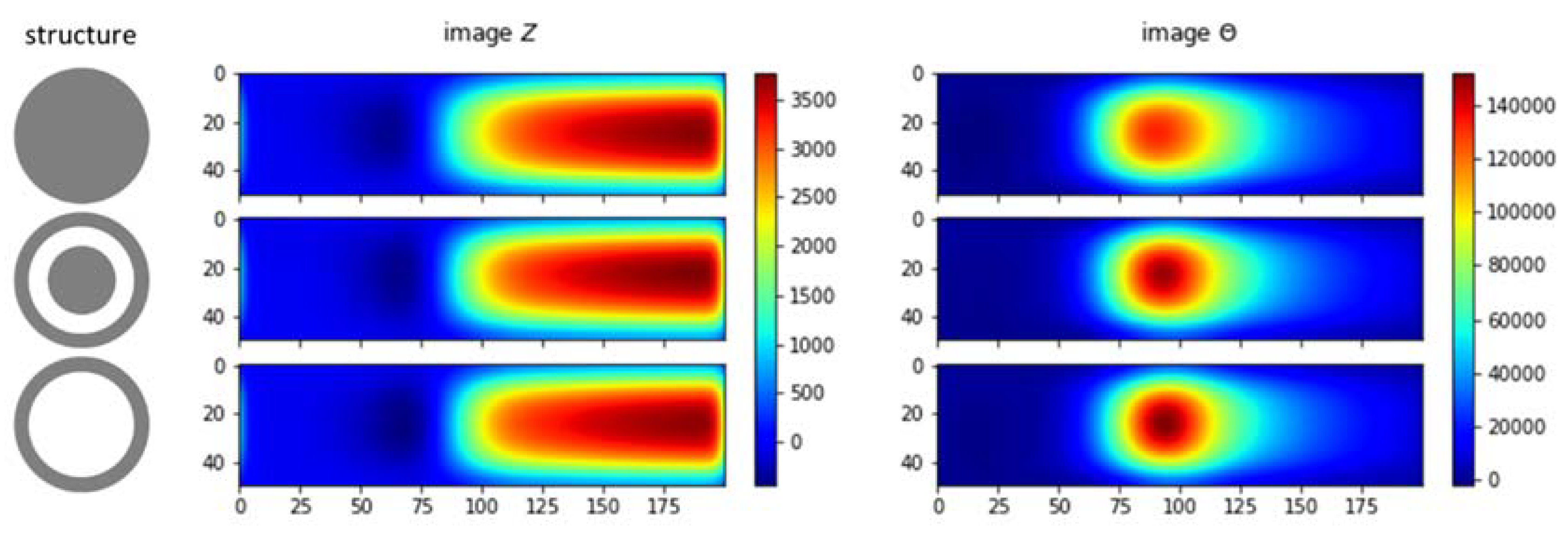
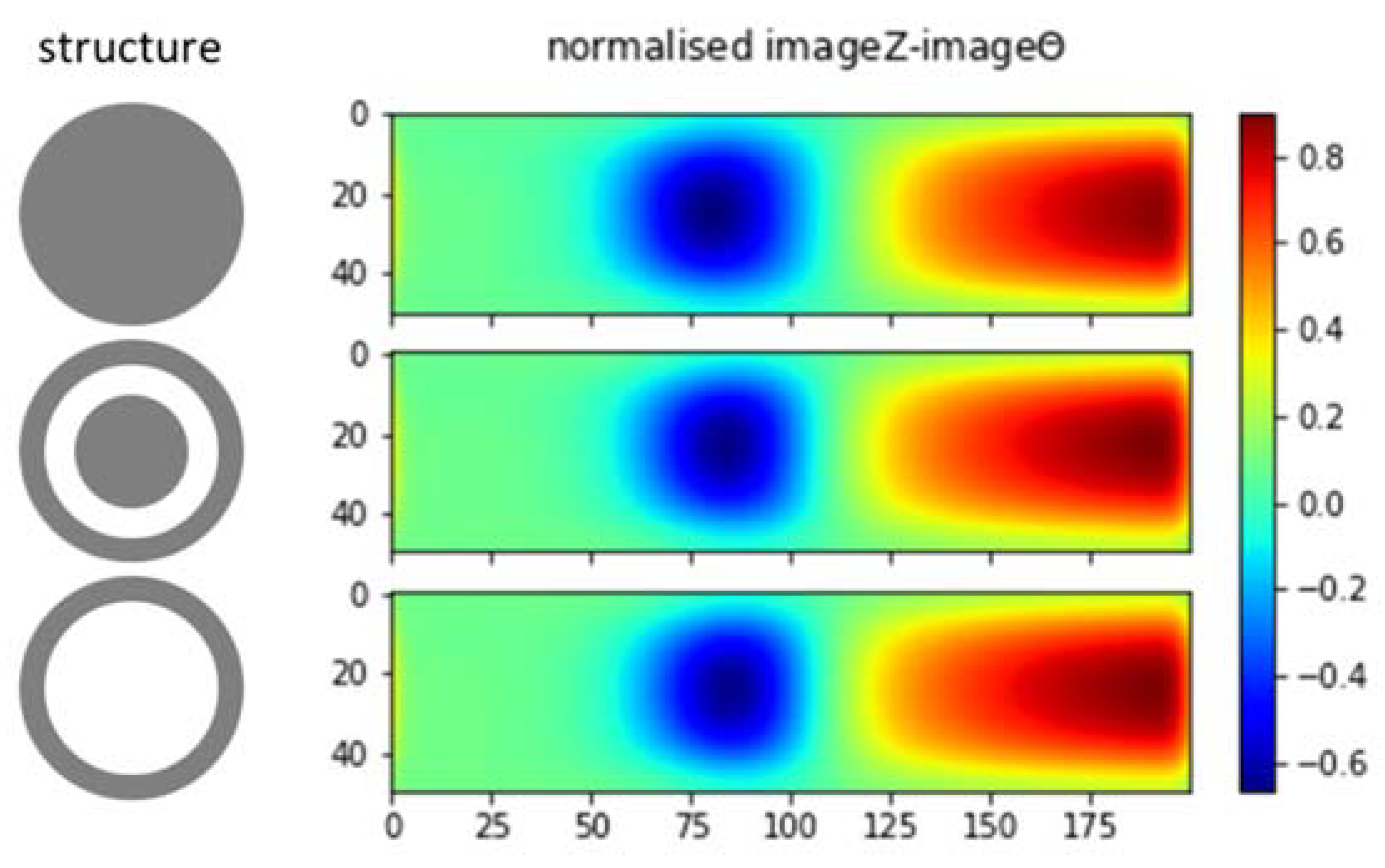
5.3. Non-Conductive Inclusion in Conductive Liquid
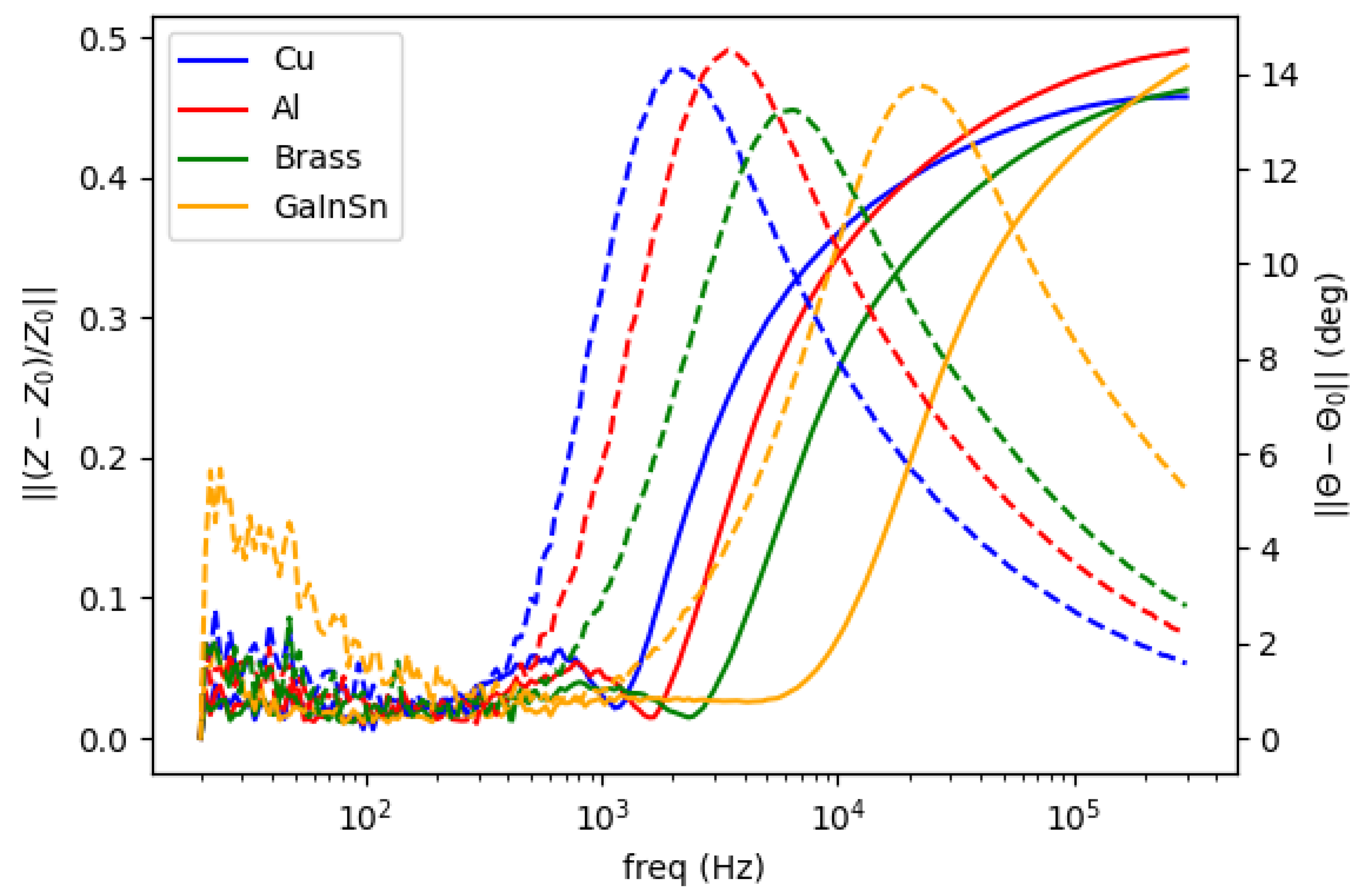
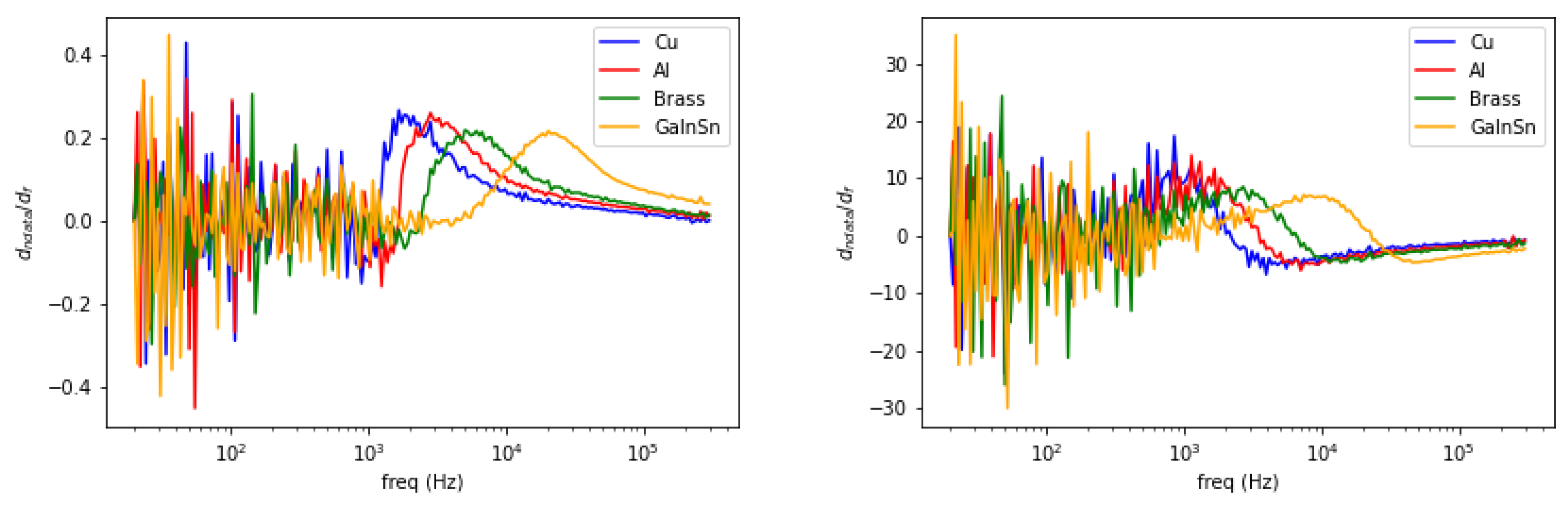
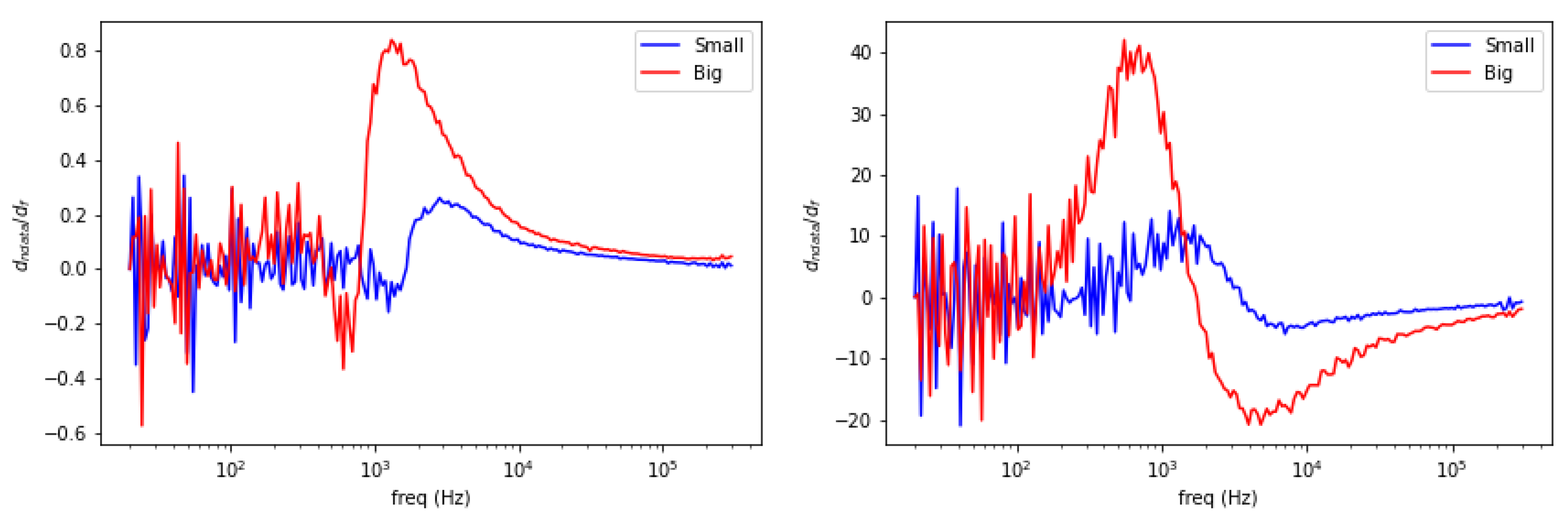
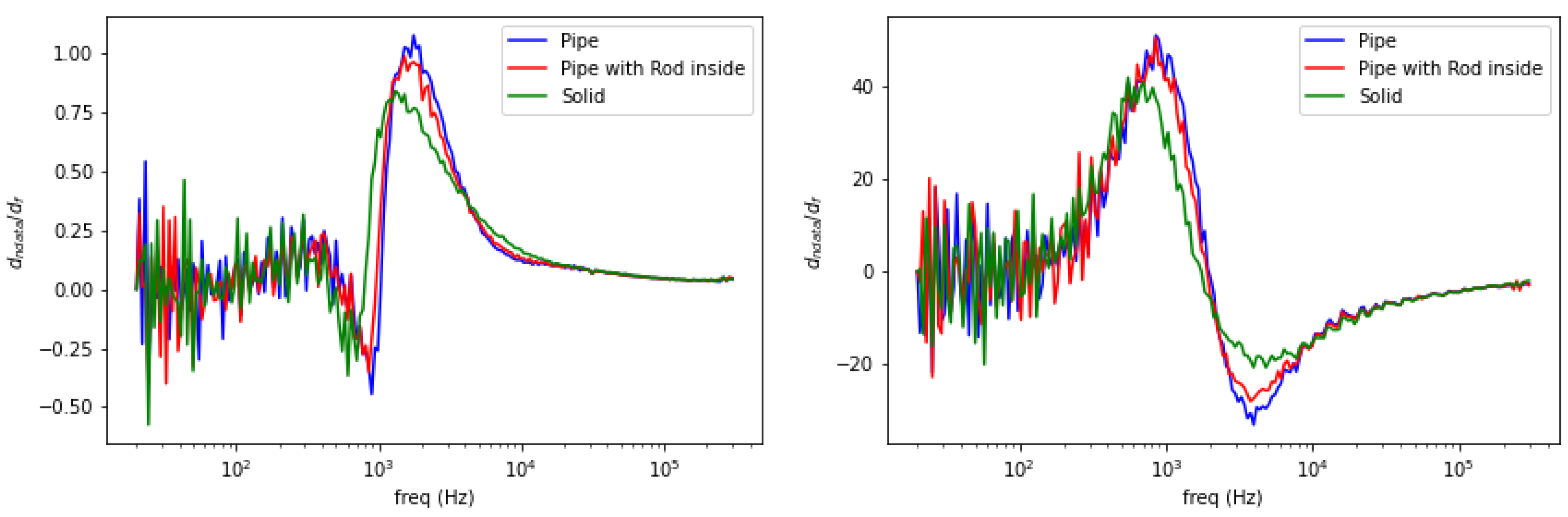
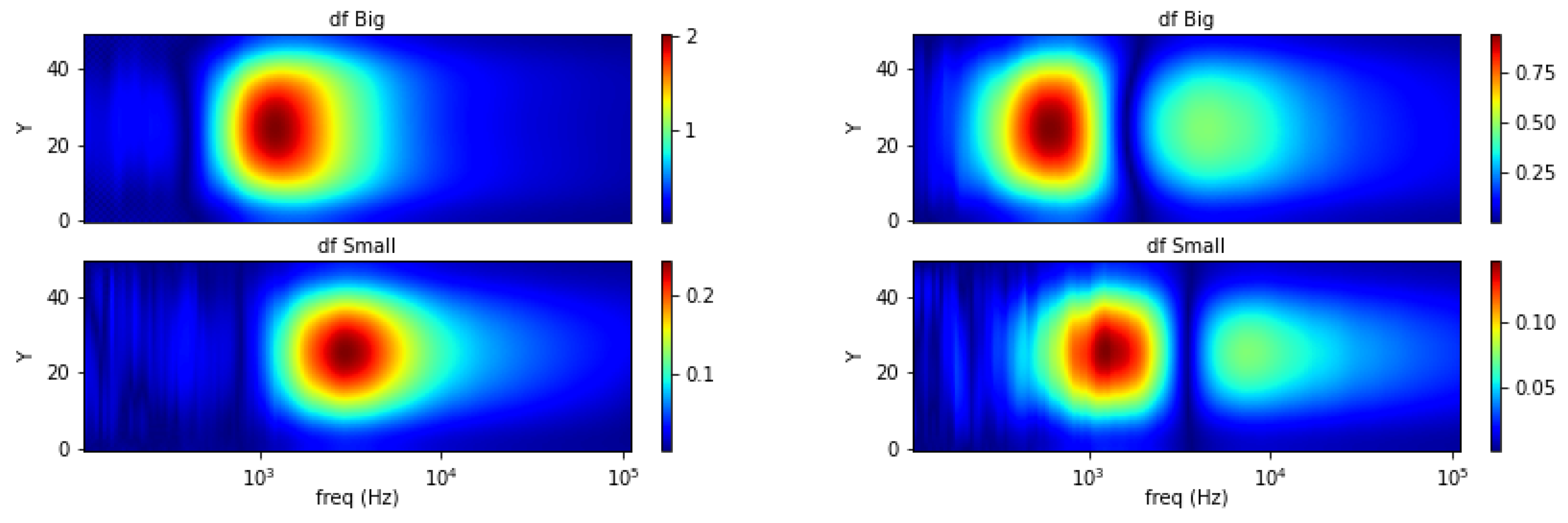
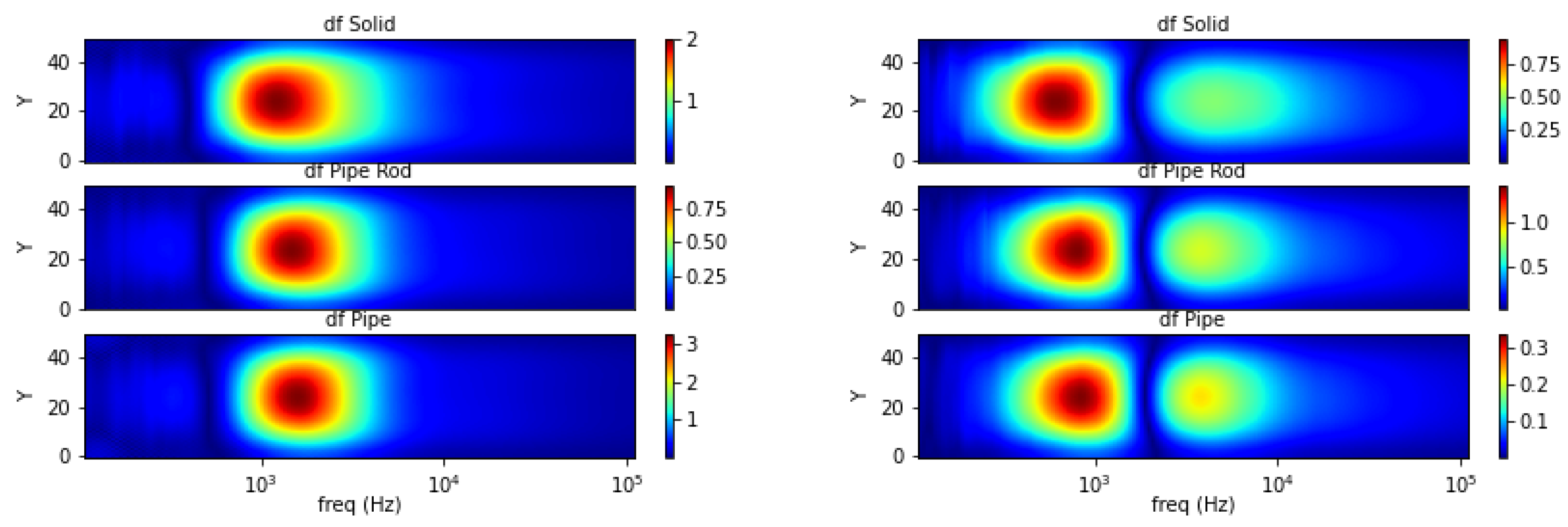
5.4. Spectral Derivative for Structural and Functional Classification
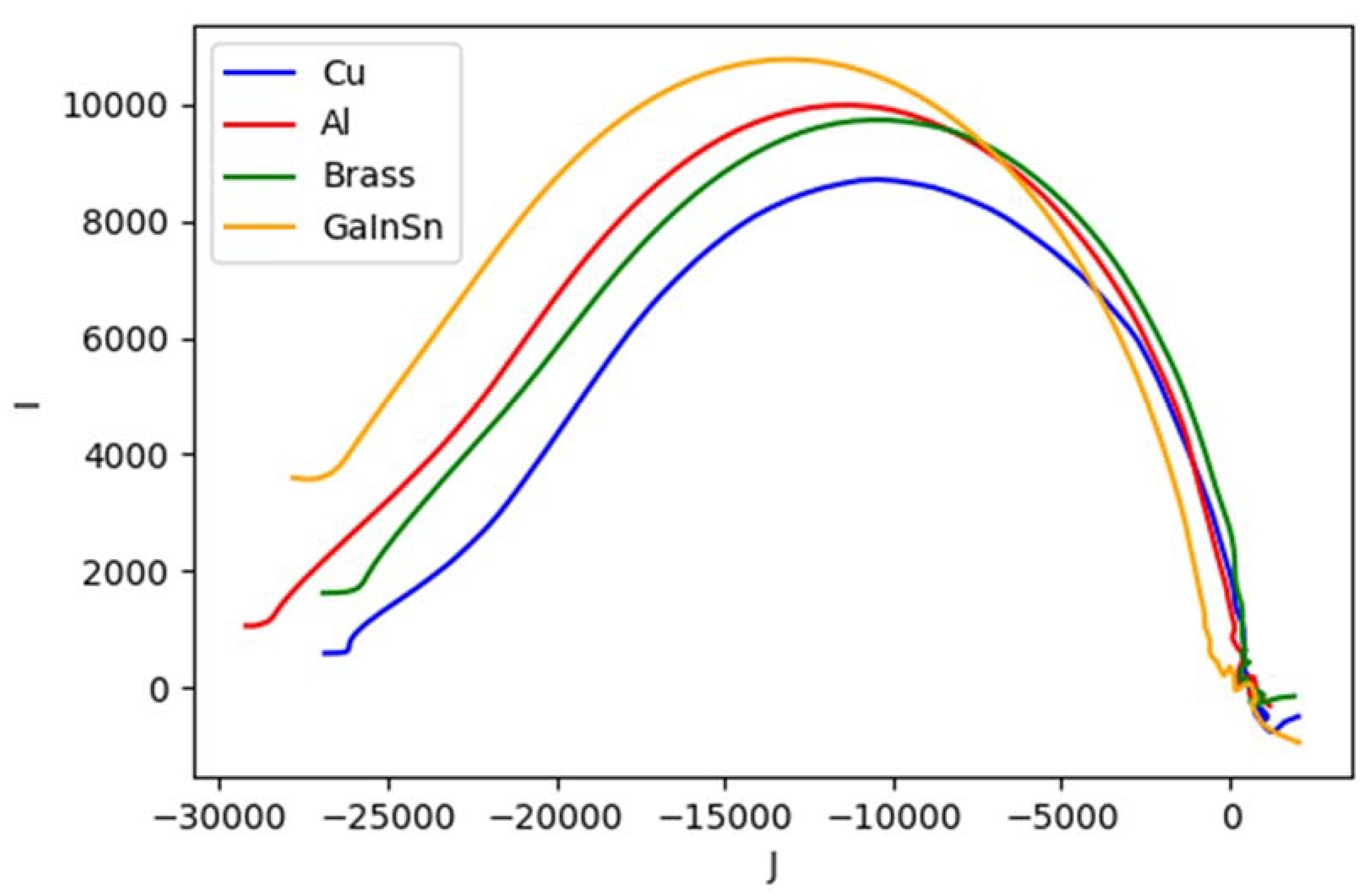
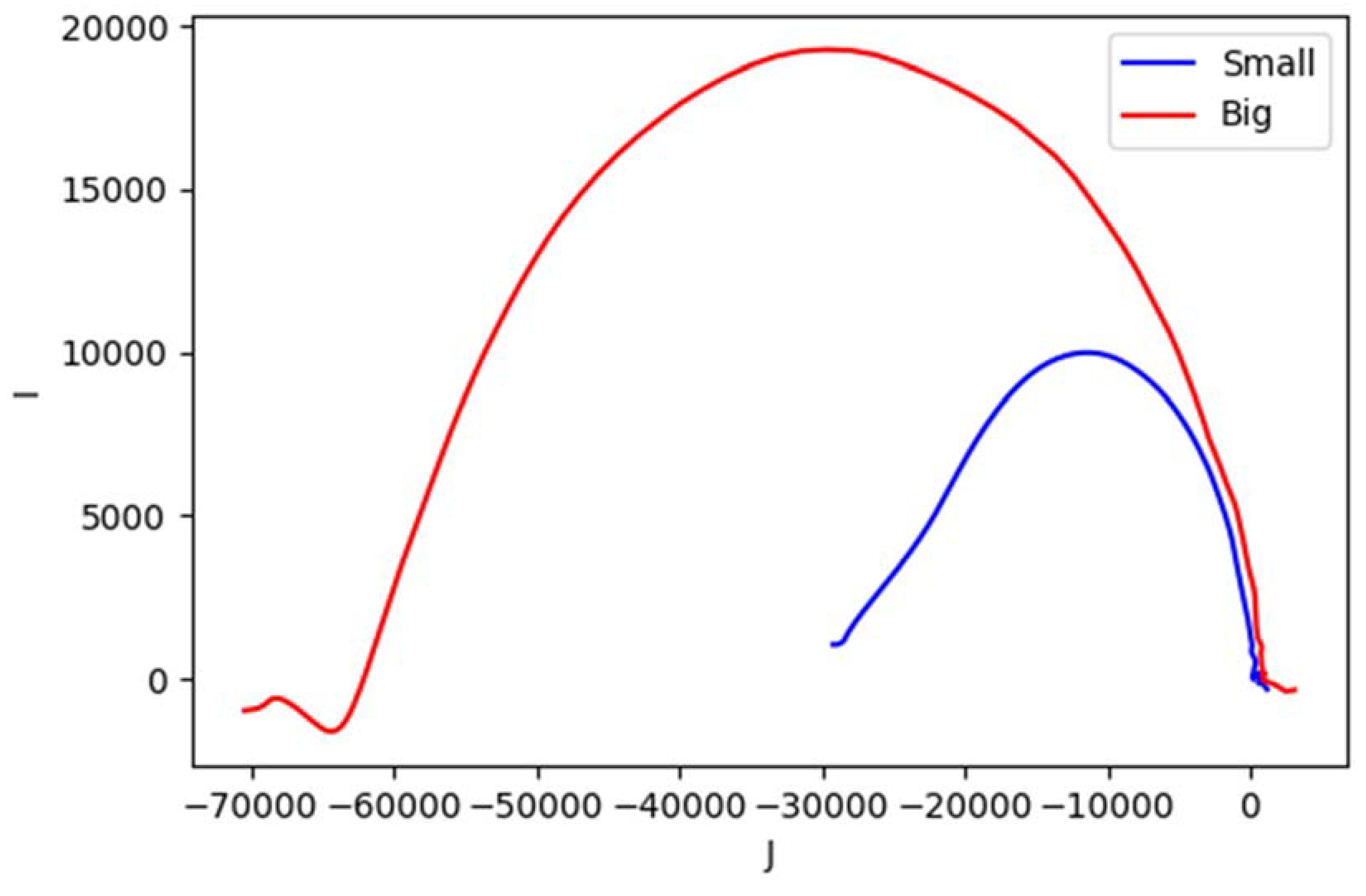
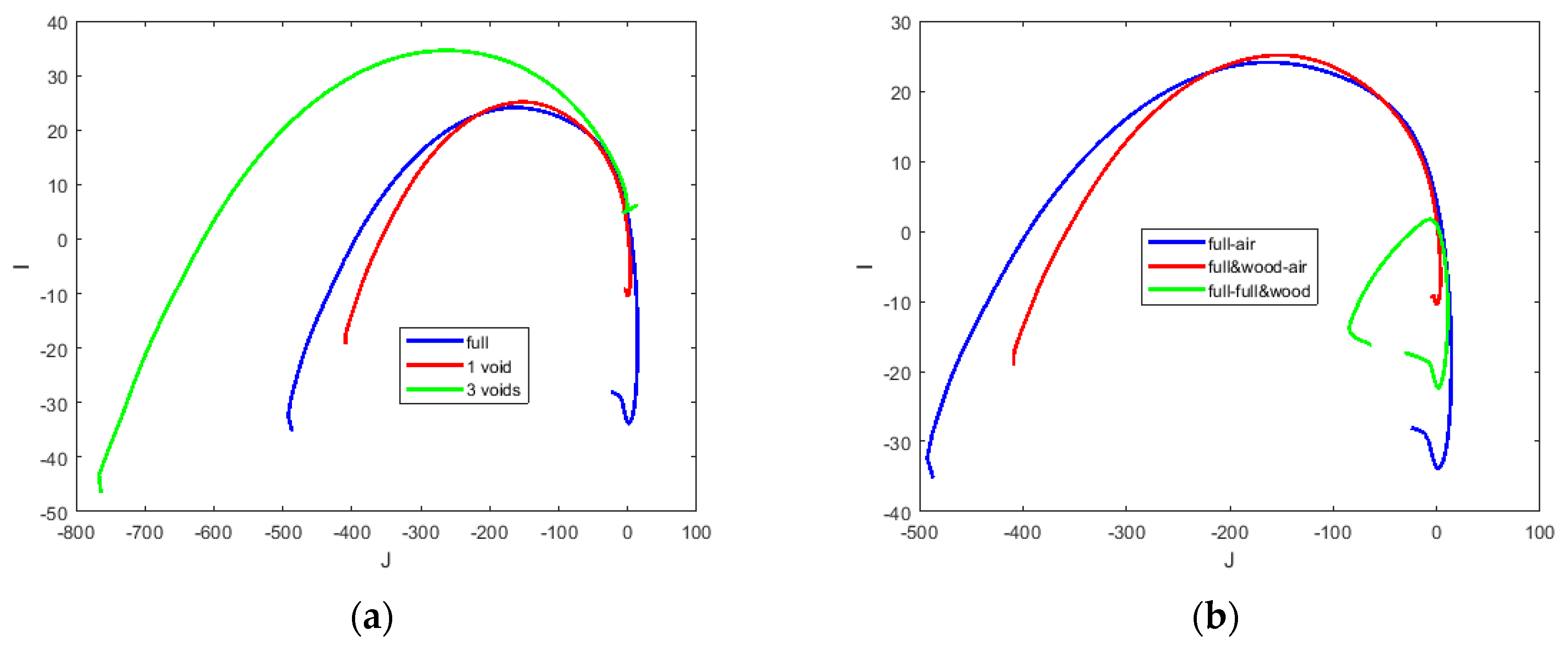
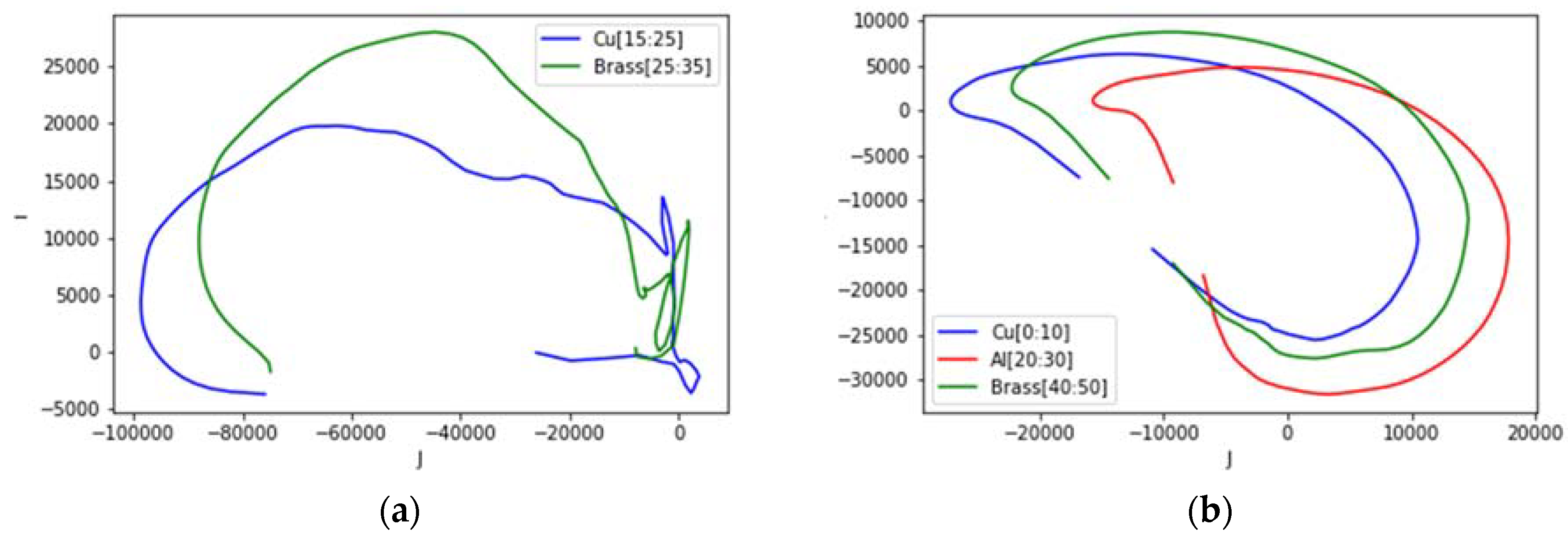
5.5. Complex Plot from Reconstruction
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- García-Martín, J.; Gómez-Gil, J.; Vázquez-Sánchez, E. Non-Destructive Techniques Based on Eddy Current Testing. Sensors 2011, 11, 2525–2565. [Google Scholar] [CrossRef]
- Chen, X.; Lei, Y. Electrical conductivity measurement of ferromagnetic metallic materials using pulsed eddy current method. NDT E Int. 2015, 75, 33–38. [Google Scholar] [CrossRef]
- Bowler, N.; Huang, Y. Electrical conductivity measurement of metal plates using broadband eddy-current and four-point methods. Meas. Sci. Technol. 2005, 16, 2193. [Google Scholar] [CrossRef]
- Sophian, A.; Tian, G.; Fan, M. Pulsed Eddy Current Non-destructive Testing and Evaluation: A Review. Chin. J. Mech. Eng. 2017, 30, 500–514. [Google Scholar] [CrossRef]
- Tian, G.; He, Y.; Adewale, I.; Simm, A. Research on spectral response of pulsed eddy current and NDE applications. Sens. Actuators A Phys. 2013, 189, 313–320. [Google Scholar] [CrossRef]
- Ko, R.T.; Blodgett, M.P.; Sathish, S.; Boehnlein, T.R. A Novel Multi-Frequency Eddy Current Measurement Technique for Materials Characterization. In AIP Conference Proceedings Vol. 820 No. 1; American Institute of Physics: New York, NY, USA, 2006; pp. 415–422. [Google Scholar]
- Cheng, W. Thickness Measurement of Metal Plates Using Swept-Frequency Eddy Current Testing and Impedance Normalization. IEEE Sens. J. 2017, 17, 4558–4569. [Google Scholar] [CrossRef]
- Lu, M.; Xie, Y.; Zhu, W.; Peyton, A.; Yin, W. Determination of the Magnetic Permeability, Electrical Conductivity, and Thickness of Ferrite Metallic Plates Using a Multifrequency Electromagnetic Sensing System. IEEE Trans. Ind. Inform. 2019, 15, 4111–4119. [Google Scholar] [CrossRef]
- Xiang, J.; Chen, Z.; Dong, Y.; Yang, Y. Image Reconstruction for Multi-frequency Electromagnetic Tomography based on Multiple Measurement Vector Model. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference, Dubrovnik, Croatia, 25–28 May 2020. [Google Scholar]
- Pirani, A.; Ricci, M.; Specogna, R.; Tamburrino, A.; Trevisan, F. Multi-frequency identification of defects in conducting media. Inverse Probl. 2008, 24, 035011. [Google Scholar] [CrossRef][Green Version]
- Zhang, Z.; Roula, M.A.; Dinsdale, R. Magnetic Induction Spectroscopy for Biomass Measurement: A Feasibility Study. Sensors 2019, 19, 2765. [Google Scholar] [CrossRef] [PubMed]
- Scharfetter, H.; Casanas, R.; Rosell, J. Biological tissue characterization by magnetic induction spectroscopy (MIS): Requirements and limitations. IEEE Trans. Biomed. Eng. 2003, 50, 870–880. [Google Scholar] [CrossRef]
- Rosell-Ferrer, J.; Merwa, R.; Brunner, P.; Scharfetter, H. A multifrequency magnetic induction tomography system using planar gradiometers: Data collection and calibration. Physiol. Meas. 2006, 27, S271. [Google Scholar] [CrossRef] [PubMed]
- Brunner, P.; Merwa, R.; Missner, A.; Rosell, J.; Hollaus, K.; Scharfetter, H. Reconstruction of the shape of conductivity spectra using differential multi-frequency magnetic induction tomography. Physiol. Meas. 2006, 27, S237. [Google Scholar] [CrossRef] [PubMed]
- Issa, S.; Scharfetter, H. Detection and elimination of signal errors due to unintentional movements in biomedical magnetic induction tomography spectroscopy (MITS). J. Electr. Bioimpedance 2018, 9, 163–175. [Google Scholar] [CrossRef]
- Yin, W.; Dickinson, S.J.; Peyton, A.J. Imaging the continuous conductivity profile within layered metal structures using inductance spectroscopy. IEEE Sens. J. 2005, 5, 161–166. [Google Scholar]
- Yin, W.; Dickinson, S.J.; Peyton, A.J. Evaluating the permeability distribution of a layered conductor by inductance spectroscopy. IEEE Trans. Magn. 2006, 42, 3645–3651. [Google Scholar] [CrossRef]
- Barai, A.; Watson, S.; Griffiths, H.; Patz, R. Magnetic induction spectroscopy: Non-contact measurement of the electrical conductivity spectra of biological samples. Meas. Sci. Technol. 2012, 23, 085501. [Google Scholar] [CrossRef]
- O’Toole, M.D.; Marsh, L.A.; Davidson, J.L.; Tan, Y.M.; Armitage, D.W.; Peyton, A.J. Non-contact multi-frequency magnetic induction spectroscopy system for industrial-scale bio-impedance measurement. Meas. Sci. Technol. 2015, 26, 035102. [Google Scholar] [CrossRef]
- Wang, J.Y.; Healey, T.; Barker, A.; Brown, B.; Monk, C.; Anumba, D. Magnetic induction spectroscopy (MIS)—Probe design for cervical tissue measurements. Physiol. Meas. 2017, 38, 729. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, C.A.; Valencia, J.A.; Mora, A.; Gonzalez, F.; Velasco, B.; Porras, M.A.; Salgado, J.; Polo, S.M.; Hevia-Montiel, N.; Cordero, S.; et al. Volumetric electromagnetic phase-shift spectroscopy of brain edema and hematoma. PLoS ONE 2013, 8, e63223. [Google Scholar] [CrossRef] [PubMed]
- Marsh, L.A.; van Verre, W.; Davidson, J.L.; Gao, X.; Podd, F.J.W.; Daniels, D.J.; Peyton, A.J. Combining Electromagnetic Spectroscopy and Ground-Penetrating Radar for the Detection of Anti-Personnel Landmines. Sensors 2019, 19, 3390. [Google Scholar] [CrossRef] [PubMed]
- El-Qady, G.; Metwaly, M.; Khozaym, A. Tracing buried pipelines using multi frequency electromagnetic. NRIAG J. Astron. Geophys. 2014, 3, 101–107. [Google Scholar] [CrossRef]
- O’Toole, M.D.; Karimian, N.; Peyton, A.J. Classification of Nonferrous Metals Using Magnetic Induction Spectroscopy. IEEE Trans. Ind. Inform. 2018, 14, 3477–3485. [Google Scholar] [CrossRef]
- Xu, H.; Lu, M.; Avila, J.R.; Zhao, Q.; Zhou, F.; Meng, X.; Yin, W. Imaging a weld cross-section using a novel frequency feature in multi-frequency eddy current testing. Insight Non Destr. Test. Cond. Monit. 2019, 61, 738–743. [Google Scholar] [CrossRef]
- Dekdouk, B.; Ktistis, C.; Armitage, D.W.; Peyton, A.J.; Chapman, R.; Brown, M. Non-contact characterisation of conductivity gradient in isotropic polycrystalline graphite using inductance spectroscopy measurements. Insight Non Destr. Test. Cond. Monit. 2011, 53, 90–95. [Google Scholar] [CrossRef]
- Peyton, A.J.; Yin, W.; Dickinson, S.J.; Davis, C.L.; Strangwood, M.; Hao, X.; Douglas, A.J.; Morris, P.F. Monitoring microstructure changes in rod online by using induction spectroscopy. Ironmak. Steelmak. 2010, 37, 135–139. [Google Scholar] [CrossRef]
- Davis, C.L.; Strangwood, M.; Peyton, A.J. Overview of non-destructive evaluation of steel microstructures using multifrequency electromagnetic sensors. Ironmak. Steelmak. 2011, 38, 510–517. [Google Scholar] [CrossRef]
- Dickinson, S.J.; Binns, R.; Yin, W.; Davis, C.; Peyton, A.J. The Development of a Multifrequency Electromagnetic Instrument for Monitoring the Phase Transformation of Hot Strip Steel. IEEE Trans. Instrum. Meas. 2007, 56, 879–886. [Google Scholar] [CrossRef]
- Yang, H.; Van Den Berg, F.D.; Bos, C.; Luinenburg, A.; Mosk, J.; Hunt, P.; Dolby, M.; Hinton, J.; Peyton, A.J.; Davis, C.L. EM sensor array system and performance evaluation for in-line measurement of phase transformation in steel. Insight Non Destr. Test. Cond. Monit. 2019, 61, 153–157. [Google Scholar] [CrossRef]
- Zhu, W.; Yang, H.; Luinenburg, A.; van den Berg, F.; Dickinson, S.; Yin, W.; Peyton, A.J. Development and deployment of online multifrequency electromagnetic system to monitor steel hot transformation on runout table of hot strip mill. Ironmak. Steelmak. 2014, 41, 685–693. [Google Scholar] [CrossRef]
- Shen, J.; Zhou, L.; Jacobs, W.; Hunt, P.; Davis, C. Real-time in-line steel microstructure control through magnetic properties using an EM sensor. J. Magn. Magn. Mater. 2019, 490, 165504. [Google Scholar] [CrossRef]
- Lyons, S.; Wei, K.; Soleimani, M. Wideband precision phase detection for magnetic induction spectroscopy. Measurement 2018, 115, 45–51. [Google Scholar] [CrossRef]
- Ma, L.; Soleimani, M. Magnetic induction spectroscopy for permeability imaging. Sci. Rep. 2018, 8, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Soleimani, M. Computational aspects of low frequency electrical and electromagnetic tomography: A review study. Int. J. Numer. Anal. Model. 2008, 5, 407–440. [Google Scholar]
- Li, F.; Abascal, J.F.P.J.; Desco, M.; Soleimani, M. Total Variation Regularization with Split Bregman-Based Method in Magnetic Induction Tomography Using Experimental Data. IEEE Sens. J. 2017, 17, 976–985. [Google Scholar] [CrossRef]
- Soleimani, M.; Li, F.; Spagnul, S.; Palacios, J.; Barbero, J.I.; Gutiérrez, T.; Viotto, A. In situ steel solidification imaging in continuous casting using magnetic induction tomography. Meas. Sci. Technol. 2020, 31, 065401. [Google Scholar] [CrossRef]
- Soleimani, M.; Lionheart, W.R.; Peyton, A.J. Image reconstruction for high-contrast conductivity imaging in mutual induction tomography for industrial applications. IEEE Trans. Instrum. Meas. 2007, 56, 2024–2032. [Google Scholar] [CrossRef]
- Bíró, O. Edge element formulations of eddy current problems. Comput. Methods Appl. Mech. Eng. 1999, 169, 391–405. [Google Scholar] [CrossRef]
- Riviere, B. Discontinuous Galerkin Methods for Solving Elliptic and Parabolic Equations: Theory and Implementation; SIAM: Philadelphia, PA, USA, 2008. [Google Scholar]
- Brandstatter, B. Jacobian calculation for electrical impedance tomography based on the reciprocity principle. IEEE Trans. Magn. 2003, 39, 1309–1312. [Google Scholar] [CrossRef]
- Liu, X.; Huang, L. Split Bregman iteration algorithm for total bounded variation regularization based image deblurring. J. Math. Anal. Appl. 2010, 372, 486–495. [Google Scholar] [CrossRef]
- Chen, B.; Abascal, J.F.P.J.; Soleimani, M. Electrical Resistance Tomography for Visualization of Moving Objects Using a Spatiotemporal Total Variation Regularization Algorithm. Sensors 2018, 18, 1704. [Google Scholar] [CrossRef]
- Abascal, J.F.; Montesinos, P.; Marinetto, E.; Pascau, J.; Desco, M. Comparison of Total Variation with a Motion Estimation Based Compressed Sensing Approach for Self-Gated Cardiac Cine MRI in Small Animal Studies. PLoS ONE 2014, 9, e110594. [Google Scholar] [CrossRef] [PubMed]
- Montesinos, P.; Abascal, J.F.P.; Cussó, L.; Vaquero, J.J.; Desco, M. Application of the Compressed Sensing Technique to Self-Gated Cardiac Cine Sequences in Small Animals. Magn. Reson. Med. 2013, 72, 369–380. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, T.; Osher, S.; Burger, M.; Goldfarb, D.; Xu, J.; Yin, W. An Iterative Regularization Method for Total Variation-Based Image Restoration. Multiscale Model. Simul. 2005, 4, 460–489. [Google Scholar]
- Goldstein, T.; Osher, S. The Split Bregman Method for L1-Regularized Problems. SIAM J. Imaging Sci. 2009, 2, 323–343. [Google Scholar] [CrossRef]
- Gutknecht, M.H. A Brief Introduction to Krylov Space Methods for Solving Linear Systems. In Frontiers of Computational Science; Springer: Berlin/Heidelberg, Germany, 2007; pp. 53–62. [Google Scholar]
- Ji, Y.; Meng, X.; Shao, J.; Wu, Y.; Wu, Q. The Generalized Skin Depth for Polarized Porous Media Based on the Cole–Cole Model. Appl. Sci. 2020, 10, 1456. [Google Scholar] [CrossRef]
- Ley, S.; Schilling, S.; Fiser, O.; Vrba, J.; Sachs, J.; Helbig, M. Ultra-Wideband Temperature Dependent Dielectric Spectroscopy of Porcine Tissue and Blood in the Microwave Frequency Range. Sensors 2019, 19, 1707. [Google Scholar] [CrossRef] [PubMed]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muttakin, I.; Soleimani, M. Magnetic Induction Tomography Spectroscopy for Structural and Functional Characterization in Metallic Materials. Materials 2020, 13, 2639. https://doi.org/10.3390/ma13112639
Muttakin I, Soleimani M. Magnetic Induction Tomography Spectroscopy for Structural and Functional Characterization in Metallic Materials. Materials. 2020; 13(11):2639. https://doi.org/10.3390/ma13112639
Chicago/Turabian StyleMuttakin, Imamul, and Manuchehr Soleimani. 2020. "Magnetic Induction Tomography Spectroscopy for Structural and Functional Characterization in Metallic Materials" Materials 13, no. 11: 2639. https://doi.org/10.3390/ma13112639
APA StyleMuttakin, I., & Soleimani, M. (2020). Magnetic Induction Tomography Spectroscopy for Structural and Functional Characterization in Metallic Materials. Materials, 13(11), 2639. https://doi.org/10.3390/ma13112639




