Dynamic Ferromagnetic Hysteresis Modelling Using a Preisach-Recurrent Neural Network Model
Abstract
1. Introduction
2. Materials and Methods
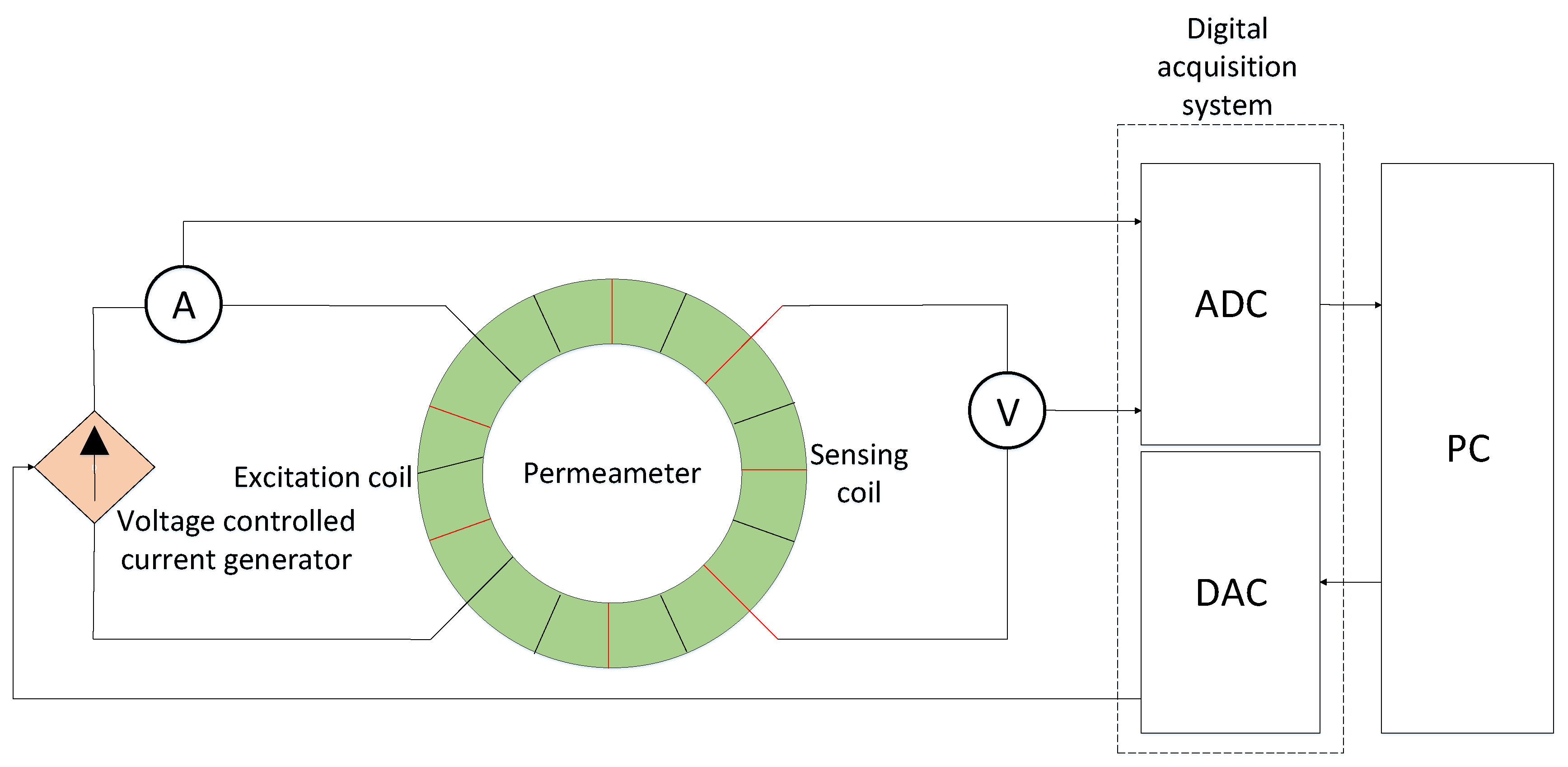
2.1. Experimental Details
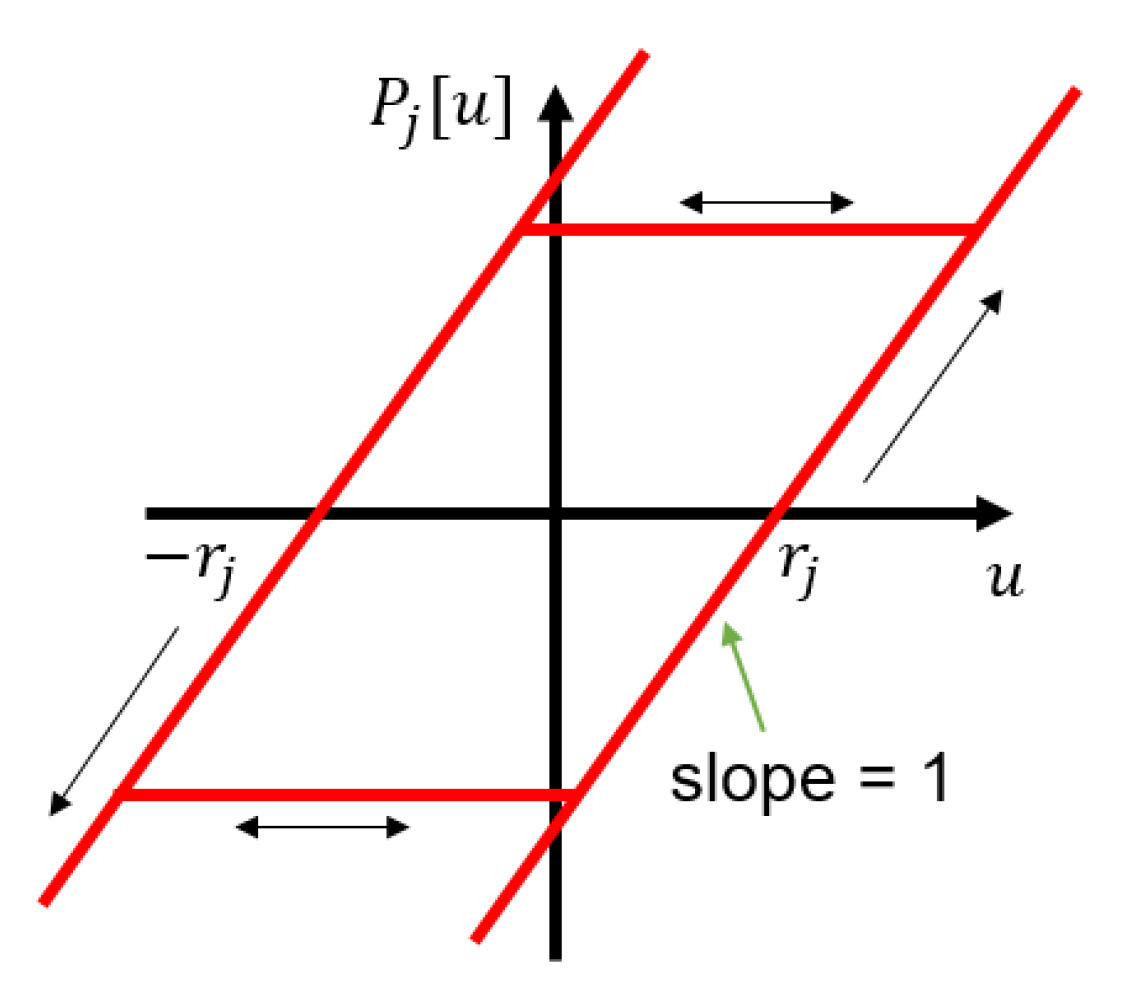
2.2. Hysteresis Modelling Based on Preisach Memory
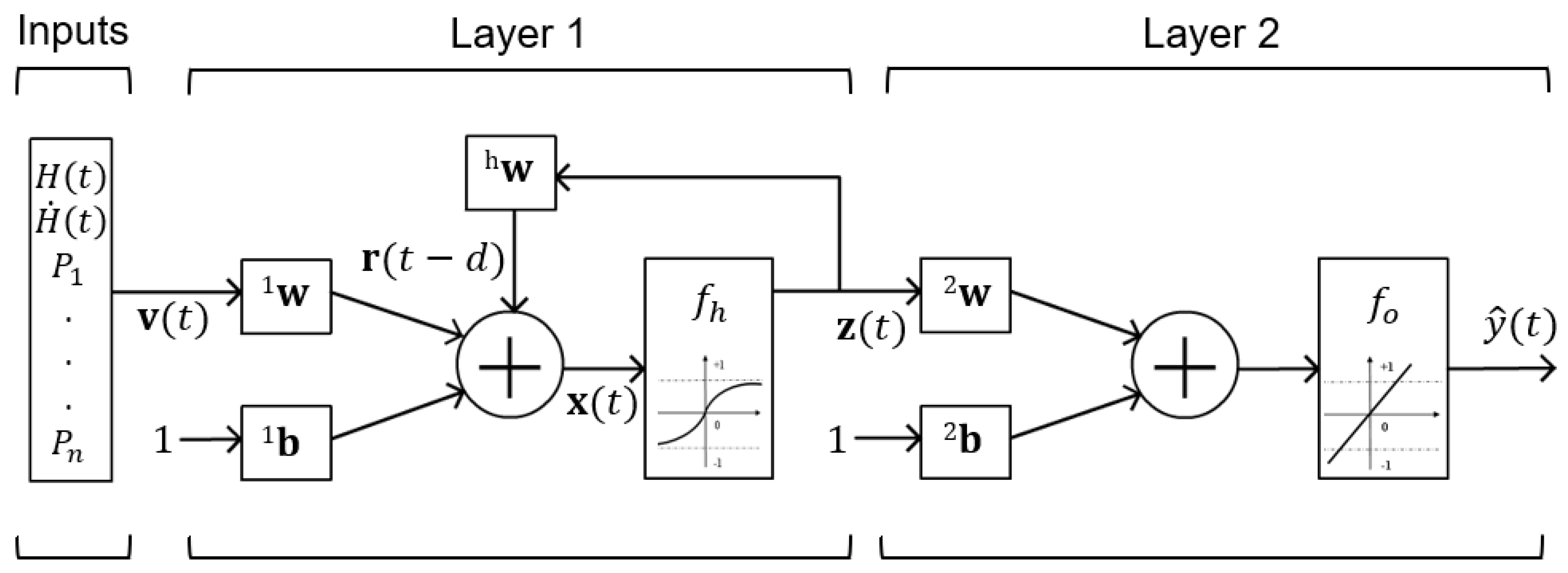
2.3. Identifying Using Recurrent Neural Networks
2.4. Data Analysis Approach
2.5. Model Validation
2.6. Performance Indicator
3. Results
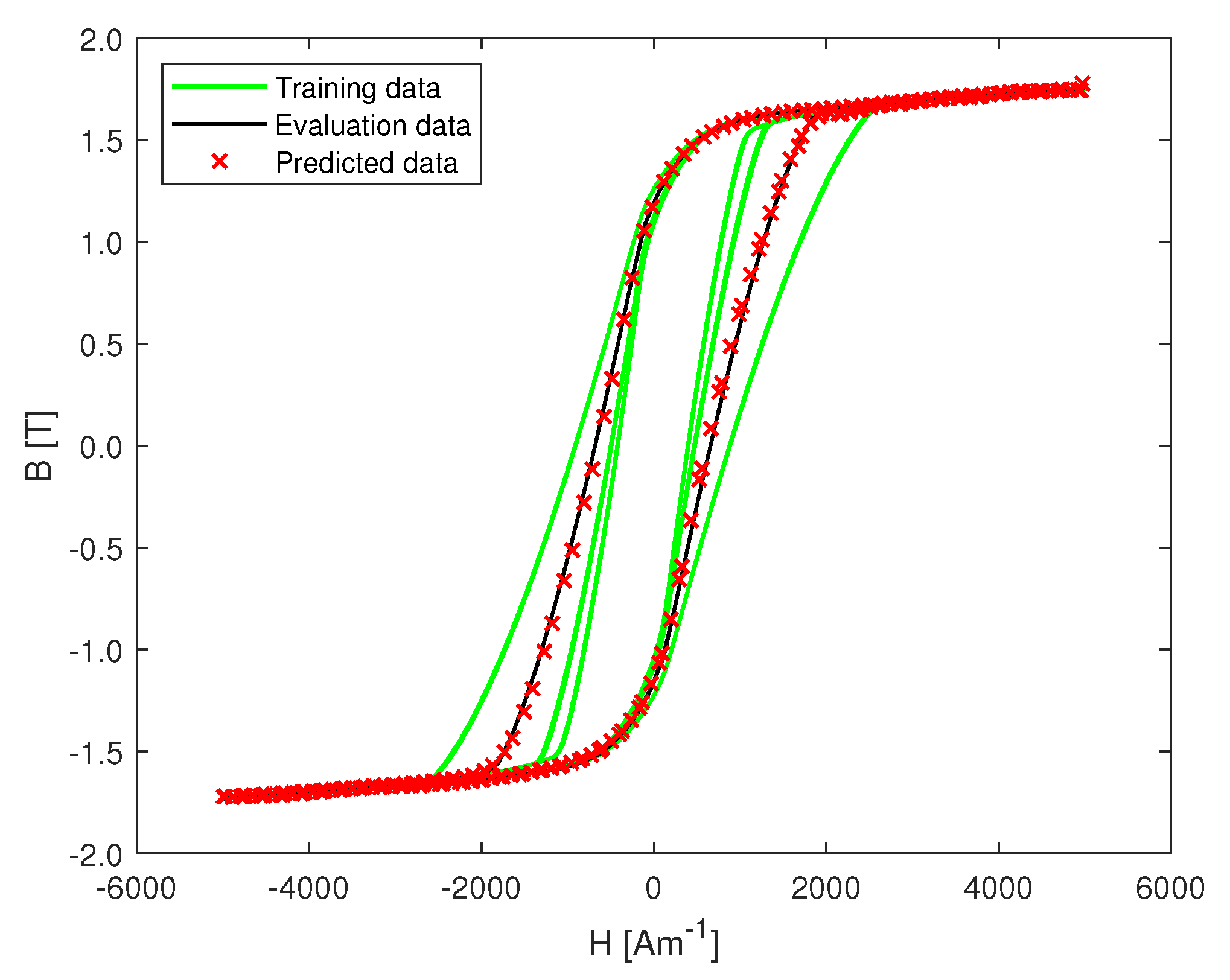
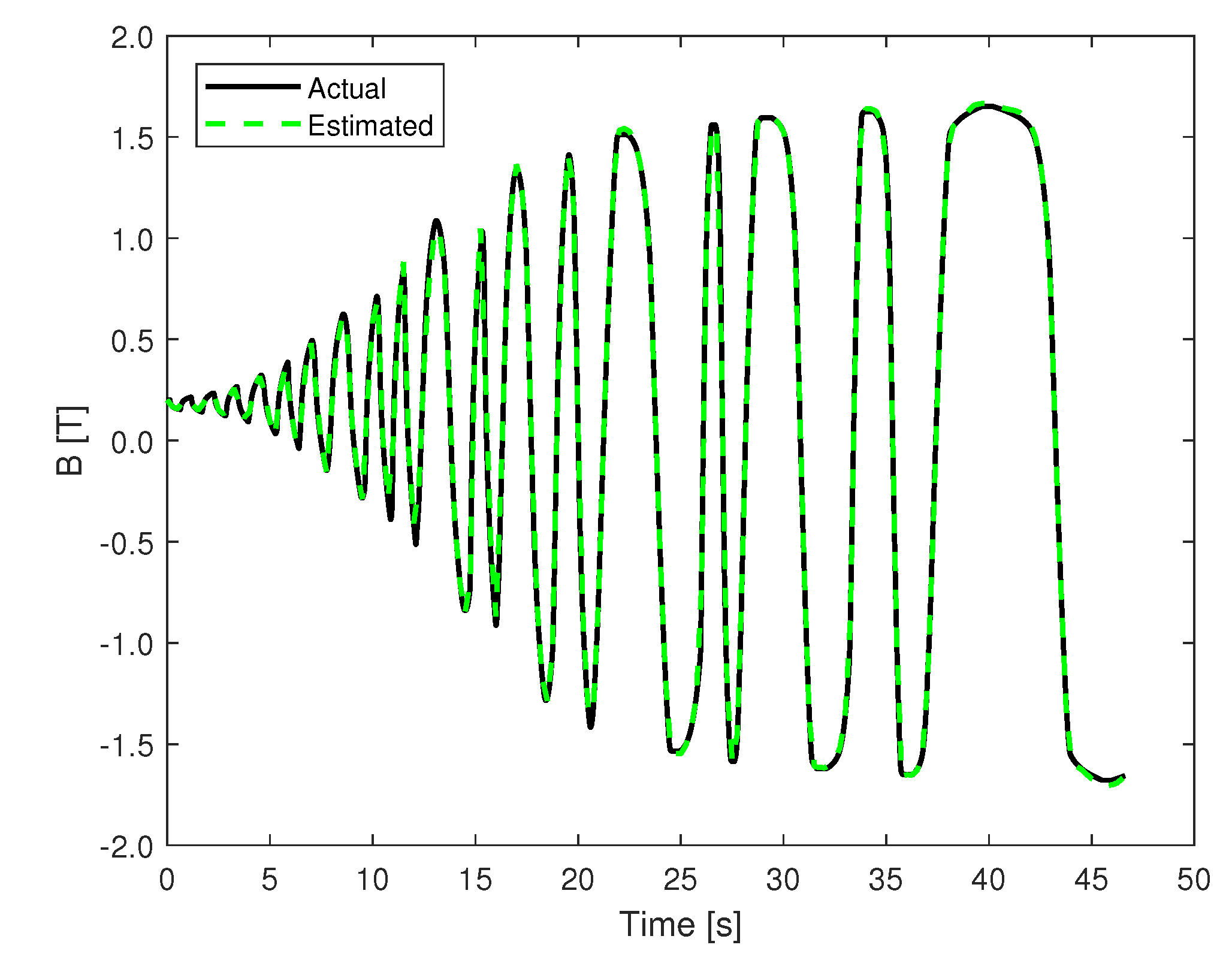
3.1. Minor and Major Loop Model Prediction
3.2. Effect of Preisach Operators on Performance
3.3. Univariate Sensitivity Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| CERN | European Organization for Nuclear Research |
| NRMSE | Normalised Root Mean Square Error |
| RNN | Recurrent Neural Network |
References
- Mayergoyz, I. (Ed.) Chapter 1—The Classical Preisach Model of Hysteresis. In Mathematical Models of Hysteresis and Their Applications; Electromagnetism; Elsevier Science: New York, NY, USA, 2003; pp. 1–63. [Google Scholar] [CrossRef]
- Saliah, H.; Lowther, D. The use of neural networks in magnetic hysteresis identification. Phys. B Condens. Matter 1997, 233, 318–323. [Google Scholar] [CrossRef]
- Iyer, R.V.; Tan, X. Control of hysteretic systems through inverse compensation. IEEE Control Syst. Mag. 2009, 29, 83–99. [Google Scholar] [CrossRef]
- Sutor, A.; Rupitsch, S.J.; Lerch, R. A Preisach-based hysteresis model for magnetic and ferroelectric hysteresis. Appl. Phys. A 2010, 100, 425–430. [Google Scholar] [CrossRef]
- Stakvik, J. Identification, Inversion and Implementaion of the Preisach Hysteresis Model in Nanopositioning. Master’s Thesis, Nowegian University of Science and Technology, Trondheim, Norway, 2014. [Google Scholar]
- Biorci, G.; Pescetti, D. Analytical theory of the behaviour of ferromagnetic materials. Il Nuovo Cimento (1955–1965) 1958, 7, 829–842. [Google Scholar] [CrossRef]
- Ruderman, M.; Bertram, T. Identification of Soft Magnetic B-H Characteristics Using Discrete Dynamic Preisach Model and Single Measured Hysteresis Loop. IEEE Trans. Magn. 2012, 48, 1281–1284. [Google Scholar] [CrossRef]
- Kozek, M.; Gross, B. Identification and Inversion of Magnetic Hysteresis for Sinusoidal Magnetization. Int. J. Online Biomed. Eng. 2005. Available online: https://online-journals.org/index.php/i-joe/article/view/299/2990 (accessed on 3 June 2020).
- Rouve, L.; Waeckerle, T.; Kedous-Lebouc, A. Application of Preisach model to grain oriented steels: Comparison of different characterizations for the Preisach function p(/spl alpha/, /spl beta/). IEEE Trans. Magn. 1995, 31, 3557–3559. [Google Scholar] [CrossRef]
- Hergli, K.; Marouani, H.; Zidi, M.; Fouad, Y.; Elshazly, M. Identification of Preisach hysteresis model parameters using genetic algorithms. J. King Saud Univ.-Sci. 2017. [Google Scholar] [CrossRef]
- Natale, C.; Velardi, F.; Visone, C. Identification and compensation of Preisach hysteresis models for magnetostrictive actuators. Phys. B Condensed Matter 2001, 306, 161–165. [Google Scholar] [CrossRef]
- Adly, A.; El-Hafiz, S.A. Using neural networks in the identification of Preisach-type hysteresis models. IEEE Trans. Magn. 1998, 34, 629–635. [Google Scholar] [CrossRef]
- Akbarzadeh, V.; Davoudpour, M.; Sadeghian, A. Neural network modeling of magnetic hysteresis. In Proceedings of the 2008 IEEE International Conference on Emerging Technologies and Factory Automation, Hamburg, Germany, 15–18 September 2008; pp. 1267–1270. [Google Scholar]
- Firouzi, M.; Shouraki, S.B.; Zakerzadeh, M.R. Hysteresis nonlinearity identification by using RBF neural network approach. In Proceedings of the 2010 18th Iranian Conference on Electrical Engineering, Isfahan, Iran, 11–13 May 2010. [Google Scholar] [CrossRef]
- Saliah, H.H.; Lowther, D.A.; Forghani, B. A neural network model of magnetic hysteresis for computational magnetics. IEEE Trans. Magn. 1997, 33, 4146–4148. [Google Scholar] [CrossRef]
- Serpico, C.; Visone, C. Magnetic hysteresis modeling via feed-forward neural networks. IEEE Trans. Magn. 1998, 34, 623–628. [Google Scholar] [CrossRef]
- Xu, R.; Zhou, M. Elman Neural Network-Based Identification of Krasnosel’skii–Pokrovskii Model for Magnetic Shape Memory Alloys Actuator. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Zhou, M.; Zhang, Q. Hysteresis Model of Magnetically Controlled Shape Memory Alloy Based on a PID Neural Network. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Mayergoyz, I.D. Dynamic Preisach models of hysteresis. IEEE Trans. Magn. 1988, 24, 2925–2927. [Google Scholar] [CrossRef]
- Mrad, R.B.; Hu, H. Dynamic modeling of hysteresis in piezoceramics. In Proceedings of the 2001 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Proceedings (Cat. No.01TH8556), Como, Italy, 8–12 July 2001. [Google Scholar] [CrossRef]
- Song, D.; Li, C.J. Modeling of piezo actuator’s nonlinear and frequency dependent dynamics. Mechatronics 1999, 9, 391–410. [Google Scholar] [CrossRef]
- Füzi, J. Computationally efficient rate dependent hysteresis model. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 1999, 18, 445–457. [Google Scholar] [CrossRef]
- Kuczmann, M. Dynamic Preisach model identification applying FEM and measured BH curve. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2014, 33, 2043–2052. [Google Scholar] [CrossRef]
- Makaveev, D.; Dupré, L.; Wulf, M.D.; Melkebeek, J. Dynamic hysteresis modelling using feed-forward neural networks. J. Magn. Magn. Mater. 2003, 254–255, 256–258. [Google Scholar] [CrossRef]
- Tan, X.; Baras, J.S. Modeling and control of hysteresis in magnetostrictive actuators. Automatica 2004, 40, 1469–1480. [Google Scholar] [CrossRef]
- Saghafifar, M.; Kundu, A.; Nafalski, A. Dynamic magnetic hysteresis modelling using Elman recurrent neural network. Int. J. Appl. Electromagn. Mech. 2001, 13, 209–214. [Google Scholar] [CrossRef]
- Wang, Q.; Su, C.Y.; Tan, Y. On the Control of Plants with Hysteresis: Overview and a Prandtl-Ishlinskii Hysteresis Based Control Approach. ACTA Autom. Sin. 2005. [Google Scholar] [CrossRef]
- Parrella, A.; Arpaia, P.; Buzio, M.; Liccardo, A.; Pentella, M.; Principe, R.; Ramos, P. Magnetic Properties of Pure Iron for the Upgrade of the LHC Superconducting Dipole and Quadrupole Magnets. IEEE Trans. Magn. 2018, 55, 1–4. [Google Scholar] [CrossRef]
- Arpaia, P.; Buzio, M.; Bermudez, S.I.; Liccardo, A.; Parrella, A.; Pentella, M.; Ramos, P.M.; Stubberud, E. A Superconducting Permeameter for Characterizing Soft Magnetic Materials at High Fields. IEEE Trans. Instrum. Meas. 2019. [Google Scholar] [CrossRef]
- Namjoshi, K.; Lavers, J.D.; Biringer, P. Eddy-current power loss in toroidal cores with rectangular cross section. IEEE Trans. Magn. 1998, 34, 636–641. [Google Scholar] [CrossRef]
- Anglada, J.; Arpaia, P.; Buzio, M.; Pentella, M.; Petrone, C. Characterization of Magnetic Steels for the FCC-ee Magnet Prototypes. In Proceedings of the 2020 IEEE Instrumentation & Measurement Technology Conference, Dubrovnik, Croatia, 25–28 May 2020. accepted for publication. [Google Scholar]
- Grossinger, R.; Mehboob, N.; Suess, D.; Turtelli, R.S.; Kriegisch, M. An eddy-current model describing the frequency dependence of the coercivity of polycrystalline Galfenol. IEEE Trans. Magn. 2012, 48, 3076–3079. [Google Scholar] [CrossRef]
- Sgobba, S. Physics and measurements of magnetic materials. In Proceedings of the CERN Accelerator School CAS 2009: Specialised Course on Magnets, Bruges, Belgium, 16–25 June 2009. [Google Scholar] [CrossRef]
- Arpaia, P.; Buzio, M.; Fiscarelli, L.; Montenero, G.; Walckiers, L. High-performance permeability measurements: A case study at CERN. In Proceedings of the 2010 IEEE Instrumentation & Measurement Technology Conference Proceedings, Austin, TX, USA, 3–6 May 2010; pp. 58–61. [Google Scholar]
- National Instruments. NI 446x Specifications. 2008. Available online: http://www.ni.com/pdf/manuals/373770j.pdf (accessed on 3 June 2020).
- Hitec. MACC 2 Plus. 2016. Available online: http://www.pm-sms.com/files/2016/02/Specifications-MACC-2-plus.pdf (accessed on 3 June 2020).
- Krejčí, P. On Maxwell equations with the Preisach hysteresis operator: The one-dimensional time-periodic case. Apl. Mat. 1989, 34, 364–374. [Google Scholar]
- Brokate, M. Some mathematical properties of the Preisach model for hysteresis. IEEE Trans. Magn. 1989, 25, 2922–2924. [Google Scholar] [CrossRef]
- Schäfer, A.M.; Zimmermann, H.G. Recurrent Neural Networks are universal approximators. Int. J. Neural Syst. 2007, 17, 253–263. [Google Scholar] [CrossRef]
- MATLAB. Deep Learning Toolbox. 2019. Available online: https://www.mathworks.com/help/deeplearning/index.html?s_tid=mwa_osa_a (accessed on 3 June 2020).
- Marquardt, D. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Hagan, M.T.; Menhaj, M.B. Training feedforward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef] [PubMed]
- Prechelt, L. Early Stopping—But When? In Neural Networks: Tricks of the Trade, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 53–67. [Google Scholar] [CrossRef]
- Yao, Y.; Rosasco, L.; Caponnetto, A. On Early Stopping in Gradient Descent Learning. Constr. Approx. 2007, 26, 289–315. [Google Scholar] [CrossRef]
- Salciccioli, J.D.; Crutain, Y.; Komorowski, M.; Marshall, D.C. Sensitivity Analysis and Model Validation. In Secondary Analysis of Electronic Health Records; Springer International Publishing: Cham, Switzerland, 2016; pp. 263–271. [Google Scholar] [CrossRef]
- Liu, Z.P.; Castagna, J.P. Avoiding overfitting caused by noise using a uniform training mode. In Proceedings of the IJCNN’99—International Joint Conference on Neural Networks. Proceedings (Cat. No.99CH36339), Washington, DC, USA, 10–16 July 1999; Volume 3, pp. 1788–1793. [Google Scholar] [CrossRef]





| Parameter | Value | |
|---|---|---|
| Model properties | Activation function (hidden layer) | sigmoid |
| Activation function (output layer) | linear | |
| delay, d | 2 | |
| hidden nodes search range, | 4:1:13 | |
| number of hidden nodes, h | 12 | |
| training repetitions, N | 10 | |
| Input | No. of play operators | 6 |
| Training set | data | 70% of data set |
| epochs | ≤1000 | |
| algorithm | Levenberg-Marquadt | |
| Validation set | data | 15% of data set |
| Testing set | data | 15% of data set |
| Evaluation set | data | unseen data |
| metric | NRMSE |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grech, C.; Buzio, M.; Pentella, M.; Sammut, N. Dynamic Ferromagnetic Hysteresis Modelling Using a Preisach-Recurrent Neural Network Model. Materials 2020, 13, 2561. https://doi.org/10.3390/ma13112561
Grech C, Buzio M, Pentella M, Sammut N. Dynamic Ferromagnetic Hysteresis Modelling Using a Preisach-Recurrent Neural Network Model. Materials. 2020; 13(11):2561. https://doi.org/10.3390/ma13112561
Chicago/Turabian StyleGrech, Christian, Marco Buzio, Mariano Pentella, and Nicholas Sammut. 2020. "Dynamic Ferromagnetic Hysteresis Modelling Using a Preisach-Recurrent Neural Network Model" Materials 13, no. 11: 2561. https://doi.org/10.3390/ma13112561
APA StyleGrech, C., Buzio, M., Pentella, M., & Sammut, N. (2020). Dynamic Ferromagnetic Hysteresis Modelling Using a Preisach-Recurrent Neural Network Model. Materials, 13(11), 2561. https://doi.org/10.3390/ma13112561







