The Meshless Analysis of Scale-Dependent Problems for Coupled Fields
Abstract
1. Introduction
2. The MLPG for Flexoelectricity
2.1. The Direct and Converse Flexoelectricity
- (1)
- Essential b.c.:
- (2)
- Natural b.c.:whereand the traction vector and the electric charge are defined aswith , , δ(x) being the Dirac delta function and is the Cartesian component of the unit tangent vector on Γ.
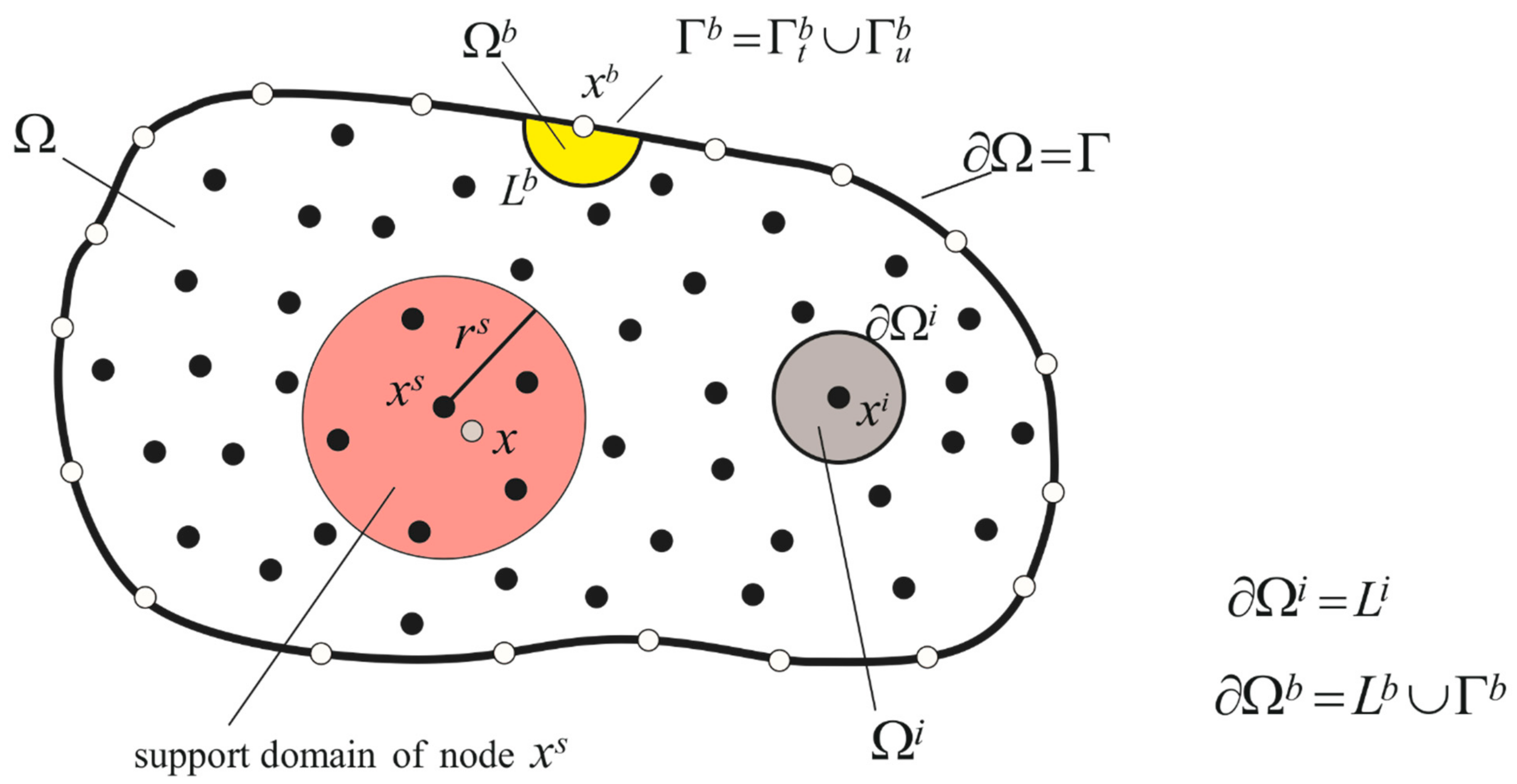
2.2. The MLPG Formulation
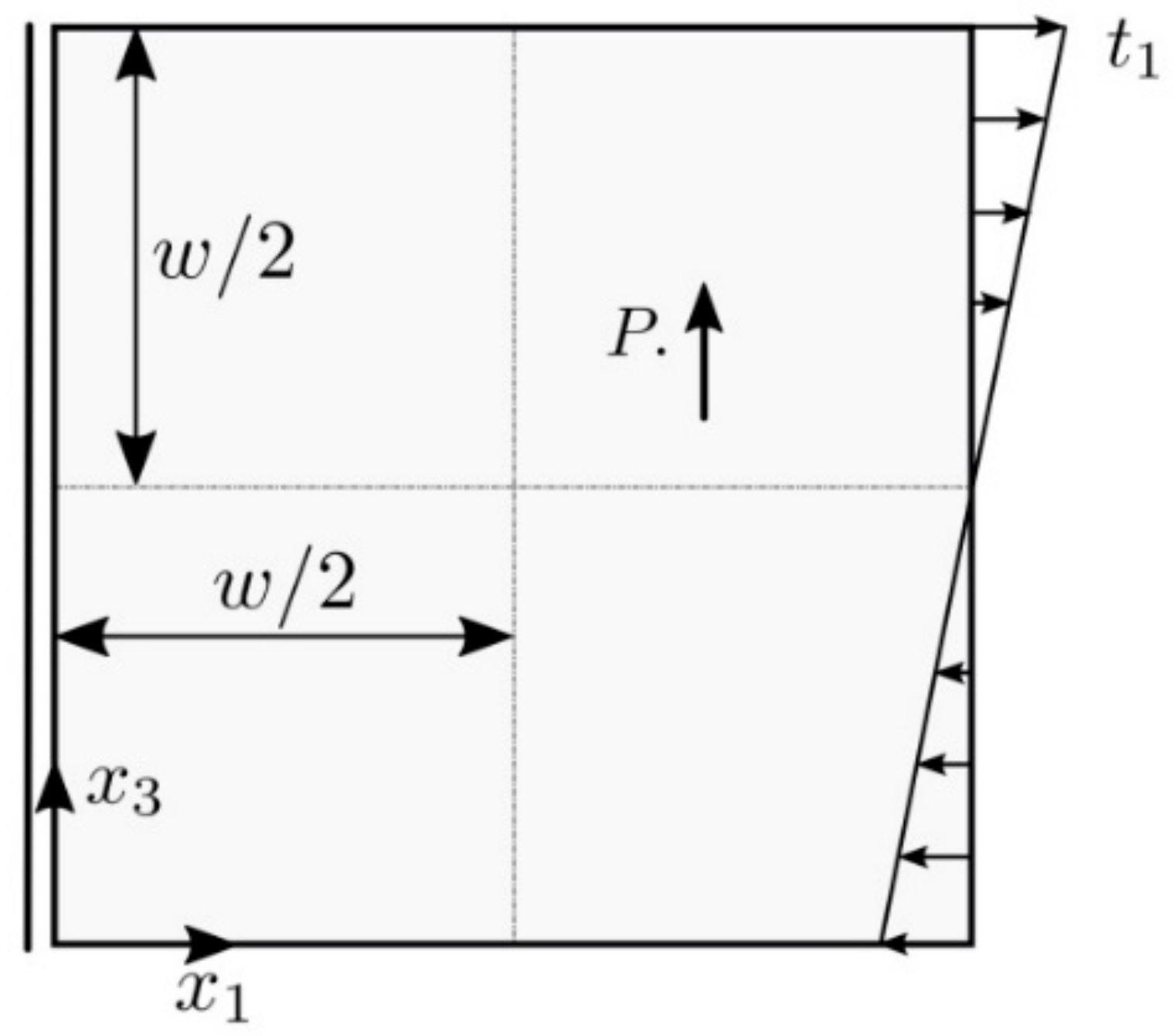
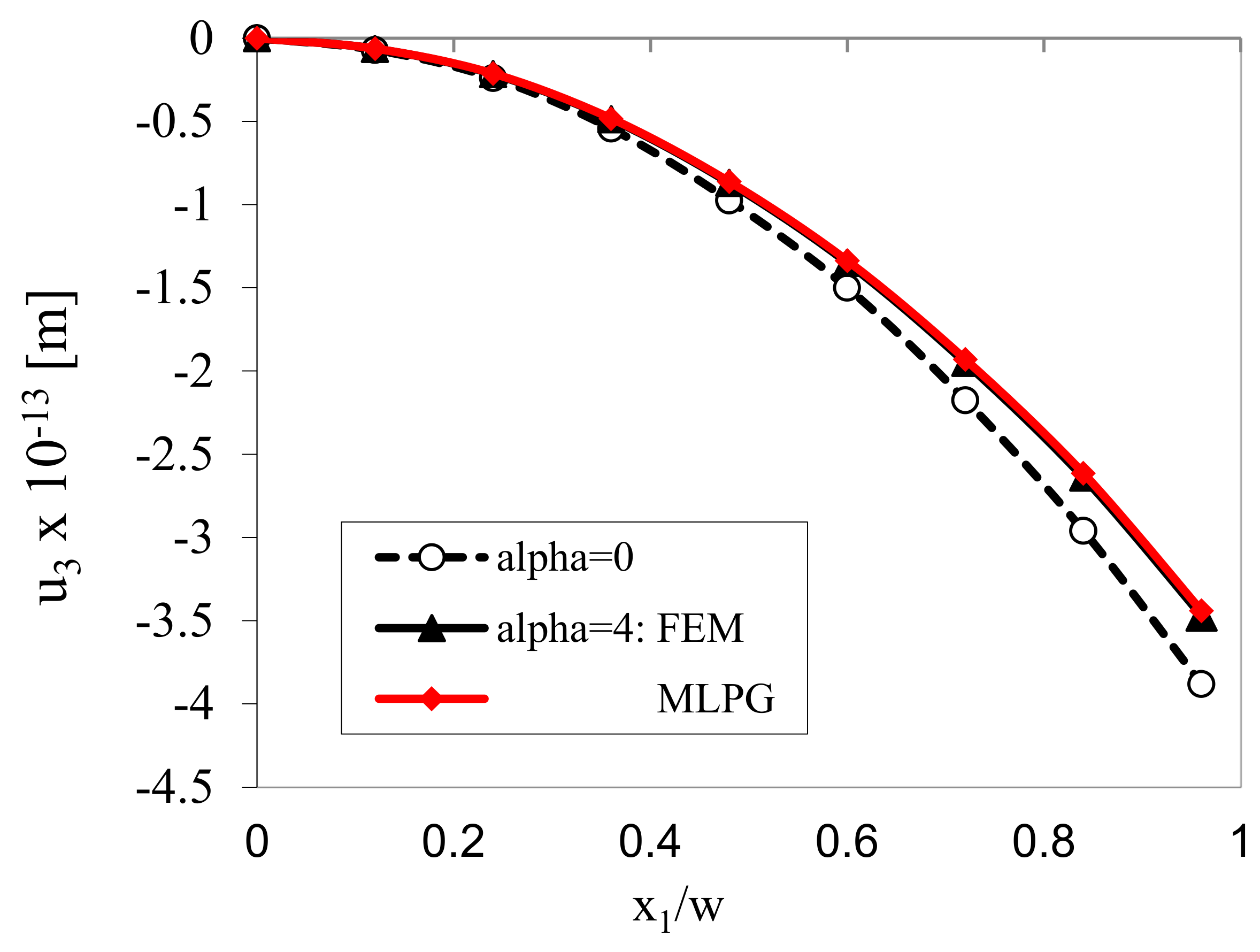
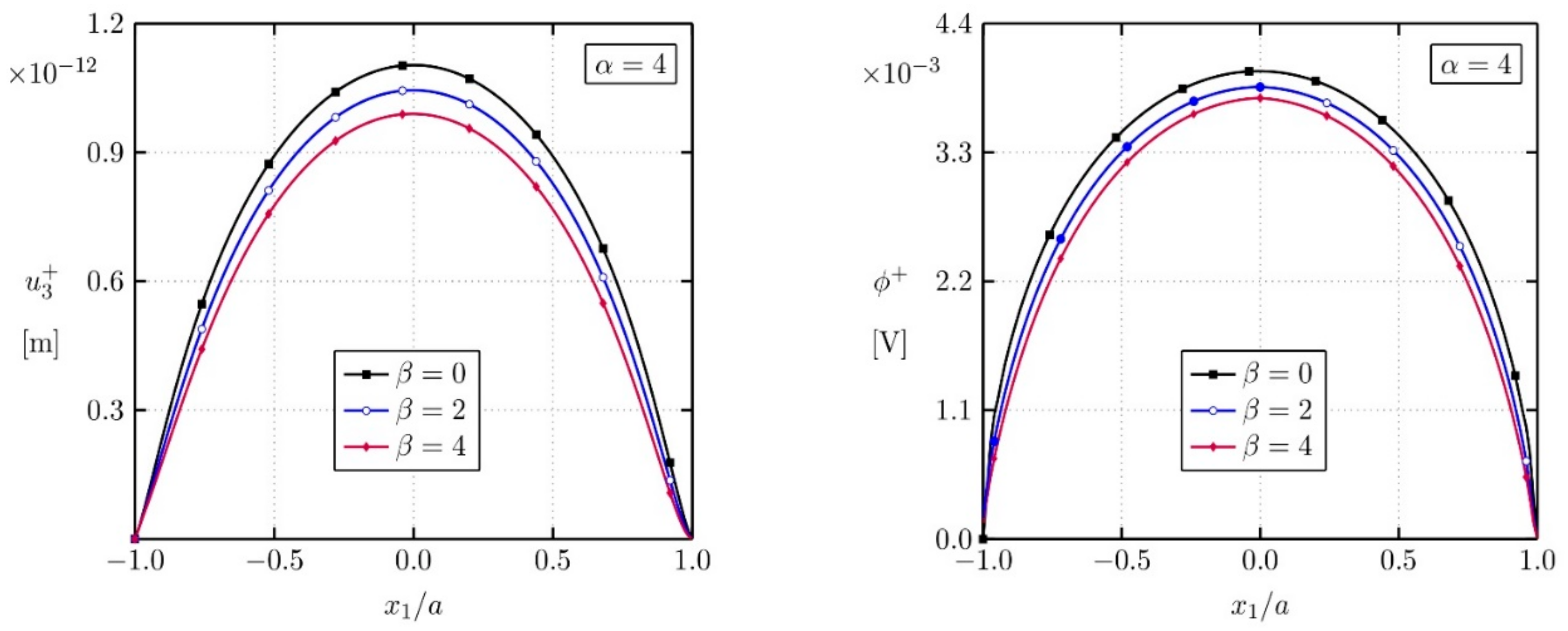
2.3. Numerical Examples
3. Gradient Theory in Thermoelectric Materials
3.1. The MLPG Formulation in Thermoelectricity
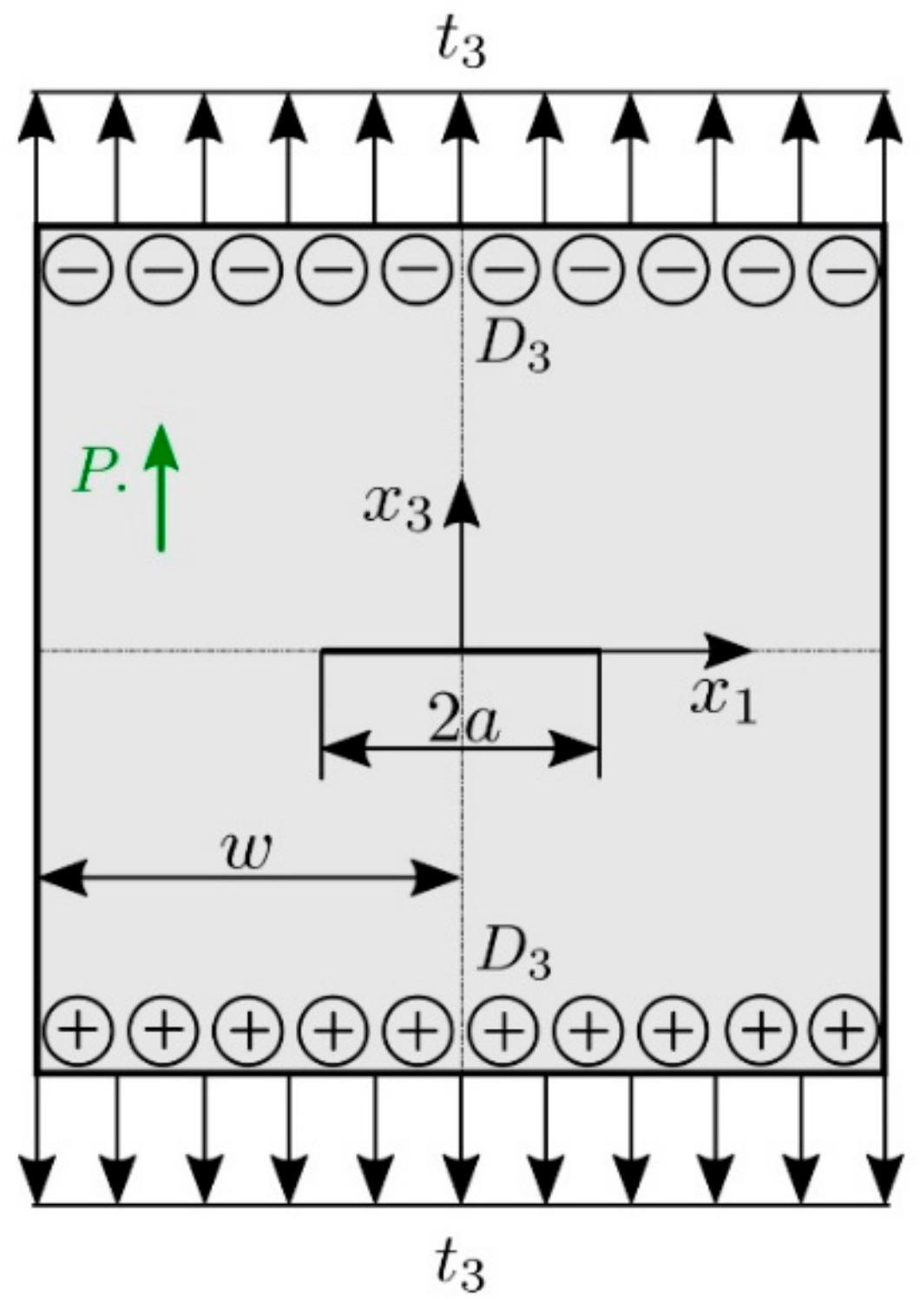
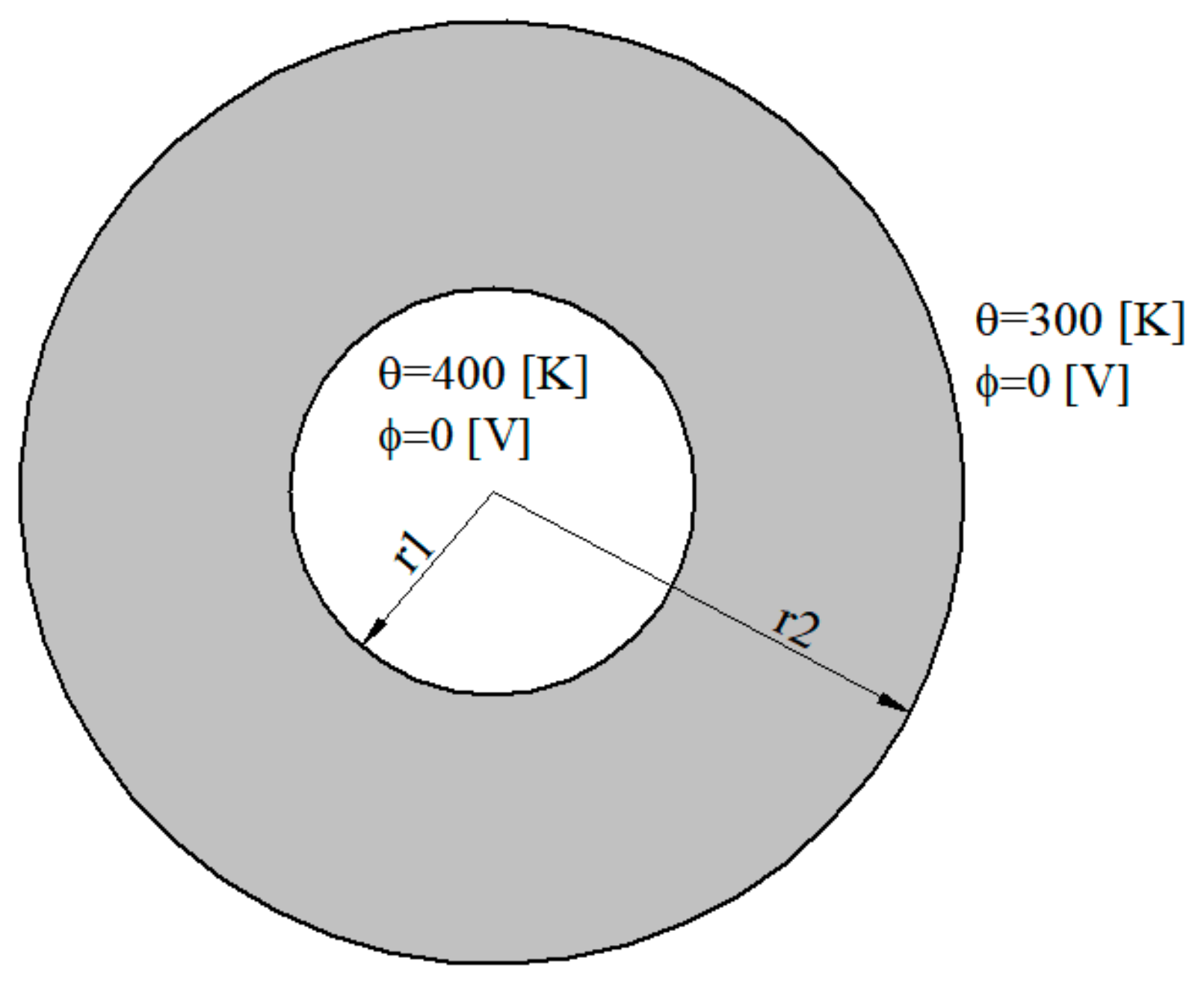
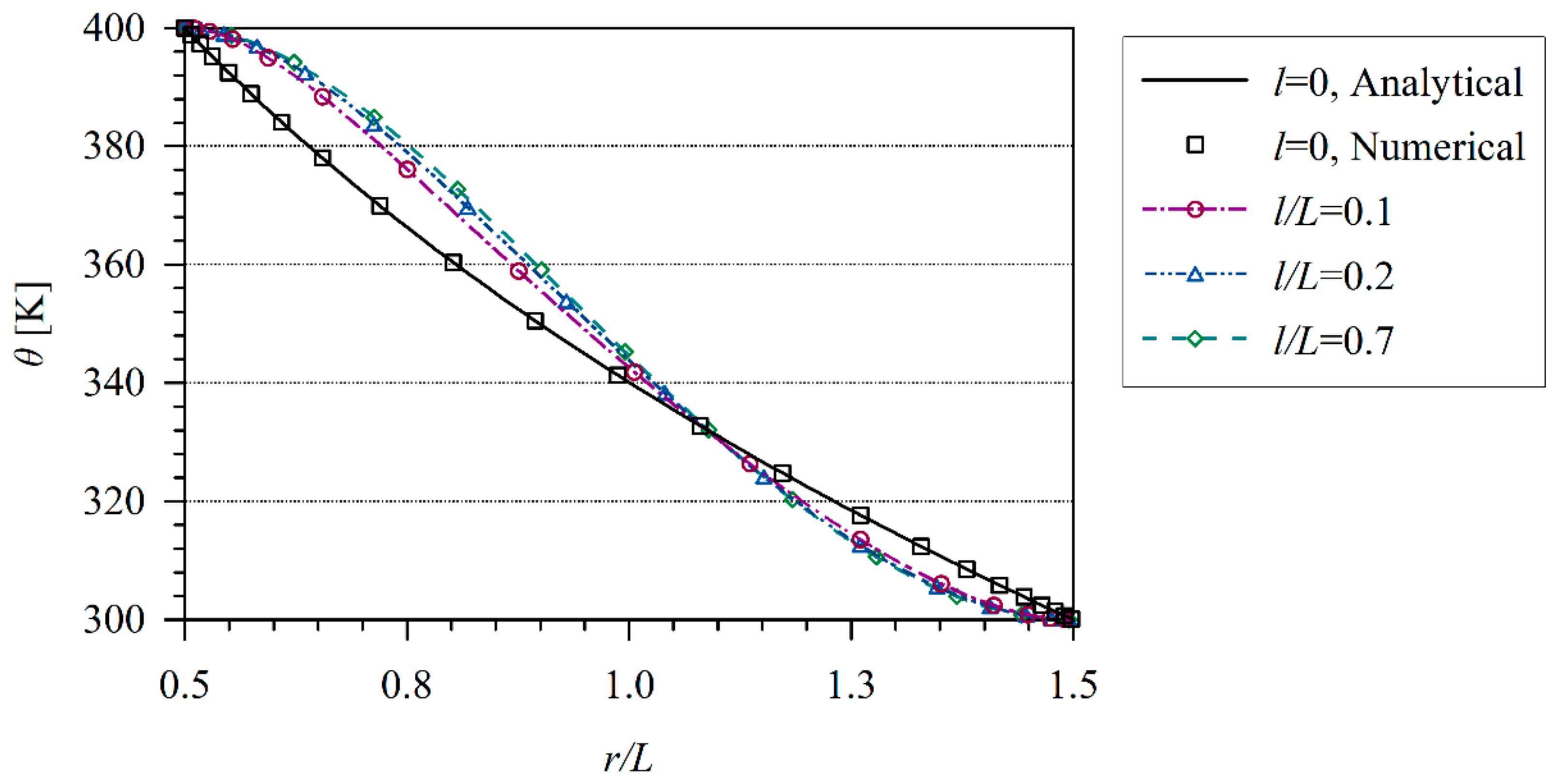
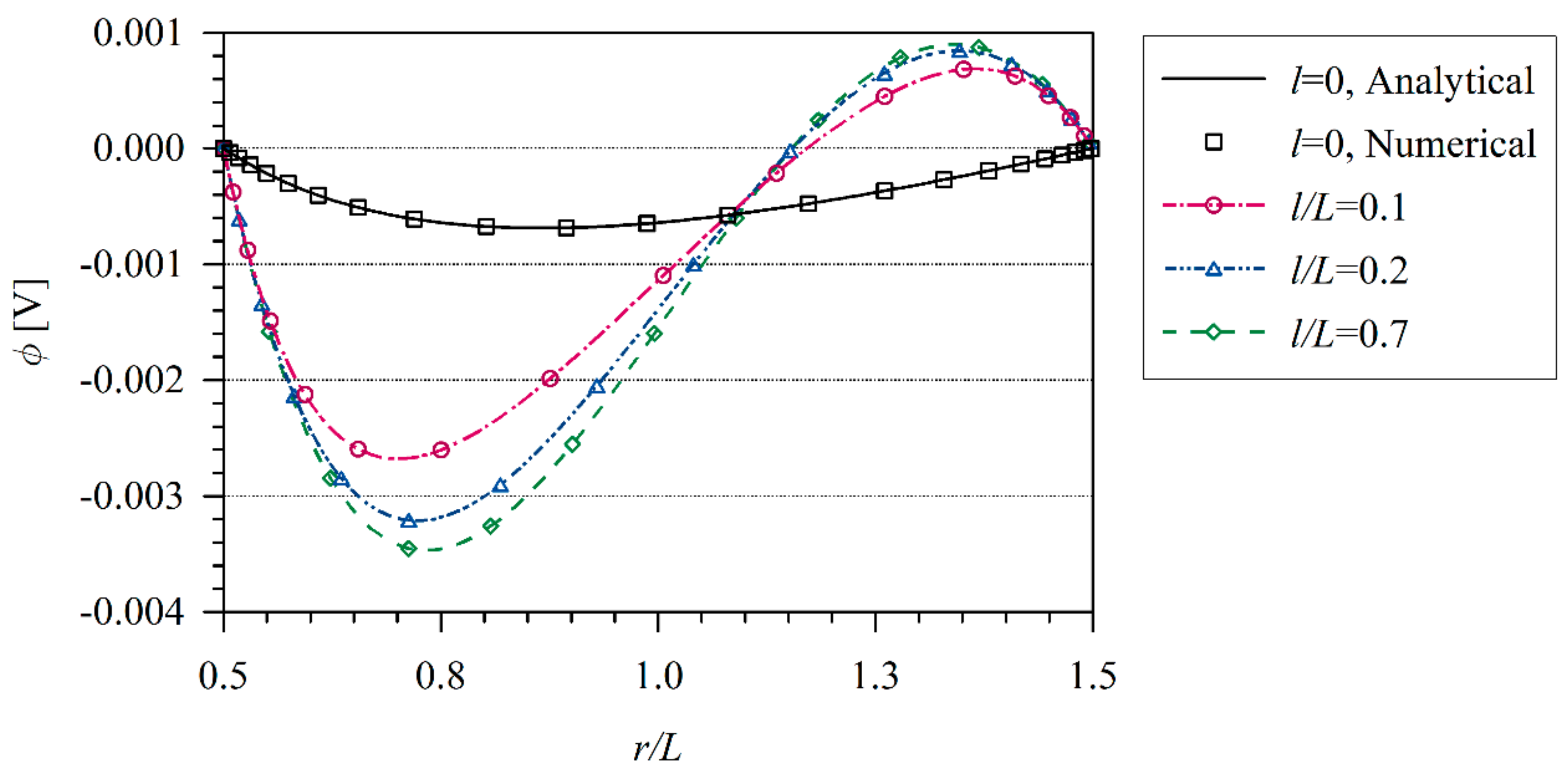
3.2. Numerical Examples
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Buhlmann, S.; Dwir, B.; Baborowski, J.; Muralt, P. Size effects in mesoscopic epitaxial ferroelectric structures: Increase of piezoelectric response with decreasing feature-size. Appl. Phys. Lett. 2002, 80, 3195–3197. [Google Scholar] [CrossRef]
- Cross, L.E. Flexoelectric effects: Charge separation in insulating solids subjected to elastic strain gradients. J. Mater. Sci. 2006, 41, 53–63. [Google Scholar] [CrossRef]
- Harden, J.; Mbanga, B.; Eber, N.; Fodor-Csorba, K.; Sprunt, S.; Gleeson, J.T.; Jakli, A. Giant flexoelectricity of bent-core nematic liquid crystals. Phys. Rev. Lett. 2006, 97, 157802. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Fu, J.Y.; Li, N.; Cross, L.E. Piezoelectric composite based on the enhanced flexoelectric effects. Appl. Phys. Lett. 2006, 89, 192904. [Google Scholar] [CrossRef]
- Catalan, G.; Lubk, A.; Vlooswijk, A.H.G.; Snoeck, E.; Magen, C.; Janssens, A.; Rispens, G.; Rijnders, G.; Blank, D.H.A.; Noheda, B. Flexoelectric rotation of polarization in ferroelectric thin films. Nat. Mater. 2011, 10, 963–967. [Google Scholar] [CrossRef]
- Kogan, S.M. Piezoelectric effect during inhomogeneous deformation and acoustic scattering of carriers in crystals. Sov. Phys. Solid State 1964, 5, 2069–2070. [Google Scholar]
- Meyer, R.B. Piezoelectric effects in liquid crystals. Phys. Rev. Lett. 1969, 22, 918–921. [Google Scholar] [CrossRef]
- Sharma, P.; Maranganti, R.; Sharma, N.D. On the possibility of piezoelectric nanocomposites without using piezoelectric materials. J. Mech. Phys. Solids 2007, 55, 2328–2350. [Google Scholar] [CrossRef]
- Deng, Q.; Liu, L.; Sharma, P. Flexoelectricity in soft materials and biological membranes. J. Mech. Phys. Solids 2014, 62, 209–227. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Electrodynamics of Continuous Media, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 1984; pp. 358–371. [Google Scholar]
- Yang, J.S. Effects of electric field gradient on an antiplane crack in piezoelectric ceramics. Int. J. Fract. 2004, 127, L111–L116. [Google Scholar] [CrossRef]
- Yang, X.M.; Hu, Y.T.; Yang, J.S. Electric field gradient effects in anti-plane problems of polarized ceramics. Int. J. Solids Struct. 2004, 41, 6801–6811. [Google Scholar] [CrossRef]
- Hicks, L.; Dresselhaus, M.S. Thermoelectric figure of merit of avone-dimensional conductor. Phys. Rev. B 1993, 47, 16631. [Google Scholar] [CrossRef] [PubMed]
- Minnich, A.J.; Dresselhaus, M.S.; Ren, Z.F.; Chen, G. Bulk nanostructured thermoelectric materials: Current research and future prospects. Energy Envir. Sci. 2009, 2, 466–479. [Google Scholar] [CrossRef]
- Eringen, A.C. Non-local polar field theory. In Continuum Physics; Eringen, A.C., Ed.; Academic Press: New York, NY, USA, 1976; Volume 4. [Google Scholar]
- Mindlin, R.D. Micro-structure in linear elasticity. Arch. Ration. Mech. Anal. 1964, 16, 51–78. [Google Scholar] [CrossRef]
- Mindlin, R.D. Second gradient of strain and surface-tension in linear elasticity. Int. J. Solids Struct. 1965, 1, 417–438. [Google Scholar] [CrossRef]
- Aifantis, E. On the microstructural origin of certain inelastic models. ASME J. Eng. Mater. Tech. 1984, 106, 326–330. [Google Scholar] [CrossRef]
- Allen, P.B. Size effects in thermal conduction by phonons. Phys. Rev. B. 2014, 90, 054301. [Google Scholar] [CrossRef]
- Silling, S.A. Reformulation of elasticity theory for discontinuities and large-range forces. J. Mech. Phys. Sol. 2000, 48, 175–209. [Google Scholar] [CrossRef]
- Silling, S.A.; Askari, E.A. meshfree method based on the peridynamic model of solid mechanic. Comput. Struct. 2005, 83, 1526–1535. [Google Scholar] [CrossRef]
- Shojaei, A.; Mudric, T.; Zaccariotto, M.; Galvanetto, V.A. Coupled meshless finite point/peridynamic method for 2D dynamic fracture analysis. Int. J. Mech. Sci. 2016, 119, 419–431. [Google Scholar] [CrossRef]
- Ren, B.; Fan, H.; Bergel, G.L.; Regueiro, R.A.; Lai, X.; Li, S. A peridynamics–SPH coupling approach to simulate soil fragmentation induced shock waves. Comput. Mech. 2015, 55, 287–302. [Google Scholar] [CrossRef]
- Shojaei, A.; Zaccariotto, M.; Galvanetto, V. Coupling of 2D discretized peridynamics with a meshless method based on classical elasticity using switching nodal behaviour. Eng. Comput. 2017, 34, 1334–1366. [Google Scholar] [CrossRef]
- Deng, F.; Deng, Q.; Yu, W.; Shen, S. Mixed finite elements for flexoelectric solids. J. Appl. Mech. 2017, 84, 081004. [Google Scholar] [CrossRef]
- Dong, L.; Atluri, S.N. A simple procedure to develop efficient & stable hybrid/mixed elements, and Voronoi cell finite elements for macro- & micromechanics. CMC: Comput. Mater. Contin. 2011, 24, 61–104. [Google Scholar]
- Atluri, S.N. The Meshless Method (MLPG) for Domain and BIE Discretizations; Tech Science Press: Forsyth, GA, USA, 2004. [Google Scholar]
- Sladek, J.; Stanak, P.; Han, Z.D.; Sladek, V.; Atluri, S.N. Applications of the MLPG method in engineering & Sciences: A review. CMES: Comput. Model. Engn. Sci. 2013, 92, 423–475. [Google Scholar]
- Sladek, J.; Sladek, V.; Repka, M.; Kasala, J.; Bishay, P. Evaluation of effective material properties in magneto-electro-elastic composite materials. Compos. Struct. 2017, 109, 176–186. [Google Scholar] [CrossRef]
- Maranganti, R.; Sharma, N.D.; Sharma, P. Electromechanical coupling in nonpiezoelectric materials due to nanoscale nonlocal size effects: Green’s function solutions and embedded inclusions. Phys. Rev. B. 2006, 74, 014110. [Google Scholar] [CrossRef]
- Hu, S.L.; Shen, S.P. Electric field gradient theory with surface effect for nano-dielectrics. CMC: Comput. Mater. Contin. 2009, 13, 63–87. [Google Scholar]
- Altan, S.; Aifantis, E. On the structure of the mode III crack-tip in gradient elasticity. Scr. Metall. Mater. 1992, 26, 319–324. [Google Scholar] [CrossRef]
- Askes, H.; Aifantis, E. Gradient elasticity in statics and dynamics: An overview of formulations, length scale identification procedures, finite element implementations and new results. Int. J. Solids Struct. 2011, 48, 1962–1990. [Google Scholar] [CrossRef]
- Gitman, I.; Askes, H.; Kuhl, E.; Aifantis, E. Stress concentrations in fractured compact bone simulated with a special class of anisotropic gradient elasticity. Int. J. Solids Struct. 2010, 47, 1099–1107. [Google Scholar] [CrossRef]
- Yaghoubi, S.T.; Mousavi, S.M.; Paavola, J. Buckling of centrosymmetric anisotropic beam structures within strain gradient elasticity. Int. J. Solids Struct. 2017, 109, 84–92. [Google Scholar] [CrossRef]
- Parton, V.Z.; Kudryavtsev, B.A. Electromagnetoelasticity, Piezoelectrics and Electrically Conductive Solids; Gordon and Breach Science Publishers: New York, NY, USA, 1988. [Google Scholar]
- Sladek, J.; Sladek, V.; Wunsche, M.; Zhang, C. Effects of electric field and strain gradients on cracks in piezoelectric solids. Eur. J. Mech. A Solids 2018, 71, 187–198. [Google Scholar] [CrossRef]
- Sladek, J.; Sladek, V.; Repka, M.; Schmauder, S. Mixed FEM for quantum nanostructured solar cells. Compos. Struct. 2019, 229, 111460. [Google Scholar] [CrossRef]
- Atluri, S.N.; Sladek, J.; Sladek, V.; Zhu, T. The local boundary integral equation (LBIE) and its meshless implementation for linear elasticity. Comput. Mech. 2000, 25, 180–198. [Google Scholar]
- Sladek, V.; Sladek, J.; Zhang, C. Computation of stresses in non-homogeneous elastic solids by local integral equation method: A comparative study. Comput. Mech. 2008, 41, 827–845. [Google Scholar] [CrossRef]
- Argyris, J.H.; Fried, I.; Scharpf, D.W. The tuba family of plate elements for the matrix displacement method. Aeronaut. J Royal Soc. 1968, 72, 701–709. [Google Scholar] [CrossRef]
- Yang, Y.; Gao, C.; Li, J. The effective thermoelectric properties of core-shell composites. Acta Mech. 2014, 225, 1211–1222. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sladek, J.; Sladek, V.; Wen, P.H. The Meshless Analysis of Scale-Dependent Problems for Coupled Fields. Materials 2020, 13, 2527. https://doi.org/10.3390/ma13112527
Sladek J, Sladek V, Wen PH. The Meshless Analysis of Scale-Dependent Problems for Coupled Fields. Materials. 2020; 13(11):2527. https://doi.org/10.3390/ma13112527
Chicago/Turabian StyleSladek, Jan, Vladimir Sladek, and Pihua H. Wen. 2020. "The Meshless Analysis of Scale-Dependent Problems for Coupled Fields" Materials 13, no. 11: 2527. https://doi.org/10.3390/ma13112527
APA StyleSladek, J., Sladek, V., & Wen, P. H. (2020). The Meshless Analysis of Scale-Dependent Problems for Coupled Fields. Materials, 13(11), 2527. https://doi.org/10.3390/ma13112527




