Dynamics of Bose–Einstein Condensates Subject to the Pöschl–Teller Potential through Numerical and Variational Solutions of the Gross–Pitaevskii Equation
Abstract
1. Introduction
2. The Dynamical Model
2.1. The Gross–Pitaevskii Equation
2.2. The External Potential
2.3. The Pöschl–Teller Potential
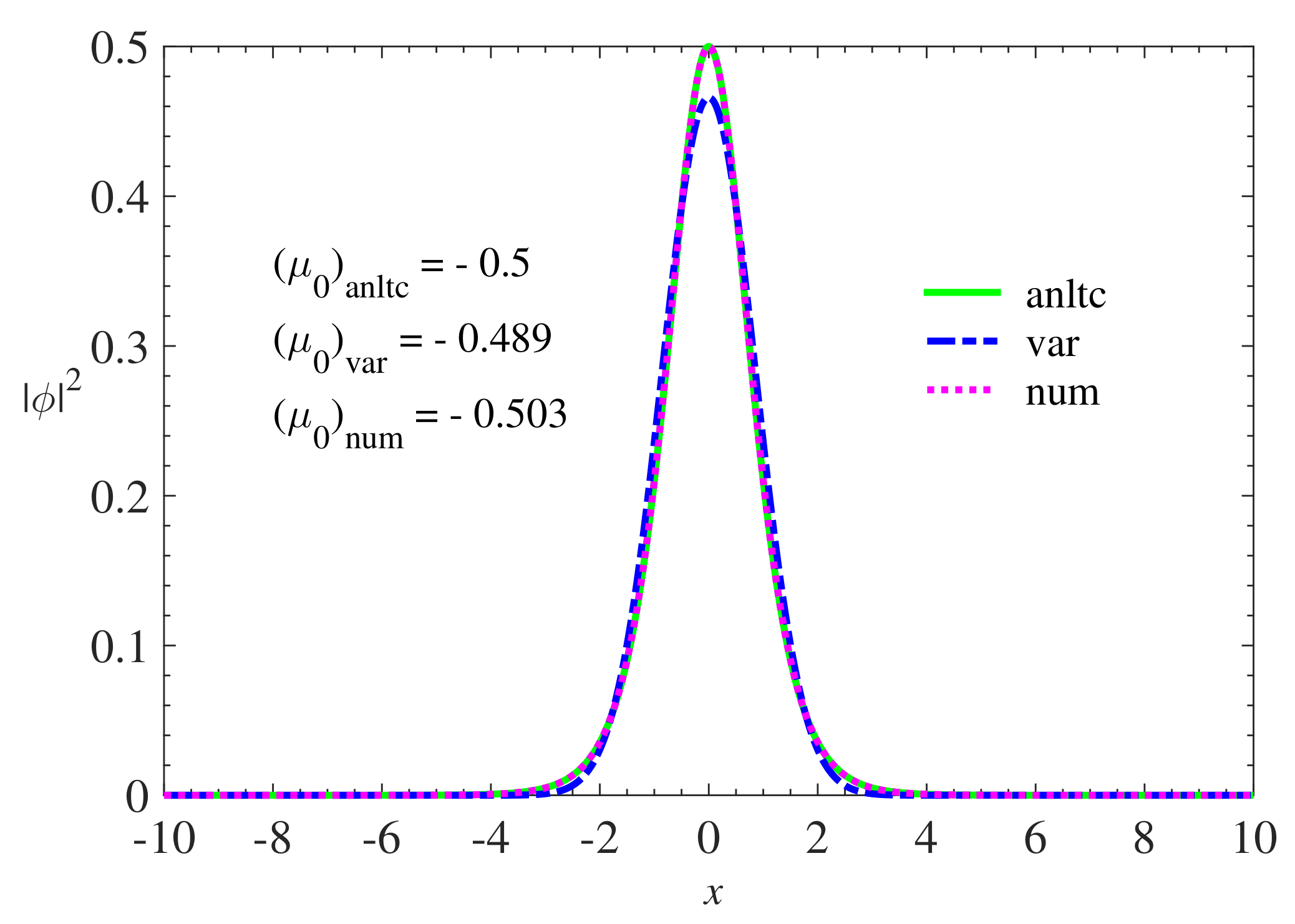
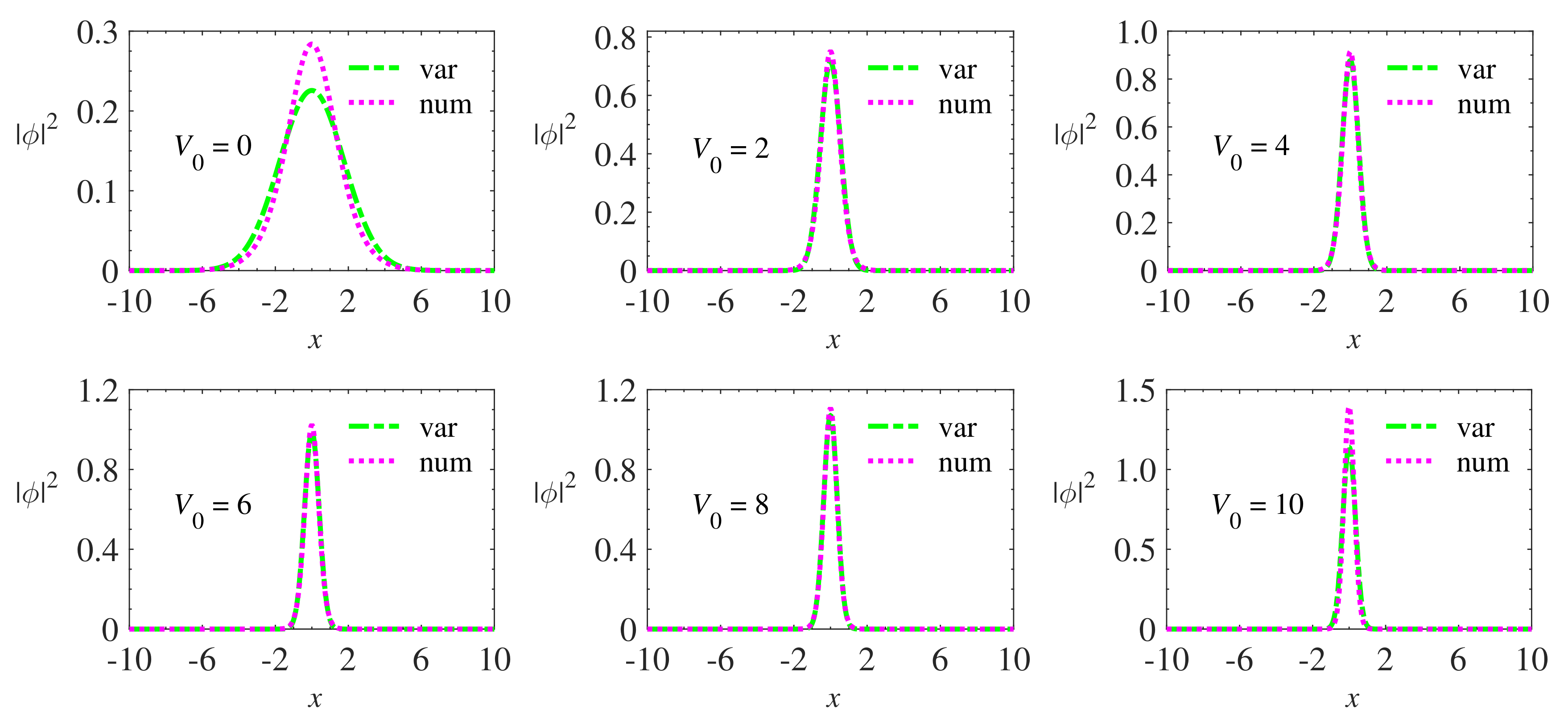
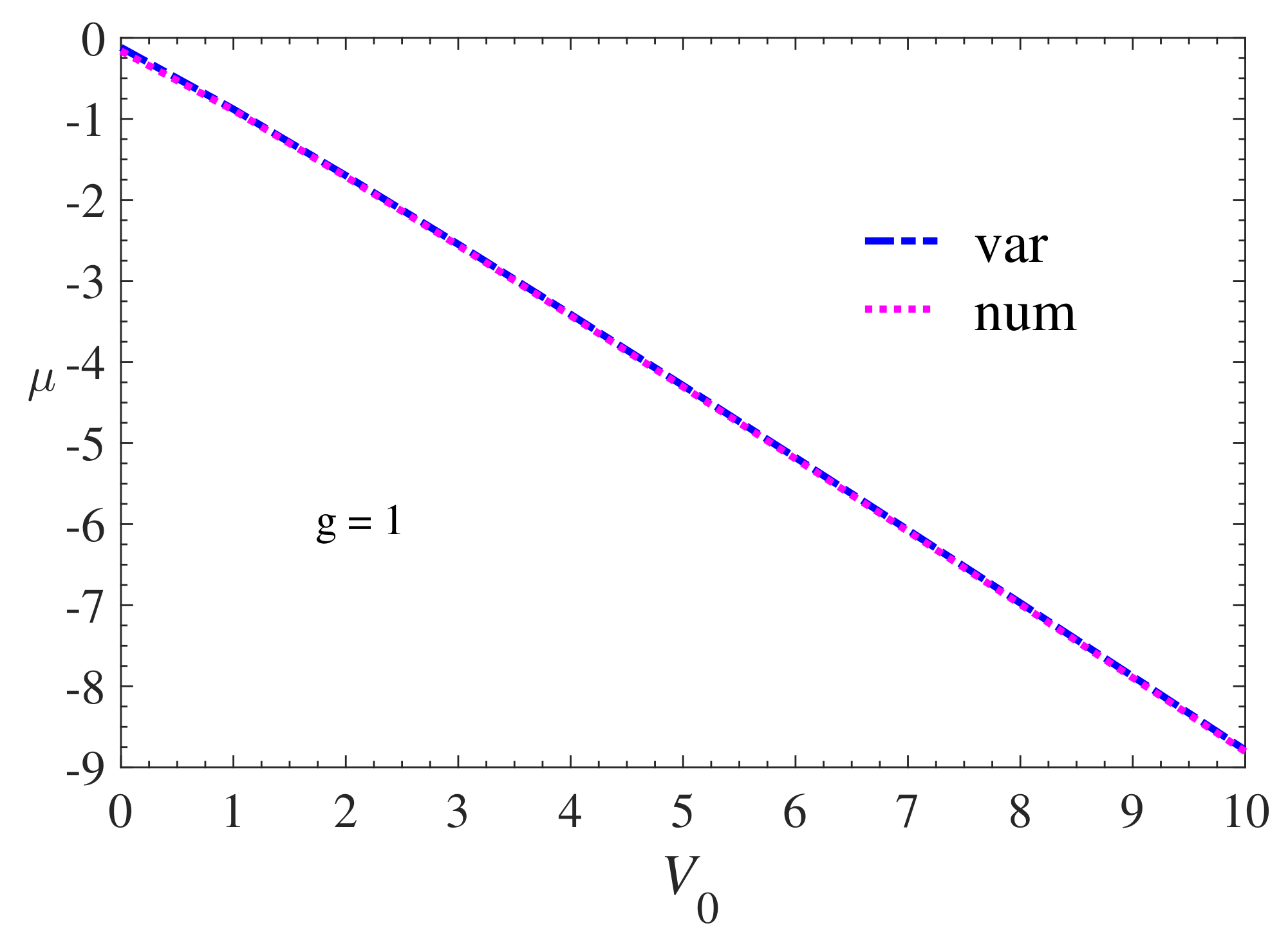
3. Results
3.1. Variational Results
3.2. Numerical Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ornes, S. Core Concept: How Bose-Einstein condensates keep revealing weird physics. Proc. Natl. Acad. Sci. USA 2017, 114, 5766–5768. Available online: https://www.pnas.org/content/114/23/5766.full.pdf (accessed on 12 April 2020). [CrossRef] [PubMed]
- Lundblad, N.; Carollo, R.A.; Lannert, C.; Gold, M.J.; Jiang, X.; Paseltiner, D.; Sergay, N.; Aveline, D.C. Shell potentials for microgravity Bose-Einstein condensates. NPJ Microgravity 2019, 5, 30. [Google Scholar] [CrossRef] [PubMed]
- Rogel-Salazar, J. The Gross-Pitaevskii equation and Bose-Einstein condensates. Eur. J. Phys. 2013, 34, 247–257. [Google Scholar] [CrossRef]
- Bloch, I. Ultracold quantum gases in optical lattices. Nat. Phys. 2005, 1, 23–30. [Google Scholar] [CrossRef]
- Dong, L.; Huang, C. Composition Relation between Nonlinear Bloch Waves and Gap Solitons in Periodic Fractional Systems. Materials 2018, 11, 1134. [Google Scholar] [CrossRef]
- Li, W.; Smerzi, A. Nonlinear Krönig-Penney model. Phys. Rev. E 2004, 70, 016605. [Google Scholar] [CrossRef]
- Charukhchyan, M.V.; Sedov, E.S.; Arakelian, S.M.; Alodjants, A.P. Spatially localized structures and oscillons in atomic Bose-Einstein condensates confined in optical lattices. Phys. Rev. A 2014, 89, 063624. [Google Scholar] [CrossRef]
- Sedov, E.S.; Charukhchyan, M.V.; Arakelian, S.M.; Alodjants, A.P.; Chuang, Y.; Lee, R. Atomic Bose–Einstein condensates as nonlinear hyperbolic metamaterials. In Proceedings of the 2015 Days on Diffraction (DD), St. Petersburg, Russia, 25–29 May 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Bradley, C.C.; Sackett, C.A.; Hulet, R.G. Bose-Einstein Condensation of Lithium: Observation of Limited Condensate Number. Phys. Rev. Lett. 1997, 78, 985–989. [Google Scholar] [CrossRef]
- Burger, S.; Bongs, K.; Dettmer, S.; Ertmer, W.; Sengstock, K.; Sanpera, A.; Shlyapnikov, G.V.; Lewenstein, M. Dark Solitons in Bose–Einstein Condensates. Phys. Rev. Lett. 1999, 83, 5198–5201. [Google Scholar] [CrossRef]
- Louis, P.J.Y.; Ostrovskaya, E.A.; Savage, C.M.; Kivshar, Y.S. Bose-Einstein condensates in optical lattices: Band-gap structure and solitons. Phys. Rev. A 2003, 67, 013602. [Google Scholar] [CrossRef]
- Louis, P.J.Y.; Ostrovskaya, E.A.; Kivshar, Y.S. Matter-wave dark solitons in optical lattices. J. Opt. Quantum Semiclassical Opt. 2004, 6, S309–S317. [Google Scholar] [CrossRef]
- Bloch, I. Quantum coherence and entanglement with ultracold atoms in optical lattices. Nature 2008, 453, 1016–1022. [Google Scholar] [CrossRef] [PubMed]
- Gross, C.; Bloch, I. Quantum simulations with ultracold atoms in optical lattices. Science 2017, 357, 995–1001. Available online: http://science.sciencemag.org/content/357/6355/995.full.pdf (accessed on 12 April 2020). [CrossRef] [PubMed]
- Adhikari, S.K.; Malomed, B.A. Gap solitons in a model of a superfluid fermion gas in optical lattices. Nonlinear Phenomena in Degenerate Quantum Gases. Phys. Nonlinear Phenom. 2009, 238, 1402–1412. [Google Scholar] [CrossRef]
- Malomed, B.A.; Nascimento, V.A.; Adhikari, S.K. Gap solitons in fermion superfluids. Nonlinear Waves: Computation and Theory VIII. Math. Comput. Simul. 2009, 80, 648–659. [Google Scholar] [CrossRef]
- Ruostekoski, J.; Walls, D.F. Bose-Einstein condensate in a double-well potential as an open quantum system. Phys. Rev. A 1998, 58, R50–R53. [Google Scholar] [CrossRef]
- Milburn, G.J.; Corney, J.; Wright, E.M.; Walls, D.F. Quantum dynamics of an atomic Bose-Einstein condensate in a double-well potential. Phys. Rev. A 1997, 55, 4318–4324. [Google Scholar] [CrossRef]
- Jia, C.S.; Zhang, L.H.; Peng, X.L. Improved Pöschl-Teller potential energy model for diatomic molecules. Int. J. Quantum Chem. 2017, 117, e25383. Available online: https://onlinelibrary.wiley.com/doi/pdf/10.1002/qua.25383 (accessed on 12 April 2020). [CrossRef]
- Yahya, W.; Oyewumi, K. Thermodynamic properties and approximate solutions of the l-state Pöschl-Teller-type potential. J. Assoc. Arab. Univ. Basic Appl. Sci. 2016, 21, 53–58. [Google Scholar] [CrossRef]
- Park, C.S. Two-dimensional transmission through modified Pöschl-Teller potential in bilayer graphene. Phys. Rev. B 2015, 92, 165422. [Google Scholar] [CrossRef]
- Ikhdair, S.M.; Falaye, B.J. Approximate analytical solutions to relativistic and nonrelativistic Pöschl-Teller potential with its thermodynamic properties. Chem. Phys. 2013, 421, 84–95. [Google Scholar] [CrossRef]
- Lekner, J. Reflectionless eigenstates of the sech2 potential. Am. J. Phys. 2007, 75, 1151–1157. [Google Scholar] [CrossRef]
- Umarov, B.A.; Messikh, A.; Regaa, N.; Baizakov, B.B. Variational analysis of soliton scattering by external potentials. J. Phys. Conf. Ser. 2013, 435, 012024. [Google Scholar] [CrossRef]
- Sarath, R.; Vinodkumar, P.C. Bose-Einstein condensation in generalized Pöschl-Teller potential. Pramana 2015, 85, 77–89. [Google Scholar] [CrossRef]
- Madeira, L.; Gandolfi, S.; Schmidt, K.E.; Bagnato, V.S. Vortices in low-density neutron matter and cold Fermi gases. Phys. Rev. C 2019, 100, 014001. [Google Scholar] [CrossRef]
- Nath, A.; Roy, U. A unified model for an external trap in a cigar-shaped Bose-Einstein condensate. J. Phys. Math. Theor. 2014, 47, 415301. [Google Scholar] [CrossRef]
- Mück, W.; Pozzo, G. Quantum portrait of a black hole with Pöschl-Teller potential. J. High Energy Phys. 2014, 2014, 128. [Google Scholar] [CrossRef]
- Pérez-García, V.M.; Michinel, H.; Cirac, J.I.; Lewenstein, M.; Zoller, P. Dynamics of Bose-Einstein condensates: Variational solutions of the Gross-Pitaevskii equations. Phys. Rev. A 1997, 56, 1424–1432. [Google Scholar] [CrossRef]
- Muruganandam, P.; Adhikari, S. Fortran programs for the time-dependent Gross-Pitaevskii equation in a fully anisotropic trap. Comput. Phys. Commun. 2009, 180, 1888–1912. [Google Scholar] [CrossRef]
- Barenghi, C.; Parker, N. A Primer on Quantum Fluids; Springer Briefs in Physics; Springer International Publishing: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Kevrekidis, P.G.; Frantzeskakis, D.J.; Carretero-González, R. Basic Mean-Field Theory for Bose–Einstein Condensates. In Emergent Nonlinear Phenomena in Bose–Einstein Condensates: Theory and Experiment; Kevrekidis, P.G., Frantzeskakis, D.J., Carretero-González, R., Eds.; Springer: Berlin/Heidelberg, Germnay, 2008; pp. 3–21. [Google Scholar] [CrossRef]
- Salasnich, L. Bright solitons in ultracold atoms. Opt. Quantum Electron. 2017, 49, 409. [Google Scholar] [CrossRef]
- Pöschl, G.; Teller, E. Bemerkungen zur Quantenmechanik des anharmonischen Oszillators. Z. Phys. 1933, 83, 143–151. [Google Scholar] [CrossRef]
- Brown, E.; Hernández de la Peña, L. A Simplified Pöschl-Teller Potential: An Instructive Exercise for Introductory Quantum Mechanics. J. Chem. Educ. 2018, 95, 1989–1995. [Google Scholar] [CrossRef]
- Butkov, E. Física Matemática; LTC: Rio de Janeiro, Brazil, 1988. [Google Scholar]
- Arfken, G.; Weber, H. Física Matemática: Métodos Matemáticos Para Engenharia e Física; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Wang, H. Numerical studies on the split-step finite difference method for nonlinear Schrödinger equations. Appl. Math. Comput. 2005, 170, 17–35. [Google Scholar] [CrossRef]
- Sakurai, J. Advanced Quantum Mechanics; Always Learning, Incorporated; Pearson Education: London, UK, 1967. [Google Scholar]
- Inguscio, M.; Ketterle, W.; Salomon, C.; Italiana di Fisica, S. Gas Di Fermi Ultrafreddi; International School of Physics “Enrico Ferm”; IOS Press: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Nascimento, V. Estudo de gases quânticos em uma rede óptica utilizando aproximação variacional. Rev. Bras. Ensino FÍsica 2011, 33, 1–6. [Google Scholar] [CrossRef][Green Version]
- Sekh, G.A. Effects of spatially inhomogeneous atomic interactions on Bose-Einstein condensates in optical lattices. Phys. Lett. A 2012, 376, 1740–1747. [Google Scholar] [CrossRef]
- Nascimento, V.; Silva, C.; Lanoa, A.; Nascimento, V.A.; Silva, A.; Cassino, P. Uma abordagem variacional ao estudo de condensados de Bose–Einstein aprisionados por redes ópticas. Rev. Bras. Ensino FÍsica 2014, 36, 01–10. [Google Scholar] [CrossRef]
- Nascimento, V.; Silva, C.; Silva, A.; Guimarães, R.; Melo, E. Método variacional aplicado ao estudo de um gás de Átomos de Fermi em um estado superfluido aprisionados por uma rede óptica quase periódica. Rev. Bras. Ensino FÍSica 2016, 38. [Google Scholar] [CrossRef]
- Paes, R.; Nascimento, V.A.d.; Melo, E.S.d.P.; Guimarães, R.d.C.A.; Nascimento, V. Gases de átomos Fermiônicos aprisionados por uma rede quase periódica e um potencial harmônico bidimensional. Rev. Bras. Ensino FÍsica 2019, 41. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pereira, L.C.; Nascimento, V.A.d. Dynamics of Bose–Einstein Condensates Subject to the Pöschl–Teller Potential through Numerical and Variational Solutions of the Gross–Pitaevskii Equation. Materials 2020, 13, 2236. https://doi.org/10.3390/ma13102236
Pereira LC, Nascimento VAd. Dynamics of Bose–Einstein Condensates Subject to the Pöschl–Teller Potential through Numerical and Variational Solutions of the Gross–Pitaevskii Equation. Materials. 2020; 13(10):2236. https://doi.org/10.3390/ma13102236
Chicago/Turabian StylePereira, Lucas Carvalho, and Valter Aragão do Nascimento. 2020. "Dynamics of Bose–Einstein Condensates Subject to the Pöschl–Teller Potential through Numerical and Variational Solutions of the Gross–Pitaevskii Equation" Materials 13, no. 10: 2236. https://doi.org/10.3390/ma13102236
APA StylePereira, L. C., & Nascimento, V. A. d. (2020). Dynamics of Bose–Einstein Condensates Subject to the Pöschl–Teller Potential through Numerical and Variational Solutions of the Gross–Pitaevskii Equation. Materials, 13(10), 2236. https://doi.org/10.3390/ma13102236




