Design of a 2 × 4 Hybrid MMI-MZI Configuration with MMI Phase-Shifters
Abstract
1. Introduction
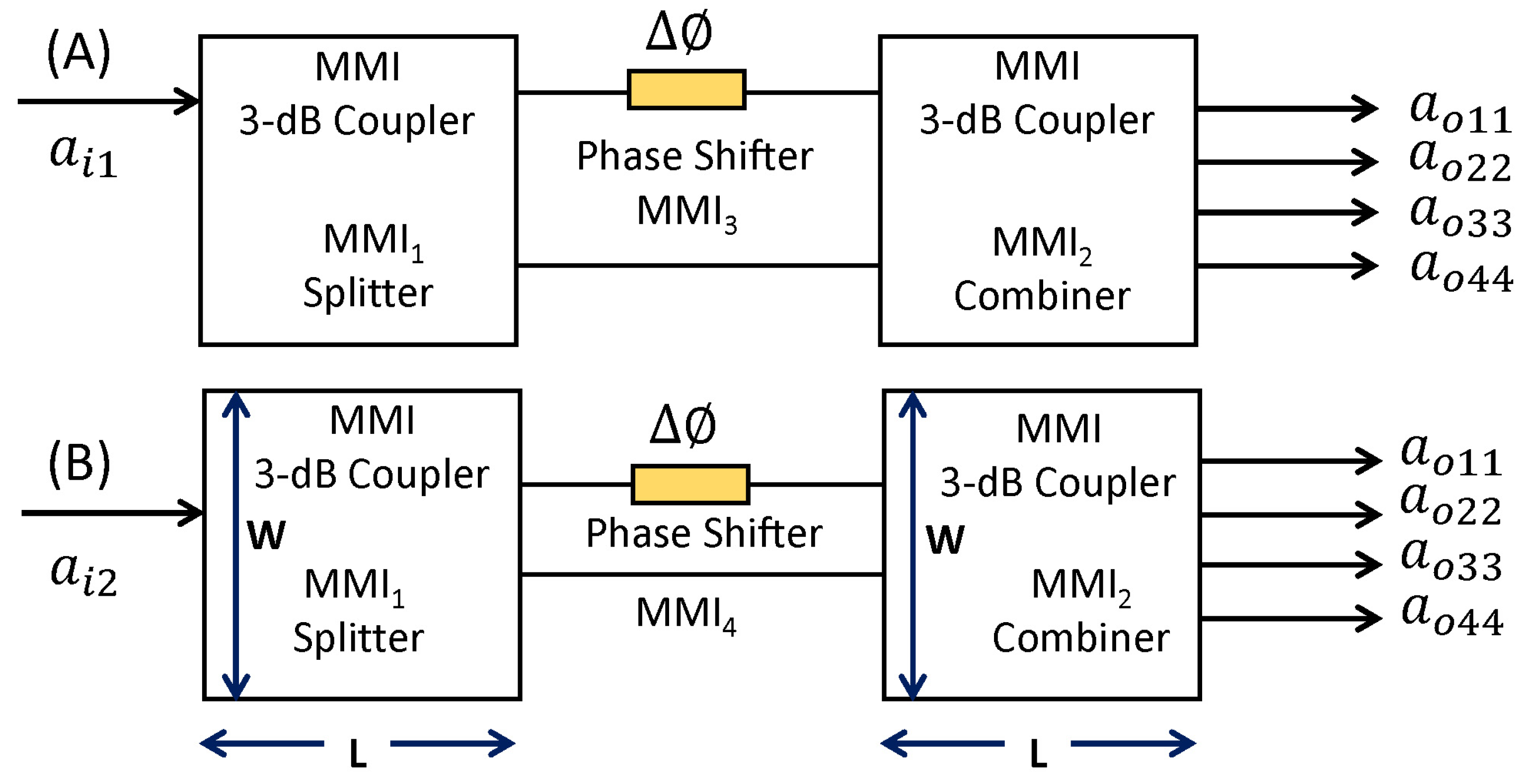
2. Design, Simulation, and Optimization
2.1. Multimode Interferometers
2.2. Access Waveguides
2.3. Phase Shifters
2.4. Thermo-Optic Heaters
3. Principle of Operation of the Device
4. Results and Discussions
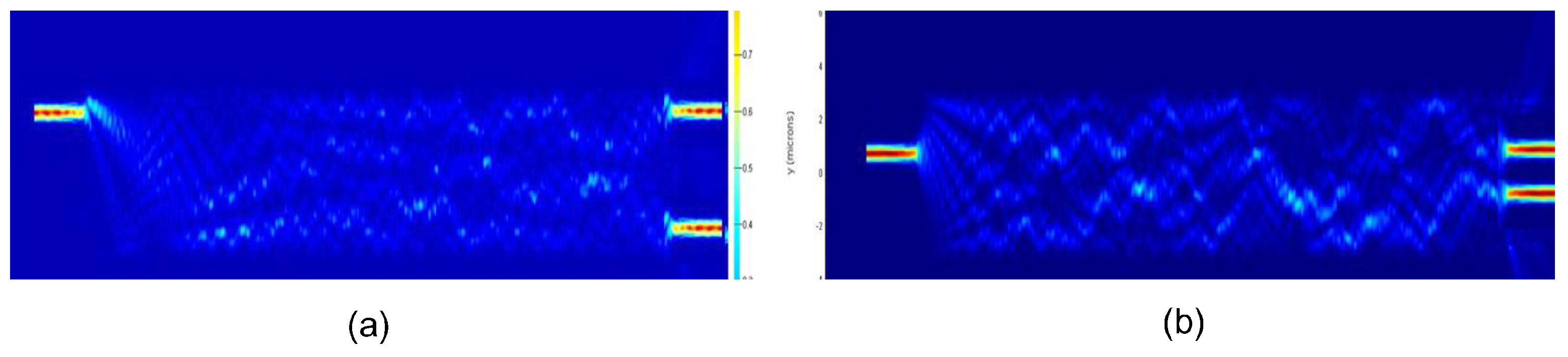
4.1. Field Distribution in the MMI Couplers /Decouplers
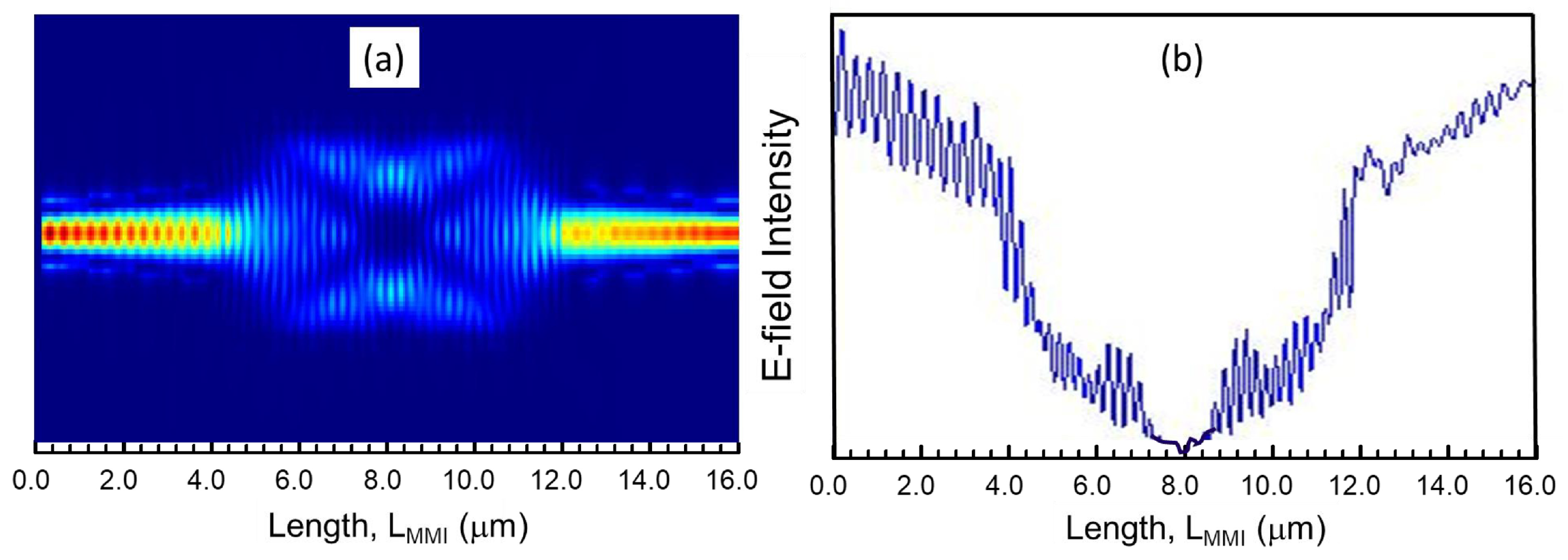
4.2. Field Distribution in the MMI Phase Shifters
4.3. Optical Characteristics of the Switching Device
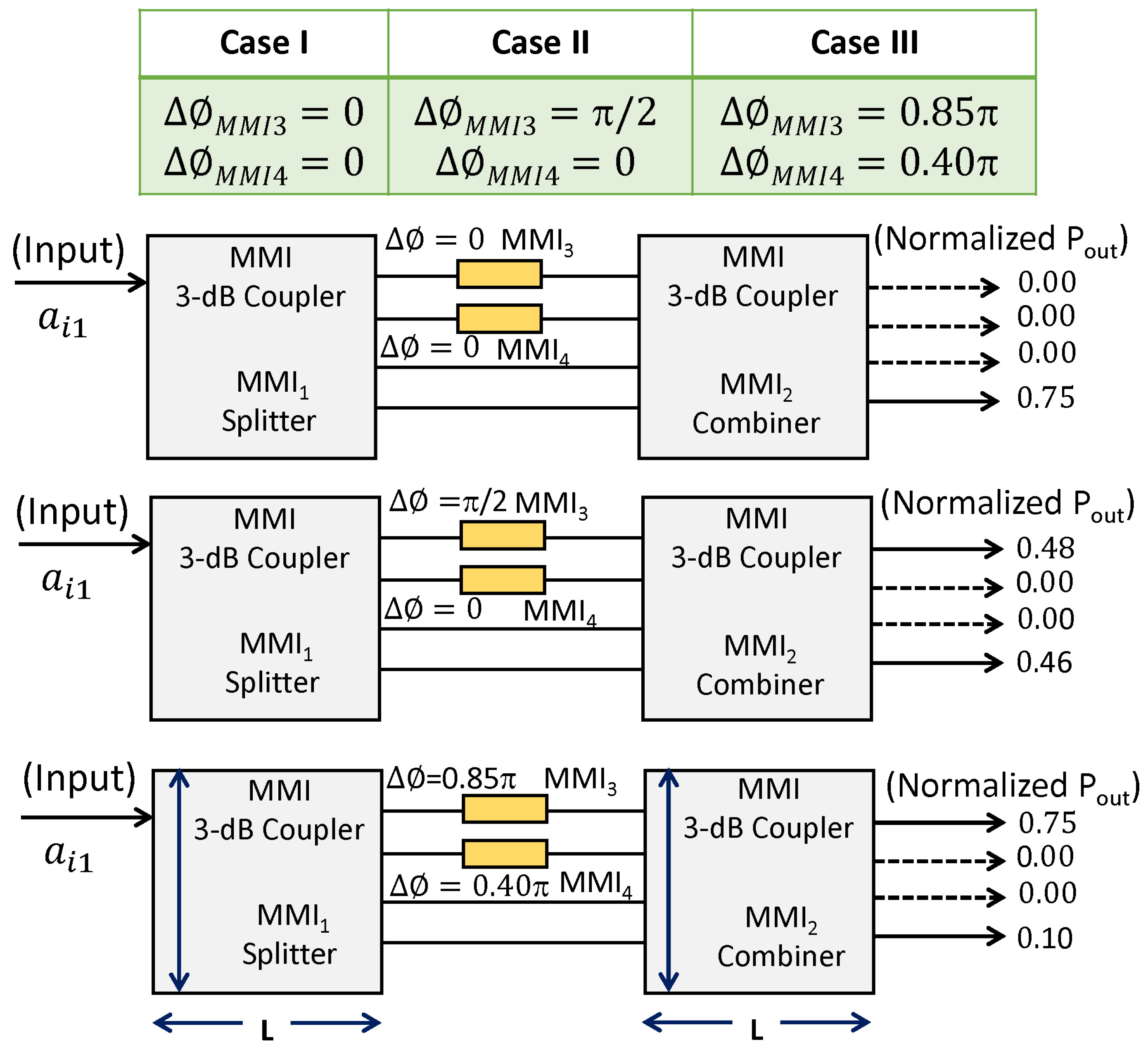
4.3.1. Case I: = 0, 0 (Heating Pads in MMI are Disabled)
4.3.2. Case II: = /2, 0 (Heating Pads in MMI are Enabled)
4.3.3. Case III: = 0.85, 0.40 (Heating Pads in MMI are Enabled)
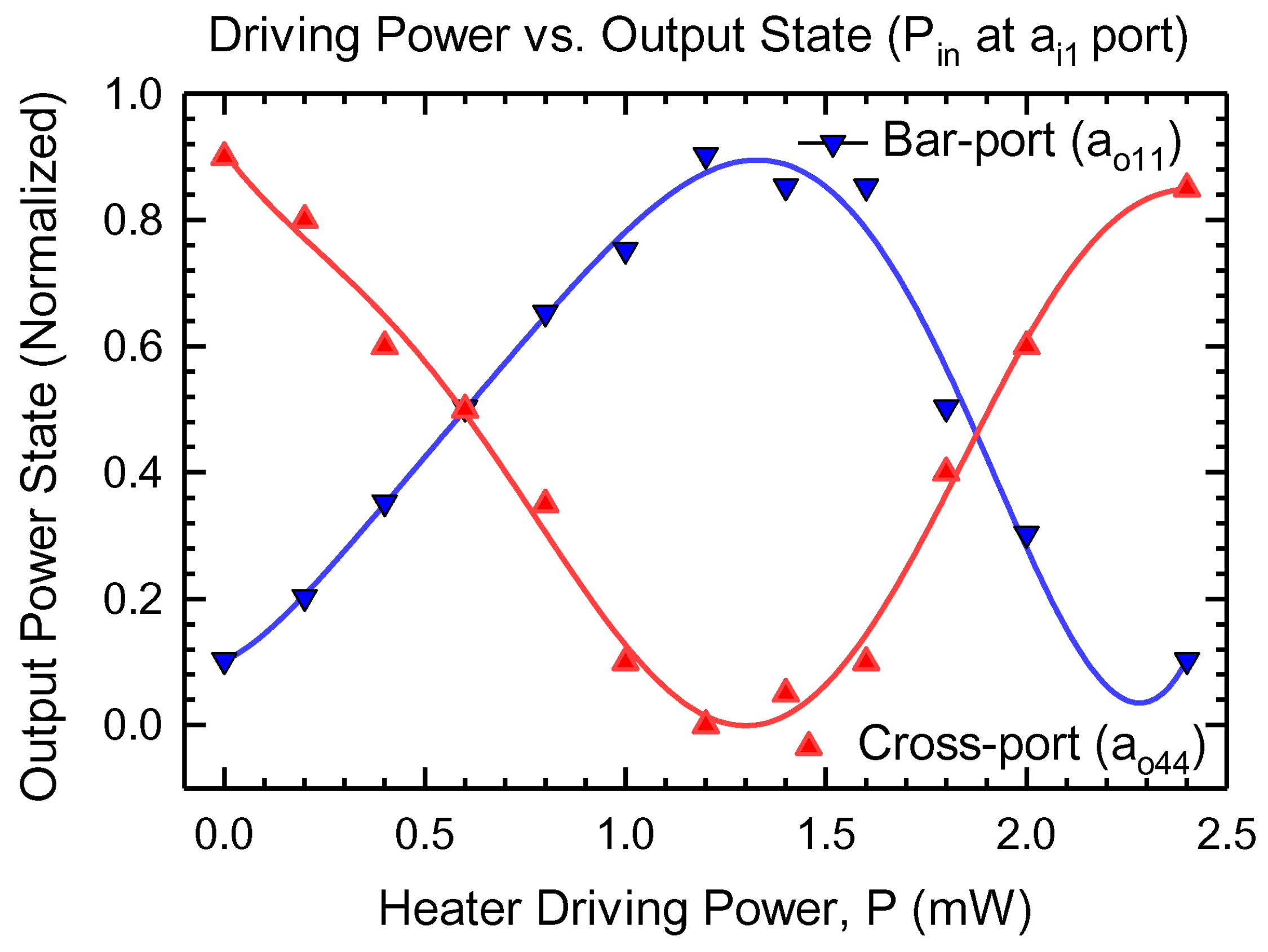
4.4. Output Power State vs Input Driving Power
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bonani, L.H. Modeling an optical network operating with hybrid-switching paradigms. J. Microw. Optoelectron. Electromagn. Appl. 2016, 15, 275–292. [Google Scholar] [CrossRef]
- For EpiPhotonics. Available online: http://www.epiphotonics.com (accessed on 18 March 2019).
- Gautam, R. Silicon Microring Resonator Loaded Mach-Zehnder Interferometer for Low Power Optical Modulation, Switching and Bio-Sensing. Ph.D. Thesis, Yokohama National University, Yokohama, Japan, 2014; pp. 1–153. [Google Scholar]
- Lu, L.; Zhou, L.; Li, S.; Li, Z.; Li, X.; Chen, J. 4 × 4 nonblocking silicon thermo-optic switches based on multimode interferometers. J. Lightwave Technol. 2015, 33, 857–864. [Google Scholar] [CrossRef]
- Boeck, R.; Caverley, M.; Chrostowski, L.; Jaeger, N.A.F. Experimental demonstration of a silicon-on-insulator high-performance double microring filter using MZI-based coupling. Opt. Lett. 2015, 40, 276–279. [Google Scholar] [CrossRef] [PubMed]
- Bryngdahl, O. Image formation using self-imaging techniques. J. Opt. Soc. Am. 1973, 63, 416–419. [Google Scholar] [CrossRef]
- Rizal, C.; Niraula, B. Compact Si-based asymmetric MZI waveguide on SOI as a thermo-optical switch. J. Opt. Commun. 2018, 410, 947–955. [Google Scholar] [CrossRef]
- Bryngdahl, O. Self-Imaging with an Optical Tunnel For Image Formation. U.S. Patent US3832029A, 27 August 1974. [Google Scholar]
- Heaton, J.M.; Jenkins, R.M. General matrix theory of self-imaging in multimode interference (MMI) couplers. IEEE Photonics Technol. Lett. 1999, 11, 212–214. [Google Scholar] [CrossRef]
- Bogaerts, W.; Fiers, M.; Dumon, P. Design challenges in silicon photonics. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 1–8. [Google Scholar] [CrossRef]
- Hamada, H. Theoretical time-domain study of self-imaging properties in a multimode interference coupler. Appl. Opt. 2007, 46, 3843–3849. [Google Scholar] [CrossRef] [PubMed]
- He, S.; Ao, X.; Romanov, V. General properties of N × M self-images in a strongly confined rectangular waveguide. Appl. Opt. 2003, 42, 4855–4859. [Google Scholar] [CrossRef] [PubMed]
- Soldano, L.B.; Pennings, E.C. Optical multi-mode interference devices based on self-imaging: Principles and applications. J. Lightwave Technol. 1995, 13, 615–627. [Google Scholar] [CrossRef]
- Berry, G.; Burke, S. Analysis of optical rib self-imaging multimode interference (MMI) waveguide devices using the discrete spectral index method. J. Opt. Quantum Electron. 1995, 27, 921–934. [Google Scholar] [CrossRef]
- Bachmann, M.; Besse, P.; Melchior, H. Overlapping-image multimode interference couplers with a reduced number of self-images for uniform and nonuniform power splitting. Appl. Opt. 1995, 34, 6898–6910. [Google Scholar] [CrossRef] [PubMed]
- Pennings, E.; Deri, R.J.; Scherer, A.; Bhat, R.; Hayes, T.R.; Andreadakis, N.C.; Smit, M.K.; Soldano, L.B.; Hawkins, R.J. Ultracompact, low-loss directional couplers on InP based on self-imaging by multimode interference. Appl. Phys. Lett. 1991, 59, 1926–1928. [Google Scholar] [CrossRef]
- Ulrich, R.; Ankele, G. Self-imaging in homogeneous planar optical waveguides. Appl. Phys. Lett. 1975, 27, 337–339. [Google Scholar] [CrossRef]
- Fallahkhair, A.B.; Kai, L.S.; Murphy, T.E. Vector finite difference modesolver for anisotropic dielectric waveguides. J. Lightwave Technol. 2008, 26, 1423–1431. [Google Scholar] [CrossRef]
- Sullivan, D.M.; Mossman, S.; Kuzyk, M.G. Time-Domain Simulation of Three Dimensional Quantum Wires. PLoS ONE 2016, 11, e0153802. [Google Scholar] [CrossRef] [PubMed]
- Pokharel, R.K.; Rizal, C.S. Design and characterization of a compact optical device based on Mach-zehnder interferometer in Silicon-on-insulator technology. In Proceedings of the 15th Annual Meeting of the Pacific Center for Advanced Materials (PCAMM), Vancouver, BC, Canada, 10 December 2011. [Google Scholar]
- Rizal, C.; Niraula, B. Nanoscale silicon waveguide based thermo-optic sensor using a compact Mach-zehnder interferometer. MDPI Photonics Electr. Electron. Eng. 2016. [Google Scholar] [CrossRef]
- Al-hetar, A.M.; Yulianti, I.; Supaat, A.S.M.; Mohammad, A. Thermo-optic multimode interference switches with air and silicon trenches. J. Opt. Commun. 2008, 281, 4653–4657. [Google Scholar] [CrossRef]
- Chrostowski, L.; Hochberg, M. Silicon Photonics Design—From Devices to Systems; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Le, T.-T.; Le, D.-T. Multimode waveguides on an SOI platform for arbitrary power splitting ratio couplers. In Emerging Waveguide Technology; You, K.Y., Ed.; IntechOpen: London, UK, 2018. [Google Scholar]
- Yoshioka, K. KyPlot—A user-oriented tool for statistical data analysis and visualization. Comput. Stat. 2002, 17, 425–437. [Google Scholar] [CrossRef]
- CMC Microsystem. Nano Silicon-on-Insulator Process Technology. 2019. Available online: http://www.cmc.ca/ (accessed on 18 March 2019).
| Components | Width (m) | Length (m) | Core Thickness (m) |
|---|---|---|---|
| MMIs: MMI, MMI | W = 6.0 | L = 140 | t = 0.22 |
| Access Waveguides, AWs | W = 0.5–8.0 | L = 4 | t = 0.22 |
| PSs: MMI, MMI | W = 1–2 | L = 8 | t = 0.22 |
| SN | Material | Thermal Conductivity, W/(m·K) | Heating Coefficient (/K) |
|---|---|---|---|
| 1 | Si | 163.25 | 160 × 10 |
| 2 | SiO | 1.405 | 8 × 10 |
| 3 | Al | 204 | 24 × 10 |
| Case | Output Position | Output State (Normalized Power) | |
|---|---|---|---|
| I | 0, 0 | a, a, a, a | 0,0,0,0.75 |
| II | /2, 0 | a, a, a, a | 0.48,0,0,0.46 |
| III | 0.85, 0.40 | a, a, a, a | 0.75,0,0,0.10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niraula, B.B.; Rizal, C. Design of a 2 × 4 Hybrid MMI-MZI Configuration with MMI Phase-Shifters. Materials 2019, 12, 1555. https://doi.org/10.3390/ma12091555
Niraula BB, Rizal C. Design of a 2 × 4 Hybrid MMI-MZI Configuration with MMI Phase-Shifters. Materials. 2019; 12(9):1555. https://doi.org/10.3390/ma12091555
Chicago/Turabian StyleNiraula, Boris B., and Conrad Rizal. 2019. "Design of a 2 × 4 Hybrid MMI-MZI Configuration with MMI Phase-Shifters" Materials 12, no. 9: 1555. https://doi.org/10.3390/ma12091555
APA StyleNiraula, B. B., & Rizal, C. (2019). Design of a 2 × 4 Hybrid MMI-MZI Configuration with MMI Phase-Shifters. Materials, 12(9), 1555. https://doi.org/10.3390/ma12091555






