Prediction and Sensitivity Analysis of Bubble Dissolution Time in 3D Selective Laser Sintering Using Ensemble Decision Trees
Abstract
:1. Introduction
2. Materials and Methods
2.1. Physical Problem and Data Preparation
2.1.1. Mechanical Description of the Bubble Dissolution Process
2.1.2. Factors that Affecting Bubble Dissolution Time
2.1.3. Datasets
2.2. Background of Models Used
2.2.1. Decision Trees Methods
Ensemble Bagged Trees (EDT Bagged)
Ensemble Boosted Trees (EDT Boosted)
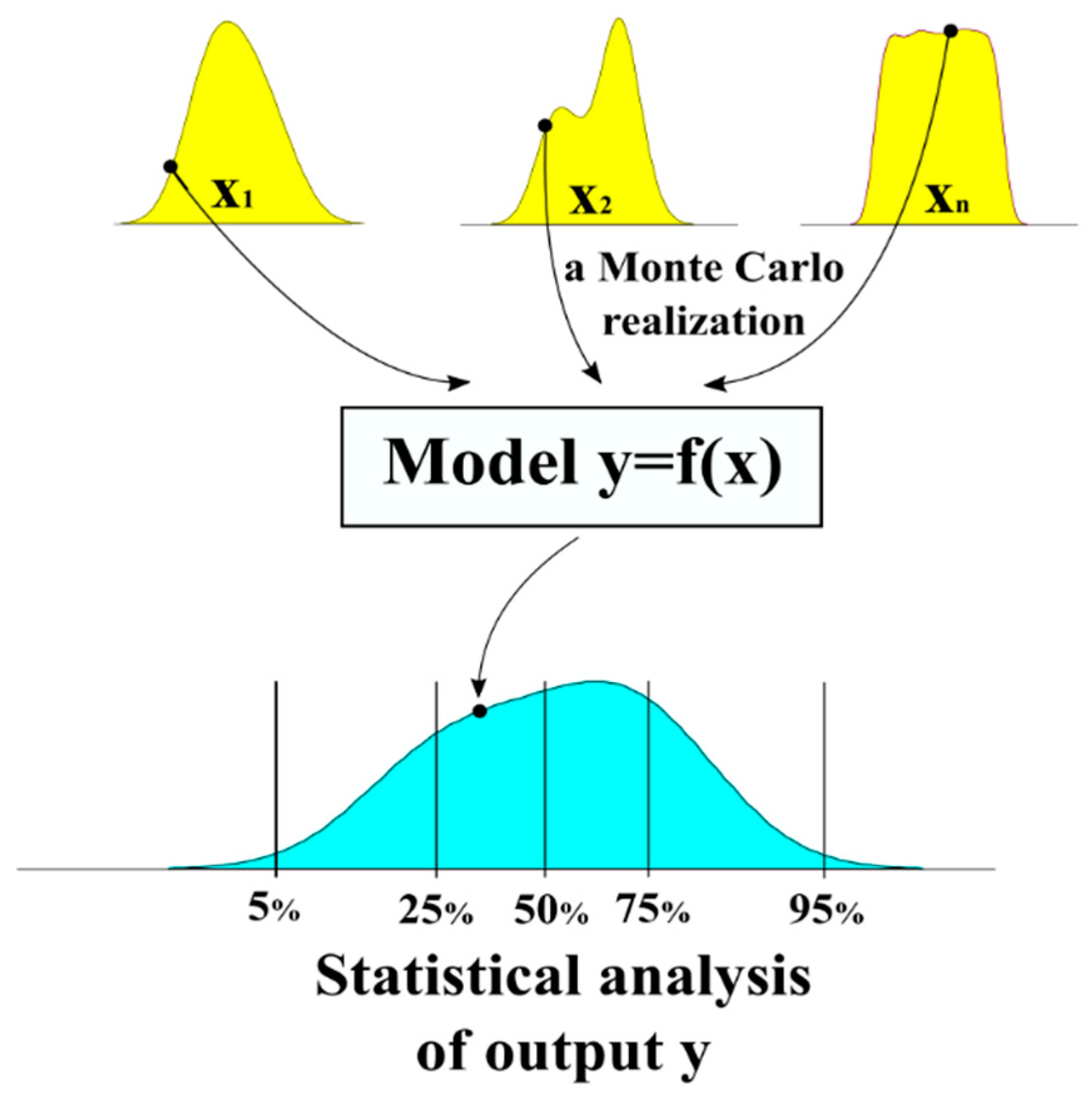
2.2.2. Monte Carlo Method
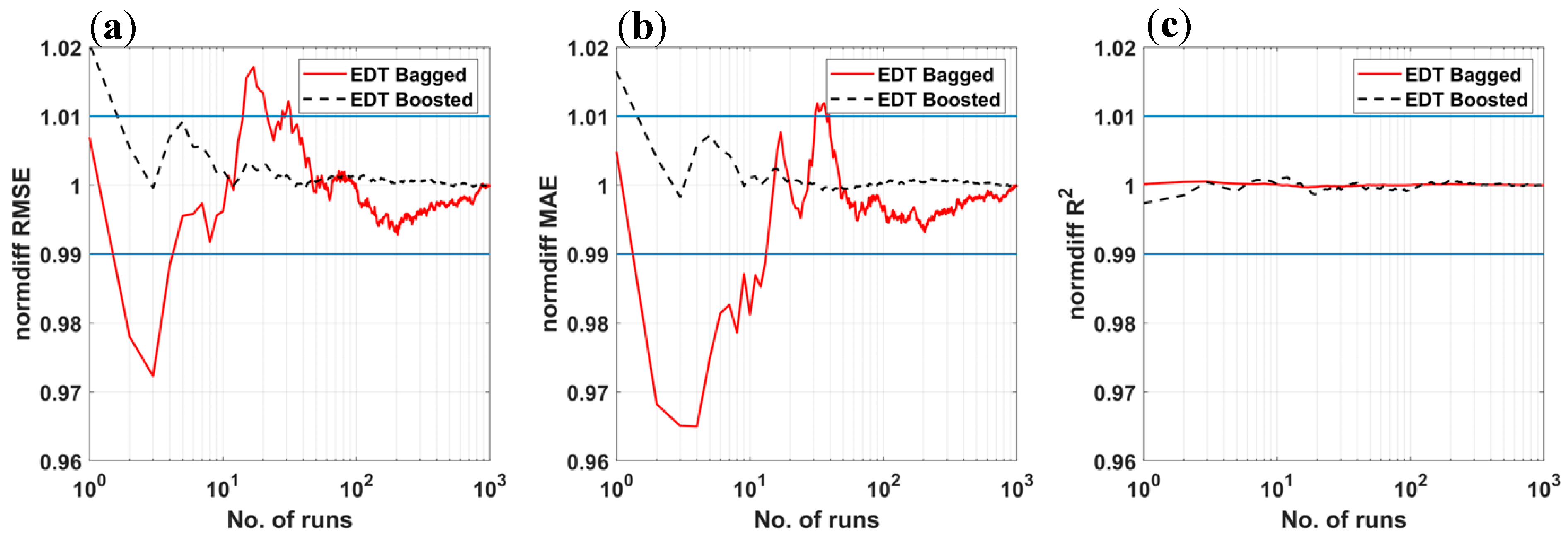
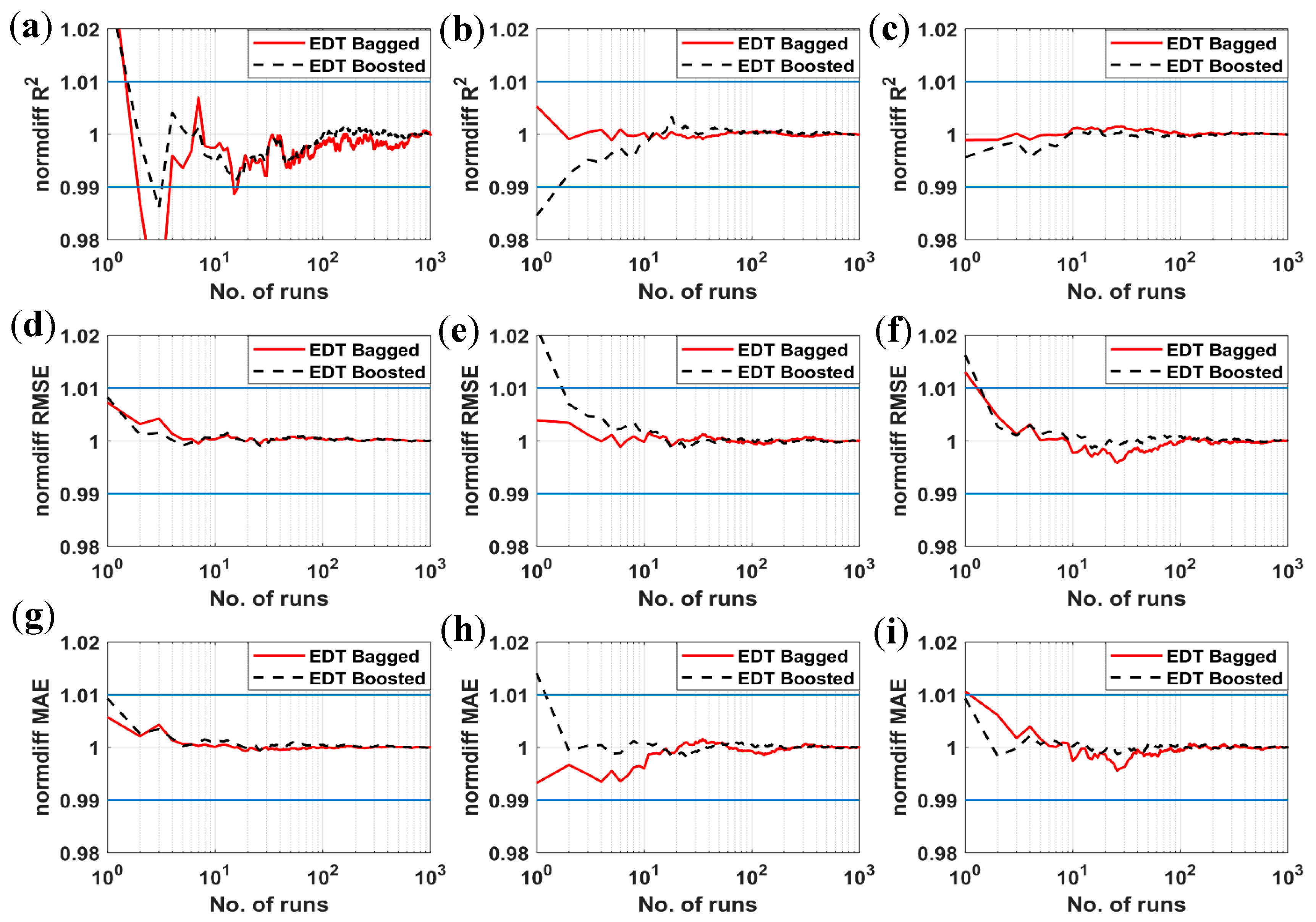
2.2.3. Validation Criteria
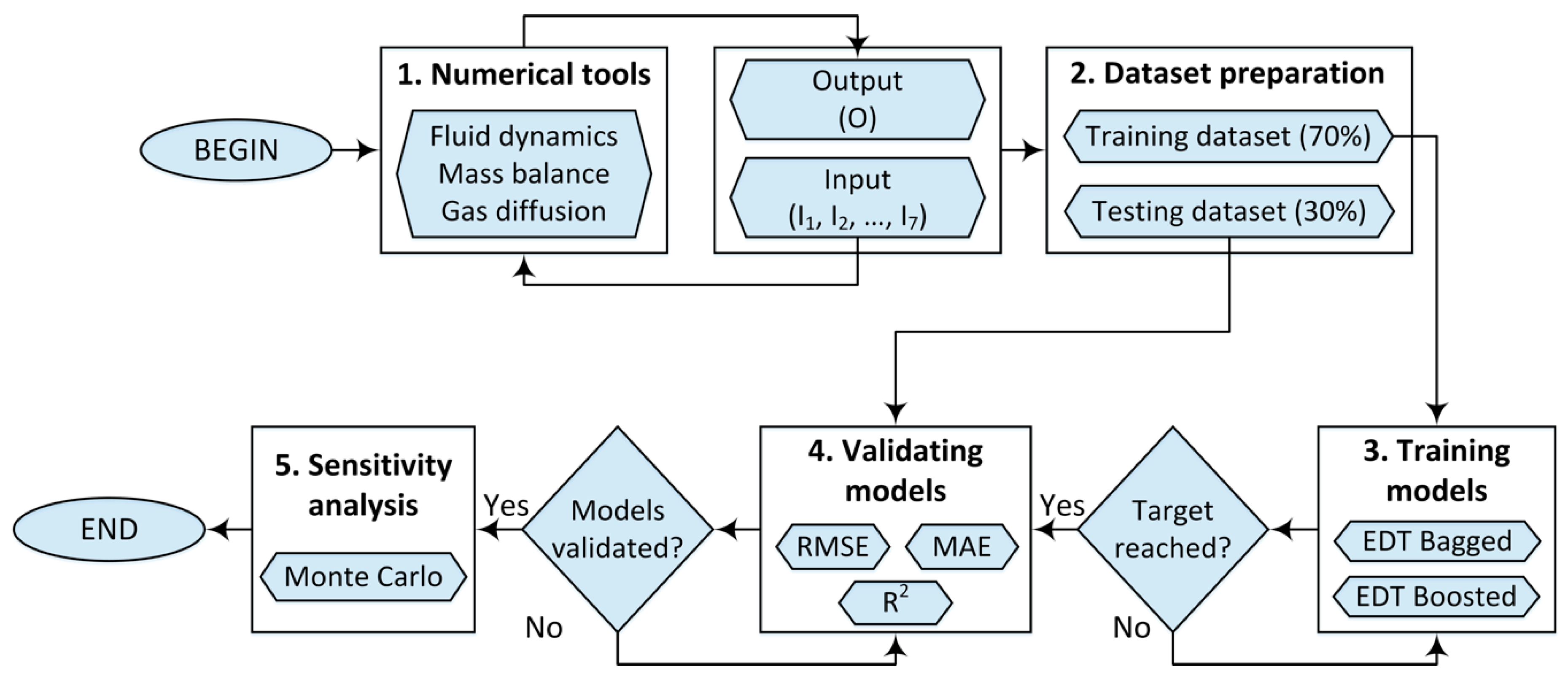
2.2.4. Methodology Chart
3. Results and Discussion
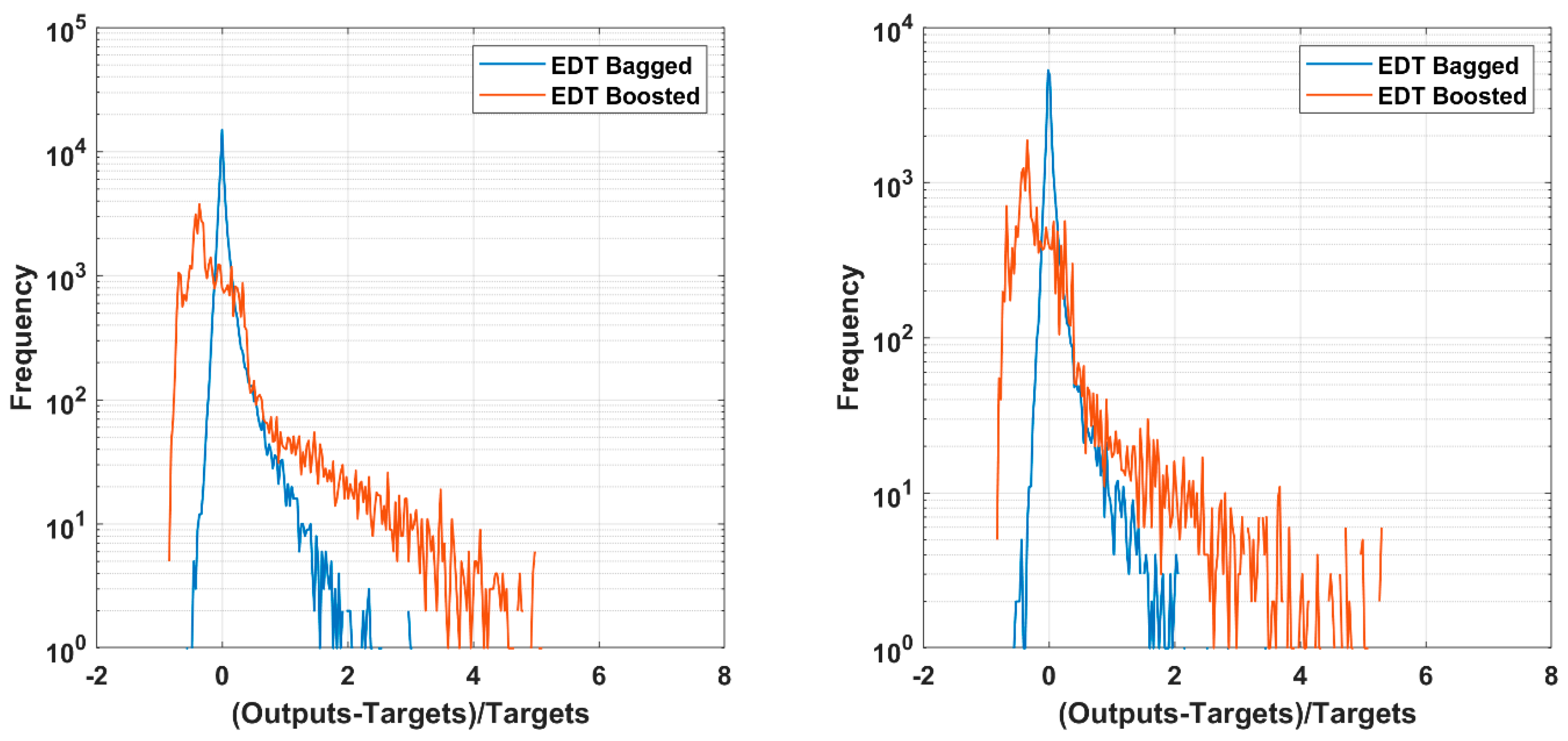
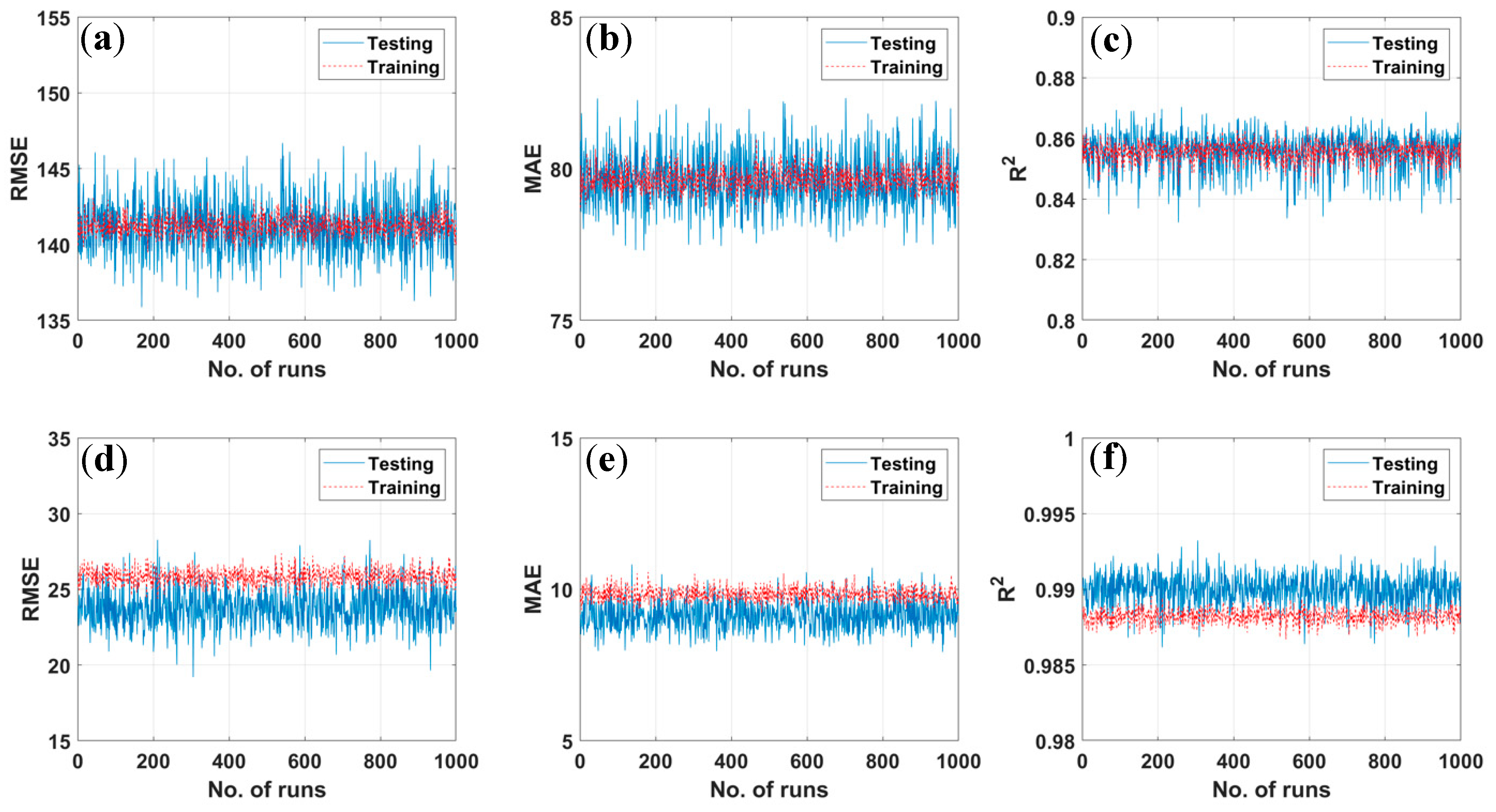
3.1. Comparison of Ensemble Decision Trees (EDT) Algorithms
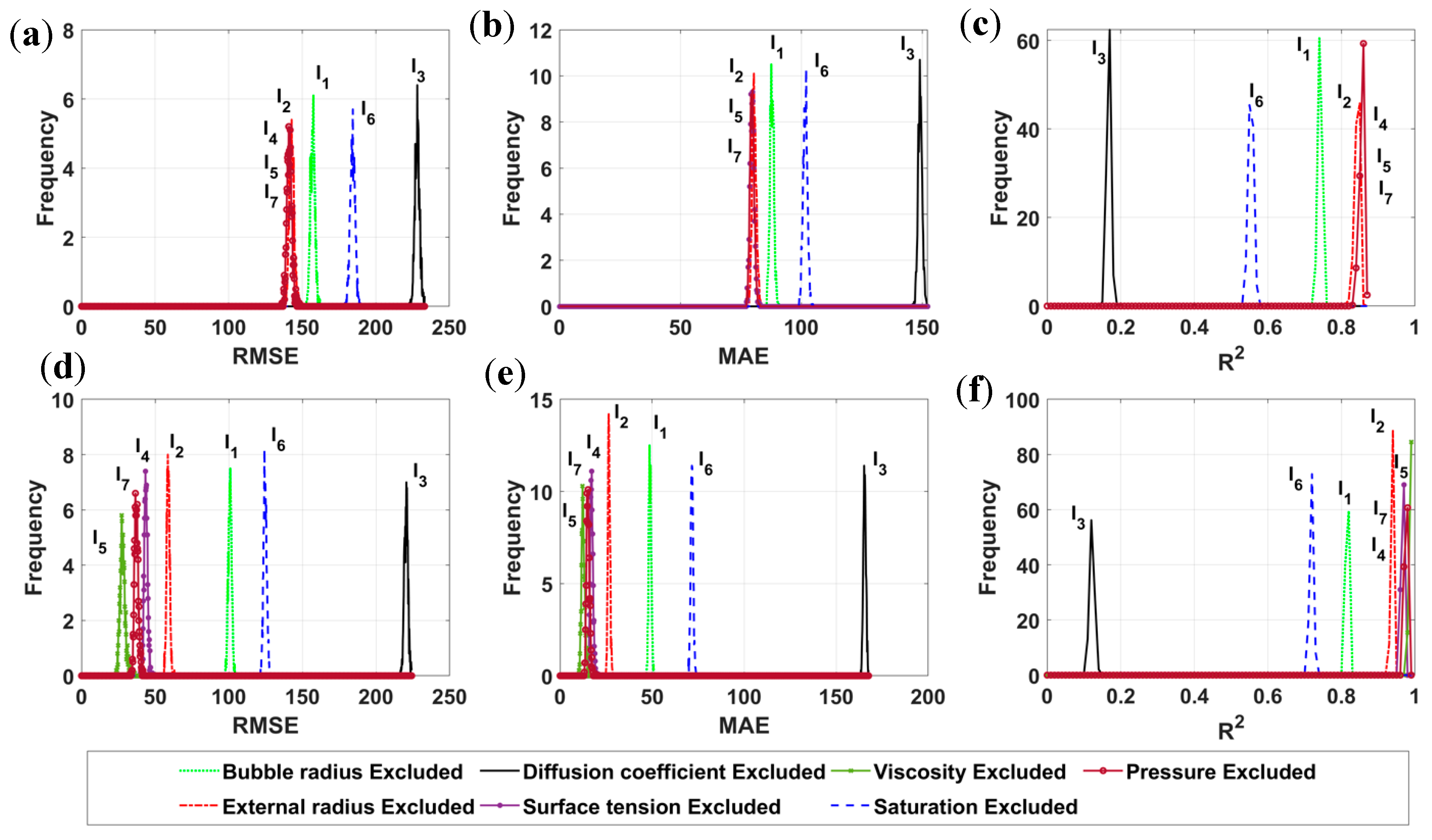
3.2. Sensitivity Analysis of Input Parameters
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Schmid, M. Laser Sintering with Plastics: Technology, Processes, and Materials; Carl Hanser Verlag GmbH & Co. KG: München, Germany, 2018; ISBN 978-1-56990-683-5. [Google Scholar]
- Nelson, J.C. Selective Laser Sintering: A Definition of the Process and an Empirical Sintering Model; University of Texas at Austin: Austin, TX, USA, 1993. [Google Scholar]
- Oter, Z.C.; Coskun, M.; Akca, Y.; Surmen, O.; Yilmaz, M.S.; Ozer, G.; Tarakci, G.; Khan, H.M.; Koc, E. Support optimization for overhanging parts in direct metal laser sintering. Optik 2019, 181, 575–581. [Google Scholar] [CrossRef]
- Cheng, B.; Chou, K. Geometric consideration of support structures in part overhang fabrications by electron beam additive manufacturing. Comput. Aided Des. 2015, 69, 102–111. [Google Scholar] [CrossRef]
- Calignano, F. Design optimization of supports for overhanging structures in aluminum and titanium alloys by selective laser melting. Mater. Des. 2014, 64, 203–213. [Google Scholar] [CrossRef]
- Yuan, S.; Zheng, Y.; Chua, C.K.; Yan, Q.; Zhou, K. Electrical and thermal conductivities of MWCNT/polymer composites fabricated by selective laser sintering. Compos. Part A Appl. Sci. Manuf. 2018, 105, 203–213. [Google Scholar] [CrossRef]
- Josupeit, S.; Ordia, L.; Schmid, H.-J. Modelling of temperatures and heat flow within laser sintered part cakes. Addit. Manuf. 2016, 12, 189–196. [Google Scholar] [CrossRef]
- Kontopoulou, M.; Vlachopoulos, J. Bubble dissolution in molten polymers and its role in rotational molding. Polym. Eng. Sci. 1999, 39, 1189–1198. [Google Scholar] [CrossRef]
- Griskey, R. Polymer Process Engineering; Springer Science & Business Media: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Doremus, R.H. Diffusion of Oxygen from Contracting Bubbles in Molten Glass. J. Am. Ceram. Soc. 1960, 43, 655–661. [Google Scholar] [CrossRef]
- Wei, Q.; Zhong, J.; Xu, Z.; Xu, Q.; Liu, B. Microstructure evolution and mechanical properties of ceramic shell moulds for investment casting of turbine blades by selective laser sintering. Ceram. Int. 2018, 44, 12088–12097. [Google Scholar] [CrossRef]
- Mokrane, A.; Boutaous, M.; Xin, S. Process of selective laser sintering of polymer powders: Modeling, simulation, and validation. C. R. Méc. 2018, 346, 1087–1103. [Google Scholar] [CrossRef]
- Venuvinod, P.K.; Ma, W. Selective Laser Sintering (SLS). In Rapid Prototyping: Laser-based and Other Technologies; Venuvinod, P.K., Ma, W., Eds.; Springer: Boston, MA, USA, 2004; pp. 245–277. ISBN 978-1-4757-6361-4. [Google Scholar]
- Bourell, D.L.; Watt, T.J.; Leigh, D.K.; Fulcher, B. Performance Limitations in Polymer Laser Sintering. Phys. Procedia 2014, 56, 147–156. [Google Scholar] [CrossRef]
- Schmid, M.; Wegener, K. Additive Manufacturing: Polymers Applicable for Laser Sintering (LS). Procedia Eng. 2016, 149, 457–464. [Google Scholar] [CrossRef]
- Wudy, K.; Lanzl, L.; Drummer, D. Selective Laser Sintering of Filled Polymer Systems: Bulk Properties and Laser Beam Material Interaction. Phys. Procedia 2016, 83, 991–1002. [Google Scholar] [CrossRef]
- Ly, H.-B.; Monteiro, E.; Dal, M.; Regnier, G. On the factors affecting porosity dissolution in selective laser sintering process. AIP Conf. Proc. 2018, 1960, 120014. [Google Scholar]
- Gogos, G. Bubble removal in rotational molding. Polym. Eng. Sci. 2004, 44, 388–394. [Google Scholar] [CrossRef]
- Weinberg, M.C. Surface tension effects in gas bubble dissolution and growth. Chem. Eng. Sci. 1981, 36, 137–141. [Google Scholar] [CrossRef]
- Duda, J.; Vrentas, J. Mathematical analysis of bubble dissolution. AIChE J. 1969, 15, 351–356. [Google Scholar] [CrossRef]
- Naji Meidani, A.R.; Hasan, M. Mathematical and physical modelling of bubble growth due to ultrasound. Appl. Math. Model. 2004, 28, 333–351. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation., 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1998; ISBN 978-0-13-273350-2. [Google Scholar]
- Jang, J.-S.R. Neuro-Fuzzy and Soft Computing: A Computational Approach to Learning and Machine Intelligence; Prentice Hall: Upper Saddle River, NJ, USA, 1997; ISBN 978-0-13-261066-7. [Google Scholar]
- Witten, I.H.; Frank, E.; Hall, M.A.; Pal, C.J. Data Mining: Practical Machine Learning Tools and Techniques, 4th ed.; Morgan Kaufmann: San Francisco, CA, USA, 2016; ISBN 978-0-12-804357-8. [Google Scholar]
- Cosmin, A.; Elena, A.; Naif, A.; Timon, R. Artificial Neural Network Methods for the Solution of Second Order Boundary Value Problems. Comput. Mater. Contin. 2019, 59, 345–359. [Google Scholar]
- Yusoff, N.I.M.; Ibrahim Alhamali, D.; Ibrahim, A.N.H.; Rosyidi, S.A.P.; Abdul Hassan, N. Engineering characteristics of nanosilica/polymer-modified bitumen and predicting their rheological properties using multilayer perceptron neural network model. Constr. Build. Mater. 2019, 204, 781–799. [Google Scholar] [CrossRef]
- Hasnaoui, H.; Krea, M.; Roizard, D. Neural networks for the prediction of polymer permeability to gases. J. Membr. Sci. 2017, 541, 541–549. [Google Scholar] [CrossRef]
- Diaconescu, R.-M.; Barbuta, M.; Harja, M. Prediction of properties of polymer concrete composite with tire rubber using neural networks. Mater. Sci. Eng. B 2013, 178, 1259–1267. [Google Scholar] [CrossRef]
- Khader, M.H.; Hamid, G.; Xiaoying, Z.; Naif, A.; Timon, R. Computational Machine Learning Representation for the Flexoelectricity Effect in Truncated Pyramid Structures. Comput. Mater. Contin. 2019, 59, 79–87. [Google Scholar]
- Dao, D.V.; Trinh, S.H.; Ly, H.-B.; Pham, B.T. Prediction of Compressive Strength of Geopolymer Concrete Using Entirely Steel Slag Aggregates: Novel Hybrid Artificial Intelligence Approaches. Appl. Sci. 2019, 9, 1113. [Google Scholar] [CrossRef]
- Xu, D.; Pop-Iliev, R.; Park, C.B.; Fenton, R. Fundamental study of CBA-blown bubble growth and collapse under atmospheric pressure. J. Cell. Plast. 2005, 41, 519–538. [Google Scholar] [CrossRef]
- Wu, S. Polymer Interface and Adhesion; CRC Press: Boca Raton, FL, USA, 1982. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Durrill, P.L.; Griskey, R.G. Diffusion and solution of gases into thermally softened or molten polymers: Part II. Relation of diffusivities and solubilities with temperature pressure and structural characteristics. AIChE J. 1969, 15, 106–110. [Google Scholar] [CrossRef]
- Khorsheed, M.S.; Al-Thubaity, A.O. Comparative evaluation of text classification techniques using a large diverse Arabic dataset. Lang Resour. Eval. 2013, 47, 513–538. [Google Scholar] [CrossRef]
- Leema, N.; Nehemiah, H.K.; Kannan, A. Neural network classifier optimization using Differential Evolution with Global Information and Back Propagation algorithm for clinical datasets. Appl. Soft Comput. 2016, 49, 834–844. [Google Scholar] [CrossRef]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Amirabadizadeh, A.; Nezami, H.; Vaughn, M.G.; Nakhaee, S.; Mehrpour, O. Identifying risk factors for drug use in an Iranian treatment sample: A prediction approach using decision trees. Subst. Use Misuse 2018, 53, 1030–1040. [Google Scholar] [CrossRef]
- Khosravi, K.; Pham, B.T.; Chapi, K.; Shirzadi, A.; Shahabi, H.; Revhaug, I.; Prakash, I.; Tien Bui, D. A comparative assessment of decision trees algorithms for flash flood susceptibility modeling at Haraz watershed, northern Iran. Sci. Total Environ. 2018, 627, 744–755. [Google Scholar] [CrossRef]
- Thai Pham, B.; Bui, D.T.; Prakash, I. Landslide susceptibility modelling using different advanced decision trees methods. Civ. Eng. Environ. Syst. 2019, 1–19. [Google Scholar] [CrossRef]
- Wang, J.; Li, P.; Ran, R.; Che, Y.; Zhou, Y. A Short-Term Photovoltaic Power Prediction Model Based on the Gradient Boost Decision Tree. Appl. Sci. 2018, 8, 689. [Google Scholar] [CrossRef]
- Akin, M.; Hand, C.; Eyduran, E.; Reed, B.M. Predicting minor nutrient requirements of hazelnut shoot cultures using regression trees. Plant Cell Tissue Organ Cult. (PCTOC) 2018, 132, 545–559. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer Series in Statistics; Springer: New York, NY, USA, 2009; ISBN 978-0-387-84857-0. [Google Scholar]
- Zhang, Y.; Haghani, A. A gradient boosting method to improve travel time prediction. Transp. Res. Part C Emerg. Technol. 2015, 58, 308–324. [Google Scholar] [CrossRef]
- Austin, P.C.; Tu, J.V.; Ho, J.E.; Levy, D.; Lee, D.S. Using methods from the data-mining and machine-learning literature for disease classification and prediction: A case study examining classification of heart failure subtypes. J. Clin. Epidemiol. 2013, 66, 398–407. [Google Scholar] [CrossRef] [PubMed]
- Winkler, D.; Haltmeier, M.; Kleidorfer, M.; Rauch, W.; Tscheikner-Gratl, F. Pipe failure modelling for water distribution networks using boosted decision trees. Struct. Infrastruct. Eng. 2018, 14, 1402–1411. [Google Scholar] [CrossRef]
- Serrano-Cinca, C.; Gutiérrez-Nieto, B. Partial Least Square Discriminant Analysis for bankruptcy prediction. Decis. Support Syst. 2013, 54, 1245–1255. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
- Zięba, M.; Tomczak, S.K.; Tomczak, J.M. Ensemble boosted trees with synthetic features generation in application to bankruptcy prediction. Expert Syst. Appl. 2016, 58, 93–101. [Google Scholar] [CrossRef]
- De’ath, G. Boosted Trees for Ecological Modeling and Prediction. Ecology 2007, 88, 243–251. [Google Scholar] [CrossRef]
- Abdar, M.; Yen, N.Y.; Hung, J.C.-S. Improving the diagnosis of liver disease using multilayer perceptron neural network and boosted decision trees. J. Med. Boil. Eng. 2017, 38, 953–965. [Google Scholar] [CrossRef]
- Chung, Y.-S. Factor complexity of crash occurrence: An empirical demonstration using boosted regression trees. Accid. Anal. Prev. 2013, 61, 107–118. [Google Scholar] [CrossRef]
- Ghasemi, H.; Rafiee, R.; Zhuang, X.; Muthu, J.; Rabczuk, T. Uncertainties propagation in metamodel-based probabilistic optimization of CNT/polymer composite structure using stochastic multi-scale modeling. Comput. Mater. Sci. 2014, 85, 295–305. [Google Scholar] [CrossRef]
- Vu-Bac, N.; Rafiee, R.; Zhuang, X.; Lahmer, T.; Rabczuk, T. Uncertainty quantification for multiscale modeling of polymer nanocomposites with correlated parameters. Compos. Part B Eng. 2015, 68, 446–464. [Google Scholar] [CrossRef]
- Le, T.T.; Guilleminot, J.; Soize, C. Stochastic continuum modeling of random interphases from atomistic simulations. Application to a polymer nanocomposite. Comput. Methods Appl. Mech. Eng. 2016, 303, 430–449. [Google Scholar] [CrossRef]
- Capillon, R.; Desceliers, C.; Soize, C. Uncertainty quantification in computational linear structural dynamics for viscoelastic composite structures. Comput. Methods Appl. Mech. Eng. 2016, 305, 154–172. [Google Scholar] [CrossRef]
- Robert, C.; Casella, G. Monte Carlo Statistical Methods, 2nd ed.; Springer Texts in Statistics; Springer: New York, NY, USA, 2004; ISBN 978-0-387-21239-5. [Google Scholar]
- Mordechai, S. Applications of Monte Carlo Method in Science and Engineering; InTech: Rijeka, Croatia, 2011; ISBN 978-953-307-691-1. [Google Scholar]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Menard, S. Coefficients of Determination for Multiple Logistic Regression Analysis. Am. Stat. 2000, 54, 17–24. [Google Scholar]
- Nagelkerke, N. A note on a general definition of the coefficient of determination. Biometrika 1991, 78, 691–692. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Dao, D.V.; Ly, H.-B.; Trinh, S.H.; Le, T.-T.; Pham, B.T. Artificial Intelligence Approaches for Prediction of Compressive Strength of Geopolymer Concrete. Materials 2019, 12, 983. [Google Scholar] [CrossRef] [PubMed]
- Epstein, P.S.; Plesset, M.S. On the stability of gas bubbles in liquid-gas solutions. J. Chem. Phys. 1950, 18, 1505–1509. [Google Scholar] [CrossRef]
- Hamdia, K.M.; Msekh, M.A.; Silani, M.; Thai, T.Q.; Budarapu, P.R.; Rabczuk, T. Assessment of computational fracture models using Bayesian method. Eng. Fract. Mech. 2019, 205, 387–398. [Google Scholar] [CrossRef]
| Input Parameter | Minimum | Maximum | Average | Standard Deviation |
|---|---|---|---|---|
| I1 (bubble radius, µm) | 30 | 150 | 112.4 | 19.37 |
| I2 (external radius, µm) | 33 | 150,000 | 333.1 | 422.15 |
| I3 (diffusion coefficient, m2·s−1) | 0.1 × 10−9 | 50 × 10−9 | 4.1 × 10−9 | 6.79 × 10−9 |
| I4 (surface tension, N·m−1) | 0.0100 | 0.0500 | 0.0288 | 0.0144 |
| I5 (viscosity, Pa·s) | 100 | 10,000 | 3670.5 | 3701.3 |
| I6 (saturation) | 0.1 | 1 | 0.54 | 0.37 |
| I7 (chamber pressure, atm) | 0.25 | 1.5 | 0.88 | 0.41 |
| O (bubble dissolution time, s) | 20 | 1200 | 194.2 | 234.9 |
| Criteria | Input Excl. | EDT Bagged | EDT Boosted | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | SD | Min | Max | Mean | SD | ||
| RMSE | No excl. | 19.20 | 28.27 | 23.78 | 1.26 | 135.86 | 146.70 | 141.16 | 1.79 |
| I1 excl. | 97.48 | 104.97 | 100.80 | 1.15 | 153.04 | 161.99 | 157.11 | 1.49 | |
| I2 excl. | 56.13 | 63.04 | 58.84 | 1.02 | 138.32 | 150.13 | 142.84 | 1.68 | |
| I3 excl. | 215.67 | 224.28 | 220.44 | 1.18 | 222.84 | 223.37 | 228.18 | 1.61 | |
| I4 excl. | 40.06 | 48.21 | 43.71 | 1.12 | 136.29 | 147.91 | 141.28 | 1.69 | |
| I5 excl. | 23.50 | 36.27 | 27.83 | 1.70 | 136.29 | 147.91 | 141.28 | 1.69 | |
| I6 excl. | 120.65 | 128.45 | 124.63 | 1.12 | 178.98 | 189.90 | 184.26 | 1.67 | |
| I7 excl. | 33.37 | 41.85 | 37.24 | 1.28 | 136.29 | 147.91 | 141.28 | 1.69 | |
| MAE | No excl. | 7.93 | 10.82 | 9.14 | 0.47 | 77.30 | 82.33 | 79.62 | 0.91 |
| I1 excl. | 46.87 | 51.16 | 48.86 | 0.69 | 85.76 | 90.81 | 87.85 | 0.82 | |
| I2 excl. | 24.95 | 31.25 | 26.57 | 0.63 | 78.39 | 83.60 | 80.54 | 0.85 | |
| I3 excl. | 163.07 | 167.72 | 165.46 | 0.73 | 145.98 | 152.37 | 149.14 | 0.88 | |
| I4 excl. | 15.13 | 20.76 | 17.15 | 0.75 | 77.41 | 82.77 | 79.65 | 0.86 | |
| I5 excl. | 10.15 | 15.99 | 12.54 | 0.92 | 77.41 | 82.77 | 79.65 | 0.86 | |
| I6 excl. | 69.15 | 73.83 | 71.64 | 0.71 | 98.73 | 104.90 | 101.63 | 0.90 | |
| I7 excl. | 13.24 | 19.13 | 15.18 | 0.83 | 77.41 | 82.77 | 79.65 | 0.86 | |
| R2 | No excl. | 0.986 | 0.993 | 0.990 | 0.001 | 0.832 | 0.870 | 0.856 | 0.006 |
| I1 excl. | 0.802 | 0.827 | 0.816 | 0.004 | 0.721 | 0.758 | 0.742 | 0.005 | |
| I2 excl. | 0.929 | 0.943 | 0.938 | 0.002 | 0.808 | 0.858 | 0.843 | 0.007 | |
| I3 excl. | 0.100 | 0.144 | 0.122 | 0.006 | 0.153 | 0.183 | 0.168 | 0.005 | |
| I4 excl. | 0.960 | 0.971 | 0.966 | 0.002 | 0.831 | 0.872 | 0.855 | 0.006 | |
| I5 excl. | 0.978 | 0.990 | 0.987 | 0.002 | 0.831 | 0.872 | 0.855 | 0.006 | |
| I6 excl. | 0.704 | 0.731 | 0.719 | 0.004 | 0.533 | 0.573 | 0.554 | 0.007 | |
| I7 excl. | 0.970 | 0.980 | 0.975 | 0.002 | 0.831 | 0.872 | 0.855 | 0.006 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ly, H.-B.; Monteiro, E.; Le, T.-T.; Le, V.M.; Dal, M.; Regnier, G.; Pham, B.T. Prediction and Sensitivity Analysis of Bubble Dissolution Time in 3D Selective Laser Sintering Using Ensemble Decision Trees. Materials 2019, 12, 1544. https://doi.org/10.3390/ma12091544
Ly H-B, Monteiro E, Le T-T, Le VM, Dal M, Regnier G, Pham BT. Prediction and Sensitivity Analysis of Bubble Dissolution Time in 3D Selective Laser Sintering Using Ensemble Decision Trees. Materials. 2019; 12(9):1544. https://doi.org/10.3390/ma12091544
Chicago/Turabian StyleLy, Hai-Bang, Eric Monteiro, Tien-Thinh Le, Vuong Minh Le, Morgan Dal, Gilles Regnier, and Binh Thai Pham. 2019. "Prediction and Sensitivity Analysis of Bubble Dissolution Time in 3D Selective Laser Sintering Using Ensemble Decision Trees" Materials 12, no. 9: 1544. https://doi.org/10.3390/ma12091544
APA StyleLy, H.-B., Monteiro, E., Le, T.-T., Le, V. M., Dal, M., Regnier, G., & Pham, B. T. (2019). Prediction and Sensitivity Analysis of Bubble Dissolution Time in 3D Selective Laser Sintering Using Ensemble Decision Trees. Materials, 12(9), 1544. https://doi.org/10.3390/ma12091544








