Nonlinear Creep Damage Constitutive Model of Concrete Based on Fractional Calculus Theory
Abstract
:1. Introduction
2. Construction of Concrete Nonlinear Creep Damage Constitutive Model
2.1. Riemann Liouville Fractional Order Software Components
2.2. Establishment and Solution of Fractional Order Creep Damage Model
- The small damage produced is neglected during the deceleration creep and steady creep stages, and only the damage caused by the accelerated creep stage is considered in the concrete indoor creep test.
- The concrete damage evolution in the accelerated creep process is consistent with the change in the exponential function.
- Stress-strain relationship of elastomer.where is the elastomer elastic modulus.
- Stress-strain relationship of visco-elasticity plasticity body.The visco-elasticity plasticity body is represented in parallel with the elastomer element, the Able dashpot and the friction element. The stress on the friction element is expressed by .where is the total stress on the visco-elasticity plasticity body, and is the ultimate stress on the visco-elasticity plasticity body friction slider.
3. Determination of Concrete Nonlinear Creep Damage Constitutive Model Parameters
3.1. Determination of Parameter
3.2. Determination of Parameters , , and
3.3. Determination of Parameters and
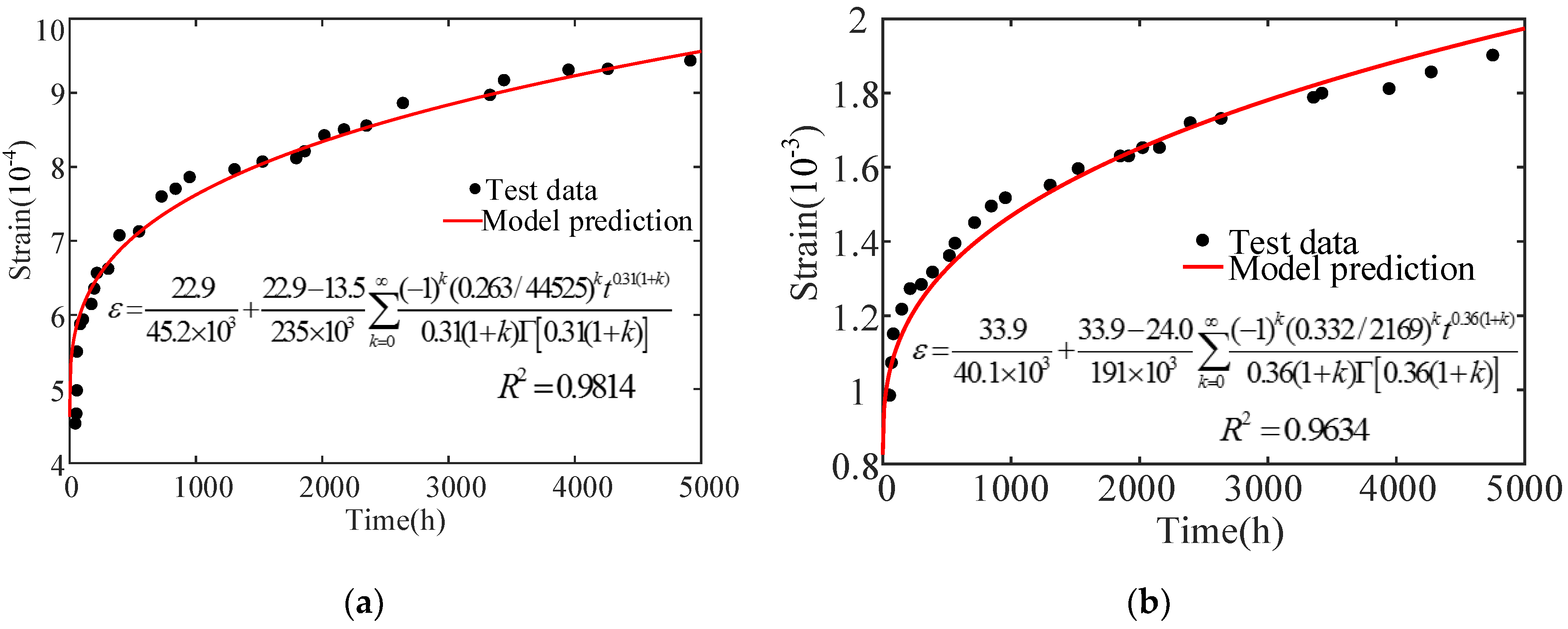
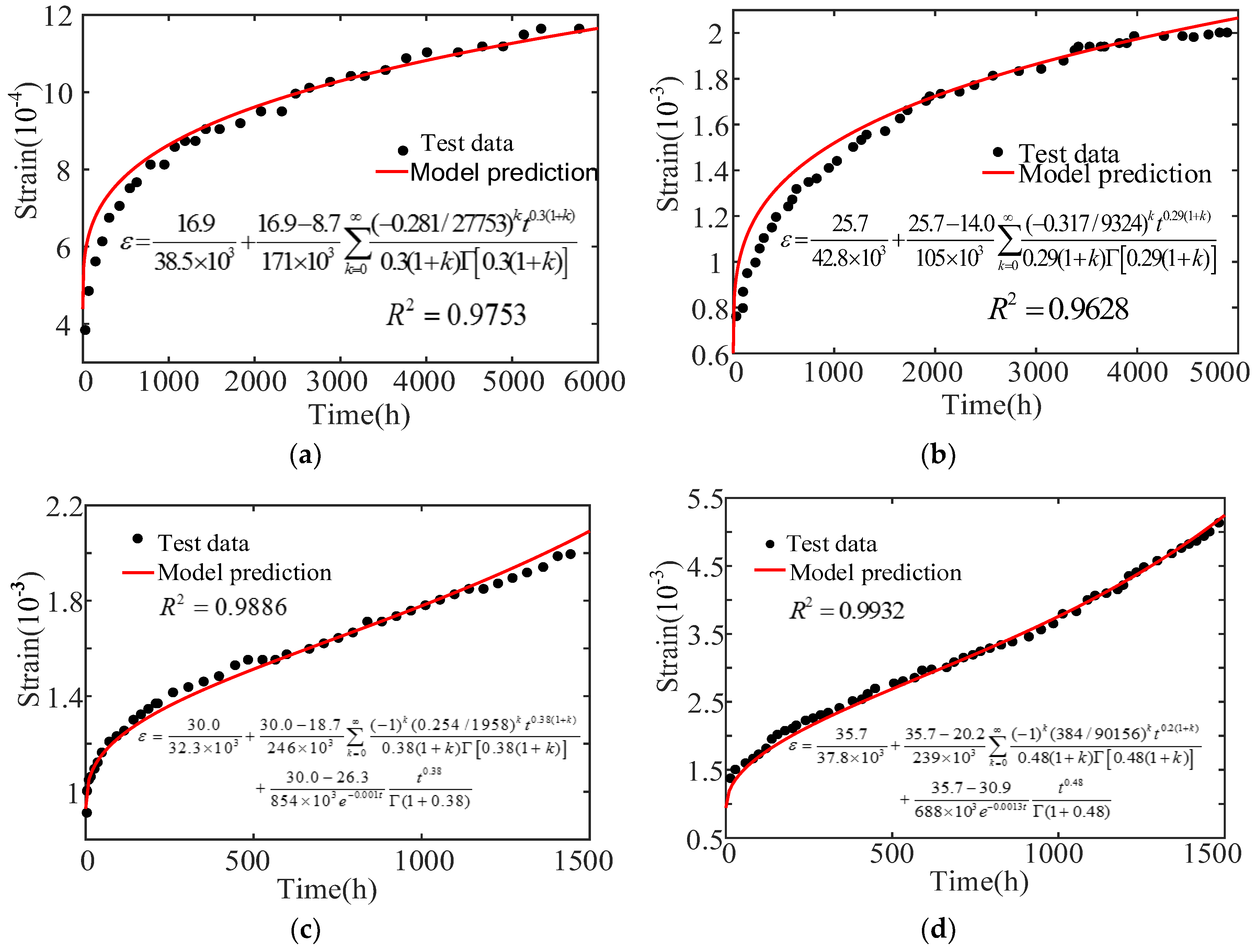
4. Verification of Concrete Nonlinear Creep Damage Constitutive Model
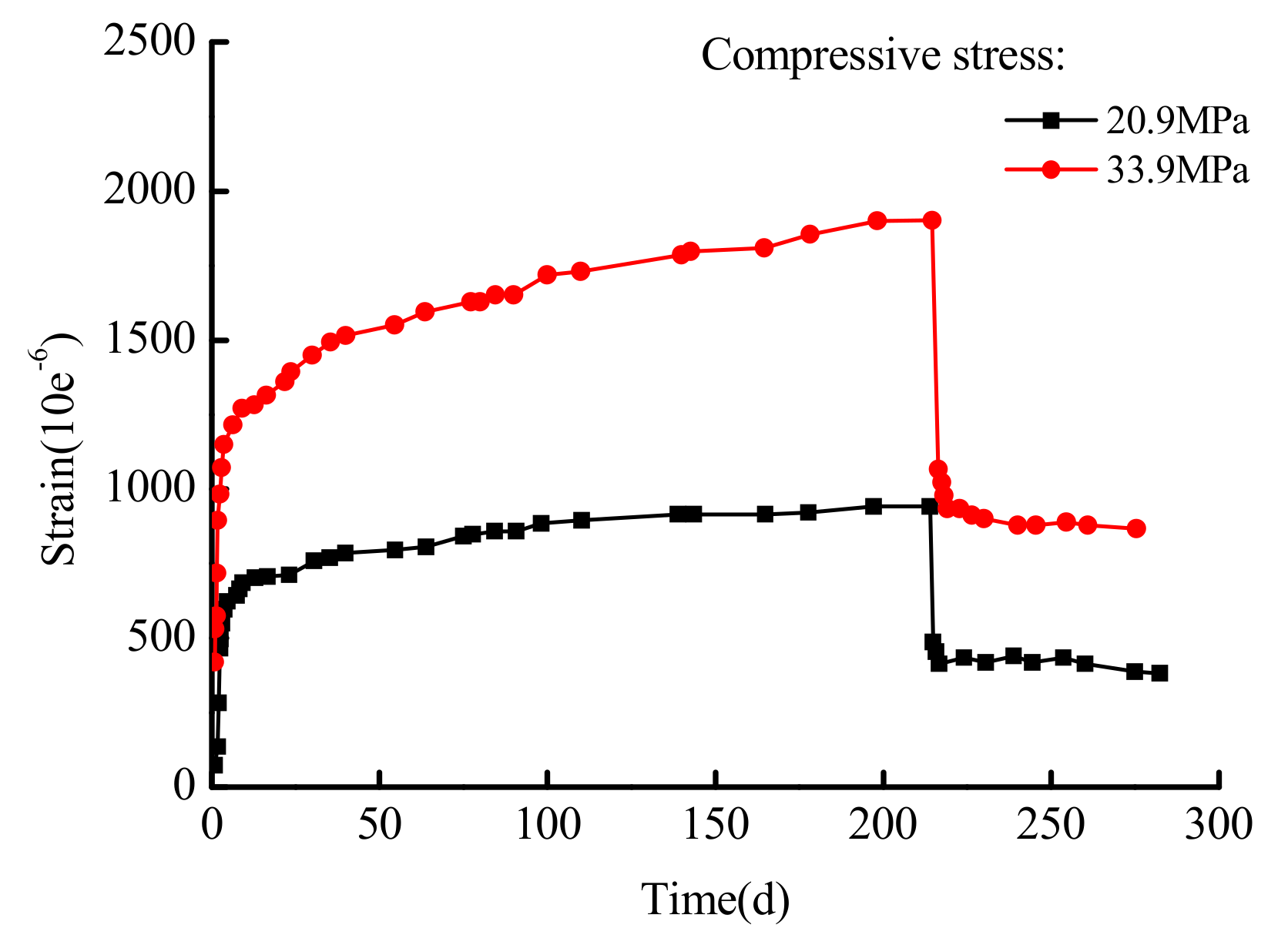
4.1. Experimental Research on Concrete Creep under High Stress
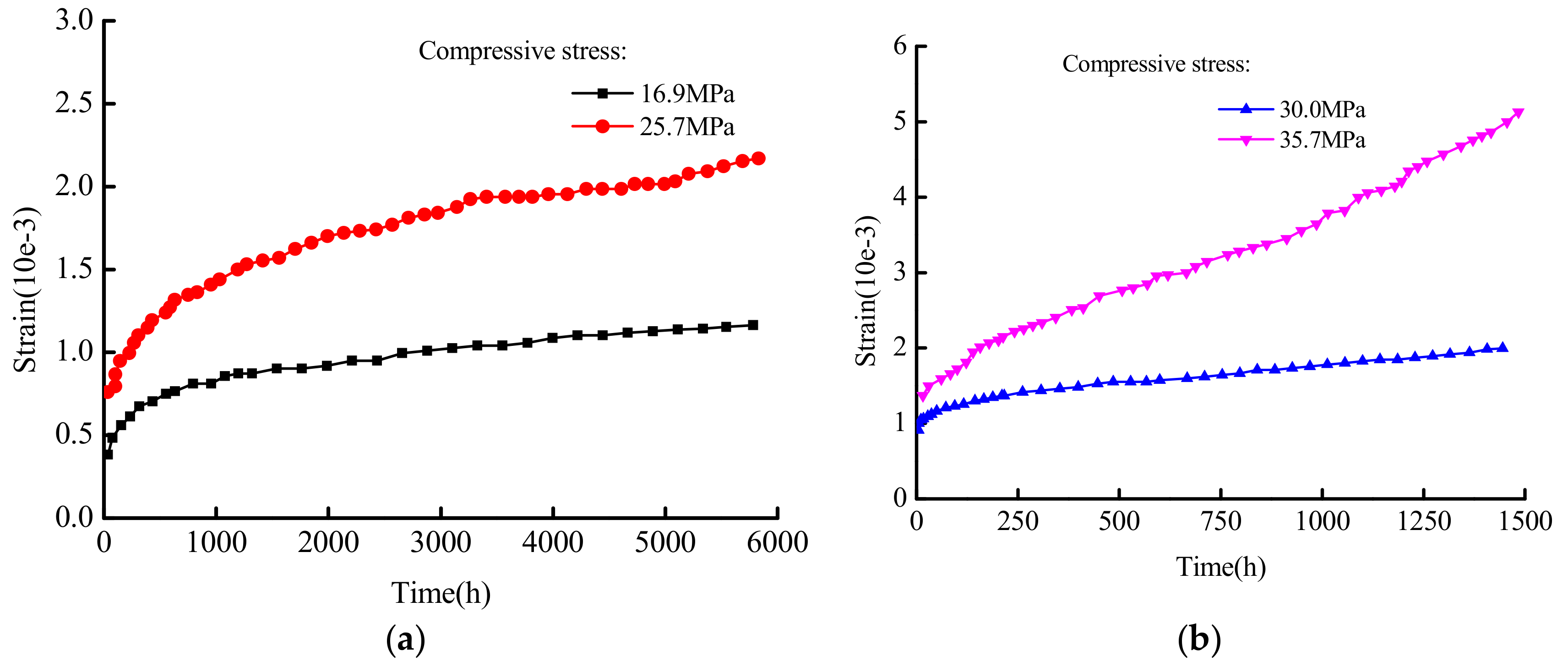
4.2. Experimental Research on Concrete Creep Under Different Stresses
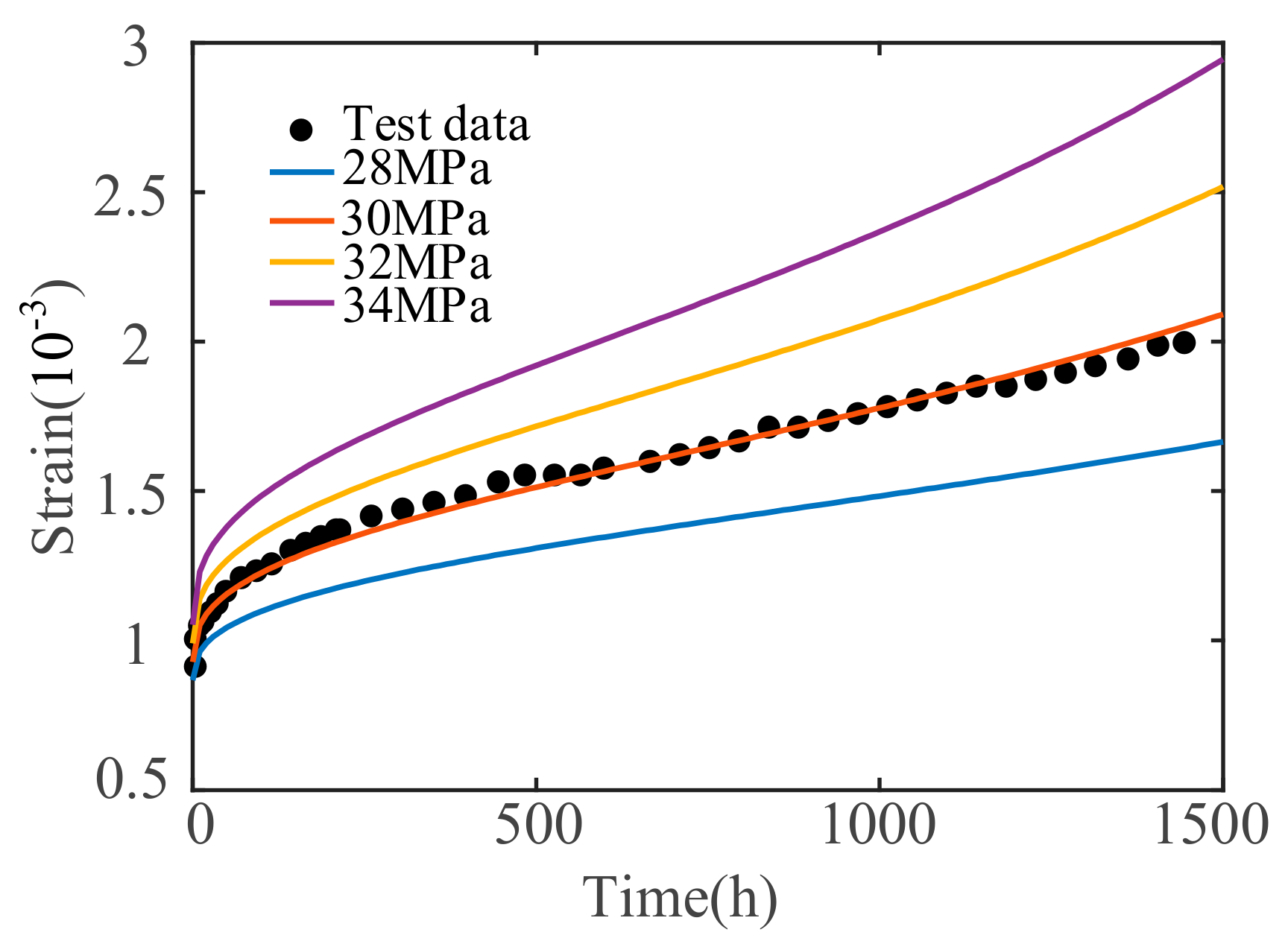
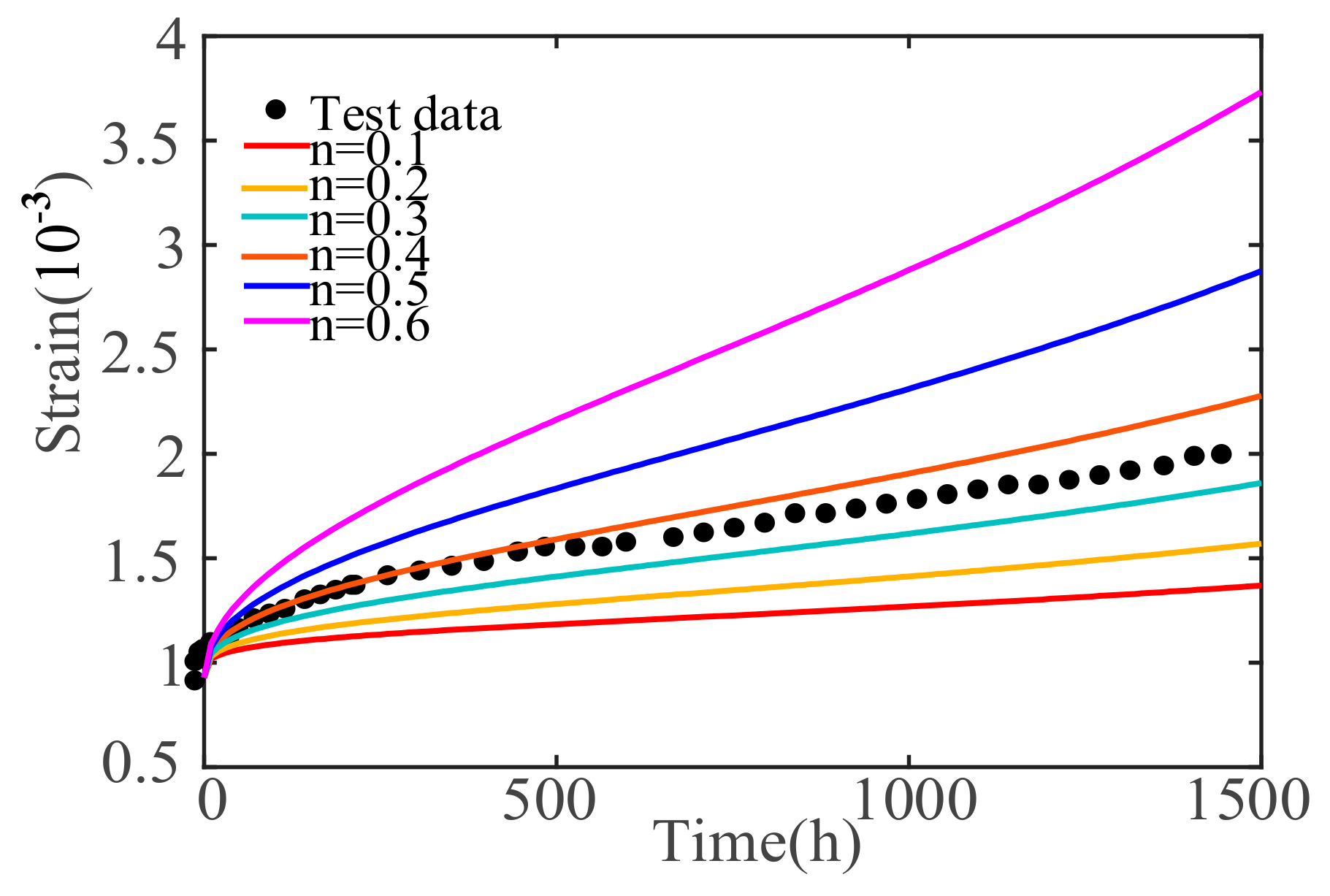
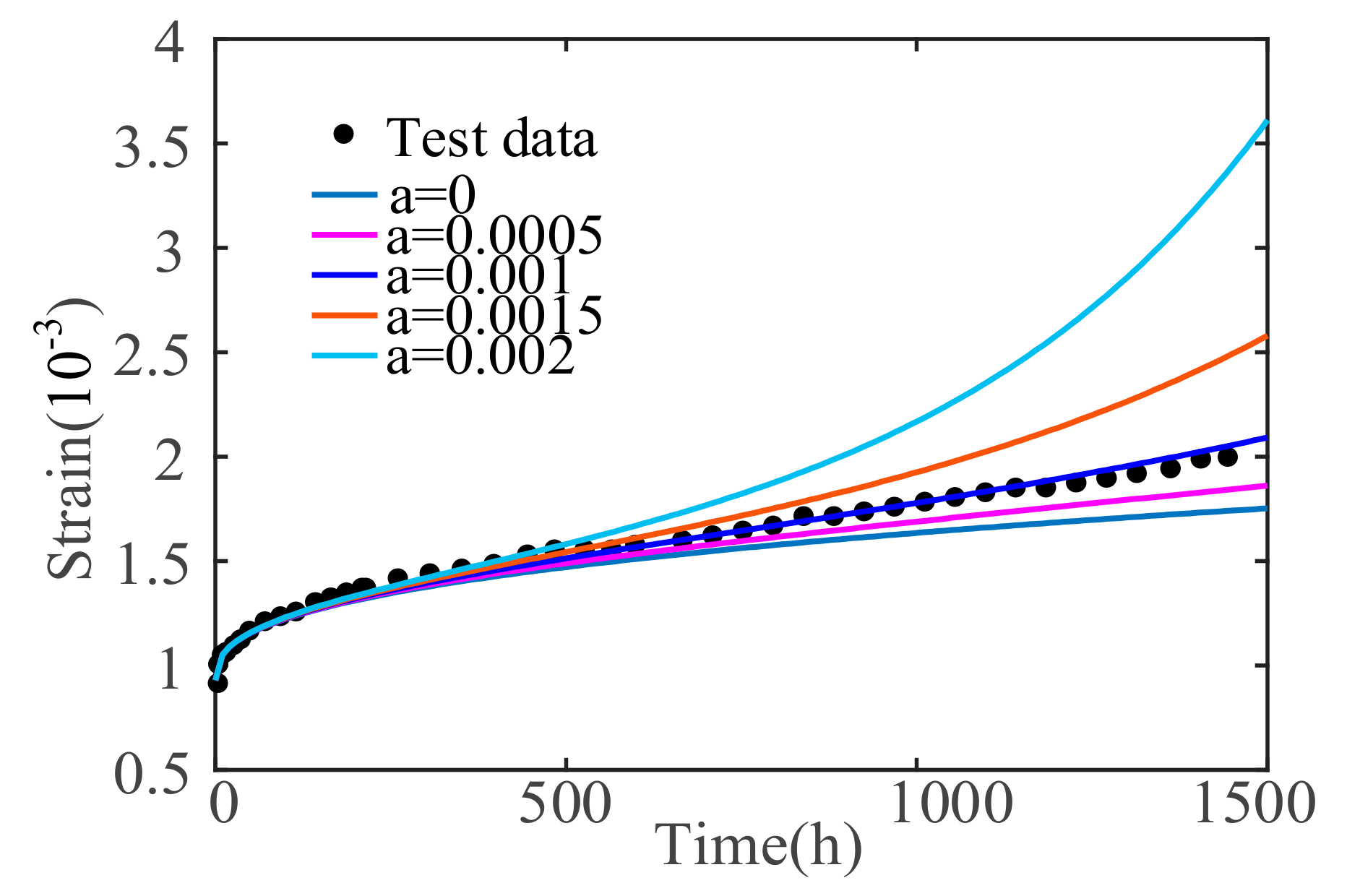
5. Parameter Sensitivity Analysis of Concrete Nonlinear Creep Damage Constitutive Model
5.1. Effect of Stress Level σ
5.2. The Influence of Fractional Order n
5.3. Effect of Material Parameter α
6. Conclusions
- The Visco-elasticity Plasticity Rheological Theory, the Riemann Liouville Theory and the Combined Model Theory are quoted to propose the stress-strain relationship expressions of the elastomer body, the visco-elasticity plasticity body, and the viscoplastic body. The nonlinear creep damage evolution equation of the concrete fractional order is conducted with consideration of damage evolution, and the parameter specific calculation method in the constructed model is given.
- The constructed concrete creep damage constitutive model in this paper is validated in high stress and different stress situations that involve uniaxial compression creep; data from the residual strain tests of Narintsoa Ranaivomanana et al. [40] and Can Tang [41] is considered. The results show that the conducted model can accurately describe the entire concrete creep process, and that it could be used as a reference for concrete non-linear creep.
- To determine the influence degree of the model parameters, the sensitivity analysis of the main influence parameters in the concrete creep damage constitutive model, including σ, material parameter α, and fractional order n, are analyzed. The results show that σ and n are positively correlated with the concrete creep deformation and rate. The creep deformation and rate will increase as σ and n increase. α is related to the time at which the concrete enters the accelerated creep stage, and the larger the value of material parameter α, the earlier the concrete will enter the accelerated creep stage.
Author Contributions
Funding
Conflicts of Interest
References
- Aitcin, P.C. Concrete structure, properties and materials. Preticehall Int. 2006, 13, 499. [Google Scholar] [CrossRef]
- Luu, C.H.; Mo, Y.L. Development of CSMM-based shell element for reinforced concrete structures. Eng. Struct. 2017, 132, 778–790. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Hubler, M.H.; Yu, Q. Damage in prestressed concrete. In Handbook of Damage Mechanics; Springer: New York, NY, USA, 2016; pp. 515–560. [Google Scholar] [CrossRef]
- Balevicius, R.; Marciukaitis, G. Linear and non-linear creep models for a multi-layered concrete composite. Arch. Civ. Mech. Eng. 2013, 13, 472–490. [Google Scholar] [CrossRef]
- Hamed, E.; Lai, C. Geometrically and materially nonlinear creep behaviour of reinforced concrete columns. Structures 2016, 5, 1–12. [Google Scholar] [CrossRef]
- Majorana, C.E. Mathematical modeling of creep and shrinkage of concrete. Int. J. Numer. Methods Biomed. Eng. 1989, 5, 423. [Google Scholar]
- Sprince, A.; Korjakins, A.; Pakrastinsh, L. Time-dependent behavior of high performance fiber-reinforced concrete. Adv. Mater. Res. 2013, 705, 75–80. [Google Scholar] [CrossRef]
- CEB-FIP Model Code 1990. Design Code; Thomas Teloford Services Ltd: London, UK, 1991.
- Eurocode BS EN 1992-1-1. Design of Concrete Structures; Department for Communities and Local Government: London, UK, 2004.
- ACI Committee 209. Prediction of Creep, Shrinkage and Temperature Effects in Concrete Structures; American Concrete Institute: Farmington Hills, MI, USA, 1999. [Google Scholar]
- Gardner, N.J.; Lockman, M.J. Design provisions for drying shrinkage and creep of normal-strength concrete. ACI Mater. J. 2001, 98, 159–167. [Google Scholar]
- Bazant, Z.P.; Baweja, S. Creep and shrinkage prediction model for analysis and design of concrete structures—Model b 3. Mater. Struct. 1995, 28, 357–365. [Google Scholar]
- Bazant, Z.P.; Baweja, S. Justification and refinements of model B3 for concrete creep and shrinkage 2. Updating and theoretical basis. Mater. Struct. 1995, 28, 488–495. [Google Scholar] [CrossRef]
- Hubler, M.H.; Wendner, R.; Bažant, Z.K. Statistical justification of model b4 for drying and autogenous shrinkage of concrete and comparisons to other models. Mater. Struct. 2015, 48, 797–814. [Google Scholar] [CrossRef]
- Wendner, R.; Hubler, M.H.; Bazant, Z.P. Optimization method, choice of form and uncertainty quantification of model b4 using laboratory and multi-decade bridge databases. Mater. Struct. 2015, 48, 771–796. [Google Scholar] [CrossRef]
- Ghasemzadeh, F.; Manafpour, A.; Sajedi, S.; Shekarchi, M.; Hatami, M. Predicting long-term compressive creep of concrete using inverse analysis method. Constr. Build. Mater. 2016, 124, 496–507. [Google Scholar] [CrossRef]
- Kindrachuk, V.M.; Galanov, B.A.; Kartuzov, V.V.; Dub, S.N. Refined model of elastic nanoindentation of a half-space by the blunted Berkovich indenter accounting for tangential displacements on the contact surface. J. Mater. Sci. 2009, 44, 2599–2609. [Google Scholar] [CrossRef]
- Grenacher, M.; Thurlimann, B. Creep buckling of reinforced concrete columns. Int. Assoc. Bridg. Struct. Eng. 1970, 6, 275–282. (In German) [Google Scholar]
- Bažant, Z.P.; Tsubaki, T. Nonlinear creep buckling of reinforced concrete columns. J. Struct. Div. 1980, 106, 2235–2257. [Google Scholar]
- Kwak, H.G.; Kim, J.K. Nonlinear behaviour of slender RC columns: Numerical formulation. Constr. Build. Mater. 2006, 20, 527–537. [Google Scholar] [CrossRef]
- Radnić, J.; Matešan, D.; Smilović, M. Nonlinear creep model for concrete in analysis of Plates and Shells. Adv. Struct. Mater. 2012, 1, 163–173. [Google Scholar]
- Briffaut, M.; Benboudjema, F.; Laborderie, C.; Torrenti, J.-M. Creep consideration effect on meso-scale modeling of concrete hydration process and consequences on the mechanical behavior. J. Eng. Mech. 2013, 139, 1808–1817. [Google Scholar] [CrossRef]
- Abdulkadir, C.A.; Arslan, A.; Rüstem, G. Mesoscale simulation of cement-based materials’ time-dependent behavior. Comput. Mater. Sci. 2008, 41, 20–26. [Google Scholar]
- Sherief, H.H.; El-Sayed, A.M.A. Fractional order theory of thermoelasticity. Int. J. Solids Struct. 2010, 47, 269–275. [Google Scholar] [CrossRef]
- Papoulia, K.D.; Panoskaltsis, V.P.; Kurup, N.V.; Korovajchuk, I. Rheological representation of fractional order viscoelastic material models. Rheol. Acta 2010, 49, 381–400. [Google Scholar] [CrossRef]
- Suzuki, J.L.; Zayernouri, M.; Bittencourt, M.L.; Karniadakis, G.E. Fractional-order uniaxial visco-elasto-plastic models for structural analysis. Comput. Methods Appl. Mech. Eng. 2016, 308, 443–467. [Google Scholar] [CrossRef]
- Bouras, Y.; Zorica, D.; Atanacković, T.M.; Vrcelj, Z. A non-linear thermo-viscoelastic rheological model based on fractional derivatives for high temperature creep in concrete. Appl. Math. Model. 2018, 55, 551–568. [Google Scholar] [CrossRef]
- Beltempo, A.; Zingales, M.; Bursi, O.S.; Deseri, L. A fractional-order model for aging materials: An application to concrete. Int. J. Solids Struct. 2018, 138, 13–23. [Google Scholar] [CrossRef]
- Adolfsson, K.; Enelund, M.; Olsson, P. On the fractional order model of viscoelasticity. Mech. Time-Depend. Mater. 2005, 9, 15–34. [Google Scholar] [CrossRef]
- Koeller, R.C. Applications of fractional calculus to the theory of viscoelasticity. Trans. ASME J. Appl. Mech. 1984, 51, 299–307. [Google Scholar] [CrossRef]
- Yin, D.; Ren, J.; He, C.; Chen, Q. A new creep model element for geomaterials. Chin. J. Rock Mech. Eng. 2007, 26, 1899–1903. [Google Scholar]
- Zhou, H.; Wang, C.; Duan, Z.; Zhang, M.; Liu, J. Time-based fractional derivative approach to creep constitutive model of salt rock. Sci. Sin. Phys. Mech. Astronomica 2012, 42, 310–318. [Google Scholar] [CrossRef]
- Gama, D.A.; Júnior, J.M.R.; De Melo, T.J.A.D.; Rodrigues, J.K.G. Rheological studies of asphalt modified with elastomeric polymer. Constr. Build. Mater. 2016, 106, 290–295. [Google Scholar] [CrossRef]
- Jun, S. Rock rheological mechanics and its advance in engineering applications. Chin. J. Rock Mech. Eng. 2007, 26, 1081–1106. [Google Scholar]
- Berdichevsky, V.L.; Herman, J.N. On rheology of cross-linked polymers: Slippage of polymer chains and its macroscopic modeling. Int. J. Eng. Sci. 2016, 100, 183–198. [Google Scholar] [CrossRef]
- Zhou, H.W.; Wang, C.P.; Han, B.B.; Duan, Z.Q. A creep constitutive model for salt rock based on fractional derivatives. Int. J. Rock Mech. Min. Sci. 2011, 48, 116–121. [Google Scholar] [CrossRef]
- Han, B.; Xie, H.B.; Zhu, L.; Jiang, P. Nonlinear model for early age creep of concrete under compression strains. Constr. Build. Mater. 2017, 147, 203–211. [Google Scholar] [CrossRef]
- Xia, C.; Xu, C.; Wang, X.; Zhang, C. Method for parameters determination with unified rheological machanical model. J. Rock Mech. Eng. 2009, 28, 425–432. [Google Scholar]
- Wang, P.; Jiang, L.; Li, X.; Qin, Q.; Wang, E. Physical Simulation of Mining Effect Caused by A Fault Tectonic. Arab. J. Geosci. 2018, 11, 741. [Google Scholar] [CrossRef]
- Ranaivomanana, N.; Stéphane, M.; Turatsinze, A. Tensile, compressive and flexural basic creep of concrete at different stress levels. Cem. Concr. Res. 2013, 52, 1–10. [Google Scholar] [CrossRef]
- Can, T. Research on compressive creep model and stress-strain relationship of concrete. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2016. [Google Scholar]
- He, Z.; Zhu, Z.; Ni, X.; Li, Z. Shear creep tests and creep constitutive model of marble with structural plane. Eur. J. Environ. Civ. Eng. 2017, 1–19. [Google Scholar] [CrossRef]
- Zhou, H.W.; Wang, C.P.; Mishnaevsky, L., Jr.; Duan, Z.Q.; Ding, J.Y. A fractional derivative approach to full creep regions in salt rock. Mech. Time Depend. Mater. 2013, 17, 413–425. [Google Scholar] [CrossRef]

| Stress/MPa | α/h-i | n | ||||||
|---|---|---|---|---|---|---|---|---|
| 20.9 | 45.2 | 13.5 | 235 | 263 | – | – | – | 0.31 |
| 33.9 | 40.1 | 24.0 | 191 | 332 | – | – | – | 0.36 |
| Stress/MPa | α/h-i | n | ||||||
|---|---|---|---|---|---|---|---|---|
| 16.9 | 38.5 | 8.7 | 171 | 281 | – | – | – | 0.3 |
| 25.7 | 42.8 | 14.0 | 105 | 317 | – | – | – | 0.29 |
| 30.0 | 32.3 | 18.7 | 246 | 254 | 26.3 | 854 | 0.001 | 0.38 |
| 35.7 | 37.8 | 20.2 | 239 | 384 | 30.9 | 688 | 0.0013 | 0.48 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Zhu, Z.; Zhu, S.; He, Z.; Zhu, D.; Liu, J.; Meng, S. Nonlinear Creep Damage Constitutive Model of Concrete Based on Fractional Calculus Theory. Materials 2019, 12, 1505. https://doi.org/10.3390/ma12091505
Zhang C, Zhu Z, Zhu S, He Z, Zhu D, Liu J, Meng S. Nonlinear Creep Damage Constitutive Model of Concrete Based on Fractional Calculus Theory. Materials. 2019; 12(9):1505. https://doi.org/10.3390/ma12091505
Chicago/Turabian StyleZhang, Cong, Zhende Zhu, Shu Zhu, Zhilei He, Duan Zhu, Jinzhong Liu, and Songsong Meng. 2019. "Nonlinear Creep Damage Constitutive Model of Concrete Based on Fractional Calculus Theory" Materials 12, no. 9: 1505. https://doi.org/10.3390/ma12091505
APA StyleZhang, C., Zhu, Z., Zhu, S., He, Z., Zhu, D., Liu, J., & Meng, S. (2019). Nonlinear Creep Damage Constitutive Model of Concrete Based on Fractional Calculus Theory. Materials, 12(9), 1505. https://doi.org/10.3390/ma12091505





