Shear-Transformation Zone Activation during Loading and Unloading in Nanoindentation of Metallic Glasses
Abstract
1. Introduction
2. Simulation Details
3. Results
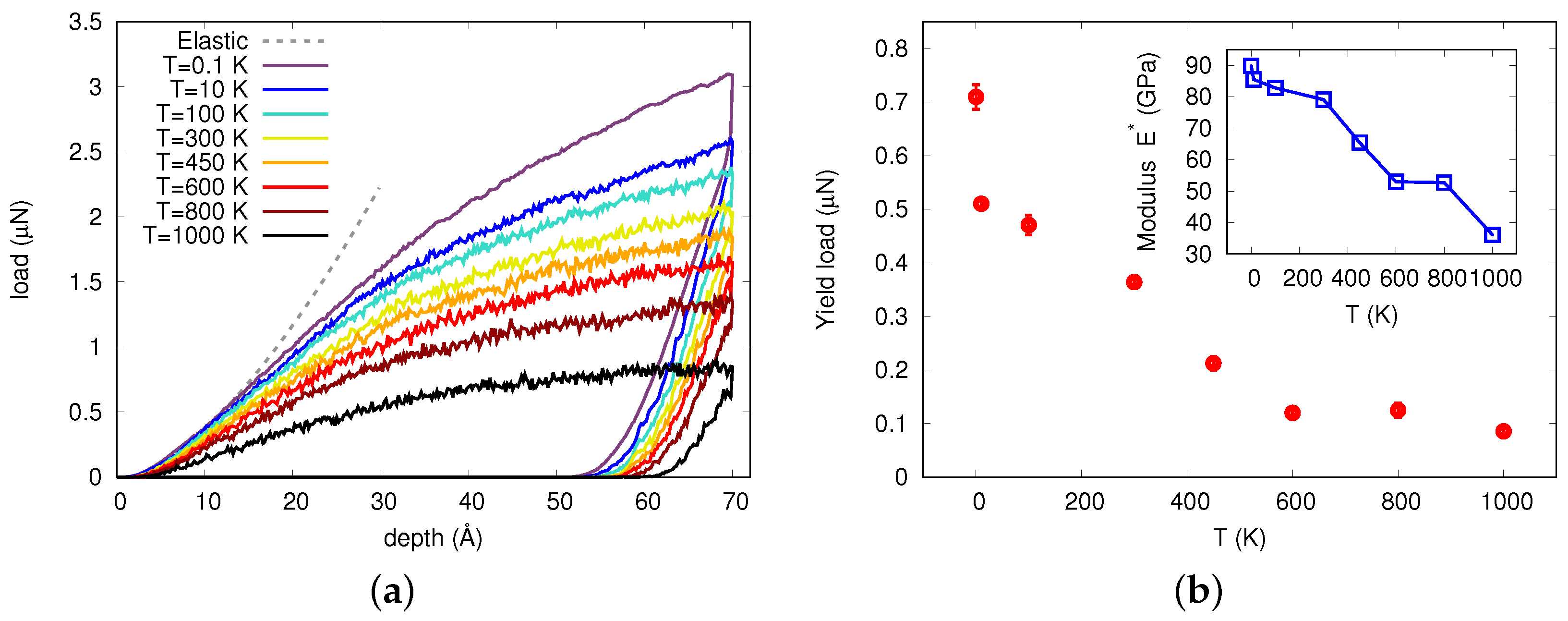
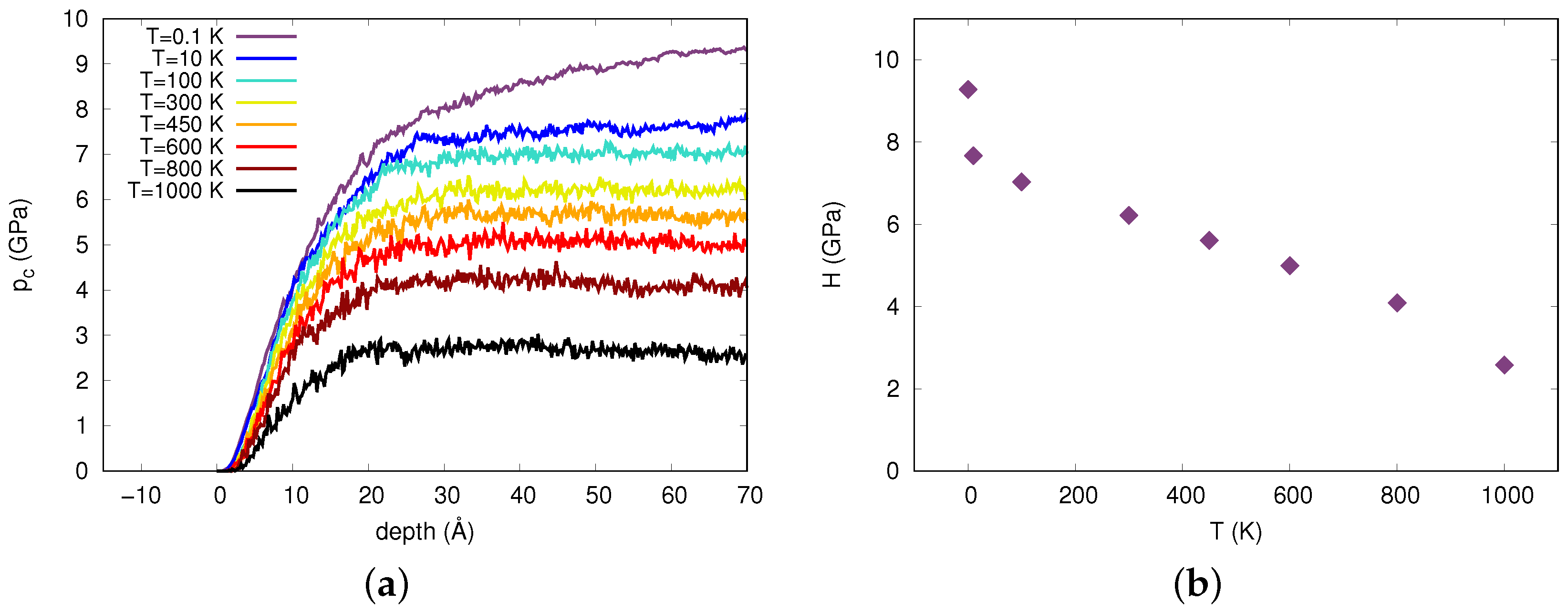
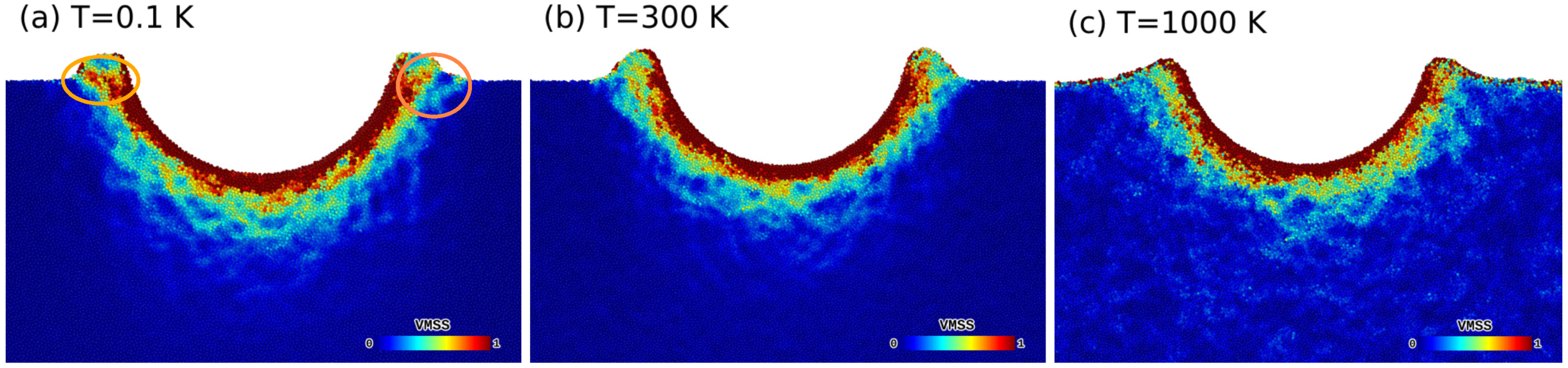
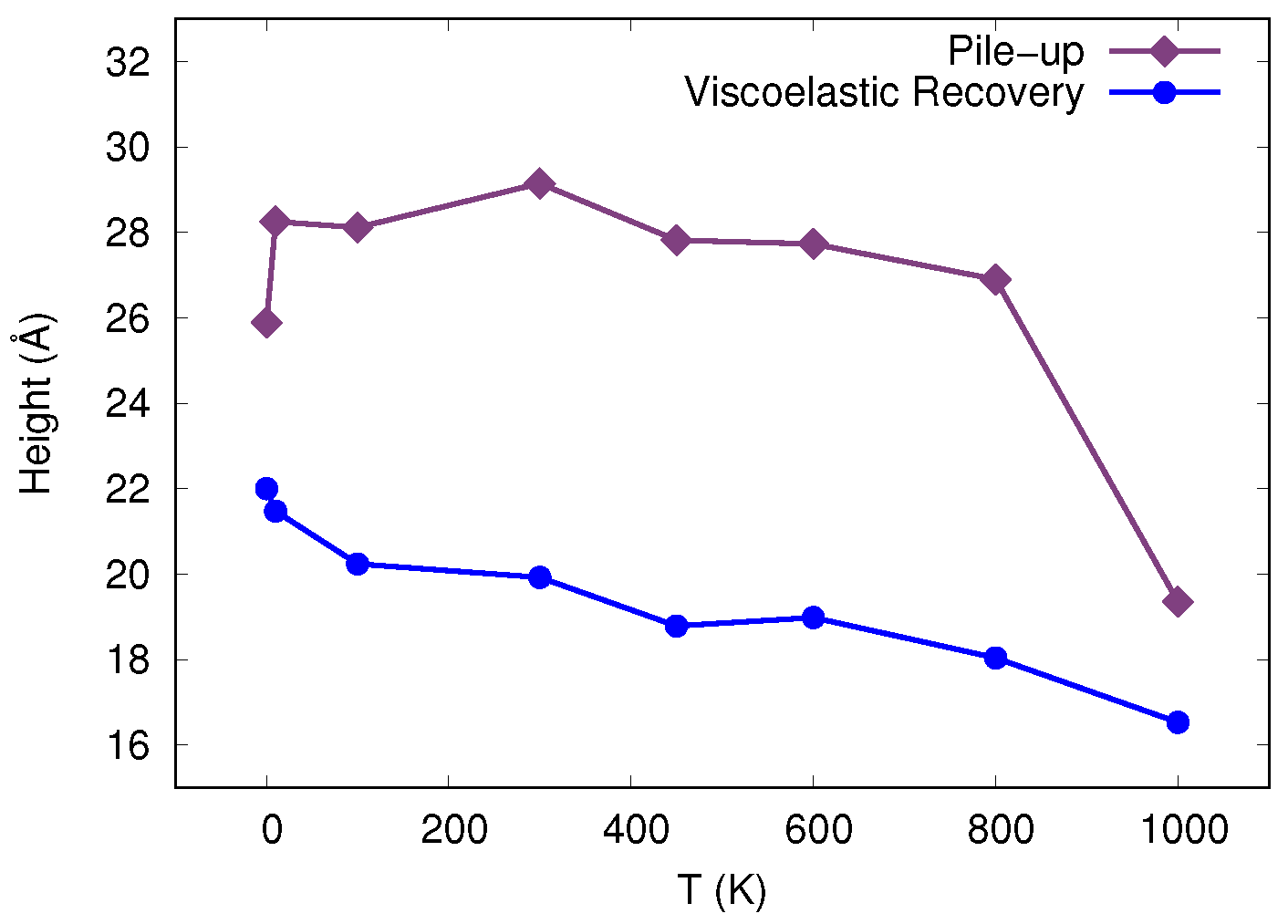
3.1. Hardness and Pit Shape
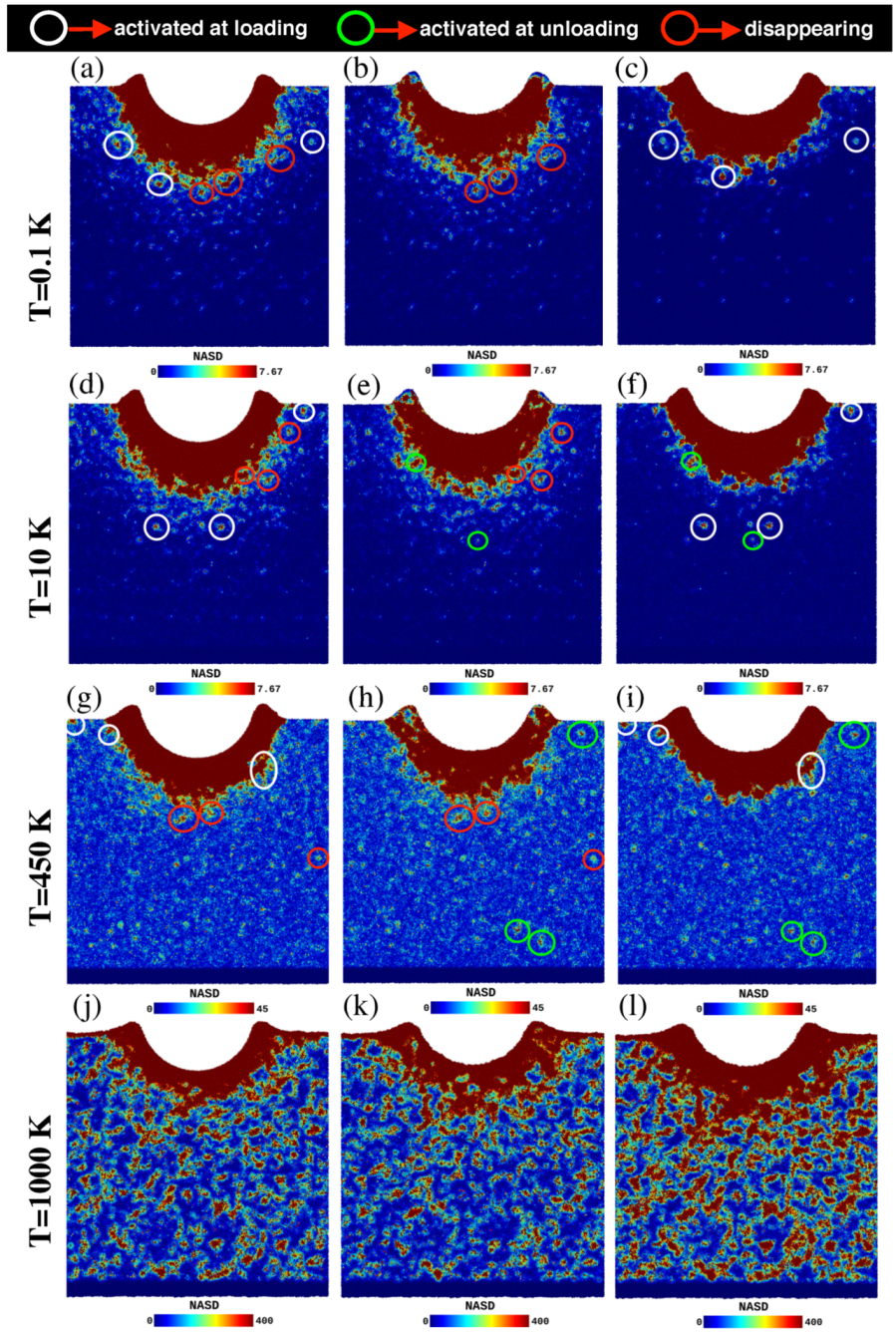
3.2. Analysis of STZs: Non-Affine Squared Displacement
- white circles enclose plastic regions that appear during loading and stay through the unloading process;
- red circles feature zones that were activated during loading, but disappear during unloading;
- green circles emphasize plastic regions that appear during unloading.
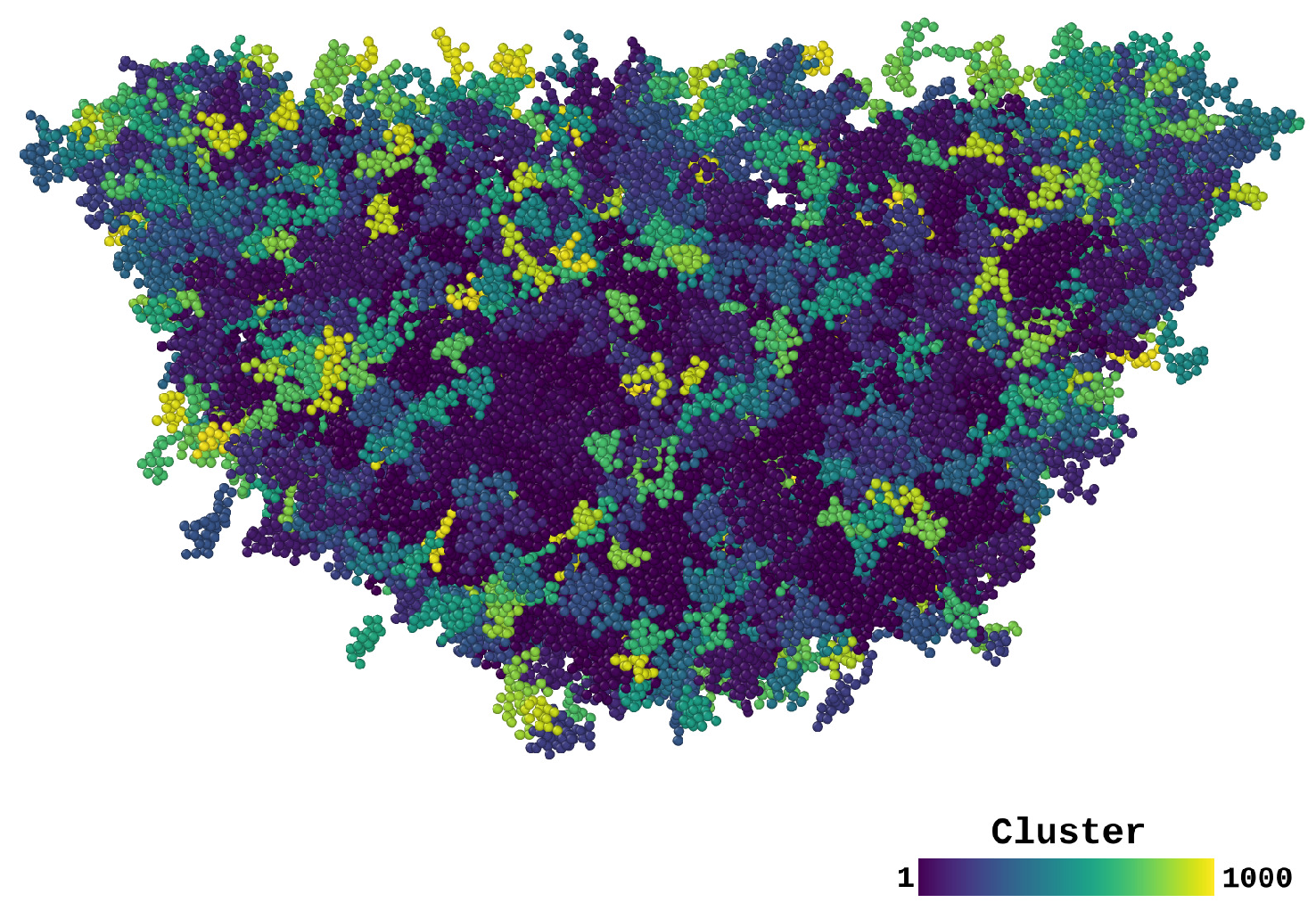
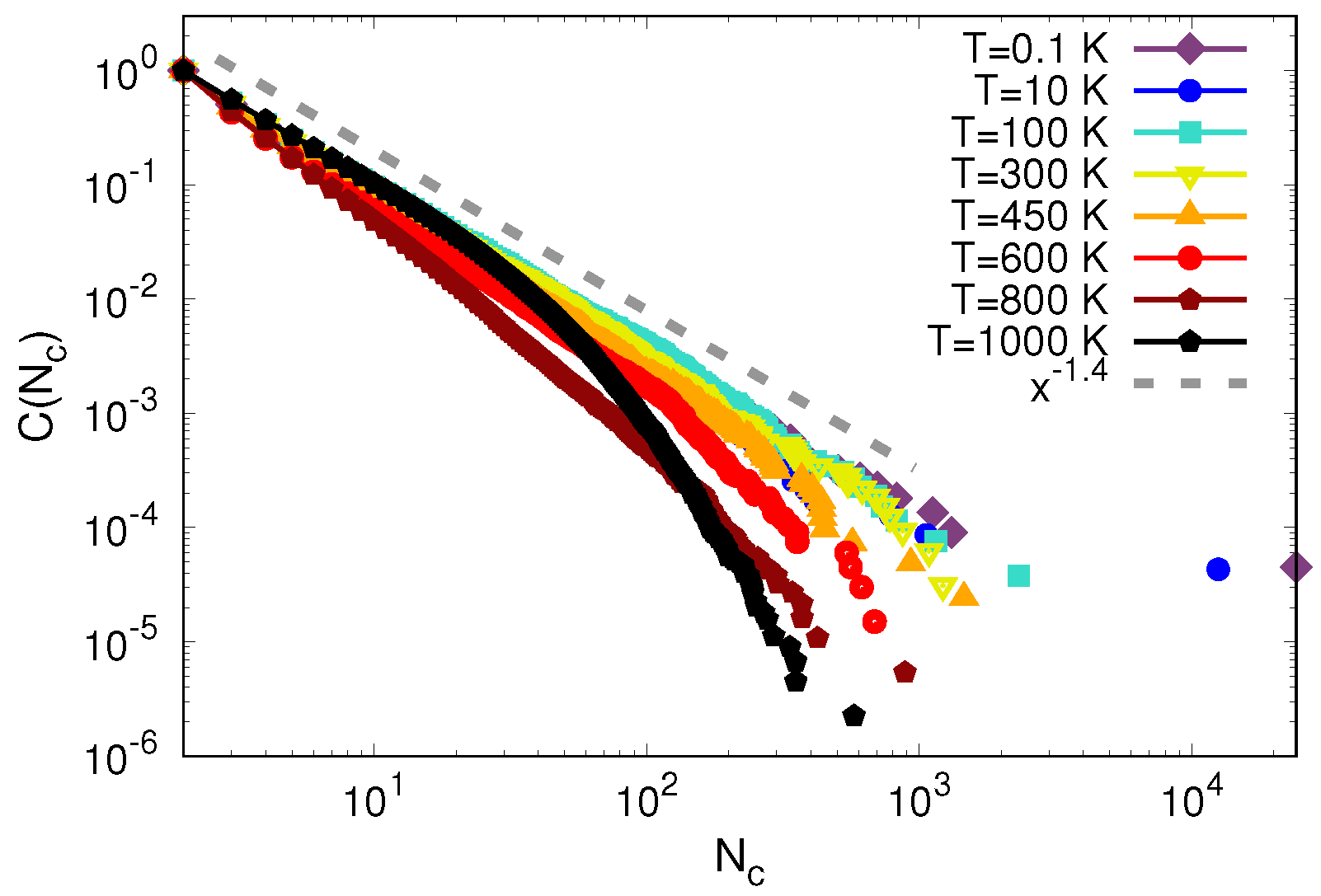
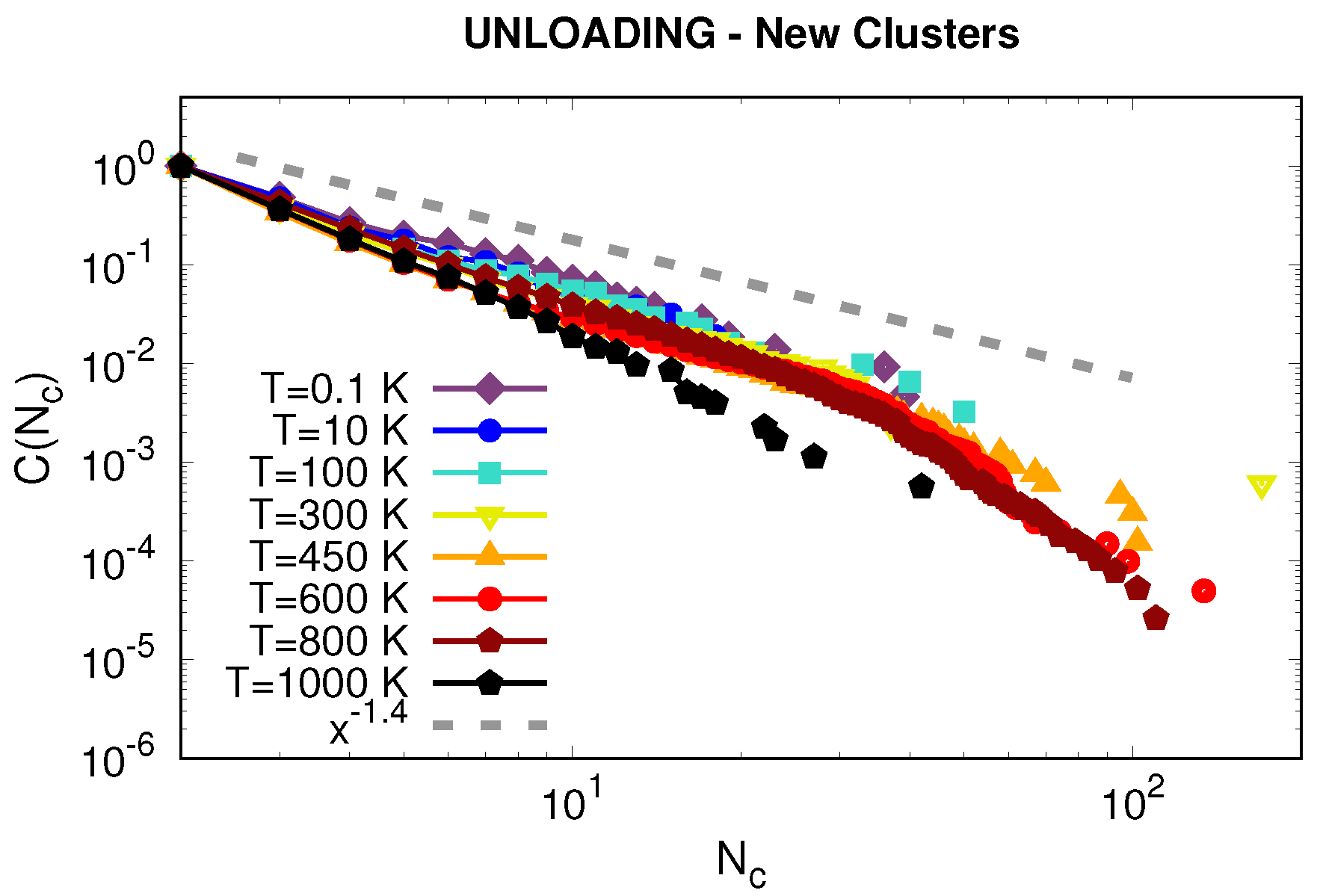
3.3. Analysis of STZs: Cluster Analysis
4. Summary
- An analysis of the plastic activity using the technique of non-affine displacements [40], together with a cluster analysis, allows us to identify the STZs created during the indentation process [48]. The complementary cumulative distribution of plastically deformed regions, , follows a power law with an exponent around . This power-law of found here is consistent with that found previously in uniaxially sheared Lennard-Jones glass and points at a percolation transition in the formation of STZs [24].
- Surprisingly, the power exponent which has been found theoretically to describe the temperature dependence of plasticity, also describes its depth dependence. In addition, the power law found during loading is the same as for the new clusters that form during unloading.
- We observe an apparent transition from STZ operation to shear banding. This shear band activity is observed at room temperature and below, and is particularly strong a the lowest temperature simulated, 0.1 K.
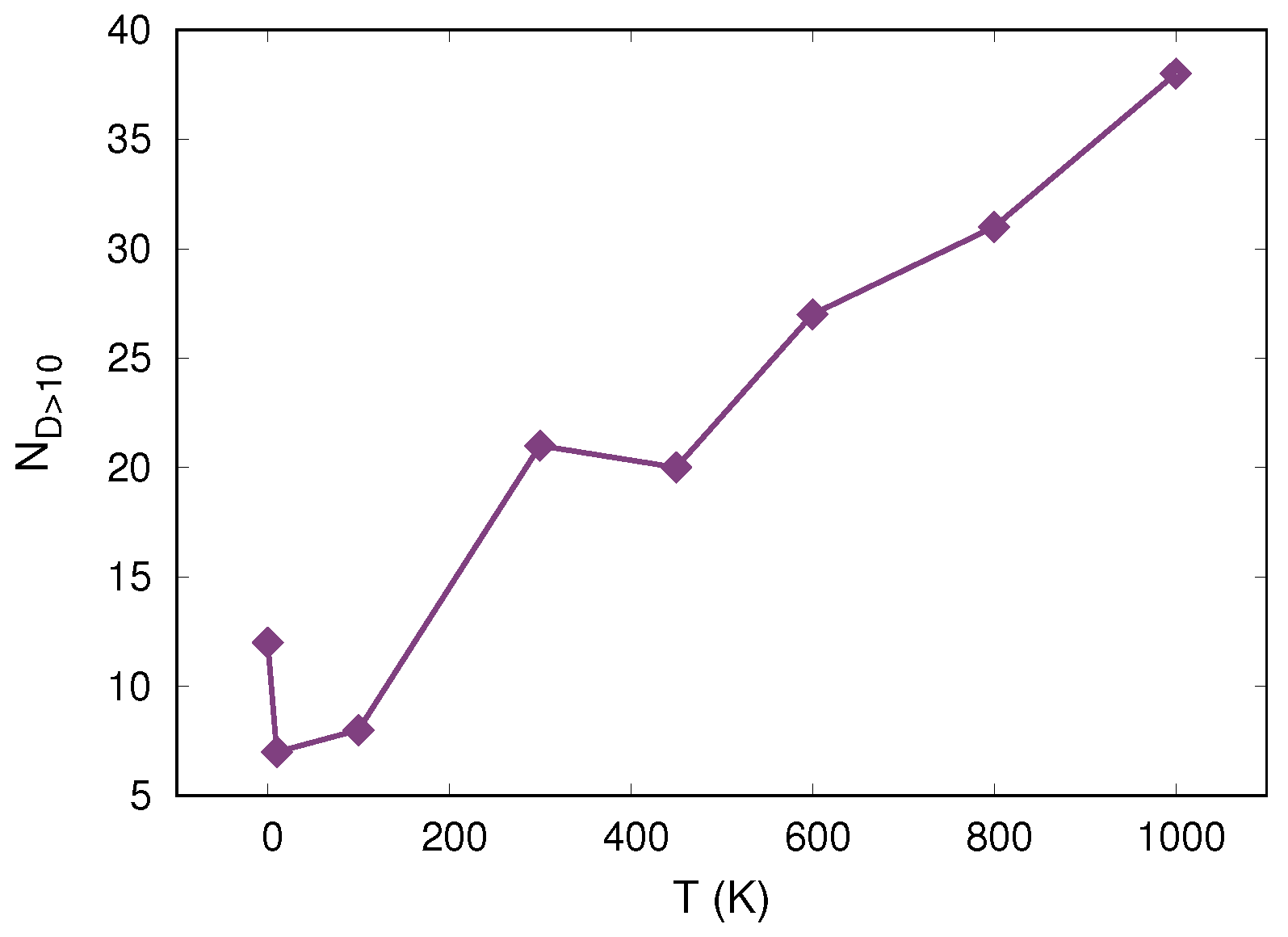
- During the unloading process, part of the created STZs deactivate and also new zones are created. The number of large disappearing STZs increases with temperature. The amount of plastic activity and STZ sizes during the unloading process strongly increases with temperature, and correlates well with the increased serration of the unloading curve at increased temperatures. In this context, the pop-outs formed in the unloading process have the same nature as the pop-ins found during loading.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
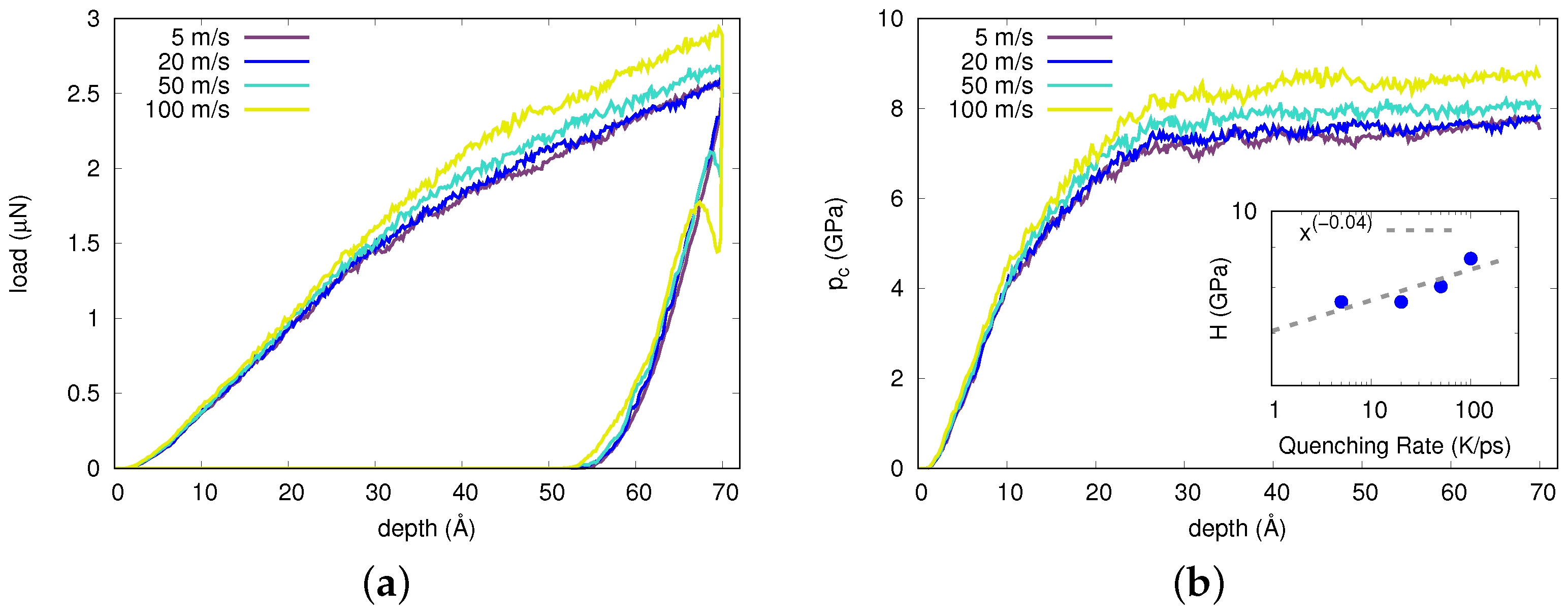
Appendix A. Quenching-Rate Dependence
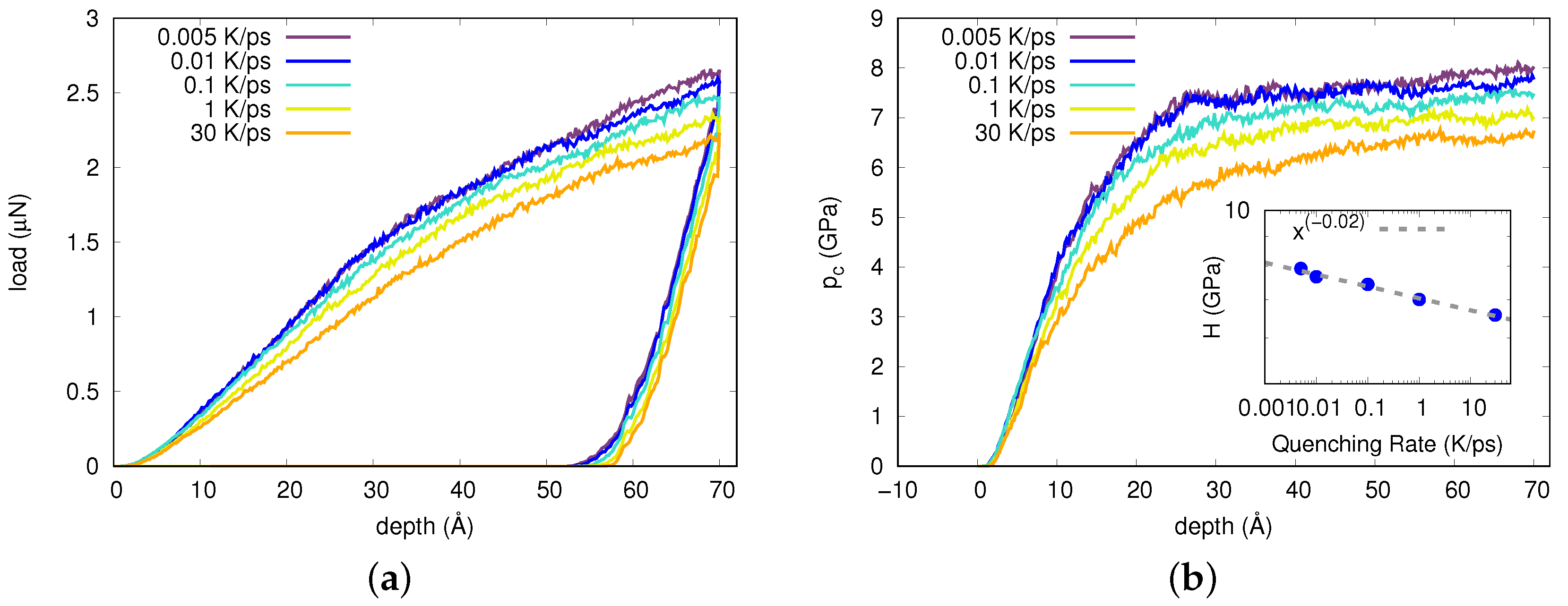

Appendix B. Cluster-Analysis Parameters

Appendix C. Statistics of STZs
References
- Spaepen, F. A microscopic mechanism for steady state inhomogeneous flow in metallic glasses. Acta Mater. 1977, 25, 407–415. [Google Scholar] [CrossRef]
- Argon, A.S. Plastic deformation in metallic glasses. Acta Mater. 1979, 27, 47–58. [Google Scholar] [CrossRef]
- Schuh, C.A.; Hufnagel, T.C.; Ramamurty, U. Mechanical behavior of amorphous alloys. Acta Mater. 2007, 55, 4067–4109. [Google Scholar] [CrossRef]
- Hufnagel, T.C.; Schuh, C.A.; Falk, M.L. Deformation of metallic glasses: Recent developments in theory, simulations, and experiments. Acta Mater. 2016, 109, 375–393. [Google Scholar] [CrossRef]
- Liu, C.; Roddatis, V.; Kenesei, P.; Maaß, R. Shear-band thickness and shear-band cavities in a Zr-based metallic glass. Acta Mater. 2017, 140, 206–216. [Google Scholar] [CrossRef]
- Küchemann, S.; Liu, C.; Dufresne, E.M.; Shin, J.; Maaß, R. Shear banding leads to accelerated aging dynamics in a metallic glass. Phys. Rev. B 2018, 97, 014204. [Google Scholar] [CrossRef]
- Maaß, R.; Birckigt, P.; Borchers, C.; Samwer, K.; Volkert, C.A. Long range stress fields and cavitation along a shear band in a metallic glass: The local origin of fracture. Acta Mater. 2015, 98, 94–102. [Google Scholar] [CrossRef]
- Shahabi, H.S.; Scudino, S.; Kaban, I.; Stoica, M.; Escher, B.; Menzel, S.; Vaughan, G.B.M.; Kühn, U.; Eckert, J. Mapping of residual strains around a shear band in bulk metallic glass by nanobeam X-ray diffraction. Acta Mater. 2016, 111, 187–193. [Google Scholar] [CrossRef]
- Mayr, S.G. Activation Energy of Shear Transformation Zones: A Key for Understanding Rheology of Glasses and Liquids. Phys. Rev. Lett. 2006, 97, 195501. [Google Scholar] [CrossRef] [PubMed]
- Krisponeit, J.O.; Pitikaris, S.; Avila, K.E.; Küchemann, S.; Krüger, A.; Samwer, K. Crossover from random three-dimensional avalanches to correlated nano shear bands in metallic glasses. Nat. Commun. 2014, 5, 3616. [Google Scholar] [CrossRef]
- Pan, D.; Inoue, A.; Sakurai, T.; Chen, M.W. Experimental characterization of shear transformation zones for plastic flow of bulk metallic glasses. Proc. Natl. Acad. Sci. USA 2008, 105, 14769–14772. [Google Scholar] [CrossRef]
- Şopu, D.; Stukowski, A.; Stoica, M.; Scudino, S. Atomic-Level Processes of Shear Band Nucleation in Metallic Glasses. Phys. Rev. Lett. 2017, 119, 195503. [Google Scholar] [CrossRef] [PubMed]
- Küchemann, S.; Derlet, P.M.; Liu, C.; Rosenthal, D.; Sparks, G.; Larson, W.S.; Maaß, R. Energy Storage in Metallic Glasses via Flash Annealing. Adv. Funct. Mater. 2018, 28, 1805385. [Google Scholar] [CrossRef]
- Schuh, C.A.; Nieh, T.G. A nanoindentation study of serrated flow in bulk metallic glasses. Acta Mater. 2003, 51, 87–99. [Google Scholar] [CrossRef]
- Schuh, C.A.; Lund, A.C.; Nieh, T.G. New regime of homogeneous flow in the formation map of metallic glasses: elevated temperature nanoindentation experiments and mechanistic modeling. Acta Mater. 2004, 52, 5879–5891. [Google Scholar] [CrossRef]
- Packard, C.E.; Homer, E.R.; Al-Aqeeli, N.; Schuh, C.A. Cyclic hardening of metallic glasses under Hertzian contacts: Experiments and STZ dynamics simulations. Philos. Mag. 2010, 90, 1373–1390. [Google Scholar] [CrossRef]
- Deng, C.; Schuh, C.A. Atomistic mechanisms of cyclic hardening in metallic glass. Appl. Phys. Lett. 2012, 100, 251909. [Google Scholar] [CrossRef]
- Greer, A.L.; Castellero, A.; Madge, S.V.; Walker, I.T.; Wilde, J.R. Nanoindentation studies of shear banding in fully amorphous and partially devitrified metallic alloys. Mater. Sci. Eng. A 2004, 375, 1182–1185. [Google Scholar] [CrossRef]
- Coleman, J.P.; Meng, F.; Tsuchiya, K.; Beadsworth, J.; LeBlanc, M.; Liaw, P.K.; Uhl, J.T.; Weaver, R.L.; Dahmen, K.A. Effect of annealing on nanoindentation slips in a bulk metallic glass. Phys. Rev. B 2017, 96, 134117. [Google Scholar] [CrossRef]
- Bian, X.L.; Wang, G.; Chan, K.C.; Ren, J.L.; Gao, Y.L.; Zhai, Q.J. Shear avalanches in metallic glasses under nanoindentation: Deformation units and rate dependent strain burst cut-off. Appl. Phys. Lett. 2013, 103, 101907. [Google Scholar] [CrossRef]
- Friedman, N.; Jennings, A.T.; Tsekenis, G.; Kim, J.Y.; Tao, M.; Uhl, J.T.; Greer, J.R.; Dahmen, K.A. Statistics of Dislocation Slip Avalanches in Nanosized Single Crystals Show Tuned Critical Behavior Predicted by a Simple Mean Field Model. Phys. Rev. Lett. 2012, 109, 095507. [Google Scholar] [CrossRef]
- Dahmen, K.A.; Ben-Zion, Y.; Uhl, J.T. A simple analytic theory for the statistics of avalanches in sheared granular materials. Nat. Phys. 2011, 7, 554–557. [Google Scholar] [CrossRef]
- Avila, K.E.; Castillo, H.E.; Vollmayr-Lee, K.; Zippelius, A. Slow and long-ranged dynamical heterogeneities in dissipative fluids. Soft Matter 2016, 12, 5461–5474. [Google Scholar] [CrossRef] [PubMed]
- Shrivastav, G.P.; Chaudhuri, P.; Horbach, J. Yielding of glass under shear: A directed percolation transition precedes shear-band formation. Phys. Rev. E 2016, 94, 042605. [Google Scholar] [CrossRef] [PubMed]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Cao, A.J.; Cheng, Y.Q.; Ma, E. Structural processes that initiate shear localization in metallic glass. Acta Mater. 2009, 57, 5146–5155. [Google Scholar] [CrossRef]
- Mendelev, M.I.; Sordelet, D.J.; Kramer, M.J. Using atomistic computer simulations to analyze x-ray diffraction data from metallic glasses. J. Appl. Phys. 2007, 102, 043501. [Google Scholar] [CrossRef]
- Shi, Y.; Falk, M.L. Stress-induced structural transformation and shear banding during simulated nanoindentation of a metallic glass. Acta Mater. 2007, 55, 4317–4324. [Google Scholar] [CrossRef]
- Lad, K.N.; Jakse, N.; Pasturel, A. Signatures of fragile-to-strong transition in a binary metallic glass-forming liquid. J. Chem. Phys. 2012, 136, 104509. [Google Scholar] [CrossRef]
- Kelchner, C.L.; Plimpton, S.J.; Hamilton, J.C. Dislocation nucleation and defect structure during surface indentation. Phys. Rev. B 1998, 58, 11085–11088. [Google Scholar] [CrossRef]
- Ruestes, C.J.; Bringa, E.M.; Gao, Y.; Urbassek, H.M. Molecular dynamics modeling of nanoindentation. In Applied Nanoindentation in Advanced Materials; Tiwari, A., Natarajan, S., Eds.; Wiley: Chichester, UK, 2017; Chapter 14; pp. 313–345. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—The Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Hertz, H. Ueber die Berührung fester elastischer Körper. J. Reine Angew. Math. 1882, 92, 156–171. [Google Scholar]
- Fischer-Cripps, A.C. Nanoindentation, 2nd ed.; Springer: New York, NY, USA, 2004. [Google Scholar]
- Johnson, W.L.; Samwer, K. A Universal Criterion for Plastic Yielding of Metallic Glasses with a (T/Tg)2/3 Temperature Dependence. Phys. Rev. Lett. 2005, 95, 195501. [Google Scholar] [CrossRef] [PubMed]
- Jang, J.i.; Lance, M.J.; Wen, S.; Tsui, T.Y.; Pharr, G.M. Indentation-induced phase transformations in silicon: influences of load, rate and indenter angle on the transformation behavior. Acta Mater. 2005, 53, 1759–1770. [Google Scholar] [CrossRef]
- Ziegenhain, G.; Urbassek, H.M.; Hartmaier, A. Influence of crystal anisotropy on elastic deformation and onset of plasticity in nanoindentation: A simulational study. J. Appl. Phys. 2010, 107, 061807. [Google Scholar] [CrossRef]
- Zhao, D.; Zhao, H.; Zhu, B.; Wang, S. Investigation on hardening behavior of metallic glass under cyclic indentation loading via molecular dynamics simulation. Appl. Surf. Sci. 2017, 416, 14–23. [Google Scholar] [CrossRef]
- Jiang, W.H.; Atzmon, M. Rate dependence of serrated flow in a metallic glass. J. Mater. Res. 2003, 18, 755–757. [Google Scholar] [CrossRef]
- Falk, M.L.; Langer, J.S. Dynamics of viscoplastic deformation in amorphous solids. Phys. Rev. E 1998, 57, 7192. [Google Scholar] [CrossRef]
- Lundberg, M.; Krishan, K.; Xu, N.; O’Hern, C.S.; Dennin, M. Reversible plastic events in amorphous materials. Phys. Rev. E 2008, 77, 041505. [Google Scholar] [CrossRef] [PubMed]
- Langer, J.S. Shear-transformation-zone theory of plastic deformation near the glass transition. Phys. Rev. E 2008, 77, 021502. [Google Scholar] [CrossRef] [PubMed]
- Zhong, C.; Zhang, H.; Cao, Q.P.; Wang, X.D.; Zhang, D.X.; Ramamurty, U.; Jiang, J.Z. Size distribution of shear transformation zones and their evolution towards the formation of shear bands in metallic glasses. J. Non-Cryst. Solids 2016, 445–446, 61–68. [Google Scholar] [CrossRef]
- Herrero-Gómez, C.; Samwer, K. Stress and temperature dependence of the avalanche dynamics during creep deformation of metallic glasses. Sci. Rep. 2016, 6, 33503. [Google Scholar] [CrossRef] [PubMed]
- Muñoz, M.A.; Dickman, R.; Vespignani, A.; Zapperi, S. Avalanche and spreading exponents in systems with absorbing states. Phys. Rev. E 1999, 59, 6175–6179. [Google Scholar] [CrossRef]
- Carvalho, M.C.T.P.; Duarte, J.A.M.S. Directed-site percolation clusters: The scaling function in dimensions two to six. Z. Phys. B Condens. Matter 1988, 70, 203–208. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, S.T.; Yang, Y.; Dong, Y.D.; Liu, C.T.; Lu, J. Unusual fast secondary relaxation in metallic glass. Nat. Commun. 2015, 6, 7876. [Google Scholar] [CrossRef]
- Ma, Y.; Peng, G.J.; Debela, T.T.; Zhang, T.H. Nanoindentation study on the characteristic of shear transformation zone volume in metallic glassy films. Scr. Mater. 2015, 108, 52–55. [Google Scholar] [CrossRef]
- Dahmen, K.A.; Ben-Zion, Y.; Uhl, J.T. Micromechanical Model for Deformation in Solids with Universal Predictions for Stress-Strain Curves and Slip Avalanches. Phys. Rev. Lett. 2009, 102, 175501. [Google Scholar] [CrossRef] [PubMed]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Avila, K.E.; Küchemann, S.; Alabd Alhafez, I.; Urbassek, H.M. Shear-Transformation Zone Activation during Loading and Unloading in Nanoindentation of Metallic Glasses. Materials 2019, 12, 1477. https://doi.org/10.3390/ma12091477
Avila KE, Küchemann S, Alabd Alhafez I, Urbassek HM. Shear-Transformation Zone Activation during Loading and Unloading in Nanoindentation of Metallic Glasses. Materials. 2019; 12(9):1477. https://doi.org/10.3390/ma12091477
Chicago/Turabian StyleAvila, Karina E., Stefan Küchemann, Iyad Alabd Alhafez, and Herbert M. Urbassek. 2019. "Shear-Transformation Zone Activation during Loading and Unloading in Nanoindentation of Metallic Glasses" Materials 12, no. 9: 1477. https://doi.org/10.3390/ma12091477
APA StyleAvila, K. E., Küchemann, S., Alabd Alhafez, I., & Urbassek, H. M. (2019). Shear-Transformation Zone Activation during Loading and Unloading in Nanoindentation of Metallic Glasses. Materials, 12(9), 1477. https://doi.org/10.3390/ma12091477






