Numerical Study on Concrete Pumping Behavior via Local Flow Simulation with Discrete Element Method
Abstract
:1. Introduction
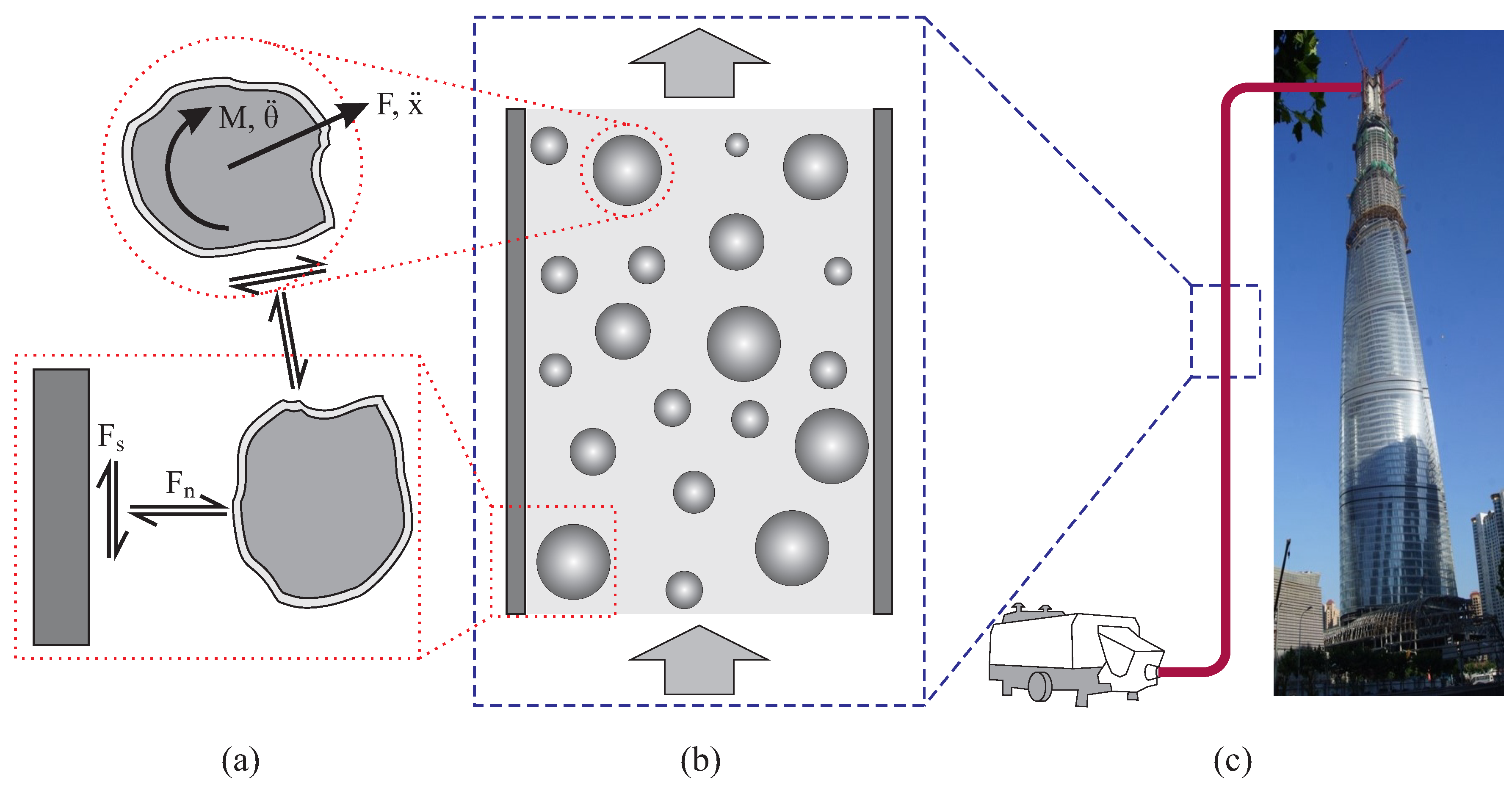
2. Fundamentals of Discrete Element Method
3. Modeling of Fresh Concrete with DEM
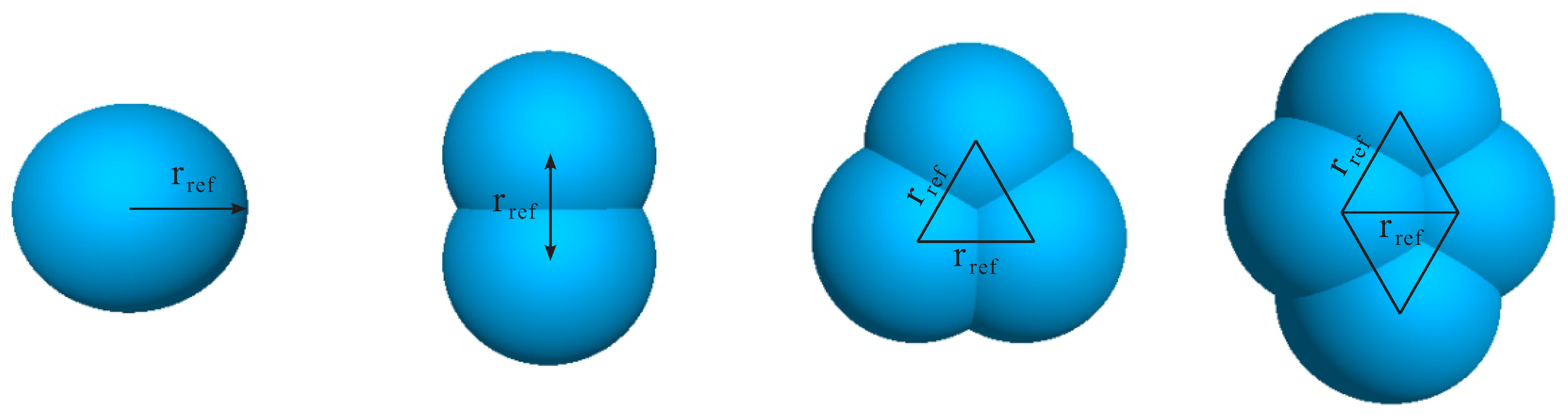
3.1. Geometrical Representation
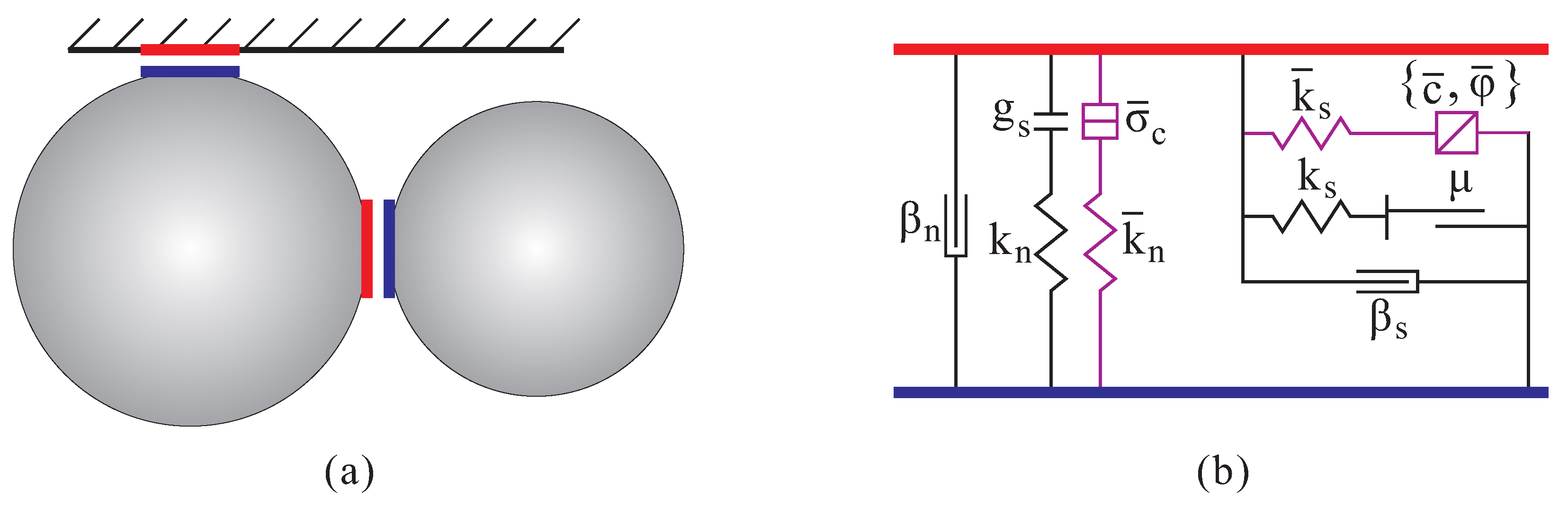
3.2. Material Model
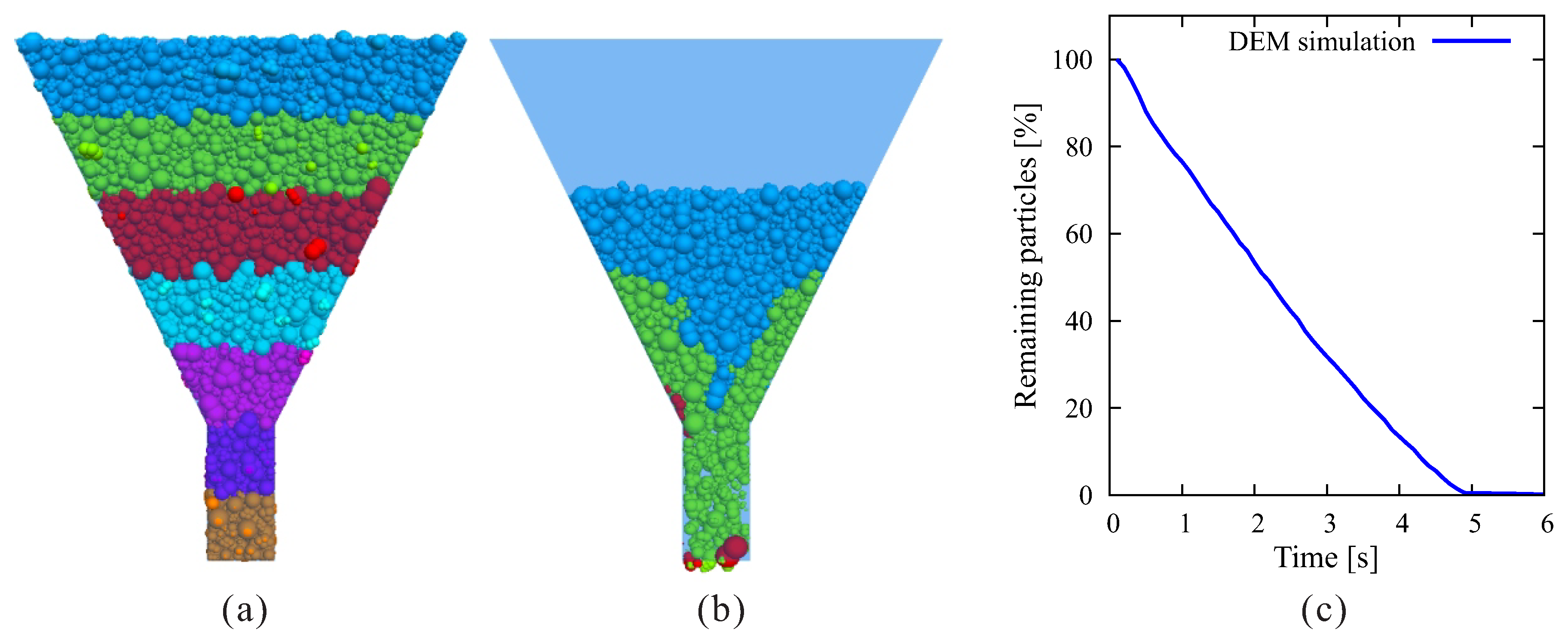
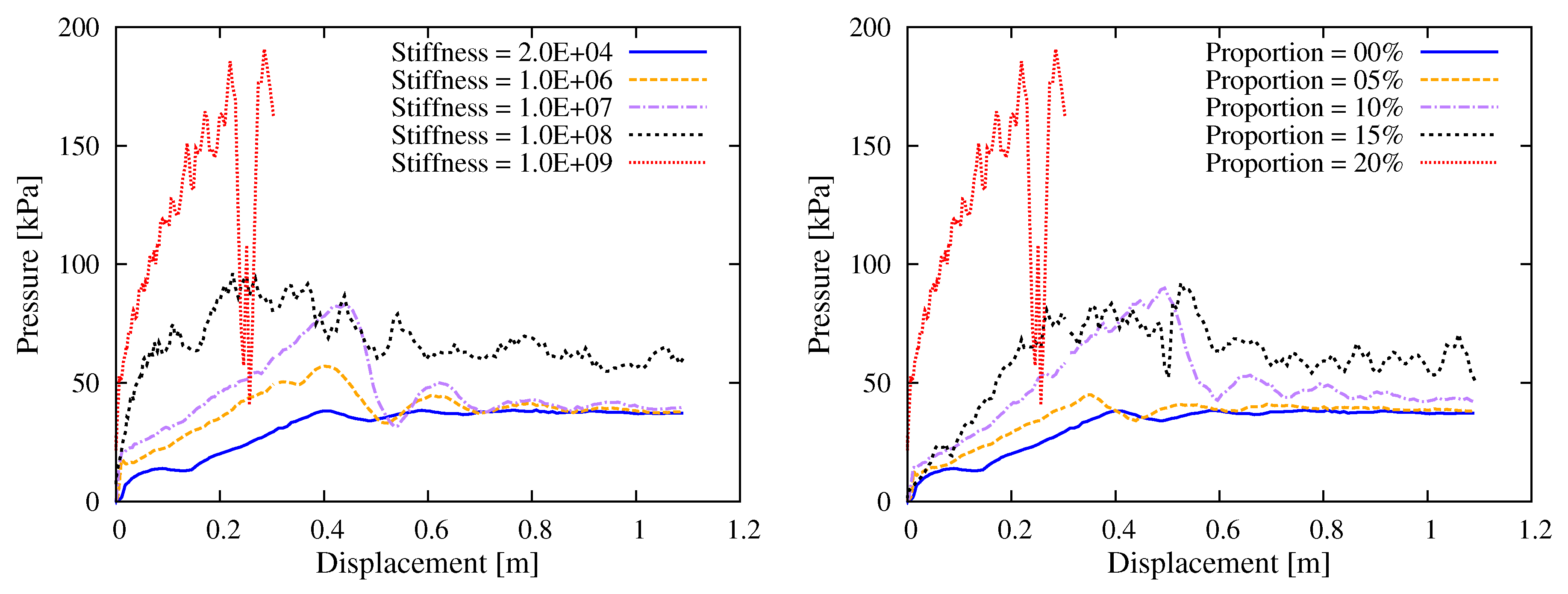
3.3. Material Parameter
4. Numerical Simulation of Pumping Behavior
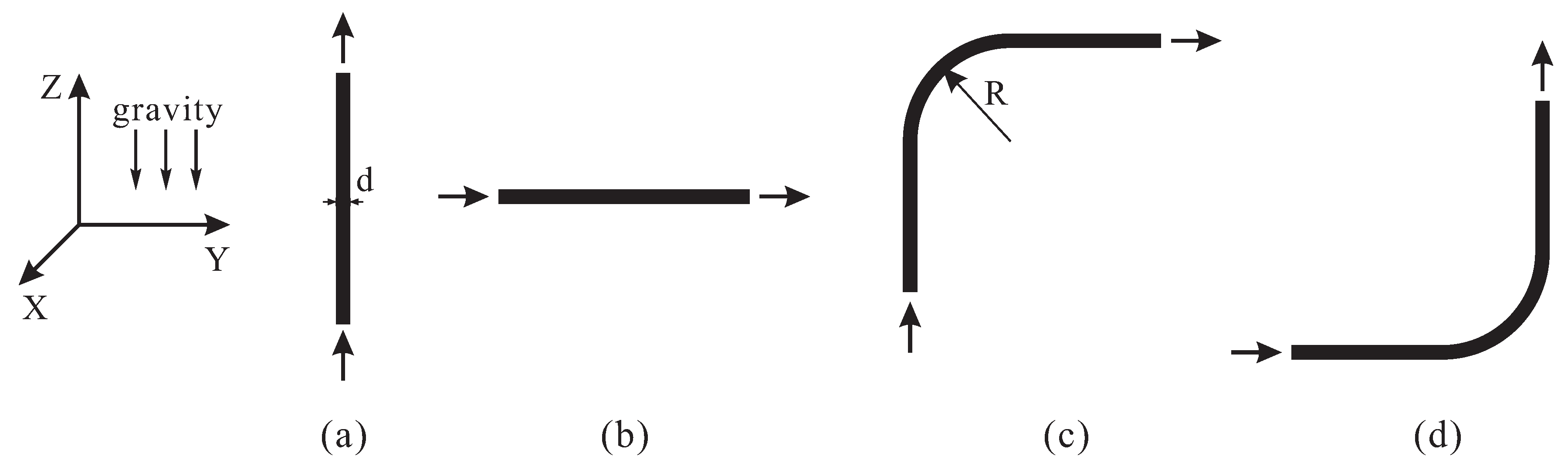
4.1. Model Geometry
4.2. Material
4.3. Simulation Process
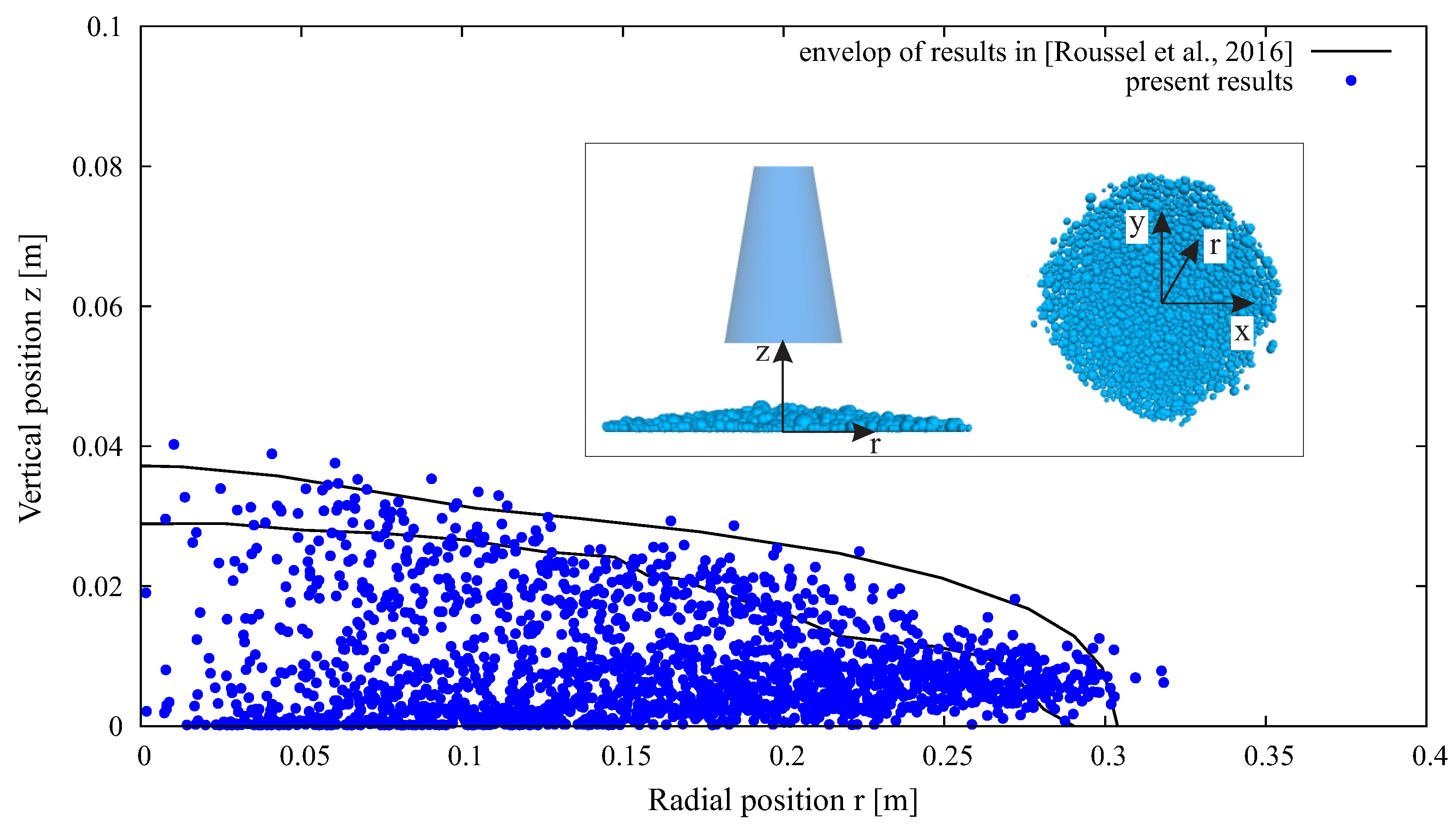
5. Results and Discussions
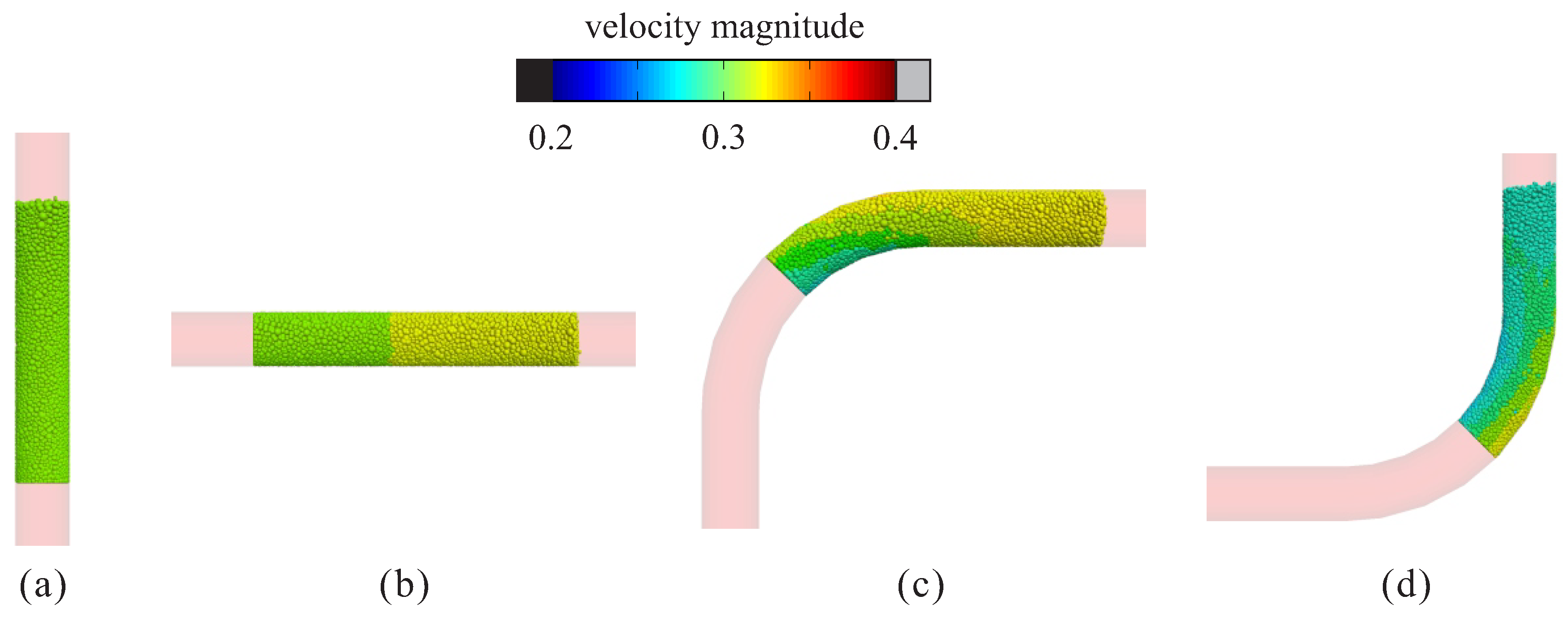
5.1. Influence of Pipe Geometry
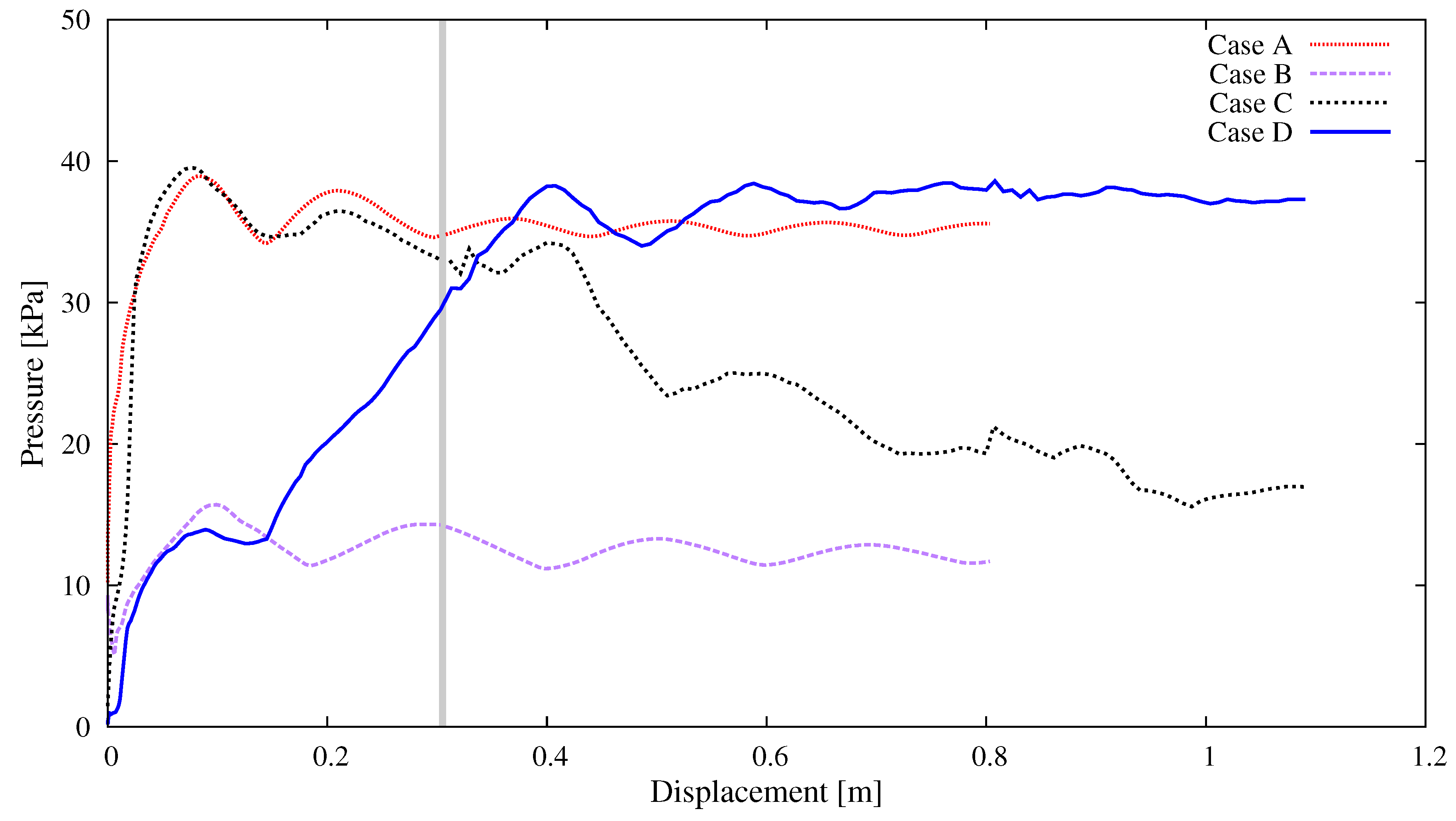
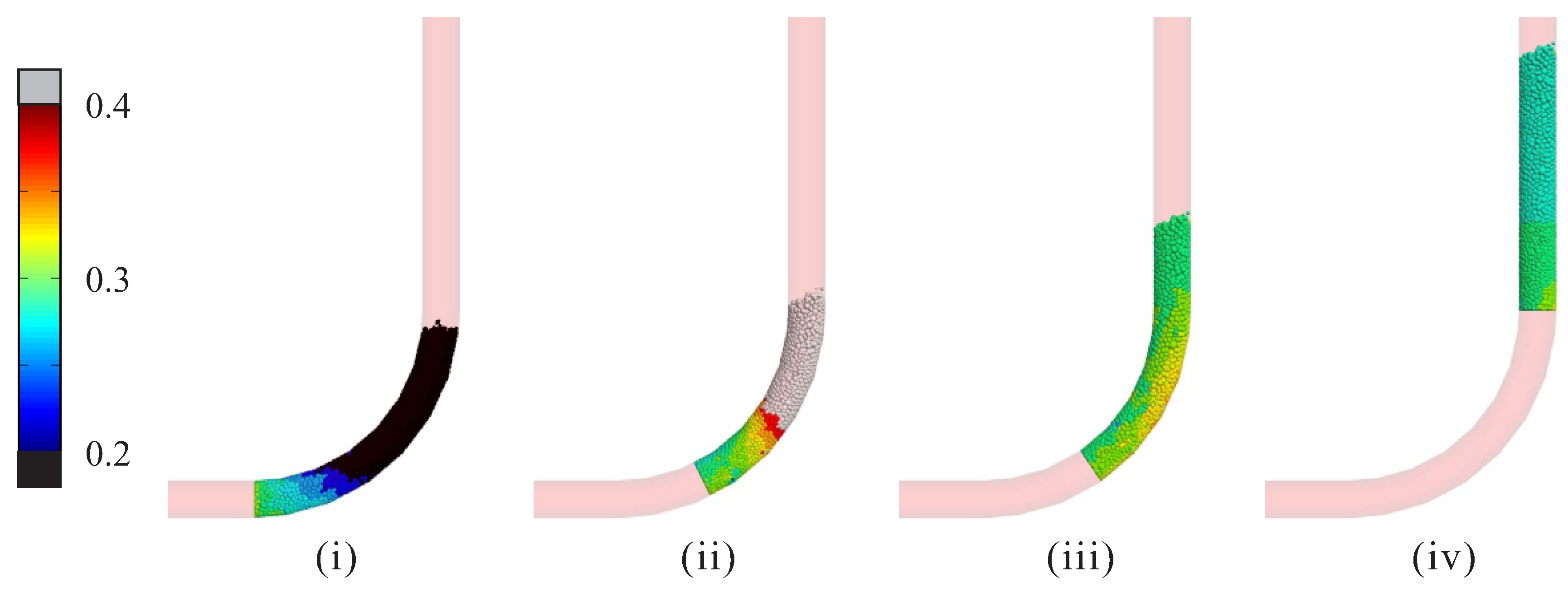
5.1.1. Pipe Section
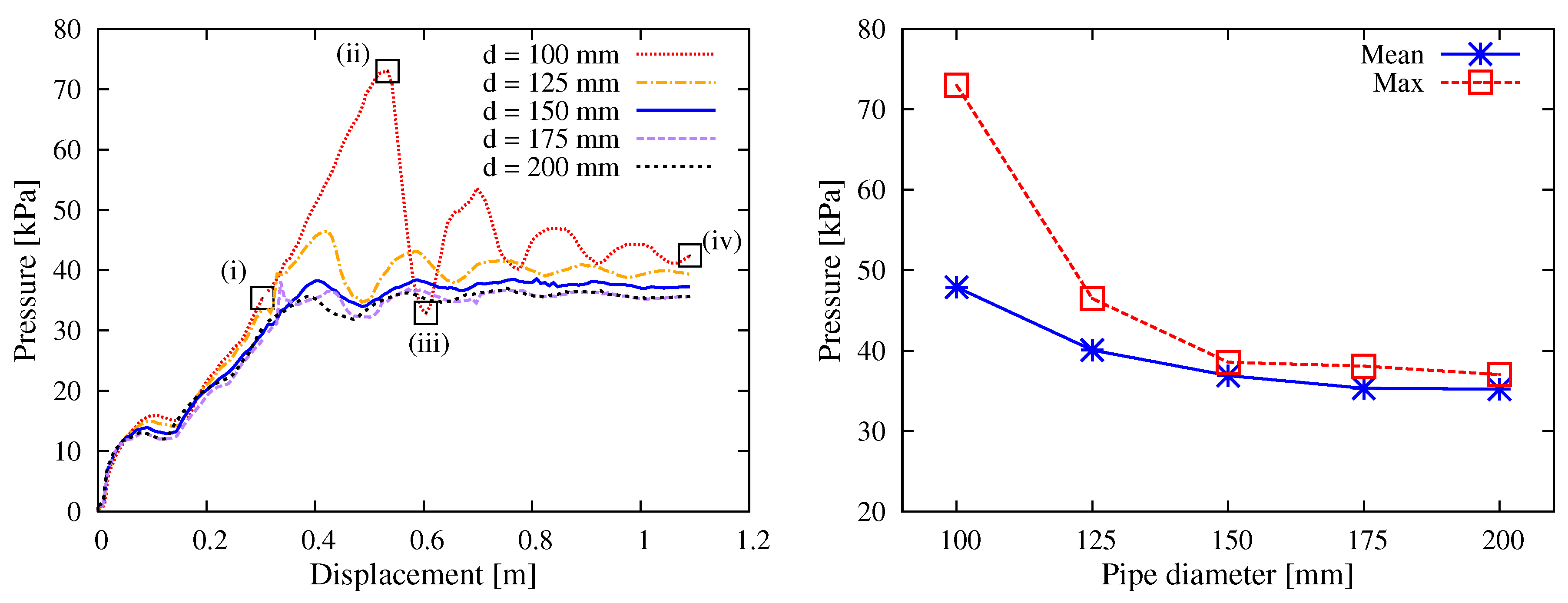
5.1.2. Pipe Diameter
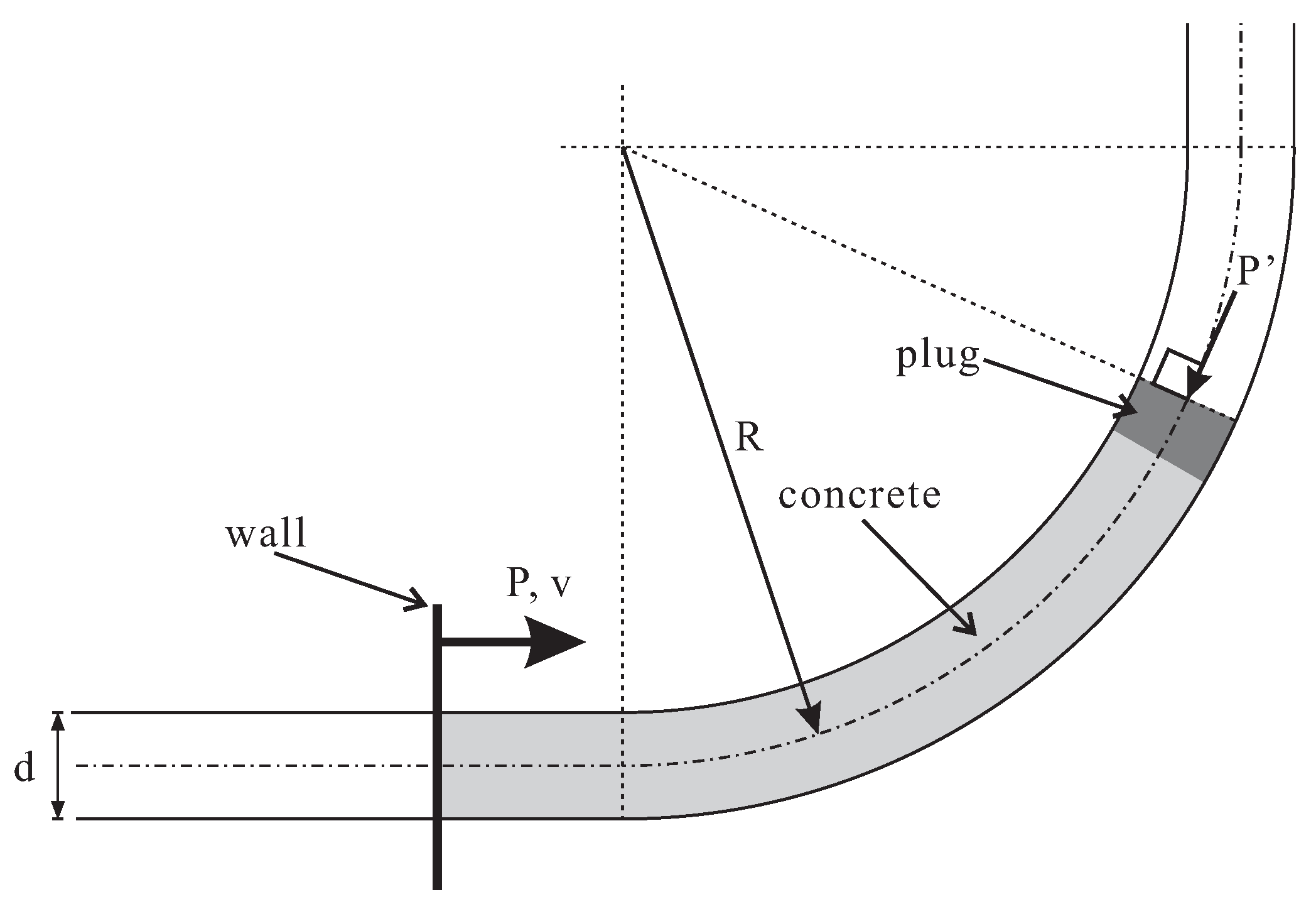
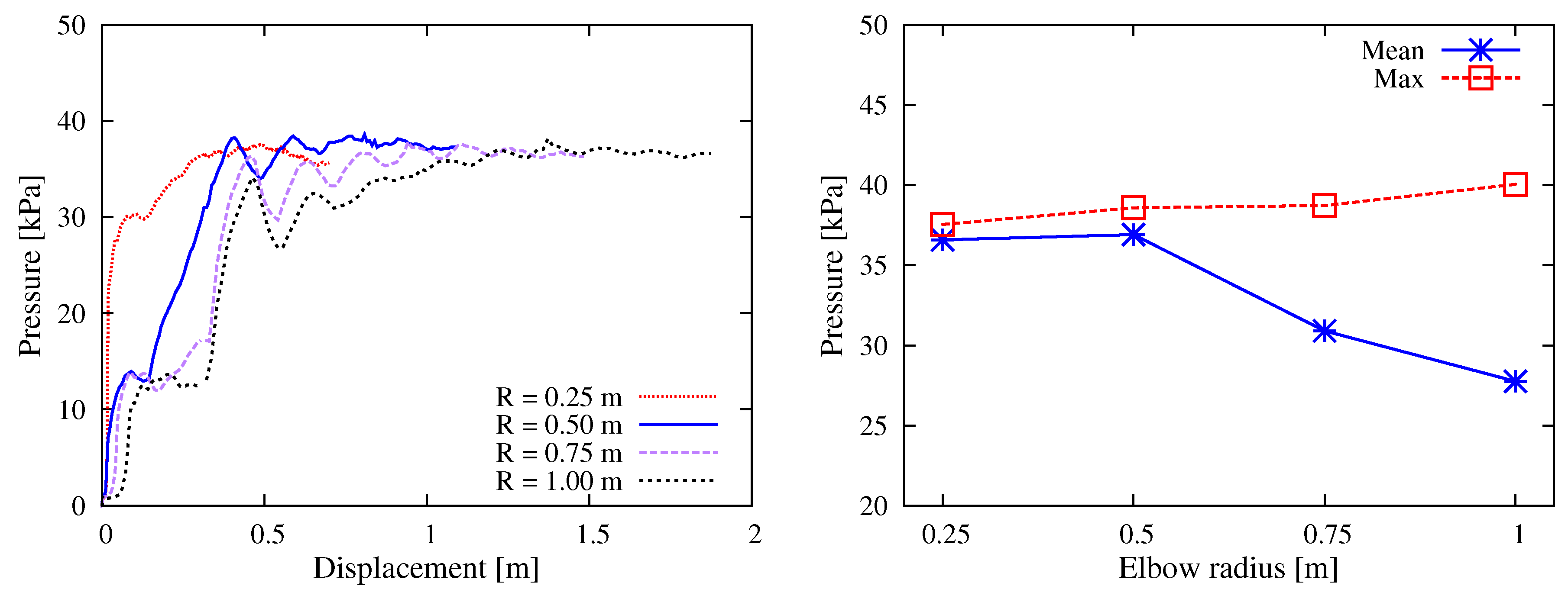
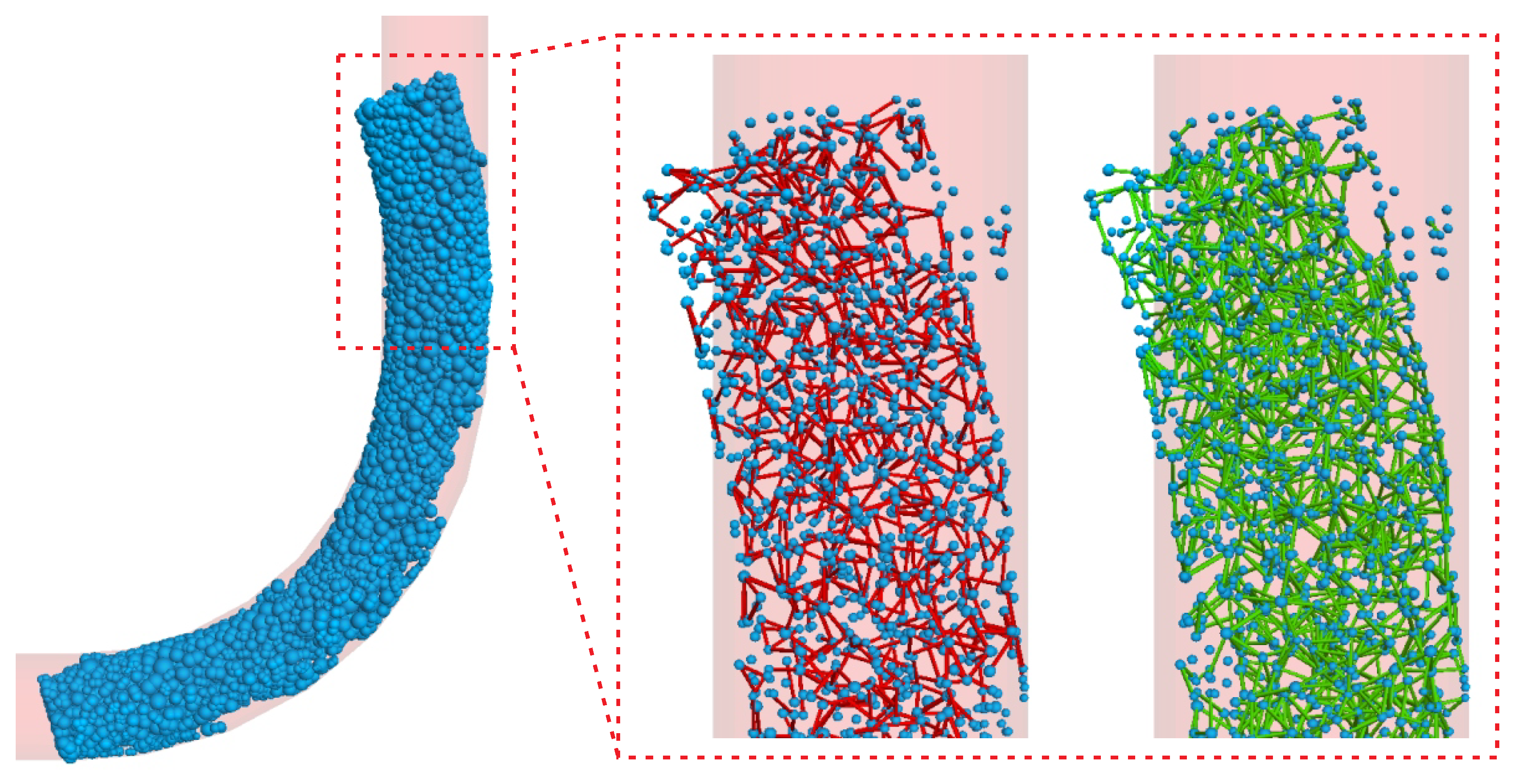
5.1.3. Elbow Curvature
5.2. Influence of Material
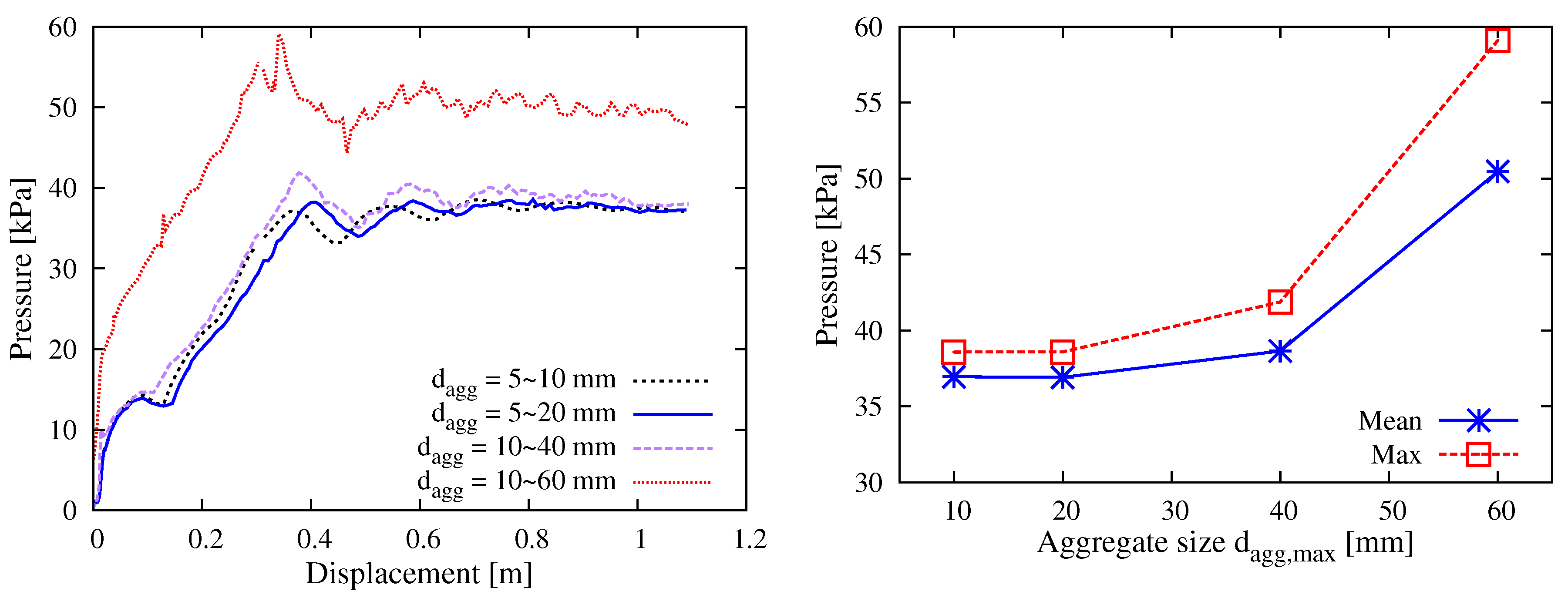
5.2.1. Aggregate Size
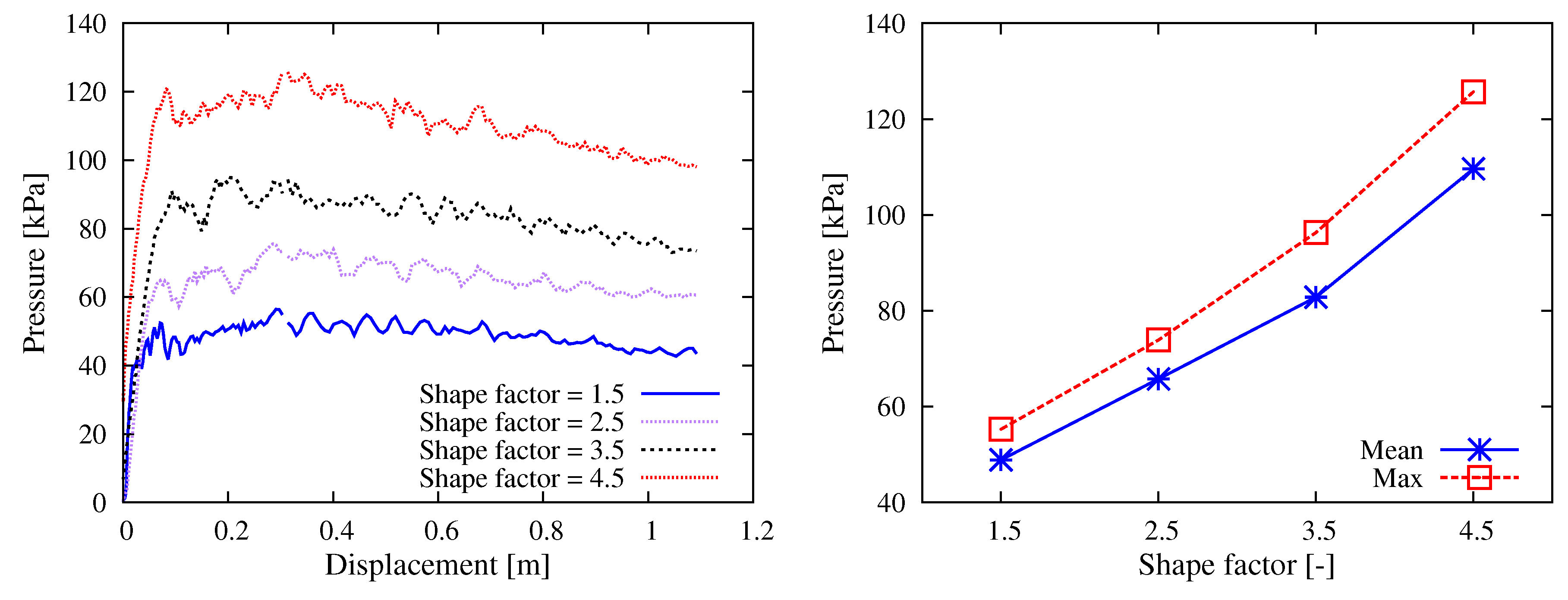
5.2.2. Aggregate Shape
5.3. Influence of Pumping Condition
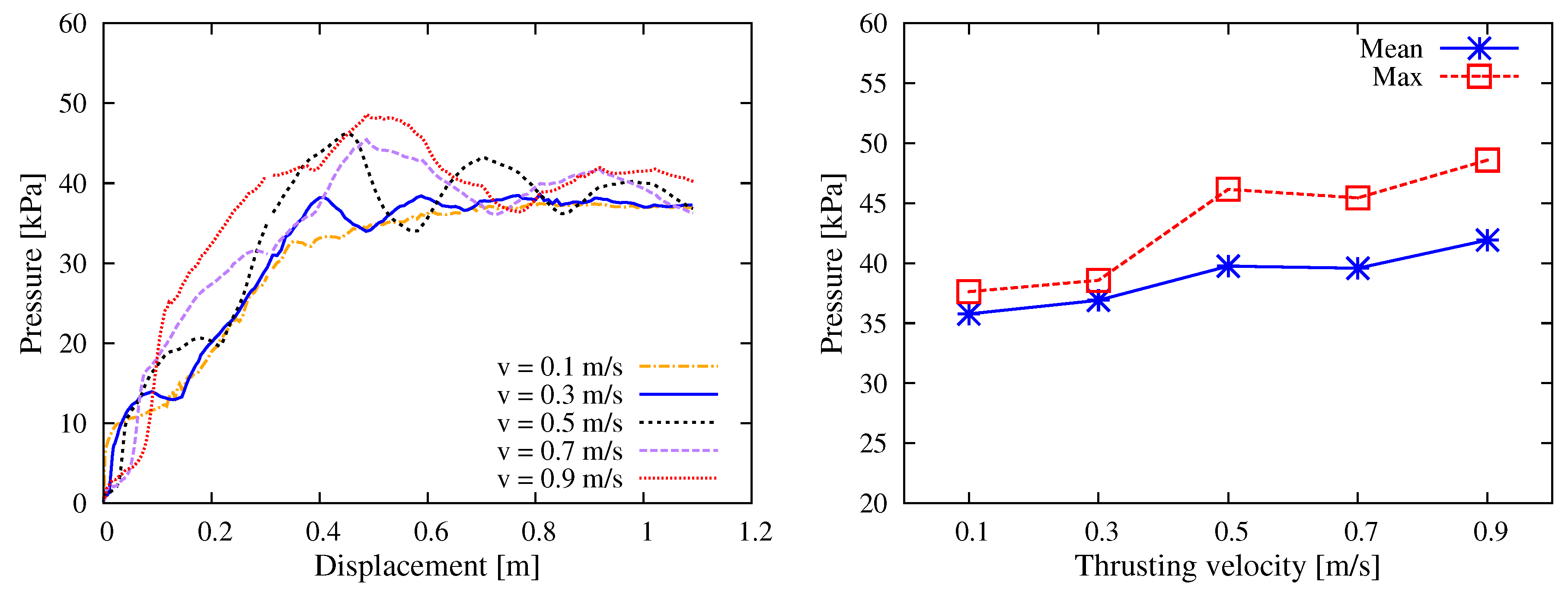
5.3.1. Pumping Velocity
5.3.2. Time Dependency
6. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Massey, B.; Ward-Smith, J. Mechanics of Fluids, 8th ed.; Taylor & Francis: Abingdon, UK, 2005. [Google Scholar]
- Banfill, P.F.G. The rheology of fresh cement and concrete—A review. In Proceedings of the 11th International Cement Chemistry Congress, Durban, South Africa, 11–16 May 2003; Volume 1, pp. 50–62. [Google Scholar]
- De Larrard, F.; Ferraris, C.F.; Sedran, T. Fresh concrete: A Herschel-Bulkley material. Mater. Struct. 1998, 31, 494–498. [Google Scholar] [CrossRef]
- Feys, D.; Wallevik, J.E.; Yahia, A.; Khayat, K.H.; Wallevik, O.H. Extension of the Reiner-Riwlin equation to determine modified Bingham parameters measured in coaxial cylinders rheometers. Mater. Struct. 2013, 46, 289–311. [Google Scholar] [CrossRef]
- ASTM C143. Standard Test Method for Slump of Hydraulic-Cement Concrete; American Society for Testing and Materials: West Conshohocken, PA, USA, 2015. [Google Scholar]
- EN 12350-2. Testing Fresh Concrete—Part 2: Slump Test; European Committee for Standardization: Brussels, Belgium, 2009. [Google Scholar]
- GB/T 50080. Standard for Test Method of Performance on Ordinary Fresh Concrete; Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2016. (In Chinese) [Google Scholar]
- Ferraris, C.F. Measurement of the rheological properties of high performance concrete: State of the art report. J. Res. Natl. Inst. Stand. Technol. 1999, 104, 461–478. [Google Scholar] [CrossRef]
- Banfill, P.F.G. Rheology Reviews 2006; Chapter Rheology of Fresh Cement and Concrete; The British Society of Rheology: UK, 2006; pp. 61–130. [Google Scholar]
- Wallevik, O.H.; Wallevik, J.E. Rheology as a tool in concrete science: The use of rheographs and workability boxes. Cem. Concr. Res. 2011, 41, 1279–1288. [Google Scholar] [CrossRef]
- Wallevik, O.H.; Feys, D.; Wallevik, J.E.; Khayat, K.H. Avoiding inaccurate interpretations of rheological measurements for cement-based materials. Cem. Concr. Res. 2015, 78, 100–109. [Google Scholar] [CrossRef]
- Feys, D.; Cepuritis, R.; Jacobsen, S.; Lesage, K.; Secrieru, E.; Yahia, A. Measuring rheological properties of cement pastes: Most common techniques, procedures and challenges. RILEM Tech. Lett. 2017, 2, 129–135. [Google Scholar] [CrossRef]
- Kaplan, D.; de Larrard, F.; Sedran, T. Design of concrete pumping circuit. ACI Mater. J. 2005, 102, 110–117. [Google Scholar]
- Choi, M.; Roussel, N.; Kim, Y.; Kim, J. Lubrication layer properties during concrete pumping. Cem. Concr. Res. 2013, 45, 69–78. [Google Scholar] [CrossRef]
- Kwon, S.H.; Park, C.K.; Jeong, J.H.; Jo, S.D.; Lee, S.H. Prediction of concrete pumping: Part I-development of new tribometer for analysis of lubricating layer & part II-analytical prediction and experimental verification. ACI Mater. J. 2013, 110, 647–667. [Google Scholar]
- Li, L.; Chen, X.; Li, L.; Yan, P. Analysis on the changes of pumping pressure of self-compacting concrete in pipes. Construct. Technol. 2016, 45, 52–56. (In Chinese) [Google Scholar]
- Jang, K.P.; Choi, M.S. How affect the pipe length of pumping circuit on concrete pumping. Constr. Build. Mater. 2019, 208, 758–766. [Google Scholar] [CrossRef]
- JGJ/T 10. Technical Specifications for Construction of Concrete Pumping; Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2011. (In Chinese) [Google Scholar]
- Khatib, R. Analysis and Prediction of Pumping Characteristics of High-Strength Self-Consolidating Concrete. Ph.D. Thesis, Université de Sherbrooke, Sherbrooke, QC, Canada, 2013. [Google Scholar]
- Feys, D.; Khayat, K.H.; Khatib, R. How do concrete rheology, tribology, flow rate and pipe radius influence pumping pressure? Cem. Concr. Compos. 2016, 66, 38–46. [Google Scholar] [CrossRef]
- Kwon, S.H.; Jang, K.P.; Kim, J.H.; Shah, S.P. State of the art on prediction of concrete pumping. Int. J. Concr. Struct. Mater. 2016, 10, 75–85. [Google Scholar] [CrossRef]
- Roussel, N.; Geiker, M.R.; Dufour, F.; Thrane, L.N.; Szabo, P. Computational modeling of concrete flow: General overview. Cem. Concr. Res. 2007, 37, 1298–1307. [Google Scholar] [CrossRef]
- Roussel, N.; Gram, A. (Eds.) Simulation of Fresh Concrete Flow: State-of-the Art Report of the RILEM Technical Committee 222-SCF; RILEM State-of-the-Art Reports; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar]
- Kitaoji, H.; Tanigawa, Y.; Mori, H.; Kurokawa, Y.; Urano, S. Flow simulation of fresh concrete cast into wall structure by viscoplastic divided space element method. Trans. Jpn. Concr. Inst. 1997, 18, 45–52. [Google Scholar]
- Ferziger, J.; Peric, M. Computational Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Cundall, P.; Hart, R. Numerical Modeling of Discontinua. In Analysis and Design Methods; Fairhurst, C., Ed.; Pergamon Press: Oxford, UK, 1993; pp. 231–243. [Google Scholar]
- Munjiza, A.A.; Knight, E.E.; Rougier, E. Computational Mechanics of Discontinua; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Cundall, P.A. A computer model for simulating progressive, large-scale movement in blocky rock system. In Proceedings of the International Symposium on Rock Mechanics, Nancy, France, 4–6 October 1971. [Google Scholar]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Mechtcherine, V.; Gram, A.; Krenzer, K.; Schwabe, J.H.; Shyshko, S.; Roussel, N. Simulation of fresh concrete flow using discrete element method (DEM): Theory and applications. Mater. Struct. 2014, 47, 615–630. [Google Scholar] [CrossRef]
- Cui, W.; Yan, W.; Song, H.; Wu, X. Blocking analysis of fresh self-compacting concrete based on the DEM. Constr. Build. Mater. 2018, 168, 412–421. [Google Scholar] [CrossRef]
- Munjiza, A. The Combined Finite-Discrete Element Method; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Dufour, F.; Pijaudier-Cabot, G. Numerical modelling of concrete flow: Homogeneous approach. Int. J. Numer. Anal. Methods Geomech. 2005, 29, 395–416. [Google Scholar] [CrossRef]
- Roussel, N.; Lemaître, A.; Flatt, R.J.; Coussot, P. Steady state flow of cement suspensions: A micromechanical state of the art. Cem. Concr. Res. 2010, 40, 77–84. [Google Scholar] [CrossRef]
- Tan, Y.; Zhang, H.; Dongmin, Y.; Jiang, S.; Song, J.; Sheng, Y. Numerical simulation of concrete pumping process and investigation of wear mechanism of the piping wall. Tribol. Int. 2012, 46, 137–144. [Google Scholar] [CrossRef]
- Leonardi, A.; Wittel, F.K.; Mendoza, M.; Herrmann, H.J. Coupled DEM-LBM method for the free-surface simulation of heterogeneous suspensions. Comput. Part. Mech. 2014, 1, 3–13. [Google Scholar] [CrossRef]
- Karakurt, C.; Çelik, A.O.; Yılmazer, C.; Kiriçi, V.; Özyaşar, E. CFD simulations of self-compacting concrete with discrete phase modeling. Constr. Build. Mater. 2018, 186, 20–30. [Google Scholar] [CrossRef]
- Chu, K.; Wang, B.; Xu, D.; Chen, Y.; Yu, A. CFD–DEM simulation of the gas–solid flow in a cyclone separator. Chem. Eng. Sci. 2011, 66, 834–847. [Google Scholar] [CrossRef]
- Xu, D.; Kaliviotis, E.; Munjiza, A.; Avital, E.; Ji, C.; Williams, J. Large scale simulation of red blood cell aggregation in shear flows. J. Biomech. 2013, 46, 1810–1817. [Google Scholar] [CrossRef]
- Xu, D.; Ji, C.; Avital, E.; Kaliviotis, E.; Munjiza, A.; Williams, J. An Investigation on the Aggregation and Rheodynamics of Human Red Blood Cells Using High Performance Computations. Scientifica 2017, 2017, 6524156. [Google Scholar] [CrossRef] [PubMed]
- Munjiza, A.; Owen, D.; Bicanic, N. A combined finite-discrete element method in transient dynamics of fracturing solids. Eng. Comput. 1995, 12, 145–174. [Google Scholar] [CrossRef]
- Mehdipour, I.; Khayat, K.H. Understanding the role of particle packing characteristics in rheo-physical properties of cementitious suspensions: A literature review. Constr. Build. Mater. 2018, 161, 340–353. [Google Scholar] [CrossRef]
- Secrieru, E.; Khodor, J.; Schröfl, C.; Mechtcherine, V. Formation of lubricating layer and flow type during pumping of cement-based materials. Constr. Build. Mater. 2018, 178, 507–517. [Google Scholar] [CrossRef]
- Lian, G.; Thornton, C.; Adams, M. Discrete particle simulation of agglomerate impact coalescence. Chem. Eng. Sci. 1998, 53, 3381–3391. [Google Scholar] [CrossRef]
- Iwashita, K.; Oda, M. Micro-deformation mechanism of shear banding process based on modified distinct element method. Powder Technol. 2000, 109, 192–205. [Google Scholar] [CrossRef]
- Langston, P.A.; Al Awamleh, M.A.; Fraige, F.Y.; Asmar, B.N. Distinct element modelling of non-spherical frictionless particle flow. Chem. Eng. Sci. 2004, 59, 425–435. [Google Scholar] [CrossRef]
- Kim, H.; Wagoner, M.P.; Buttlar, W.G. Simulation of fracture behavior in asphalt concrete using a heterogeneous cohesive zone discrete element model. J. Mater. Civ. Eng. 2008, 20, 552–563. [Google Scholar] [CrossRef]
- Shi, C.; Li, D.; Chen, K.; Zhou, J. Failure mechanism and stability analysis of the Zhenggang landslide in Yunnan province of China using 3D particle flow code simulation. J. Mt. Sci. 2016, 13, 891–905. [Google Scholar] [CrossRef]
- Shi, C.; Yang, W.; Chu, W.; Shen, J.; Kong, Y. Study of anti-sliding stability of a dam foundation based on the fracture flow method with 3D discrete element code. Energies 2017, 10, 1544. [Google Scholar] [CrossRef]
- Xiang, Y.; Liu, H.; Zhang, W.; Chu, J.; Zhou, D.; Xiao, Y. Application of transparent soil model test and DEM simulation in study of tunnel failure mechanism. Tunn. Undergr. Space Technol. 2018, 74, 178–184. [Google Scholar] [CrossRef]
- Wu, W.; Tu, Z.; Zhu, Z.; Zhang, Z.; Lin, Y. Effect of gradation segregation on mechanical properties of an asphalt mixture. Appl. Sci. 2019, 9, 308. [Google Scholar] [CrossRef]
- Ferellec, J.F.; McDowell, G.R. A method to model realistic particle shape and inertia in DEM. Granul. Matter 2010, 12, 459–467. [Google Scholar] [CrossRef]
- Taghavi, R. Automatic clump generation based on mid-surface. In Proceedings of the 2nd International FLAC/DEM Symposium, Melbourne, Australia, 14–16 February 2011; pp. 791–797. [Google Scholar]
- Shi, C.; Li, D.; Xu, W.; Wang, R. Discrete element cluster modeling of complex mesoscopic particles for use with the particle flow code method. Granul. Matter 2015, 17, 377–387. [Google Scholar] [CrossRef]
- Shi, C.; Shen, J.; Xu, W.; Wang, R.; Wang, W. Micromorphological characterization and random reconstruction of 3D particles based on spherical harmonic analysis. J. Cent. South Univ. 2017, 24, 1197–1206. [Google Scholar] [CrossRef]
- Cui, W.; Ji, T.; Li, M.; Wu, X. Simulating the workability of fresh self-compacting concrete with random polyhedron aggregate based on DEM. Mater. Struct. 2017, 50, 92. [Google Scholar] [CrossRef]
- Le, H.D.; Kadri, E.H.; Aggoun, S.; Vierendeels, J.; Troch, P.; De Schutter, G. Effect of lubrication layer on velocity profile of concrete in a pumping pipe. Mater. Struct. 2015, 48, 3991–4003. [Google Scholar] [CrossRef]
- Shyshko, S.; Mechtcherine, V. Developing a discrete element model for simulating fresh concrete: experimental investigation and modelling of interactions between discrete aggregate particles with fine mortar between them. Constr. Build. Mater. 2013, 47, 601–615. [Google Scholar] [CrossRef]
- Pieralisi, R.; Cavalaro, S.H.P.; Aguado, A. Discrete element modelling of the fresh state behavior of pervious concrete. Cem. Concr. Res. 2016, 90, 6–18. [Google Scholar] [CrossRef]
- Thornton, C.; Yin, K. Impact of elastic spheres with and without adhesion. Powder Technol. 1991, 65, 153–166. [Google Scholar] [CrossRef]
- Willett, C.; Adams, M.; Johnson, S.; Seville, J. Capillary bridges between two spherical bodies. Langmuir 2000, 16, 9396–9405. [Google Scholar] [CrossRef]
- Puri, U.C.; Uomoto, T. Numerical modeling—A new tool for understanding shotcrete. Mater. Struct. 1999, 32, 266–272. [Google Scholar] [CrossRef]
- Puri, U.C.; Uomoto, T. Characterization of distinct element modeling parameters for fresh concrete and its application in shotcrete simulations. J. Mater. Civ. Eng. 2002, 14, 137–144. [Google Scholar] [CrossRef]
- Itasca Consulting Group Inc. PFC 3D, version 5.0; ICG: Minneapolis, MN, USA, 2015. [Google Scholar]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Horn, E. The Calibration of Material Properties for Use in Discrete Element Models. Master’s Thesis, University of Stellenbosch, Stellenbosch, South Africa, 2012. [Google Scholar]
- Krenzer, K.; Schwabe, J.H. Calibration of parameters for particle simulation of building materials, using stochastic optimization procedures. In Proceedings of the 3rd International RILEM Symposium on Rheology of Cement Suspensions Such as Fresh Concrete, Reykjavik, Iceland, 19–21 August 2009; pp. 135–142. [Google Scholar]
- Li, Z.; Cao, G.; Tan, Y. Prediction of time-dependent flow behaviors of fresh concrete. Constr. Build. Mater. 2016, 125, 510–519. [Google Scholar] [CrossRef]
- Mechtcherine, V.; Shyshko, S. Simulating the behaviour of fresh concrete with the distinct element method - deriving model parameters related to the yield stress. Cem. Concr. Compos. 2015, 55, 81–90. [Google Scholar] [CrossRef]
- Roussel, N.; Gram, A.; Cremonesi, M.; Ferrara, L.; Krenzer, K.; Mechtcherine, V.; Shyshko, S.; Skocec, J.; Spangenberg, J.; Svec, O.; et al. Numerical simulations of concrete flow: A benchmark comparison. Cem. Concr. Res. 2016, 79, 265–271. [Google Scholar] [CrossRef]
- EN 12350-9. Testing Fresh Concrete—Part 9: Self-Compacting Concrete-V-Funnel Test; European Committee for Standardization: Brussels, Belgium, 2010. [Google Scholar]
- Khayat, K.H. Workability, testing, and performance of self-consolidating concrete. ACI Mater. J. 1999, 96, 346–353. [Google Scholar]
- Zhou, Y.; Xu, Y.; Wu, D. Calculation of concrete pumping resistance and its error analysis. Build. Constr. 2017, 11, 1695–1698. (In Chinese) [Google Scholar]
- Noorani, A.; Vinuesa, R.; Brandt, L.; Schlatter, P. Aspect ratio effect on particle transport in turbulent duct flows. Phys. Fluids 2016, 28, 115103. [Google Scholar] [CrossRef]
- Chin, C.; Vinuesa, R.; Örlü, R.; Cardesa, J.; Noorani, A.; Schlatter, P.; Chong, M. Flow topology of rare back flow events and critical points in turbulent channels and toroidal pipes. J. Phys. Conf. Ser. 2018, 1001, 012002. [Google Scholar] [CrossRef]

| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| aggregate density | [kg/m] | ||
| aggregate size | [m] | ||
| linear contact effective modulus | [N/m] | ||
| linear contact normal-to-shear stiffness ratio | [-] | ||
| linear contact friction coefficient | [-] | ||
| normal critical damping ratio | [-] | ||
| shear critical damping ratio | [-] | ||
| parallel bond effective modulus | [N/m] | ||
| parallel bond normal-to-shear stiffness ratio | [-] | ||
| parallel bond tensile strength | [N/m] | ||
| parallel bond cohesion | [N/m] | ||
| parallel bond friction angle | 30 | [] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhan, Y.; Gong, J.; Huang, Y.; Shi, C.; Zuo, Z.; Chen, Y. Numerical Study on Concrete Pumping Behavior via Local Flow Simulation with Discrete Element Method. Materials 2019, 12, 1415. https://doi.org/10.3390/ma12091415
Zhan Y, Gong J, Huang Y, Shi C, Zuo Z, Chen Y. Numerical Study on Concrete Pumping Behavior via Local Flow Simulation with Discrete Element Method. Materials. 2019; 12(9):1415. https://doi.org/10.3390/ma12091415
Chicago/Turabian StyleZhan, Yijian, Jian Gong, Yulin Huang, Chong Shi, Zibo Zuo, and Yiqun Chen. 2019. "Numerical Study on Concrete Pumping Behavior via Local Flow Simulation with Discrete Element Method" Materials 12, no. 9: 1415. https://doi.org/10.3390/ma12091415
APA StyleZhan, Y., Gong, J., Huang, Y., Shi, C., Zuo, Z., & Chen, Y. (2019). Numerical Study on Concrete Pumping Behavior via Local Flow Simulation with Discrete Element Method. Materials, 12(9), 1415. https://doi.org/10.3390/ma12091415





