Lifing the Effects of Crystallographic Orientation on the Thermo-Mechanical Fatigue Behaviour of a Single-Crystal Superalloy
Abstract
:1. Introduction
2. Materials and Methods
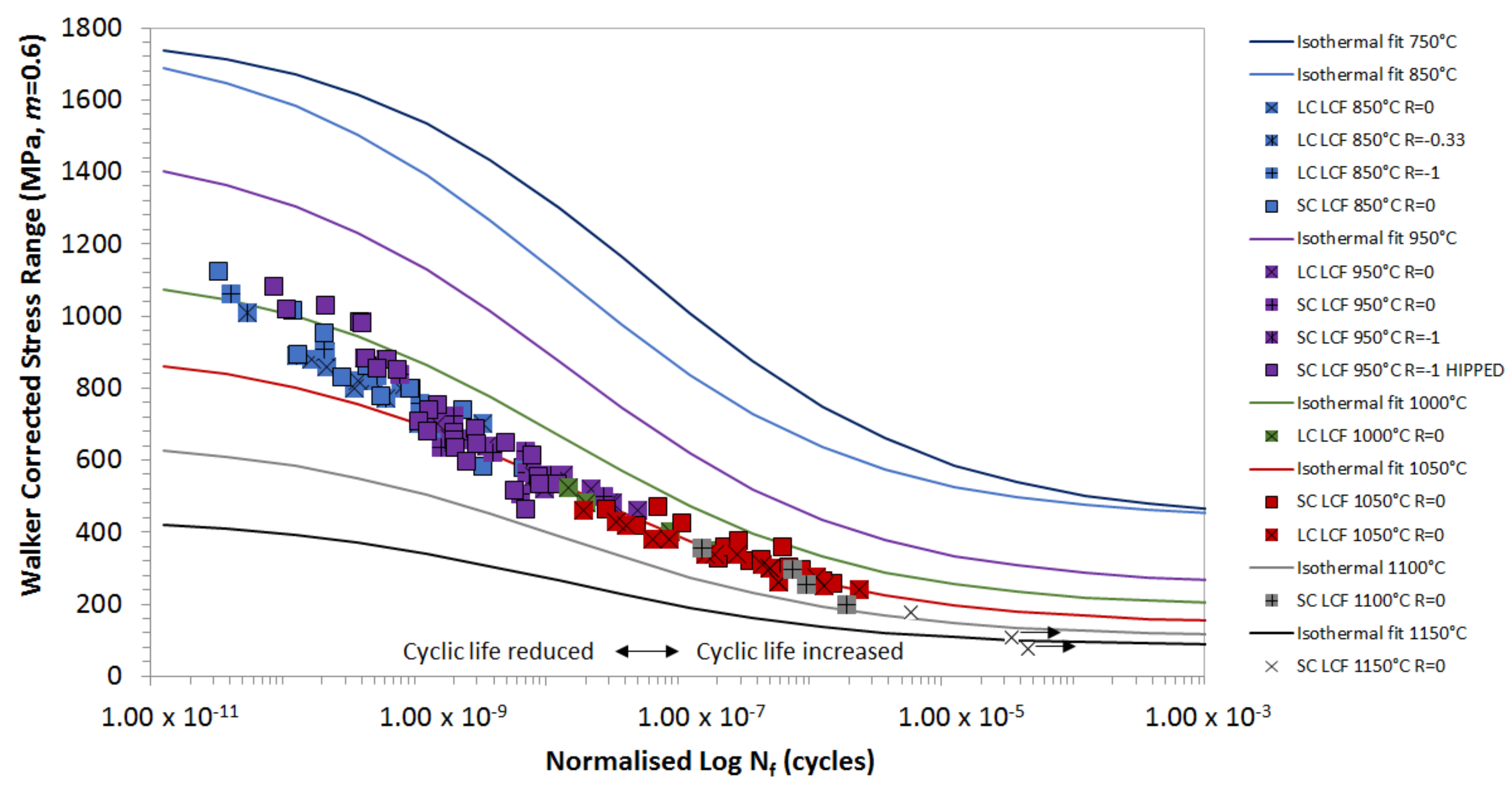
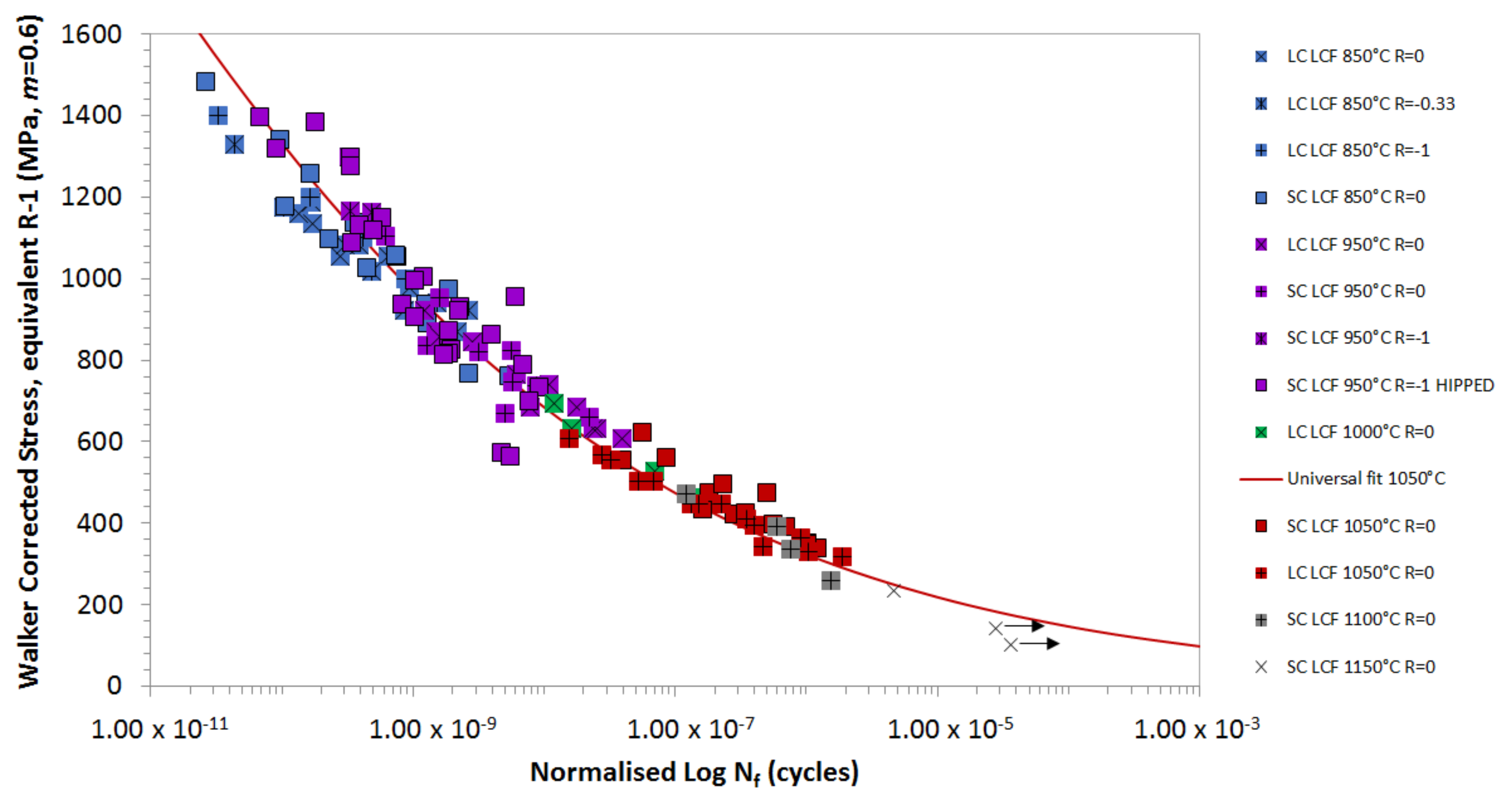
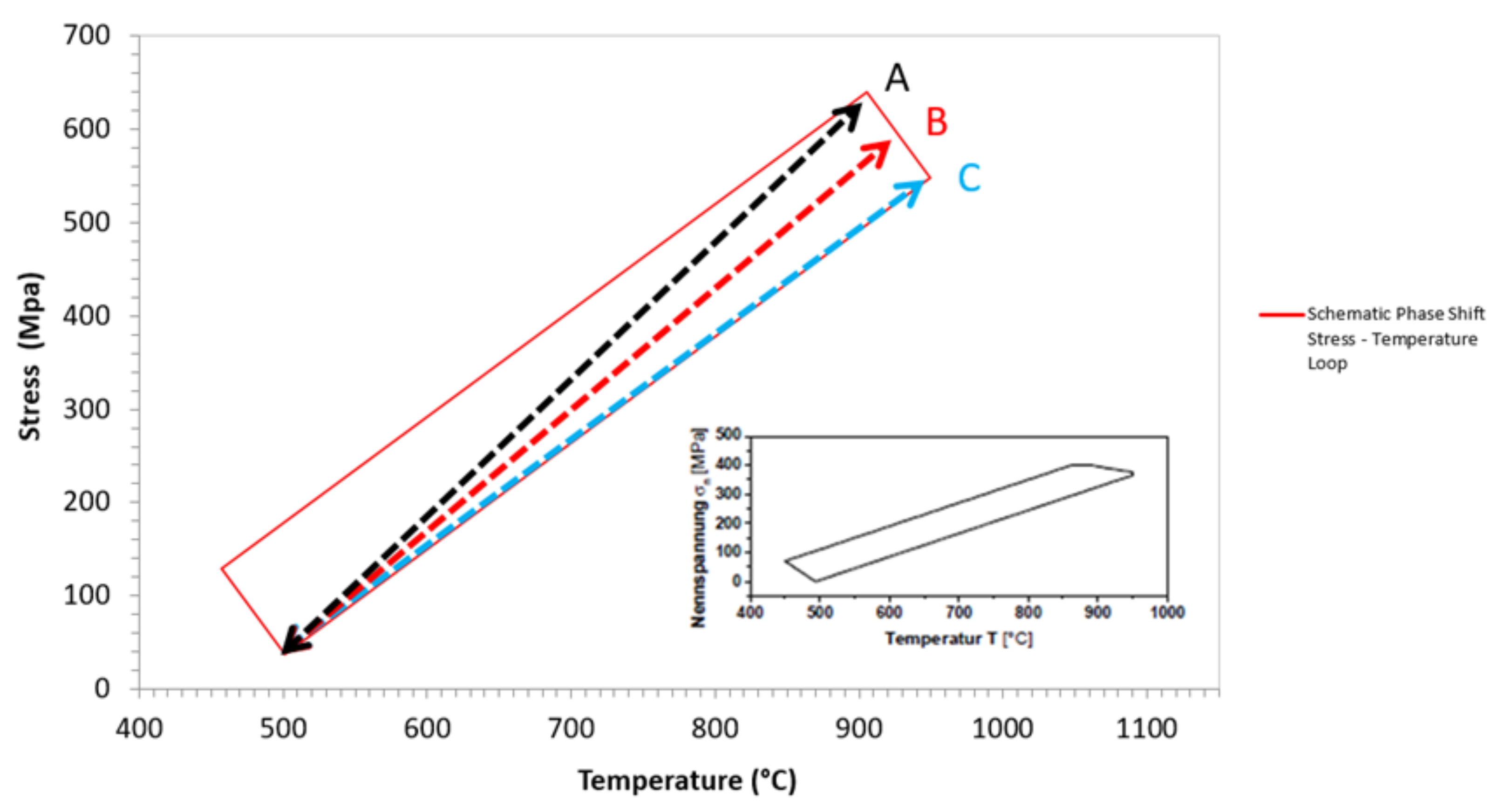
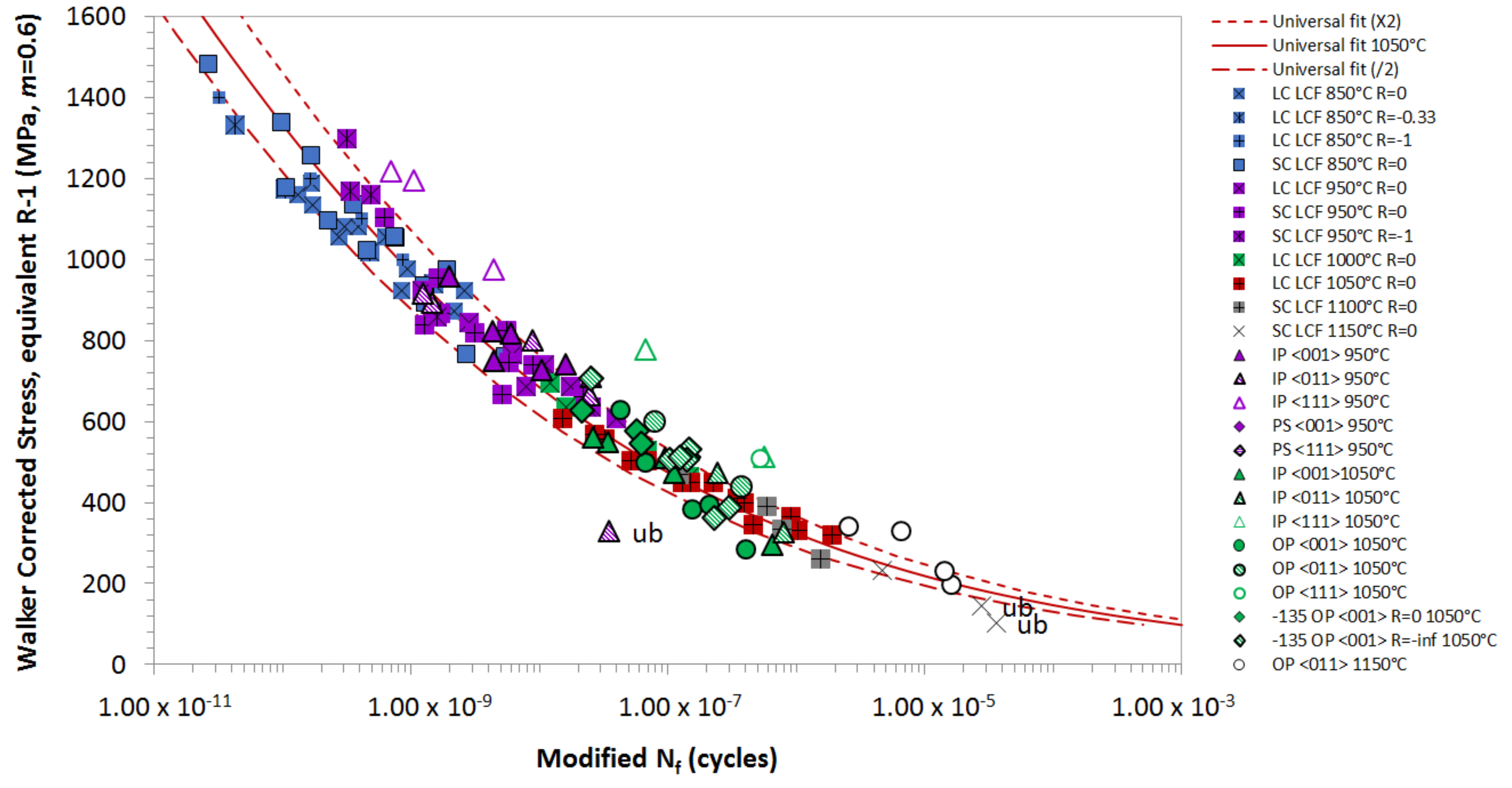
3. Development of the TMF Lifing Model
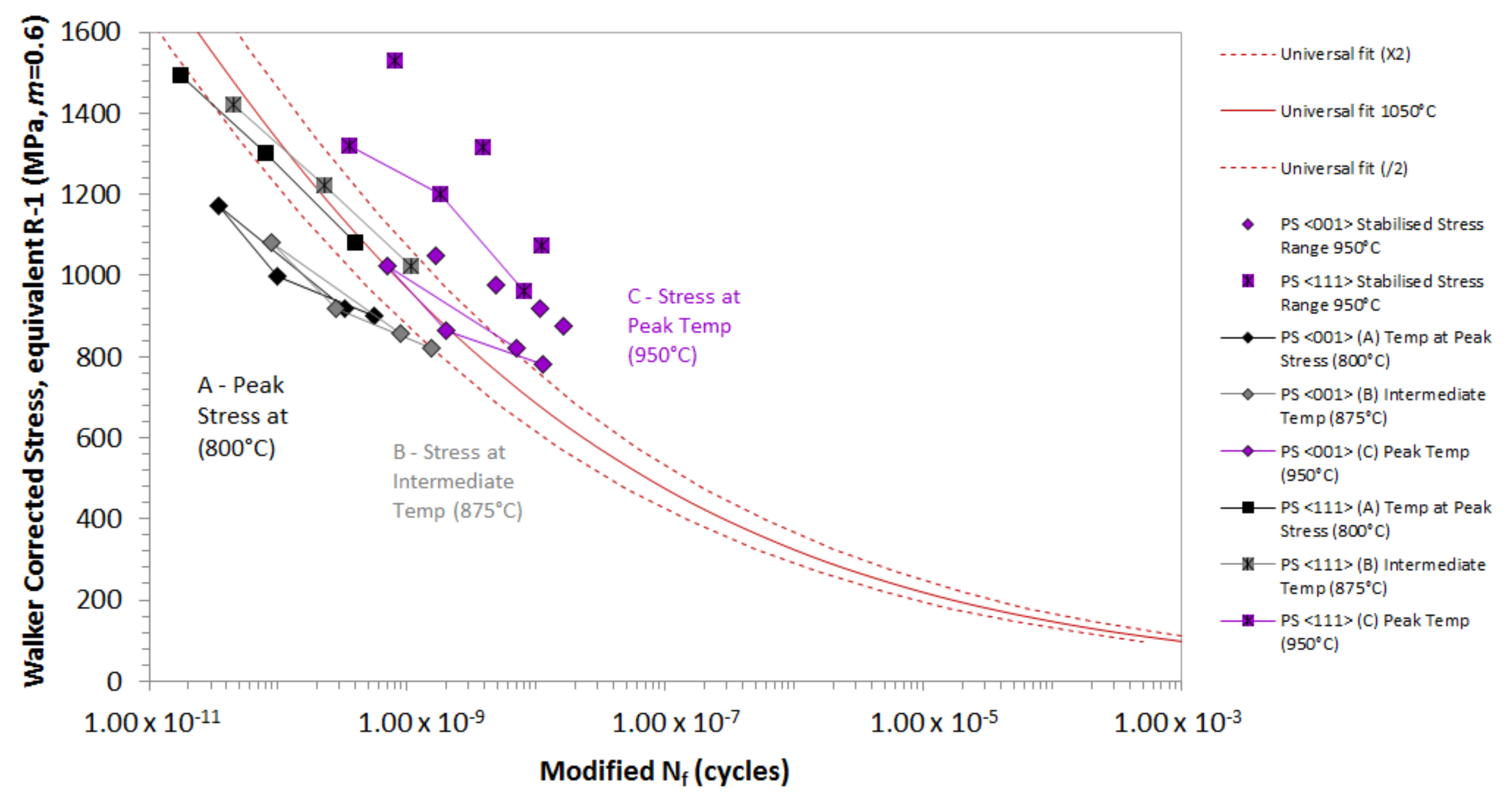
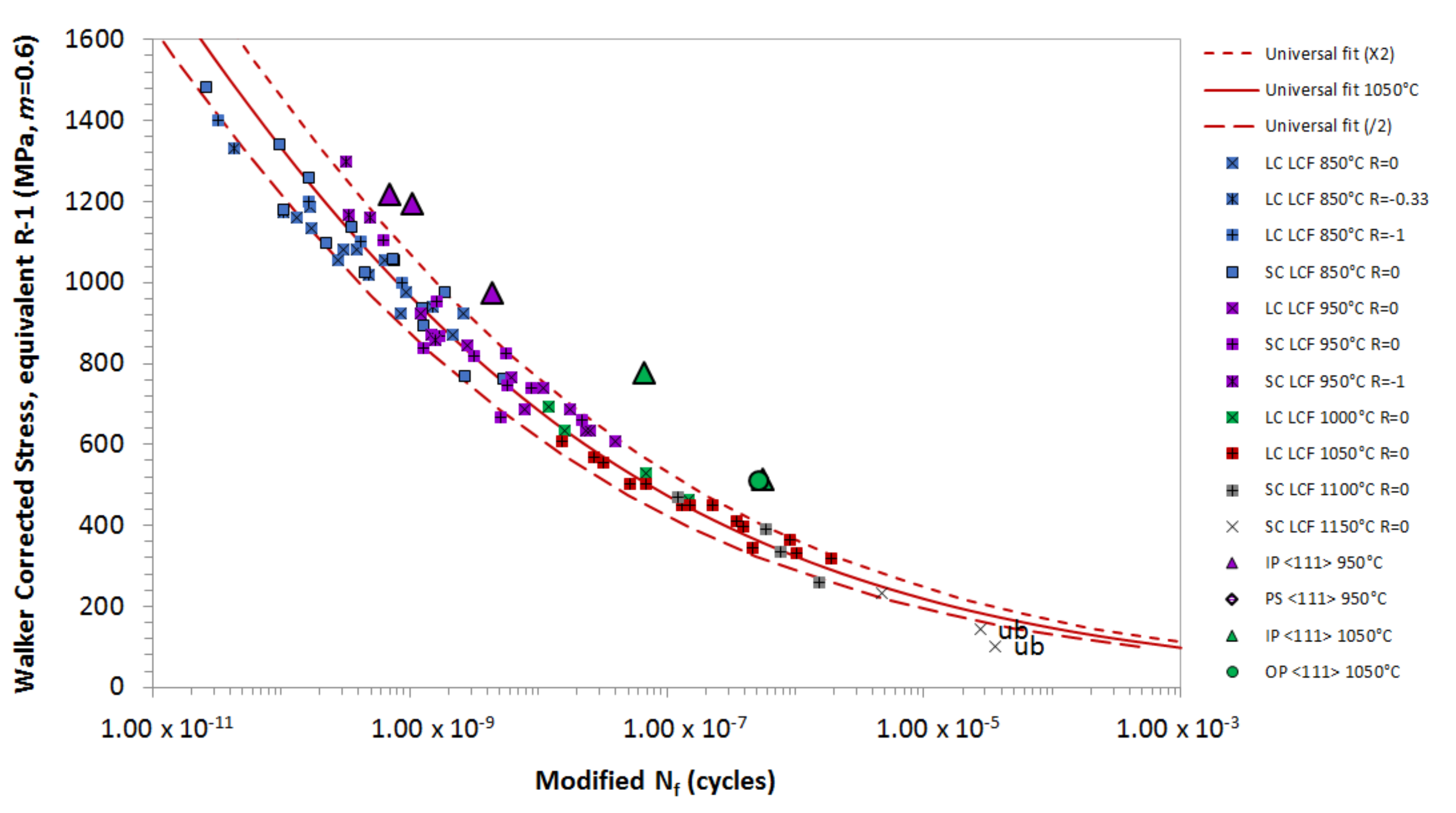
4. Effects of Orientation on TMF Life
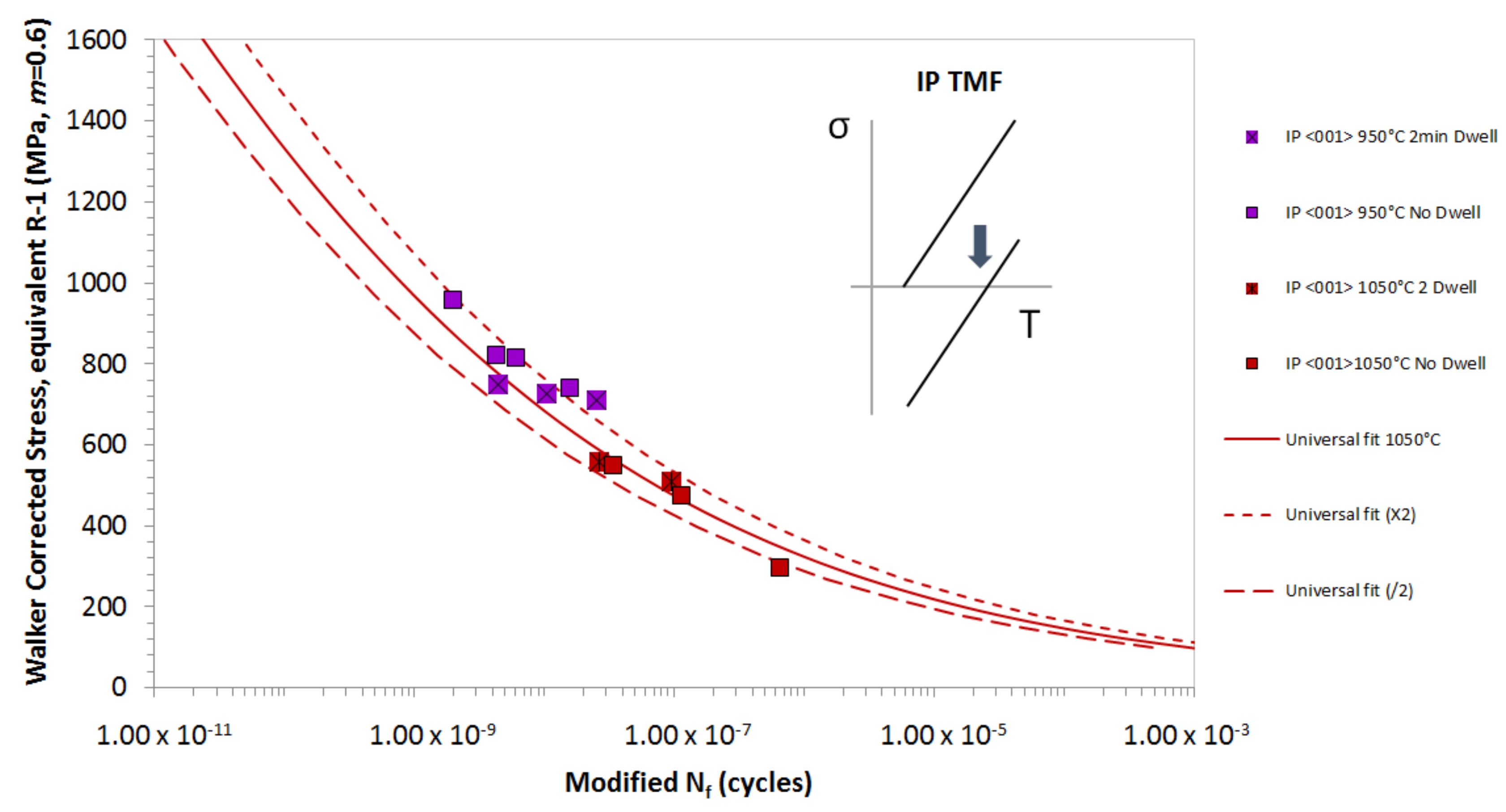
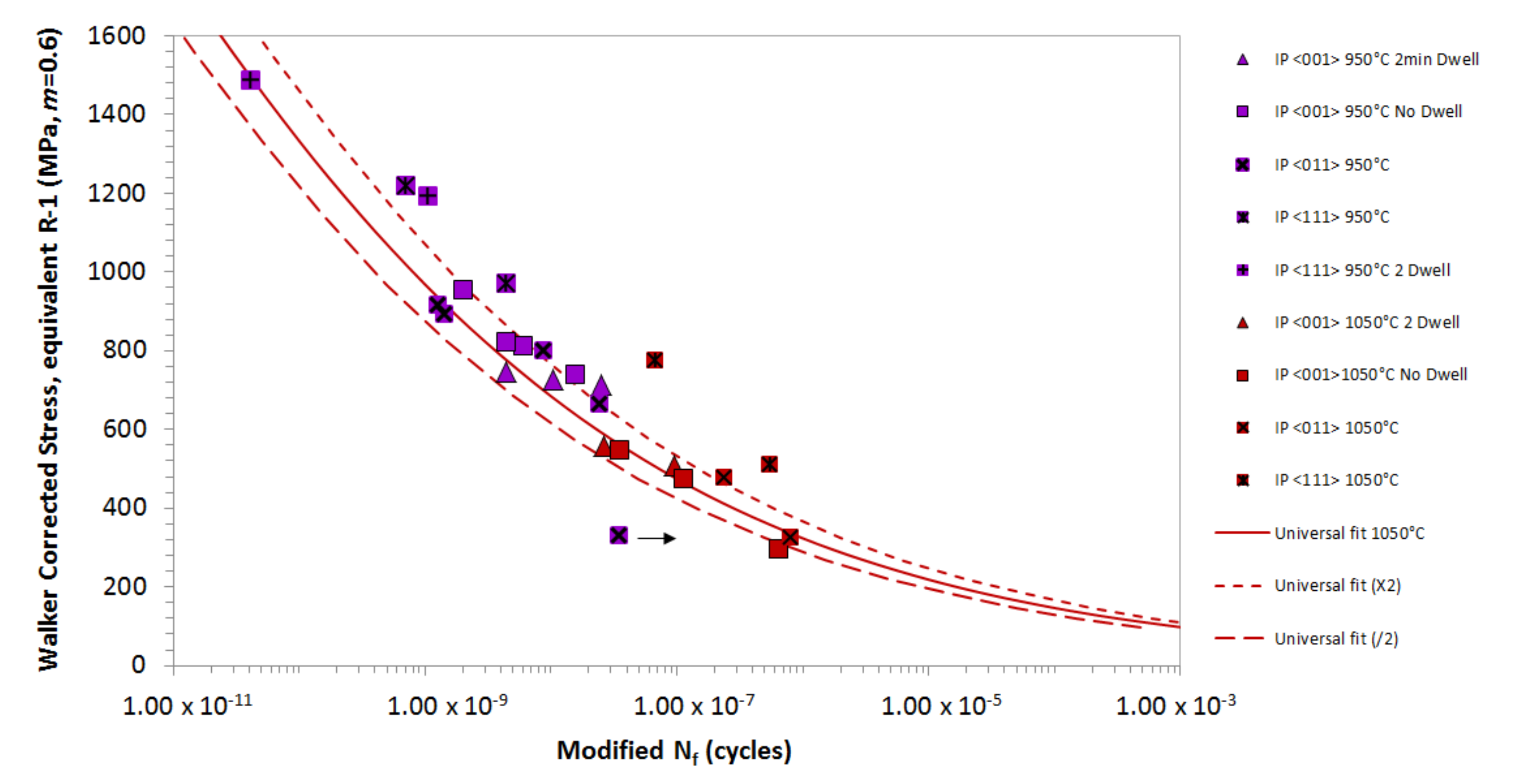
4.1. In-Phase TMF
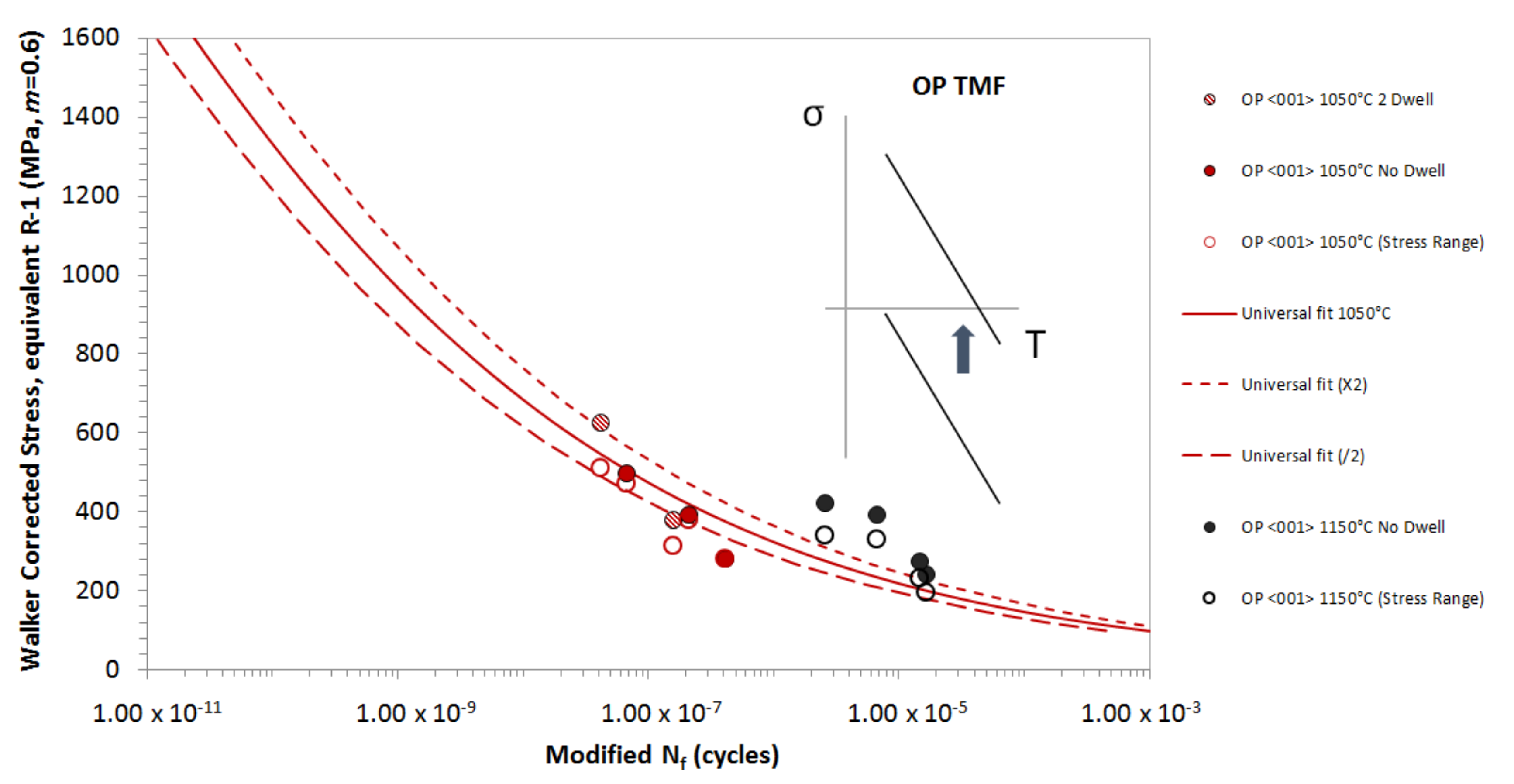
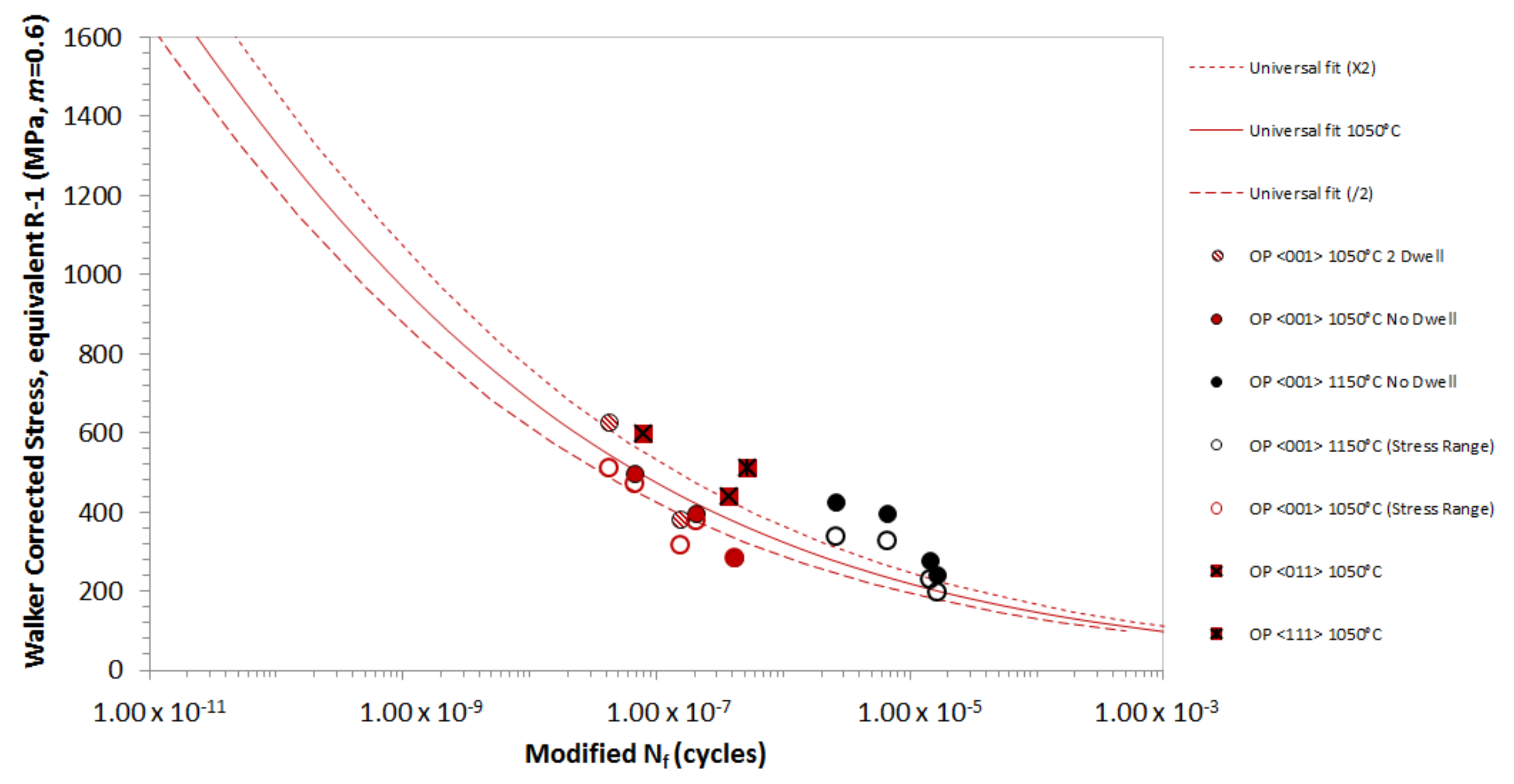
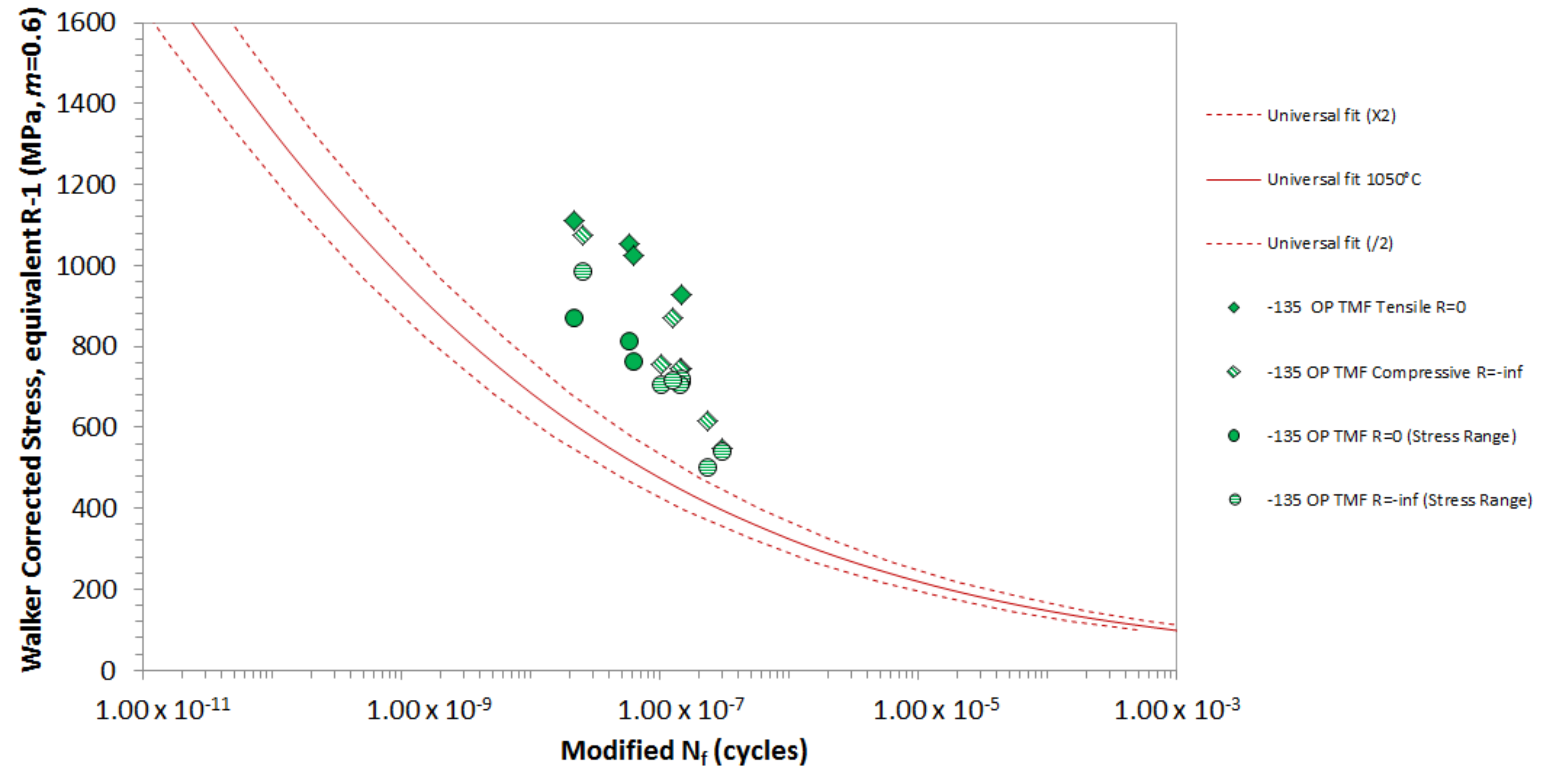
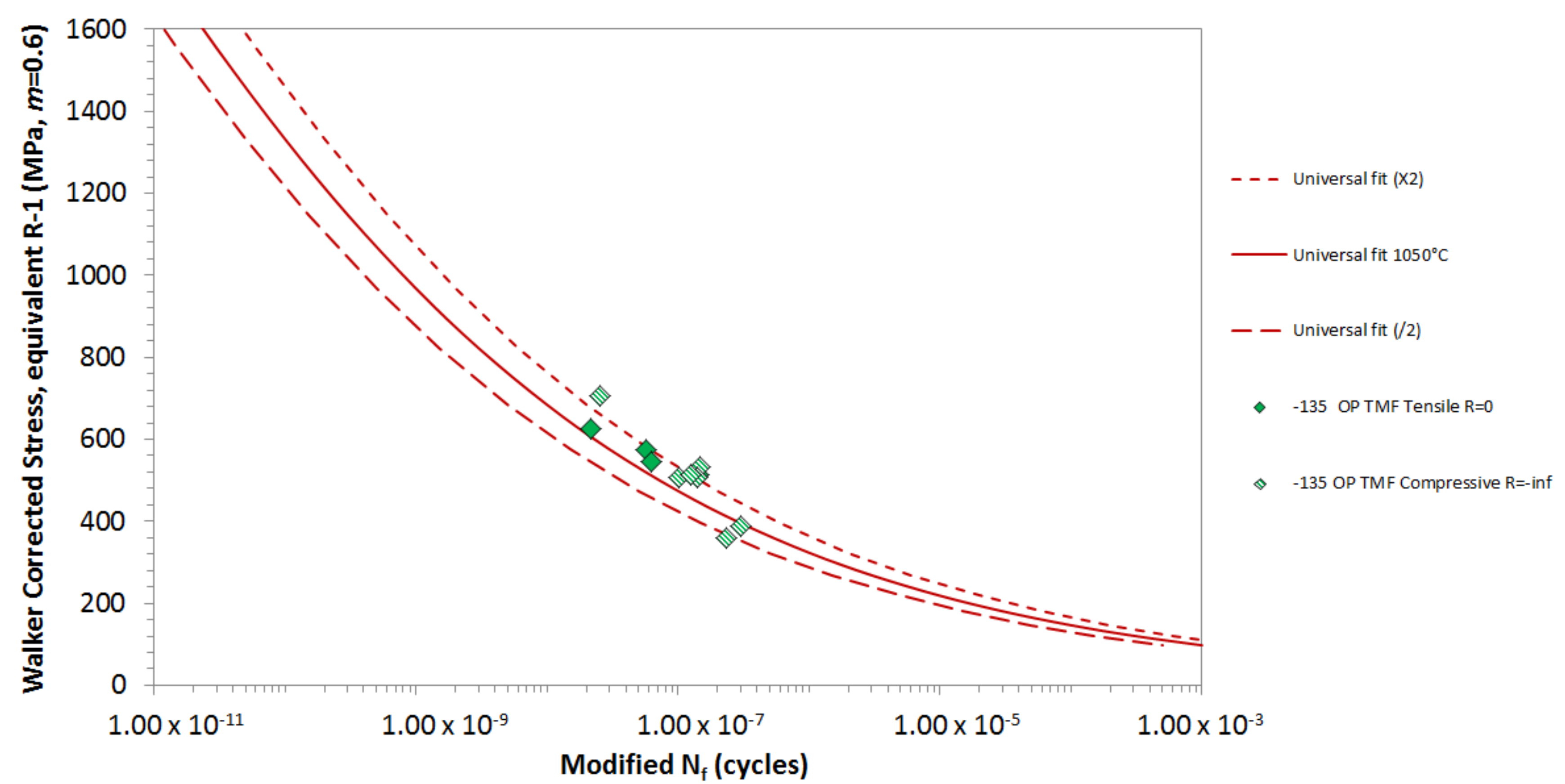
4.2. Out-of-Phase TMF
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- European Commission. Flightpath 2050 Europe’s Vision for Aviation Report of the High-Level Group on Aviation Research; Publications Office of the European Union: Luxembourg City, Luxembourg, 2011. [Google Scholar]
- ASTM. Standard practice for strain controlled thermomechanical fatigue testing. In E2368-10; ASTM: West Conshohocken, PA, USA, 2010. [Google Scholar]
- ISO. Standardisation, metallic materials, fatigue testing, strain-controlled thermomechanical fatigue testing method. In 12111; ISO: Geneva, Switzerland, 2017; p. 25. [Google Scholar]
- Pahlavanyali, S.; Drew, G.; Rayment, A.; Rae, C. Thermo-mechanical fatigue of a polycrystalline superalloy: The effect of phase angle on TMF life and failure. Int. J. Fatigue 2008, 30, 330–338. [Google Scholar] [CrossRef]
- Arrell, D.; Hasselqvist, M.; Sommer, C.; Moverare, J. On TMF damage, degradation effects, and the associated TMin influence on TMF test results in γ/γ′ alloys. In Proceedings of the 10th International Symposium on Superalloys—SUPERALLOYS 2004, Champion, PA, USA, 19–23 September 2004; pp. 291–294. [Google Scholar]
- Hahner, P.; Rinaldi, C.; Bicego, V.; Affeldt, E.; Brendel, T.; Andersson, H.; Beck, T.; Klingelhoffer, H.; Kuhn, H.; Koster, A. Research and development into a European code of practice for strain controlled thermo-mechanical fatigue testing. Int. J. Fatigue 2008, 30, 372–381. [Google Scholar] [CrossRef]
- Scholz, A.; Schmidt, A.; Walther, H.C.; Schein, M.; Schwienheer, M. Experiences in the determination of TMF, LCF and creep life of CMSX-4 in four-point bending experiments. Int. J. Fatigue 2008, 30, 357–362. [Google Scholar] [CrossRef]
- Hong, H.U.; Kang, J.G.; Choi, B.G.; Kim, I.S.; Yoo, Y.S.; Jo, C.Y. A comparative study on thermomechanical and low cycle fatigue failures of a single crystal nickel-based superalloy. Int. J. Fatigue 2011, 33, 1592–1599. [Google Scholar] [CrossRef]
- Whittaker, M.T.; Lancaster, R.J.; Harrison, W.J.; Williams, S.J. An empirical approach to aorrelating thermo-mechanical fatigue behaviour of a polycrystalline Ni-base alloy. Materials 2013, 6, 5275–5290. [Google Scholar] [CrossRef] [PubMed]
- Lancaster, R.J.; Whittaker, M.T.; Williams, S.J. A review of thermo-mechanical fatigue behaviour in polycrystalline nickel superalloys for turbine disc applications. Mater. High Temp. 2013, 30, 2–12. [Google Scholar] [CrossRef]
- Evans, W.J.; Lancaster, R.J.; Steele, A.; Whittaker, M.T.; Jones, N. Plain and notched fatigue in nickel single crystal alloys. Int. J. Fatigue 2009, 31, 1709–1718. [Google Scholar] [CrossRef]
- Okazaki, M.; Take, K.; Kakehi, K.; Yamazaki, Y.; Sakane, M.; Arai, M.; Sakurai, S.; Kaneko, H.; Harada, Y.; Itoh, A.; et al. Collaborative research on thermo-mechanical and isothermal low-cycle fatigue strength of Ni-base superalloys and protective coatings at elevated temperatures in The Society of Materials Science, Japan (JSMS). In Thermomechanical Fatigue Behavior of Materials; ASTM International: West Conshohocken, PA, USA, 2003. [Google Scholar]
- Vasseur, E.; Rémy, L. High temperature low cycle fatigue and thermal-mechanical fatigue behaviour of an oxide-dispersion-strengthened nickel-base superalloy. Mater. Sci. Eng. A 1994, 184, 1–15. [Google Scholar] [CrossRef]
- Nutting, J. An introduction to metallurgy. Met. Sci. 1976, 10, 148. [Google Scholar] [CrossRef]
- Drew, G. Thermo-Mechanical Fatigue of the Single Crystal Nickel Based Superalloy CMSX-4. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2003. [Google Scholar]
- Kraft, H.M.S. Thermo-mechanical fatigue of the superalloy CMSX-6. Materials 1996, 2, 27. [Google Scholar]
- Egly, T.A.; Lang, K.H.; Löhe, D. Influence of phase shift and strain path on the thermomechanical fatigue behavior of CMSX-4 specimens. Int. J. Fatigue 2008, 30, 249–256. [Google Scholar] [CrossRef]
- Zhang, J.X.; Harada, H.; Koizumi, Y.; Kobayashi, T. Crack appearance of single-crystal nickel-base superalloys after thermomechanical fatigue failure. Scr. Mater. 2009, 61, 1105–1108. [Google Scholar] [CrossRef]

| Alloy | Cr | Co | Mo | W | Ta | Re | Nb | Al | Ti | Hf | Nl | Density |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CMSX-4 | 6.4 | 9.6 | 0.6 | 6 | 6.5 | 3 | - | 5.6 | 1 | 0.1 | Bal. | 8.70 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smith, R.; Lancaster, R.; Jones, J.; Mason-Flucke, J. Lifing the Effects of Crystallographic Orientation on the Thermo-Mechanical Fatigue Behaviour of a Single-Crystal Superalloy. Materials 2019, 12, 998. https://doi.org/10.3390/ma12060998
Smith R, Lancaster R, Jones J, Mason-Flucke J. Lifing the Effects of Crystallographic Orientation on the Thermo-Mechanical Fatigue Behaviour of a Single-Crystal Superalloy. Materials. 2019; 12(6):998. https://doi.org/10.3390/ma12060998
Chicago/Turabian StyleSmith, Richard, Robert Lancaster, Jonathan Jones, and Julian Mason-Flucke. 2019. "Lifing the Effects of Crystallographic Orientation on the Thermo-Mechanical Fatigue Behaviour of a Single-Crystal Superalloy" Materials 12, no. 6: 998. https://doi.org/10.3390/ma12060998
APA StyleSmith, R., Lancaster, R., Jones, J., & Mason-Flucke, J. (2019). Lifing the Effects of Crystallographic Orientation on the Thermo-Mechanical Fatigue Behaviour of a Single-Crystal Superalloy. Materials, 12(6), 998. https://doi.org/10.3390/ma12060998





