A Statistical Model of Cleavage Fracture Toughness of Ferritic Steel DIN 22NiMoCr37 at Different Temperatures
Abstract
:1. Introduction
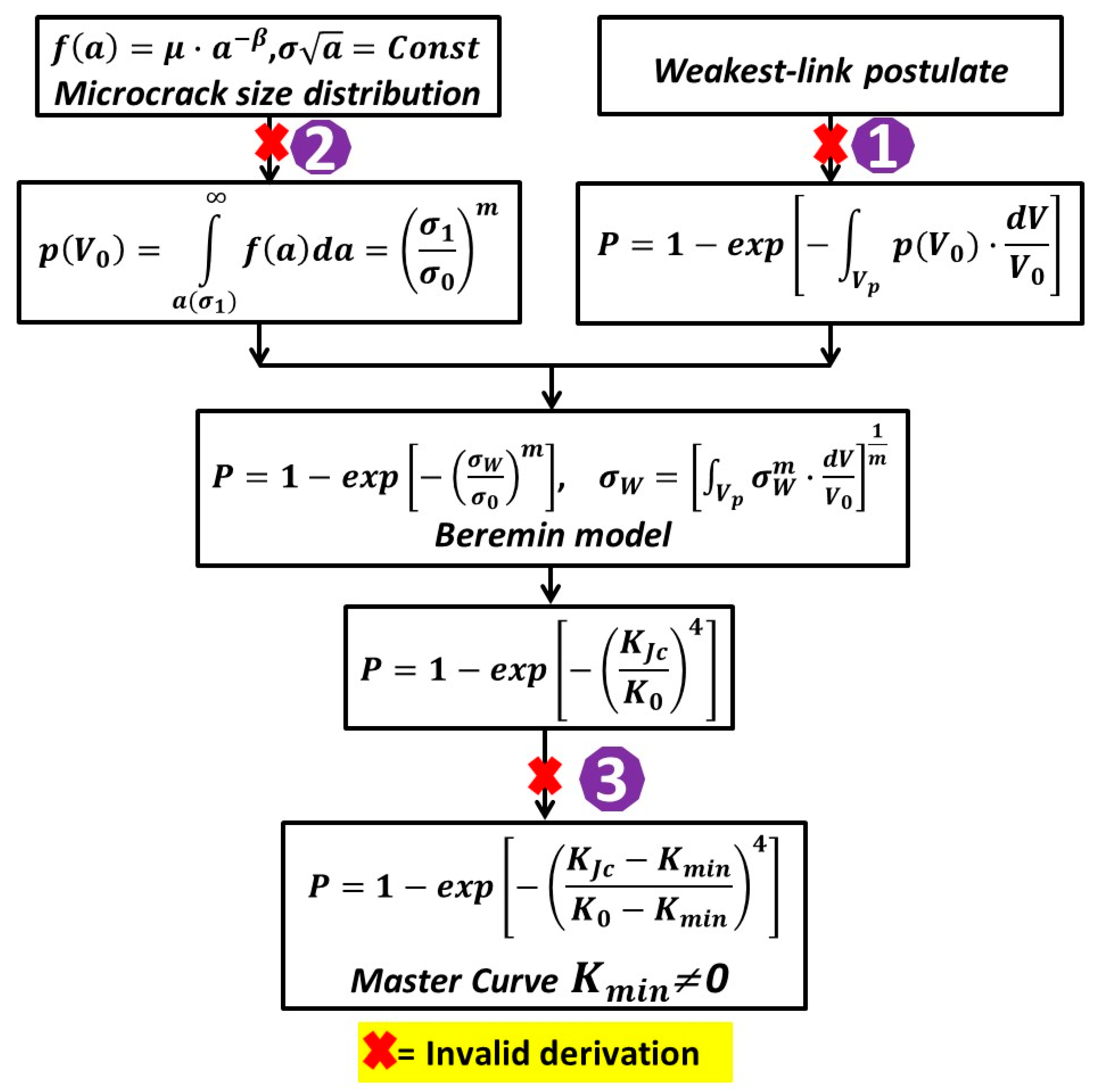
2. A Statistical Model of Cleavage Fracture Toughness
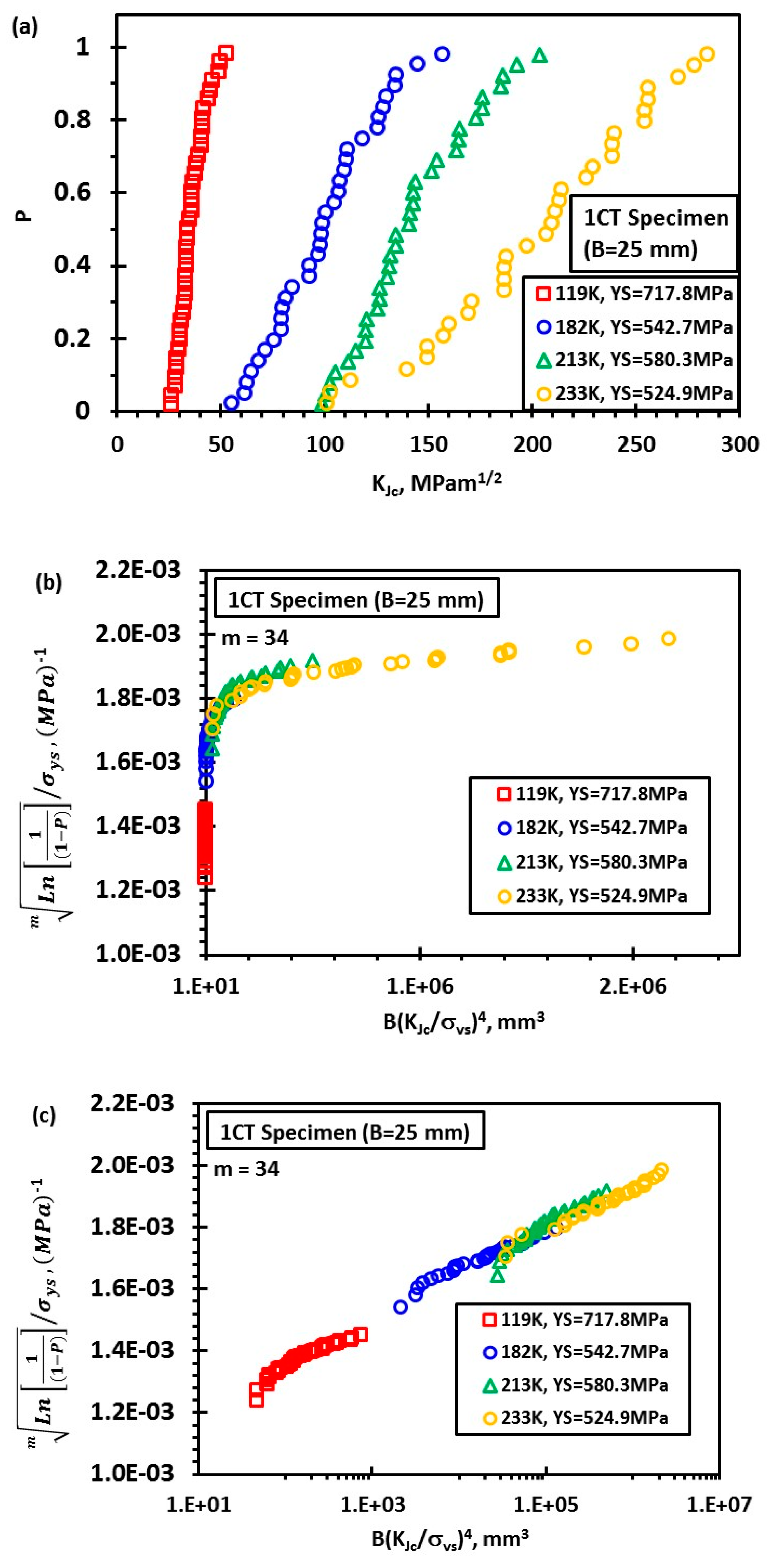
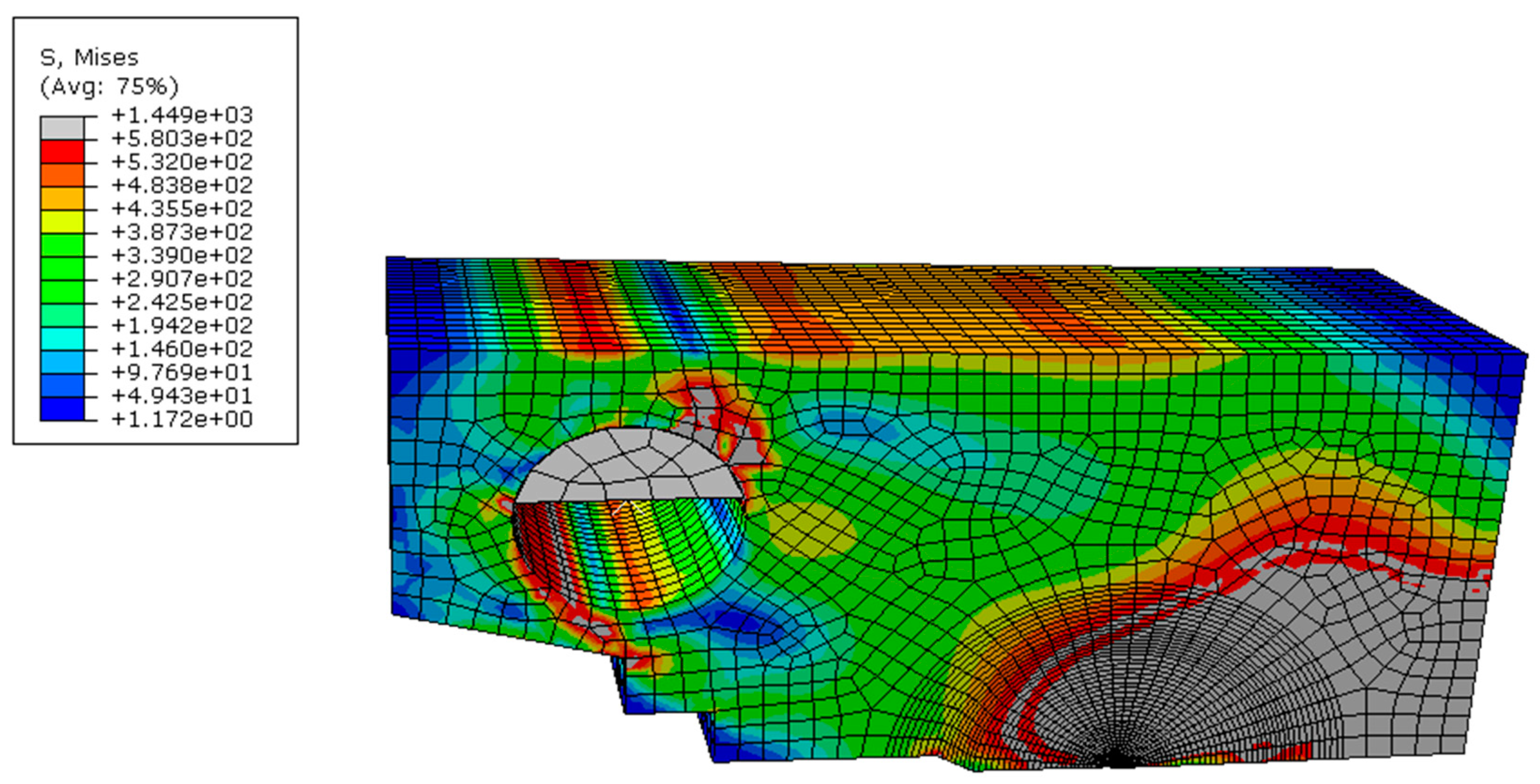
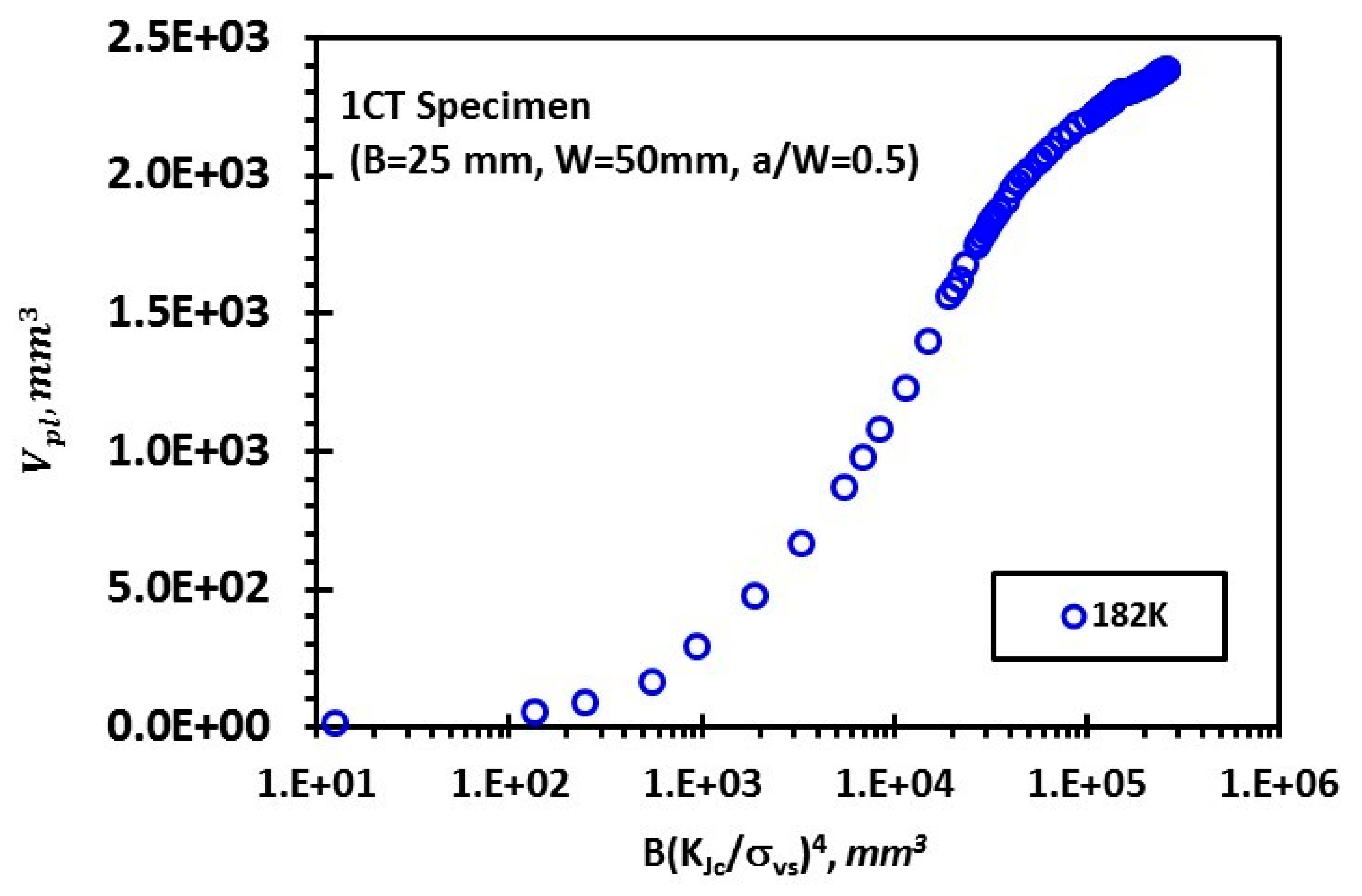
3. Model Validation
4. Conclusions
- A model for the statistical distribution of cleavage fracture toughness is proposed based on a new local approach model to collectively reflect the effect of temperature and specimen size. The model suggests that under large scale yielding, the distribution of cleavage fracture toughness may deviate from the Weibull statistics with a modulus (mK) of four.
- According to the proposed model, cleavage fracture toughness data of 1CT specimens at four different temperatures are synchronized onto a single master curve governed by the two compound parameters and .
- Finite element analysis of stress distribution in a 1CT fracture toughness specimen reveals the non-linear relationship between and under large scale yielding.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| a | crack depth |
| B, W, L | geometrical dimensions of a specimen |
| Cm,n | numerical coefficient |
| CT | compact tension |
| E | Young’s modulus, MPa |
| f(a) | probability density function of microcrack size (a) distribution |
| g(S) | probability density function of microscopic cleavage strength (S) |
| J | J-integral |
| Jc | critical J-integral at cleavage fracture |
| j | rank number |
| Jmin, Kmin | threshold values |
| J0, K0 | scale parameters |
| K | stress intensity factor |
| critical stress intensity factor at cleavage fracture | |
| m, mJ, mK | Weibull modulus |
| P | fracture probability |
| p(V0) | fracture probability of an elementary volume (V0) |
| S | fracture strength |
| S | microscopic cleavage fracture strength |
| S(εp) | microcrack propagation resistance |
| Vpl | volume of plastic deformation zone |
| V0 | mean volume occupied by each micro-crack |
| dV | differential volume |
| volume of a finite element | |
| ν | Poisson’s ratio |
| σys | yield stress |
| σ0 | scale parameter |
| σw | Weibull stress |
| σ1 | maximum tensile principal stress |
| maximum principal stress at initial yielding of a volume | |
| threshold stress | |
| σd | resistance to microcrack nucleation |
| εp | plastic strain |
| numerical coefficient |
References
- Qian, G.; Niffenegger, M.; Sharabi, M.; Lafferty, N. Effect of non-uniform reactor cooling on fracture and constraint of a reactor pressure vessel. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 1559–1575. [Google Scholar] [CrossRef]
- Liao, D.; Zhu, S.P.; Correia, J.A.; De Jesus, A.M.; Calçada, R. Computational framework for multiaxial fatigue life prediction of compressor discs considering notch effects. Eng. Fract. Mech. 2018, 202, 423–435. [Google Scholar] [CrossRef]
- Wu, Y.; Xu, Y.; Guo, X.; Bao, R. Fatigue life prediction based on equivalent initial flaw size for Al-Li alloy 2297 under spectrum loading. Int. J. Fatigue 2017, 103, 39–47. [Google Scholar] [CrossRef]
- Qian, G.; Cao, Y.; Niffenegger, M.; Chao, Y.J.; Wu, W. Comparison of constraint analyses with global and local approaches under uniaxial and biaxial loadings. Eur. J. Mech. A Solids 2018, 69, 135–146. [Google Scholar] [CrossRef]
- Zhu, S.P.; Foletti, S.; Beretta, S. Evaluation of size effect on strain-controlled fatigue behavior of a quench and tempered rotor steel: Experimental and numerical study. Mater. Sci. Eng. A 2018, 735, 423–435. [Google Scholar] [CrossRef]
- Qian, G.; Lei, W.-L.; Peng, L.; Yu, Z.; Niffengger, M. Statistical assessment of notch toughness against cleavage fracture of ferritic steels. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 1120–1131. [Google Scholar] [CrossRef]
- Li, D.; Hu, D.; Wang, R.; Ma, Q.; Liu, H. A non-local approach for probabilistic assessment of LCF life based on optimized effective-damage-parameter. Eng. Fract. Mech. 2018, 199, 188–200. [Google Scholar] [CrossRef]
- Wu, S.C.; Xiao, T.Q.; Withers, P.J. The imaging of failure in structural materials by synchrotron radiation X-ray micro-tomography. Eng. Fract. Mech. 2017, 182, 127–156. [Google Scholar] [CrossRef]
- Lei, W.S. On the statistical modeling of cleavage fracture toughness of structural Steels. Mech. Mater. 2016, 101, 81–92. [Google Scholar] [CrossRef]
- Landes, J.D.; Shaffer, D.H. Statistical characterization of fracture in the transition region. In Fracture Mechanics; ASTM STP 700; American Society for Testing and Materials: Philadelphia, PA, USA, 1980; pp. 368–382. [Google Scholar]
- Landes, J.D.; McCabe, D.E. Effect of section size on trnsition temperature behavior of structural steels. In Fracture Mechanics; Sanford, R.J., Ed.; American Society for Testing and Materials: Philadelphia, PA, USA, 1984; pp. 378–392. [Google Scholar]
- McCabe, D.E. A Comparison of Weibull and βIc analyses of transition range data. Presented at the 23rd National Symposium on Fracture Mechanics, College Station, TX, USA, 18–20 June 1991. [Google Scholar]
- Beremin, F.M. A local approach for cleavage fracture of a nuclear pressure vessel steel. Metall. Trans. A 1983, 14, 2277–2287. [Google Scholar] [CrossRef]
- Pineau, A. Development of the local approach to fracture over the past 25 years: Theory and applications. Int. J. Fract. 2006, 138, 139–166. [Google Scholar] [CrossRef]
- Wallin, K. Master curve analysis of the “Euro” fracture toughness dataset. Eng. Fract. Mech. 2002, 69, 451–481. [Google Scholar] [CrossRef]
- International Atomic Energy Agency (IAEA). Guidelines for Applications of the Master Curve Approach to Reactor Pressure Vessel Integrity in Nuclear Power Plants; Technical Reports Series No.429; International Atomic Energy Agency: Vienna, Austria, 2005; pp. 91–95. [Google Scholar]
- Wallin, K.A. Laukkanen, New developments of the Wallin, Saario, Törrönen cleavage fracture model. Eng. Fract. Mech. 2008, 75, 3367–3377. [Google Scholar] [CrossRef]
- Margolin, B.; Gulenko, A.; Shvetsova, V. Fracture toughness prediction for RPV steels with various degree of embrittlement. In Proceedings of the 17th International Conference on Structural Mechanics in Reactor Technology (SMiRT 17), Prague, Czech Republic, 17–22 August 2003. [Google Scholar]
- Margolin, B.; Shvetsova, V.; Kostylev, V. Radiation embrittlement modelling in multi-scale approach to brittle fracture of RPV steels. Int. J. Fract. 2013, 179, 87–103. [Google Scholar] [CrossRef]
- Lei, W.-S. A discussion of “An engineering methodology for constraint corrections of elastic–plastic fracture toughness—Part II: Effects of specimen geometry and plastic strain on cleavage fracture predictions” by C. Ruggieri, R.G. Savioli, R.H. Dodds [Eng. Fract. Mech. 146 (2015) 185–209]. Eng. Fract. Mech. 2017, 178, 527–534. [Google Scholar]
- Lei, W.-S. A cumulative failure probability model for cleavage fracture in ferritic steels. Mech. Mater. 2016, 93, 184–198. [Google Scholar] [CrossRef]
- Lei, W.-S. A statistical model of cleavage fracture in structural steels with power-law distribution of microcrack size. Philos. Mag. Lett. 2016, 96, 101–111. [Google Scholar] [CrossRef]
- Lei, W.-S. A framework for statistical modeling of plastic yielding initiated cleavage fracture of structural steels. Philos. Mag. 2016, 96, 3586–3631. [Google Scholar] [CrossRef]
- Qian, G.; Lei, W.-S.; Niffenegger, M. Calibration of a new local approach to cleavage fracture of ferritic steels. Mater. Sci. Eng. A 2017, 694, 10–12. [Google Scholar] [CrossRef]
- Qian, G.; Lei, W.-S.; Niffenegger, M.; Gonzalez, V.F. On the temperature independence of statistical model parameters for cleavage fracture in ferritic steels. Philos. Mag. 2018, 98, 959–1004. [Google Scholar] [CrossRef]
- Shen, A.; Li, P.; Wang, K.; Qian, G.; Berto, F. A simplified method for parameters calibration of the new local approach model for cleavage fracture in ferritic steels. Theor. Appl. Fract. Mech. 2019. [Google Scholar] [CrossRef]
- Heerens, J.; Hellmann, D. Development of the Euro fracture toughness dataset. Eng. Fract. Mech. 2002, 69, 421–449. [Google Scholar] [CrossRef]
- Zhu, S.P.; Liu, Q.; Peng, W.; Zhang, X.C. Computational-experimental approaches for fatigue reliability assessment of turbine bladed disks. Int. J. Mech. Sci. 2018, 142–143, 502–517. [Google Scholar] [CrossRef]
- Hu, D.; Mao, J.; Wang, X.; Meng, F.; Song, J.; Wang, R. Probabilistic evaluation on fatigue crack growth behavior in nickel based GH4169 superalloy through experimental data. Eng. Fract. Mech. 2018, 196, 71–82. [Google Scholar] [CrossRef]
- Kamiński, M. On probabilistic fatigue models for composite materials. Int. J. Fatigue 2002, 24, 477–495. [Google Scholar] [CrossRef]
- Qian, G.; Zhai, J.; Yu, Z.; Lei, W.; Wu, W. Non-proportional size scaling of strength of concrete in uniaxial and biaxial loading conditions. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 1733–1745. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, G.; Lei, W.-S.; Tong, Z.; Yu, Z. A Statistical Model of Cleavage Fracture Toughness of Ferritic Steel DIN 22NiMoCr37 at Different Temperatures. Materials 2019, 12, 982. https://doi.org/10.3390/ma12060982
Qian G, Lei W-S, Tong Z, Yu Z. A Statistical Model of Cleavage Fracture Toughness of Ferritic Steel DIN 22NiMoCr37 at Different Temperatures. Materials. 2019; 12(6):982. https://doi.org/10.3390/ma12060982
Chicago/Turabian StyleQian, Guian, Wei-Sheng Lei, Zhenfeng Tong, and Zhishui Yu. 2019. "A Statistical Model of Cleavage Fracture Toughness of Ferritic Steel DIN 22NiMoCr37 at Different Temperatures" Materials 12, no. 6: 982. https://doi.org/10.3390/ma12060982
APA StyleQian, G., Lei, W.-S., Tong, Z., & Yu, Z. (2019). A Statistical Model of Cleavage Fracture Toughness of Ferritic Steel DIN 22NiMoCr37 at Different Temperatures. Materials, 12(6), 982. https://doi.org/10.3390/ma12060982



