Transmittance and Reflectance Effects during Thermal Diffusivity Measurements of GNP Samples with the Flash Method
Abstract
1. Introduction
- a very short energy pulse can produce a meaningful temperature increase on the irradiated surface which can even damage it; this can be avoided with a low power source (a photographic flash), but temperature increase on the opposite side results very low, and temperature detection becomes difficult;
- an error can arise when the time length of the flash pulse is comparable with the temperature transition on the opposite face: In such case the approximation of the analytical trend of the pulse with a Dirac-delta function cannot be considered any more valid, and a meaningful systematic error is introduced [6,9].
2. Analytical Solution
2.1. Parker Solution
- homogeneous and isotropic materials;
- pulse heating (Dirac δ);
- adiabatic condition of the slab after the pulse;
- homogeneously irradiated surface;
- one-dimensional heat propagation;
- thermo-physical properties constant in the temperature range of the test;
2.2. Double Exponential
2.3. Solution Involving GNP Partial Transparency
3. Sample Preparation and Test Setup
- a quantum radiation detector (mercury cadmium telluride, MCT, active area 1 mm2, Pro-Lite Technology Ltd, Melton Mowbray, Leicestershire, UK), cooled with liquid nitrogen (77 K) in a dewar surrounding it;
- a ZnSe infrared lens (focal length 50 mm, manufacturer, city, state, country), transparent to visible and IR radiation from 0.5 to 13 µm, located in front of the MCT detector (ZSL);
- a photographic flash Universal 1500 S Elinchrom (F), 200 W nominal maximum power (Elinchrom SA, Renens, Switzerland). Tests were carried out with one half of this maximum power;
- data acquisition system (NI USB-6229, National Instruments, Austin, Texas, USA) set at a sampling rate of 25 kHz, and ±10 V range.
4. Results
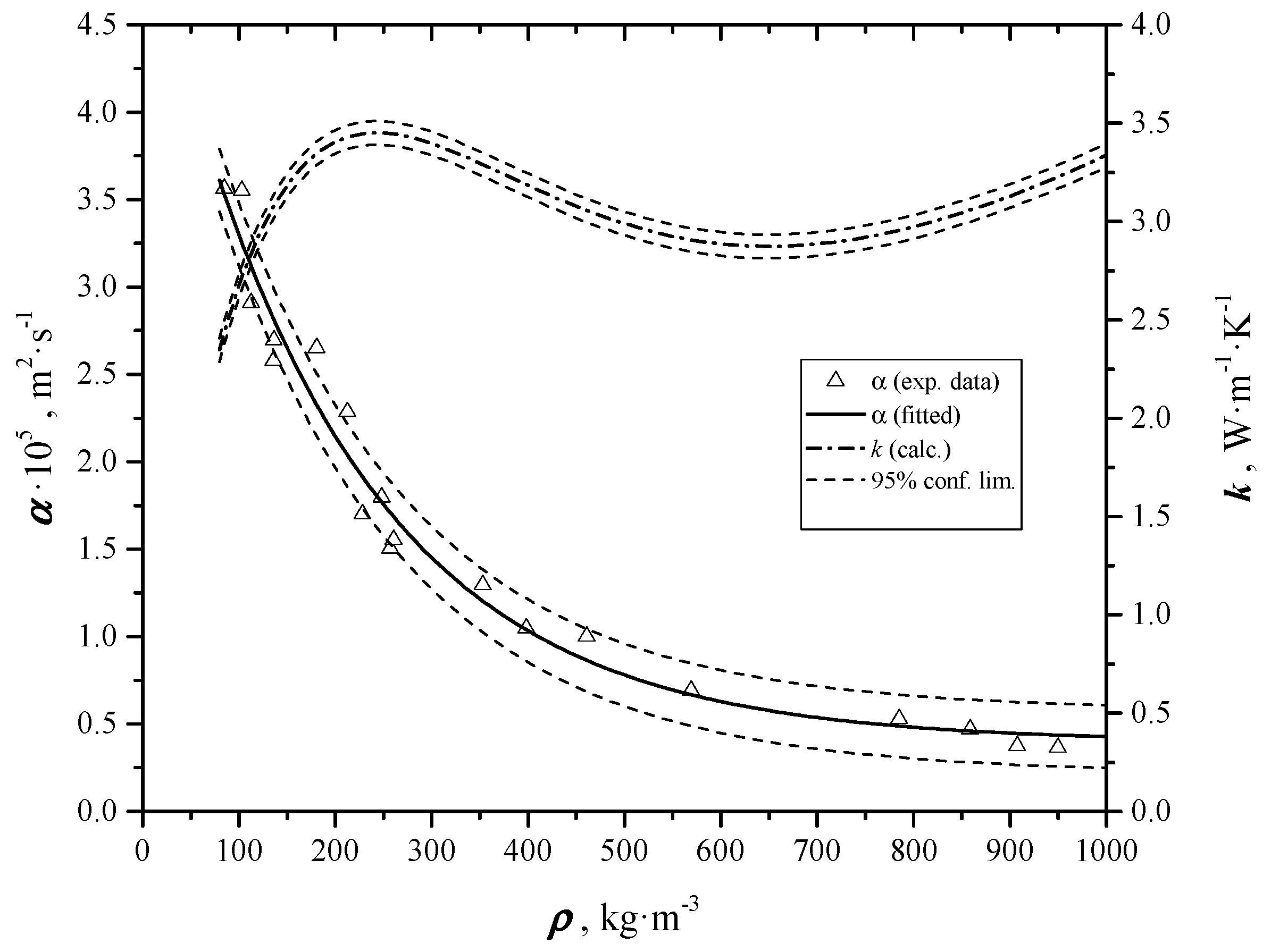
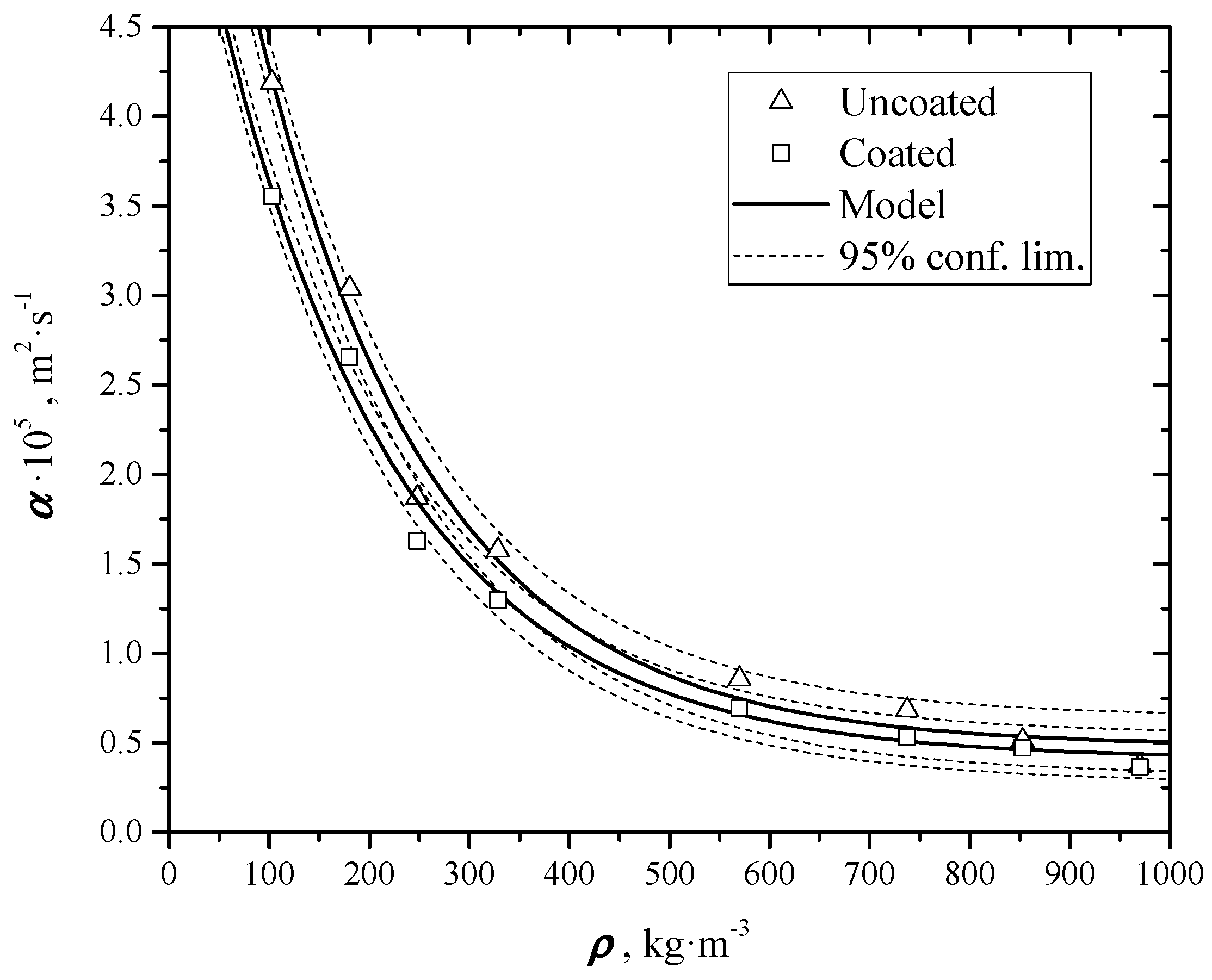
4.1. Thermal Diffusivity
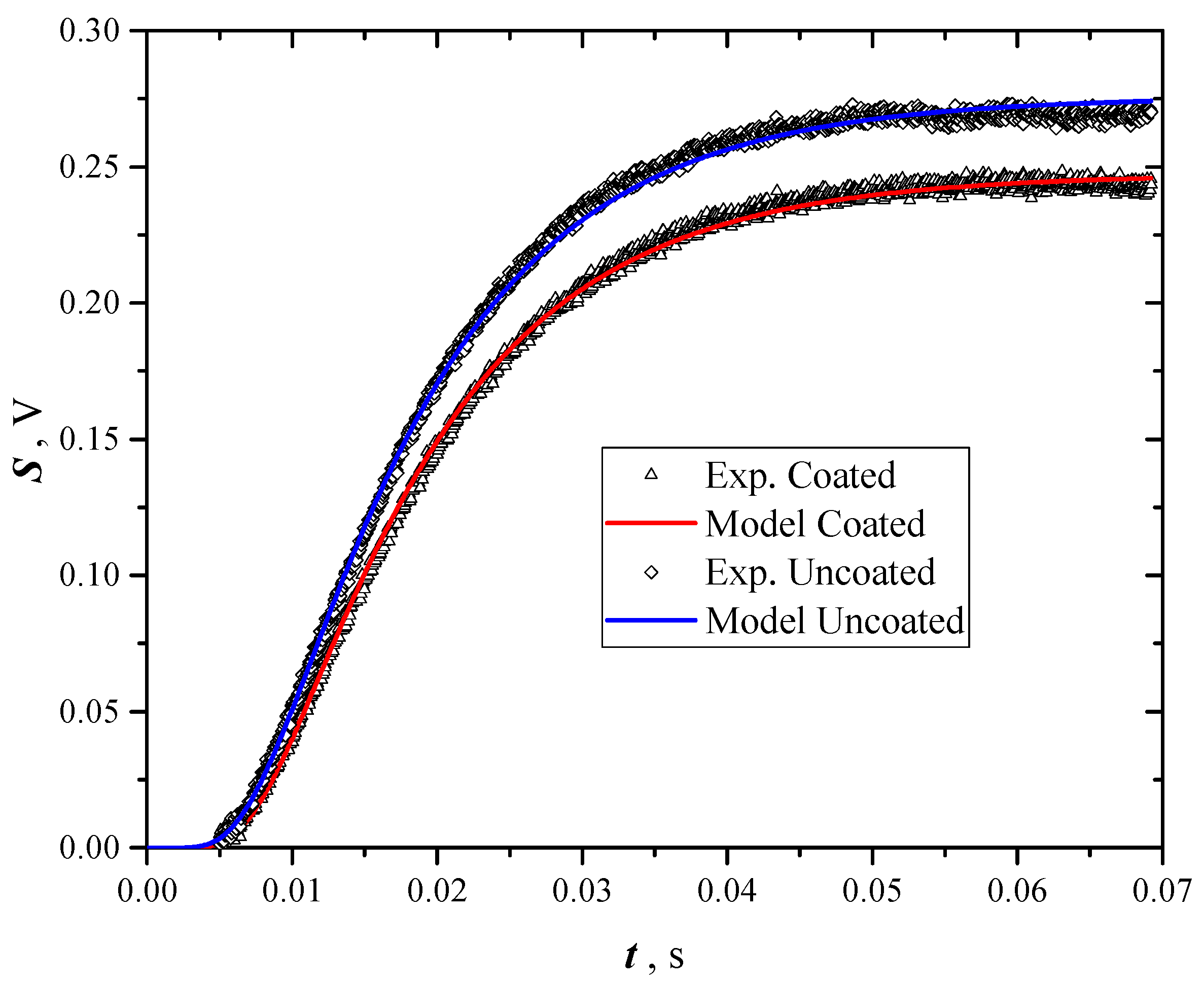
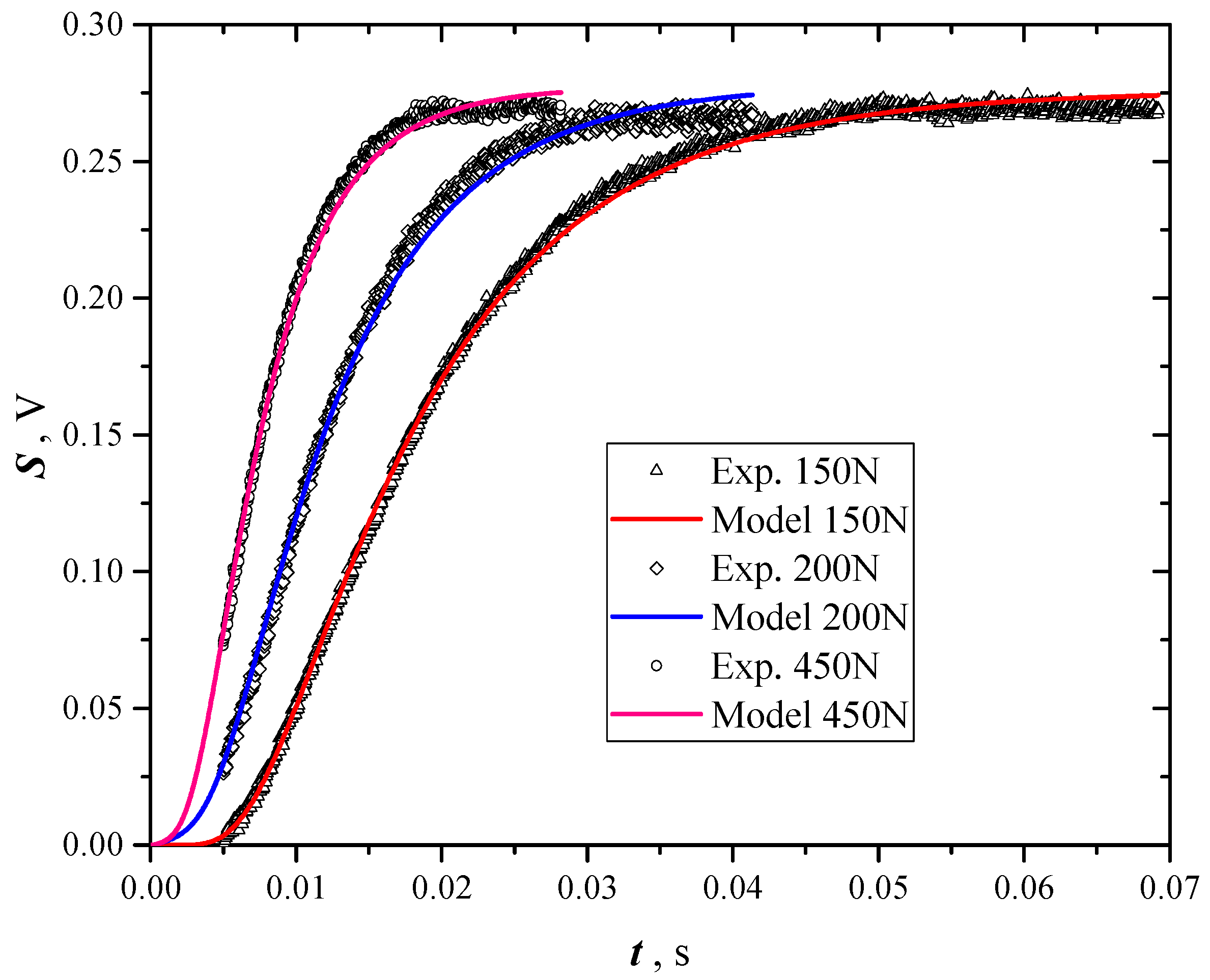
- pressing samples at predefined loads;
- testing uncoated samples five times each, and evaluating the thermal diffusivity with NL-LSF analysis using Equation (3) as model;
- coating samples and testing them again five times, evaluating their thermal diffusivity again using NL-LSF with Equation (3).
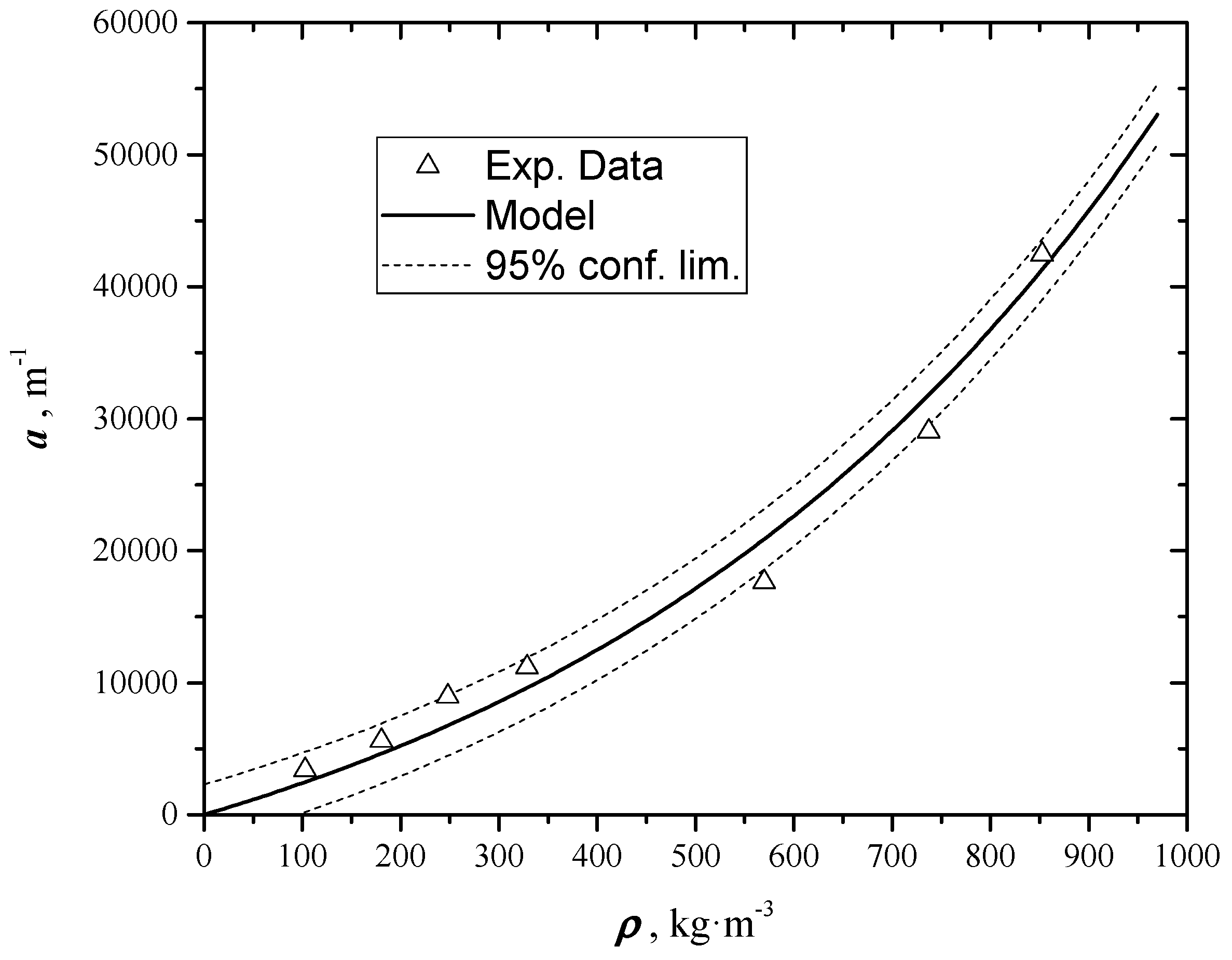
4.2. Extinction Coefficient Results
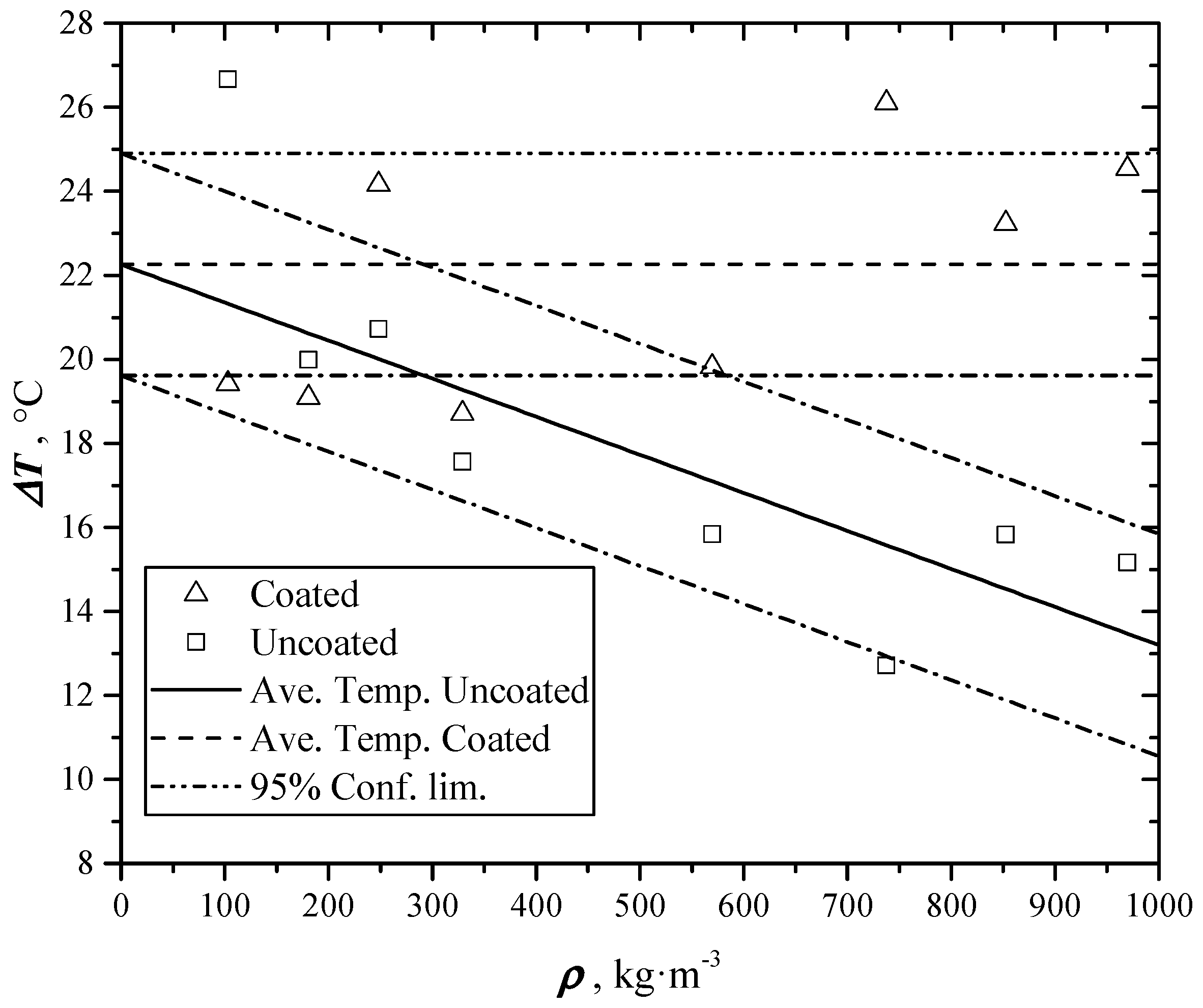
4.3. Reflectance
5. Extinction Coefficient Uncertainty Analysis
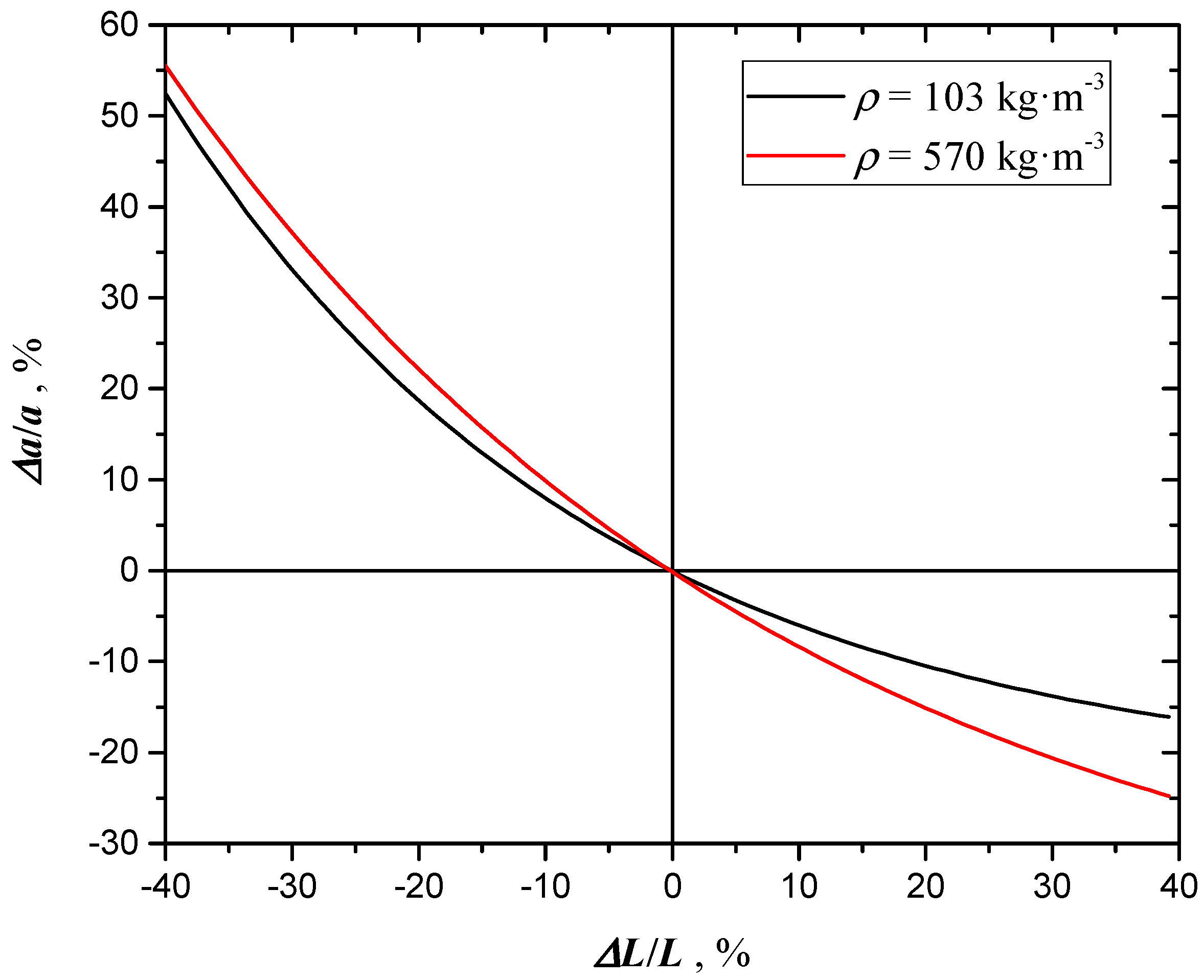
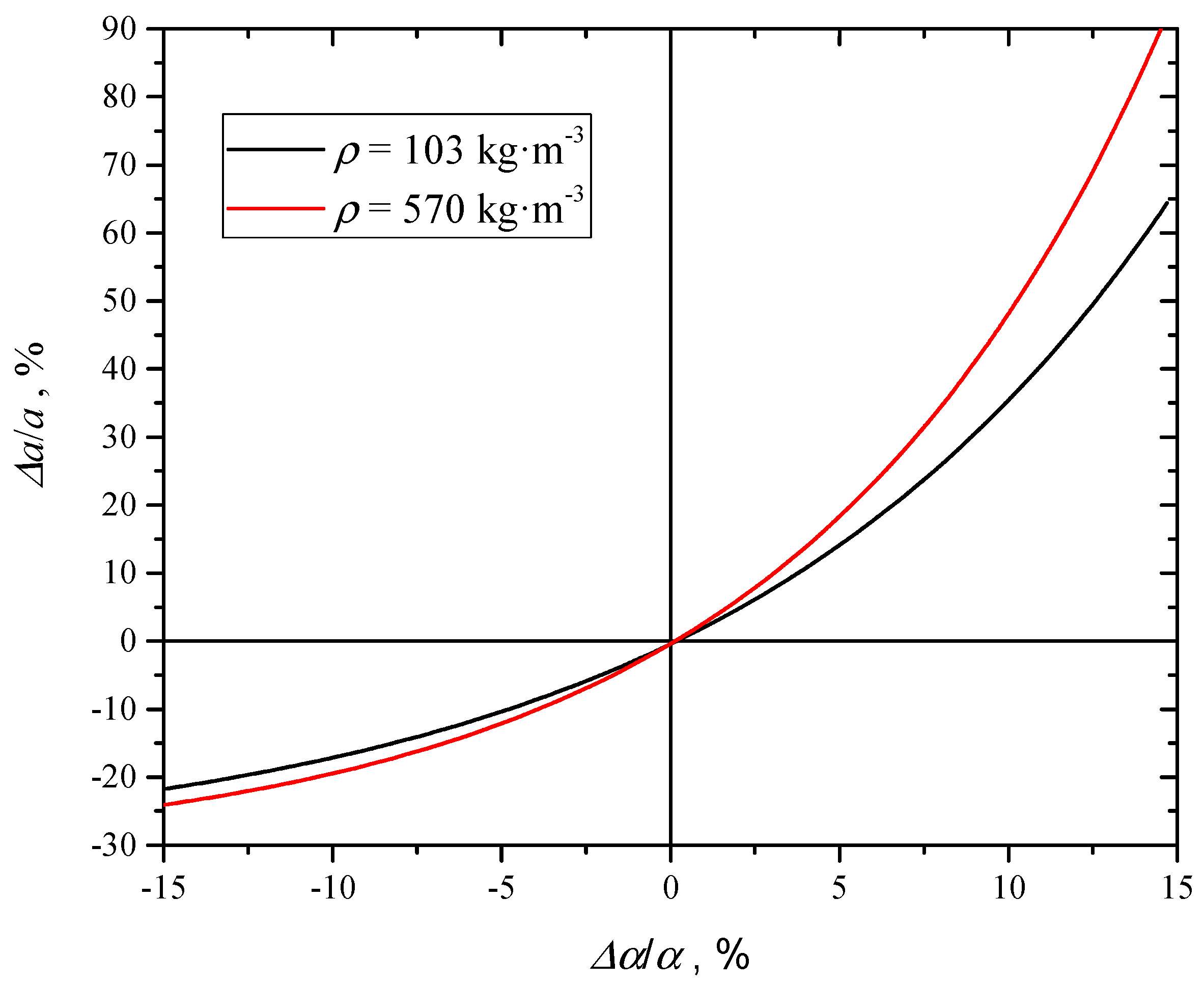
5.1. Uncertainty due to Thermal Diffusivity and Sample Thickness
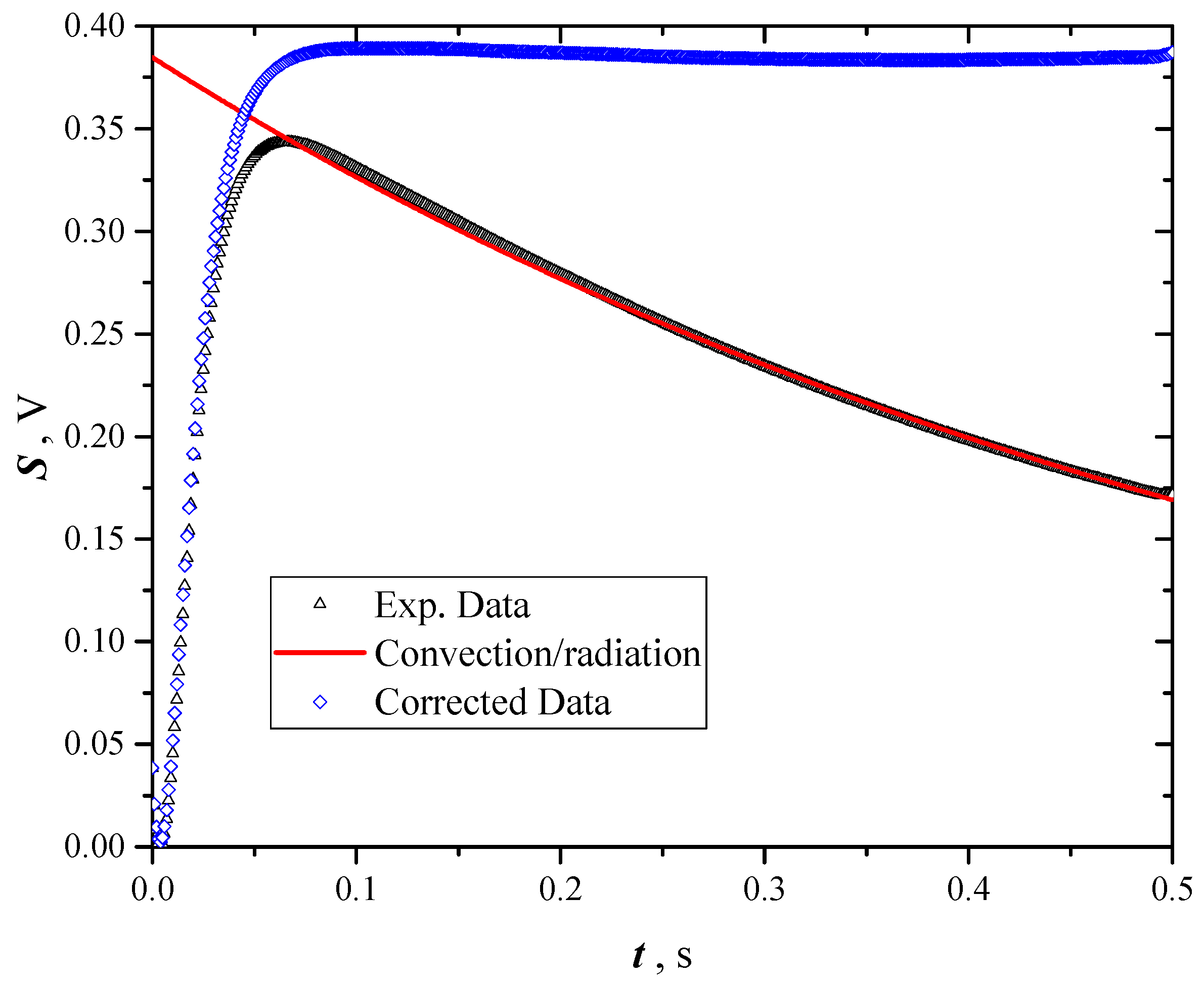
5.2. Uncertainty due to Convection/Radiation Effects
- data after the inflection point of the whole trend (including the temperature decrease) are processed with a nonlinear least square regression using the lumped parameter solution as model:where and are the initial and asymptotic temperatures of the considered time range, and a constant function of the convection and radiation heat transfer coefficients, the thermal capacity of the sample and the area exposed to the fluid (air);
- exponential decreasing data are extrapolated till to the start of the pulse heating;
- data used for thermal diffusivity calculation are corrected adding the difference between Equation (6) and its extrapolated initial value. This procedure returns data not influenced by convection/radiation, in fact their asymptote results horizontal.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Latin | ||
| A | proportional factor on light intensity in Equation (2) | [V] |
| a | extinction coefficient | [m−1] |
| B | proportional factor on light intensity in Equation (5) | [V] |
| b | nonlinear least square regression coefficient | |
| c | constant in Equation (7) | [V] |
| cp | specific heat capacity | [J·kg−1·K−1] |
| d | constant in Equation (7) | [V·°C−1] |
| I | light intensity | [W·m−2] |
| k | thermal conductivity | [W·m−1·K−1] |
| L | sample thickness | [m] |
| m | mass | [kg] |
| Q | thermal energy | [J] |
| specific thermal flux | [W·m−1] | |
| R | inverse of the time constant | [s−1] |
| S | signal | [V] |
| s | standard uncertainty (estimated) | |
| T | temperature | [°C or K] |
| t | temperature | [°C] |
| x | abscissa along the sample thickness | [m] |
| Greek and composite symbols | ||
| α | thermal diffusivity | [m2·s−1] |
| β | reflectance | |
| δ | Dirac delta function | |
| ρ | density | [kg·m−3] |
| τ | time | [s] |
| constant function of Equation (11) | [s−1] | |
| Subscript | ||
| 0 | start, initial value | |
| ∞ | infinity, asymptotic value | |
| coat | coated | |
| unc | uncoated | |
| Acronyms | ||
| D | Dewar | |
| F | Flash | |
| GNP | Graphene Nano-Plates | |
| MCT | Mercury Cadmium Telluride detector | |
| NL-LSF | Nonlinear least square fitting | |
| PTFE | Polytetrafluoroethylene | |
| SA | Sensor Amplifier | |
| SH | Sample holder | |
| SPS | Sensor Power Supply | |
| ZSL | Zinc Selenide Lenses | |
Appendix A. Analytical Expression of the Propagation of a Double Exponential Pulse in a Solid Slab by Conduction
References
- Ferrari, A.C.; Bonaccorso, F.; Fal’ko, V.; Novoselov, K.S.; Roche, S.; Bøggild, P.; Borini, S.; Koppens, F.H.L.; Palermo, V.; Pugno, N.; et al. Science and technology roadmap for graphene, related two-dimensional crystals, and hybrid systems. Nanoscale 2015, 7, 4598–4810. [Google Scholar] [CrossRef] [PubMed]
- Mattevi, C.; Kim, H.; Chhowalla, M. A review of chemical vapour deposition of graphene on copper. J. Mater. Chem. 2011, 21, 3324–3334. [Google Scholar] [CrossRef]
- Matsumoto, K. Frontiers of Graphene and Carbon Nanotubes: Devices and Applications; Springer: Tokyo, Japan, 2015; pp. 1–289. ISBN 978-4-431-55372-4. [Google Scholar]
- Maffucci, A.; Micciulla, F.; Cataldo, A.; Miano, G.; Bellucci, S. Bottom-up realization and electrical characterization of a graphene-based device. Nanotechnology 2016, 27, 095204. [Google Scholar] [CrossRef] [PubMed]
- Dabrowska, A.; Bellucci, S.; Cataldo, A.; Micciulla, F.; Huczko, A. Nanocomposites of epoxy resin with graphene nanoplates and exfoliated graphite: Synthesis and electrical properties. Phys. Status Solidi B 2014, 251, 2599–2602. [Google Scholar] [CrossRef]
- Potenza, M.; Cataldo, A.; Bovesecchi, G.; Corasaniti, S.; Coppa, P.; Bellucci, S. Graphene nanoplatelets: Thermal diffusivity and thermal conductivity by the flash method. AIP Adv. 2017, 7, 075214. [Google Scholar] [CrossRef]
- Parker, W.J.; Jenkins, R.J.; Butler, C.P.; Abbott, G.L. Flash method of determining thermal diffusivity, heat capacity, and thermal conductivity. J. Appl. Phys. 1961, 32, 1679–1684. [Google Scholar] [CrossRef]
- Netzsch-Gerätebau GmbH. Selb, Germany. Available online: https://www.netzsch-thermal-analysis.com/us/products-solutions/thermal-diffusivity-conductivity/ (accessed on 7 January 2019).
- Bocchini, G.F.; Bovesecchi, G.; Coppa, P.; Corasaniti, S.; Montanari, R.; Varone, A. Thermal Diffusivity of Sintered Steels with Flash Method at Ambient Temperature. Int. J. Thermophys. 2016, 37, 1–14. [Google Scholar] [CrossRef]
- Mehling, H.; Hautzinger, G.; Nilsson, O.; Fricke, J.; Hofmann, R.; Hahn, O. Thermal diffusivity of semitransparent materials determined by the laser-flash method applying a new analytical model. Int. J. Thermophys. 1998, 19, 941–949. [Google Scholar] [CrossRef]
- Tischler, M.; Kohanoff, J.J.; Rangugni, G.A. Pulse method of measuring thermal diffusivity and optical absorption depth for partially transparent materials. J. Appl. Phys. 1988, 63, 1259–1264. [Google Scholar] [CrossRef]
- Andre, S.; Degiovanni, A. A theoretical study of the transient coupled conduction and radiation heat transfer in glass: phonic diffusivity measurements by the flash technique. Int. J. Heat Mass Transf. 1995, 38, 3401–3412. [Google Scholar] [CrossRef]
- Salazar, A.; Mendioroz, A.; Apiñaniz, E.; Pradere, C.; Noë, F.; Batsale, J. Extending the flash method to measure the thermal diffusivity of semitransparent solids. Meas. Sci. Technol. 2014, 25, 035604. [Google Scholar] [CrossRef]
- Maglić, K.D.; Taylor, R.E. Compendium of Thermophysical Property Measurement Methods: Volume 2 Recommended Measurement Techniques and Practices; Maglić, K.D., Cezairliyan, A., Peletsky, V.E., Eds.; Springer: Boston, MA, USA, 1992; pp. 281–314. [Google Scholar]
- Taylor, R.E.; Clark, L.M., III. Finite Pulse Time Effects in Flash Diffusivity Method. High Temp. High Press. 1974, 6, 65–72. [Google Scholar]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Clarendon Press: Oxford, UK, 1959. [Google Scholar]
- Brandt, S. Data Analysis, Statistical and Computational Methods for Scientists and Engineers, 4th ed.; Springer: Berlin, Germany, 2014. [Google Scholar]
- ISO-IEC, 98-3: 2008. Uncertainty of Measurement—Part 3: Guide to the Expression of Uncertainty in Measurement (GUM:1995); ISO/TMBG: Geneva, Switzerland, 2008. [Google Scholar]
- Coppa, P.; Giamberardini, F. Low temperature (20–200°C) pyrometry for flash method applications: tricks in carrying out experiments and data processing. In Proceedings of the 7th AIPT Conference, Pisa, Italy, 21 September 2001; pp. 35–49. [Google Scholar]



| Sample # | Load (N) | Diameter (mm) | Thickness (mm) | Mass (g) | ρ (kg⋅m−3) |
|---|---|---|---|---|---|
| 1 | 100 | 31 | 2.36 | 0.184 | 103.1 ± 1.7 |
| 2 | 200 | 31 | 1.49 | 0.201 | 180.7 ± 3.1 |
| 3 | 450 | 34 | 0.88 | 0.200 | 248.1 ± 4.8 |
| 4 | 550 | 32 | 0.65 | 0.186 | 352.9 ± 9.3 |
| 5 | 1500 | 34 | 0.39 | 0.200 | 569.3 ± 9.7 |
| 6 | 3000 | 34 | 0.29 | 0.201 | 785 ± 27 |
| 7 | 5000 | 34 | 0.23 | 0.184 | 859 ± 38 |
| 8 | 7000 | 35 | 0.21 | 0.184 | 950 ± 28 |
| Sample # | Load (N) | ρ (kg⋅m−3) | α·107 (m2·s−1) * | sα/α (%) | α·107 (m2·s−1) ** | sα/α (%) |
|---|---|---|---|---|---|---|
| 1 | 100 | 103.1 ± 1.7 | 419 ± 2.1 | 0.5 | 355 ± 10.3 | 2.9 |
| 2 | 200 | 180.7 ± 3.1 | 304 ± 1.2 | 0.4 | 265 ± 2.6 | 1.0 |
| 3 | 450 | 248.1 ± 4.8 | 187 ± 1.6 | 0.9 | 163 ± 1.5 | 0.9 |
| 4 | 550 | 352.9 ± 9.3 | 158 ± 0.8 | 0.5 | 130 ± 1.4 | 1.1 |
| 5 | 1500 | 569.3 ± 9.7 | 85.6 ± 1.8 | 2.1 | 69.1 ± 0.8 | 1.1 |
| 6 | 3000 | 785 ± 27 | 68.3 ± 3.7 | 5.4 | 53.0 ± 0.2 | 0.4 |
| 7 | 5000 | 859 ± 38 | 51.1 ± 0.6 | 1.1 | 47.2 ± 0.4 | 0.9 |
| 8 | 7000 | 950 ± 28 | 37.1 ± 0.6 | 1.6 | 36.6 ± 0.5 | 1.4 |
| ρ (kg⋅m−3) | L (mm) | α·107 (m2⋅s−1) * | α·107 (m2⋅s−1) ** | a (m−1) |
|---|---|---|---|---|
| 103.1 | 2.36 | 419 | 355 | 3406 |
| 180.7 | 1.49 | 304 | 265 | 5607 |
| 248.1 | 0.88 | 187 | 163 | 8975 |
| 352.9 | 0.65 | 158 | 130 | 11,170 |
| 569.3 | 0.39 | 85.6 | 69.1 | 17,629 |
| 785 | 0.29 | 68.3 | 53.0 | 29,034 |
| 859 | 0.23 | 51.1 | 47.2 | 42,451 |
| ρ (kg⋅m−3) | T (°C) * | T (°C) ** | β |
|---|---|---|---|
| 103.1 | 26.7 | 19.4 | 0 |
| 180.7 | 20 | 19.1 | 0.02 |
| 248.1 | 20.7 | 24.2 | 0.05 |
| 352.9 | 17.6 | 18.7 | 0.09 |
| 569.3 | 15.8 | 19.8 | 0.21 |
| 785 | 12.7 | 26.1 | 0.29 |
| 859 | 15.8 | 23.2 | 0.35 |
| 950 | 15.15 | 24.5 | 0.41 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bellucci, S.; Bovesecchi, G.; Cataldo, A.; Coppa, P.; Corasaniti, S.; Potenza, M. Transmittance and Reflectance Effects during Thermal Diffusivity Measurements of GNP Samples with the Flash Method. Materials 2019, 12, 696. https://doi.org/10.3390/ma12050696
Bellucci S, Bovesecchi G, Cataldo A, Coppa P, Corasaniti S, Potenza M. Transmittance and Reflectance Effects during Thermal Diffusivity Measurements of GNP Samples with the Flash Method. Materials. 2019; 12(5):696. https://doi.org/10.3390/ma12050696
Chicago/Turabian StyleBellucci, Stefano, Gianluigi Bovesecchi, Antonino Cataldo, Paolo Coppa, Sandra Corasaniti, and Michele Potenza. 2019. "Transmittance and Reflectance Effects during Thermal Diffusivity Measurements of GNP Samples with the Flash Method" Materials 12, no. 5: 696. https://doi.org/10.3390/ma12050696
APA StyleBellucci, S., Bovesecchi, G., Cataldo, A., Coppa, P., Corasaniti, S., & Potenza, M. (2019). Transmittance and Reflectance Effects during Thermal Diffusivity Measurements of GNP Samples with the Flash Method. Materials, 12(5), 696. https://doi.org/10.3390/ma12050696








