Nonlinear Acoustic Modeling and Measurements during the Fatigue Process in Metals
Abstract
1. Introduction
2. Theoretical Models
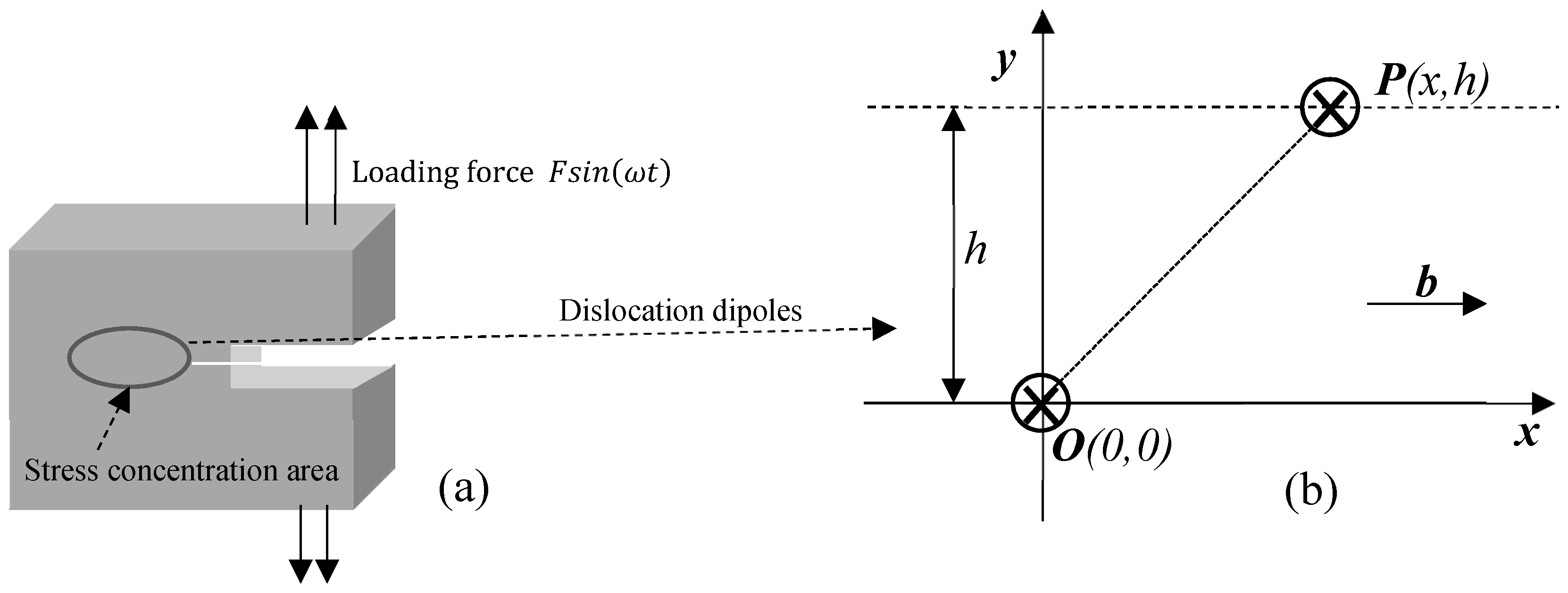
2.1. Nonlinearity Due to Lattice Dislocations at Early Stage Fatigue
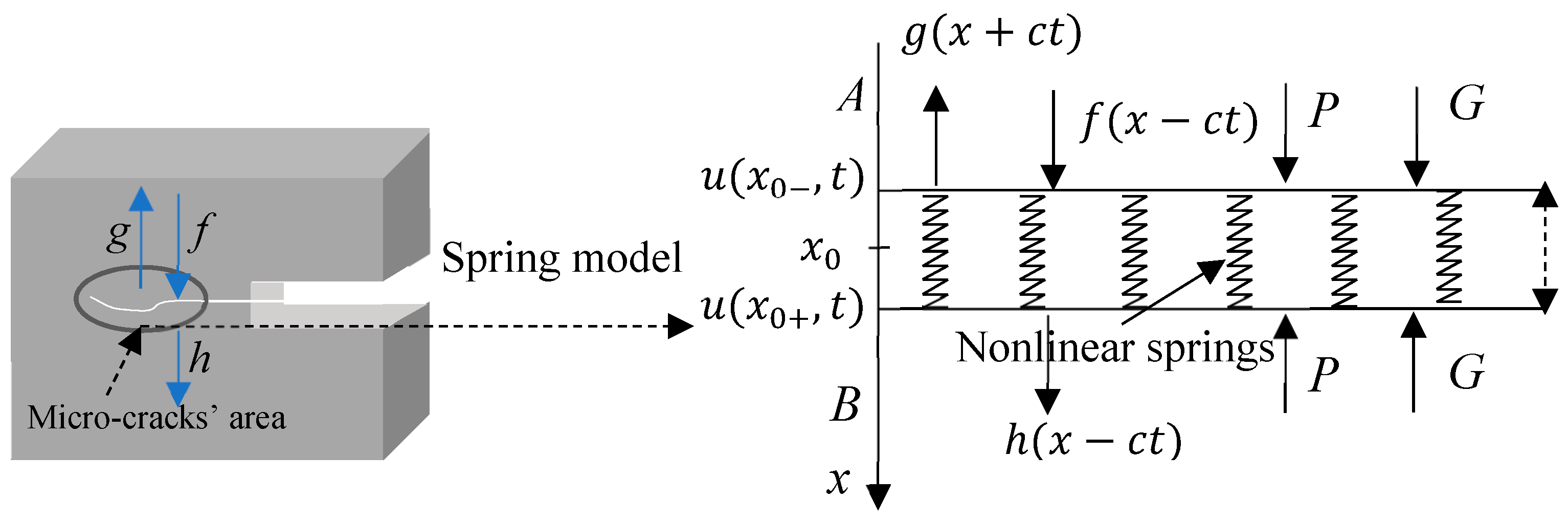
2.2. Nonlinearity Due to Micro-Cracks at Late Stage Fatigue
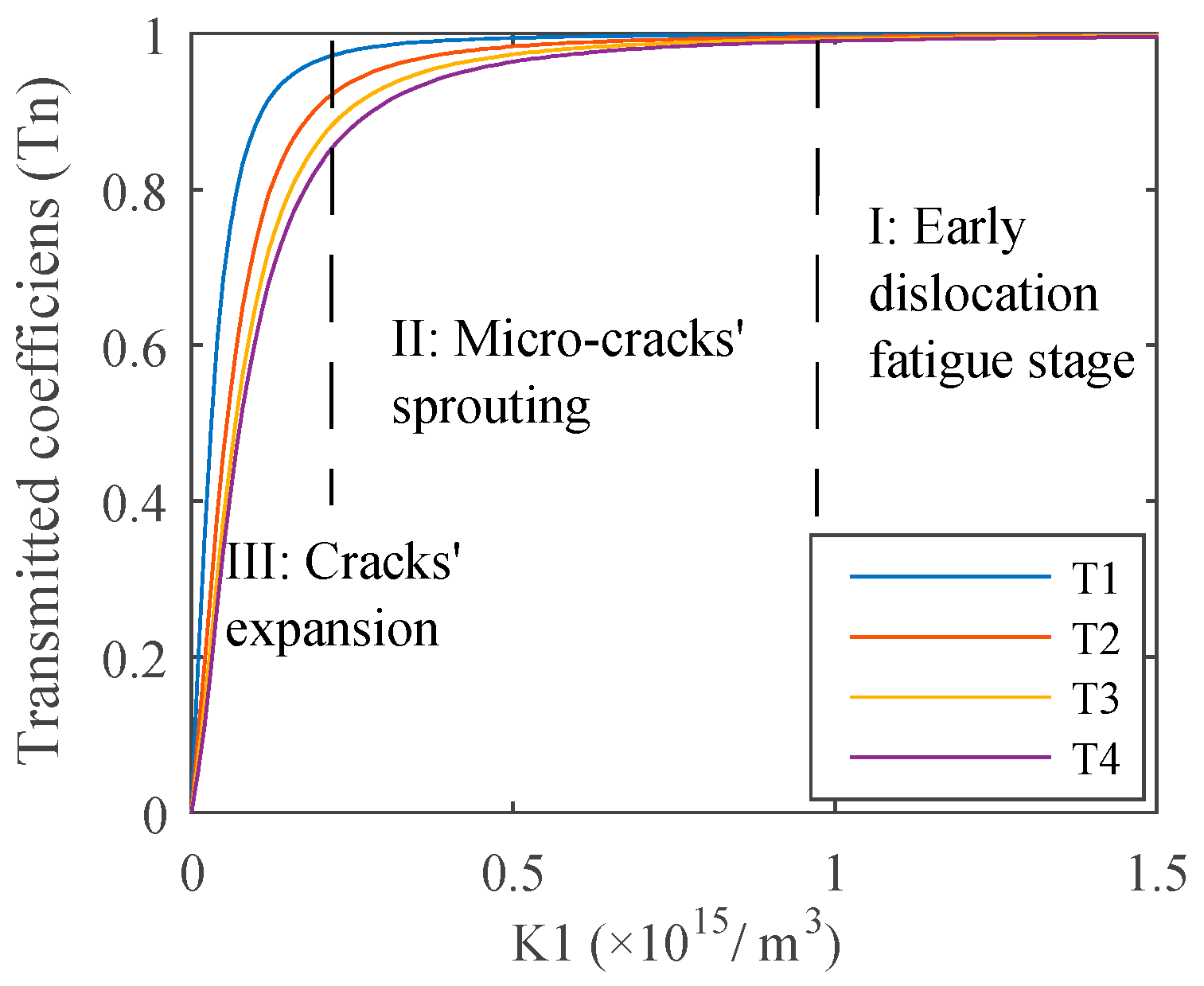
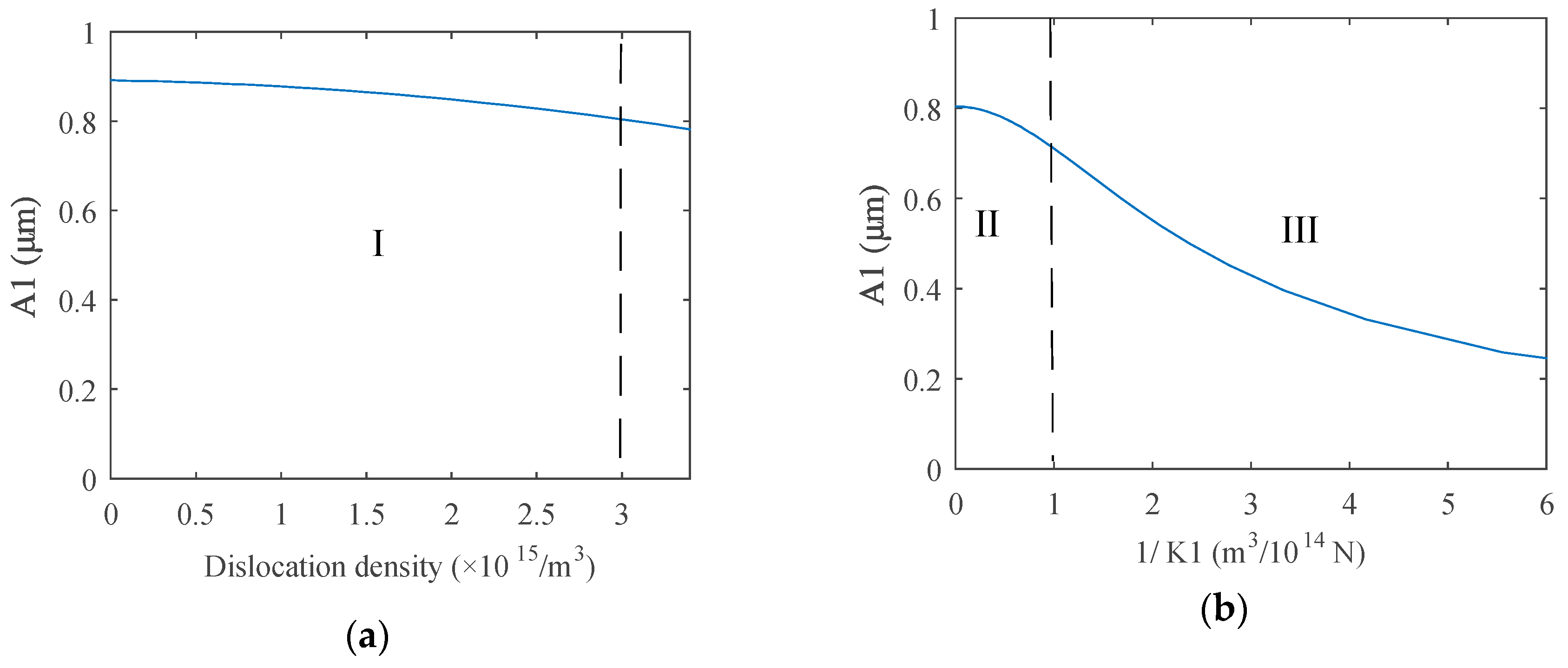
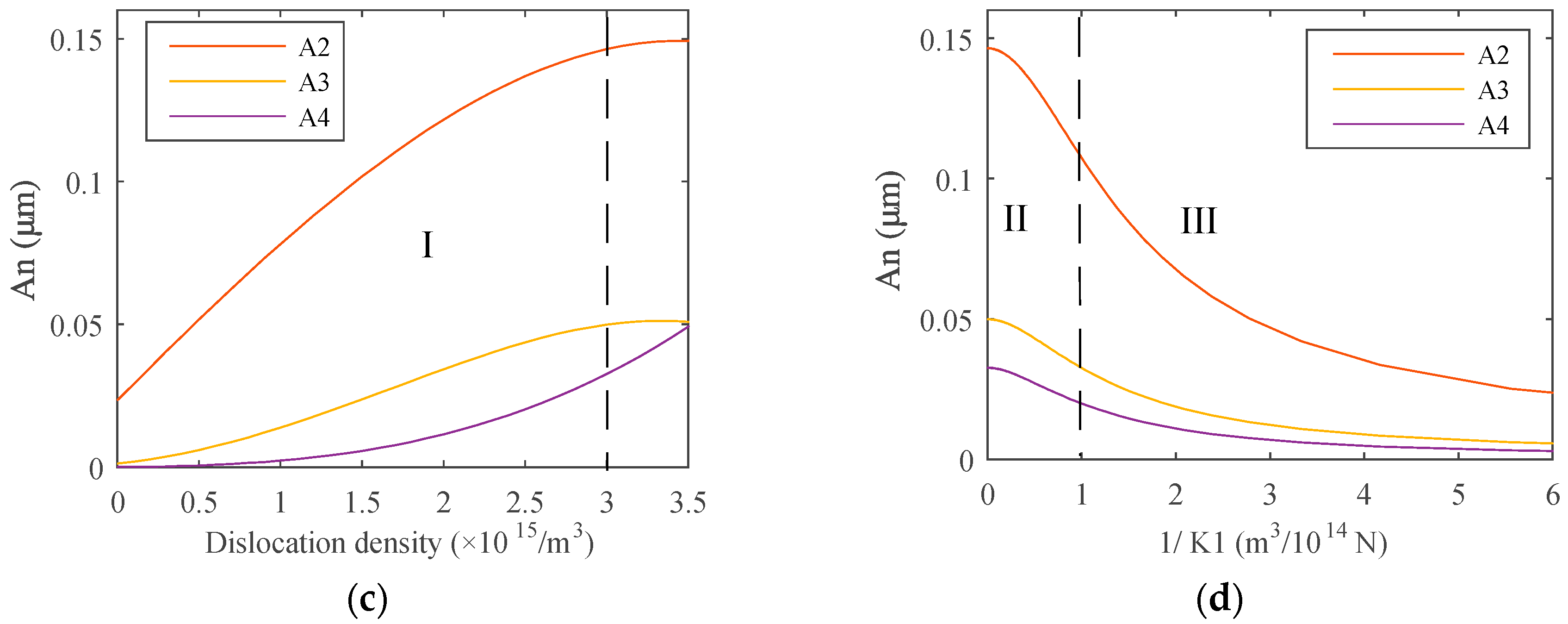
2.3. Computation Results
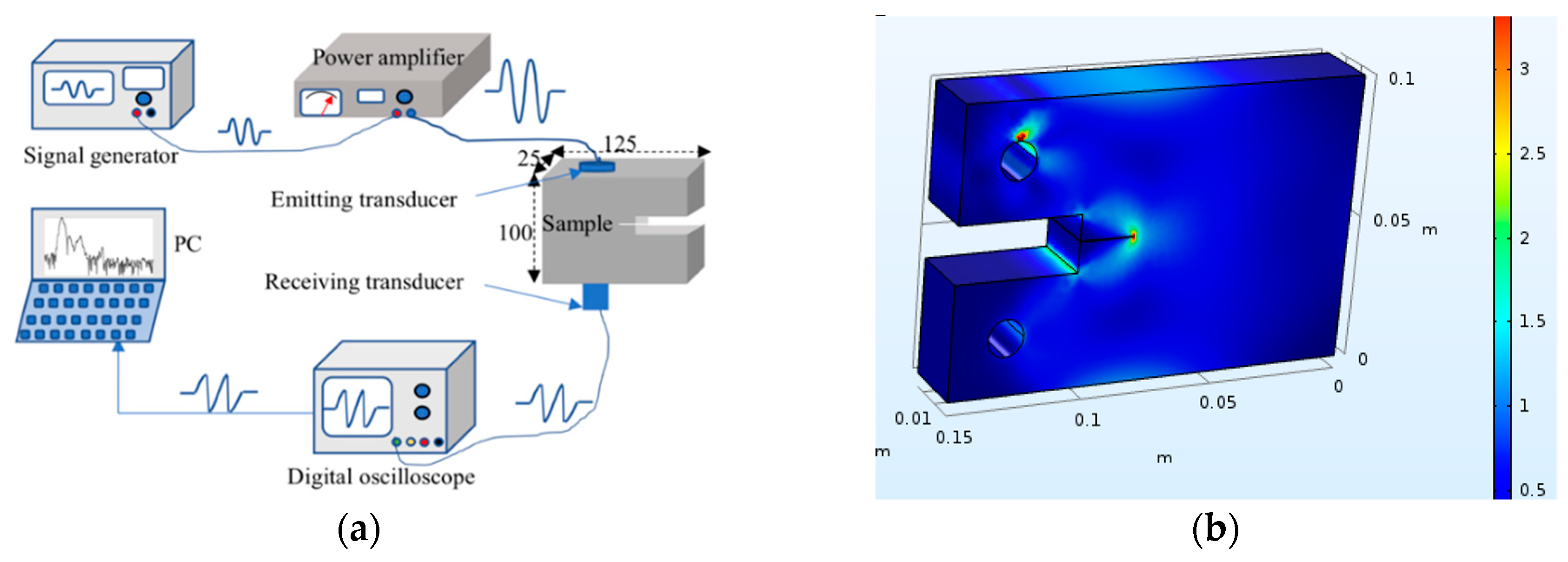
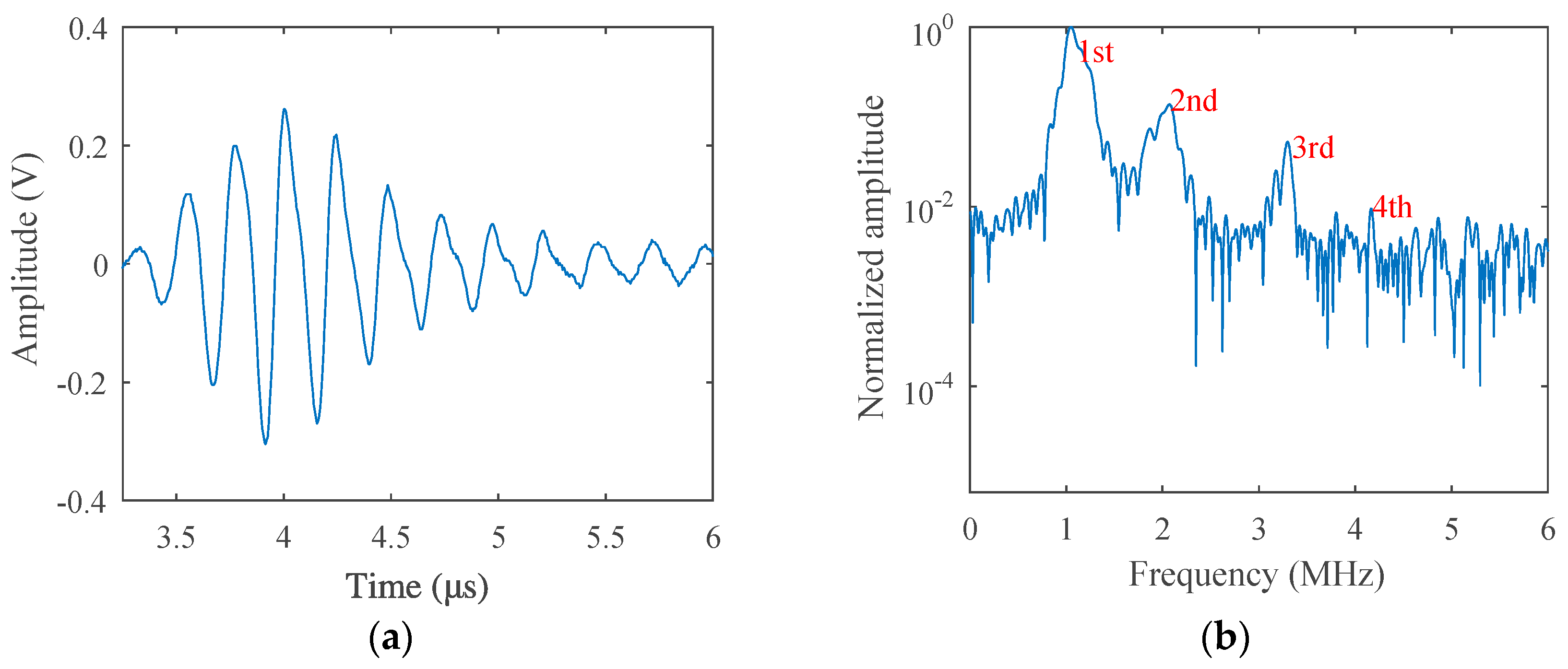
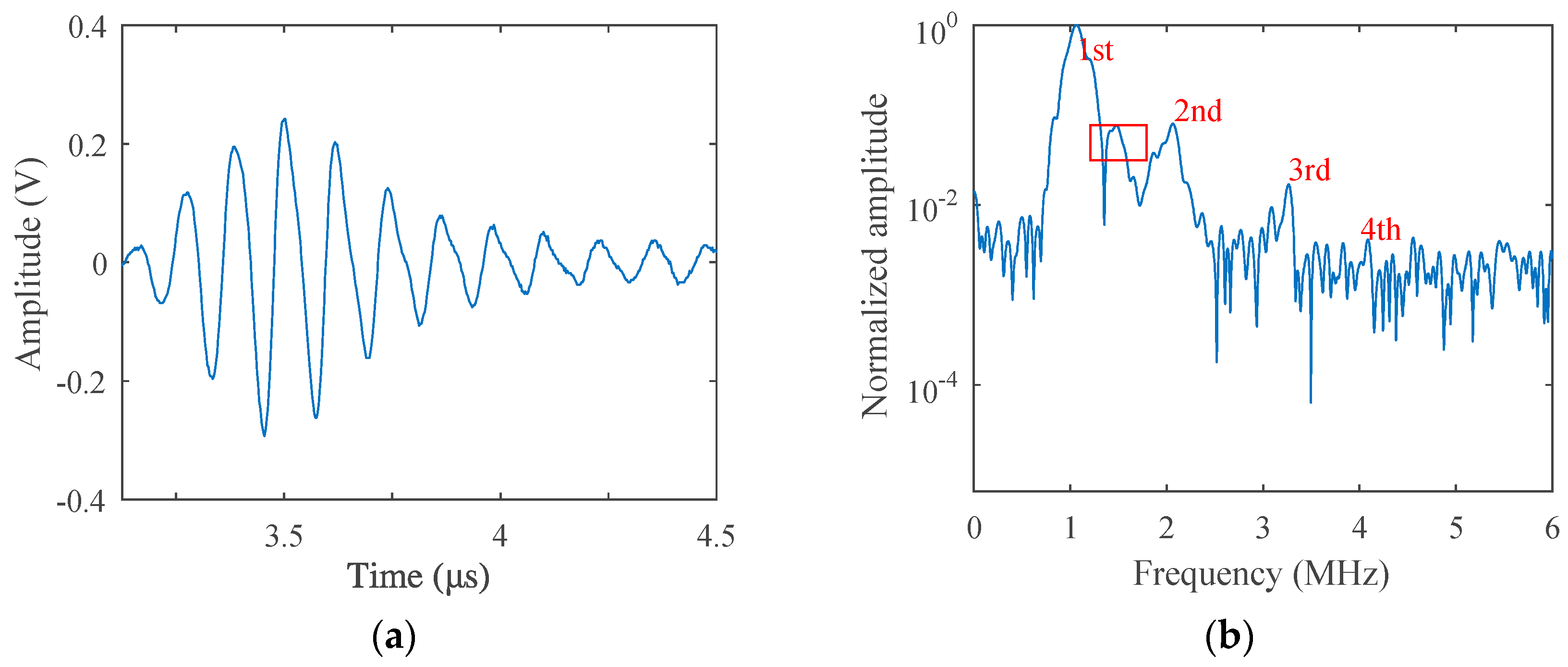
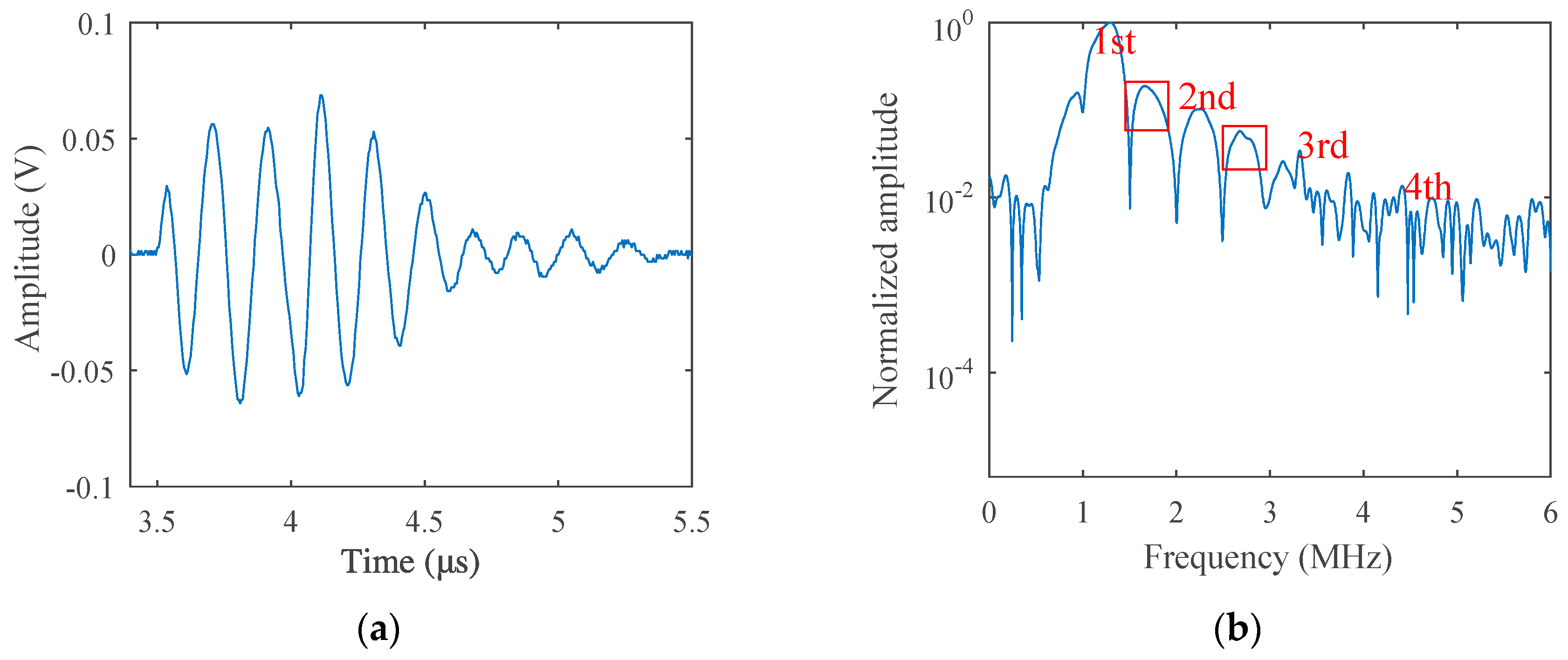
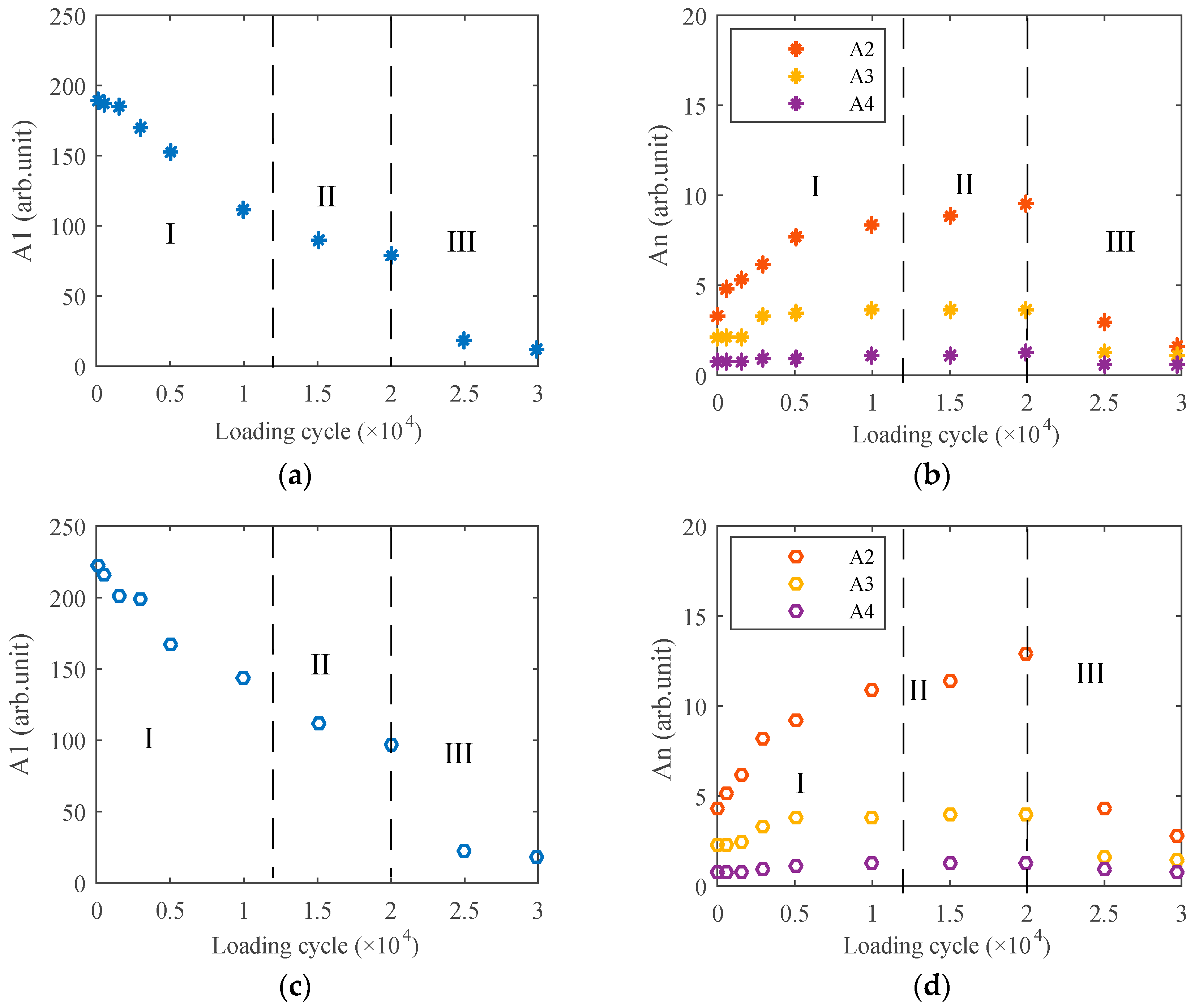
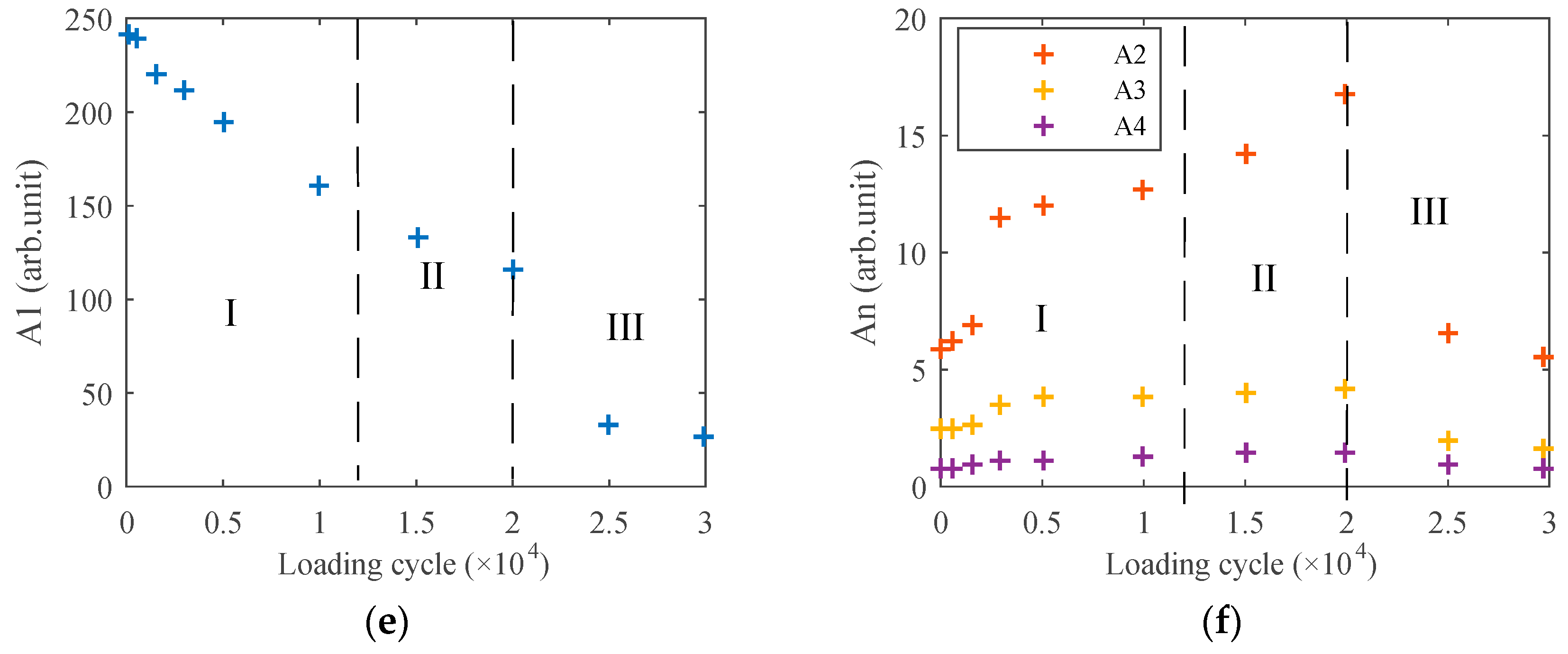
3. Experiment Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Klepka, A.; Staszewski, W.; Jenal, R.; Szwedo, M.; Iwaniec, J.; Uhl, T. Nonlinear acoustics for fatigue crack detection—Experimental investigations of vibro-acoustic wave modulations. Struct. Health Monit. 2012, 11, 197–211. [Google Scholar] [CrossRef]
- Tsyfansky, S.; Beresnevich, V. Non-linear vibration method for detection of fatigue cracks in aircraft wings. J. Sound Vib. 2000, 236, 49–60. [Google Scholar] [CrossRef]
- Palitsagar, S.; Das, S.; Parida, N.; Bhattacharya, D. Non-linear ultrasonic technique to assess fatigue damage in structural steel. Scr. Mater. 2006, 55, 199–202. [Google Scholar] [CrossRef]
- Nagy, P.B. Fatigue damage assessment by nonlinear ultrasonic materials characterization. Ultrasonics 1998, 36, 375–381. [Google Scholar] [CrossRef]
- Yang, Z.; Tian, Y.; Li, W.; Zhou, H.; Zhang, W. Experimental Investigation of the Acoustic Nonlinear Behavior in Granular Polymer Bonded Explosives with Progressive Fatigue Damage. Materials 2017, 10, 660. [Google Scholar] [CrossRef] [PubMed]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity, 3rd ed.; Pergamon Press: New York, NY, USA, 1959; pp. 104–107. [Google Scholar]
- Murnaghan, F.D. Finite Deformations of an Elastic Solid; John Wiley: New York, NY, USA, 1951; pp. 60–66. [Google Scholar]
- Granato, A.V.; Lücke, K. The Vibrating String Model of Dislocation Damping. In Physical Acoustics; Mason, W.P., Ed.; Academic Press: New York, NY, USA, 1966; Volume 3, pp. 225–276. [Google Scholar]
- Cantrell, J.H.; Yost, W.T. Nonlinear ultrasonic characterization of fatigue microstructures. Int. J. Fatigue 2001, 23, 487–490. [Google Scholar] [CrossRef]
- Cantrell, J.H.; Yost, W.T. Acoustic harmonic generation from fatigue-induced dislocation dipoles. Philos. Mag. A 1994, 69, 315–326. [Google Scholar] [CrossRef]
- Mayergoyz, I.D. Hysteresis models from the mathematical and control theory points of view. J. Appl. Phys. 1985, 57, 3803–3805. [Google Scholar] [CrossRef]
- Gonzalez-Valadez, M.; Baltazar, A.; Dwyer-Joyce, R. Study of interfacial stiffness ratio of a rough surface in contact using a spring model. Wear 2010, 268, 373–379. [Google Scholar] [CrossRef]
- Wu, X.; Li, H.; Lv, W.; Zhang, S.; Zhang, D. Numerical analysis on acoustic nonlinear phenomena between rough contact interfaces. In Proceedings of the 2016 IEEE International Ultrasonics Symposium (IUS), Tours, France, 18–21 September 2016; pp. 1–4. [Google Scholar]
- An, Z.; Wang, X.; Deng, M.; Mao, J.; Li, M. A nonlinear spring model for an interface between two solids. Wave Motion 2013, 50, 295–309. [Google Scholar] [CrossRef]
- Takahashi, S.; Motegi, R. Measurement of third-order elastic constants and applications to loaded structural materials. SpringerPlus 2015, 4, 325. [Google Scholar] [CrossRef] [PubMed]
- Richardson, J.M. Harmonic generation at an unbonded interface—I. Planar interface between semi-infinite elastic media. Int. J. Eng. Sci. 1979, 17, 73–85. [Google Scholar] [CrossRef]
- Buck, O. Acoustic harmonic generation at unbonded interfaces and fatigue cracks. J. Acoust. Soc. Am. 1978, 33, 371–373. [Google Scholar]
- Cantrell, J.H.; Pan, E. Substructural organization, dislocation plasticity and harmonic generation in cyclically stressed wavy slip metals. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2004, 460, 757–780. [Google Scholar] [CrossRef]
- Cantrell, J.H.; Yost, W.T. Effect of precipitate coherency strains on acoustic harmonic generation. J. Appl. Phys. 1997, 81, 2957–2962. [Google Scholar] [CrossRef]
- Deng, M. Cumulative second-harmonic generation of Lamb-mode propagation in a solid plate. J. Appl. Phys. 1999, 85, 3051–3058. [Google Scholar] [CrossRef]
- Pei, J.; Deng, M. Assessment of accumulated fatigue damage in solid plates using nonlinear Lamb wave approach. Appl. Phys. Lett. 2007, 90, 121902. [Google Scholar]
- Shah, A.; Ribakov, Y. Non-linear ultrasonic evaluation of damaged concrete based on higher order harmonic generation. Mater. Des. 2009, 30, 4095–4102. [Google Scholar] [CrossRef]
- Yan-Xun, X.; Fu-Zhen, X.; Ming-Xi, D. Evaluation of Thermal Degradation Induced Material Damage Using Nonlinear Lamb Waves. Chin. Phys. Lett. 2010, 27, 016202. [Google Scholar] [CrossRef]
- Khelladi, H.; Rahmi, F. Perturbation methods for the spectral analysis of a weakly nonlinear acoustic field generated by a transient insonation. J. Acoust. Soc. Am. 2013, 19, 045079. [Google Scholar]
- Liu, G.; Jayathilake, P.G.; Khoo, B.C. Perturbation method for the second-order nonlinear effect of focused acoustic field around a scatterer in an ideal fluid. Ultrasonics 2014, 54, 576–585. [Google Scholar] [CrossRef] [PubMed]
- Momani, S.; Odibat, Z. Homotopy perturbation method for nonlinear partial differential equations of fractional order. Phys. Lett. A 2007, 365, 345–350. [Google Scholar] [CrossRef]
- Blackstock, D.T. Convergence of the Keck-Beyer Perturbation Solution for Plane Waves of Finite Amplitude in a Viscous Fluid. J. Acoust. Soc. Am. 1966, 39, 411–413. [Google Scholar] [CrossRef]
- Born, M. Dynamical Theory of Crystal Lattices. Am. J. Phys. 1955, 23, 474. [Google Scholar] [CrossRef]


| Parameters | Value | Unit |
|---|---|---|
| 109 | GPa | |
| −510 | GPa | |
| 28.6 | GPa | |
| b | 0.4 | mm |
| 0.33 | / | |
| R | 0.33 | / |
| 5 | nm | |
| 0.33 | / | |
| c | 6250 | m/s |
| 2700 | kg/m3 | |
| f | 1 | MHz |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyu, W.; Wu, X.; Xu, W. Nonlinear Acoustic Modeling and Measurements during the Fatigue Process in Metals. Materials 2019, 12, 607. https://doi.org/10.3390/ma12040607
Lyu W, Wu X, Xu W. Nonlinear Acoustic Modeling and Measurements during the Fatigue Process in Metals. Materials. 2019; 12(4):607. https://doi.org/10.3390/ma12040607
Chicago/Turabian StyleLyu, Wenhan, Xianmei Wu, and Weijiang Xu. 2019. "Nonlinear Acoustic Modeling and Measurements during the Fatigue Process in Metals" Materials 12, no. 4: 607. https://doi.org/10.3390/ma12040607
APA StyleLyu, W., Wu, X., & Xu, W. (2019). Nonlinear Acoustic Modeling and Measurements during the Fatigue Process in Metals. Materials, 12(4), 607. https://doi.org/10.3390/ma12040607





