Corrosion Investigation of Reinforced Concrete Based on Piezoelectric Smart Materials
Abstract
1. Introduction
2. Experiments
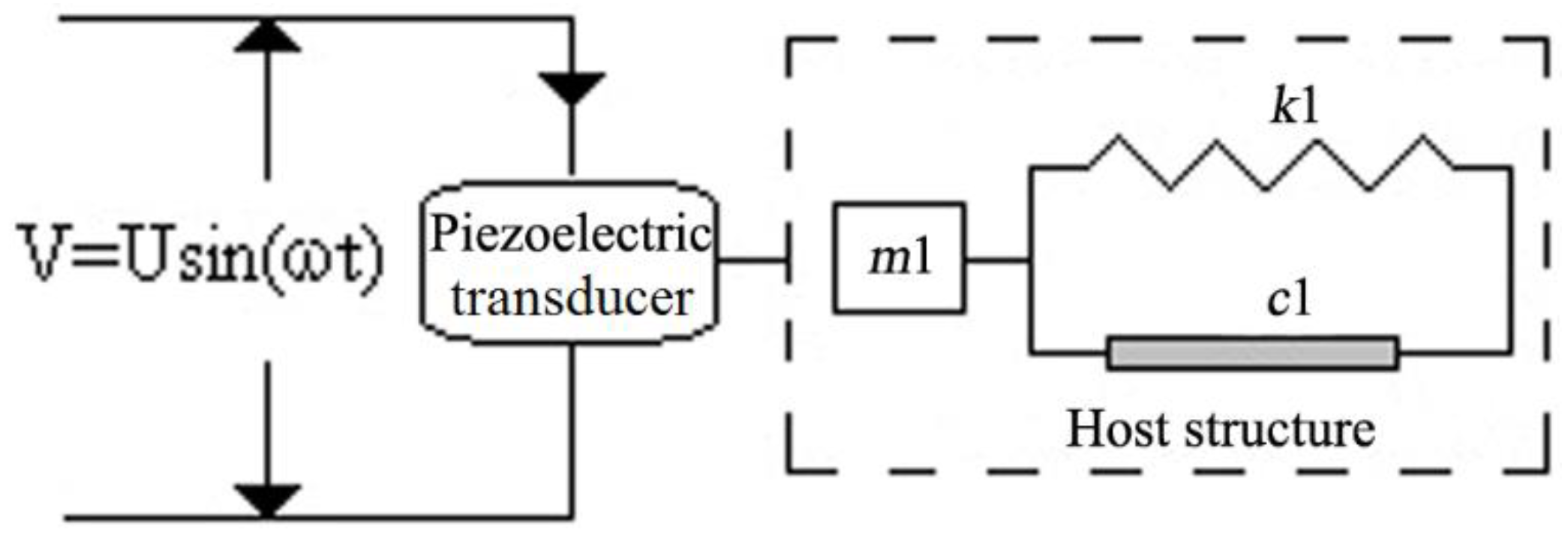
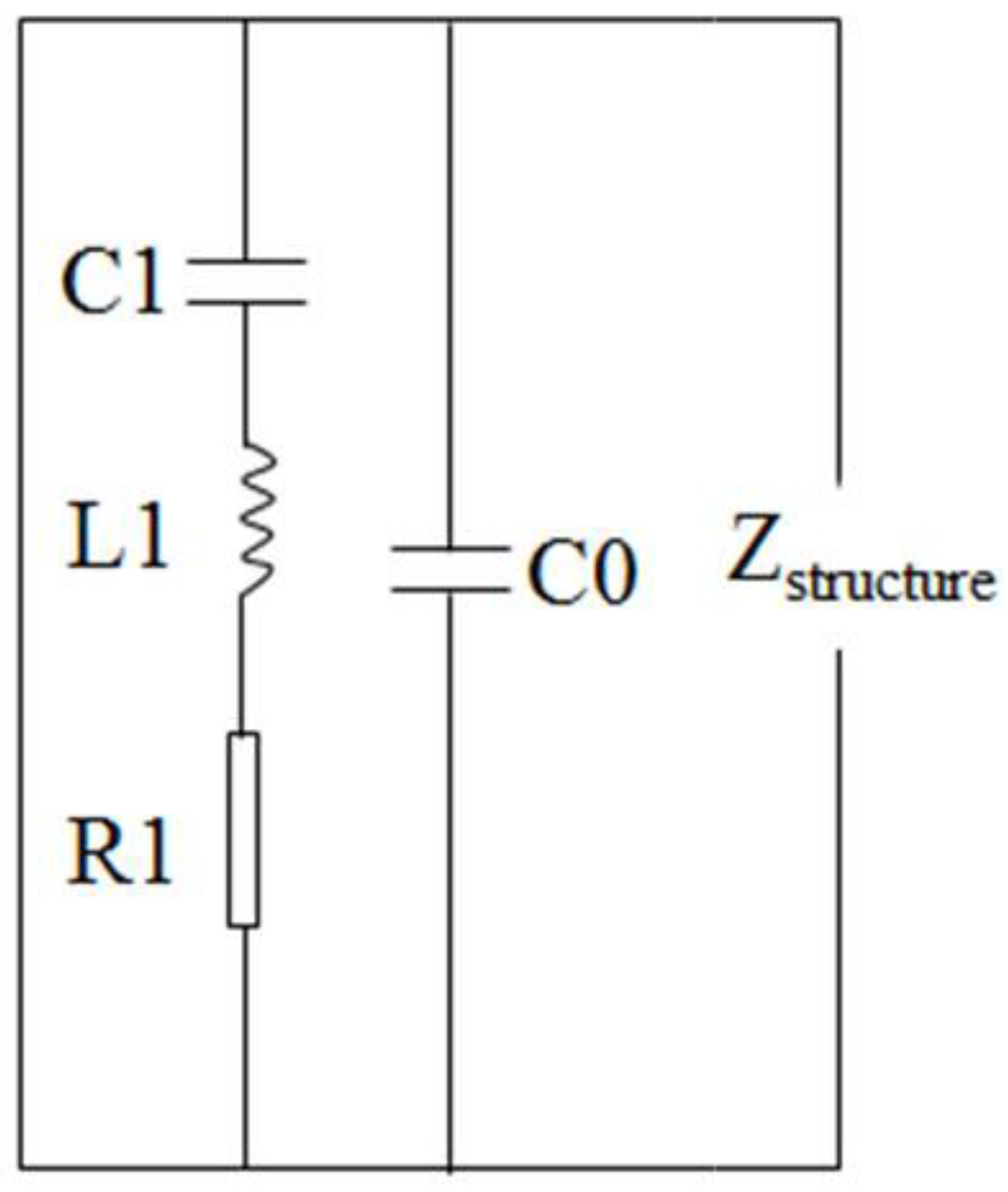
2.1. Principle of the Piezoelectric Impedance Technique
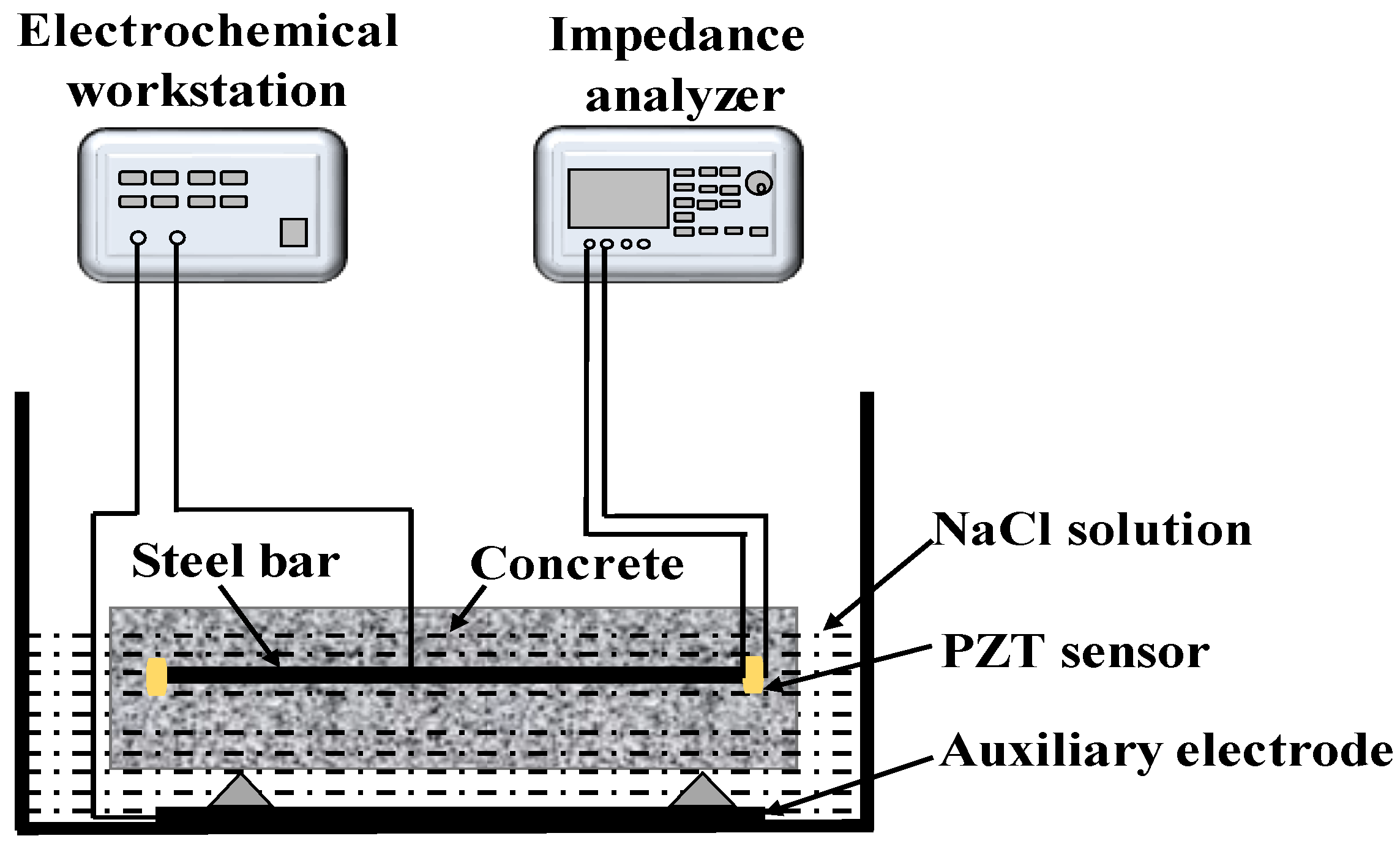
2.2. Corrosion Experiment of the Reinforcement Bar in Concrete
2.3. Electric Impedance Test of PZT Transducers
3. Results and Discussion
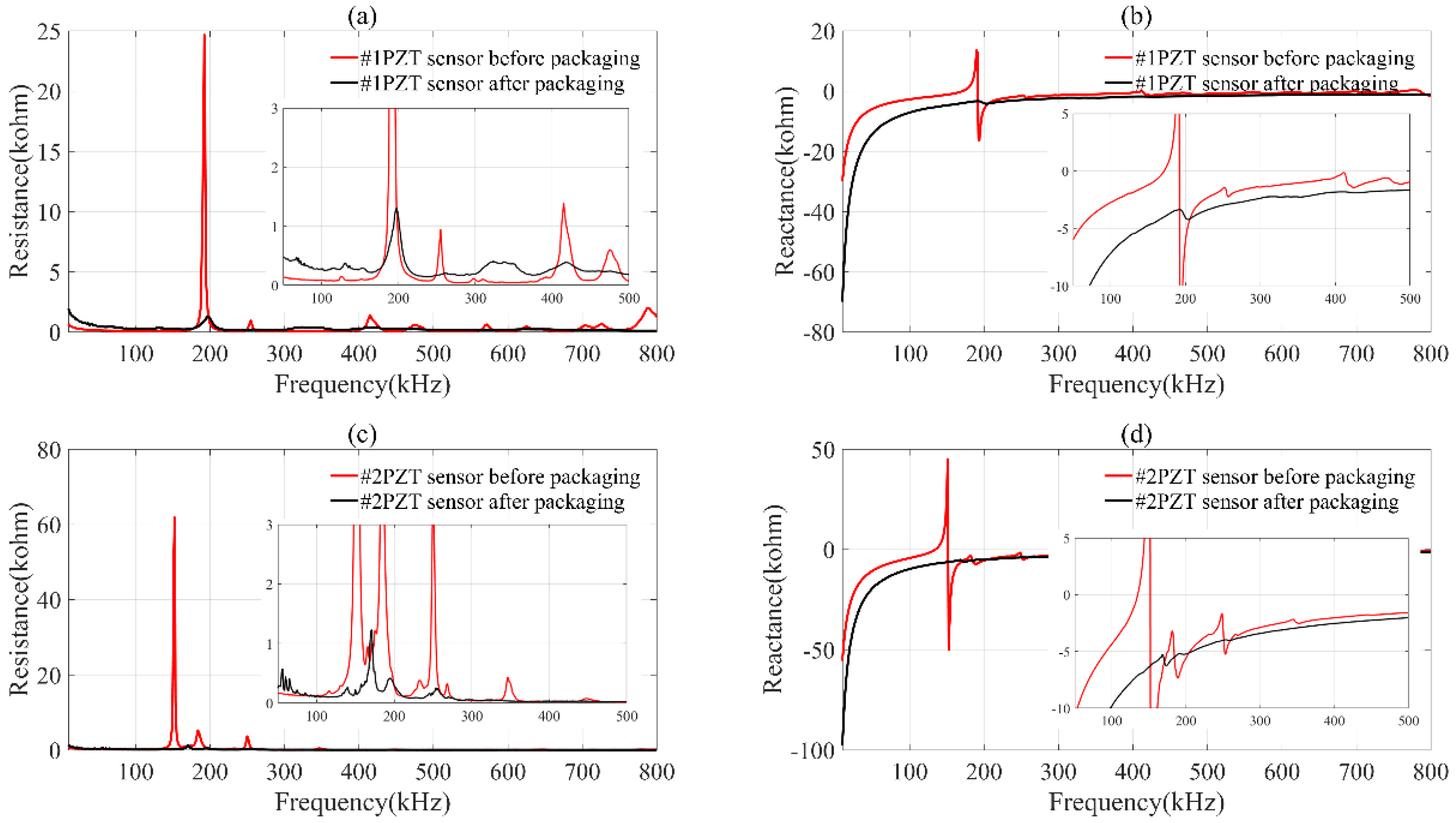
3.1. Impedance Spectra Comparison of PZT Transducers before and after Packaging
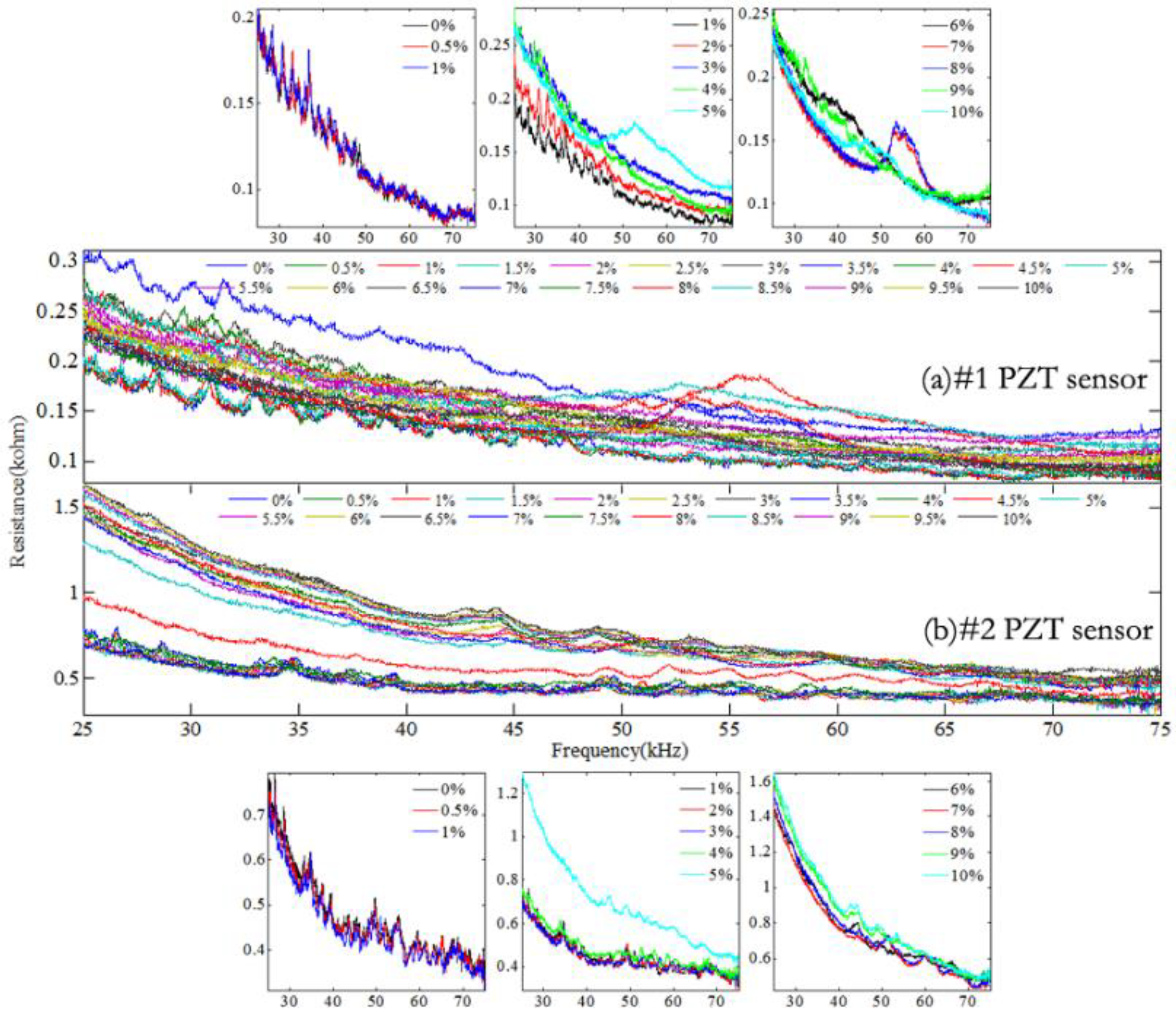
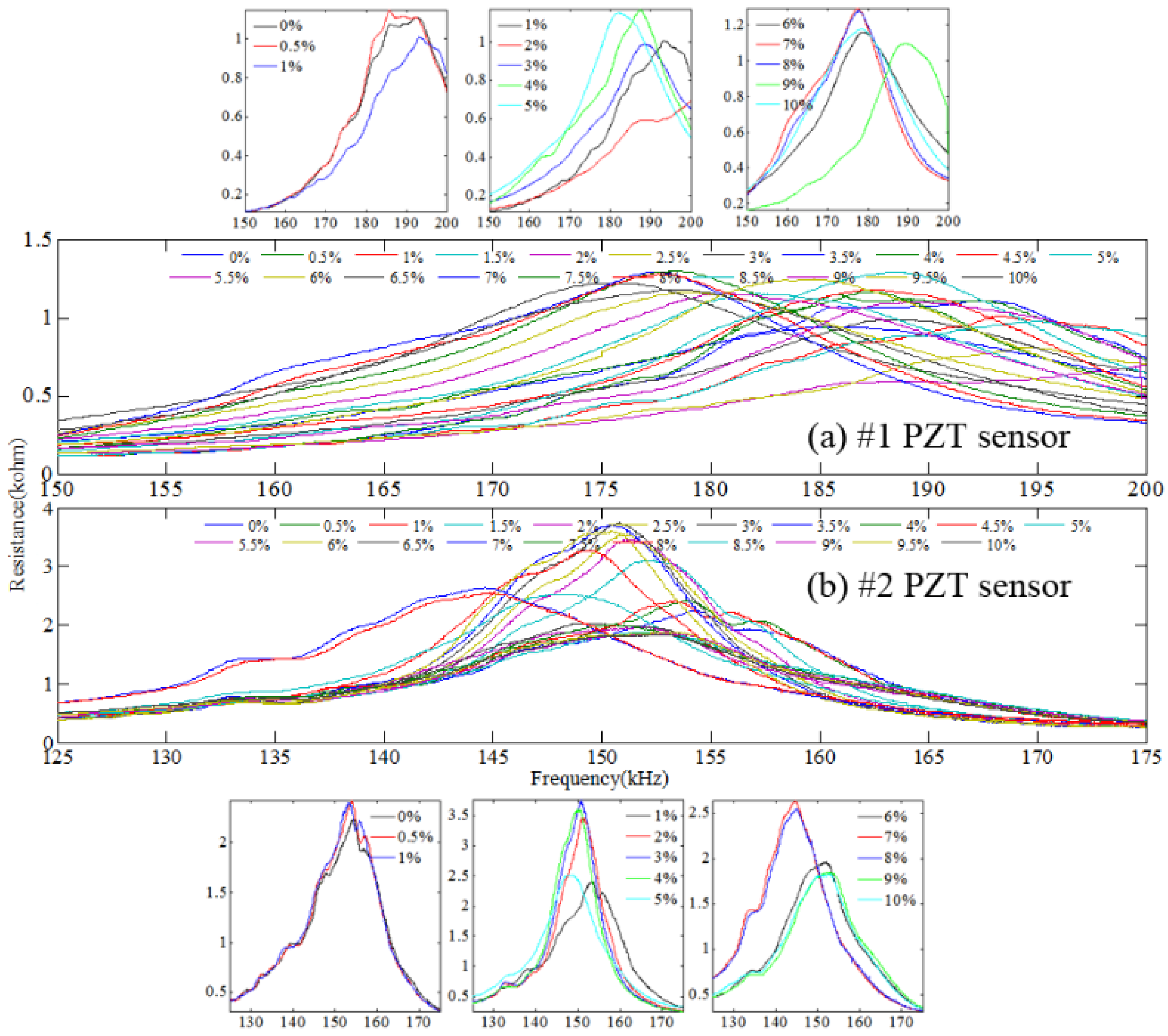
3.2. Impedance Spectra of PZT Transducers under Different Relative Mass Losses
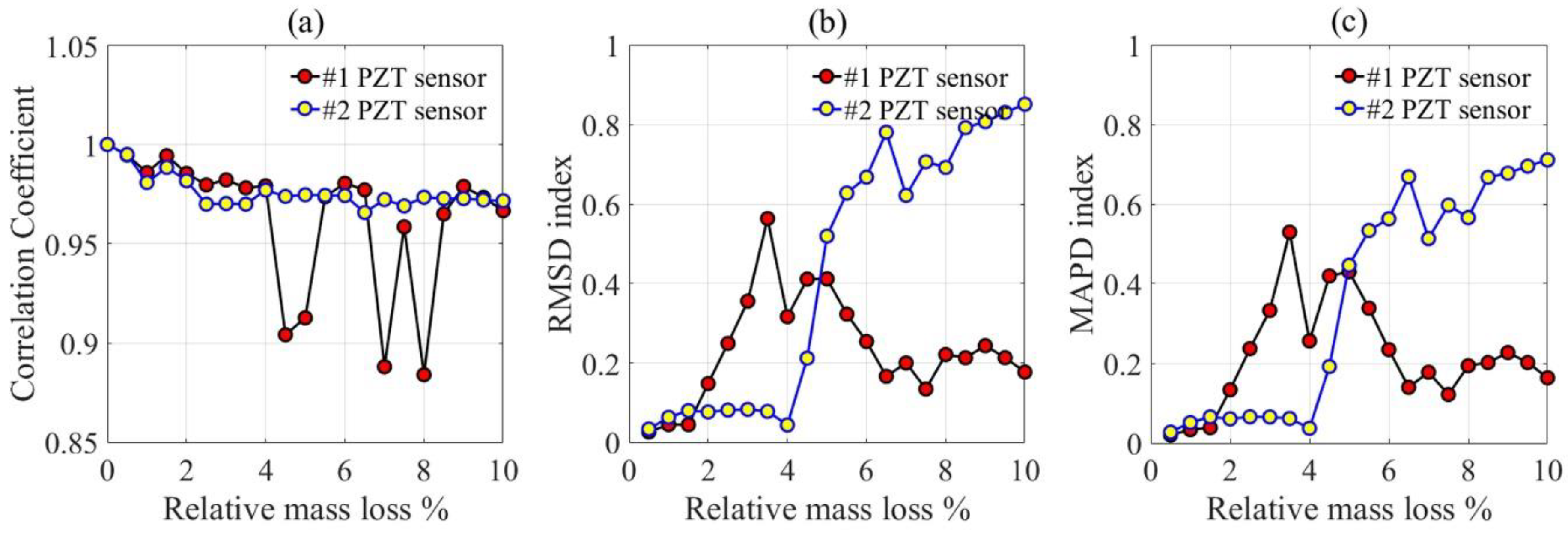
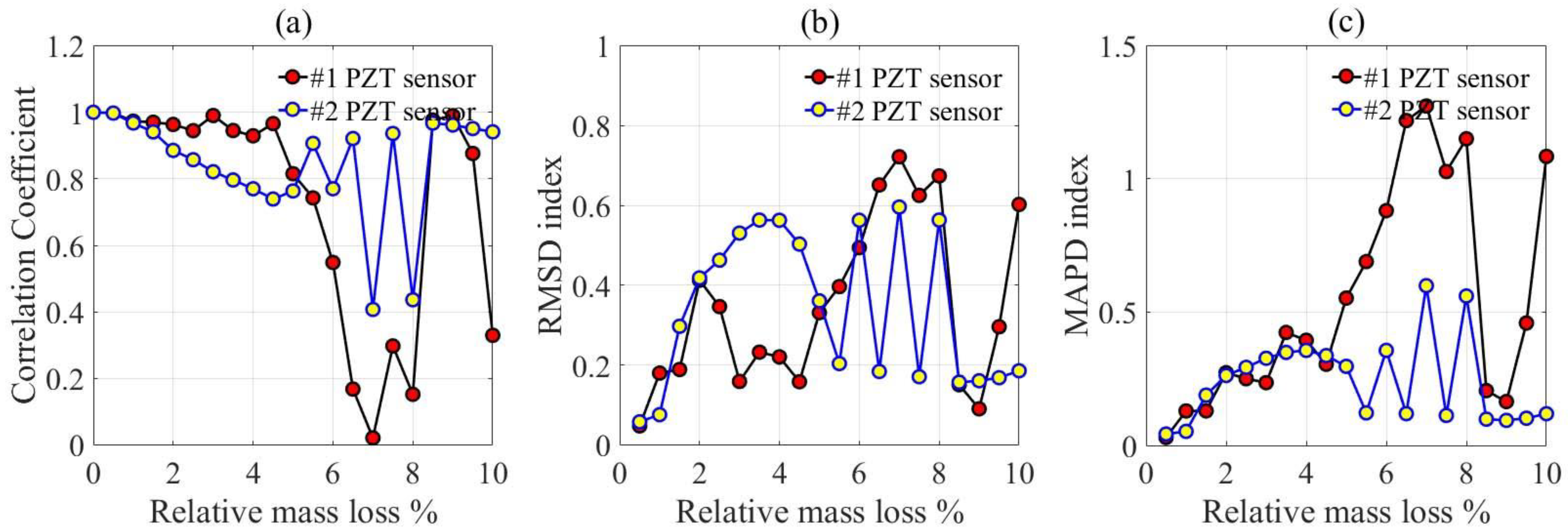
3.3. Statistical Analysis of Impedance Spectra
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Metha, P.K. Durability-critical issues for the future. Conc. Int. 1997, 19, 27–33. [Google Scholar]
- Cabrera, J.G. Deterioration of concrete due to reinforcement steel corrosion. Cement Conc. Comp. 1996, 18, 47–59. [Google Scholar] [CrossRef]
- Ahmad, S. Reinforcement corrosion in concrete structures, its monitoring and service life prediction-a review. Cement Conc. Comp. 2003, 25, 459–471. [Google Scholar] [CrossRef]
- Raupach, M. Chloride-induced macrocell corrosion of steel in concrete-theoretical background and practical consequences. Constr. Build. Mater. 1996, 10, 329–338. [Google Scholar] [CrossRef]
- Bertolini, L.; Gastaldi, M.; Pedeferri, M.P.; Redaelli, E. Prevention of steel corrosion in concrete exposed to seawater with submerged sacrificial anodes. Corros. Sci. 2002, 44, 1497–1513. [Google Scholar] [CrossRef]
- Isgor, O.B.; Razaqpur, A.G. Modelling steel corrosion in concrete structures. Mater. Struct. 2006, 39, 291–302. [Google Scholar] [CrossRef]
- Jung, W.Y.; Yoon, Y.S.; Sohn, Y.M. Predicting the remaining service life of land concrete by steel corrosion. Cement Conc. Res. 2003, 33, 663–677. [Google Scholar] [CrossRef]
- Kranc, S.C.; Sagüés, A.A. Computation of reinforcing steel corrosion distribution in concrete marine bridge substructures. Corrosion 1994, 50, 50–61. [Google Scholar] [CrossRef]
- Gonzalez, J.A.; Feliu, S.; Andrade, M.C. Confinement of electrical signal for in-situ measurement of polarization resistance in reinforced concrete. ACI Mater. J. 1990, 87, 457–460. [Google Scholar]
- Gaydecki, P.; Fernandes, B.; Quek, S.; Benitez, D.; Miller, G.; Zaid, M. Inductive and magnetic field inspection systems for rebar visualization and corrosion estimation in reinforced and pre-stressed concrete. Nondestruct. Test. Eva. 2007, 22, 255–298. [Google Scholar] [CrossRef]
- Idrissi, H.; Limam, A. Study and characterization by acoustic emission and electrochemical measurements of concrete deterioration caused by reinforcement steel corrosion. NDT E Int. 2003, 36, 563–569. [Google Scholar] [CrossRef]
- Weng, M.S.; Dunn, S.E.; Hartt, W.H.; Brown, R.P. Application of acoustic emission to detection of reinforcing steel corrosion in concrete. Corrosion 1982, 38, 9–14. [Google Scholar] [CrossRef]
- Fuhr, P.L.; Huston, D.R. Corrosion detection in reinforced concrete roadways and bridges via embedded fiber optic sensors. Smart Mater. Struct. 1998, 7, 217–228. [Google Scholar] [CrossRef]
- Bertolini, L.; Carsana, M.; Pedeferri, P. Corrosion behaviour of steel in concrete in the presence of stray current. Corros. Sci. 2007, 49, 1056–1068. [Google Scholar] [CrossRef]
- Hussaina, R.R.; Ishidab, T. Enhanced electro-chemical corrosion model for reinforced concrete under severe coupled action of chloride and temperature. Constr. Build. Mater. 2011, 25, 1305–1315. [Google Scholar] [CrossRef]
- Chen, W.; Du, R.G.; Ye, C.Q.; Zhu, Y.F.; Lin, C.J. Study on the corrosion behavior of reinforcing steel in simulated concrete pore solutions using in situ Raman spectroscopy assisted by electrochemical techniques. Electrochim. Acta 2010, 55, 5677–5682. [Google Scholar] [CrossRef]
- Song, G.; Gu, H.; Mo, Y.L.; Hsu, T.T.C.; Dhonde, H. Concrete structural health monitoring using embedded piezoceramic transducers. Smart Mater. Strut. 2007, 16, 959–968. [Google Scholar] [CrossRef]
- Lau, K.; Yuan, L.; Zhou, L.; Wu, J.; Woo, C. Strain monitoring in FRP laminates and concrete beams using FBG sensors. Compos. Struct. 2001, 51, 9–20. [Google Scholar] [CrossRef]
- Lee, H.K.; Lee, K.M.; Kim, Y.H.; Yim, H.; Bae, D.B. Ultrasonic in-situ monitoring of setting process of high-performance concrete. Cement Conc. Res. 2004, 34, 631–640. [Google Scholar] [CrossRef]
- Shin, S.W.; Oh, T.K. Application of electro-mechanical impedance sensing technique for online monitoring of strength development in concrete using smart PZT patches. Constr. Build. Mater. 2009, 23, 1185–1188. [Google Scholar] [CrossRef]
- Inci, P.; Goksu, C.; Ilki, A.; Kumbasar, N. Effects of reinforcement corrosion on the performance of RC frame buildings subjected to seismic actions. J. Perform. Constr. Fac. 2012, 27, 683–696. [Google Scholar] [CrossRef]
- Goksu, C.; Ilki, A. Seismic behavior of reinforced concrete columns with corroded deformed reinforcing bars. ACI Struct. J. 2016, 113, 1053–1064. [Google Scholar]
- Zhang, D.; Zhao, Y.; Jin, W.; Ueda, T.; Nakai, H. Shear strengthening of corroded reinforced concrete columns using pet fiber based composites. Eng. Struct. 2017, 153, 757–765. [Google Scholar] [CrossRef]
- Tracy, M.; Chang, F.K. Identifying impacts in composite plates with piezoelectric strain sensors, Part II: Experiment. J. Intel. Mater. Syst. Strut. 1998, 9, 929–937. [Google Scholar] [CrossRef]
- Soh, C.K.; Bhalla, S. Calibration of piezo-impedance transducers for strength prediction and damage assessment of concrete. Smart Mater. Strut. 2005, 14, 671–684. [Google Scholar] [CrossRef]
- Liang, C.; Sun, F.P.; Rogers, C.A. Electro-mechanical impedance modeling of active material systems. J. Intel. Mat. Syst. Strut. 1994, 21, 232–252. [Google Scholar] [CrossRef]
- Giurgiutiu, V.; Zagrai, A.; Bao, J.J. Piezoelectric wafer embedded active sensors for aging aircraft structural health monitoring. Struct. Health. Monit. 2002, 1, 41–61. [Google Scholar] [CrossRef]
- Xu, D.Y.; Huang, S.F.; Cheng, X. Electromechanical impedance spectra investigation of impedance-based PZT and cement/polymer based piezoelectric composite sensors. Constr. Build. Mater. 2014, 65, 543–550. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, W.; Chen, Y.; Liu, P.; Xu, D. Corrosion Investigation of Reinforced Concrete Based on Piezoelectric Smart Materials. Materials 2019, 12, 519. https://doi.org/10.3390/ma12030519
Shi W, Chen Y, Liu P, Xu D. Corrosion Investigation of Reinforced Concrete Based on Piezoelectric Smart Materials. Materials. 2019; 12(3):519. https://doi.org/10.3390/ma12030519
Chicago/Turabian StyleShi, Weihua, Ying Chen, Peng Liu, and Dongyu Xu. 2019. "Corrosion Investigation of Reinforced Concrete Based on Piezoelectric Smart Materials" Materials 12, no. 3: 519. https://doi.org/10.3390/ma12030519
APA StyleShi, W., Chen, Y., Liu, P., & Xu, D. (2019). Corrosion Investigation of Reinforced Concrete Based on Piezoelectric Smart Materials. Materials, 12(3), 519. https://doi.org/10.3390/ma12030519






