Abstract
Three series of binary, FeTi (Ti-rich), FeAl and TiAl (Al-rich) alloy samples were produced in an argon arc furnace. An annealing treatment of 72 h at 1000 °C was applied to the samples, giving rise to different equilibrium microstructures depending on chemical composition. Their mechanical properties were studied through the determination of elastic constants that measure the stiffness of the elaborated materials. Young’s modulus of the binary alloys was determined using Resonance Ultrasonic Vibration (RUV). The accuracy of this technique was demonstrated. A scanning electron microscope (SEM) with an energy dispersive spectrometer (EDS) and X-ray diffraction (XRD) made it possible to identify intermetallic compounds FeTi and Ti, FeAl and Fe, and TiAl and Ti in respective systems Fe–Ti, Fe–Al, and Ti–Al. The link between their composition, microstructure, and elastic properties was established.
1. Introduction
The development of the intermetallic alloys Ti–Al, Fe–Al and Fe–Ti is essentially related to the properties and performance of these materials compared to steel’s constituent pure elements, namely, iron, titanium, aluminum, and for some uses, nickel-based superalloys. Indeed, economic reasons (reduction of costs) and industrial reasons (reduction of material density or environmental nuisances) explain why they are highly sought after by certain industries, in particular, aeronautics industries. Today, they are used for properties such as friction resistance, hardness, and high-temperature and corrosion resistance [1,2,3]. As a result, Ti–Al alloys are potential materials for the aerospace, chemical, and energy industries [4,5]. Fe–Ti alloys have excellent resistance to friction, and are widely used in the automotive industry [6]. Fe–Ti and Fe–Al alloys have particular advantages: they are very affordable raw materials, and they have low density, excellent corrosion resistance, even in aggressive environments, and good mechanical properties [7,8].
The influence of different microstructures on macroscopic mechanical properties has been the subject of numerous studies [9,10,11]. Ti–Al alloys have a fully lamellar microstructure and offer a good balance between mechanical properties such as elasticity at room temperature [4,12]. The mechanical properties of Fe–Al and Fe–Ti alloys are not only influenced by the chemical composition contained in the alloy, but also by the dendritic microstructure formed in intermetallic alloys [13]. The main microstructural constituent formed during the solidification process of single- or dual-phase Fe-based intermetallic alloys is the dendritic microstructure [14]. The dendritic microstructure plays an important role in giving better mechanical properties, such as elasticity and hardness [6]. This study focuses on the effect of alloy microstructures on the mechanical properties. The microstructure is strongly linked to the mechanical properties; therefore, its identification and the determination of its influence on the different phases and on the phase diagrams are important [15]. The literature reports a number of studies where the Young’s modulus of the studied alloys in the present work was experimentally determined using nanoindentation, and very few using ultrasonic vibration (see Table 1).

Table 1.
Existing mechanical (elastic modulus) data in the literature for the studied alloys and methods employed to obtain them.
Studies linking the microstructure and Young’s modulus obtained using acoustic methods are scarce.
Many theoretical and experimental methods are available to evaluate elastic constants, including the ab initio method used to theoretically predict mechanical properties. The ab initio method is based on density functional theory (DFT), which is used to perform quantum calculations of the solid’s electronic structure. This is the approach that was employed to explore the relationship between chemical composition and elastic properties. Experimentally, the Resonant Ultrasonic Vibration (RUV) method was developed in this study and used to recover Young’s modulus of the alloys. These constants can be easily calculated knowing Hooke’s law [22,23]. A variant of the method developed in this study is Resonant Ultrasound spectroscopy (RUS), which is an accurate and efficient method for characterizing the elasticity of isotropic or anisotropic solid materials [24]. RUS often involves the use of shear-wave type piezoelectric transducers (PZT) making dry-point contact with the sample’s corners (corners are used because they provide elastically weak coupling, reducing loading). However, sample sizes in RUS are often very small (typically between 1.0 mm and 1.0 cm in size). The Lagrangian minimization (the Rayleigh–Ritz variational method) is the most used in RUS analyses for forward problems [22,23].
In this part of our work, the objective was to identify the formed phases in the series of binary alloys being investigated and understand their solidification microstructures (their phase distribution, compositions, and morphologies). This allows control of solidification and the industrial development of viable alloys, together with the determination of their mechanical properties and of the effect of the microstructure on their elasticity, the elastic properties, that is, Young’s modulus here. These binary alloys guide the choice of ternary grades that might be promising solutions to overcoming problems arising during the development or use of industrial alloy Fe–Al or intermetallic base Ti–Al. The effect of the chemical composition on Young’s modulus was also highlighted.
2. Materials and Methods
The set of binary alloys, Ti–Fe, Ti–Al and Fe–Al, were synthesized using pure metals (Fe → 99.98%, Ti → 99.99%, Al → 99.98%), in an arc furnace under argon flow. The purity of the argon (Ar) gas used to prepare the alloys was 99.9999%. In order to ensure good homogeneity of the samples, the fusion process was repeated four times for each. Verification of the nominal composition after elaboration was performed using X-ray fluorescence spectrometry (XRF) (Horiba XGT-5000, Kyoto, Japan). This XRF apparatus typically covers all elements, from Sodium (Na) to Uranium (U), (Z Na = 11 to Z U = 92). Each chemical element present in the alloy, ranging from Na to U is characterized by two essential peaks, K and K. The K peak is more intense than the K peak. The intensity of each characteristic radiation is directly related to the amount of each element in the material. Once composition was verified, our alloys were annealed for 72 h at 1000 °C (heating rate 20 °C/min) and then cooled (slow cooling rate of 5 °C/min), which gave them their physicochemical, mechanical, and structural balance. Thus, the obtained structure is that reported on the equilibrium diagrams at room temperature (part of another study). They were then prepared and polished for observation. This was achieved using a scanning electron microscope coupled with a dispersive energy spectrometer (SEM-EDS) (Fei QUANTA 600-EDAX, Hillsboro, Oregon, USA). An X-ray diffractometer (Bruker D8 Advance, Billerica, MA, USA) was used to identify the formed phases using the following parameters: voltage 40 keV, intensity 30 mA, , and CuK = 1.54056 Å.
3. Preparation of Disc Surfaces for Mechanical Characterization
Prior to experimental analysis, the disc samples were first shaped so that the diameter-to-thickness ratio was approximately 4 (for simplicity of analysis of the experimental data). They were then polished using sheets of sandpaper with different grit sizes (240, 400, 600, 800, and 1200), resulting in well-polished surfaces and well-adjusted sample sizes, with a diameter of 14 ± 0.5 mm and thickness of 3 ± 0.5 mm.
Configuration with Piezoelectric Discs
The configuration employed two thin piezoelectric transducer (PZT) discs. The PZT discs were retrieved from the resonators of the piezoelectric audio transducers used as sounders. Since their response characteristics were not known beforehand, three different discs were tested on the specimens and their responses evaluated to obtain the best choice for the experiment. They were referenced as KPEG827, KPEG110, KPEG165 (Kingstate, Taipei, Taiwan), with diameters of 25, 20, and 10 mm, respectively. Two thin PZT discs were necessary and had the same diameter. The first PZT disc was used as the exciter and the second as sensor to capture the spectral vibration response of the metal sample. The carefully polished metal-disc alloy sample was placed between the pair of PZT transducer discs. The PZT disc, Kingstate KPEG 110, 20 mm diameter, gave the best response for the tested samples. The experimental setup diagram and photograph are shown in Figure 1. A lock amplifier (Signal Recovery 7265 DSP, Oak Ridge, TN, USA) was employed to drive the exciter in discrete frequency steps. Thin double-sided adhesive tape was used to assure good contact between the two flat surfaces of the sample and the PZT. The PZT disc and sample taped to it were then suspended to ensure stressfree vibrations, i.e., without constraint (Figure 1). The adhesive tape was cut to exactly fit PZT-disc size in order to limit the impact of damping on the measurements that the tape may add. The sample was then excited using continuous harmonic stimulation, realizing a frequency sweep (frequency, 50–250 kHz in 200 Hz steps). The response was captured by the second piezoelectric disc connected to a low-noise amplifier (EO80dB, Ciprian, Grenoble, France). Rotation of the alloy-disc sample in several directions was performed to confirm the similarity of vibration response spectra, verify the isotropy of the samples, and confirm the repeatability and consistency of the obtained experimental data.
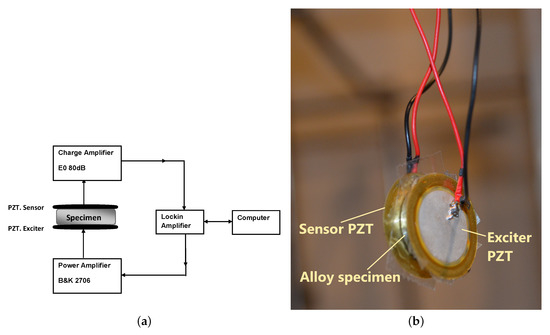
Figure 1.
(a) Diagram and (b) photography of the setup employed for the vibration spectroscopy experimental setup.
4. Ingredients for Estimating Alloy-Disc-Sample Elastic Modulus
To simplify mechanical behavior analysis, the alloy samples in this study were considered as equivalent single-crystal elastic bodies. Their mechanical behavior was accurately captured using the elastodynamic model of an anisotropic elastic solid. Two elastodynamic models of vibration were candidates for solving the direct problem; the first incorporated more physical and geometric information on the sample, but required more intensive computations. The second model was not computationally intensive and was chosen as a candidate to solve the inverse problem, which was the recovery of Young’s modulus and Poisson ratio from the resonance frequencies of the samples. The second model was validated using the first model. The first model was then used to finely adjust the two parameters that had been identified through solving the inverse problem.
4.1. First Model for Solving Direct Problem
The choice of the correct model for solving the direct problem is a key issue for the validation of data retrieved from experimental measurements. The inversion process can be one in which a set of computed observables, in this case, eigenfrequencies, are used to calculate a succession of trial values of the sought for parameters of the configuration from experimental data. In such a process, there is need to compute the resonance frequencies of a given structure configuration and then compare them with the measured resonance frequencies of the test sample to recover its elastic modulus and Poisson ratio. In this study, the computed eigenfrequencies were obtained using an interaction model based on the finite element method. They were then compared with the experimental resonance frequencies recovered from the measured spectral response. This permitted the retrieval of the optimal values of the elastic modulus and Poisson ratio that were recovered by the second model. Precisely, the computations were done in three dimensions (3D) using an elastodynamic finite-element method (FEM) [25,26] implemented in commercial software Abaqus (version 6.14, Dassault Systèmes Simulia Corporation, Providence, RI, USA) [27]. This constituted the first interaction model.
4.2. Second Model for Solving Direct Problem
The resonance frequencies resulting from harmonic excitation applied to the sample, a thick circular disc, were computed using a quasianalytic model. This model was developed by Martinceck [28] and has also been adopted in the standard testing method [29]. The model equation defines the relationship between resonance frequency, and the elastic properties of the material and dimensions of the disc-shaped sample. It is written as follows:
where is the resonance frequency (i = 1, 2), is the geometry factor for the resonance frequency, r is the radius of the disc, disc constant , E is Young’s modulus, t is disc thickness, is the Poisson ratio, and is the density. In this study, the ratio was equal to 0.42.
4.3. Solving the Inverse Problem of Vibrational Spectroscopy
The second interaction model equation was rewritten in order to retrieve Young’s modulus as a function of resonance frequency. The expression calculated from Equation (1) is rewritten as:
This quasianalytical equation makes the inversion process instantaneous. The geometric factors computed for the ratio = 0.42 are = 4.6356 and = 7.3284. Poisson ratio read from nomograms [28] in terms of ratio = 0.4 and resonance-frequency ratio (for most alloys in this study) was . The Poisson ratio was initialized using this value. Once Young’s modulus and Poisson ratio were recovered, they were injected into the sophisticated 3D FEM to calculate the resonance frequencies, which were then compared to the measured frequencies. The values of Young’s moduli and Poisson ratios were further adjusted so that the RUV experimental frequencies and those generated by the 3D FEM matched. These were then the parameter values considered as final.
4.4. Identification and Classification of Vibration Modes in the Response Spectrum
A simple argument was employed to resolve the issue of identifying the modes of vibration corresponding to the observed spectral vibration peaks. The elastic properties of an alloy depend on the crystallographic structure, which depends on the chemical composition of the alloy (see Table 4). The eigenvalues of one of the components of the metallic alloy of the disc sample composed of single crystals were computed. These provided orientation where the first, second, and third modes would be situated in the vibration spectrum. The elastic moduli of the single-crystal components from ab initio computation for pure metals that make up the alloy, and parameters such as density and Poisson ratio, were employed. The values for the single crystal were from the literature; therefore, computations were completed for confirmation and to evaluate the different first-principle DFT-method calculation tools. For titanium, density functional theory using the projector augmented-wave (PAW) method in Quantum Espresso associated with the Exciting [30,31] package was employed. The mechanical parameters were then injected into the 3D finite-element model to calculate the eigenfrequencies and plot mode shapes/deformation. The identification of mode types was also theoretically confirmed. A 3D elastodynamic finite-element direct-solution steady-state dynamic analysis was used to calculate the steady-state dynamic linearized response of the disc submitted to a concentrated harmonic-force excitation [32]. The concentrated force was applied at the center of the disc to only excite longitudinal modes as confirmed in the computed response [33]. In a second step, force was applied to the edge of the disc to excite all modes. This enabled the identification of mode types (whether shear or longitudinal) captured in the vibration spectrum.
5. Results
5.1. XRF Analysis
The XRF analysis results are listed in Table 2. The average compositions of the different binary alloys, obtained by XRF, were fairly close to the nominal compositions, as shown by the results of the analysis carried out on the alloy (Figure 2).

Table 2.
Effective compositions of the studied binary alloys obtained by X-ray fluorescence (XRF) analysis.
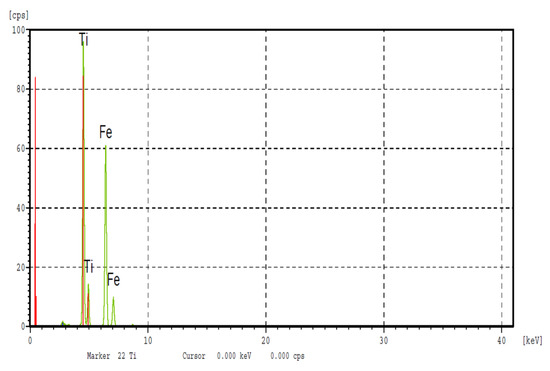
Figure 2.
Fluorescence analysis of the XRF alloy.
5.2. Energy Dispersive Spectrometer (EDS) Analysis
The nominal chemical compositions of the various binary alloys were verified. The effective levels of Fe, Ti, and Al were provided by EDS analysis and are listed in Table 3, in which we also reported the chemical compositions of the different observed phases in each of the studied alloys here.

Table 3.
Effective compositions of the studied alloys obtained by Energy Dispersive Spectrometer (EDS) analysis.
5.3. Phase Identification
The diffractograms of the various FeTi, FeAl, and TiAl binary alloys are shown in Figure 3a–c, respectively. The different identified phases, as well as the crystalline structures and their literature references for each phase, are listed in Table 4.
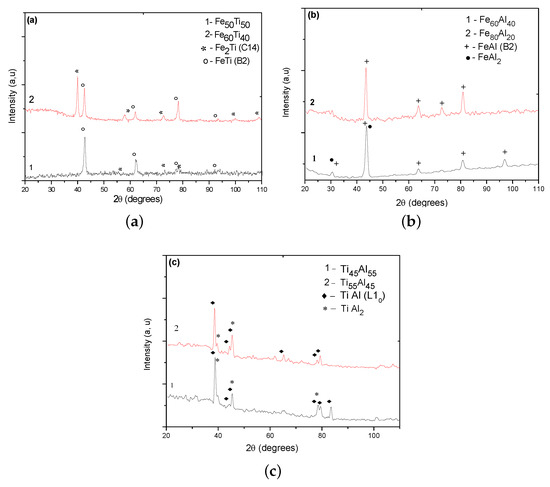
Figure 3.
Diffractograms of the studied binary alloys: (a) FeTi, (b) FeAl, (c) TiAl.

Table 4.
Identified phases and corresponding crystal structures.
5.4. Metallography
To confirm the phases found by X-ray diffraction (XRD) analysis, we studied the morphology of the phases formed in the binary alloys (annealed at 1000 °C for 72 h at a heating rate of 20 °C/min) by scanning electron microscopy (SEM). Mcrostructures are depicted in Figure 4.

Figure 4.
Scanning electron microscopy (SEM) micrographs of binary alloys of respective compositions (percent by weight): (a) , (b) , (c) , (d) .
5.5. Vibration Modes
In order to calculate the Young’s modulus of the alloys in disc form, it was important to identify the modes of vibration to which the first and second resonance frequencies corresponded (Section 4.4), as illustrated by the mode shapes in Figure 5.
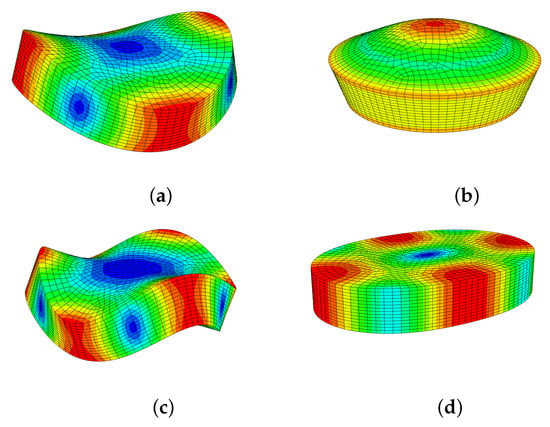
Figure 5.
Natural vibration mode shapes of the thick discs: (a) first flexural mode (≈70 kHz—Table 4); (b) first compressional mode (≈110 kHz); (c) second flexural mode (≈134 kHz); (d) first wine-glass mode (≈165 kHz).
The results of the computation of the resonance frequencies of the single-crystal elements and the Young’s moduli found in the literature (from ab initio calculations) are given in Table 5. These results guided the choice of the first and second resonance family of modes from the spectral vibrational response of the alloy-disc specimens.

Table 5.
Mechanical properties calculated by an ab initio method (density functional theory), and resonance frequencies of single-crystal metals computed using the 3D finite-element method (, ). and are the recovered Young’s moduli (in GPa) using synthetic resonance frequencies (, ) and the second interaction model (Equation (2)).
Figure 6 shows the positions of peaks corresponding to different modes of vibration, occurring by the excitation of piezoelectric crystals stuck onto the sample. The peaks appear sharp and well-defined with respect to the spectra obtained by the piezoelectric discs.
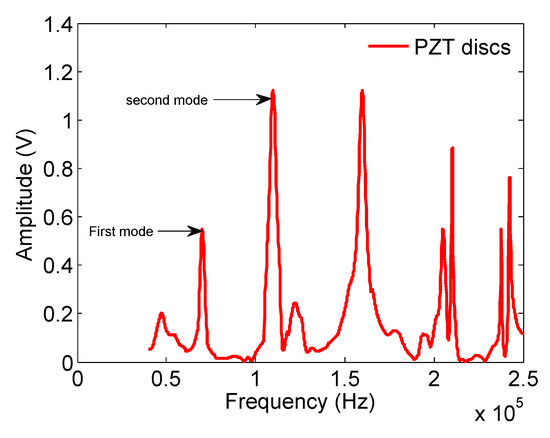
Figure 6.
Vibration spectrum obtained using piezoelectric-disc transducers for the binary disc sample composition (percentage by weight).
The final step of the inversion procedure was to obtain the elastic modulus and Poisson ratio of all alloy samples. This was achieved by minimizing the differences between the measured spectral responses and the calculated responses of the two models, which consisted of calculating the error percentages between the results of the two configuration methods as well as the experimental values obtained with the 3D finite-element method.
The recovered values of Young’s modulus and Poisson ratio obtained from calculations are shown in Table 5.
6. Discussion
6.1. Fe–Ti Binary Alloys
The diffractograms of Fe–Ti alloys (Figure 3a) show the existence of two Fe–Ti and Ti phases in the alloy. However, only the Fe–Ti phase is revealed with certainty. Indeed, two lines of very low intensities relative to Ti were found in this sample, whereas, in , where Ti is unambiguously highlighted. At this stage of the investigation, only the Fe–Ti phase was clearly identified in our two samples at a time. The microstructures of the and binary alloys (Figure 4a,b) showed Ti phase dendrites surrounded by interdendritic Fe–Ti phase space. This might suggest that the Fe–Ti phase appears after the Ti phase. In this case, it would probably result from a peritectic-type reaction, which would then be written as L + Ti ↔ FeTi, as predicted by the FeTi binary diagram [43]. EDS analysis (Figure 4b) revealed the chemical compositions of each of the Fe–Ti and Ti phases and confirmed their formation in the two studied alloys, even if X-ray diffraction only allowed the identification of Ti in the alloy. All of our results are in perfect agreement with what we can obtain using the Fe–Ti diagram given by Reference [44]. Moreover, our measurements of the densities of these alloys (Table 4) did not show any significant influence of the substitution of iron by titanium.
6.2. Fe–Al Binary Alloys
As for Fe–Al binary alloys, X-ray diffraction strongly indicated the presence of a Fe–Al phase (Figure 3b). However, some lines could be assigned to Fe–Al and Fe at the same time, which means that we cannot ignore the presence of Fe. In Fe–Al alloys, a dendritic structure was observed thanks to EDS analysis (Figure 4d). It was identified as Fe–Al and a fine eutectic structure Fe/Fe–Al structure localised in the interdentritic space, where Fe–Al is in the form of lamellae and Fe occupies the rest of the interdendritic space. Moreover, we could not detect the presence of the Al phase, widely coveted in the industry. In terms of lightening, it has been shown previously that density decreases with aluminum content [45], which was aimed at in the first place in the choice of our compositions. However, it was previously noted [46] that problems arise in the production of high-aluminum Fe–Al alloys, hence the use of vacuum or powder-metallurgy techniques. These problems include excessive metal oxidation, and the occurrence of significant internal stresses on parts, resulting in cracks and porosities. None of these problems was encountered during the development of our samples, partly because it was performed under an inert atmosphere (under argon) to prevent the evaporation of aluminum and the formation of oxides. It was also because we ensured the absence of oxide layers by stripping our metals just before shade elaboration, onto which we imposed slow cooling (rate 5 °C/min). Indeed, we, at no stage of the analysis, noted the presence of oxide in our alloys, porosity, or cracks. However, we could not rule out the possibility that a ceramic film was formed on the surface of our samples, given the high aluminum content when subjected to an oxidizing medium. This layer would then have the role of improving samples’ resistance to corrosion. On the other hand, the role of iron substitution by aluminum in Fe–Al alloys is shown in Table 4, which shows that density decreased by 28% when aluminum content increased by 24%.
6.3. Ti–Al Binary Alloys
As for Ti–Al alloys with a high aluminum content, the formation of two Ti–Al and Ti intermetallics in and (Figure 3b) were clearly shown. At this stage of the investigation, it seems difficult to decide on the stability of intermetallic. Indeed, this compound formed as Ti–Al in the “as-cast condition” and in those having undergone 72 h of annealing. Figure 4c is a typical microstructure of the Ti–Al alloys that we studied. It shows the existence of a two-phase structure, composed of Ti–Al lamellae in a matrix, itself lamellar, which has not been observed before. It is important to point out that a Ti–Al structure is highly dependent on the heat treatment of our alloys. In previous work [47] on aluminum-rich Ti–Al alloys, two types of duplex or lamellar Ti–Al and Ti (stable) microstructures were obtained following the appropriate heat treatment. In crude-cast alloys, precipitates of the metastable Ti and phases are often observed in the Ti–Al matrix, but are transformed into Ti–Al by heating at 900 °C. In this case, we also did not note the presence of oxides, pores, or cracks in our samples. The characteristic temperatures of predicted phase transitions only agreed well with the experimentally observed ones at high temperatures [48]. In this study, it was highlighted that the total substitution of Fe by Ti strongly affects the density of the studied alloys. They became lighter compared with the previous intermetallic base alloys (Fe–Ti and Fe–Al) (Table 4). Thus, the alloys became lighter and probably improved in corrosion resistance since Ti–Al and Ti both have a much better resistance to oxidation than [49].
6.4. Retrieved Young’s Modulus Values
Alloy composition and content result in microstructural adjustment and, therefore, improvement of the mechanical properties. Yield and ultimate strengths, Young’s modulus, and creep resistance are drastically enhanced, and the high-temperature limit is also expanded [48]. In this study, we focused on the microstructure and Young’s modulus.
Before starting the discussion about a mechanical property (Young’s modulus) of aluminum-rich alloys, it should be noted that very few researchers have ventured to study this type of alloy for the problems mentioned earlier regarding their elaboration. The results reported in Table 6 show that Young’s modulus values, calculated from the spectra obtained using the piezoelectric discs, are very close to the final estimated values obtained by adjusting the parameters in the 3D finite-element model. Thus, and by way of example, the Young’s modulus of the and alloys are 201.44 and 199.56 GPa for frequencies corresponding to and , respectively. The error ratio in all cases does not exceed 1% (Table 6), and the values are very close to the measured Young’s modulus of 200 GPa in Reference [2]. The similarity of and confirms that frequencies and are of the same family, and also that our alloys were homogeneous. By examining the results of Fe–Al binary alloys, it can be seen that, when Al content increases, the modulus decreases. In this case, two compounds are formed; one rich in aluminum, Fe (small volume fraction) and the other rich in iron, Fe–Al, which could possibly explain this decrease compared with pure iron and steel, since the Young’s modulus is closely related to the bonds between atoms and the atomic stack [50]. Young’s modulus values for the and alloys are, respectively, 165.92 and 163.70 GPa, compared with those of titanium and its alloys [51] and that of Ti–Al (160 GPa). One might think that Ti also contributes to this increase given its volume fraction. However, given the scarcity of data concerning this intermetallic alloy, it is still difficult to estimate its contribution. These results show that the addition of titanium aluminum significantly increases the elastic modulus. The respective values of the Young’s modulus for and alloys are 191.57 and 183.47 GPa. This shows that titanium lowers the rigidity of iron. Thus, the higher the titanium content is, the more its modulus decreases. Note that all of the values obtained with the method developed herein are close to those found in the literature [18]. As a result, alloys with a dendritic to lamellar microstructure (Figure 4) have the highest Young’s modulus, which explains why the microstructure plays an important role in the elasticity of materials.

Table 6.
Resonance frequencies (, ) recovered from vibration spectra obtained using piezoelectric-disc transducers and the corresponding Young’s moduli (, ), retrieved using Equation (2). Final 3D finite-element method (FEM) Young’s moduli (E) after adjustment to fit experimental resonance frequencies. The difference between and E is given as a percentage. The indicates ab initio calculated results found in the literature. Values of = 4.6356, = 7.3284, and initial = 0.27.
7. Conclusions
In this work, a series of binary alloys, Fe–Al, Ti–Al (all rich in aluminum), and Fe–Ti (titanium-rich) were developed by fusion in an argon arc furnace using pure metals, etched just before fabrication. The important precautions taken in the solidification process revealed that, for aluminum-rich alloys, the formation of oxides, porosities, and cracks, so much feared when Al content is important, was avoided. As a result, the intermetallic Ti in TiAl alloys, whose properties are not well-known, were formed.
Fe–Ti and Ti, Ti–Al and Ti, Fe–Al and Fe phases were identified, respectively, in the Fe–Ti, Ti–Al, and Fe–Al alloys, for which the microstructures were described. The density obtained for each of the alloys did not seem to be affected by the substitution of iron with titanium, but was moderately affected when aluminum replaced titanium. However, density dropped dramatically when titanium, in the presence of aluminum, replaced iron. The experimental method of Resonance Ultrasonic Vibration, combined with theoretical approaches, were used to determine Young’s modulus of binary alloys (Fe–Al, Fe–Ti, and Ti–Al) with different chemical compositions and microstructures (dendritic, lamellar). It was found that dendritic microstructures had a higher Young’s modulus than lamellar ones. These measurements also helped reveal the isotropy of the material. This conclusion was only possible because it was found that, for all tested samples, the Young’s modulus values determined using the method agreed with the modulus retrieved using resonance frequencies and 3D finite-element formulation for the isotropic elastic model.
The accuracy of the nondestructive method developed herein using piezoelectric discs has been demonstrated by comparing the recovered Young’s modulus with those from already published results, and particularly those from first-principle calculations. The method permitted to conclude that the elaborated alloy samples were homogeneous. The mastery of the elaboration process, as well as the study of the mechanical properties and corrosion resistance of these intermetallic base alloys, appeals to the optimization of the parameters in order to find the best combination of composition and properties. This provides for the possibility of applying Al-rich Ti–Al alloys, substituted for iron and/or other elements, as alloys having high performance at high temperatures. The idea of producing a Ti–Al-like microstructure was used in the second part of our current study, which is based on the results obtained from Fe–Ti, Fe–Al, and Ti–Al binary studies.
Author Contributions
D.C. and E.O. conceived, designed, performed the experiments, and wrote the paper; Z.E.A.F. contributed the analysis tools; S.E.A. and L.A.A., funding acquisition.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank the Algerian government for the grant that supported D. Chanbi during his stay at LMA, Marseilles, France, and finally B. Mourot of LMA for helping with the administrative paper work.
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Zamanzade, M.; Barnoush, A.; Motz, C. A Review on the Properties of Iron Aluminide Intermetallics. Crystals 2016, 6, 10. [Google Scholar] [CrossRef]
- Moret, F.; Baccino, R.; Martel, P.; Guetaz, L. Propriétés et applications des alliages intermétalliques B2-FeAl. J. Phys. IV Fr. 1996, 06, C2-281–C2-289. [Google Scholar] [CrossRef]
- Meshram, S.; Mohandas, T.; Reddy, G.M. Friction welding of dissimilar pure metals. J. Mater. Process. Technol. 2007, 184, 330–337. [Google Scholar] [CrossRef]
- He, W.W.; Tang, H.P.; Liu, H.Y.; Jia, W.P.; Liu, Y.; Yang, X. Microstructure and tensile properties of containerless near-isothermally forged TiAl alloys. Trans. Nonferrous Met. Soc. China 2011, 21, 2605–2609. [Google Scholar] [CrossRef]
- Kim, Y.W. Intermetallic alloys based on gamma titanium aluminide. JOM 1989, 41, 24–30. [Google Scholar] [CrossRef]
- Barbier, D.; Huang, M.; Bouaziz, O. A novel eutectic Fe-15 wt.% Ti alloy with an ultrafine lamellar structure for high temperature applications. Intermetallics 2013, 35, 41–44. [Google Scholar] [CrossRef]
- Stoloff, N. Iron aluminides: Present status and future prospects. Mater. Sci. Eng. A 1998, 258, 1–14. [Google Scholar] [CrossRef]
- Hartig, C.; Yoo, M.H.; Koeppe, M.; Mecking, H. Effect of temperature on elastic constants and deformation behavior in shear tests of Fe-30%Al single crystals. Mater. Sci. Eng. A 1998, 258, 59–64. [Google Scholar] [CrossRef]
- Skrotzki, W.; Kegler, K.; Tamm, R.; Oertel, C.G. Grain structure and texture of cast iron aluminides. Cryst. Res.Technol. 2005, 40, 90–94. [Google Scholar] [CrossRef]
- Ikeda, O.; Ohnuma, I.; Kainuma, R.; Ishida, K. Phase equilibria and stability of ordered BCC phases in the Fe-rich portion of the Fe-Al system. Intermetallics 2001, 9, 755–761. [Google Scholar] [CrossRef]
- Cebulski, J.; Lalik, S. Changes in the structure of alloy on the matrix of FeAl intermetallic phase after primary crystallization and homogenizing treatment. J. Mater. Process. Technol. 2005, 162–163, 4–8. [Google Scholar] [CrossRef]
- Engelier, C.; Béchet, J. Transformations structurales dans l’alliage de titane, β-CEZ études des mécanismes de précipitation après traitement de mise en solution. J. Phys. IV Fr. 1994, 04, 111–116. [Google Scholar] [CrossRef]
- Palm, M.; Sauthoff, G. Deformation Behaviour and Oxidation Resistance of Single-Phase and Two-Phase L21 Fe-Al-Ti Alloys. Intermetallics 2004, 12, 1345–1359. [Google Scholar] [CrossRef]
- Ruan, Y.; Mohajerani, A.; Dao, M. Microstructural and Mechanical-Property Manipulation through Rapid Dendrite Growth and Undercooling in an Fe-based Multinary Alloy. Sci. Rep. 2016, 6, 31684. [Google Scholar] [CrossRef] [PubMed]
- Bendjeddou, L.; Debili, M. Structure and Hardness of Al-Fe-Ti Alloys. In Defects and Diffusion in Metals XII; Defect and Diffusion Forum; Trans Tech Publications: Zürich, Switzerland, 2010; Volume 305, pp. 23–32. [Google Scholar]
- Brotzu, A.; Felli, F.; Marra, F.; Pilone, D.; Pulci, G. Mechanical properties of a TiAl-based alloy at room and high temperatures. Mater. Sci. Technol. 2018, 34, 1847–1853. [Google Scholar] [CrossRef]
- He, Y.; Schwarz, R.; Migliori, A.; Whang, S. Elastic constants of single crystal γ–TiAl. J. Mater. Res. 1995, 10, 1187–1195. [Google Scholar] [CrossRef]
- Wen, Y.; Wang, L.; Liu, H.; Song, L. Ab Initio Study of the Elastic and Mechanical Properties of B19 TiAl. Crystals 2017, 7, 39. [Google Scholar] [CrossRef]
- Liebertz, J.; Stähr, S.; Haussühl, S. Growth and properties of single crystals of FeTi. Krist. Tech. 1980, 15, 1257–1260. [Google Scholar] [CrossRef]
- Harmouche, M.R.; Wolfenden, A. Temperature and Composition Dependence of Young’s Modulus for Ordered B2 Polycrystalline CoAl and FeAI. Mater. Sci. Eng. 1986, 84, 35–42. [Google Scholar] [CrossRef]
- Zhang, C.H.; Huang, S.; Shen, J.; Chen, N.X. Structural and mechanical properties of Fe-Al compounds: An atomistic study by EAM simulation. Intermetallics 2014, 52, 86–91. [Google Scholar] [CrossRef]
- Migliori, A.; Sarrao, J.L.; Visscher, W.M.; Bell, T.; Lei, M.; Fisk, Z.; Leisure, R.G. Resonant ultrasound spectroscopic techniques for measurement of the elastic moduli of solids. Phys. B Condens. Matter 1993, 183, 1–24. [Google Scholar] [CrossRef]
- Migliori, A.; Maynard, J.D. Implementation of a modern resonant ultrasound spectroscopy system for the measurement of the elastic moduli of small solid specimens. Rev. Sci. Instrum. 2005, 76, 121301. [Google Scholar] [CrossRef]
- Bernard, S.; Grimal, Q.; Laugier, P. Resonant ultrasound spectroscopy for viscoelastic characterization of anisotropic attenuative solid materials. J. Acoust. Soc. Am. 2014, 135, 2601. [Google Scholar] [CrossRef] [PubMed]
- Hughes, T.J.R. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis; Dover Civil and Mechanical Engineering, Dover Publications: New York, NY, USA, 2012. [Google Scholar]
- Ogam, E.; Fellah, Z.; Ogam, G. Identification of the mechanical moduli of closed-cell porous foams using transmitted acoustic waves in air and the transfer matrix method. Compos. Struct. 2016, 135, 205–216. [Google Scholar] [CrossRef]
- ABAQUS Theory Manual, v6.14 ed.; Hibbitt, Karlsson, Sorensen: Pawtucket, RI, USA, 2014.
- Martinček, G. The determination of poisson’s ratio and the dynamic modulus of elasticity from the frequencies of natural vibration in thick circular plates. J. Sound Vib. 1965, 2, 116–127. [Google Scholar] [CrossRef]
- ASTM E1876-01(2006). Standard Test Method for Dynamic Young’s Modulus, Shear Modulus, and Poisson’s Ratio by Impulse Excitation of Vibration; ASTM International: West Conshohocken, PA, USA, 2006. [Google Scholar]
- Gulans, A.; Kontur, S.; Meisenbichler, C.; Nabok, D.; Pavone, P.; Rigamonti, S.; Sagmeister, S.; Werner, U.; Draxl, C. Exciting: A full-potential all-electron package implementing density-functional theory and many-body perturbation theory. J. Phys. Condens. Matter 2014, 26, 363202. [Google Scholar] [CrossRef] [PubMed]
- Golesorkhtabar, R.; Pavone, P.; Spitaler, J.; Puschnig, P.; Draxl, C. ElaStic: A tool for calculating second-order elastic constants from first principles. Comput. Phys. Commun. 2013, 184, 1861–1873. [Google Scholar] [CrossRef]
- Ogam, E.; Wirgin, A.; Schneider, S.; Fellah, Z.; Xu, Y. Recovery of elastic parameters of cellular materials by inversion of vibrational data. J. Sound Vib. 2008, 313, 525–543. [Google Scholar] [CrossRef]
- Chanbi, D.; Ogam, E.; Amara, S.E.; Fellah, Z.E. Synthesis and Mechanical Characterization of Binary and Ternary Intermetallic Alloys Based on Fe-Ti-Al by Resonant Ultrasound Vibrational Methods. Materials 2018, 11, 746. [Google Scholar] [CrossRef]
- Palm, M.; Lacaze, J. Assessment of the Al-Fe-Ti system. Intermetallics 2006, 14, 1291–1303. [Google Scholar] [CrossRef]
- Rigaud, V. Contribution à L’étude De La Solidification Et à La Description Thermodynamique des éQuilibres de Phases du Système Quaternaire Fe-Al-Ti-Zr. Ph.D. Thesis, Université de Lorraine, Vandoeuvre-les-Nancy, France, 2009. [Google Scholar]
- Kwiatkowska, M.; Zasada, D.; Bystrzycki, J.; Polański, M. Synthesis of Fe-Al-Ti Based Intermetallics with the Use of Laser Engineered Net Shaping (LENS). Materials 2015, 8, 2311–2331. [Google Scholar] [CrossRef]
- Agote, I.; Coleto, J.; Gutiérrez, M.; Sargsyan, A.; de Cortazar, M.G.; Lagos, M.; Borovinskaya, I.; Sytschev, A.; Kvanin, V.; Balikhina, N.; et al. Microstructure and mechanical properties of gamma TiAl based alloys produced by combustion synthesis+compaction route. Intermetallics 2008, 16, 1310–1316. [Google Scholar] [CrossRef]
- Connétable, D.; Maugis, P. First principle calculations of the k-Fe3AlC perovskite and iron aluminium intermetallics. Intermetallics 2008, 16, 345–352. [Google Scholar] [CrossRef]
- Friàk, M.; Hickel, T.; Körmann, F.; Udyansky, A.; Dick, A.; von Pezold, J.; Ma, D.; Kim, O.; Counts, W.; Šob, M.; et al. Determining the Elasticity of Materials Employing Quantum-mechanical Approaches: From the Electronic Ground State to the Limits of Materials Stability. Steel Res. Int. 2011, 82, 86–100. [Google Scholar] [CrossRef]
- Zhu, L.F.; Friák, M.; Udyansky, A.; Ma, D.; Schlieter, A.; Kühn, U.; Eckert, J.; Neugebauer, J. Ab initio based study of finite-temperature structural, elastic and thermodynamic properties of FeTi. Intermetallics 2014, 45, 11–17. [Google Scholar] [CrossRef]
- Friák, M.; Counts, W.; Ma, D.; Sander, B.; Holec, D.; Raabe, D.; Neugebauer, J. Theory-Guided Materials Design of Multi-Phase Ti-Nb Alloys with Bone-Matching Elastic Properties. Materials 2012, 5, 1853–1872. [Google Scholar] [CrossRef]
- Sai, S.V.; Satyanarayana, R.S.M.; Murthy, B.K.V.; Rao, S.G.; Prasad, S.A. An Experimental Simulation to Validate FEM to Predict Transverse Young’s Modulus of FRP Composites. Adv. Mater. Sci. Eng. 2013, 2013, 648527. [Google Scholar] [CrossRef]
- Pande, M.M.; Guo, M.; Blanpain, B. Inclusion Formation and Interfacial Reactions between FeTi Alloys and Liquid Steel at an Early Stage. ISIJ Int. 2013, 53, 629–638. [Google Scholar] [CrossRef]
- Nagai, H.; Kitagaki, K.; Shoji, K. Microstructure and hydriding characteristics of FeTi alloys containing manganese. J. Less Common Met. 1987, 134, 275–286. [Google Scholar] [CrossRef]
- Sarreal, J.; Koch, C. Metastable microstructures of rapidly solidified and undercooled Fe-Al-C and Fe-(Ni,Mn)-Al-C alloys. Mater. Sci. Eng. A 1991, 136, 141–149. [Google Scholar] [CrossRef]
- Bednarczyk, I.; Kuc, D.; Niewielski, G. Influence of Cumulative Plastic Deformation on Microstructure of the Fe-Al Intermetallic Phase Base Alloy. Arch. Metall. Mater. 2014, 59, 987–991. [Google Scholar] [CrossRef]
- Guo, F. Influence of Microstructure on the Mechanical Properties And Internal Stresses of a Two-Phase TiAl-Based Alloy. Ph.D. Thesis, Arts et Métiers ParisTech, Paris, France, 2001. [Google Scholar]
- Kartavykh, A.; Asnis, E.; Piskun, N.; Statkevich, I.; Stepashkin, A.; Gorshenkov, M.; Akopyan, T. Complementary thermodynamic and dilatometric assessment of phase transformation pathway in new β-stabilized TiAl intermetallics. Mater. Lett. 2017, 189, 217–220. [Google Scholar] [CrossRef]
- Kelm, K.; Irsen, S.; Paninski, M.; Drevermann, A.; Schmitz, G.J.; Palm, M.; Stein, F.; Engberding, N.; Heilmaier, M.; Saage, H.; et al. Characterization of the Microstructure of Al-rich TiAl-Alloys by Combined TEM Imaging Techniques. Microsc. Microanal. 2007, 13, 294–295. [Google Scholar] [CrossRef]
- Matysik, P.; Jóźwiak, S.; Czujko, T. Characterization of Low-Symmetry Structures from Phase Equilibrium of Fe-Al System–Microstructures and Mechanical Properties. Materials 2015, 8, 914–931. [Google Scholar] [CrossRef] [PubMed]
- Nazarova, T.; Imayev, V.; Imayev, R.; Fecht, H.J. Study of microstructure and mechanical properties of Ti-45Al-(Fe,Nb) (at.%) alloys. Intermetallics 2017, 82, 26–31. [Google Scholar] [CrossRef]
- Acharyan, N.; Fatima, B.; Chouhan, S.S.; Sanyal, S.P. First Principles Study on Structural, Electronic, Elastic and Thermal Properties of Equiatomic MTi (M = Fe, Co, Ni). Chem. Mater. Res. 2013, 3, 22–30. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).