Mode Conversion of the Edge Modes in the Graphene Double-Ribbon Bend
Abstract
1. Introduction
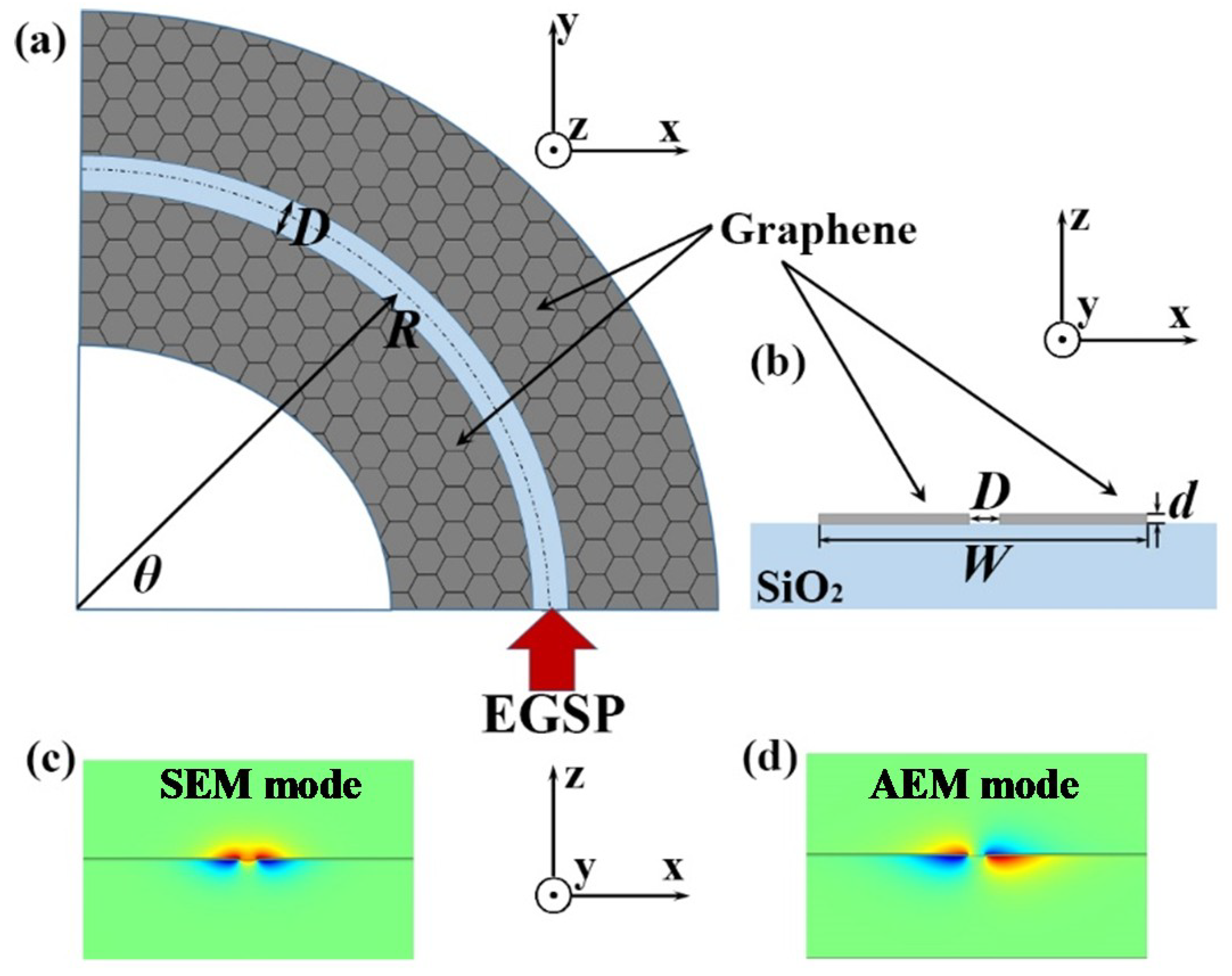
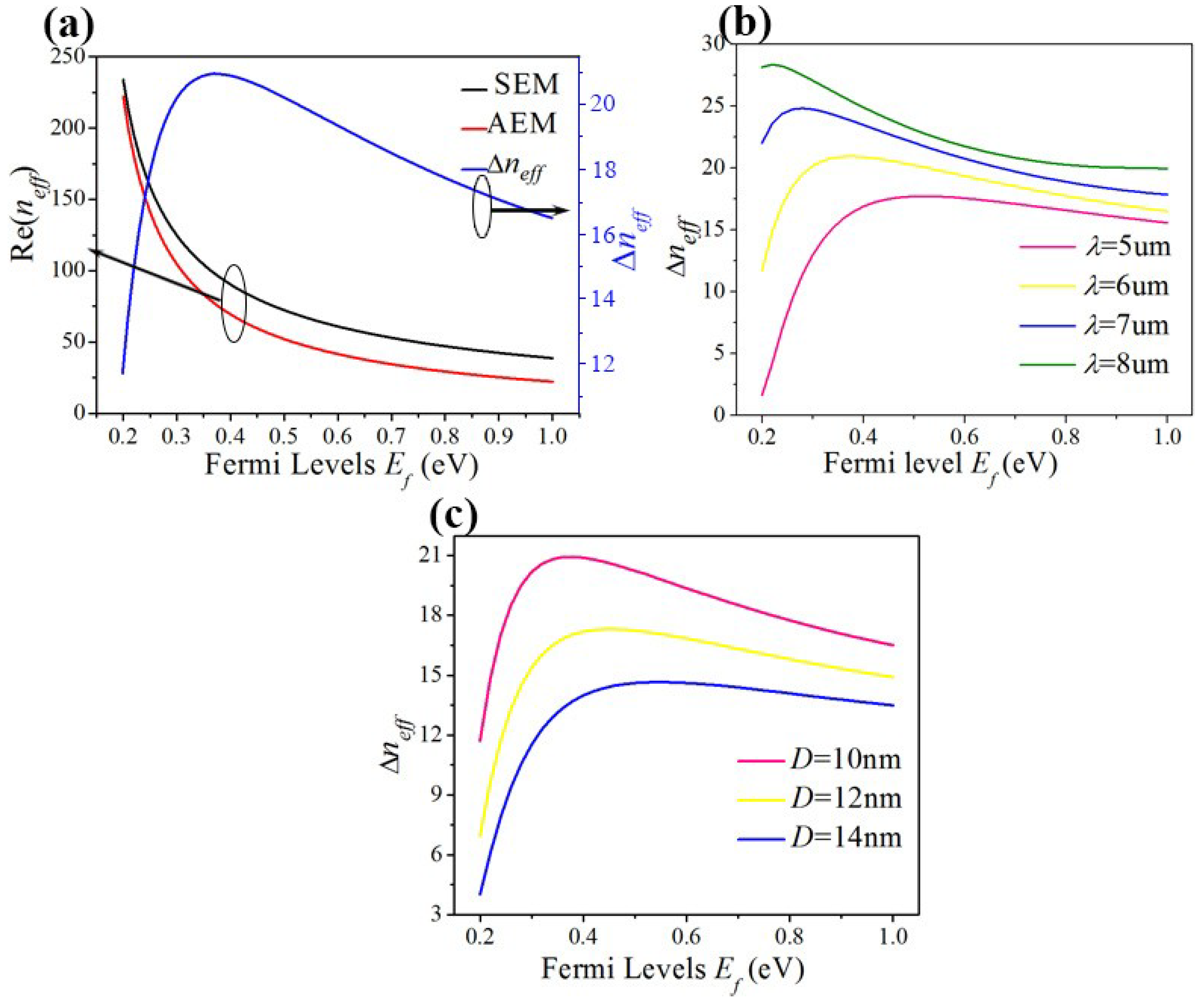
2. Structure and EGSPs Dispersion
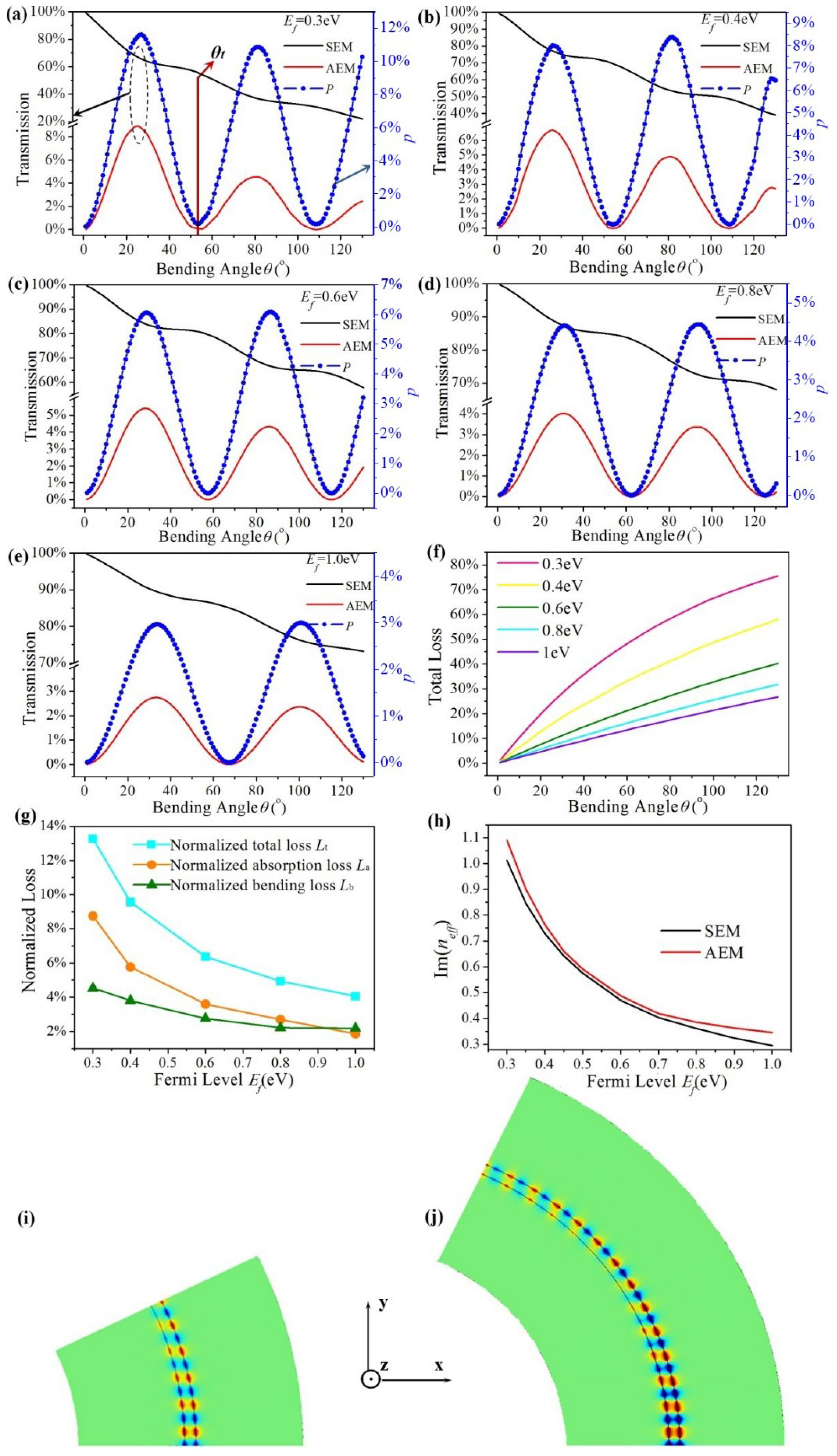
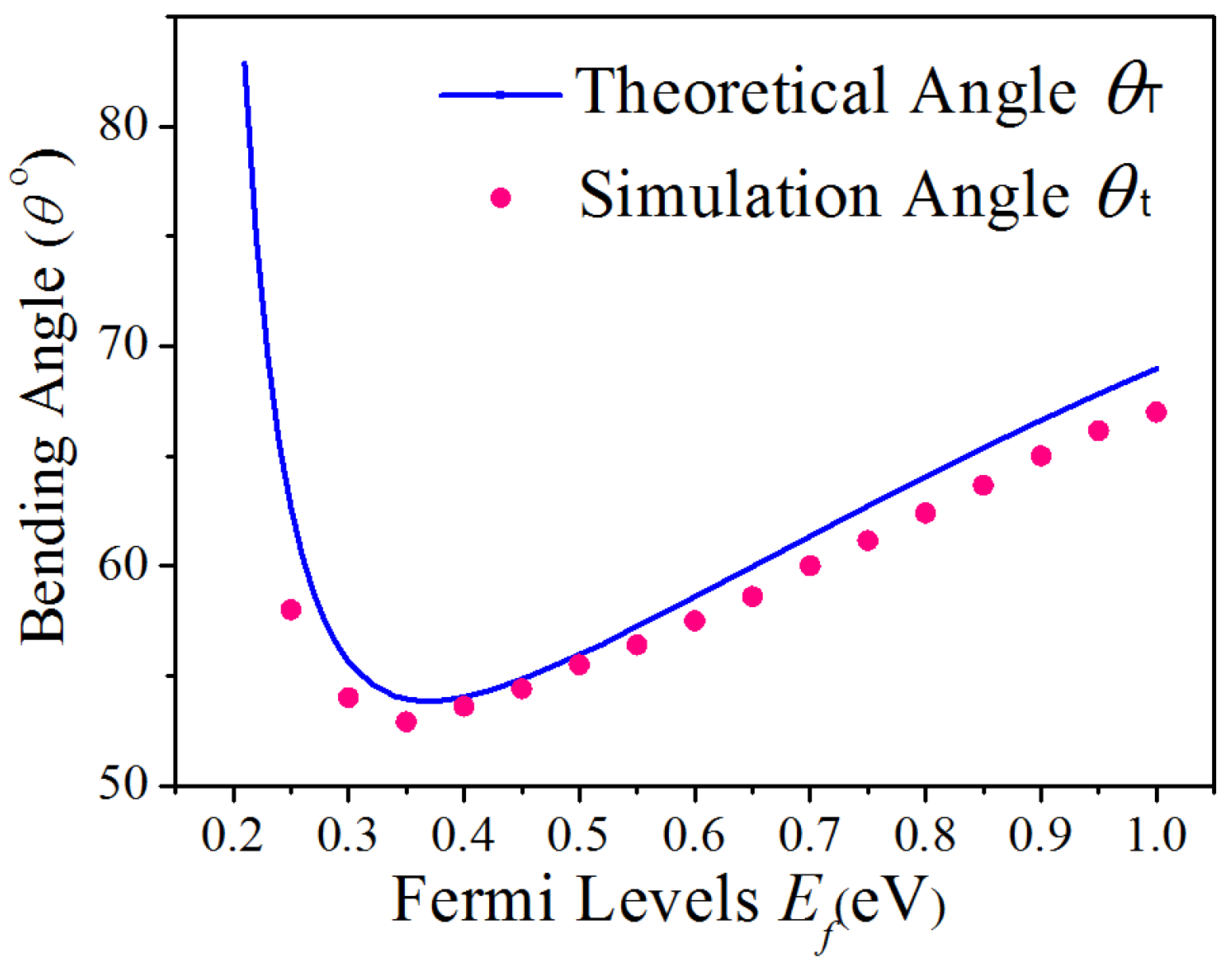
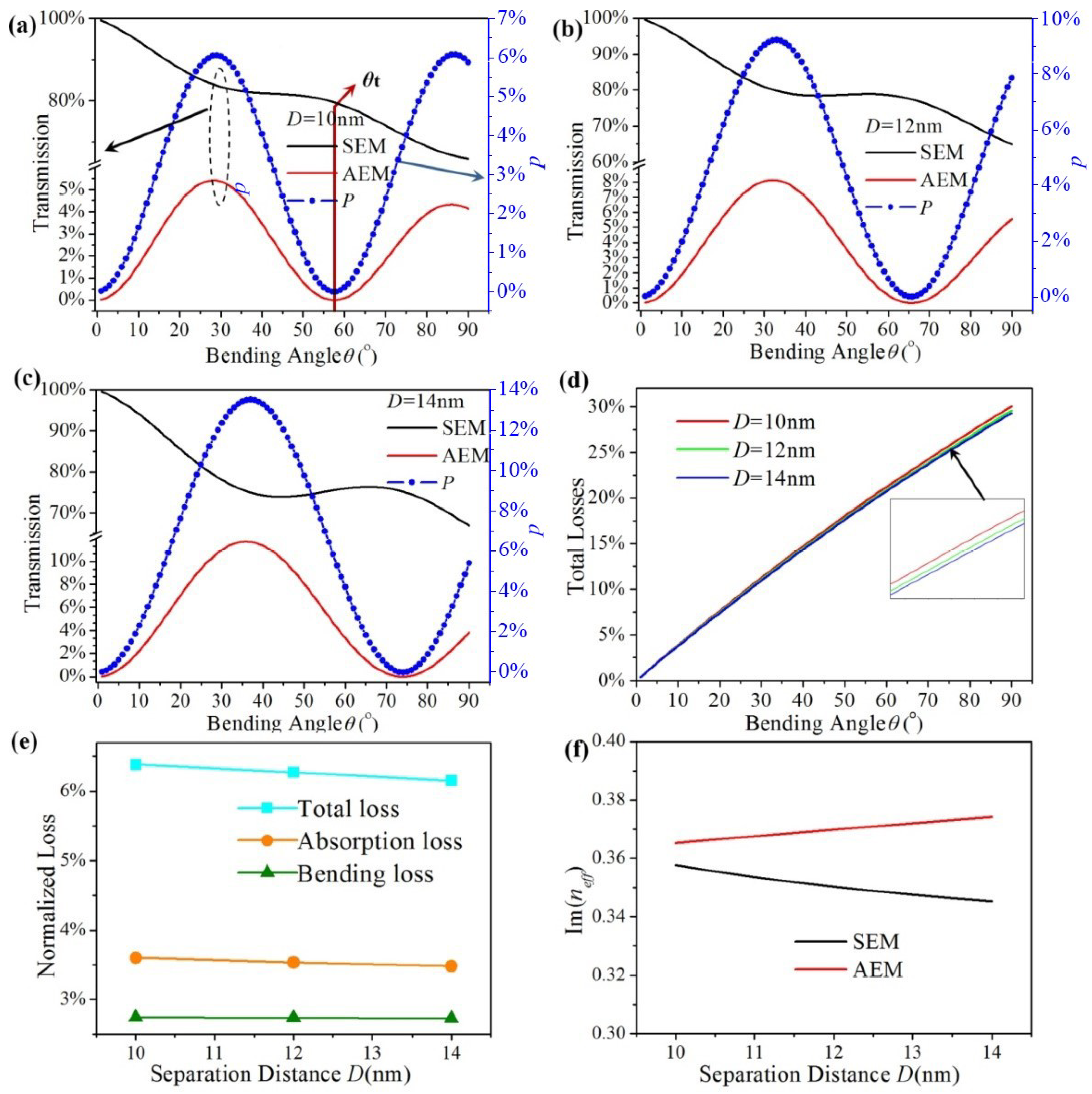
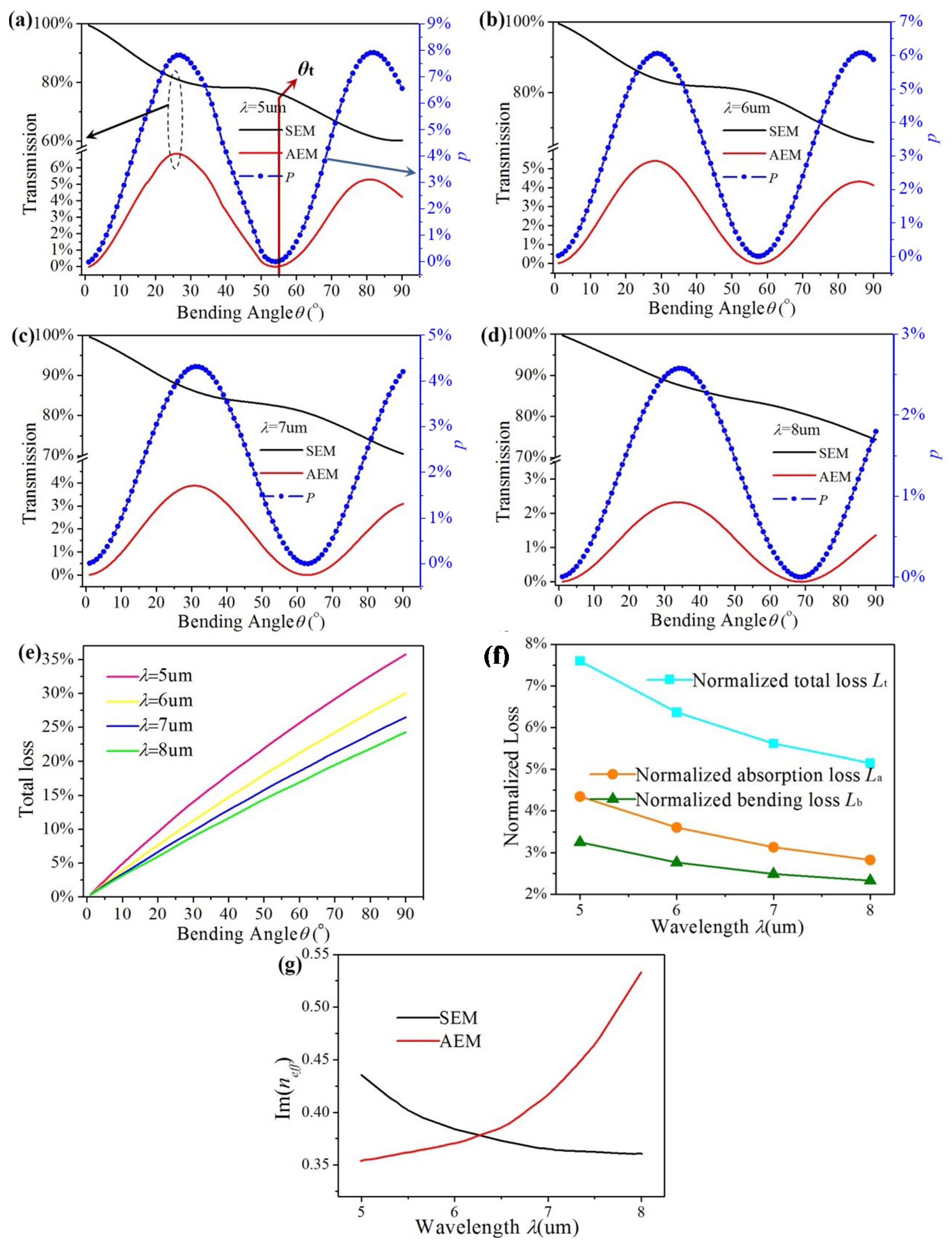
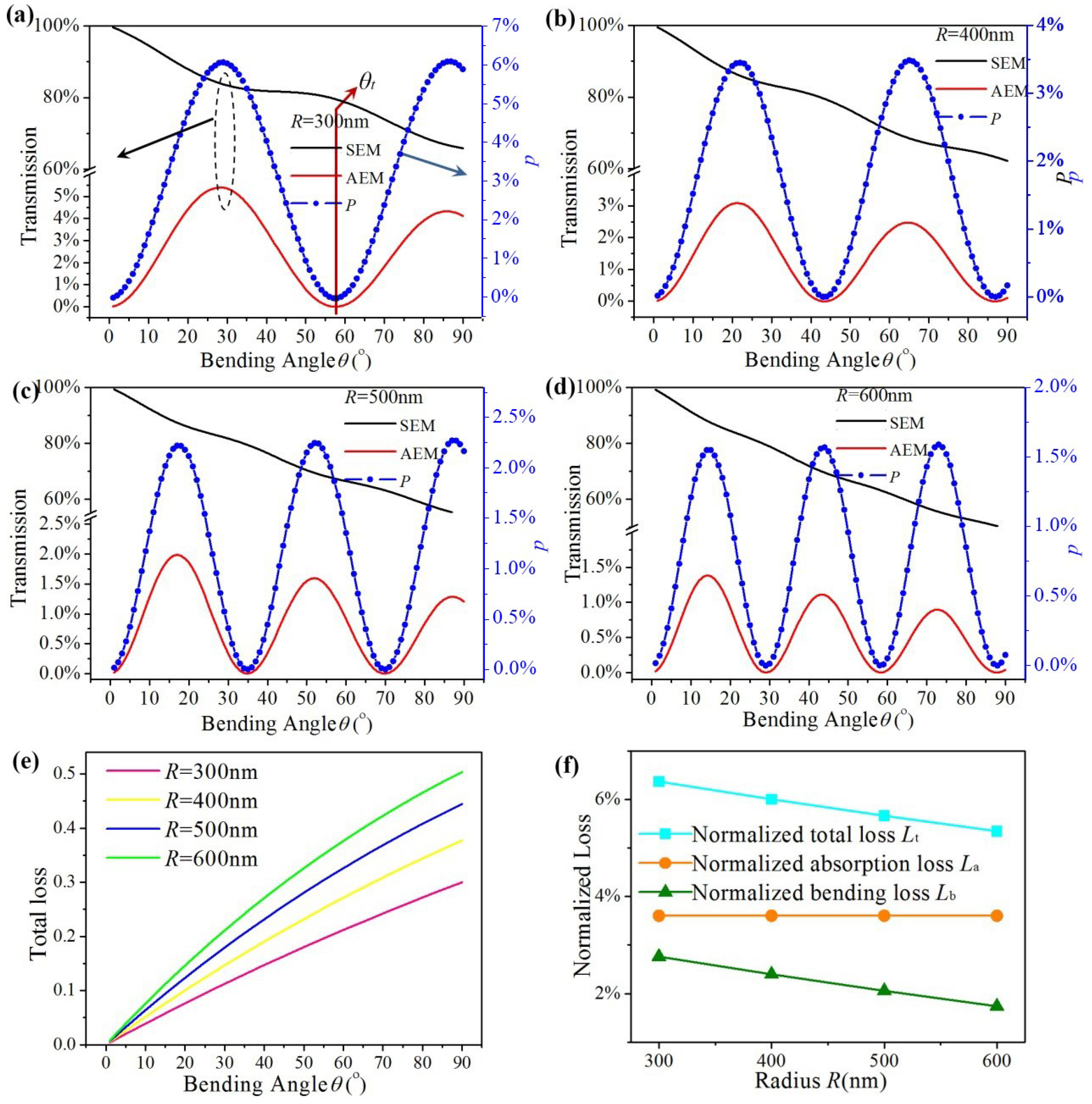
3. Mode Conversion and Simulations Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Bonaccorso, F.; Sun, Z.; Hasan, T.; Ferrari, A.C. Graphene photonics and optoelectronics. Nat. Photonics 2010, 4, 611–622. [Google Scholar] [CrossRef]
- Emani, N.K.; Kildishev, A.V.; Shalaev, V.M.; Boltasseva, A. Graphene: A dynamic platform for electrical control of plasmonic resonance. Nanophotonics 2015, 4, 214–223. [Google Scholar] [CrossRef]
- Constant, T.J.; Hornett, S.M.; Chang, D.E.; Hendry, E. All-optical generation of surface plasmons in graphene. Nat. Phys. 2015, 12, 124–128. [Google Scholar] [CrossRef]
- Garcia de Abajo, F.J. Graphene plasmonics: Challenges and opportunities. ACS Photonics 2014, 1, 135–152. [Google Scholar] [CrossRef]
- Koppens, F.H.; Chang, D.E.; Garcia de Abajo, F.J. Graphene plasmonics: A platform for strong light–matter interactions. Nano. Lett. 2011, 11, 3370–3377. [Google Scholar] [CrossRef]
- Ju, L.; Geng, B.; Horng, J.; Girit, C.; Martin, M.; Hao, Z.; Bechtel, H.A.; Liang, X.; Zettl, A.; Shen, Y.R. Graphene plasmonics for tunable terahertz metamaterials. Nat. Nanotechnol. 2011, 6, 630–634. [Google Scholar] [CrossRef]
- Vakil, A.; Engheta, N. Transformation optics using graphene. Science 2011, 332, 1291–1294. [Google Scholar] [CrossRef]
- Jablan, M.; Buljan, H.; Soljačić, M. Plasmonics in graphene at infrared frequencies. Phys. Rev. B 2009, 80, 245435. [Google Scholar] [CrossRef]
- Shalaev, V.M. Optical negative-index metamaterials. Nature 2007, 1, 41–48. [Google Scholar] [CrossRef]
- Sreekanth, K.; De Luca, A.; Strangi, G. Negative refraction in graphene-based hyperbolic metamaterials. Appl. Phys. Lett. 2013, 103, 023107. [Google Scholar] [CrossRef]
- Chen, P.-Y.; Alu, A. Atomically thin surface cloak using graphene monolayers. ACS Nano 2011, 5, 5855–5863. [Google Scholar] [CrossRef] [PubMed]
- Naserpour, M.; Zapata-Rodríguez, C.J.; Vuković, S.M.; Pashaeiadl, H.; Belić, M.R. Tunable invisibility cloaking by using isolated graphene-coated nanowires and dimers. Sci. Rep. 2017, 7, 12186. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Taubner, T. Broadband subwavelength imaging using a tunable graphene-lens. ACS Nano 2012, 6, 10107–10114. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Tang, C.; Yan, Z.; Wang, Q.; Liu, F.; Chen, J.; Xu, Z.; Sui, C. Graphene-based superlens for subwavelength optical imaging by graphene plasmon resonances. Plasmonics 2016, 11, 515–522. [Google Scholar] [CrossRef]
- Alaee, R.; Menzel, C.; Rockstuhl, C.; Lederer, F. Perfect absorbers on curved surfaces and their potential applications. Opt. Lett. 2012, 20, 18370–18376. [Google Scholar] [CrossRef]
- Hedayati, M.K.; Zillohu, A.; Strunskus, T.; Faupel, F.; Elbahri, M. Plasmonic tunable metamaterial absorber as ultraviolet protection film. Appl. Phys. Lett. 2014, 104, 041103. [Google Scholar] [CrossRef]
- Liu, M.; Yin, X.; Ulin-Avila, E.; Geng, B.; Zentgraf, T.; Ju, L.; Wang, F.; Zhang, X. A graphene-based broadband optical modulator. Nature 2011, 474, 64–67. [Google Scholar] [CrossRef]
- Sensale-Rodriguez, B.; Yan, R.; Kelly, M.M.; Fang, T.; Tahy, K.; Hwang, W.S.; Jena, D.; Liu, L.; Xing, H.G. Broadband graphene terahertz modulators enabled by intraband transitions. Nat. Commun. 2012, 3, 780. [Google Scholar] [CrossRef]
- AlSayem, A.; Mahdy, M.R.C.; Jahangir, I.; Rahman, M.S. Ultrathin ultra-broadband electro-absorption modulator based on few-layer graphene based anisotropic metamaterial. Opt. Commun. 2017, 384, 50–58. [Google Scholar]
- Shao, Y.; Wang, J.; Wu, H.; Liu, J.; Aksay, I.A.; Lin, Y. Graphene based electrochemical sensors and biosensors: A review. Electroanal. Int. J. Devoted Fundam. Pract. Asp. Electroanal. 2010, 22, 1027–1036. [Google Scholar] [CrossRef]
- Goossens, S.; Navickaite, G.; Monasterio, C.; Gupta, S.; Piqueras, J.J.; Pérez, R.; Burwell, G.; Nikitskiy, I.; Lasanta, T.; Galán, T. Broadband image sensor array based on graphene–CMOS integration. Nat. Photonics 2017, 11, 366–371. [Google Scholar] [CrossRef]
- Nikitin, A.Y.; Guinea, F.; García-Vidal, F.; Martín-Moreno, L. Edge and waveguide terahertz surface plasmon modes in graphene microribbons. Phys. Rev. B 2011, 84, 161407. [Google Scholar] [CrossRef]
- Fei, Z.; Goldflam, M.D.; Wu, J.S.; Dai, S.; Wagner, M.; McLeod, A.S.; Liu, M.K.; Post, K.W.; Zhu, S.; Janssen, G.C.; et al. Edge and surface plasmons in graphene nanoribbons. Nano Lett. 2015, 15, 8271–8276. [Google Scholar] [CrossRef] [PubMed]
- Hou, H.W.; Teng, J.H.; Palacios, T.; Chua, S.J. Edge plasmons and cut-off behavior of graphene nano-ribbon waveguides. Opt. Commun. 2016, 370, 226–230. [Google Scholar] [CrossRef]
- Hajati, M.; Hajati, Y. Investigation of plasmonic properties of graphene multilayer nano-ribbon waveguides. Appl. Opt. 2016, 55, 1878–1884. [Google Scholar] [CrossRef]
- Wang, Y.K.; Hong, X.R.; Yang, G.F.; Sang, T. Filtering characteristics of a graphene ribbon with a rectangle ring in infrared region. AIP Adv. 2016, 6, 115311. [Google Scholar] [CrossRef]
- Yuan, L.; Yan, X.; Wang, Y.K.; Sang, T.; Yang, G.F. Transmittance characteristics of plasmonic graphene ribbons with a wing. Appl. Phys. Express 2016, 9, 092202. [Google Scholar] [CrossRef]
- Zhu, X.; Yan, W.; Mortensen, N.A.; Xiao, S. Bends and splitters in graphene nanoribbon waveguides. Opt. Express 2013, 21, 3486–3491. [Google Scholar] [CrossRef]
- Zhu, B.; Ren, G.; Gao, Y.; Yang, Y.; Wu, B.; Lian, Y.; Wang, J.; Jian, S. Spatial splitting and coupling of the edge modes in the graphene bend waveguide. Plasmonics 2015, 10, 745–751. [Google Scholar] [CrossRef]
- Christensen, J.; Manjavacas, A.; Thongrattanasiri, S.; Koppens, F.H.; García de Abajo, F.J. Graphene plasmon waveguiding and hybridization in individual and paired nanoribbons. ACS Nano 2011, 6, 431–440. [Google Scholar] [CrossRef] [PubMed]
- Hanson, G.W. Quasi-transverse electromagnetic modes supported by a graphene parallel-plate waveguide. J. Appl. Phys. 2008, 104, 084314. [Google Scholar] [CrossRef]
- Nikitin, A.Y.; Alonso-González, P.; Hillenbrand, R. Efficient coupling of light to graphene plasmons by compressing surface polaritons with tapered bulk materials. Nano Lett. 2014, 14, 2896–2901. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Wang, B.; Zhang, X.; Yuan, X.; Teng, J. Optical coupling of surface plasmons between graphene sheets. Appl. Phys. Lett. 2012, 100, 131111. [Google Scholar] [CrossRef]
- Zhernovnykova, O.A.; Popova, O.V.; Deynychenko, G.V.; Deynichenko, T.I.; Bludov, Y.V. Surface plasmon-polaritons in graphene, embedded into medium with gain and losses. J. Phys. Condens. Matter 2019, 31, 465301. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Xue, B.; Wang, Y. Mode Conversion of the Edge Modes in the Graphene Double-Ribbon Bend. Materials 2019, 12, 4008. https://doi.org/10.3390/ma12234008
Zhang L, Xue B, Wang Y. Mode Conversion of the Edge Modes in the Graphene Double-Ribbon Bend. Materials. 2019; 12(23):4008. https://doi.org/10.3390/ma12234008
Chicago/Turabian StyleZhang, Lanlan, Binghan Xue, and Yueke Wang. 2019. "Mode Conversion of the Edge Modes in the Graphene Double-Ribbon Bend" Materials 12, no. 23: 4008. https://doi.org/10.3390/ma12234008
APA StyleZhang, L., Xue, B., & Wang, Y. (2019). Mode Conversion of the Edge Modes in the Graphene Double-Ribbon Bend. Materials, 12(23), 4008. https://doi.org/10.3390/ma12234008



