Calculation of Volume Fractions of In Situ TiB and Residual Stress Distributions in Functionally Graded Composite of Ti–TiB–TiB2
Abstract
:1. Introduction
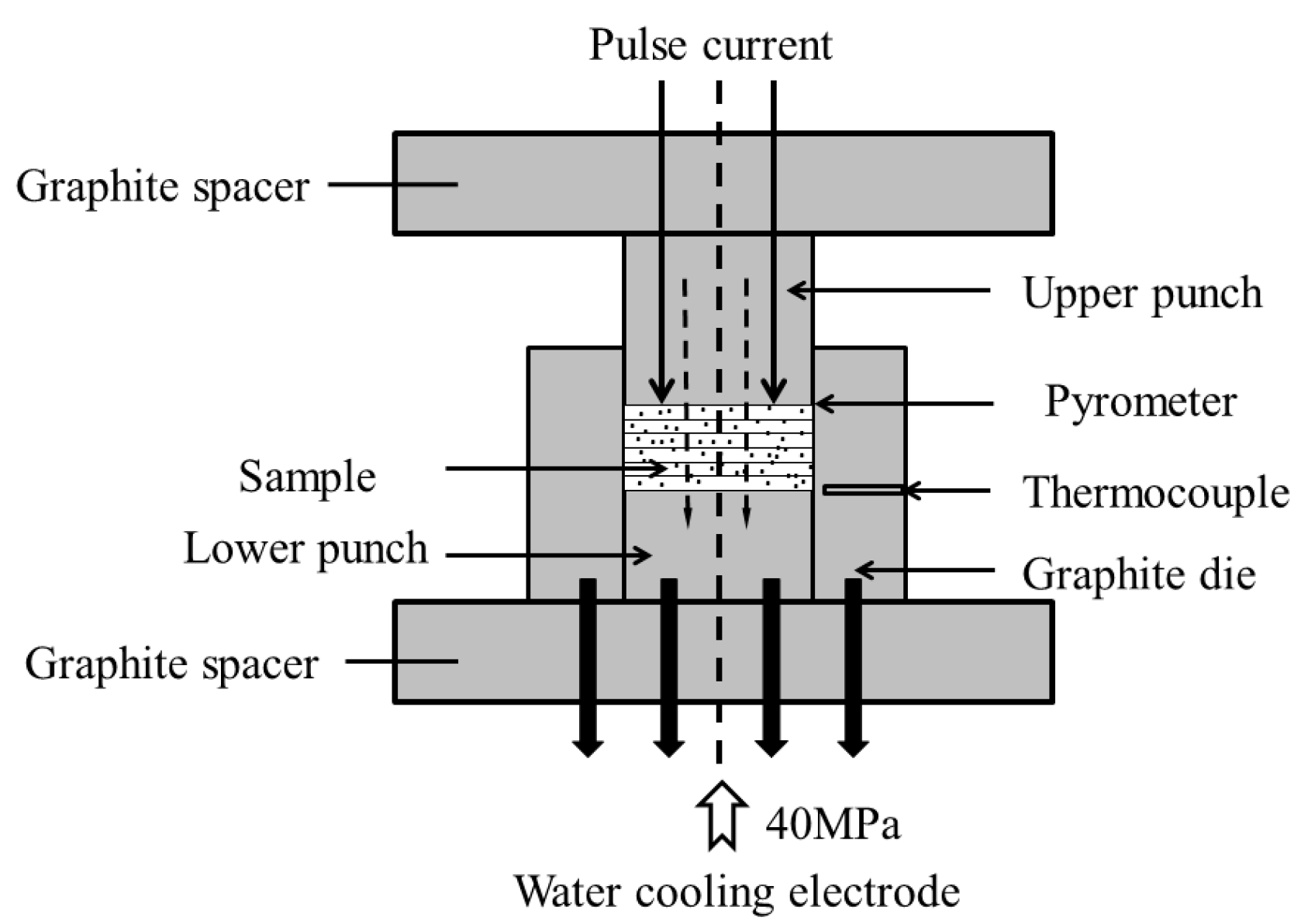
2. Methods and materials
3. Results and Discussion
3.1. Calculation of Actual TiB Fraction
3.2. Microstructure
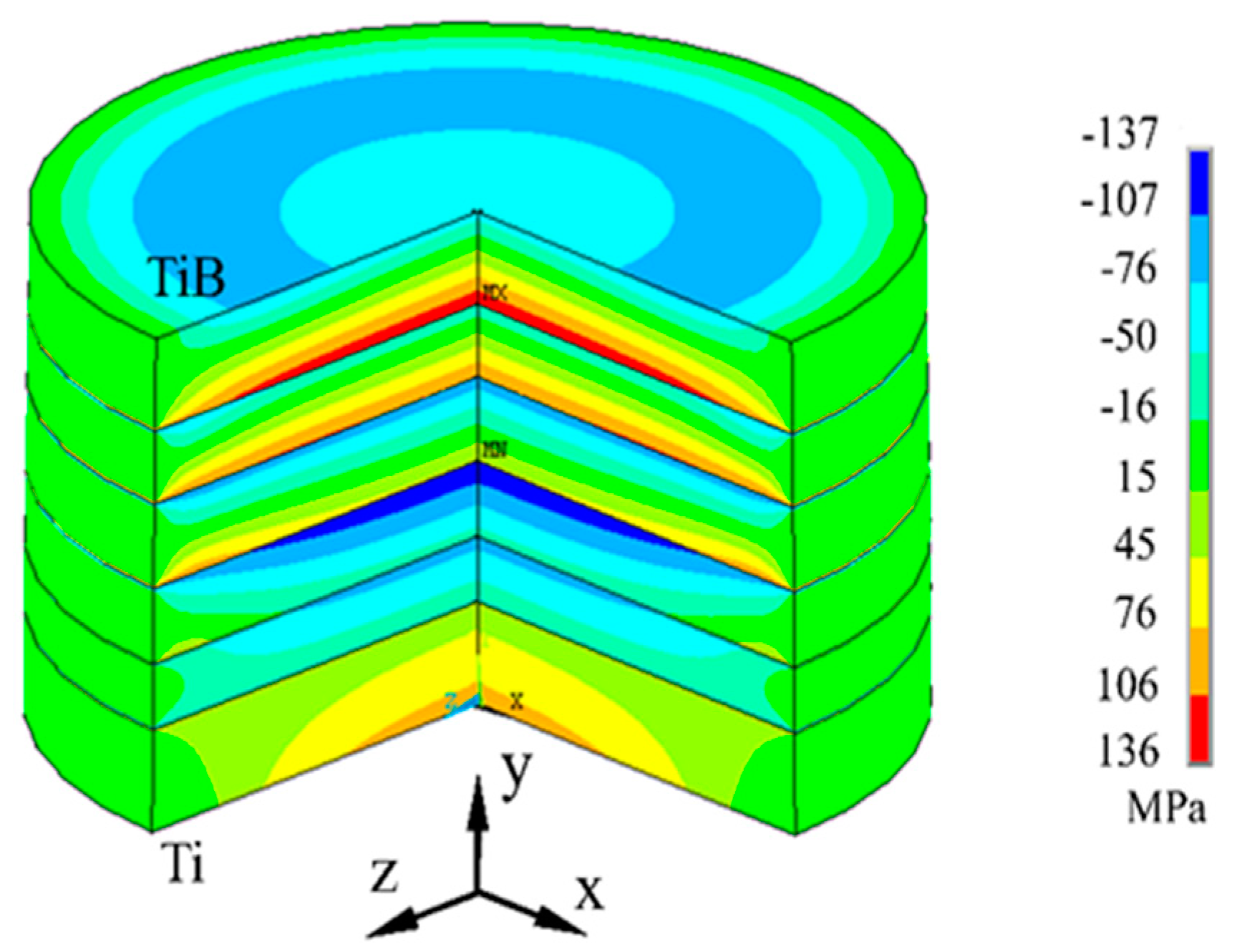
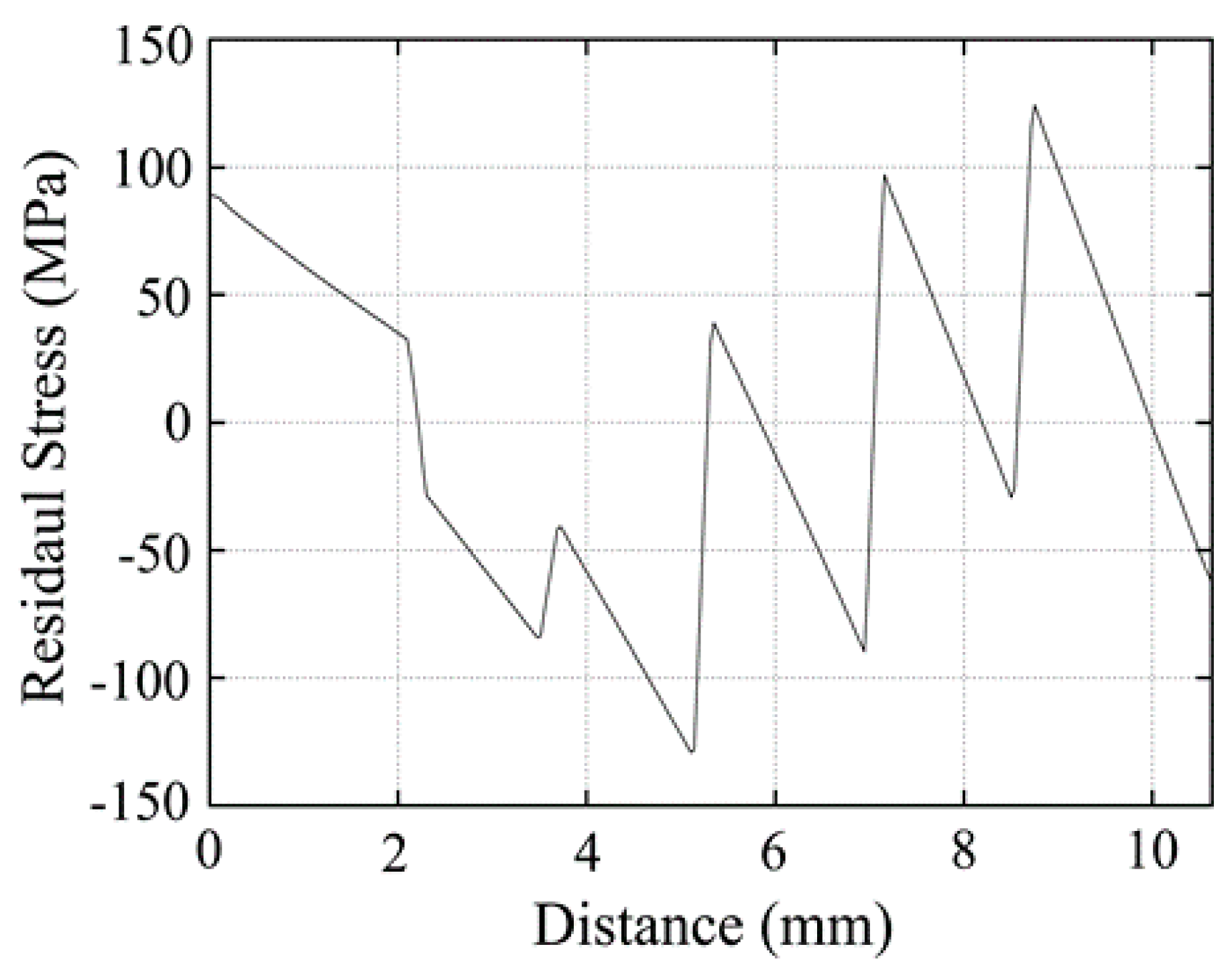
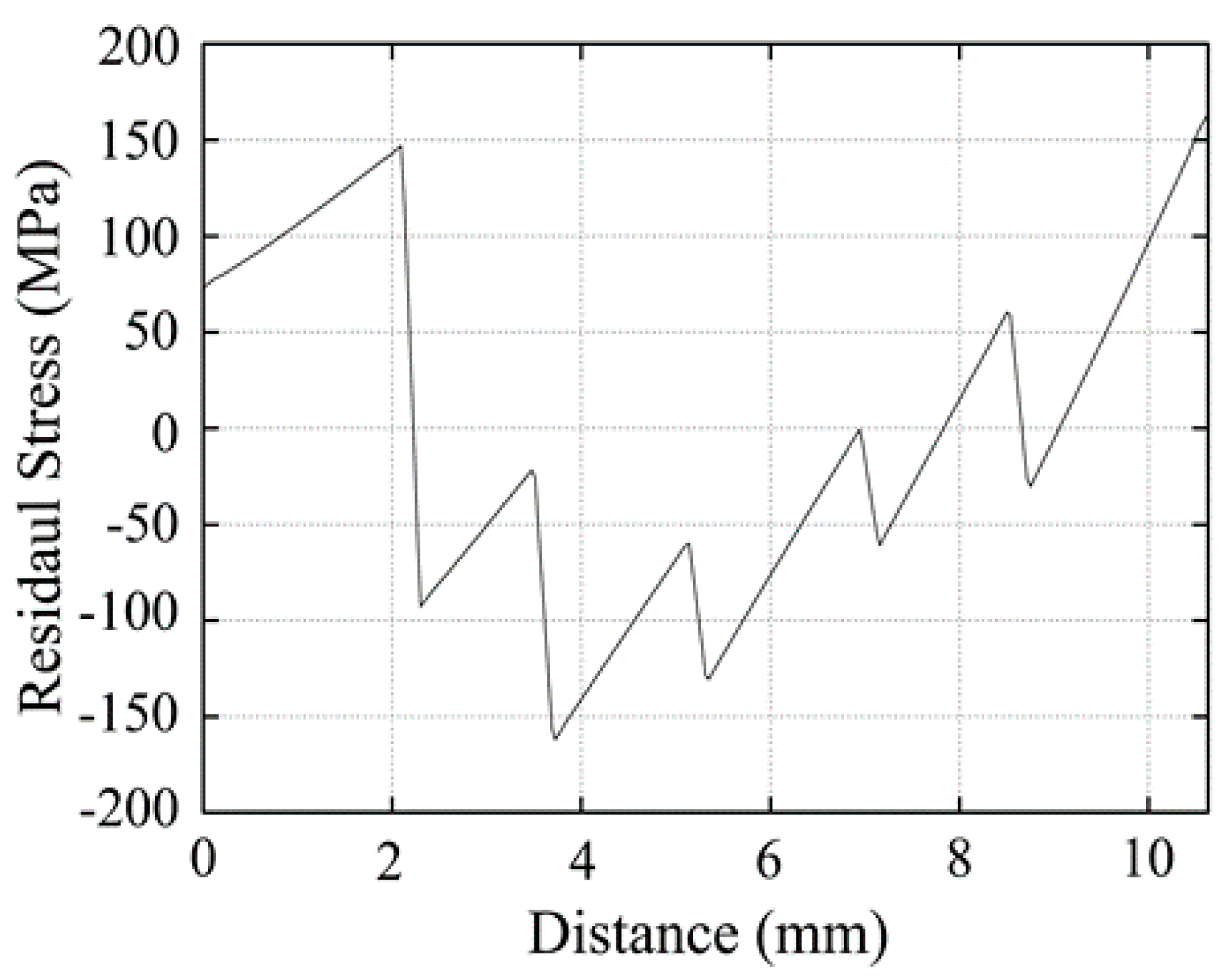
3.3. Residual Stress Distributions in the FGM
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Koizumi, M. FGM activities in Japan. Compos. Part B 1997, 28, 1–4. [Google Scholar] [CrossRef]
- Tsuda, K.; Ikegaya, A.; Isobe, K.; Kitagawa, N.; Nomura, T. Development of functionally graded sintered hard materials. Powder Metall. 2009, 39, 296–300. [Google Scholar] [CrossRef]
- Ma, X.X.; Xiao, B.; Cao, S.H.; Chen, B.; Xu, H. A novel approach to fabricate W/Cu functionally gradient materials. Int. J. Refract. Met. Hard Mater. 2018, 72, 183–193. [Google Scholar] [CrossRef]
- Bhavar, V.; Kattire, P.; Thakare, S.; Patil, S.; Singh, R.K.P. A review on functionally gradient materials (FGMs) and their applications. IOP Conf. Ser. Mater. Sci. Eng. 2017, 229, 012021. [Google Scholar] [CrossRef]
- Liu, T.; Wang, Q.; Gao, A.; Zhang, C.; Wang, C.; He, J. Fabrication of functionally graded materials by a semi-solid forming process under magnetic field gradients. Scr. Mater. 2017, 57, 992–995. [Google Scholar] [CrossRef]
- Gorsse, S.; Chaminade, J.P.; Petitcorps, Y.L. In situ preparation of titanium base composites reinforced by TiB single crystals using a powder metallurgy technique. Compos. Part A 1998, 29, 1229–1234. [Google Scholar] [CrossRef]
- Lu, W.J.; Zhang, D.; Zhang, X.N.; Wu, R.J. HREM study of TiB/Ti interfaces in a TiB-TiC in situ composite. Scr. Mater. 2001, 44, 1069–1075. [Google Scholar] [CrossRef]
- Zhang, Z.; Shen, X.; Zhang, C. A new rapid route to in-situ synthesize TiB-Ti system functionally graded materials using spark plasma sintering method. Mater. Sci. Eng. A 2013, 565, 326–332. [Google Scholar] [CrossRef]
- Wang, F.C.; Zhang, Z.H.; Luo, J.; Huang, C.C.; Lee, S.K. A novel rapid route for in situ synthesizing TiB-TiB2 composites. Compos. Sci. Technol. 2009, 69, 2682–2687. [Google Scholar] [CrossRef]
- Asl, M.S.; Zambarir, M.J.; Ahmadi, Z.; Parvizi, S. Effects of nano-graphite content on the characteristics of spark plasma sintered ZrB2-SiC composites. Mater. Sci. Eng. A 2018, 716, 99–106. [Google Scholar]
- Guillon, O.; Gonzalez-Julian, J.; Dargatz, B.; Kessel, T.; Schierning, G.; Räthel, J.; Herrmann, M. Field-assisted sintering technology/spark plasma sintering: Mechanisms, materials and technology. Adv. Eng. Mater. 2014, 16, 830–849. [Google Scholar] [CrossRef]
- Jiang, W.; Zhang, J.F.; Wang, L.J.; Tu, R.; Yang, X.Q.; Chen, G.; Zhai, P.C. Ti3SiC2-(Ti3SiC2-SiC) functionally graded materials by spark plasma sintering reactive synthesis method part 1-gradient optimizations. Mater. Technol. 2010, 25, 283–288. [Google Scholar] [CrossRef]
- Omori, M. Sintering, consolidation, reaction and crystal growth by the spark plasma system (SPS). Mater. Sci. Eng. A 2000, 287, 183–188. [Google Scholar] [CrossRef]
- Feng, H.B.; Meng, Q.; Zhou, Y.; Jia, D. Spark plasma sintering of functionally graded material in the Ti-TiB2-B system. Mater. Sci. Eng. A 2005, 397, 92–97. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Li, Z.W.; Li, C.G.; Yu, Z.S. Temperature gradient field sintering of Ti-TiB-TiB2 functionally graded materials. Ceram. Int. 2015, 41, 13844–13849. [Google Scholar] [CrossRef]
- Meng, Q.C. Microscopy of Transmission Electron; Harbin Institute of Technology Press: Harbin, China, 1998; pp. 154–156. [Google Scholar]
- Zhang, X.H.; Xu, Q.; Han, J.C.; Kvanin, V.L. Self-propagating high temperature combustion synthesis of TiB/Ti composites. Mater. Sci. Eng. A 2003, 348, 41–46. [Google Scholar]
- Cirakoglu, M.; Watt, G.L.; Bhaduri, S.B. Controlled combustion synthesis in the Ti–B system with ZrO2 addition. Mater. Sci. Eng. A 2000, 282, 223–231. [Google Scholar] [CrossRef]
- Nardone, V.C.; Prewo, K.M. On the strength of discontinuous silicon carbide reinforced aluminum composites. Scr. Metall. 1986, 20, 43–48. [Google Scholar] [CrossRef]
- Feng, H.B.; Jia, D.C.; Zhou, Y. Spark plasma sintering reaction synthesized TiB reinforced titanium matrix composites. Compos. Part A 2005, 36, 558–563. [Google Scholar] [CrossRef]
- Saito, T.; Furuta, T.; Yamaguchi, T. Development of Low Cost Titanium Matrix Composite. In Recent Advances in Titanium Metal Matrix Composites; Froes, F.H., Storer, J., Eds.; The Minerals, Metals and Materials Society: Pittsburgh, PA, USA, 1995; pp. 33–44. [Google Scholar]
- Alman, D.E.; Hawk, J.A. The abrasive wear of sintered titanium matrix-ceramic particle reinforced composites. Wear 1999, 225–229, 629–639. [Google Scholar] [CrossRef]
- Panda, K.B.; Ravi Chandran, K.S. Titanium-titanium boride (Ti-TiB) functionally graded materials through reaction sintering: Synthesis, microstructure, and properties. Metall. Mater. Trans. A 2003, 34, 1993–2003. [Google Scholar] [CrossRef]


| hkl | 2θ(Deg) | d(A) | |Fhkl|2 | L | p | ITiB in JCPDS | ITiB Computed | ITiB in XRD | R Calculated |
|---|---|---|---|---|---|---|---|---|---|
| 101 | 24.502 | 3.633 | 906 | 41.20 | 4 | 20 | 82 | 14 | 20.46 |
| 200 | 29.252 | 3.053 | 2501 | 29.08 | 2 | 32 | 80 | 17 | 19.92 |
| 201 | 35.293 | 2.543 | 1089 | 19.14 | 4 | 80 | 46 | 11 | 11.42 |
| 111 | 38.368 | 2.346 | 718 | 15.80 | 8 | 80 | 50 | 8 | 12.44 |
| 210 | 41.799 | 2.161 | 1142 | 13.09 | 4 | 64 | 33 | 84 | 8.19 |
| 102 | 42.229 | 2.140 | 3549 | 12.81 | 4 | 100 | 100 | 100 | 24.91 |
| 211 | 46.422 | 1.956 | 713 | 10.35 | 8 | 40 | 32 | - | 8.09 |
| 301 | 48.887 | 1.863 | 377 | 9.23 | 4 | 56 | 8 | - | 1.91 |
| 112 | 52.113 | 1.755 | 722 | 7.92 | 8 | 40 | 25 | 30 | 6.27 |
| 020 | 60.598 | 1.528 | 4315 | 5.65 | 2 | 32 | 2 | - | 6.68 |
| 401 | 63.694 | 1.461 | 452 | 5.08 | 4 | 28 | 5 | - | 1.26 |
| 312 | 68.944 | 1.362 | 2508 | 4.27 | 8 | 72 | 47 | 54 | 11.73 |
| hkl | 2θ(Deg) | d(A) | |Fhkl|2 | L | p | Iβ-Ti in JCPDS | Iβ-Ti Computed | Iβ-Ti in XRD | R Calculated |
|---|---|---|---|---|---|---|---|---|---|
| 110 | 38.482 | 2.3375 | 1277 | 15.80 | 12 | 100 | 100 | 100 | 202.68 |
| 200 | 55.543 | 1.6532 | 907 | 6.86 | 6 | 12 | 15 | 9 | 31.25 |
| 211 | 69.607 | 1.3496 | 646 | 4.19 | 24 | 17 | 27 | 27 | 54.38 |
| 220 | 82.447 | 1.1689 | 639 | 3.12 | 12 | 4 | 10 | 7 | 20.03 |
| 310 | 94.927 | 1.0454 | 462 | 2.74 | 24 | 5 | 13 | 6 | 25.43 |
| 222 | 107.628 | 0.9544 | 462 | 2.84 | 8 | 1 | 4 | - | 8.79 |
| hkl | 2θ(Deg) | d(A) | |Fhkl|2 | L | p | Iα-Ti in JCPDS | Iα-Ti Computed | Iα-Ti in XRD | R Calculated |
|---|---|---|---|---|---|---|---|---|---|
| 100 | 35.063 | 2.557 | 34161 | 19.38 | 6 | 30 | 23 | 17 | 27.38 |
| 002 | 38.402 | 2.342 | 37134 | 15.80 | 2 | 26 | 25 | 28 | 29.77 |
| 101 | 40.150 | 2.244 | 151026 | 14.28 | 12 | 100 | 100 | 100 | 121.06 |
| 102 | 53.008 | 1.726 | 19115 | 7.65 | 12 | 19 | 13 | - | 15.32 |
| 110 | 62.960 | 1.475 | 25887 | 5.18 | 6 | 17 | 17 | 18 | 20.75 |
| 103 | 70.657 | 1.332 | 214175 | 4.07 | 12 | 16 | 14 | - | 17.17 |
| 200 | 74.263 | 1.276 | 0 | 3.70 | 6 | 2 | 0 | - | 0 |
| 112 | 76.294 | 1.247 | 24626 | 3.51 | 12 | 16 | 16 | - | 19.74 |
| hkl | 2θ(Deg) | d(A) | |Fhkl|2 | L | p | ITiB2 in JCPDS | ITiB2 Computed | ITiB2 in XRD | R Calculated |
|---|---|---|---|---|---|---|---|---|---|
| 001 | 27.598 | 3.2295 | 110 | 32.31 | 2 | 22 | 19 | 19 | 10.78 |
| 100 | 34.133 | 2.6246 | 208 | 20.38 | 6 | 55 | 67 | 44 | 38.60 |
| 101 | 44.438 | 2.0370 | 279 | 11.43 | 12 | 100 | 100 | 100 | 58.05 |
| 002 | 56.992 | 1.6145 | 339 | 6.48 | 2 | 12 | 11 | 10 | 6.67 |
| 110 | 61.106 | 1.5153 | 402 | 5.52 | 6 | 27 | 35 | 37 | 20.207 |
| 102 | 68.134 | 1.3751 | 86 | 4.37 | 12 | 16 | 12 | - | 6.847 |
| 111 | 68.328 | 1.3717 | 42 | 4.35 | - | 18 | - | - | - |
| 200 | 71.895 | 1.3121 | 108 | 3.94 | 6 | 7 | 7 | - | 3.88 |
| 201 | 78.642 | 1.2156 | 190 | 3.35 | 12 | 16 | 20 | 9 | 11.58 |
| Layers | Target Volume Fraction of TiB(%) | Calculated Volume Fraction (%) | Estimated Composition (wt%) | CTE(/K) | |||
| TiB | TiB2 | TiB | TiB2 | Ti | |||
| Layer1 | 0 | 0 | 0 | 0 | 0 | 100 | 9.00 |
| Layer2 | 20 | 24.4 | 0 | 23.3 | 0 | 76.7 | 7.89 |
| Layer3 | 40 | 45.7 | 0 | 44.2 | 0 | 55.8 | 7.52 |
| Layer4 | 60 | 61.6 | 0 | 60.2 | 0 | 39.8 | 7.36 |
| Layer5 | 80 | 76.5 | 2.2 | 75.5 | 2.2 | 22.3 | 7.22 |
| Layer6 | 100 | 73.0 | 16.0 | 72.5 | 15.9 | 11.6 | 7.03 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; He, S.; Yang, W.; Ren, J.; Kong, H. Calculation of Volume Fractions of In Situ TiB and Residual Stress Distributions in Functionally Graded Composite of Ti–TiB–TiB2. Materials 2019, 12, 4006. https://doi.org/10.3390/ma12234006
Zhang Y, He S, Yang W, Ren J, Kong H. Calculation of Volume Fractions of In Situ TiB and Residual Stress Distributions in Functionally Graded Composite of Ti–TiB–TiB2. Materials. 2019; 12(23):4006. https://doi.org/10.3390/ma12234006
Chicago/Turabian StyleZhang, Youfeng, Shasha He, Wanwan Yang, Jiangwei Ren, and Haijuan Kong. 2019. "Calculation of Volume Fractions of In Situ TiB and Residual Stress Distributions in Functionally Graded Composite of Ti–TiB–TiB2" Materials 12, no. 23: 4006. https://doi.org/10.3390/ma12234006
APA StyleZhang, Y., He, S., Yang, W., Ren, J., & Kong, H. (2019). Calculation of Volume Fractions of In Situ TiB and Residual Stress Distributions in Functionally Graded Composite of Ti–TiB–TiB2. Materials, 12(23), 4006. https://doi.org/10.3390/ma12234006





