Atomic Study on Tension Behaviors of Sub-10 nm NanoPolycrystalline Cu–Ta Alloy
Abstract
1. Introduction
2. Materials and Methods
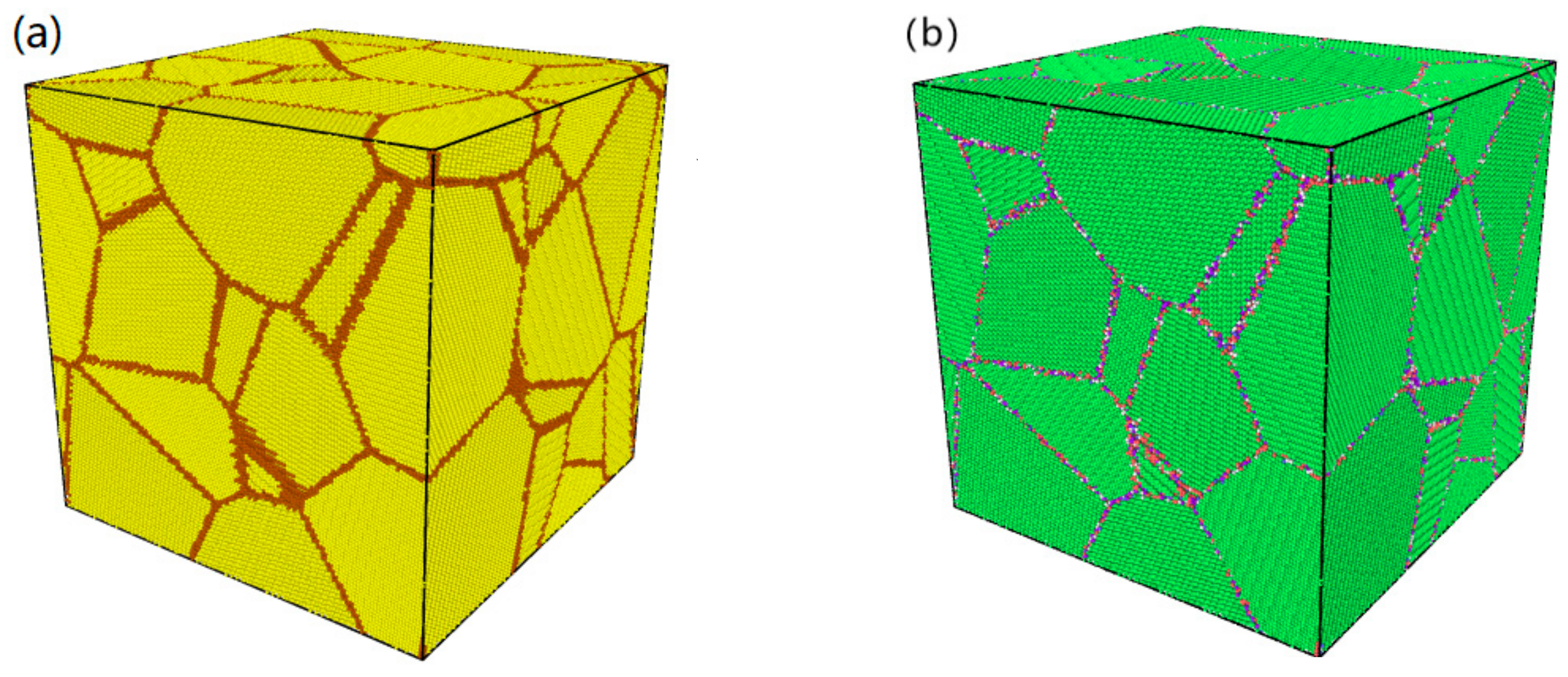
2.1. Physical Modeling
2.2. Methodology of Atomistic Simulations
3. Results and Discussion
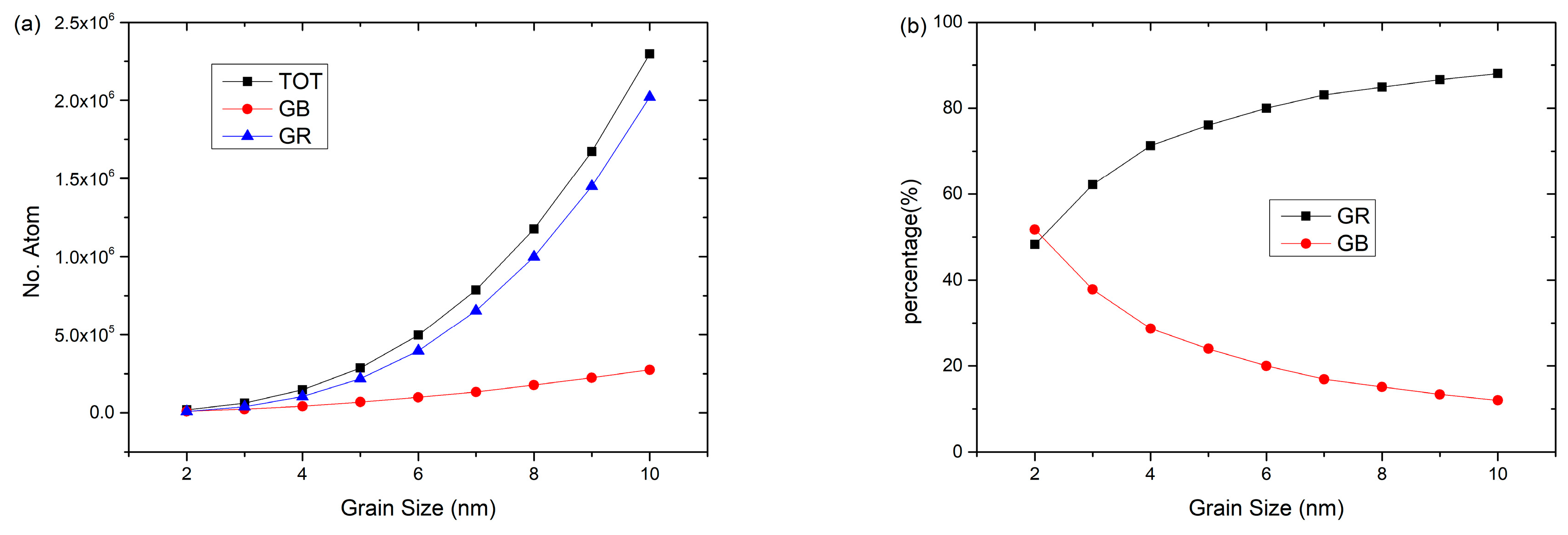
3.1. Dependence of Grain Size
3.2. Dependence of Strain Rate
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dewaele, A.; Mezouar, M.; Guignot, N.; Loubeyre, P. High melting point of tantalum in a laser-heated diamond anvil cell. Phys. Rev. Lett. 2010, 104, 5701. [Google Scholar] [CrossRef] [PubMed]
- Burakovsky, L.; Chen, S.P.; Preston, D.L.; Belonoshko, A.B.; Rosengren, A.; Mikhaylushkin, A.S.; Simak, S.I.; Moriarty, J.A. High-pressure-high-temperature polymoephism in Ta: resolving an ongoing experimental controversy. Phys. Rev. Lett. 2010, 104, 5702. [Google Scholar] [CrossRef] [PubMed]
- Cynn, H.; Yoo, C.S. Equation of tantalum to 174 GPa. Phys. Rev. B 1999, 59, 8526–8529. [Google Scholar] [CrossRef]
- Shigeaki, O. First-principles molecular dynamics calculations of the equation of state for tantalum. Int. J. Mol. Sci. 2009, 10, 4342–4351. [Google Scholar]
- Wu, J.H.; Zhao, X.L.; Song, Y.L.; Wu, G.D. First-principles high-pressure elastic and thermodynamic properties of tantalum. Int. J. Mod. Phys. B 2011, 25, 1393–1407. [Google Scholar] [CrossRef]
- Liu, Z.L.; Zhang, X.L.; Cai, L.C.; Chen, X.R.; Wu, Q.; Jing, F.Q. Thermal equation of state, and melting and thermos elastic properties of bcc tantalum from molecular dynamics. J. Phys. Chem. Solids 2008, 69, 2833–2840. [Google Scholar] [CrossRef]
- Li, W.B.; Li, K.; Fan, K.Q.; Zhang, D.X.; Wang, W.D. Temperature and pressure dependences of the elastic properties of tantalum. Nanoscale Res. Lett. 2018, 13, 118. [Google Scholar] [CrossRef]
- Zeng, F.; Gao, Y.; Li, L.; Li, D.M.; Pan, F. Elastic modulus and hardness of Cu-Ta amorphous films. J Alloy. Compd. 2005, 389, 75–79. [Google Scholar] [CrossRef]
- Zhu, X.F.; Li, Y.P.; Zhang, G.P.; Zhu, S.J. On strain-localized damage in nanoscale Cu-Ta multilayers on a flexible substrate. Mater. Sci. Eng. A 2010, 527, 3279–3283. [Google Scholar] [CrossRef]
- Wang, F.; Huang, P.; Xu, M.; Lu, T.J.; Xu, K.W. Shearing banding deformation in Cu/Ta nano-multilayers. Mater. Sci. Eng. A 2011, 528, 7290–7294. [Google Scholar] [CrossRef]
- Huang, P.; Wang, F.; Xu, M.; Lu, T.J.; Xu, K.W. Strain rate sensitivity of unequal grained nano-multilayers. Mater. Sci. Eng. A 2011, 528, 5908–5913. [Google Scholar] [CrossRef]
- Frolov, T.; Darling, K.A.; Kecskes, L.J.; Mishin, Y. Stablization and strengthening of nanocrystalline copper by alloying with tantalum. Acta Mater. 2012, 60, 2158–2168. [Google Scholar] [CrossRef]
- Hashibon, A.; Lozovoi, A.Y.; Mishin, Y.; Elsässer, C.; Gumbsch, P. Interatomic potential for the Cu-Ta system and its application to surface wetting and dewetting. Phys. Rev. B 2008, 77, 4131. [Google Scholar] [CrossRef]
- Gu, C.; Wang, F.; Huang, P.; Xu, K.W.; Lu, T.J. Structure-dependent size effects in CuTa/Cu nanolaminates. Mater. Sci. Eng. A 2016, 658, 381–388. [Google Scholar] [CrossRef]
- Gong, H.R.; Liu, B.X. Influence of interfacial texture on solid-state amorphization and associated asymmetric growth in immiscible Cu-Ta multilayers. Phys. Rev. B 2004, 70, 4202. [Google Scholar] [CrossRef]
- Gong, H.R.; Liu, B.X. Interface stability and solid-state amorphization in an immiscible Cu-Ta system. Appl. Phys. Lett. 2003, 83, 4515. [Google Scholar] [CrossRef]
- Gong, H.R.; Kong, L.T.; Lai, W.S.; Liu, B.X. Atomistic modeling of solid-state amorphization in an immiscible Cu-Ta system. Phys. Rev. B 2002, 66, 4204. [Google Scholar] [CrossRef]
- Francis, M.F.; Neurock, M.N.; Zhou, X.W.; Quan, J.J.; Wadley, H.N.; Webb, E.B., III. Atomic assembly of Cu/Ta multilayers: surface roughness, grain structure, misfit dislocation and amorphization. J. Appl. Phys. 2008, 104, 4310. [Google Scholar] [CrossRef]
- Chen, L.; Magtoto, N.; Ekstrom, B.; Kelber, J. Efeect of surface impurities on the Cu/Ta interface. Thin Solid Films 2000, 376, 115–123. [Google Scholar] [CrossRef]
- Darling, K.A.; Roberts, A.J.; Mishin, Y.; Mathaudhu, S.N.; Kecskes, L.J. Grain size stabilization of nanocrystalline copper at high temperatures by alloying with tantalum. J. Alloy. Compd. 2013, 573, 142–150. [Google Scholar] [CrossRef]
- Rajagopalan, M.; Darling, K.; Turnage, S.; Koju, R.K.; Hornbuckle, B.; Mishin, Y.; Solanki, K.N. Microstructural evolution in a nanocrystalline Cu-Ta Alloy: A combined in-situ TEM and atomistic study. Mater. Des. 2017, 113, 178–185. [Google Scholar] [CrossRef]
- Pierre, H. Atomsk: A tool for manipulating and coverting atomic data files. Comput. Phys. Commun. 2015, 197, 212–219. [Google Scholar]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Pun, G.P.; Darling, K.A.; Kecskes, L.J.; Mishin, Y. Angular-dependent interatomic potential for the Cu-Ta system and its application to structural stability of nano-crystalline alloys. Acta Mater. 2015, 100, 377–391. [Google Scholar]
- Pan, Z.; Li, Y.; Wei, Q. Tensile properties of nanocrystalline tantalum from molecular dynamics simulations. Acta Mater. 2008, 56, 3470–3480. [Google Scholar] [CrossRef]
- Chang, L.; Zhou, C.Y.; Wen, L.L.; Li, J.; He, X.H. Molecular dynamics study of strain rate effects on tensile behavior of single crystal titanium nanowire. Comput. Mater. Sci. 2017, 128, 348–358. [Google Scholar] [CrossRef]
- Wang, W.; Pi, Z.; Lei, F.; Lu, Y. Understanding the tensile behaviors of ultra-thin ZnO nanowires via molecular dynamics simulations. AIP Adv. 2016, 6, 26–33. [Google Scholar] [CrossRef]
- Huang, C.; Peng, X.; Yang, B.; Chen, X.; Li, Q.; Yin, D.; Fu, T. Effects of strain rate and annealing temperature on tensile properties of nanocrystalline diamond. Carbon 2018, 4, 320–328. [Google Scholar] [CrossRef]
- Meyers, M.A.; Chen, Y.J.; Marquis, F.D.; Kim, D.S. High-strain-rate behavior of tantalum. Metall. Mater. Trans. A 1995, 26, 2493–2501. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Isaacs, J.B.; Liu, M. Microstructure of high-strain, high-strain-rate deformed tantalum. Acta Mater. 1998, 46, 1307–1325. [Google Scholar] [CrossRef]
- Shang, G.Q.; Wang, X.N.; Fei, Y.; Li, J.; Zhu, L.W.; Zhu, Z.S. Effect of hot forging strain rate on the microstructure and mechanical properties of TC4-DT Titanium Alloy. Mater. Sci. Forum 2016, 849, 271–275. [Google Scholar] [CrossRef]
- Hahn, E.N.; Meyers, M.A. Grain-size dependent mechanical behavior of nanocrystalline metals. Mater. Sci. Eng. A 2015, 646, 101–134. [Google Scholar] [CrossRef]
- Quek, S.S.; Chooi, Z.H.; Wu, Z.; Zhang, Y.W.; Srolovitz, D.J. The inverse Hall-Petch relation in nanocrystalline metals: a discrete dislocation dynamics analysis. J. Mech. Phys. Solids 2016, 88, 252–266. [Google Scholar] [CrossRef]
- Wang, L.; Teng, J.; Liu, P.; Hirata, A.; Ma, E.; Zhang, Z.; Chen, M.; Han, X. Grain rotation by grain boundary dislocations in nanocrystalline platinum. Nat. Commun. 2014, 5, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Schiiotz, J.; Jacobsen, K.W. A maximum in the strength of nanocrystalline copper. Science 2003, 301, 1357–1359. [Google Scholar] [CrossRef]
- Rupert, T.J.; Gianola, D.S.; Gan, Y.; Hemker, K.J. Experimental observations of stress-driven grain boundary migration. Science 2009, 326, 1686–1690. [Google Scholar] [CrossRef]
- Huang, Z.; Bartels, M.; Xu, R.; Osterhoff, M.; Kalbfleisch, S.; Sprung, M.; Suzuki, A.; Takahashi, Y.; Blanton, T.N.; Salditt, T.; et al. Grain rotation and lattice deformation during photoinduced chemical reactions revealed by in situ X-ray nanodiffraction. Nat. Mater. 2015, 14, 691–695. [Google Scholar] [CrossRef][Green Version]
- Wang, X.; Li, K.; Zhu, Y.M.; Li, W.B.; Wang, W.D. Molecular Dynamics Study on Mechanical Properties of Nanocrystalline tantalum. In Proceedings of the 2019 IEEE International Conference on Nanotechnology, Macau, China, 22–26 July 2019. [Google Scholar]
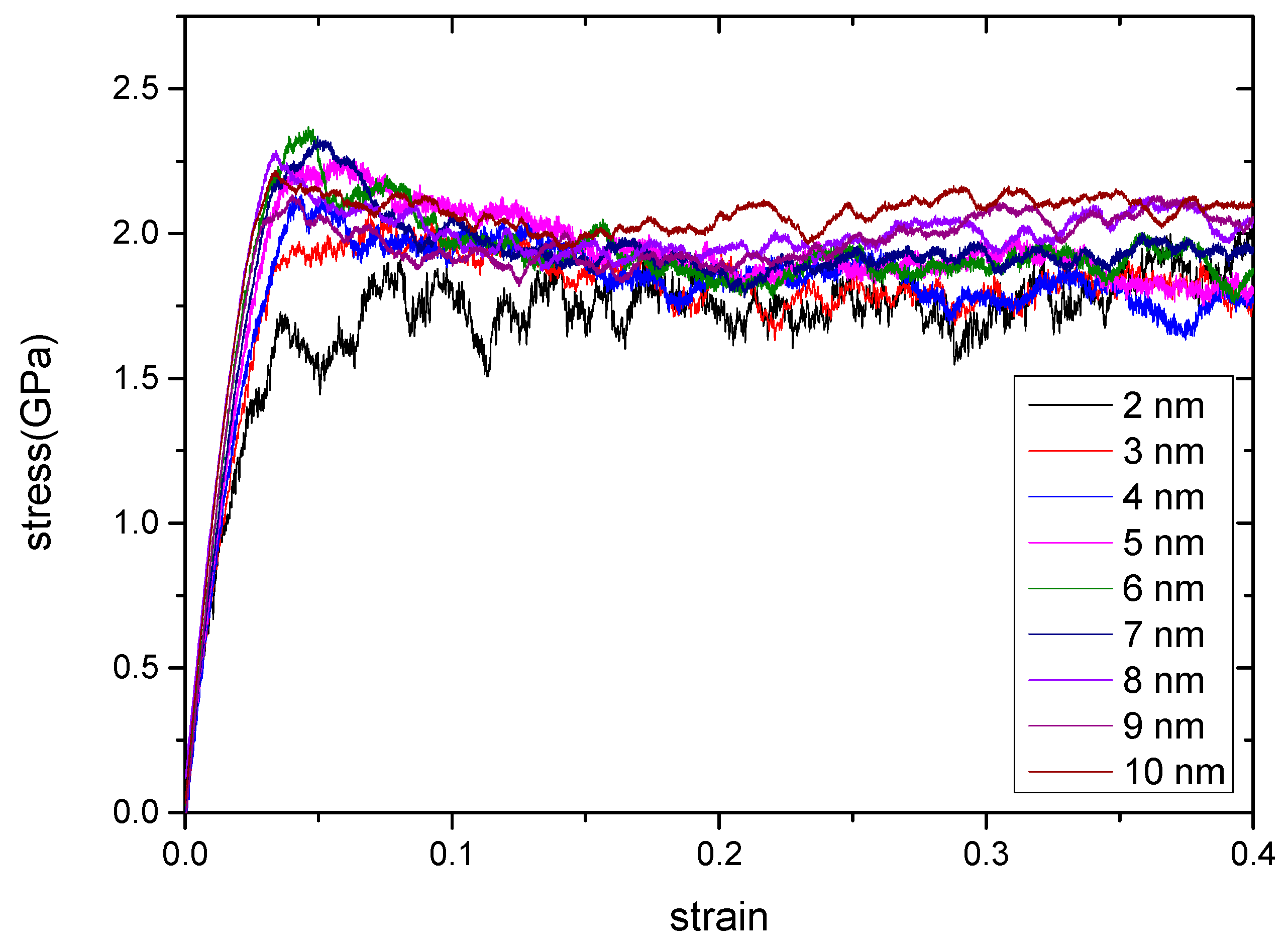

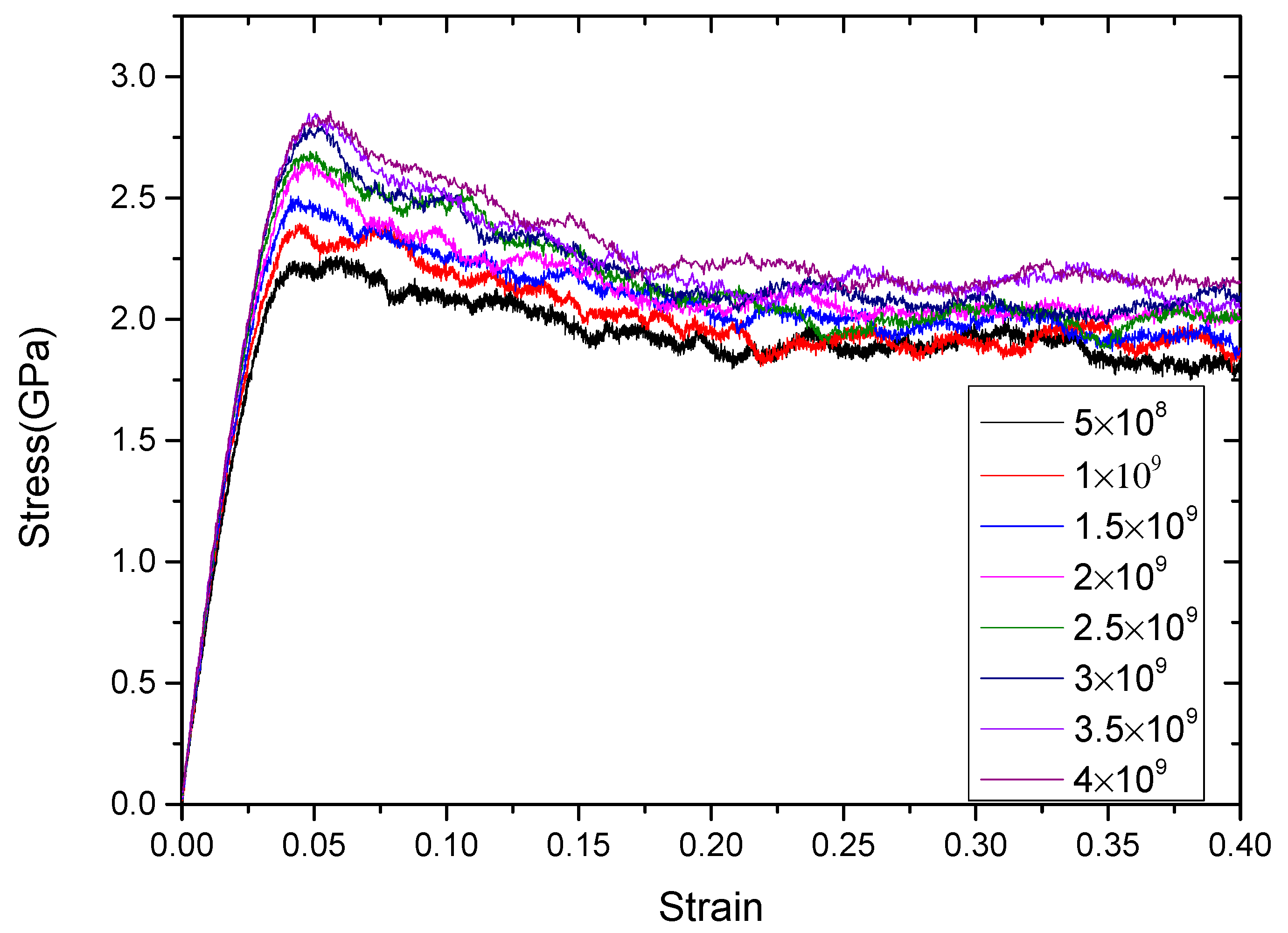
| Grain Size (nm) | Elastic Modulus (GPa) | Flow Strength (GPa) |
|---|---|---|
| 2 | 48.26 | 1.78 |
| 3 | 61.92 | 1.79 |
| 4 | 68.86 | 1.81 |
| 5 | 69.73 | 1.87 |
| 6 | 75.76 | 1.89 |
| 7 | 76.13 | 1.91 |
| 8 | 80.44 | 2.01 |
| 9 | 81.53 | 2.03 |
| 10 | 85.44 | 2.09 |
| Strain Rate (s−1) | 5 nm | 10 nm | ||
|---|---|---|---|---|
| Elastic Modulus (GPa) | Flow Strength (GPa) | Elastic Modulus (GPa) | Flow Strength (GPa) | |
| 5.0 × 108 | 68.38 | 1.87 | 75.98 | 2.09 |
| 1.0 × 109 | 72.71 | 1.91 | 80.26 | 2.16 |
| 1.5 × 109 | 74.17 | 1.97 | 81.64 | 2.21 |
| 2.0 × 109 | 77.97 | 2.04 | 85.37 | 2.23 |
| 2.5 × 109 | 78.43 | 2.05 | 86.72 | 2.27 |
| 3.0 × 109 | 78.88 | 2.07 | 86.54 | 2.31 |
| 3.5 × 109 | 78.55 | 2.13 | 86.33 | 2.34 |
| 4.0 × 109 | 78.46 | 2.17 | 86.64 | 2.36 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Wang, X.; Gao, L.; Lu, Y.; Wang, W. Atomic Study on Tension Behaviors of Sub-10 nm NanoPolycrystalline Cu–Ta Alloy. Materials 2019, 12, 3913. https://doi.org/10.3390/ma12233913
Li W, Wang X, Gao L, Lu Y, Wang W. Atomic Study on Tension Behaviors of Sub-10 nm NanoPolycrystalline Cu–Ta Alloy. Materials. 2019; 12(23):3913. https://doi.org/10.3390/ma12233913
Chicago/Turabian StyleLi, Weibing, Xiao Wang, Libo Gao, Yang Lu, and Weidong Wang. 2019. "Atomic Study on Tension Behaviors of Sub-10 nm NanoPolycrystalline Cu–Ta Alloy" Materials 12, no. 23: 3913. https://doi.org/10.3390/ma12233913
APA StyleLi, W., Wang, X., Gao, L., Lu, Y., & Wang, W. (2019). Atomic Study on Tension Behaviors of Sub-10 nm NanoPolycrystalline Cu–Ta Alloy. Materials, 12(23), 3913. https://doi.org/10.3390/ma12233913








