The Effect of Co-Doping at the A-Site on the Structure and Oxide Ion Conductivity in (Ba0.5−xSrx)La0.5InO3−δ: A Molecular Dynamics Study
Abstract
1. Introduction
2. Experimental and Simulation Methods
2.1. Experimental Method
2.2. Simulation Method
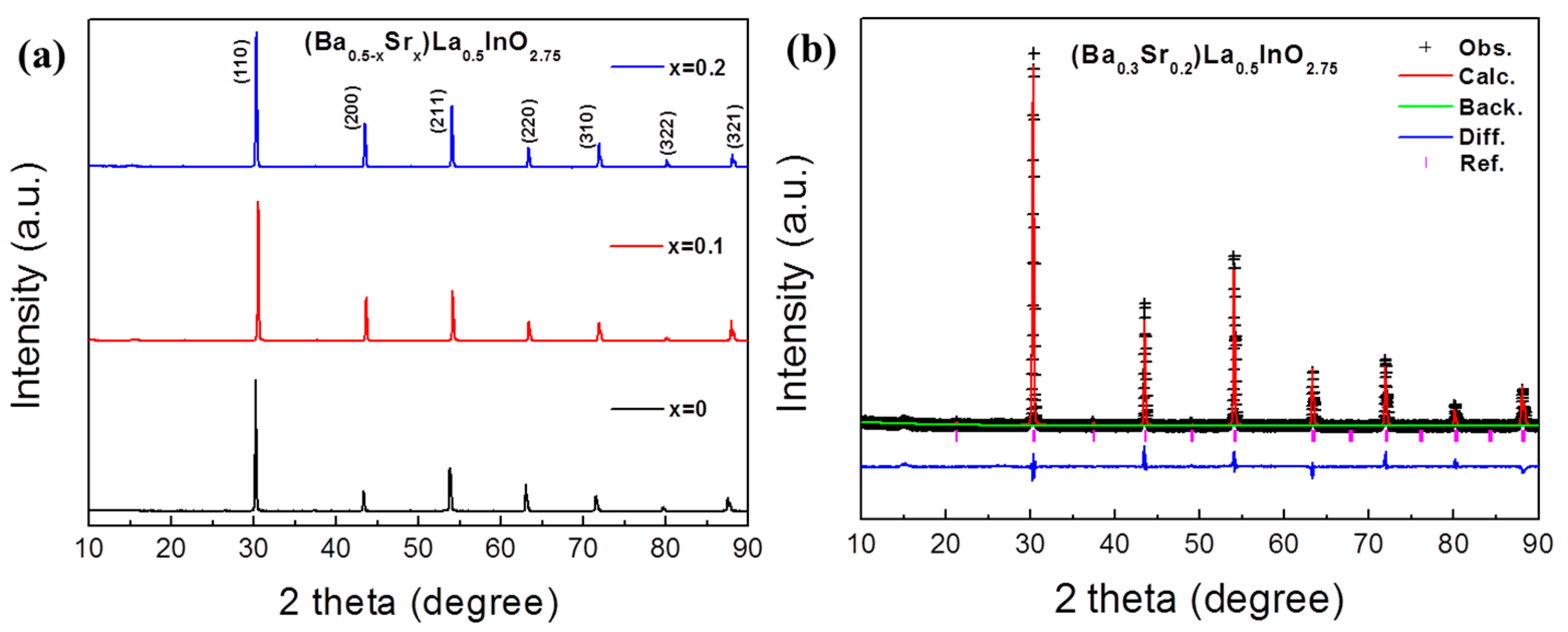
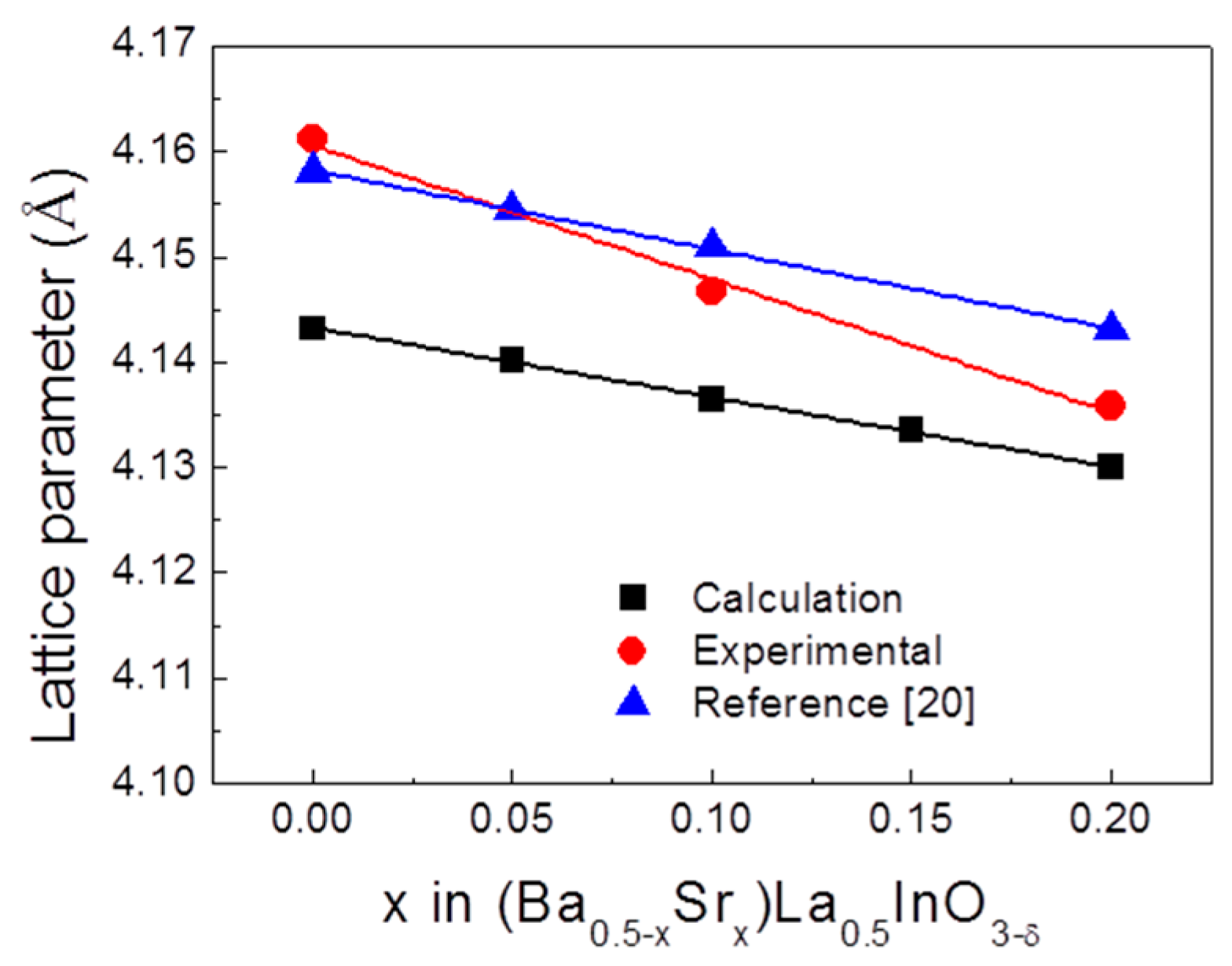
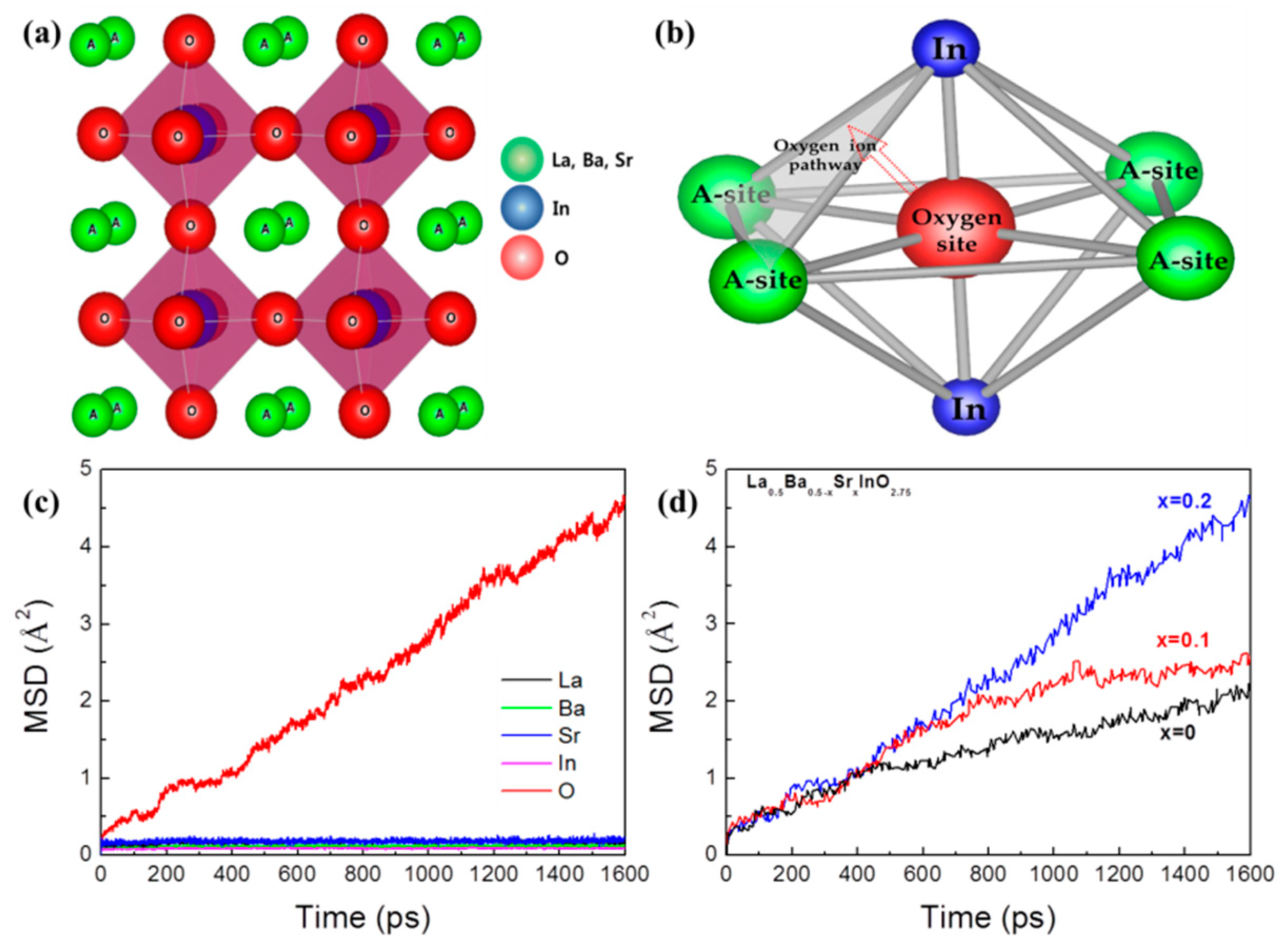
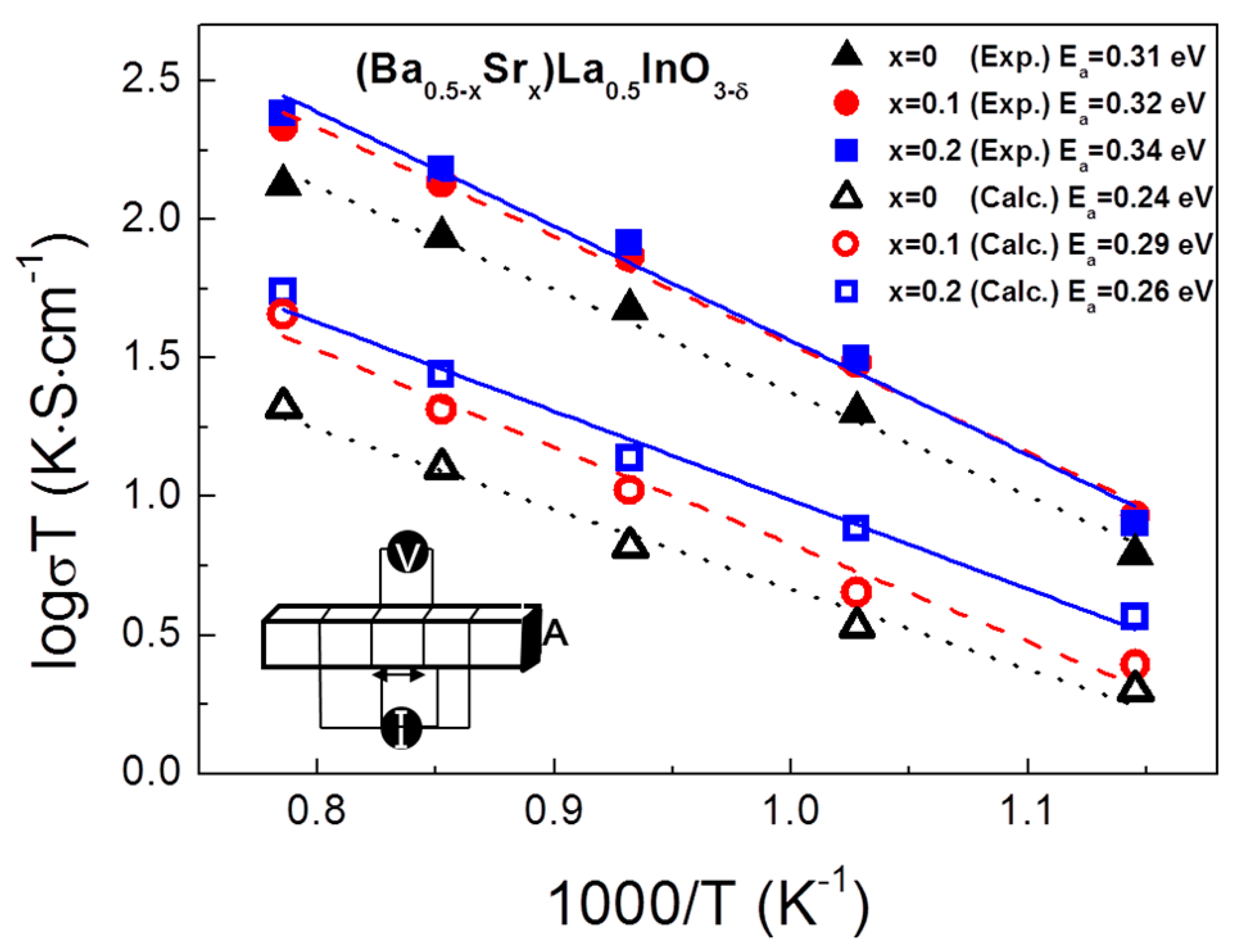
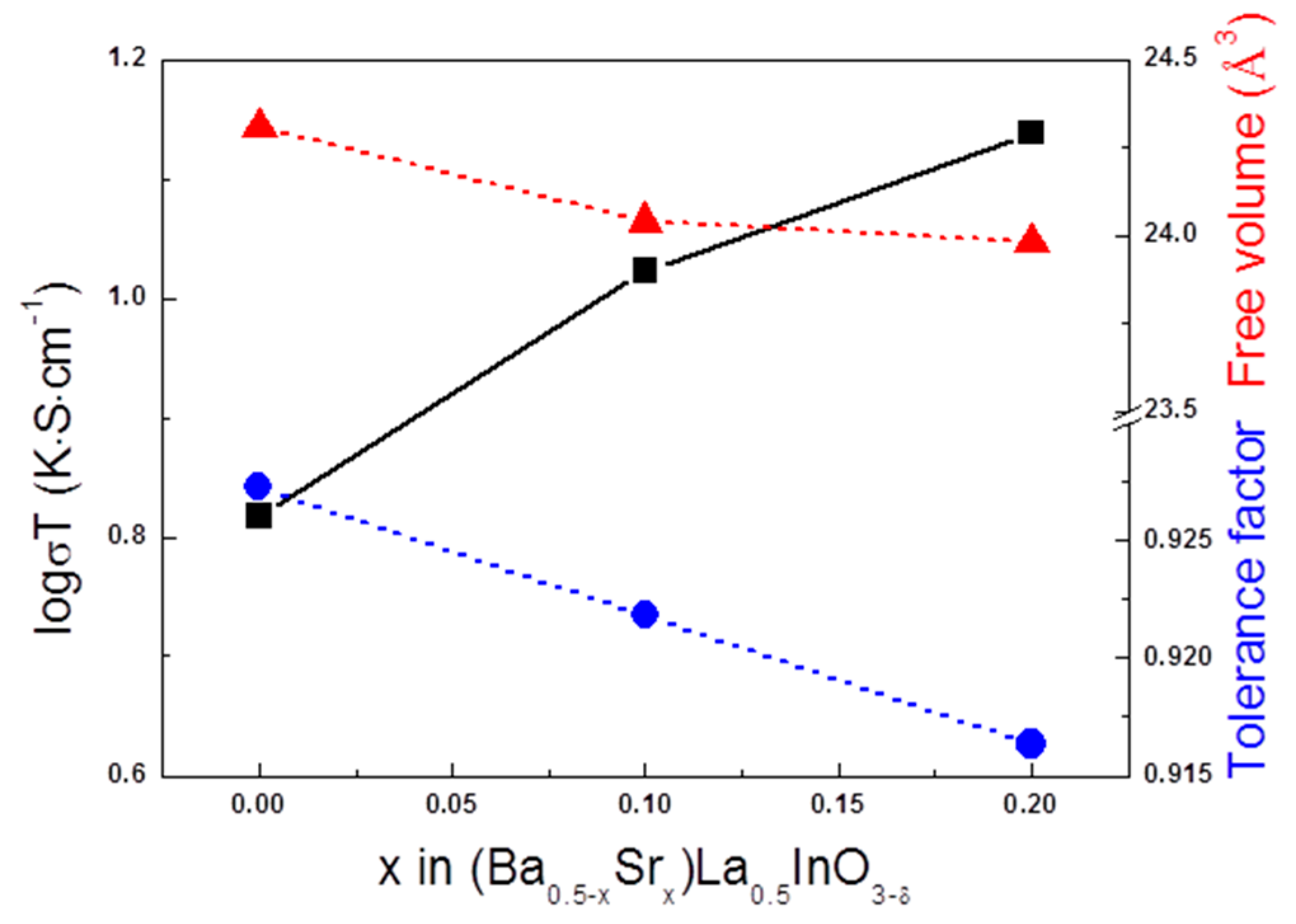
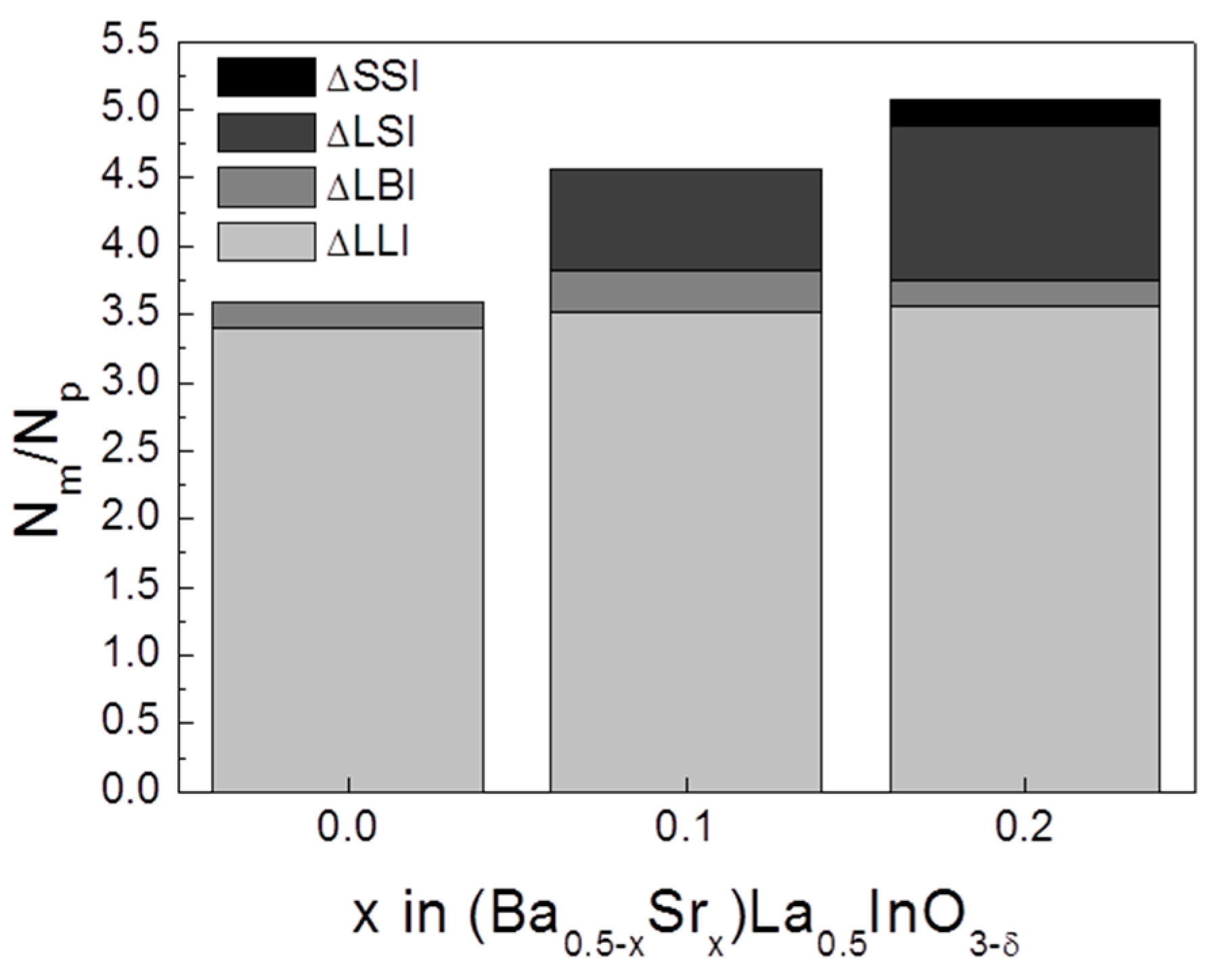
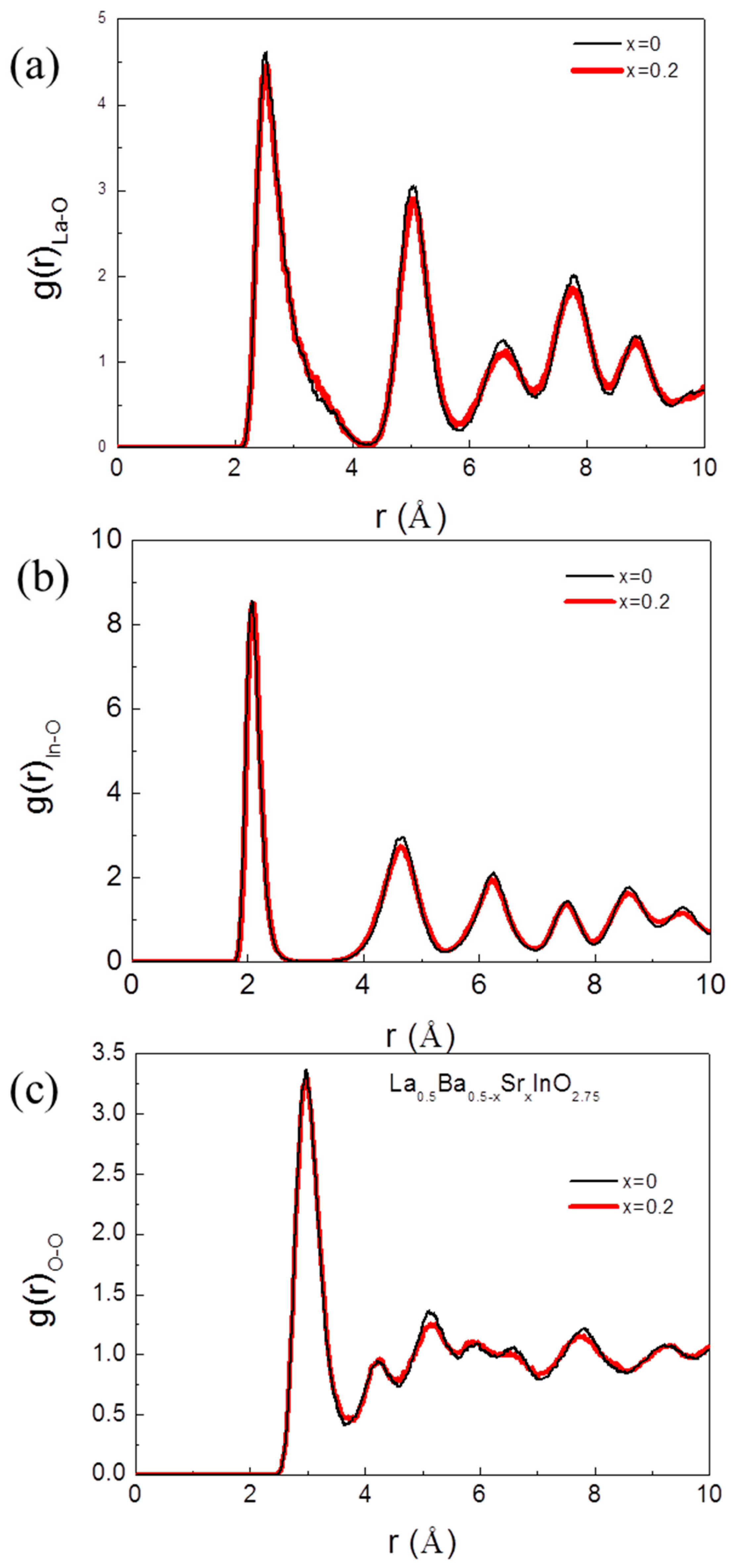
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fergus, J.W. Electrolytes for solid oxide fuel cells. J. Power Sources. 2006, 162, 30–40. [Google Scholar] [CrossRef]
- Ramamoorthy, R.; Dutta, P.K.; Akbar, S.K. Oxygen Sensors: Materials, methods, designs and applications. J. Mater. Sci. 2003, 38, 4271–4282. [Google Scholar] [CrossRef]
- Badwal, S.P.S.; Drennan, J. Yttria-zirconia: Effect of microstructure on conductivity. J. Mater. Sci. 1987, 22, 3231–3239. [Google Scholar] [CrossRef]
- Xia, C. Electrolytes, in Solid Oxide Fuel Cells Materials Properties and Performance; Fergus, J.W., Hui, R., Li, X., Wilkinson, D.P., Zhang, J., Eds.; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2009; pp. 3–5. [Google Scholar] [CrossRef]
- Kharton, V.V.; Marques, F.M.B.; Atkinson, A. Transport properties of solid oxide electrolyte ceramics: A brief review. Solid State Ion. 2004, 174, 135–149. [Google Scholar] [CrossRef]
- Yamamoto, O.; Arati, Y.; Takeda, Y.; Imanishi, N.; Mizutani, Y.; Kawai, M.; Nakamura, Y. Electrical conductivity of stabilized zirconia with ytterbia and scandia. Solid State Ion. 1995, 79, 137–142. [Google Scholar] [CrossRef]
- Wang, S.; Jiang, Y.; Zhang, Y.; Yan, J.; Li, W. Promoting effect of YSZ on the electrochemical performance of YSZ+LSM composite electrodes. Solid State Ion. 1998, 113–115, 291–303. [Google Scholar] [CrossRef]
- Lybye, D.; Poulsen, F.W.; Mogensen, M. Conductivity of A- and B-site doped LaAlO3, LaGaO3, LaScO3 and LaInO3 perovskites. Solid State Ion. 2000, 128, 91–103. [Google Scholar] [CrossRef]
- Huang, P.; Petric, A. Superior oxygen ion conductivity of lanthanum gallate doped with strontium and magnesium. J. Electrochem. Soc. 1996, 143, 1644–1648. [Google Scholar] [CrossRef]
- Nomura, K.; Tanase, S. Electrical conduction behavior in (La0.9Sr0.1)MIIIO3−δ (MIII = Al, Ga, Sc, In, and Lu) perovskites. Solid State Ion. 1997, 98, 229–236. [Google Scholar] [CrossRef]
- Nomura, K.; Takeuchi, T.; Tanase, S.; Kageyama, H.; Tanimoto, K.; Miyazaki, Y. Proton conduction in (La0.9Sr0.1)MIIIO3−δ (MIII = Al, Ga, Sc, In, and Lu) perovskites. Solid State Ion. 2002, 154–155, 647–652. [Google Scholar] [CrossRef]
- Ishihara, T.; Matsuda, H.; Takita, Y. Doped LaGaO3 perovskite type oxide as a new oxide ionic conductor. J. Am. Chem. Soc. 1994, 116, 3801–3803. [Google Scholar] [CrossRef]
- He, H.; Huang, X.; Chen, L. Sr-doped LaInO3 and its possible application in a single layer SOFC. Solid State Ion. 2000, 130, 183–193. [Google Scholar] [CrossRef]
- Kim, H.; Lee, K.; Kim, S.; Lee, H. Electrical conduction behavior of BaO-doped LaInO3 perovskite oxide. Jpn. J. Appl. Phys. 2006, 45, 872–874. [Google Scholar] [CrossRef]
- Kakinuma, K.; Arisaka, T.; Yamamura, H.; Atake, T. Solid oxide fuel cell using (Ba0.3Sr0.2La0.5)InO2.75 electrolyte. Solid State Ion. 2004, 175, 139–143. [Google Scholar] [CrossRef]
- Byeon, D.; Jeong, S.; Hwang, K.; Yoon, M.; Hwang, H.; Kim, S.; Lee, H. Oxide ion diffusion in Ba-doped LaInO3 perovskite: A molecular dynamics study. J. Power Sources. 2013, 222, 282–287. [Google Scholar] [CrossRef]
- Larson, A.C.; Von Dreele, R.B. General Structure Analysis System (GSAS); Los Alamos National Laboratory Report LAUR: Los Alamos, NM, USA, 2004; pp. 86–748.
- Toby, B.H. EXPGUI, A graphical user interface for GSAS. J. Appl. Cryst. 2001, 34, 210–213. [Google Scholar] [CrossRef]
- Uchimoto, Y.; Takagi, H.; Yao, T.; Ozawa, N.; Inagaki, T.; Yoshida, H. EXAFS study of crystal structures of (Ba1−xLax)2In2O5+x and their oxide ion conductivity. J. Sync. Rad. 2001, 8, 857–859. [Google Scholar] [CrossRef]
- Kakinuma, K.; Yamamura, H.; Atake, T. High oxide ion conductivity of (Ba1−x−ySrxLay)InO2.5+y/2 members derived from Ba2In2O5 system. Defect. Diffus. Forum. 2005, 242–244, 159–168. [Google Scholar] [CrossRef]
- Fumi, F.G.; Tosi, M.P. Ionic sizes and born repulsive parameters in the NaCl-type alkali halides-I: The Huggins-Mayer and pauling forms. J. Phys. Chem. Solids. 1964, 25, 31–43. [Google Scholar] [CrossRef]
- Tosi, M.P.; Fumi, F.G. Ionic sizes and born repulsive parameters in the NaCl-type alkali halides-II: The generalized Huggins-Mayer form. J. Phys. Chem. Solids. 1964, 25, 45–52. [Google Scholar] [CrossRef]
- Buckingham, R.A. The classical equation of state of gaseous helium, neon and argon. Proc. R. Soc. Lond. A Math. Phys. Sci. 1938, 168, 264. [Google Scholar] [CrossRef]
- Yamamura, Y.; Ihara, C.; Kawasaki, S.; Sakai, H.; Suzuki, K.; Takami, S.; Kubo, M.; Miyamoto, A. Materials design of perovskite-based oxygen ion conductor by molecular dynamics method. Solid State Ion. 2003, 160, 93–101. [Google Scholar] [CrossRef]
- Tamai, Y.; Kawamoto, Y. Molecular dynamics simulation of permanet densification of fluorozirconate glass. Chem. Phys. Lett. 1999, 302, 15–19. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Ishigaki, T.; Yamauchi, S.; Kishio, K.; Mizusaki, J.; Fueki, K. Diffusion of oxide ion vacancies in perovskite-type oxides. J. Solid State Chem. 1998, 73, 179–187. [Google Scholar] [CrossRef]
- Ruiz-Trejo, E.; Tavizon, G.; Arroyo-Landeros, A. Structure, point defects and ion migration in LaInO3. J. Phys. Chem. Solids. 2003, 64, 515–521. [Google Scholar] [CrossRef]
- Burbano, M.; Norberg, S.T.; Hull, S.; Eriksson, S.G.; Marrocchelli, D.; Madden, P.A.; Watson, G.W. Oxygen vacancy ordering and the conductivity maximum in Y2O3-doped CeO2. Chem. Mater. 2012, 24, 222–229. [Google Scholar] [CrossRef]
- Islam, M.S.; Cherry, M.; Catlow, C.R.A. Oxygen diffusion in LaMnO3 and LaCoO3 perovskite-type oxides: A molecular dynamics study. J. Solid State Chem. 1996, 124, 230–237. [Google Scholar] [CrossRef]
- Goldschmidt, V.M. Die Gesetze Der Krystallochemie. Naturwissenschaften 1926, 14, 477–485. [Google Scholar] [CrossRef]
- Cook, R.L.; Sammells, A.F. On the systematic selection of perovskite solid electrolytes for intermediate temperature fuel cells. Solid State Ion. 1991, 45, 311–321. [Google Scholar] [CrossRef]
- Kilner, J.A.; Brook, R.J. A study of oxygen ion conductivity in doped non-stoichiometric oxides. Solid State Ion. 1982, 6, 237–252. [Google Scholar] [CrossRef]
- Inaguma, Y.; Katsumata, T.; Mori, D. Predominant factor of activation energy for ionic conductivity in perovskite-type lithium ion-conducting oxides. J. Phys. Soc. Jpn. 2010, 79, 69–71. [Google Scholar] [CrossRef]
- Clarke, A.S.; Jonsson, H. Structural changes accompanying densification of random hard-sphere packings. Phys. Rev. E 1993, 47, 3975–3984. [Google Scholar] [CrossRef] [PubMed]
- Hwang, K.; Yoon, M.; Hwang, H.; Choi, S.; Jeong, S. Molecular dynamics simulation of oxygen ion conduction in orthorhombic perovskite Ba-doped LaInO3 using cubic and orthorhombic model. J. Nanosci. Nanotechnol. 2015, 15, 8947–8950. [Google Scholar] [CrossRef]
- Fabris, S.; Paxton, A.T.; Finnis, M.W. A stabilization mechanism of zirconia based on oxygen vacancies only. Acta Mater. 2002, 50, 5171–5178. [Google Scholar] [CrossRef]
| Interatomic Potential Parameters | ||||||
|---|---|---|---|---|---|---|
| - | La | Ba | Sr | In | O | |
| a (Å) | 2.149 | 1.800 | 2.028 | 2.013 | 1.568 | |
| b (Å) | 0.205 | 0.077 | 0.194 | 0.220 | 0.087 | |
| c (kcal·Å6/mol)0.5 | 0 | 0 | 0 | 0 | 27 | |
| Configurations of Oxide Ion Conduction Pathways | ||||||
| x | △LaLaIn | △LaBaIn | △LaSrIn | △BaSrIn | △SrSrIn | △BaBaIn |
| 0 | 572 | 1256 | 572 | |||
| 0.1 | 572 | 964 | 292 | 172 | 8 | 392 |
| 0.2 | 572 | 716 | 540 | 284 | 68 | 220 |
| - | △LaLaIn | △LaBaIn | △BaBaIn | △LaSrIn | △SrSrIn | △BaSrIn |
|---|---|---|---|---|---|---|
| x = 0 | 0.993 | 0.925 | 0.832 | - | - | - |
| x = 0.1 | 0.998 | 0.918 | 0.829 | 0.962 | 0.967 | 0.874 |
| x = 0.2 | 0.996 | 0.906 | 0.832 | 0.954 | 0.95 | 0.883 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hwang, K.-J.; Hwang, H.-J.; Lee, M.-H.; Jeong, S.-M.; Shin, T.H. The Effect of Co-Doping at the A-Site on the Structure and Oxide Ion Conductivity in (Ba0.5−xSrx)La0.5InO3−δ: A Molecular Dynamics Study. Materials 2019, 12, 3739. https://doi.org/10.3390/ma12223739
Hwang K-J, Hwang H-J, Lee M-H, Jeong S-M, Shin TH. The Effect of Co-Doping at the A-Site on the Structure and Oxide Ion Conductivity in (Ba0.5−xSrx)La0.5InO3−δ: A Molecular Dynamics Study. Materials. 2019; 12(22):3739. https://doi.org/10.3390/ma12223739
Chicago/Turabian StyleHwang, Kuk-Jin, Hae-Jin Hwang, Myung-Hyun Lee, Seong-Min Jeong, and Tae Ho Shin. 2019. "The Effect of Co-Doping at the A-Site on the Structure and Oxide Ion Conductivity in (Ba0.5−xSrx)La0.5InO3−δ: A Molecular Dynamics Study" Materials 12, no. 22: 3739. https://doi.org/10.3390/ma12223739
APA StyleHwang, K.-J., Hwang, H.-J., Lee, M.-H., Jeong, S.-M., & Shin, T. H. (2019). The Effect of Co-Doping at the A-Site on the Structure and Oxide Ion Conductivity in (Ba0.5−xSrx)La0.5InO3−δ: A Molecular Dynamics Study. Materials, 12(22), 3739. https://doi.org/10.3390/ma12223739







