Experimental and Numerical Studies of Low-Profile, Triangular Grid-Stiffened Plates Subjected to Shear Load in the Post-Critical States of Deformation
Abstract
1. Introduction
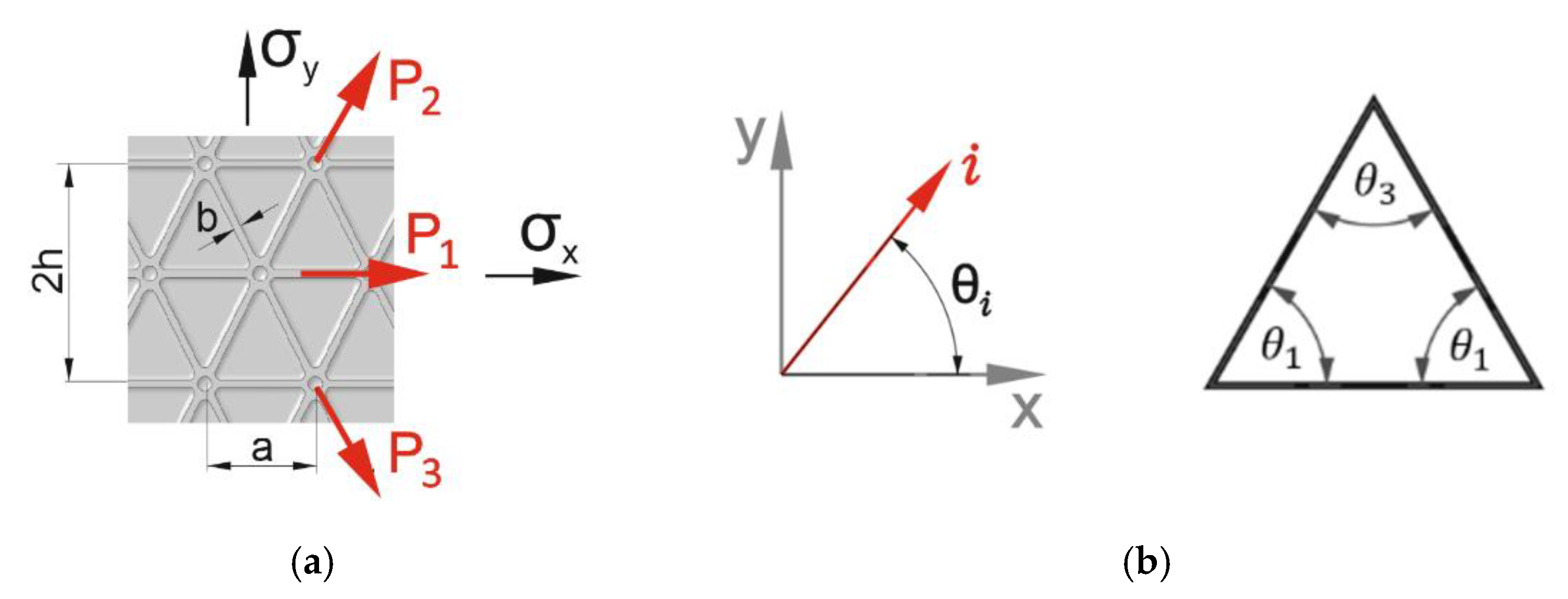
2. Theoretical Basis
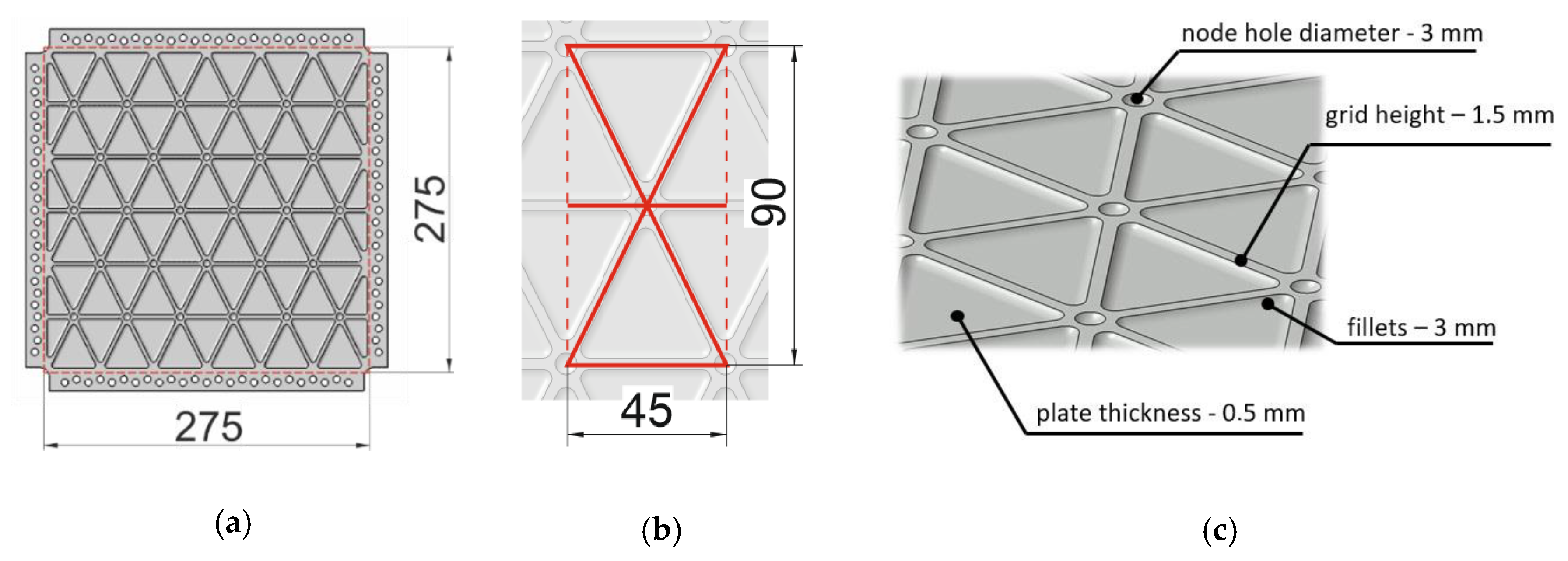
3. The Object of the Study
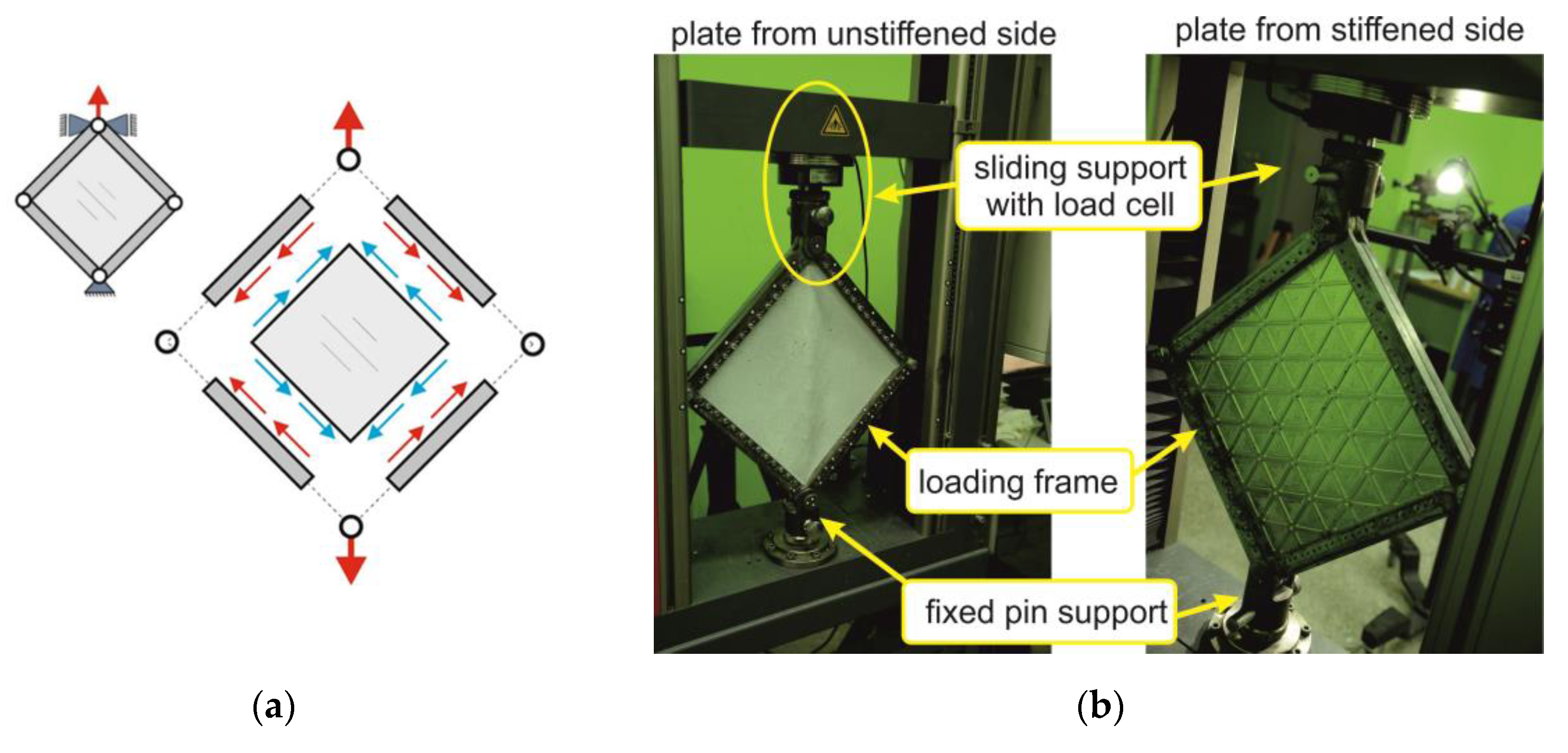
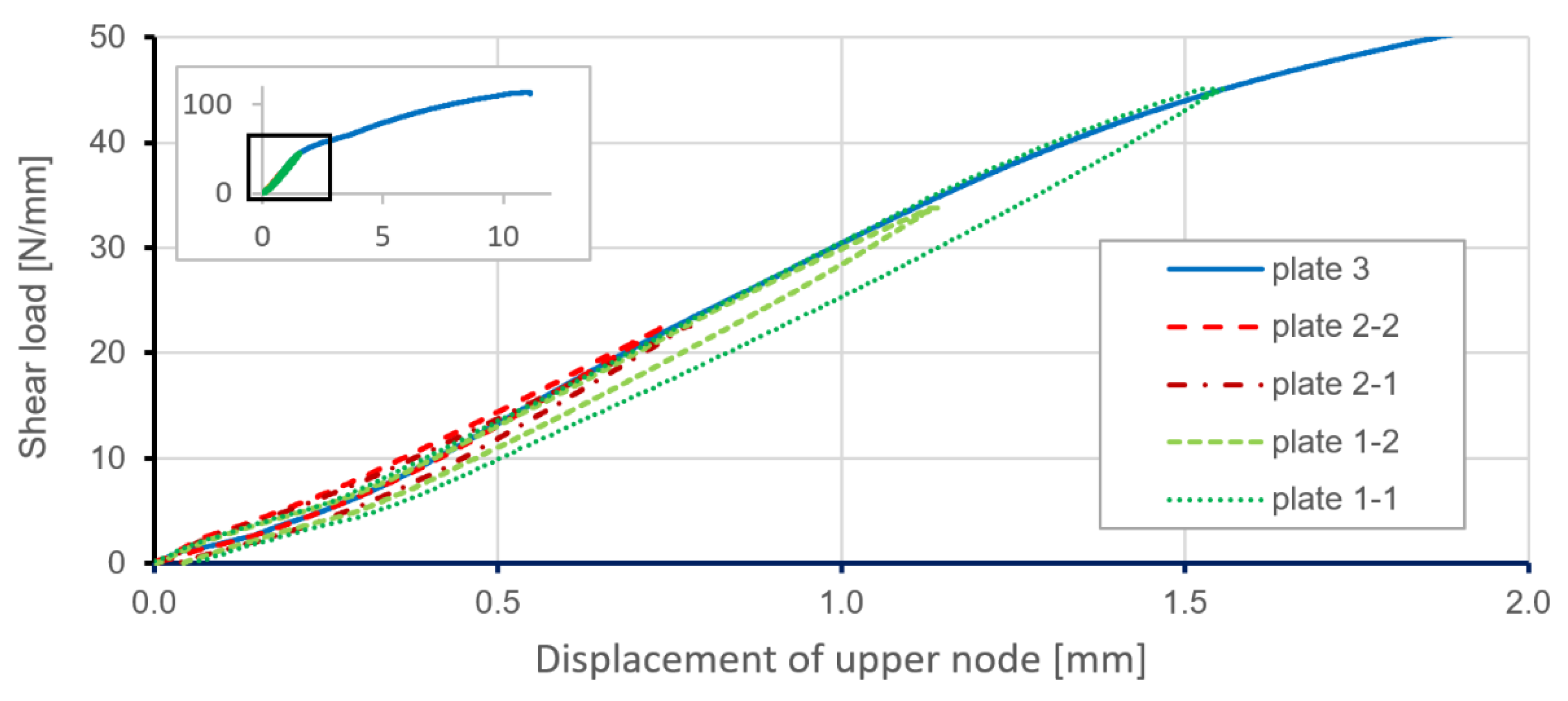
4. Experimental Test Stand
5. Numerical Modelling
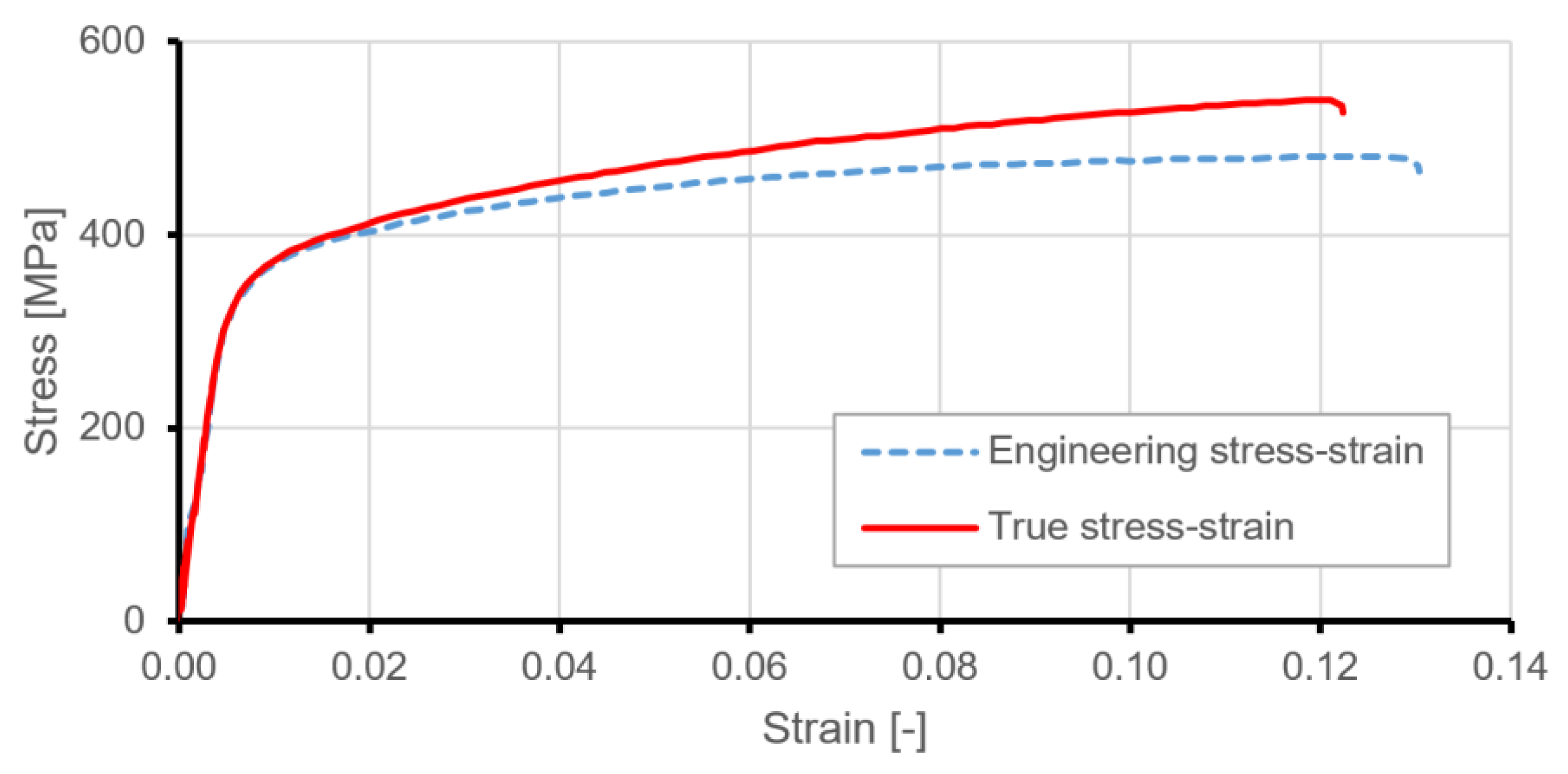
5.1. Material Modeling
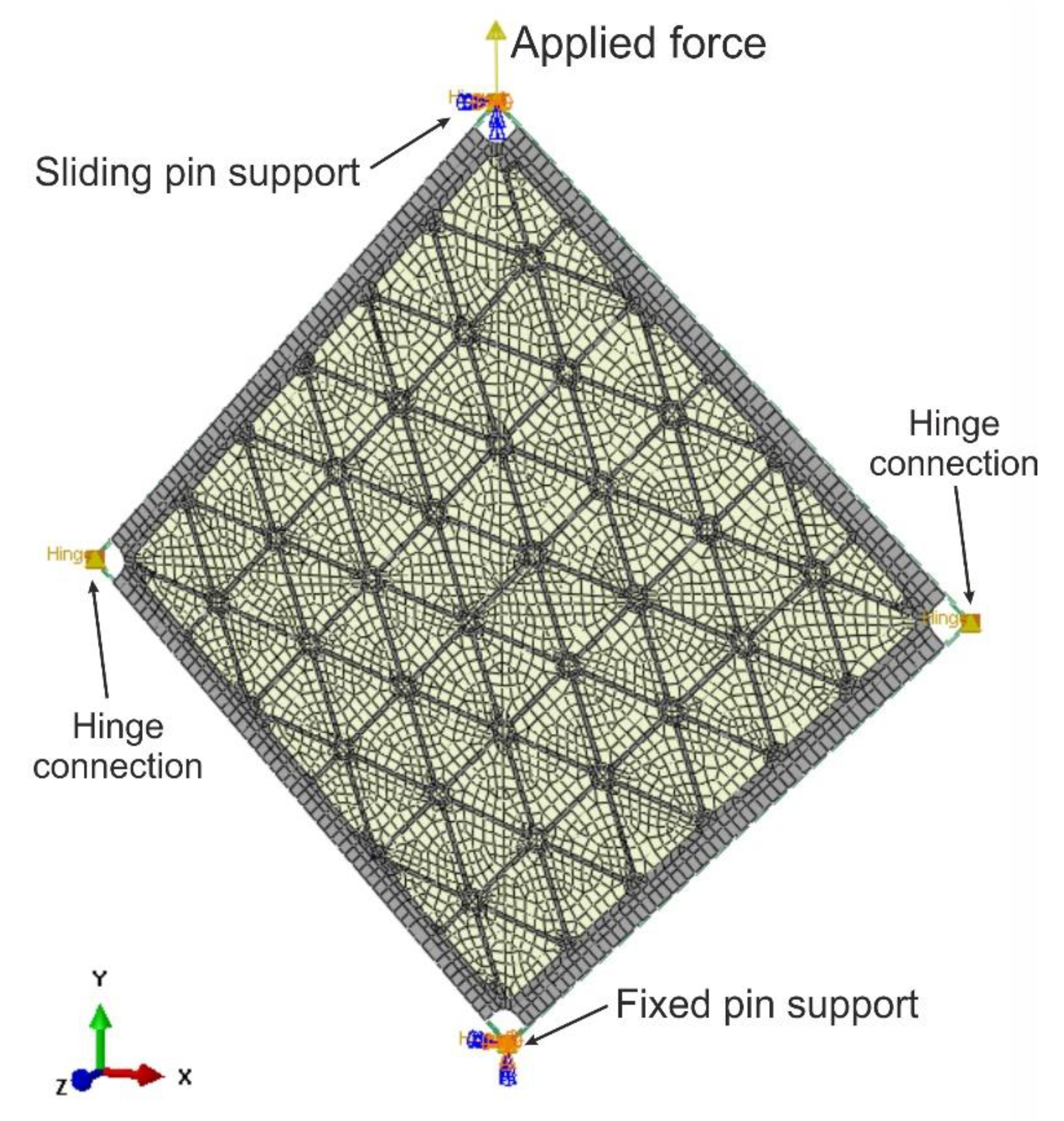
5.2. Boundary Conditions
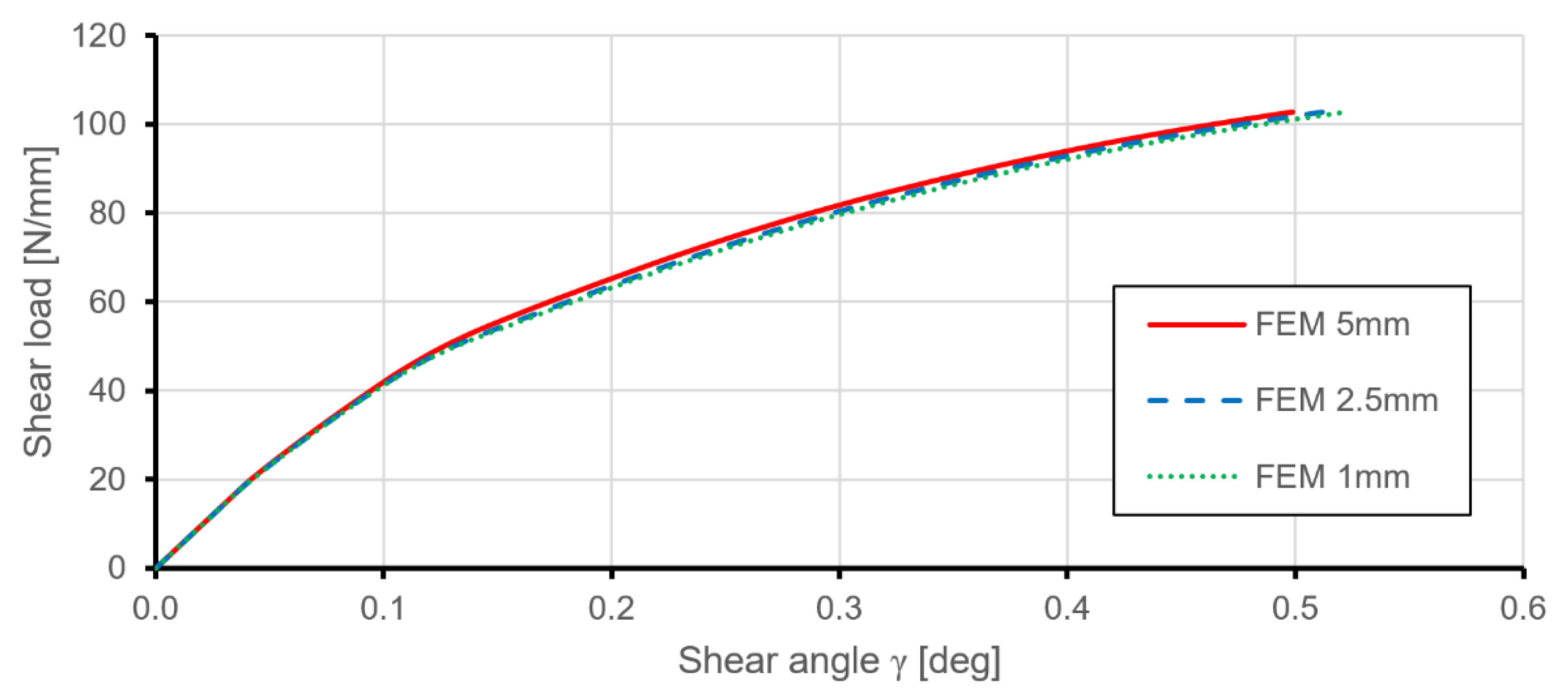
5.3. Mesh and Elements
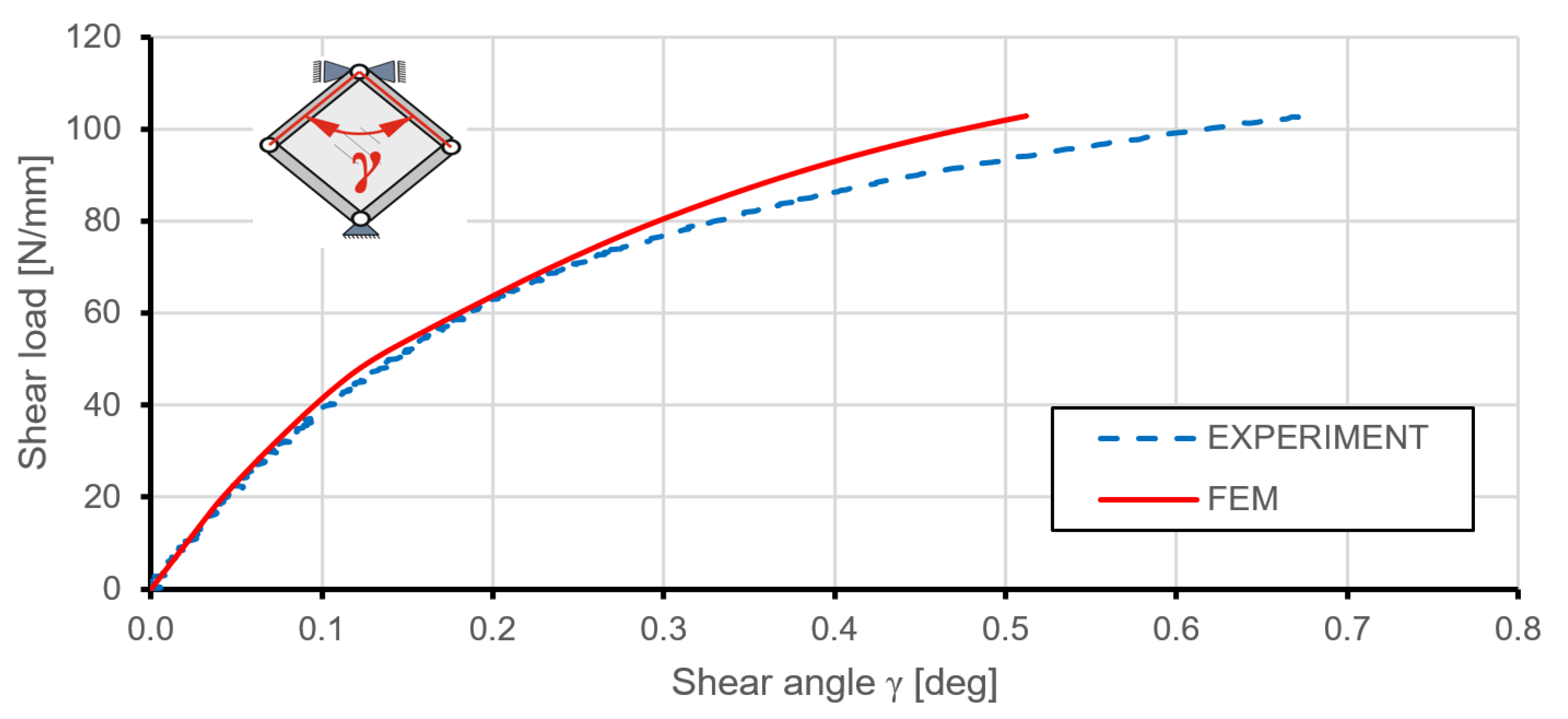
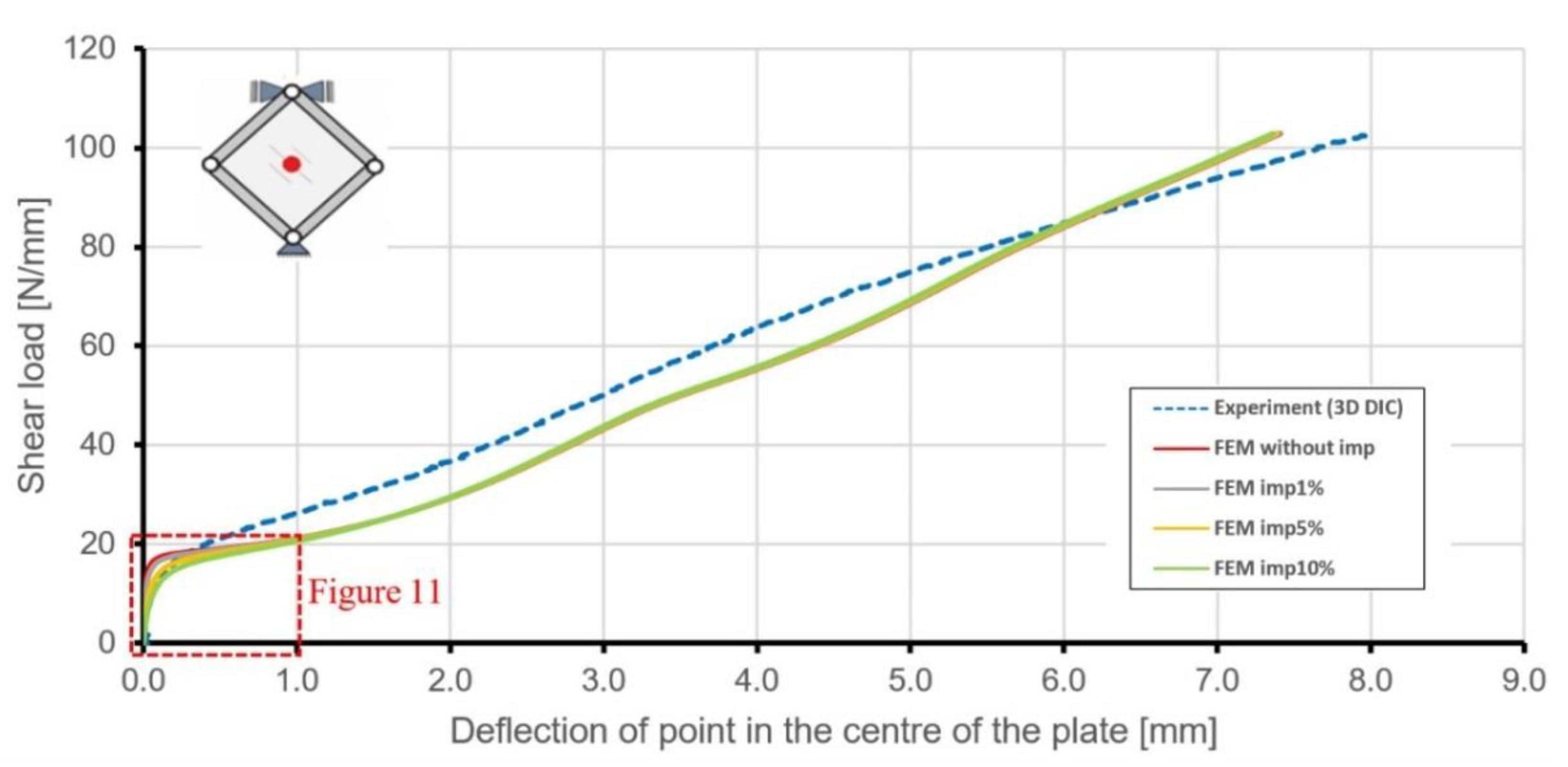
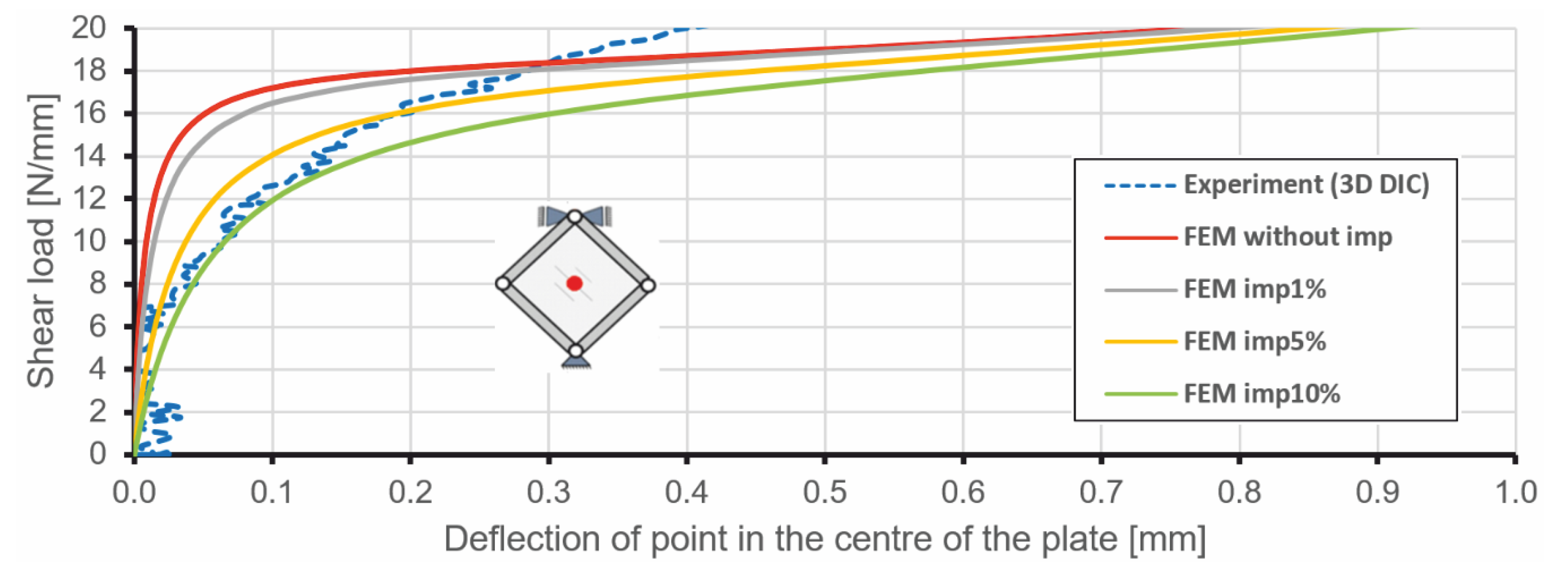
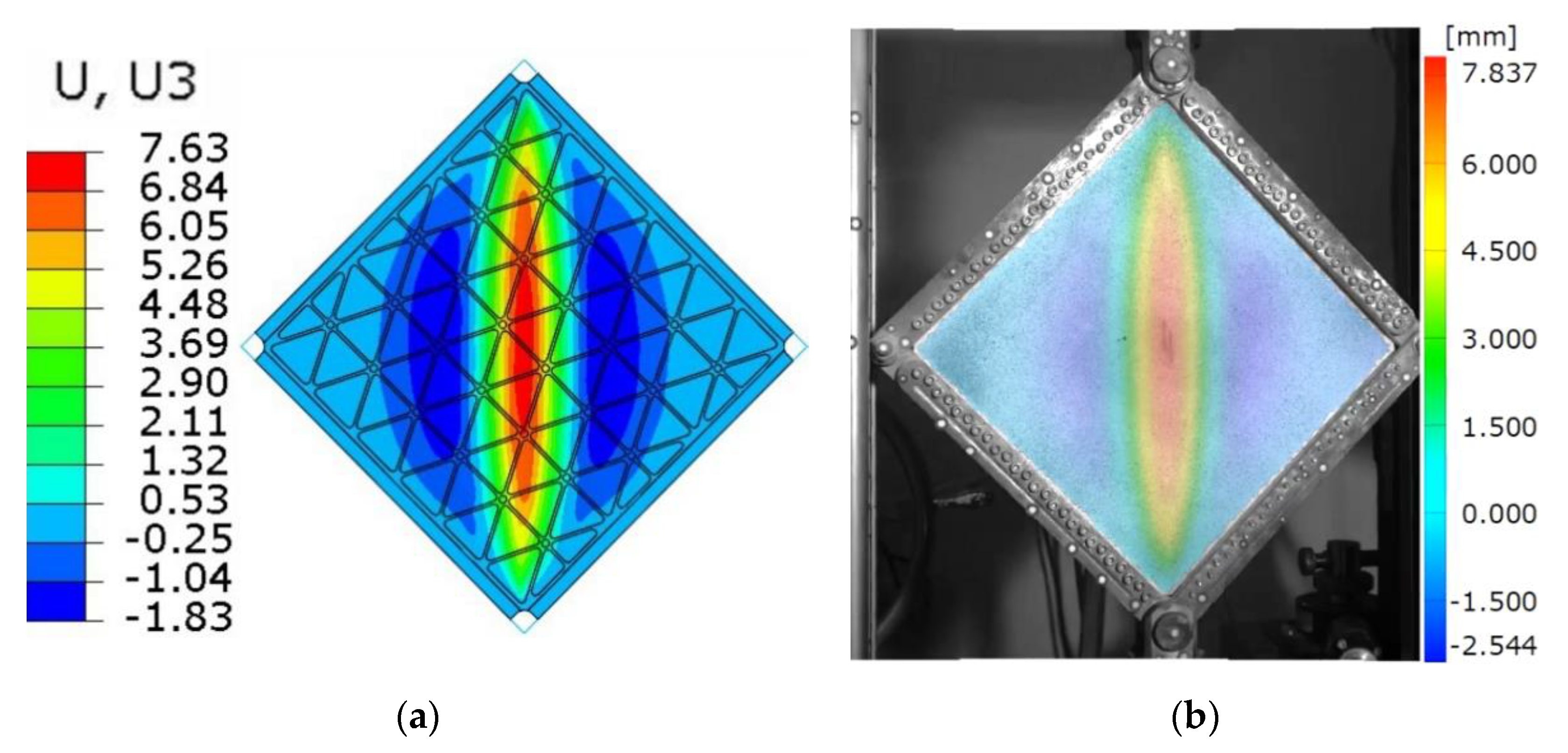
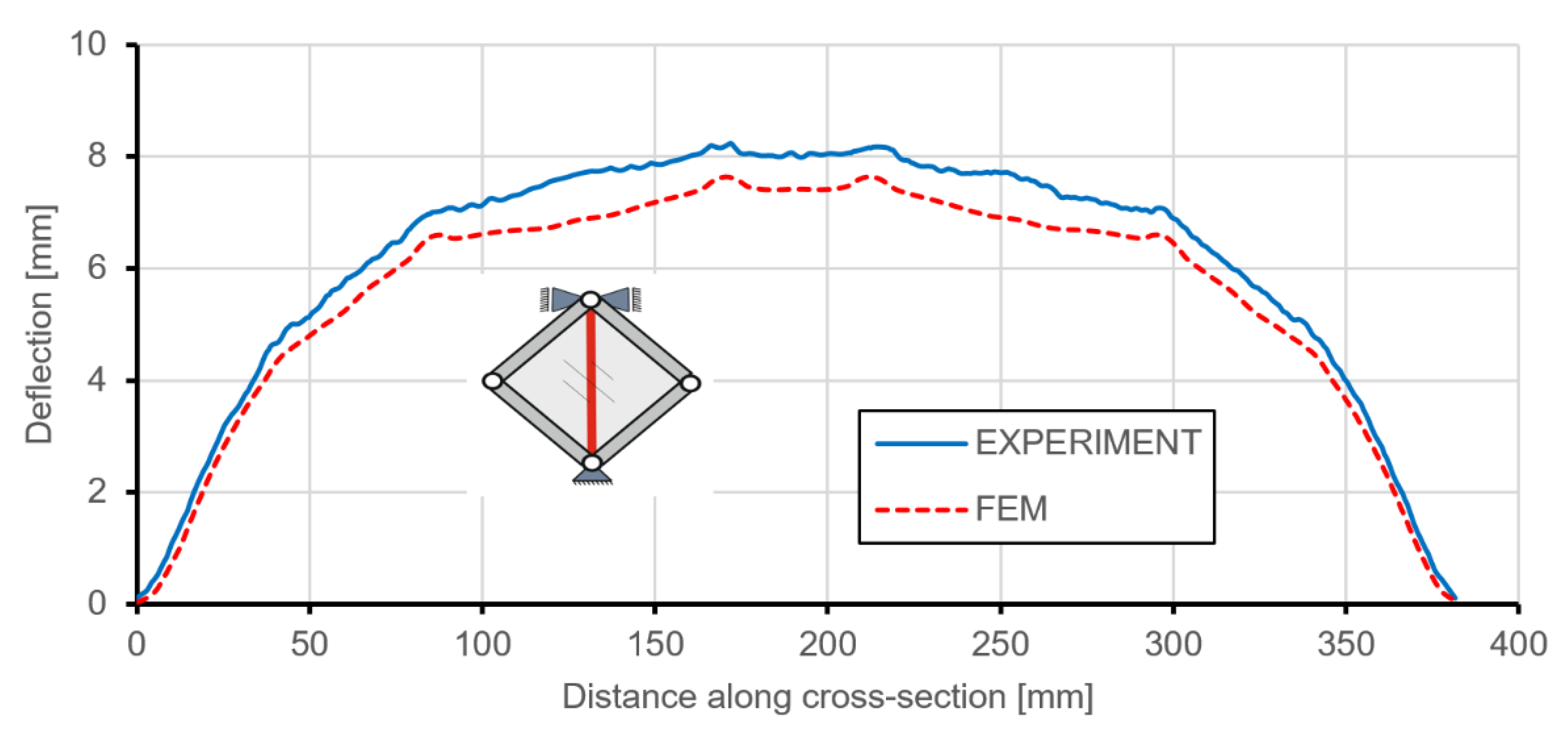
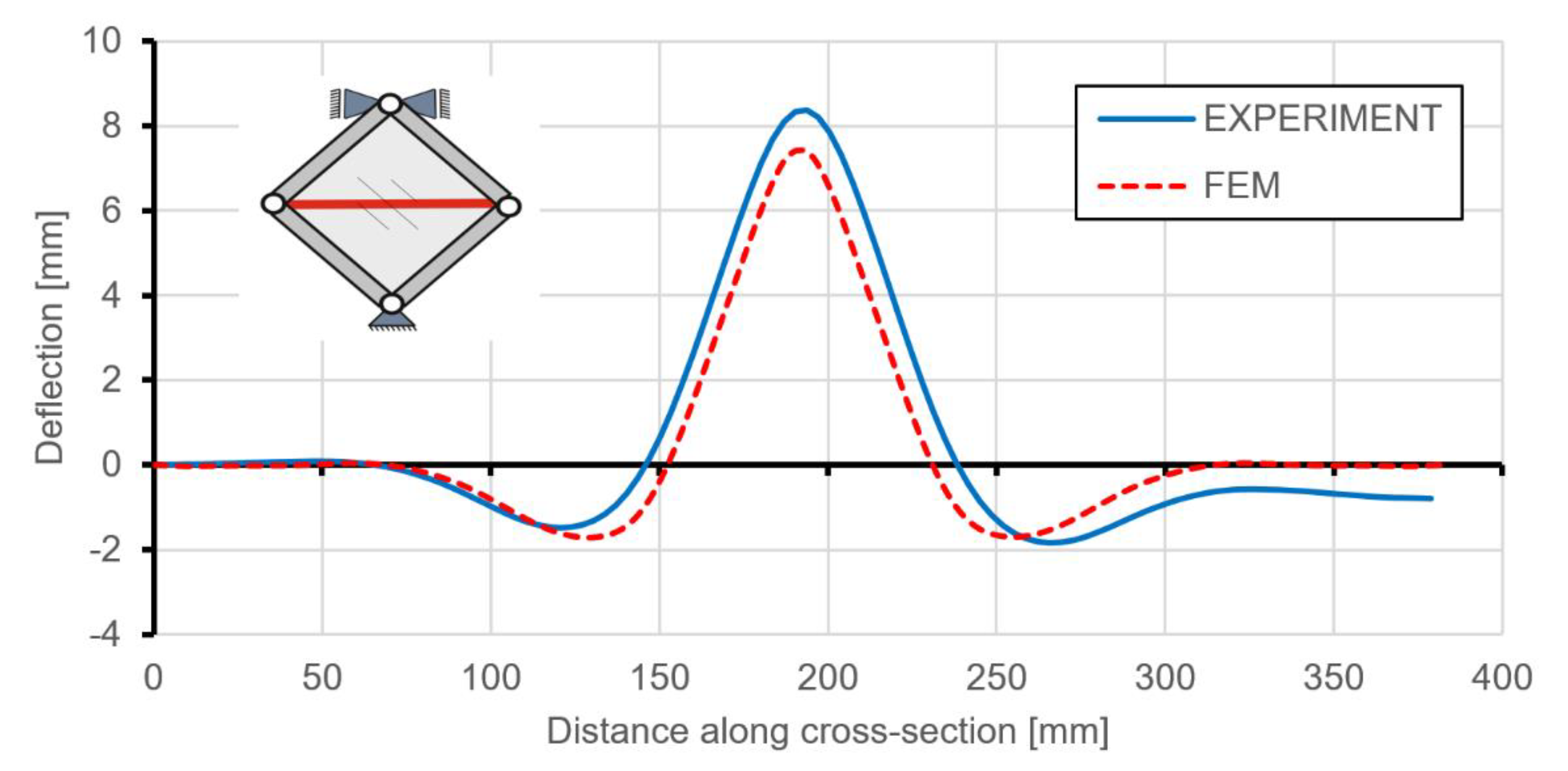
5.4. Validation
6. Results
6.1. Comparison of FE Results and the Experiment for the Stiffened Plate
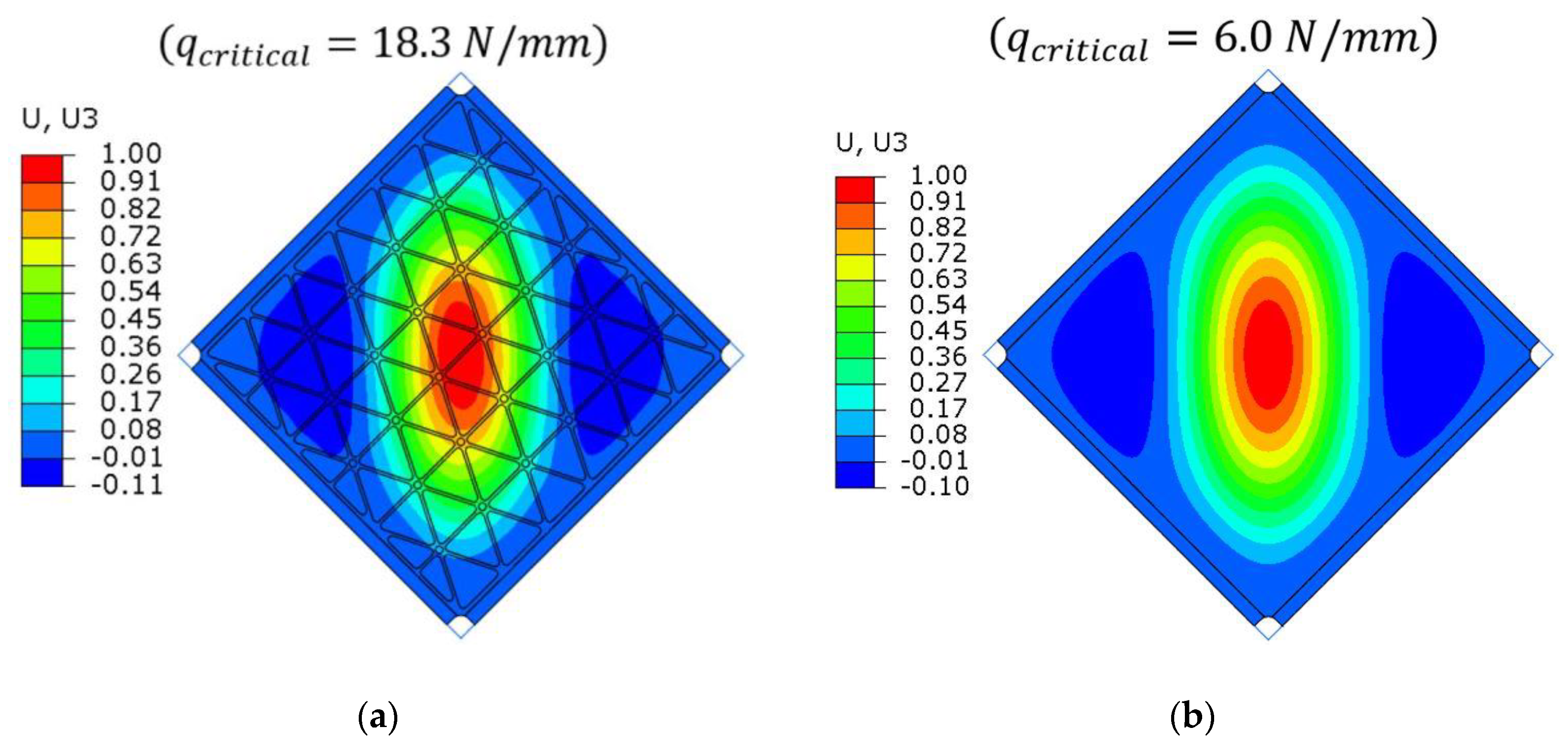
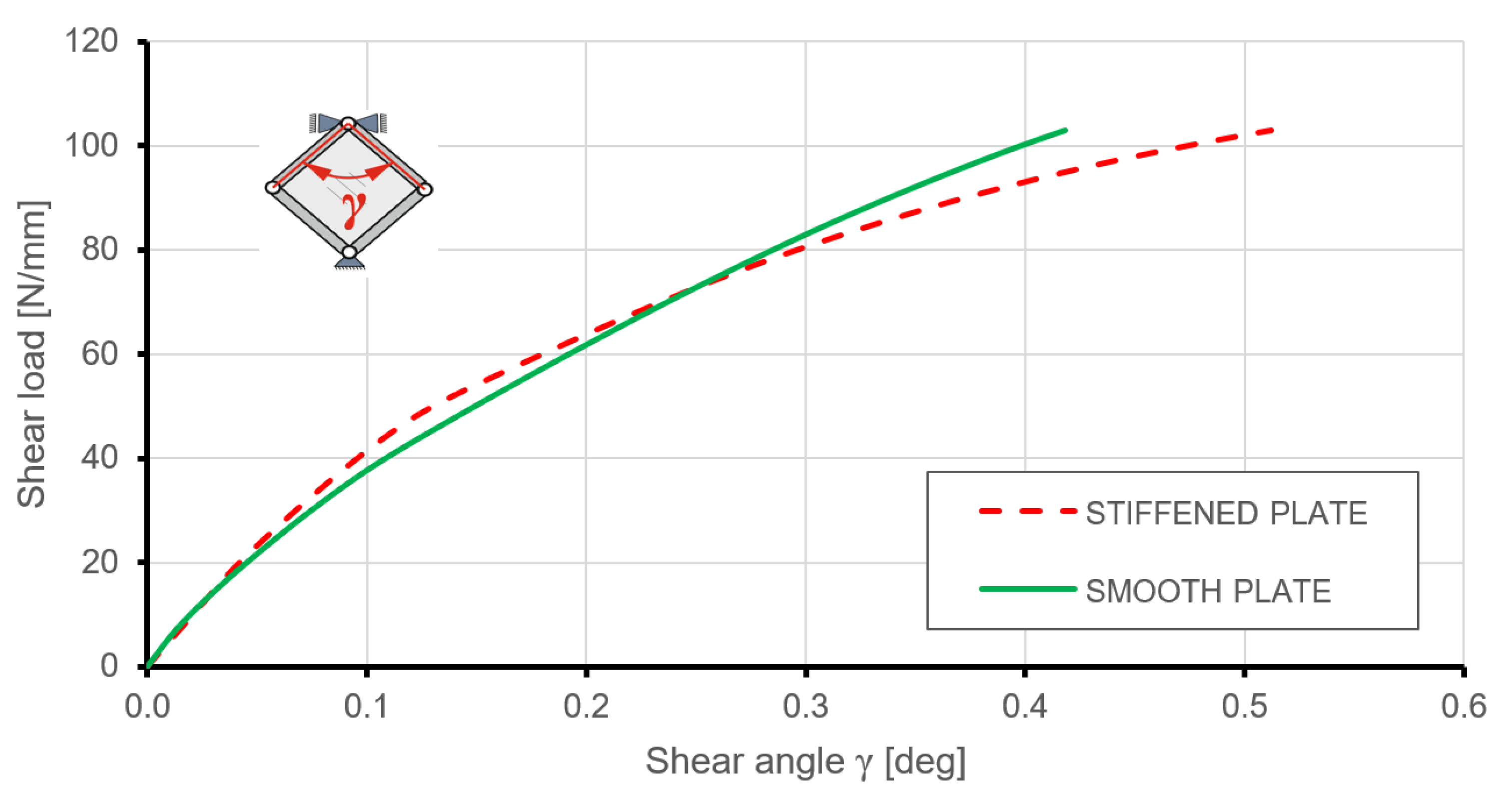
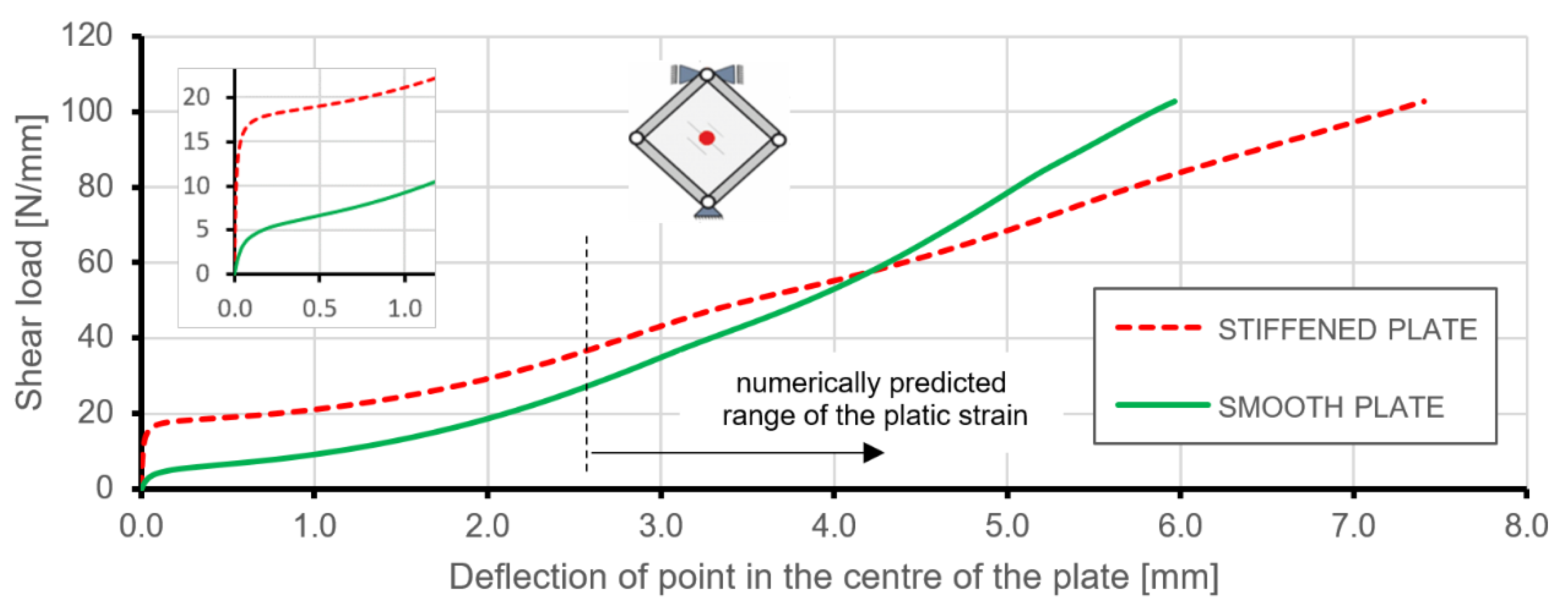
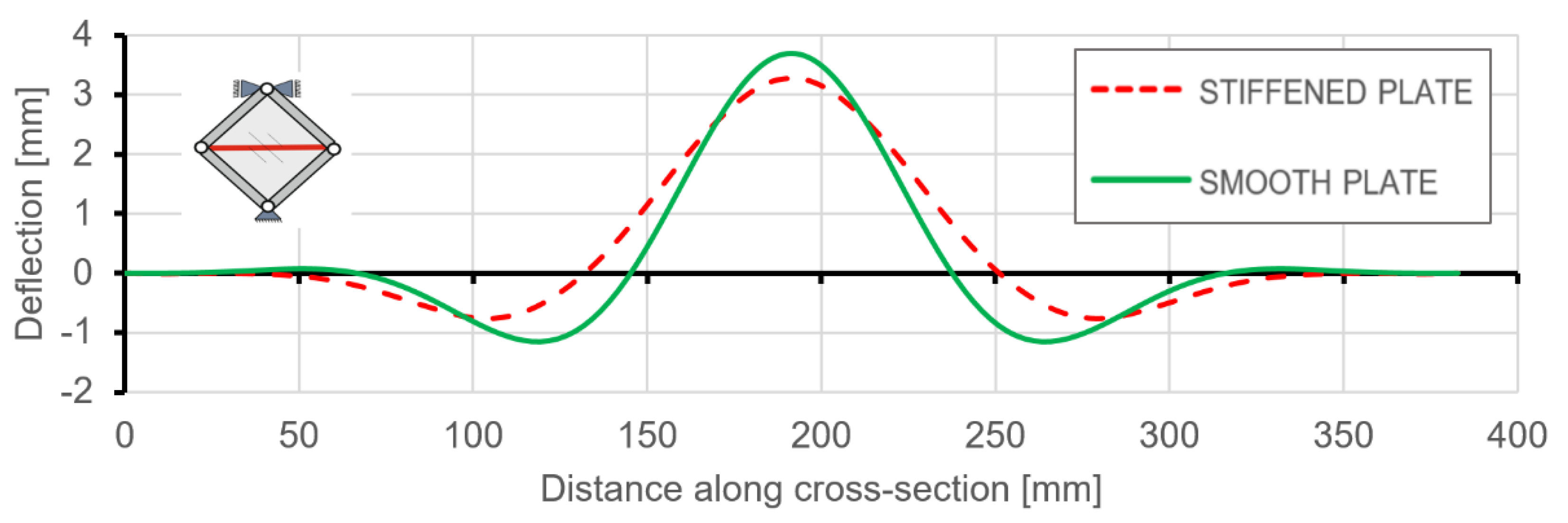
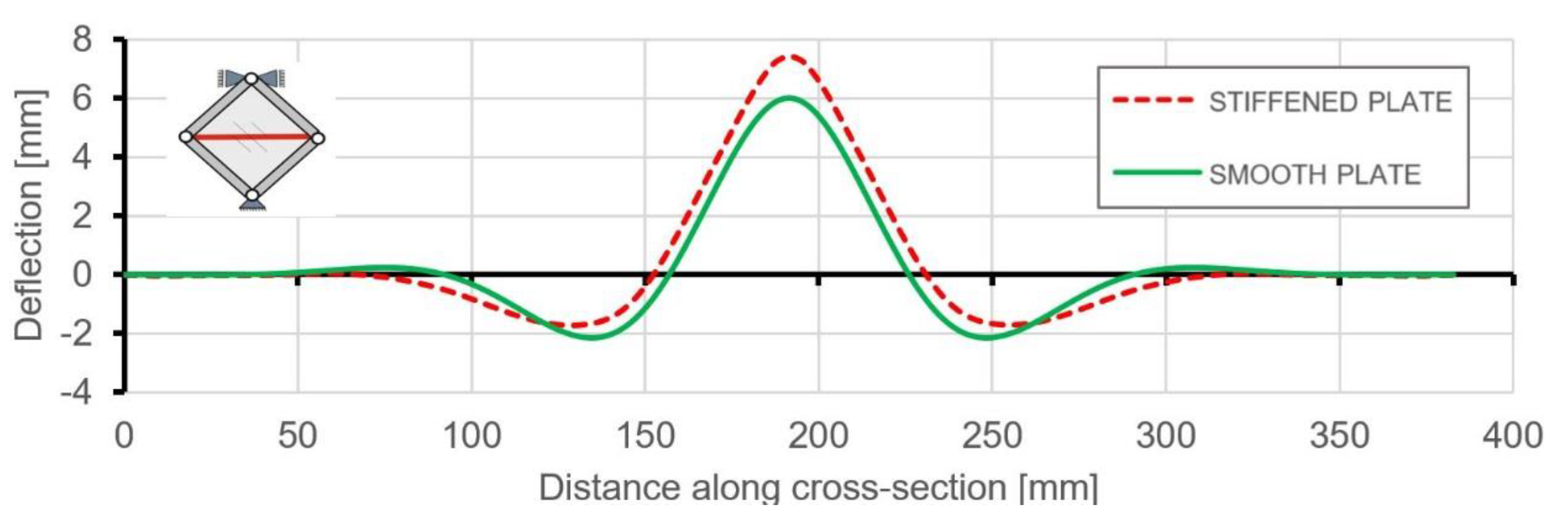
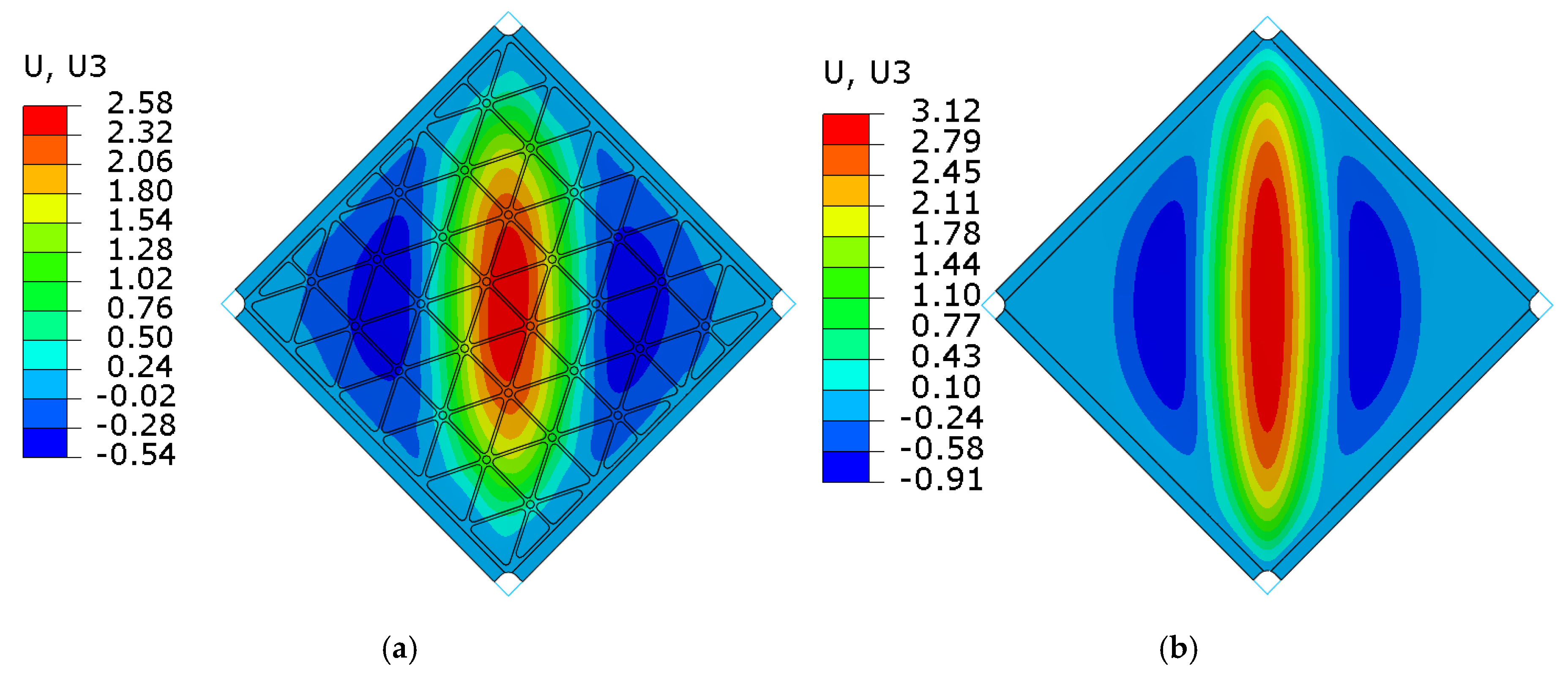
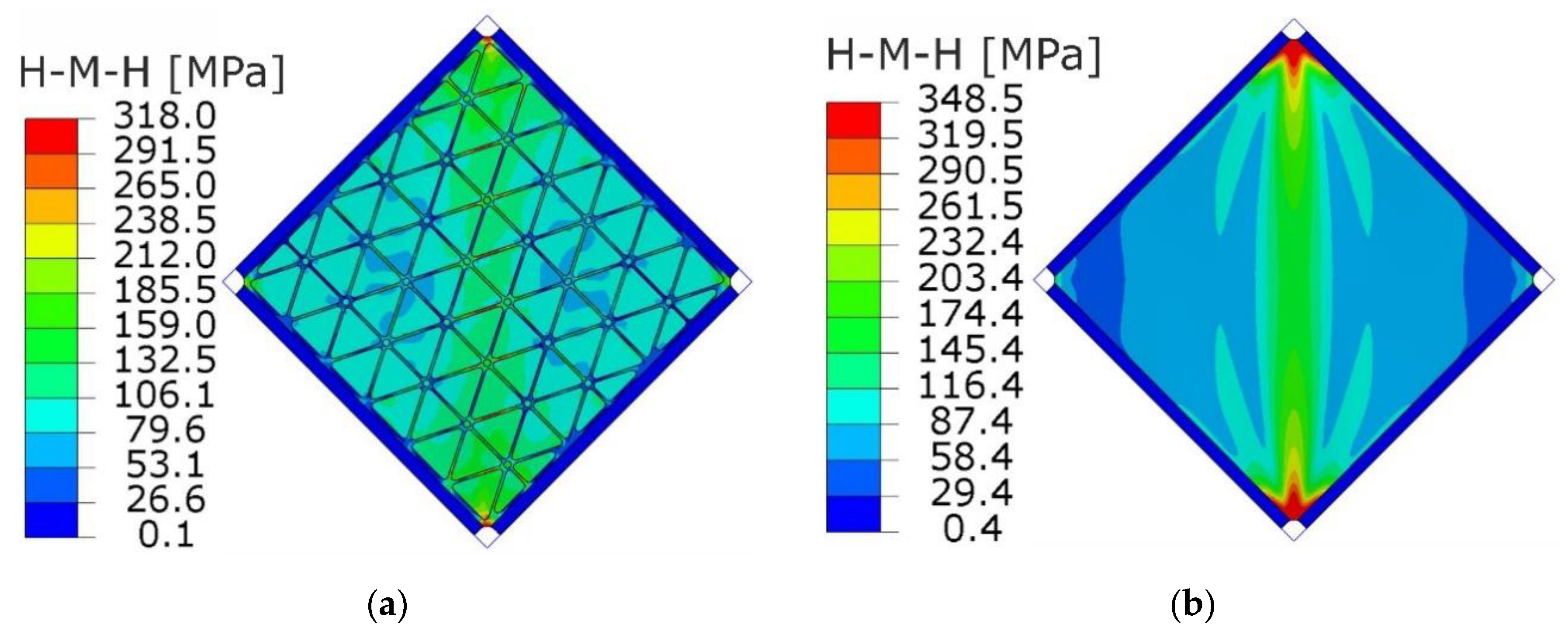
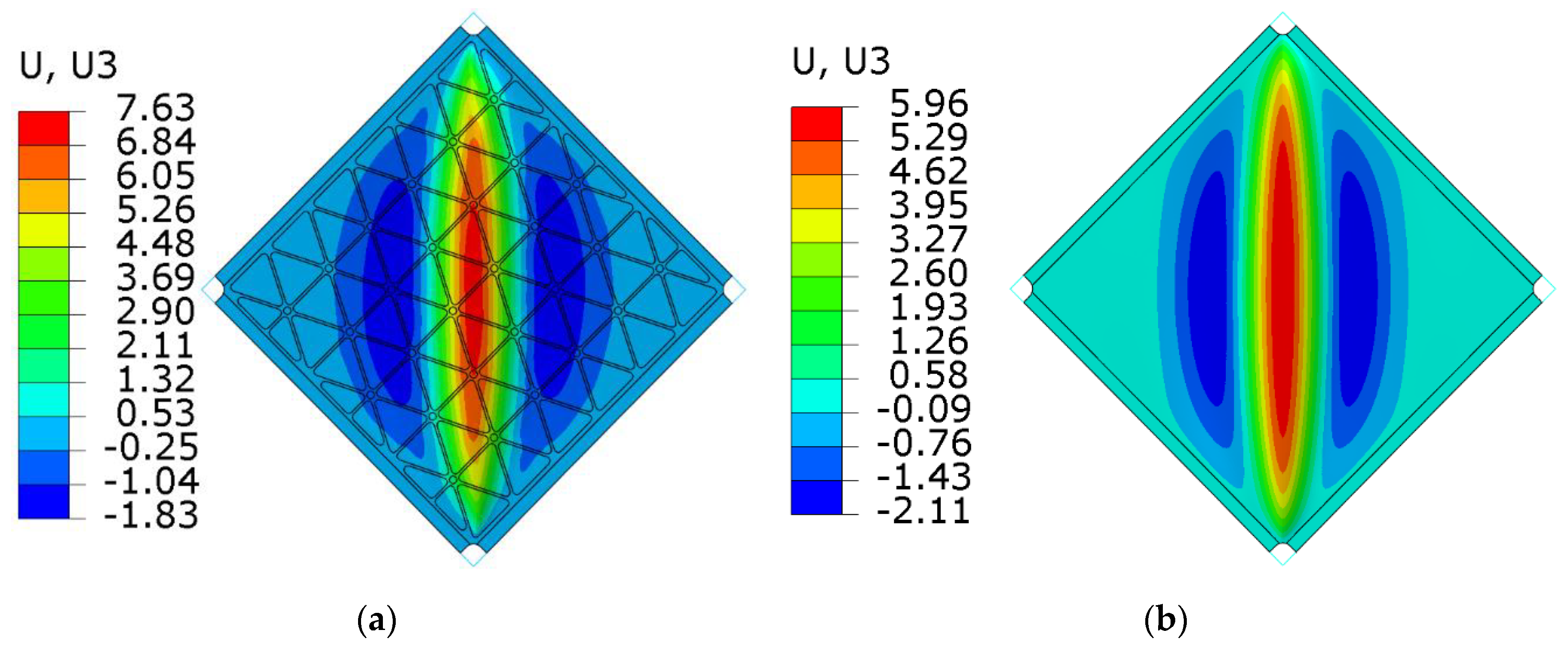
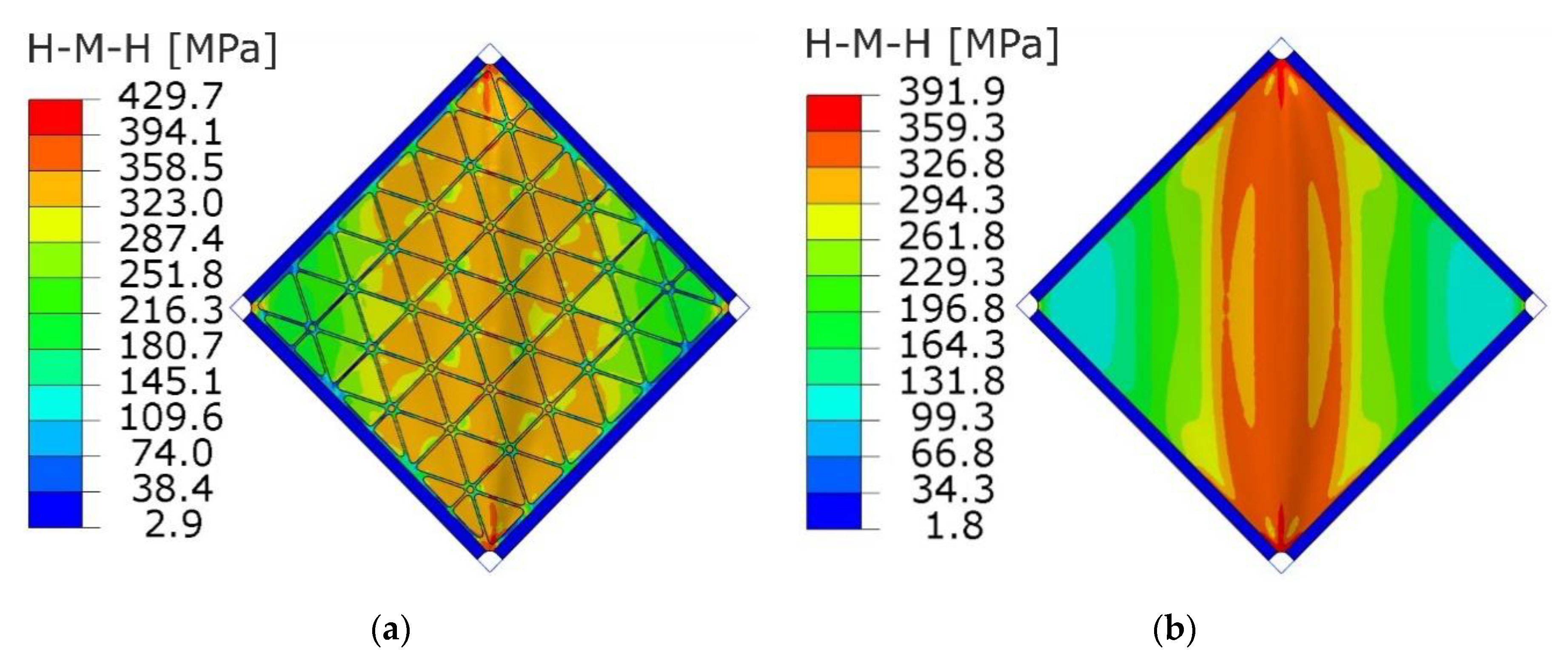
6.2. Comparison of FE Results for Stiffened and Smooth Plates
7. Conclusions
- (1)
- Introduction of triangularly arranged ribs increased the critical load by 300% in comparison to the smooth plate with equivalent mass. This phenomenon can be used in situations where it is intentional to maintain the shape of the structure (e.g., impact on aerodynamics), or directly when the local loss of stability is not permissible and critical load is equal to limit load.
- (2)
- Comparisons of post-critical behaviours of the investigated structures proved that in the range of elastic deformation, the stiffened plate may have significantly better properties in the case of deflection and stress level, without an increase in the mass of the structure.
- (3)
- Use of integral triangular stiffening in the design of thin-walled elements made it also possible to reduce the mass of the load-bearing structures maintaining the critical and limit load. This issue will be the subject of further work.
- (4)
- Despite the use of certain simplifications covering both the geometry of the structure and the material model in the FEM analyses, it should be noted that results with a satisfactory degree of convergence were obtained.
- (5)
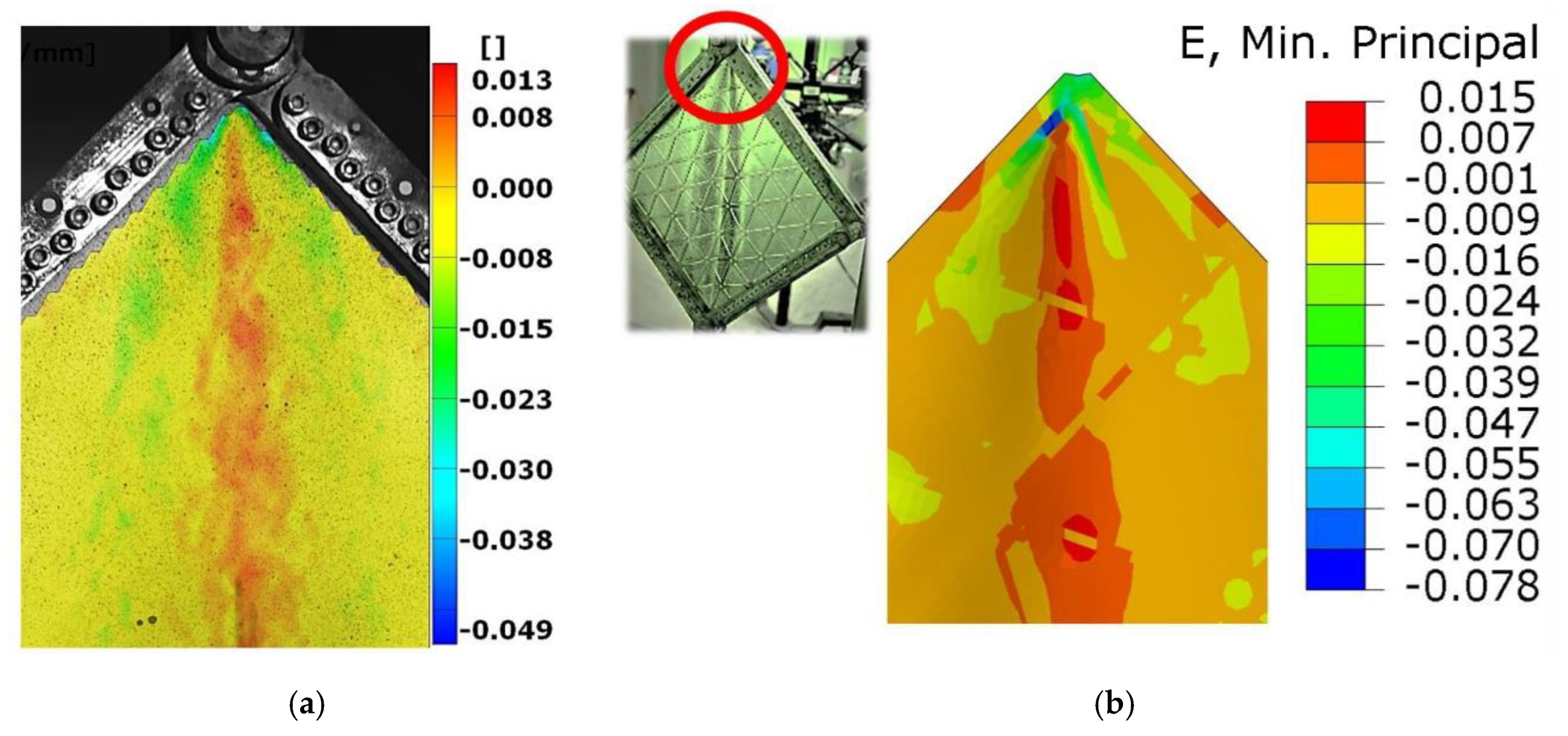
- Reduced properties of the stiffened plate in the range of the plastic deformations are related to the stress concentrations. Such effects are probably caused by the incorrect geometry of the rib pattern around the corners of the plate, resulting in changes to the rigidity of the structure in the areas under consideration. More research should be carried out to obtain the methodology of the correct selection of geometry near the attachment areas. This fact should be taken into consideration when designing real construction solutions.
- (6)
- Considering the occurrence of significant stress concentrations, it is necessary to carry out fatigue tests that will prove the impact of introducing the isosceles grid pattern of low-profile, integral ribs on the service life of the structure.
Supplementary Materials
Funding
Conflicts of Interest
References
- Megson, T.H.G. Introduction to Aircraft Structural Analysis, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2014. [Google Scholar]
- Niu, M.C. Airframe Structural Design, 2nd ed.; Conmilit Press Ltd.: Granada Hills, CA, USA, 2011. [Google Scholar]
- Bedair, O. Analysis and limit states design of stiffened plates and shell: A world view. Appl. Mech. Rev. 2009, 62, 1–16. [Google Scholar] [CrossRef]
- Neto, E.L.; Monteiro, F.A.C.; Ruela, H.H. A Comparison of Buckling Performance of Rivet and Friction Stir Welding Stiffened Panels. In Proceedings of the 31th Iberian Latin-American Congress on Computational Methods in Engineering, Buenos Aires, Argentina, 15–18 November 2010. [Google Scholar]
- Kubit, A.; Trzepiecinski, T.; Faes, K.; Drabczyk, M.; Bochnowski, W.; Korzeniowski, M. Analysis of the effect of structural defects on the fatigue strength of RFSSW joints using C-scan scanning acoustic microscopy and SEM. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 1308–1321. [Google Scholar] [CrossRef]
- Kubit, A.; Trzepiecinski, T.; Święch, Ł.; Faes, K.; Slota, J. Experimental and Numerical Investigations of Thin-Walled Stringer-Stiffened Panels Welded with RFSSW Technology under Uniaxial Compression. Materials 2019, 12, 1785. [Google Scholar] [CrossRef] [PubMed]
- Sepe, R.; Armentani, E.; di Lascio, P.; Citarella, R. Crack growth behavior of welded stiffened panel. Procedia Eng. 2015, 109, 473–483. [Google Scholar] [CrossRef]
- Nesterenko, G.I. Comparison of Damage Tolerance of Integrally Stiffened and Riveted Structures. In Proceedings of the 22nd International Council of the Aeronautical Sciences. Comparison of Damage Tolerance of Integrally Stiffened and Riveted Structures, Harrogate, UK, 27 August–1 September 2000. [Google Scholar]
- Shantharaja, M.; Srinivas, K.R. Comparison of Riveted Panel and Integral Panel for Damage Tolerance by Using FEA. Int. J. Sci. Res. 2014, 3, 426–431. [Google Scholar]
- Quinn, D.; Murphy, A.; McEwan, W.; Lemaitre, F. Stiffened panel stability behaviour and performance gains with plate prismatic sub-stiffening. Thin Walled Struct. 2009, 47, 1457–1468. [Google Scholar] [CrossRef]
- Quinn, D.; Murphy, A.; Glazebrook, C. Aerospace stiffened panel initial sizing with novel skin sub-stiffening features. Int. J. Struct. Stab. Dyn. 2012, 12. [Google Scholar] [CrossRef]
- Kopecki, T.; Święch, Ł. Experimental and numerical analysis of post-buckling deformation states of integrally stiffened thin-walled components of load-bearing aircraft structures. J. Theor. Appl. Mech. 2014, 54, 905–915. [Google Scholar] [CrossRef][Green Version]
- NASA Marshall Space Flight Center. Isogrid Design Handbook; Report, CR-124075; NASA Marshall Space Flight Center: Huntsville, AL, USA, 1973.
- Vasiliev, V.; Barynin, V.; Rasin, A. Anisogrid lattice structures—Survey of development and application. Comp. Struct. 2001, 54, 361–370. [Google Scholar] [CrossRef]
- Li, M.; Lai, C.; Zheng, Q.; Han, B.; Wu, H.; Fan, H. Design and mechanical properties of hierarchical isogrid structures validated by 3D printing technique. Mat. Des. 2019, 168. [Google Scholar] [CrossRef]
- Szilard, R. Theories and Applications of Plate Analysis: Classical, Numerical and Engineering Methods; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Troytsky, M.S. Stiffened Plates: Bending, Stability and Vibrations; Elsevier: Amsterdam, The Netherlands, 1976. [Google Scholar]
- Wang, B.; Tian, K.; Hao, P.; Zheng, Y.; Ma, Y.; Wang, J. Numerical-based smeared stiffener method for global buckling analysis of grid-stiffened composite cylindrical shells. Compos. Struct. 2016, 152, 807–815. [Google Scholar] [CrossRef]
- Jaunky, N.; Knight, N.; Ambur, D. Formulation of an improved smeared stiffener theory for buckling analysis of grid-stiffened composite panels. Compos. Part B Eng. 1996, 27, 519–526. [Google Scholar] [CrossRef]
- Xu, Y.; Tong, Y.; Liu, M.; Suman, B. A new effective smeared stiffener method for global buckling analysis of grid stiffened composite panels. Compos. Struct. 2016, 158, 83–91. [Google Scholar] [CrossRef]
- Wang, D.; Abdalla, M. Global and local buckling analysis of grid-stiffened composite panels. Compos. Struct. 2015, 119, 767–776. [Google Scholar] [CrossRef]
- Luan, Y.; Ohlrich, M.; Jacobsen, F. Improvements of the smearing technique for cross-stiffened thin rectangular plates. J. Sound Vib. 2011, 330, 4274–4286. [Google Scholar] [CrossRef]
- Huybrechts, S.; Tsai, S.W. Analysis and behaviour of grid structures. Compos. Sci. Technol. 1996, 56, 1001–1015. [Google Scholar] [CrossRef]
- Kopecki, T.; Mazurek, P.; Lis, T.; Chodorowska, D. Post-buckling deformation states of semi-monocoque cylindrical structures with large cut-outs under operating load conditions. Numerical analysis and experimental tests. Eksploatacja Niezawodn. 2016, 18, 16–24. [Google Scholar] [CrossRef]
- Kopecki, T.; Mazurek, P. Determination of stress distribution patterns in post-critical deformation states of thin-walled skins subjected to operating loads. Eksploatacja Niezawodn. 2014, 16, 608–615. [Google Scholar]
- Li, X.; Wang, H.; Li, G. Reanalysis assisted metaheuristic optimization for free vibration problems of composite laminates. Compos. Struct. 2018, 206, 380–391. [Google Scholar] [CrossRef]
- Huang, G.; Wang, H.; Li, G. An efficient reanalysis assisted optimization for variable-stiffness composite design by using path functions. Compos. Struct. 2016, 153, 409–420. [Google Scholar] [CrossRef]
- Liang, K.; Sun, Q.; Zhang, Y. Nonlinear buckling analysis of variable stiffness composite plates based on the reduced order model. Compos. Struct. 2018, 206, 681–692. [Google Scholar] [CrossRef]
- GOM GmbH. GOM Software; v.2019; GOM GmbH: Braunschweig, Germany, 2019. [Google Scholar]
- GOM GmbH. Digital Image Correlation and Strain Computation Basics; v.2016; GOM GmbH: Braunschweig, Germany, 2016. [Google Scholar]
- Dassault Systemes. ABAQUS User’s & Theory Manuals—Release 6.13-1; Dassault Systemes: Providence, RI, USA, 2013. [Google Scholar]
- Arborcz, J. Post-buckling behavior of structures. Numerical techniques for more complicated structures. Lect. Notes Phys. 1985, 288, 83–142. [Google Scholar]
- Bathe, K.J. Finite Element Procedures; Prentice Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Doyle, J.F. Nonlinear Analysis of Thin-Walled Structures; Springer: Luxembourg, 2001. [Google Scholar]
- Felippa, C.A. Procedures for Computer Analysis of Large Nonlinear Structural System in Large Engineering Systems; Pergamon Press: London, UK, 1976. [Google Scholar]


| Parameter Name | Young’s Modulus E, GPa | Poisson Ratio | Ultimate Tensile Stress Rm, MPa | Yield Stress Rp0.2, MPa |
|---|---|---|---|---|
| Al2024 | 70 | 0.33 | 488 | 345 |
| Steel | 210 | 0.3 | - | - |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Święch, Ł. Experimental and Numerical Studies of Low-Profile, Triangular Grid-Stiffened Plates Subjected to Shear Load in the Post-Critical States of Deformation. Materials 2019, 12, 3699. https://doi.org/10.3390/ma12223699
Święch Ł. Experimental and Numerical Studies of Low-Profile, Triangular Grid-Stiffened Plates Subjected to Shear Load in the Post-Critical States of Deformation. Materials. 2019; 12(22):3699. https://doi.org/10.3390/ma12223699
Chicago/Turabian StyleŚwięch, Łukasz. 2019. "Experimental and Numerical Studies of Low-Profile, Triangular Grid-Stiffened Plates Subjected to Shear Load in the Post-Critical States of Deformation" Materials 12, no. 22: 3699. https://doi.org/10.3390/ma12223699
APA StyleŚwięch, Ł. (2019). Experimental and Numerical Studies of Low-Profile, Triangular Grid-Stiffened Plates Subjected to Shear Load in the Post-Critical States of Deformation. Materials, 12(22), 3699. https://doi.org/10.3390/ma12223699






