Analytical Method for Predicting Early Age Thermal Effects in Thick Foundation Slabs
Abstract
:1. Introduction
2. Proposal of the Analytical Method
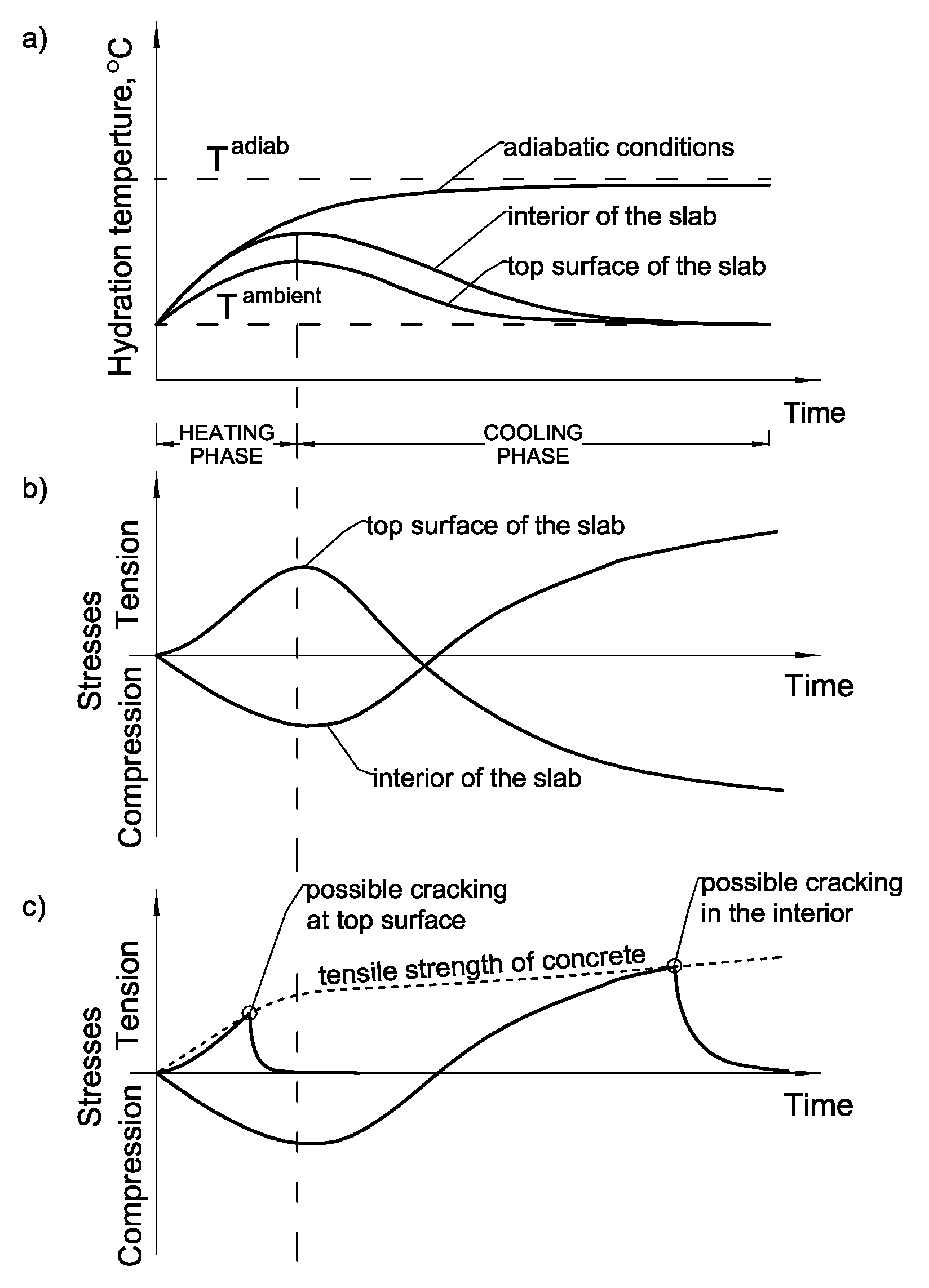
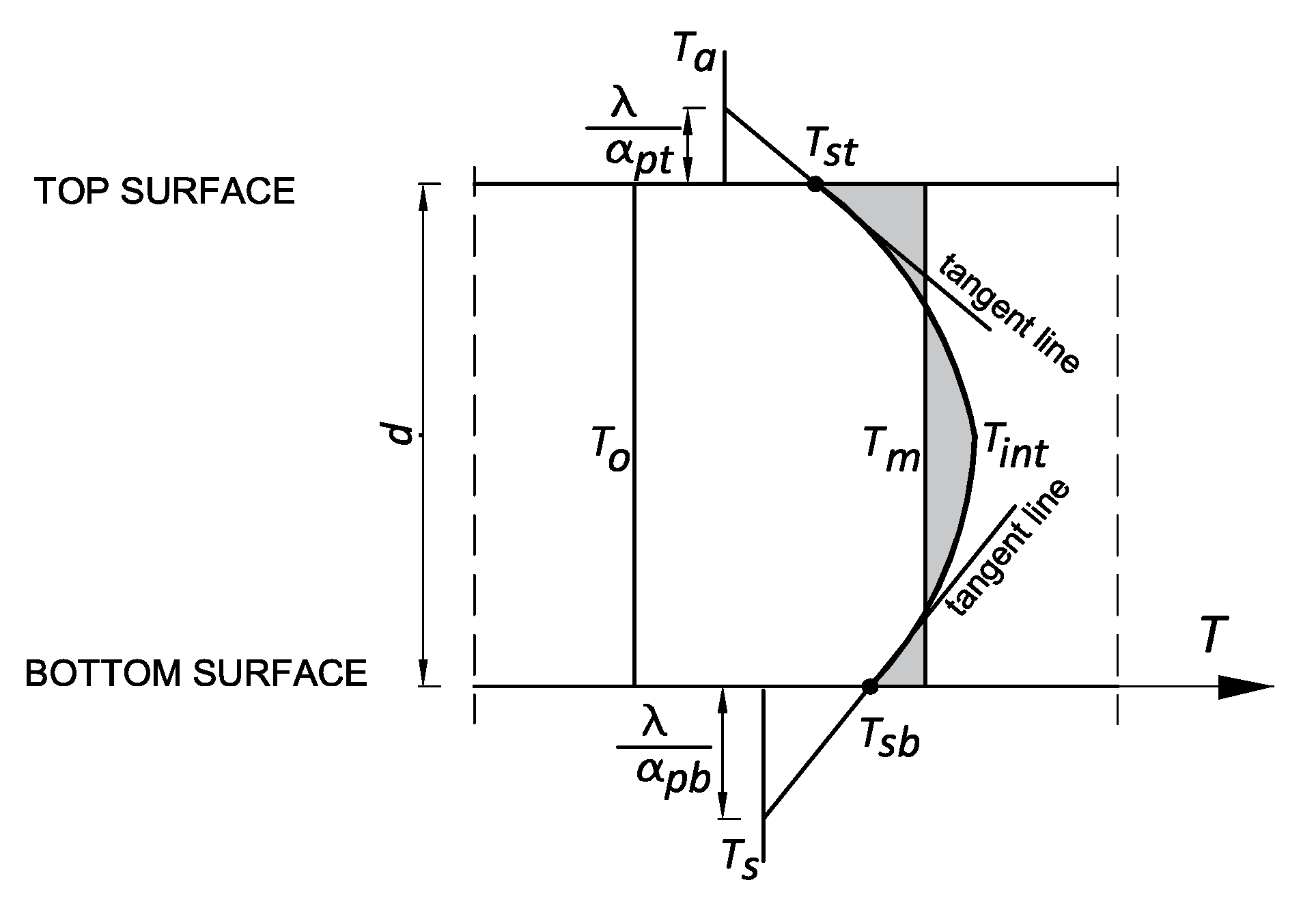
2.1. Hydration Temperature Rise and the Temperature Differentials at the Slab Thickness
- for the top surface of the slab:
- for the bottom surface of the slab:
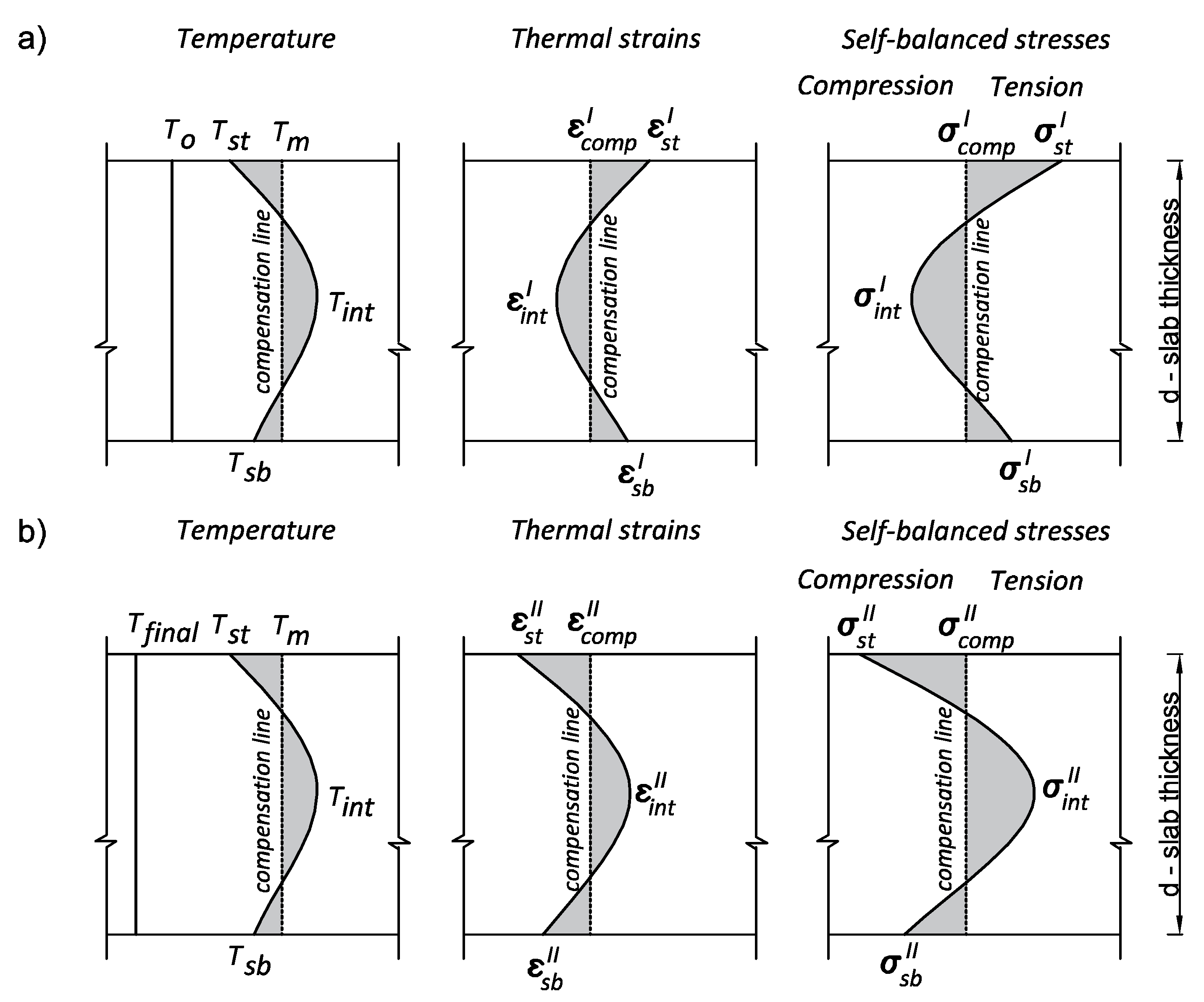
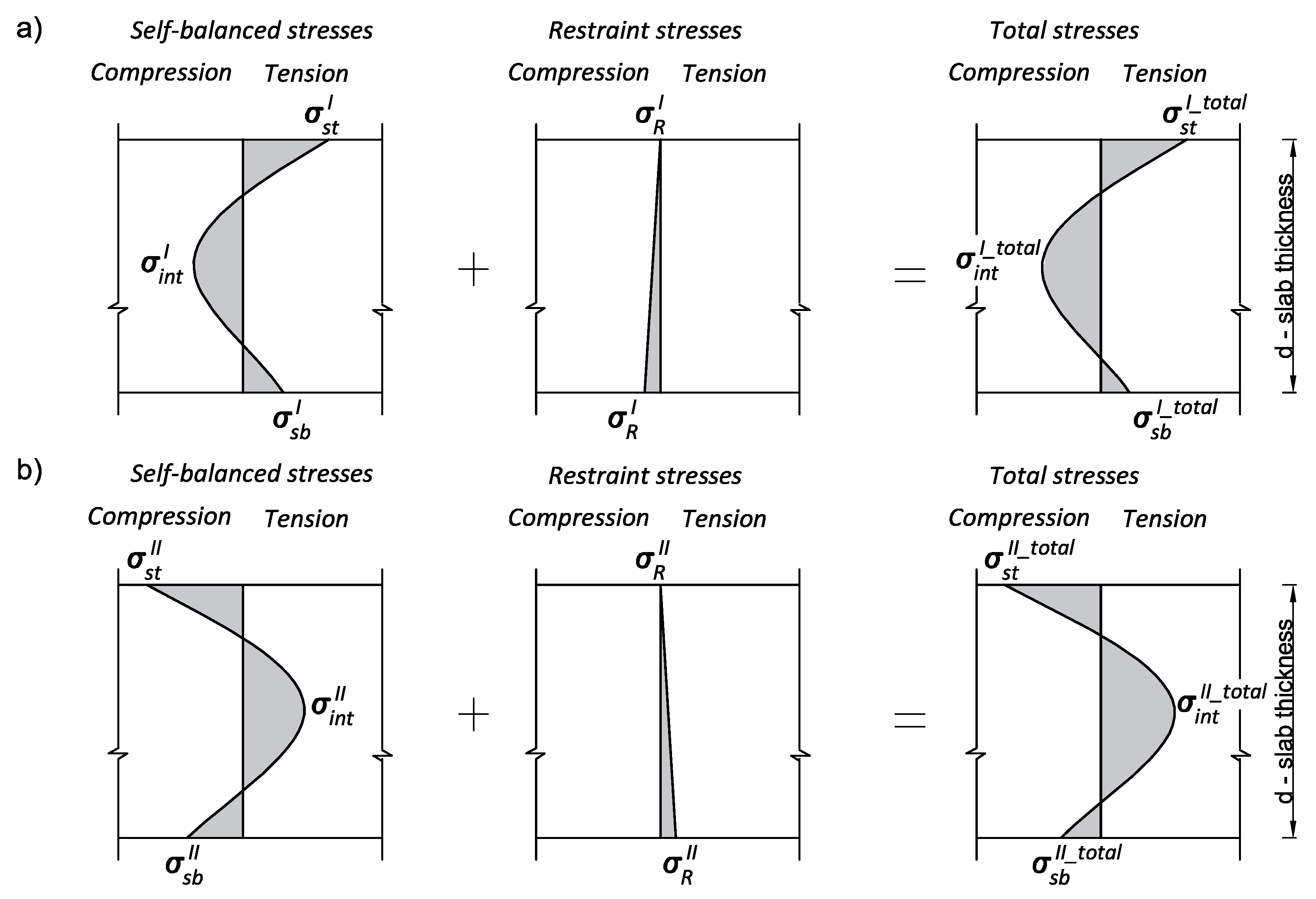
2.2. Thermal Strains and Stresses
- In the center of the slab:
- At the top surface of the slab:
- At the bottom surface of the slab:
- Strains on the compensation line:
- Strains in the center of the slab:
- Strains at the top surface of the slab:
- Strains at the bottom surface of the slab:
3. Numerical Validation
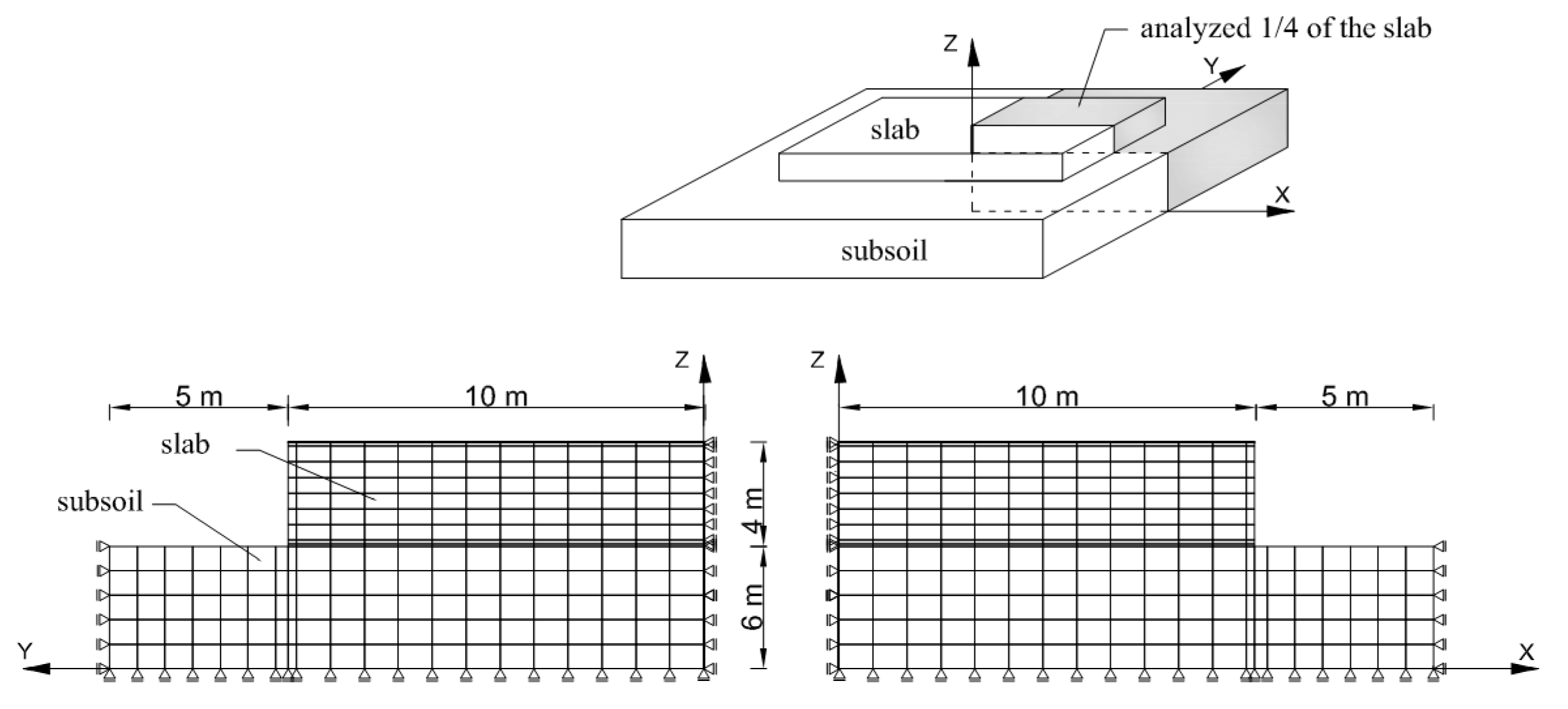
3.1. Data for Analysis
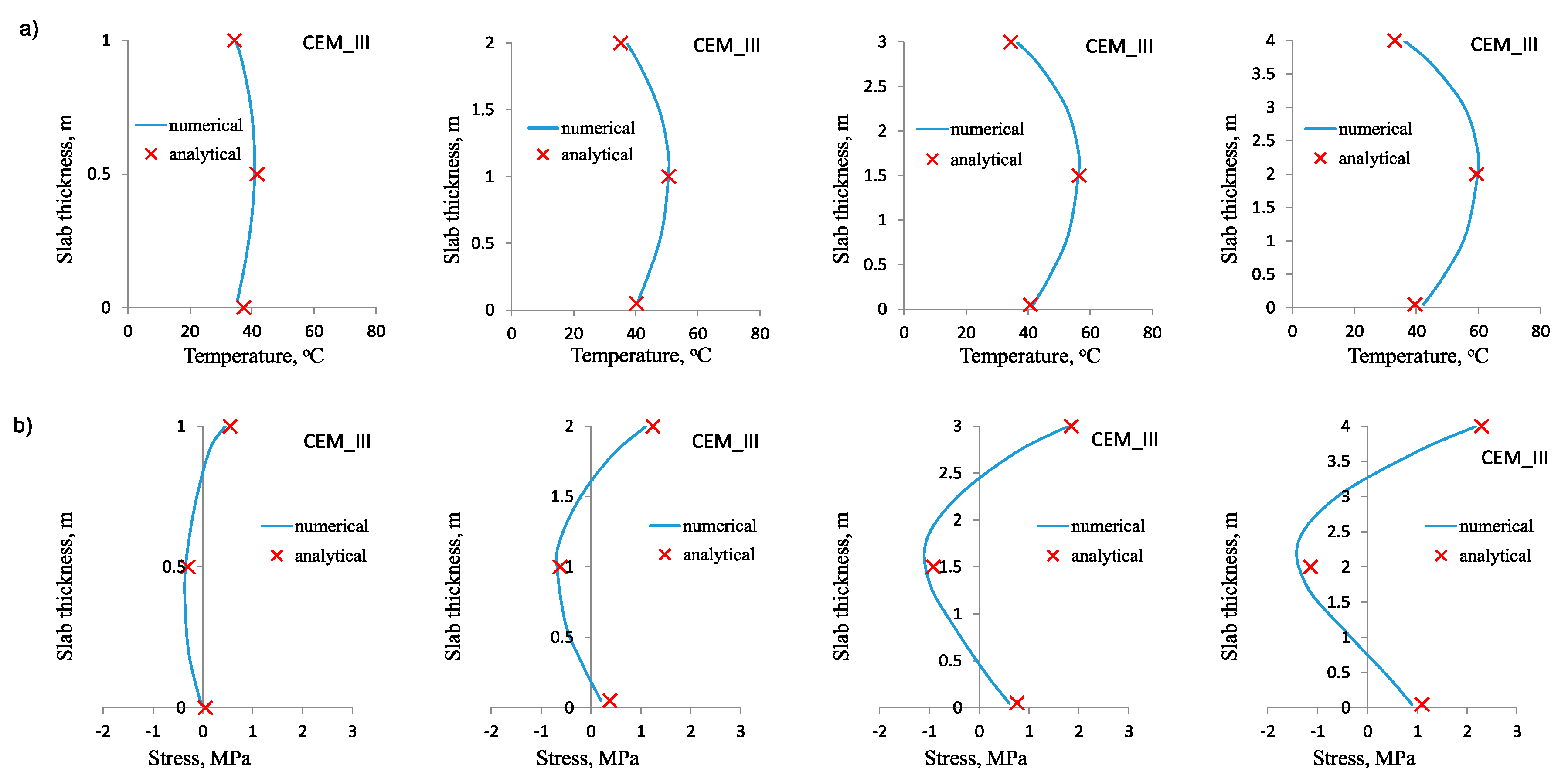
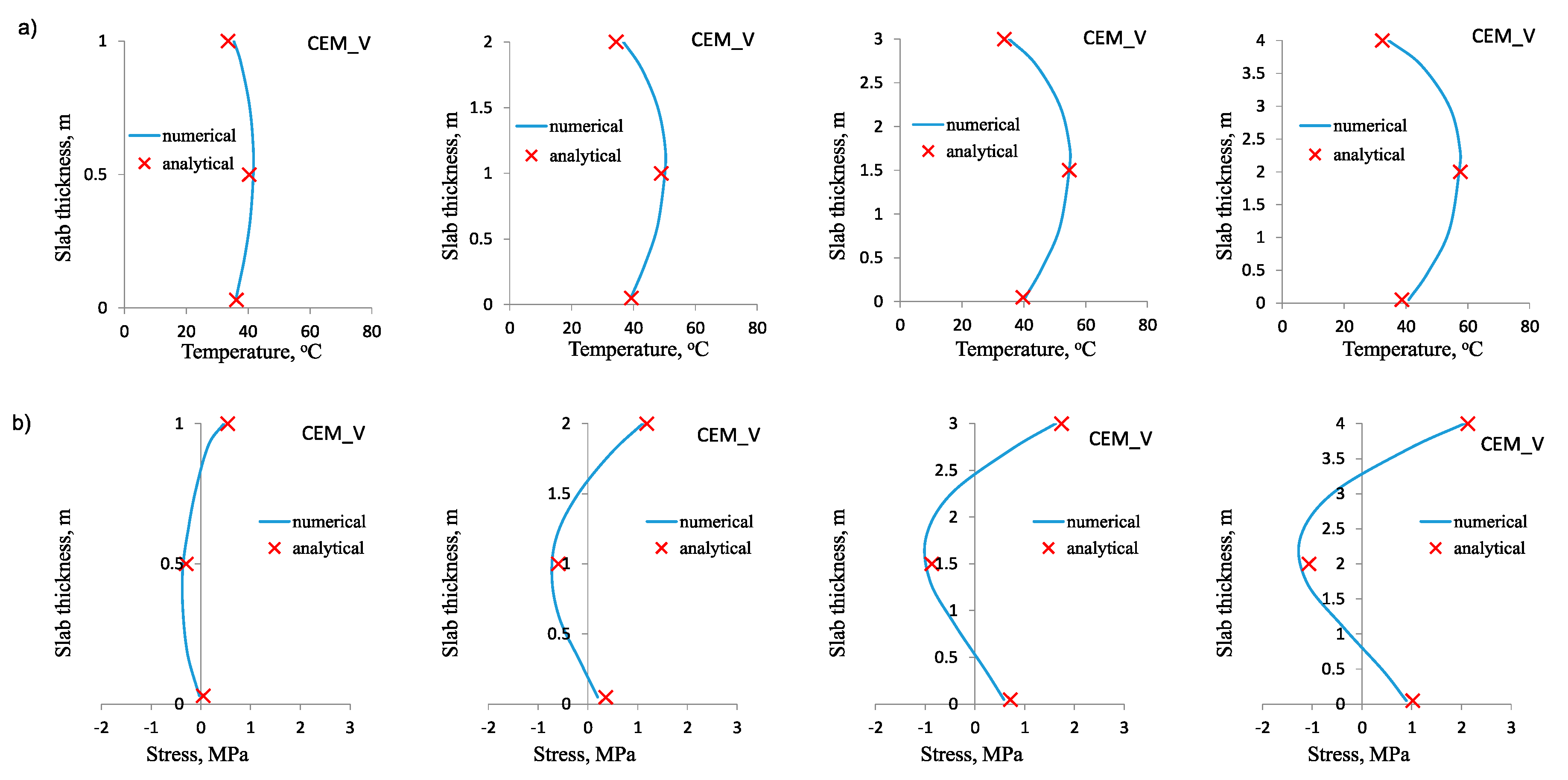
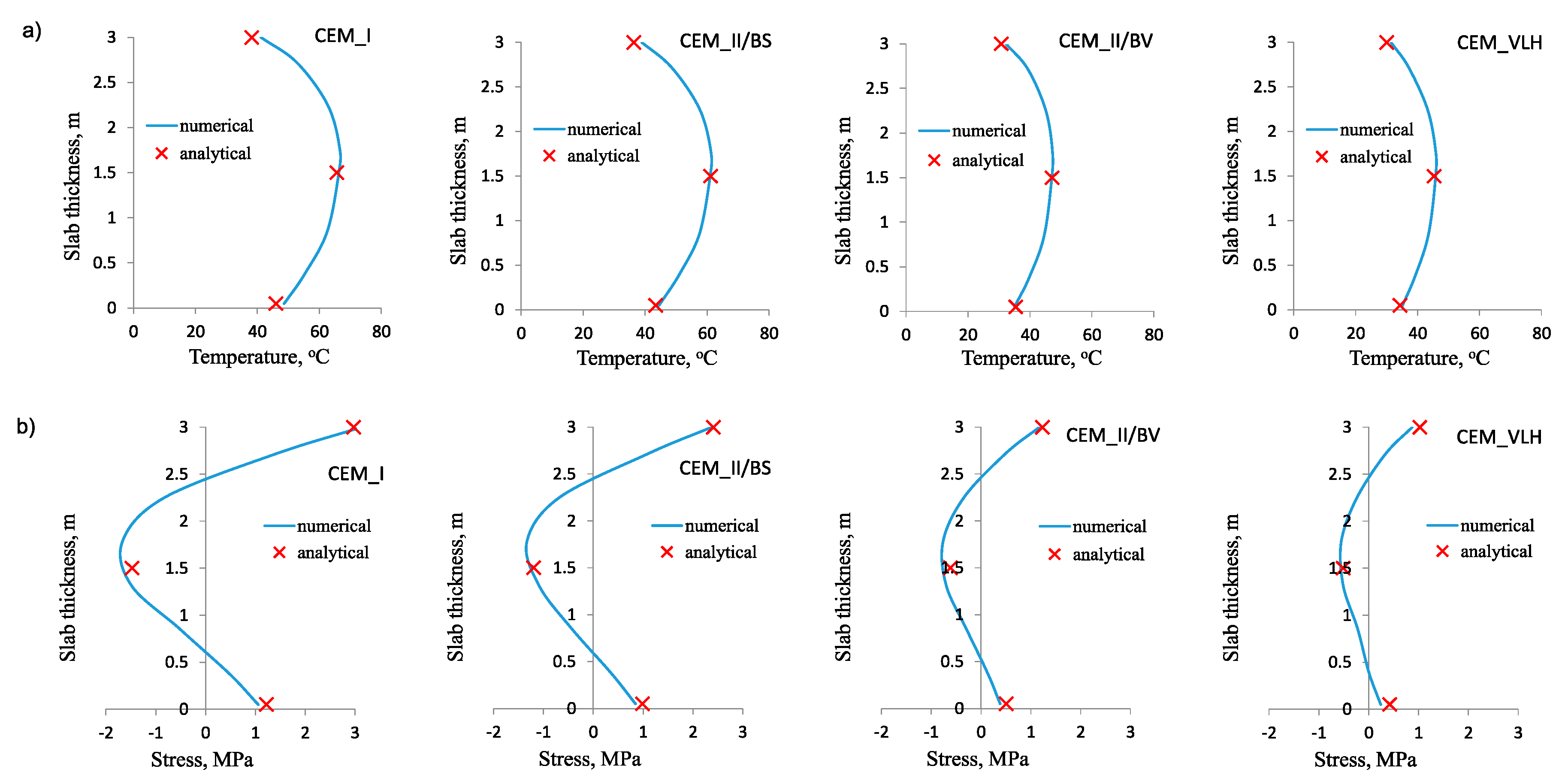
3.2. Results of Validation
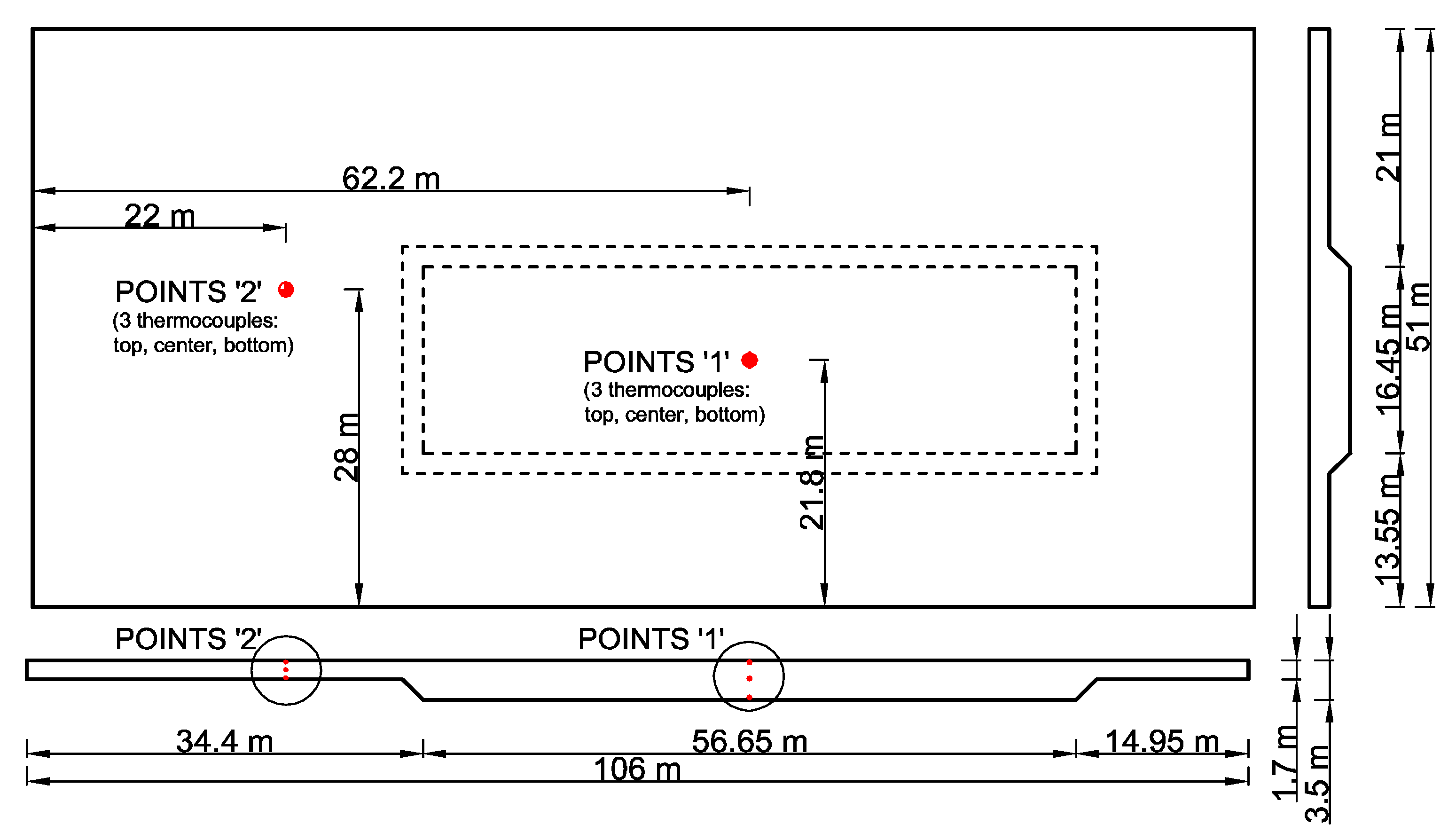
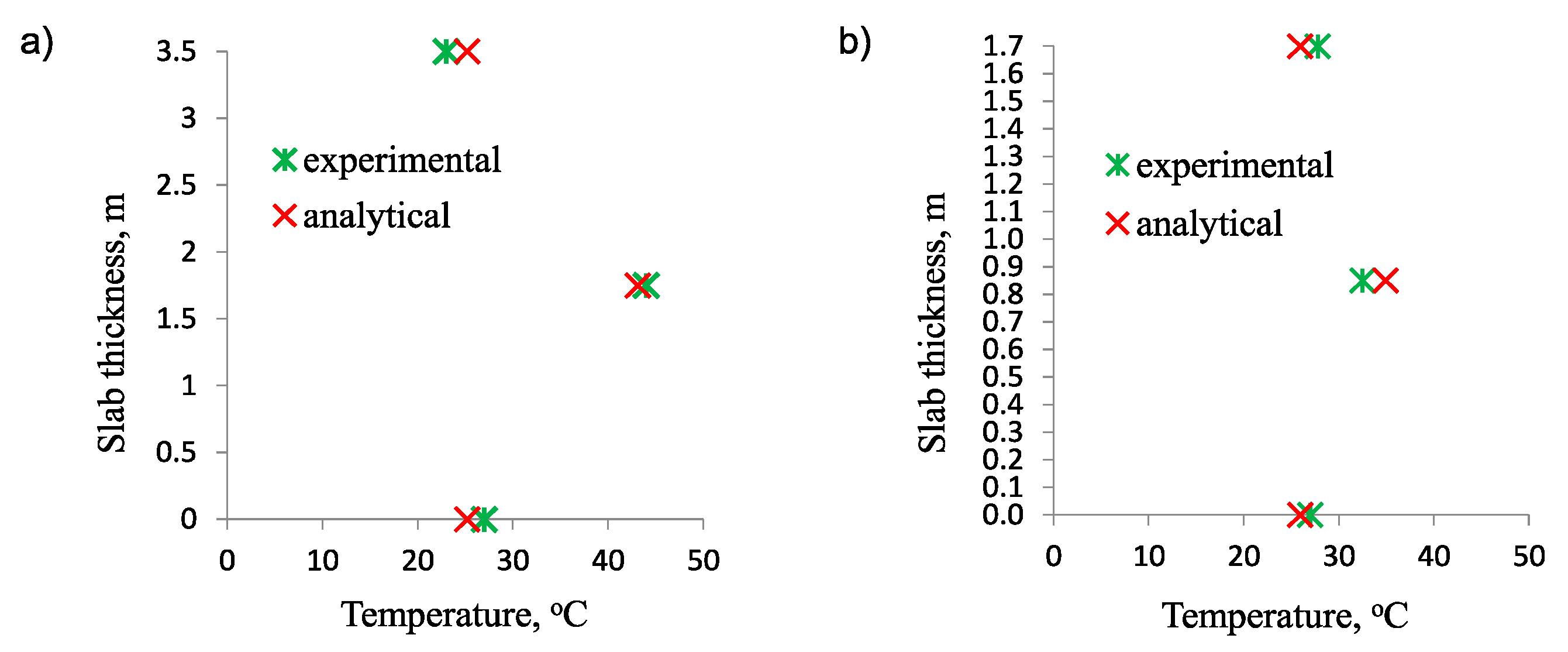
4. Experimental Validation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bamforth, P.B. Early-Age Thermal Crack Control in Concrete; CIRIA C660; CIRIA Classic House: London, UK, 2007. [Google Scholar]
- Neville, A.M. Properties of Concrete; Pearson Education: Harlow, UK, 2012. [Google Scholar]
- Azenha, A.; Sousa, C.; Faria, R.; Neves, A. Thermo-hygro-mechanical modelling of self-induced stresses during the service life of RC structures. Eng. Struct. 2011, 33, 3442–3453. [Google Scholar] [CrossRef]
- Barre, F.; Bisch, P.; Chauvel, D.; Cortade, J.; Coste, J.F.; Dubois, J.P.; Erlicher, S.; Gallitre, E.; Labbé, P.; Mazars, J.; et al. Guidelines for the Control of Cracking in Reinforced Concrete Structures, Outcomes of the French Research Project CEOS.fr; CEOS: Beijing, China, 2016. [Google Scholar]
- Klemczak, B.; Batog, M.; Giergiczny, Z.; Żmij, A. Complex Effect of Concrete Composition on the Thermo-Mechanical Behaviour of Mass Concrete. Materials 2018, 11, 2207. [Google Scholar] [CrossRef] [PubMed]
- Batog, M.; Giergiczny, Z. Influence of mass concrete constituents on its properties. Constr. Build. Mater. 2017, 146, 221–230. [Google Scholar] [CrossRef]
- Shen, D.; Wang, W.; Liu, J.; Zhao, X.; Jiang, G. Influence of Barchip fiber on early-age cracking potential of high-performance concrete under restrained condition. Constr. Build. Mater. 2018, 187, 118–130. [Google Scholar] [CrossRef]
- American Concrete Institute. ACI Committee 207. Guide to Mass Concrete; ACI: Farmington Hills, MI, USA, 2006. [Google Scholar]
- Japan Concrete Institute. Guidelines for Control of Cracking of Mass Concrete; JCI: Tokyo, Japan, 2016. [Google Scholar]
- DIANA FEA. Available online: https://dianafea.com/diana-downloads (accessed on 12 September 2019).
- ATENA. Available online: https://www.cervenka.cz/products/atena/ (accessed on 12 September 2019).
- MIDAS Engineering Software. Available online: https://en.midasuser.com/ (accessed on 12 September 2019).
- Huang, Y.; Liu, G.; Huang, S.; Rao, R.; Hu, C. Experimental and finite element investigations on the temperature field of a massive bridge pier caused by the hydration heat of concrete. Constr. Build. Mater. 2018, 163, 240–252. [Google Scholar] [CrossRef]
- Azenha, M.; Leitão, L.; Granja, J.L.; Sousa, C.; Faria, R.; Barros, J.A.O. Experimental validation of a framework for hygro-mechanical simulation of self-induced stresses in concrete. Cem. Concr. Compos. 2017, 80, 41–54. [Google Scholar] [CrossRef]
- Jędrzejewska, A.; Benboudjema, F.; Lacarriere, L.; Azenha, M.; Schlicke, D.; Dal Pont, S.; Delaplace, A.; Granja, J.; Hajkova, K.; Heinrich, P.J. COST TU1404 benchmark on macroscopic modelling of concrete and concrete structures at early age: Proof-of-concept stage. Constr. Build. Mater. 2018, 174, 173–189. [Google Scholar] [CrossRef]
- ACI Committee 231. Report on Early-Age Cracking: Causes, Measurement, and Mitigation; American Concrete Institute: Farmington Hills, MI, USA, 2010. [Google Scholar]
- Klemczak, B.; Flaga, K.; Knoppik-Wróbel, A. Analytical model for evaluation of thermal–shrinkage strains and stresses in RC wall-on-slab structures. Arch. Civ. Mech. Eng. 2017, 17, 75–95. [Google Scholar] [CrossRef]
- Japan Society of Civil Engineers. JSCE Guidelines for Concrete No. 15: Standard Specifications for Concrete Structures, DESIGN; Japan Society of Civil Engineers: Tokyo, Japan, 2011. [Google Scholar]
- Kiernożycki, W. Massive Concrete Structures; Polski Cement: Cracow, Poland, 2003. (In Polish) [Google Scholar]
- Schindler, A.K.; Folliard, K.J. Heat of hydration models for cementitious materials. ACI Mater. J. 2005, 102, 24–33. [Google Scholar]
- Bamforth, P.B. Temperature Prediction and Its Significance. Proc. Seminar Carry on Casting, Cement and Concrete Association; Fulmer Grange: Slough, UK, 1976. [Google Scholar]
- CEB-FIP. CEB-FIP Model Code 90; Thomas Telford: London, UK, 1991. [Google Scholar]
- Altoubat, S.A.; Lange, D.A. Creep, shrinkage and cracking of restrained concrete at early-age. ACI Mater. J. 2001, 98, 323–331. [Google Scholar]
- Klemczak, B. Modelling thermal–shrinkage stresses in early age massive concrete structures—comparative study of basic models. Arch. Civ. Mech. Eng. 2014, 14, 721–733. [Google Scholar] [CrossRef]
- Klemczak, B.; Knoppik-Wróbel, A. Reinforced concrete tank walls and bridge abutments: Early-age behaviour, analytic approaches and numerical models. Eng. Struct. 2015, 84, 233–251. [Google Scholar] [CrossRef]
- Golda, A. Concrete Resistance on the Environmental effecst in Massive Structures, on the Example of Block no. 5 and 6 of Opole Power Station. Ph.D. Thesis, Silesian University of Technology, Gliwice, Poland, 2017. (In Polish). [Google Scholar]
- Hu, C. Microstructure and mechanical properties of fly ash blended cement pastes. Constr. Build. Mater. 2014, 73, 618–625. [Google Scholar] [CrossRef]
- Hu, C.; Li, Z. Property investigation of individual phases in cementitious composites containing silica fume and fly as. Cem. Concr. Comp. 2015, 57, 17–26. [Google Scholar] [CrossRef]
| Component | , kJ/(kg °C) |
|---|---|
| water | 4.18 |
| cement | 0.56 |
| sand | 0.74 |
| basalt | 0.77 |
| dolomite | 0.82 |
| granite | 0.47 |
| quartz | 0.72 |
| riolite | 0.78 |
| Cement Type | Component, % | |||
|---|---|---|---|---|
| Portland Clinker | Slag (S) | Siliceous Fly Ash (V) | kJ/kg | |
| CEM I 42.5R | 95.7 | – | – | 501 |
| CEM II/B-V 32.5R | 67.3 | – | 29.1 | 410 |
| CEM II/B-S 32.5R | 68.3 | 27.1 | – | 490 |
| CEM III/A 32.5N-LH/HSR/NA | 41.1 | 58.9 | – | 498 |
| CEM V/A (S-V) 32.5R-LH | 62.2 | 18.2 | 19.6 | 430 |
| VLH V/B (S-V) 22.5 | 32.3 | 34.4 | 33.3 | 362 |
| Cement Type | |
|---|---|
| CEM I 42.5R | 0.65 |
| CEM II/B-V 32.5R | 0.48 |
| CEM II/B-S 32.5R | 0.60 |
| CEM III/A 32.5N-LH/HSR/NA | 0.52 |
| CEM V/A (S-V) 32.5R-LH | 0.58 |
| VLH V/B (S-V) 22.5 | 0.50 |
| Slab Thickness, m | |
|---|---|
| 1.0 | 0.70 |
| 2.0 | 0.85 |
| 3.0 | 0.95 |
| 4.0 | 1.0 |
| Component | , W/(m∙°C) |
|---|---|
| water | 0.60 |
| cement | 1.28 |
| sand | 3.08 |
| basalt | 1.91 |
| dolomite | 4.32 |
| granite | 2.94 |
| quartz | 4.60 |
| riolite | 1.88 |
| Wind Speed [m/s] | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| [W/(m2·°C)] | 6.0 | 10.4 | 14.5 | 18.6 | 22.6 | 26.7 | 34.5 |
| Coarse Aggregate Applied in Concrete | |
|---|---|
| Basalt | 10 |
| Flint gravel | 12 |
| Quartzite | 14 |
| Granite | 10 |
| Limestone | 9 |
| Sandstone | 12.5 |
| Slab Thickness, m | t, Days |
|---|---|
| 1.0 | 3 |
| 2.0 | 4 |
| 3.0 | 5 |
| 4.0 | 6 |
| Symbol | Cement | Aggregate | ||||
|---|---|---|---|---|---|---|
| W/m °C | kJ/(kg °C) | kg/m3 | MPa | |||
| CEM I | CEM I 42.5R | gravel | 2.96 | 0.84 | 2370 | 36400 |
| CEM II/BS | CEM II/B-S 32.5R | gravel | 2.96 | 0.84 | 2370 | 33900 |
| CEM II/BV | CEM II/B-V 32.5R | gravel | 2.96 | 0.84 | 2366 | 26200 |
| CEM III | CEM III/A 32.5N-LH/HSR/NA | gravel | 2.96 | 0.84 | 2343 | 32100 |
| CEM V | CEM V/A (S-V) 32.5R-LH | gravel | 2.96 | 0.84 | 2366 | 28800 |
| CEM VLH | VLH V/B (S-V) 22.5 | gravel | 2.96 | 0.84 | 2330 | 25700 |
| Coefficient | Notation | Value | Comment |
|---|---|---|---|
| Initial temperature | , °C | 20 | – |
| Ambient, soil temperature | , °C | 20 | – |
| Coefficient of thermal diffusion | , m2/s | – | calculated: |
| Rate of hydration heat | W/m3 | – | based on Table 1 and [5] |
| Thermal transfer coefficient | , W/(m2°C) | 6.0 3.5 3.0 | top surface side surfaces bottom surface |
| Coefficient of thermal expansion | , 1/°C | 10 × 10−6 | – |
| Coefficient of mechanical development | s | 0.2 0.25 0.25 0.38 0.25 0.38 | CEM I 42.5R CEM II/B-S 32.5R CEM II/B-V 32.5R CEM III/A 32.5N-LH/HSR/NA CEM V/A (S-V) 32.5R-LH VLH V/B (S-V) 22.5 |
| Data | Unit | Value | Comment |
|---|---|---|---|
| Cement CEM III/A 32.5N-LH/HSR/NA | kg/m3 | 235 | The composition of the binder is close to the cement VLH (28% of Portland clinker, 40% of slag and 32% of fly ash in the total amount 345 kg/m3 of the binder), thus the coefficients were taken as for this cement with 345 kg/m3 in Equation (1) |
| Fly ash | kg/m3 | 110 | |
| Density, | kg/m3 | 2306 | On the base of experimental data |
| Specific heat, | kJ/(kg °C) | 0.84 | Gravel aggregate |
| Thermal conductivity, | W/(m °C) | 2.96 | Gravel aggregate |
| Initial temperature, | °C | 12 | On the base of experimental data |
| Ambient, soil temperature, | °C | 5 | On the base of experimental data |
| Thermal transfer coefficient, | W/(m2 °C) | 3.0 3.0 | top surface (with insulation) bottom surface |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klemczak, B. Analytical Method for Predicting Early Age Thermal Effects in Thick Foundation Slabs. Materials 2019, 12, 3689. https://doi.org/10.3390/ma12223689
Klemczak B. Analytical Method for Predicting Early Age Thermal Effects in Thick Foundation Slabs. Materials. 2019; 12(22):3689. https://doi.org/10.3390/ma12223689
Chicago/Turabian StyleKlemczak, Barbara. 2019. "Analytical Method for Predicting Early Age Thermal Effects in Thick Foundation Slabs" Materials 12, no. 22: 3689. https://doi.org/10.3390/ma12223689
APA StyleKlemczak, B. (2019). Analytical Method for Predicting Early Age Thermal Effects in Thick Foundation Slabs. Materials, 12(22), 3689. https://doi.org/10.3390/ma12223689





