Nanoindentation of Aluminum Single Crystals: Experimental Study on Influencing Factors
Abstract
:1. Introduction
2. Theoretical Background
2.1. Young’s Modulus
2.2. Indentation Modulus
2.3. Determination of the Indentation Hardness and Modulus from Indentation Curves
2.4. Statistical Pop-In Analysis
3. Materials and Methods
3.1. Materials and Sample Preparation
3.2. Pile-Up and Sink-In Corrections
3.3. Indentation Setup
3.4. Design of the Fit Function
4. Results
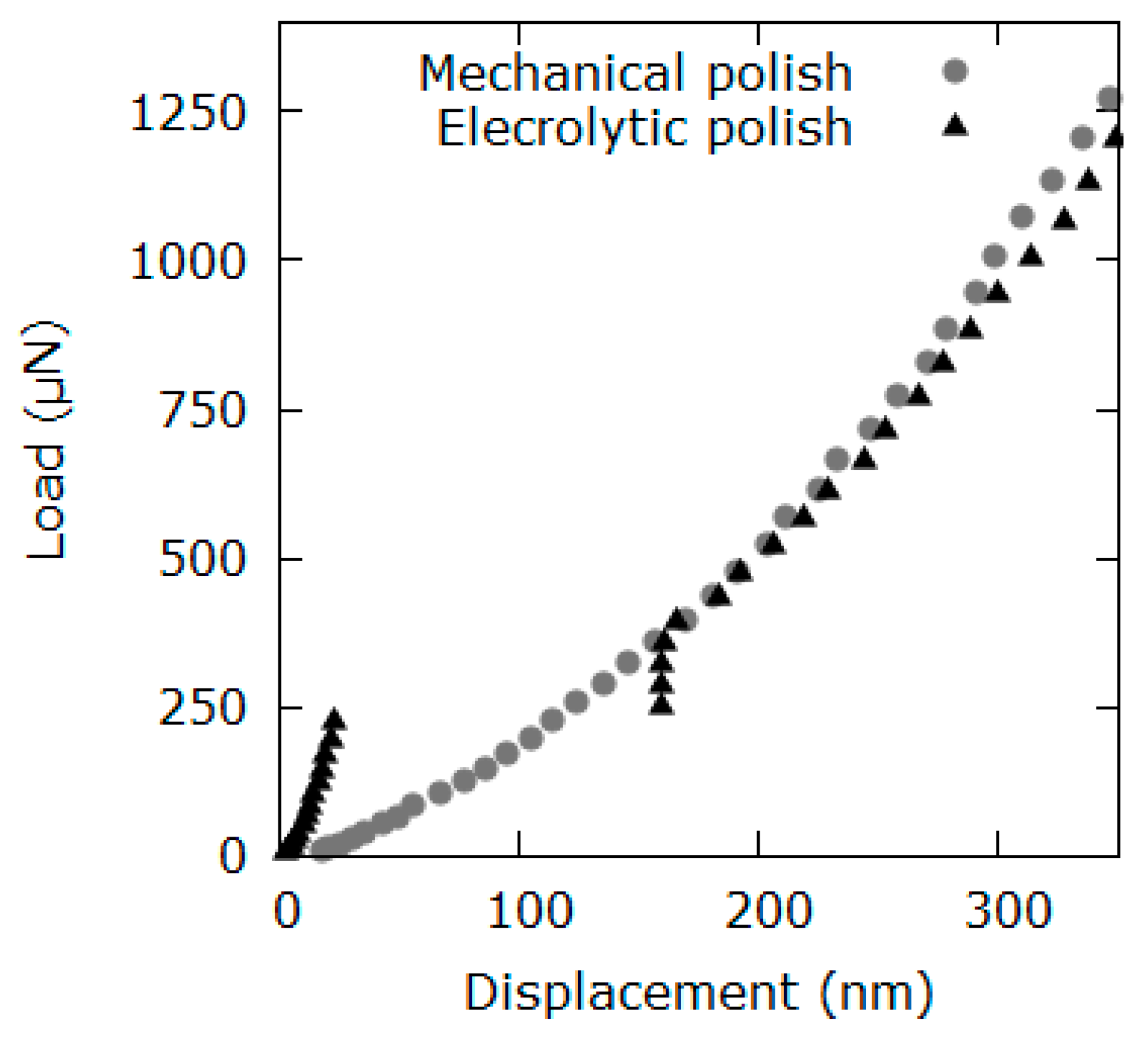
4.1. Quality of Sample Preparation
4.2. Pile-Up and Sink-In Corrections
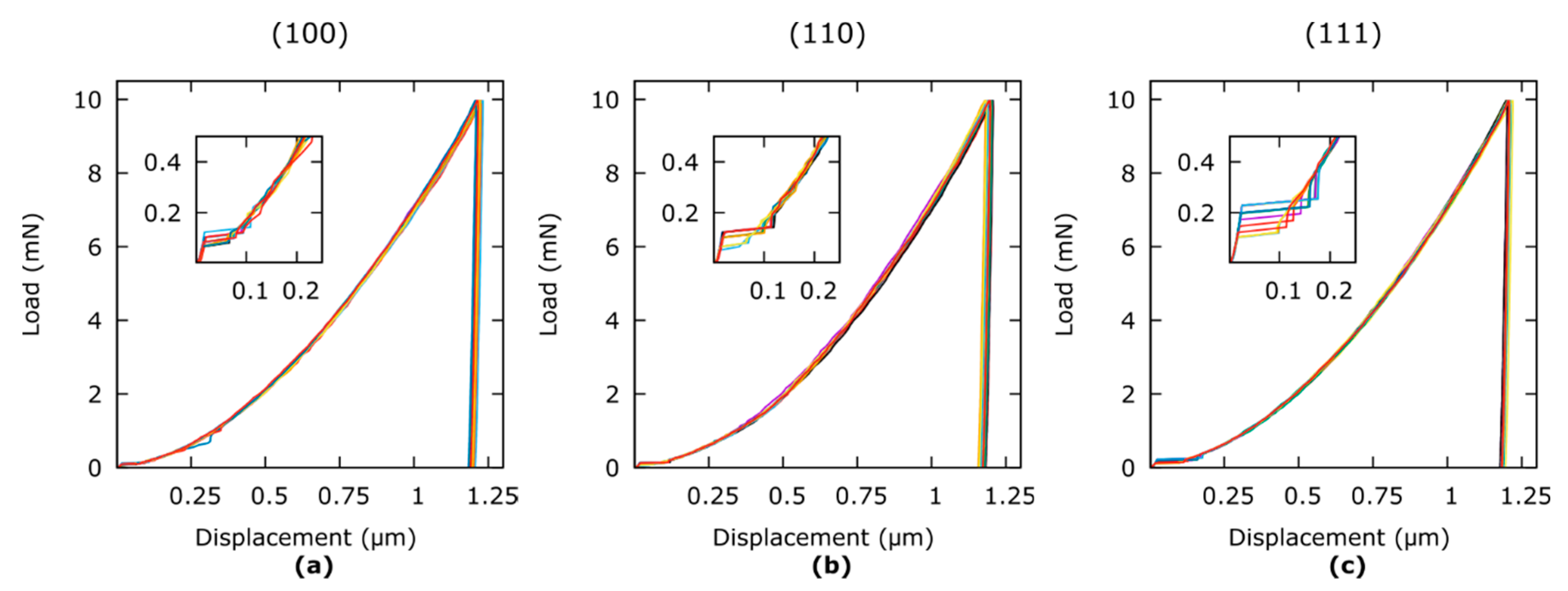
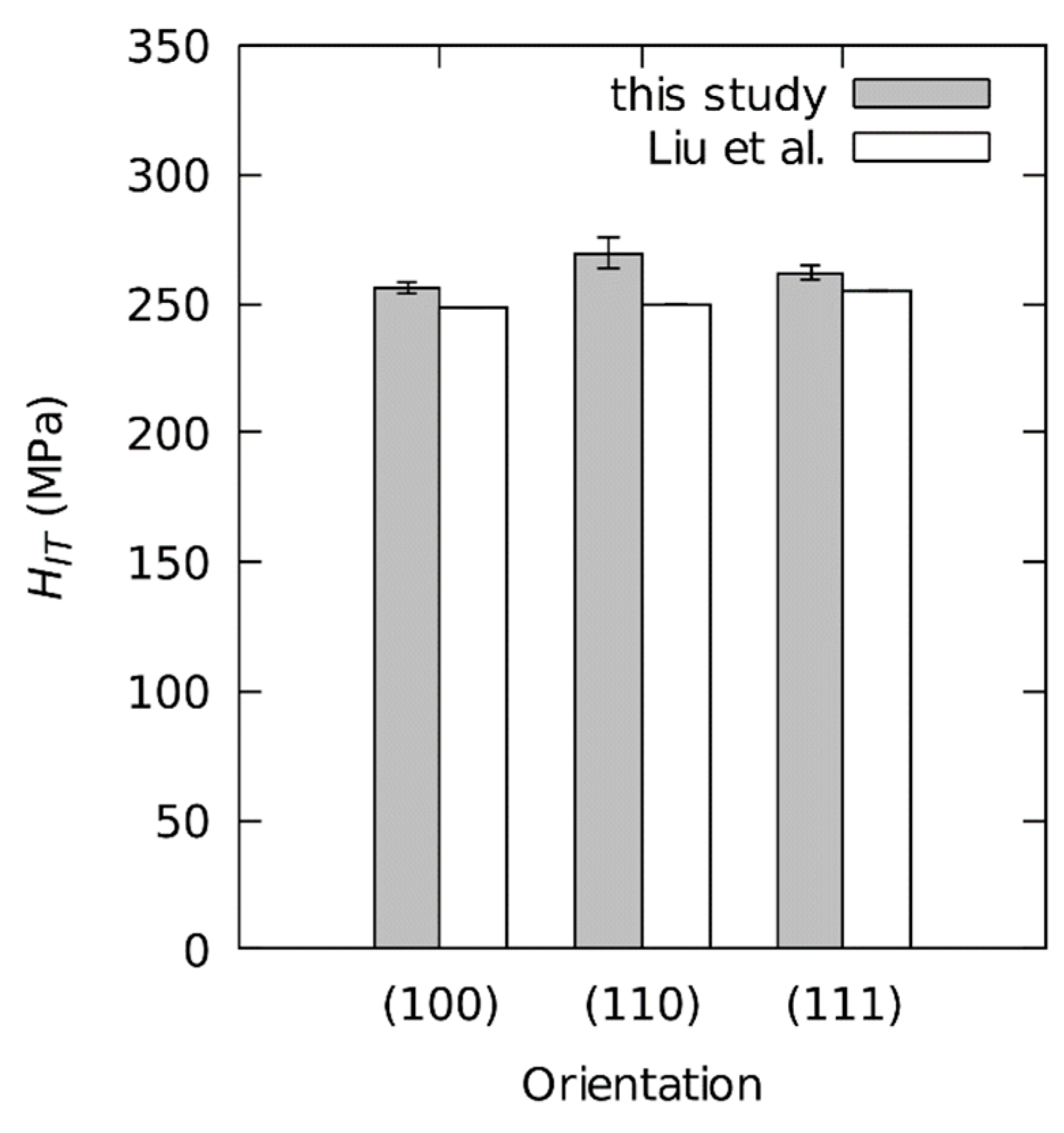
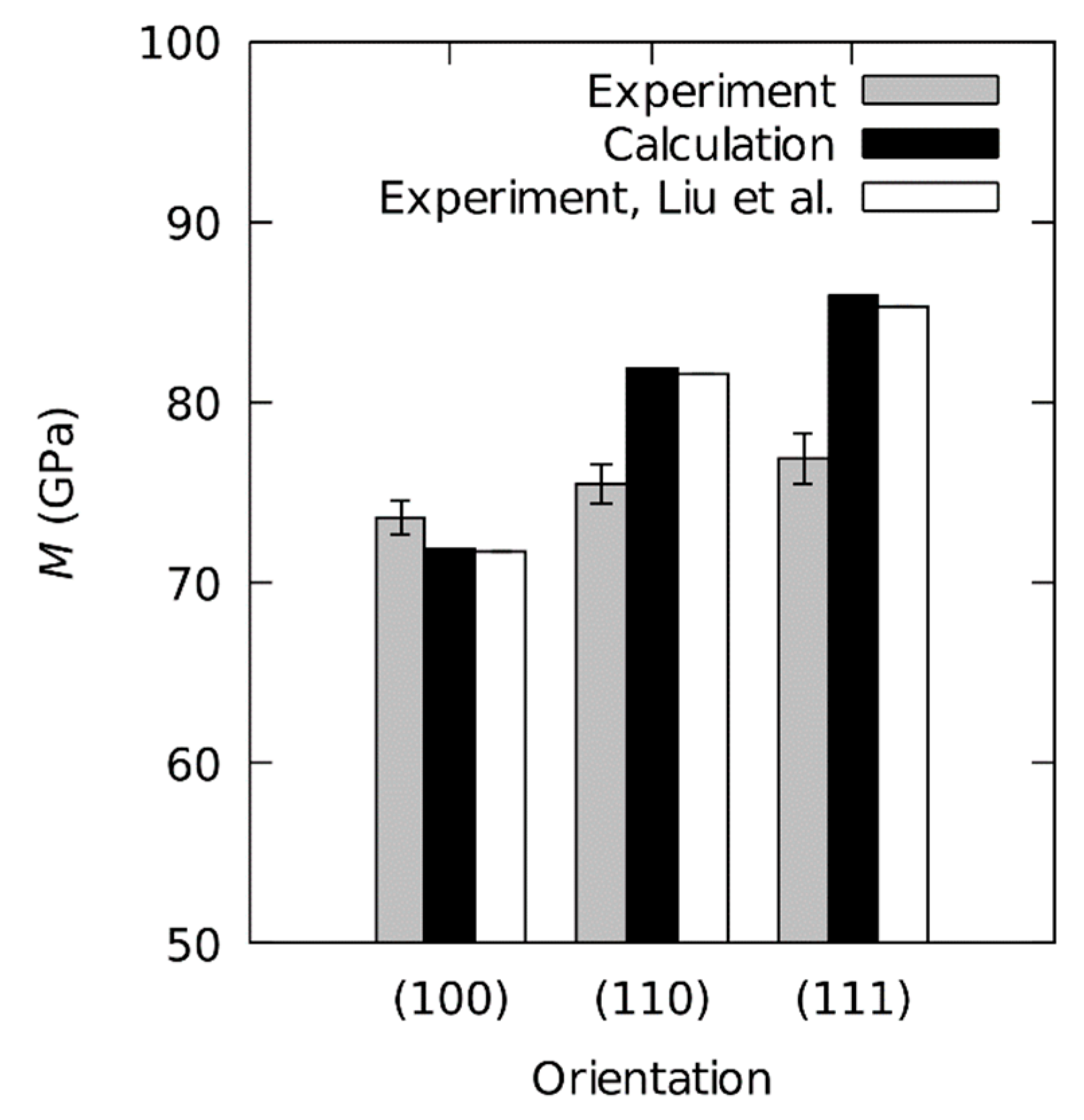
4.3. Influence of the Crystal Orientation on and
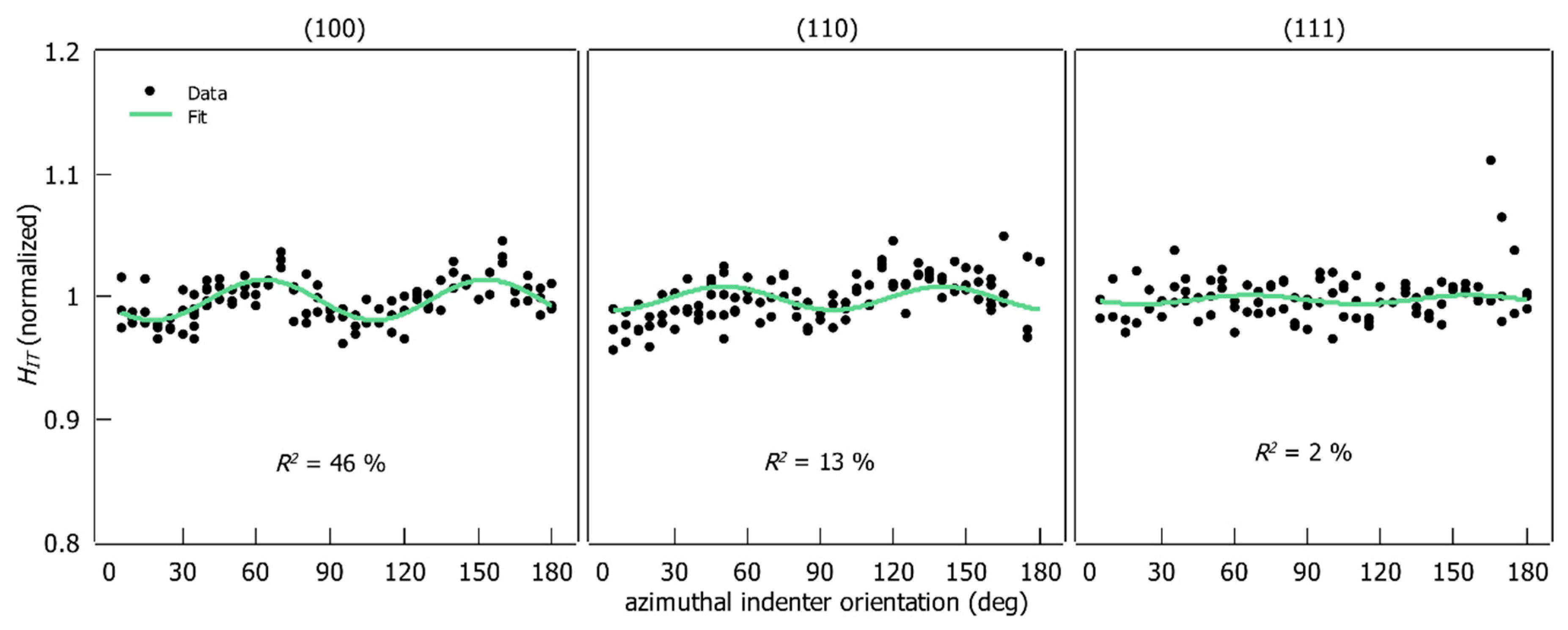
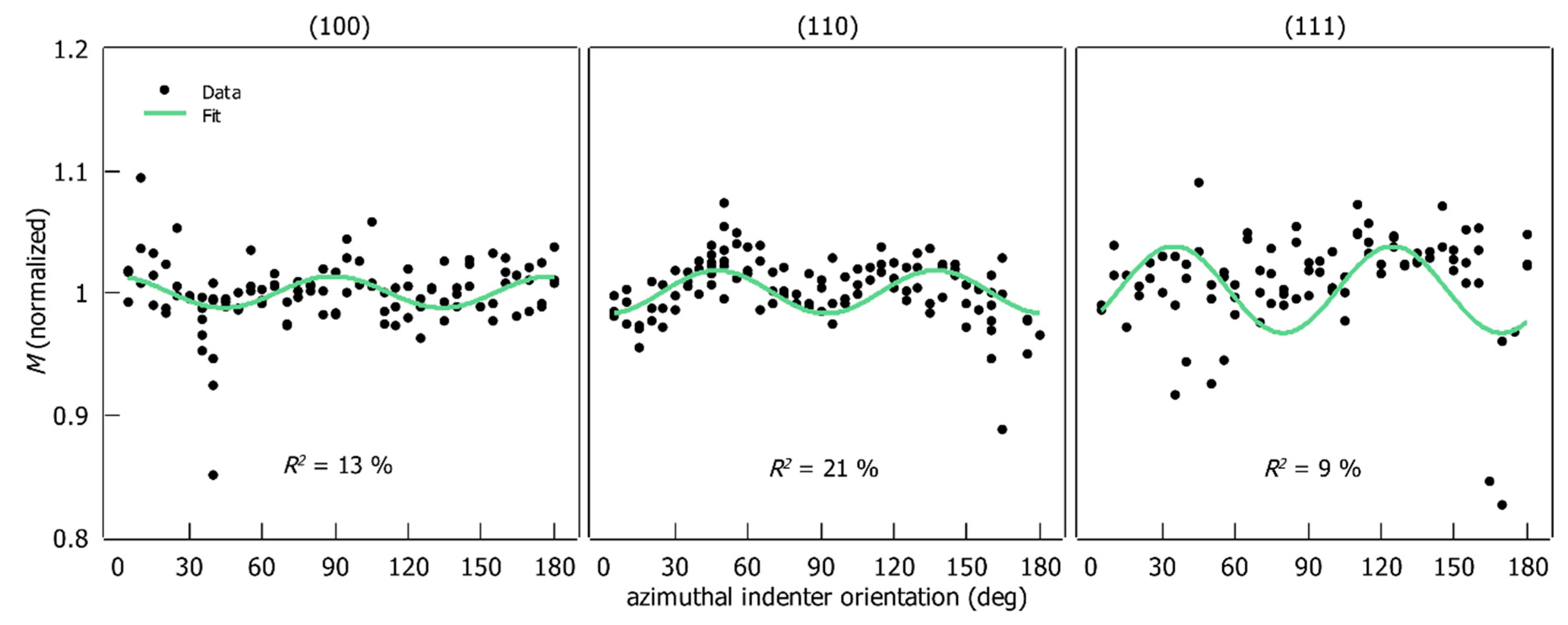
4.4. Influence of the Indenter Orientation on and
5. Discussion
5.1. Quality of Sample Preparation
5.2. Correction for Plastic Behavior
5.3. Influence of the Crystal Orientation on and Values
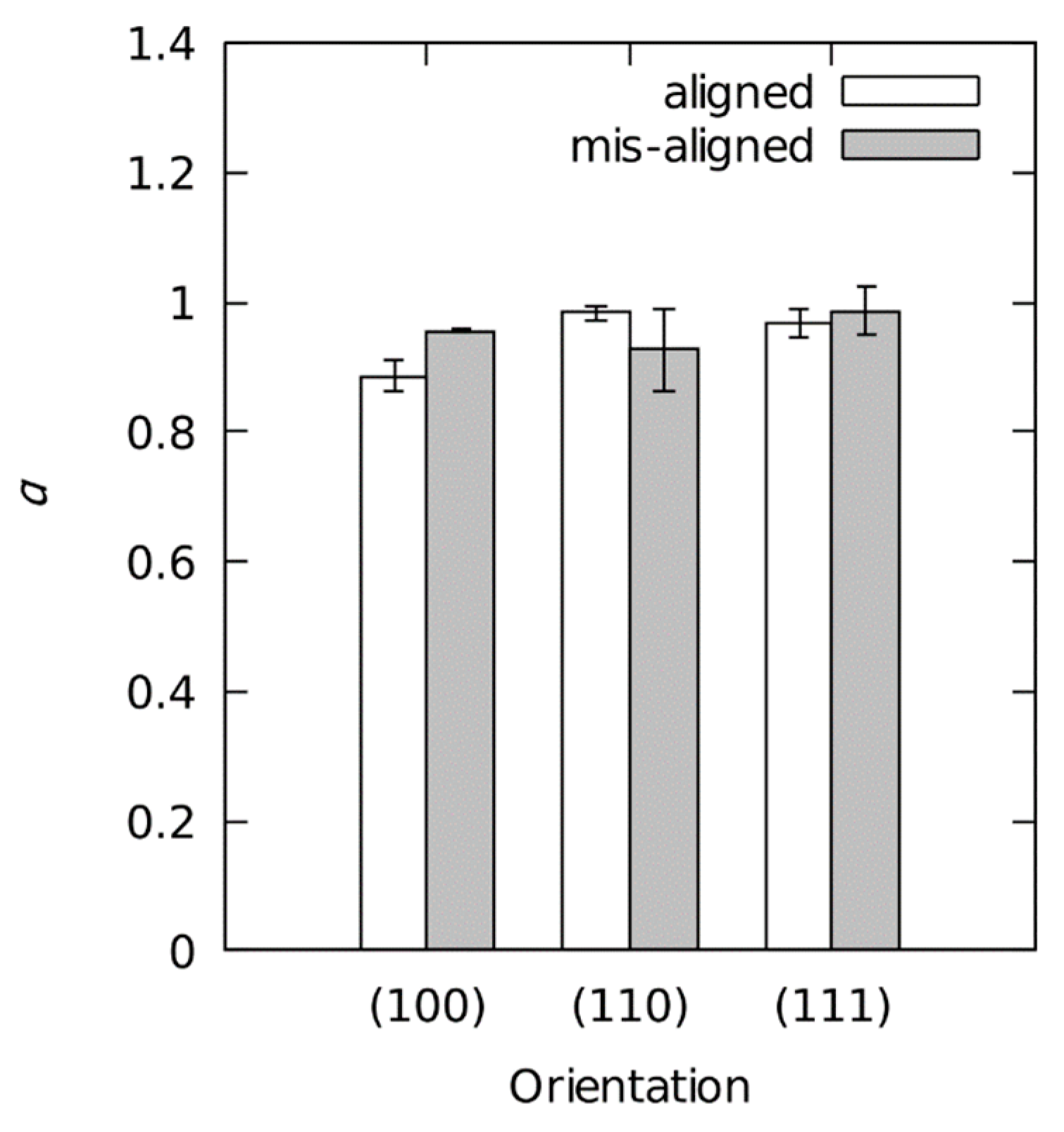
5.4. Influence of the Azimuthal Indenter Orientation
6. Conclusions
- Distinctive surface deformation patterns (crystal integrity) and the pop-in effect (low dislocation density) demonstrated that the combination of mechanical and electrolytic sample preparation has almost no influence on the acquired results.
- No correction method for the true contact area could be applied due to the directionality of the sink-in behavior.
- The range of the effect of crystallographic orientation on was found to be 7.3% relative to average hardness, which corresponds to a of 1.8%.
- The variation of indentation modulus on three different crystallographic orientations can be assigned to elastic anisotropy of aluminum. The anisotropy of the indentation modulus is reduced as a result of indentation averaging. This is correctly predicted by the implemented data analysis model.
- The periodic behavior of and as a function of azimuthal indenter orientation is assigned to the combined effect of indenter geometry and crystal symmetry. Therefore, only the interaction of even-numbered symmetries results in periodic behavior.
- Through the analysis of a harmonic function fitted to the experimental data, a significant fraction of the data scatter can be assigned to the effect of the azimuthal orientation of the indenter. For the first time, it is possible to quantify this effect on the basis of experimental data.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Doerner, M.F.; Nix, W.D. A method for interpreting the data from depth-sensing indentation instruments. J. Mater. Res. 1986, 1, 601–609. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation. J. Mater. Res. 1992, 7, 1654–1853. [Google Scholar] [CrossRef]
- Armstrong, R.W.; Walley, S.M.; Elban, W.L. Crystal Indentation Hardness. Crystals 2017, 7, 21. [Google Scholar] [CrossRef]
- Fischer-Cripps, A.C. A review of analysis methods for sub-micron indentation testing. Vacuum 2000, 58, 569–585. [Google Scholar] [CrossRef]
- Armstrong, R.W.; Elban, W.L.; Walley, S.M. Elastic, plastic, cracking aspects of the hardness of materials. Int. J. Mod. Phys. B 2013, 27, 1330004. [Google Scholar] [CrossRef]
- Shuman, D.J.; Costa, A.L.M.; Andrade, M.S. Calculating the elastic modulus from nanoindentation and microindentation reload curves. Mater. Charact. 2007, 58, 380–389. [Google Scholar] [CrossRef]
- Nemecek, J. Nanoindentation Based Analysis of Heterogeneous Structural Materials. In Nanoindentation in Materials Science; Nemecek, J., Ed.; InTech: London, UK, 2012; pp. 89–108. [Google Scholar]
- Liu, M.; Lu, C.; Tieu, K.A.; Peng, C.-T.; Kong, C. A combined experimental-numerical approach for determining mechanical properties of aluminum subjects to nanoindentation. Sci. Rep. 2015, 5, 15072. [Google Scholar] [CrossRef]
- Pharr, G.M.; Bolshakov, A. Understanding nanoindentation unloading curves. J. Mater. Res. 2002, 17, 2660–2671. [Google Scholar] [CrossRef]
- Field, J.S.; Swain, M.V. A simple predictive model for spherical indentation. J. Mater. Res. 1993, 8, 297–306. [Google Scholar] [CrossRef]
- Haušild, P.; Materna, A.; Nohava, J. Effect of crystallographic orientation on hardness and indentation modulus in austenitic stainless steel. In Local Mechanical Properties IX; Pešek, L., Zubko, P., Eds.; TTP Trans Tech Publ.: Durnten-Zurich, Switzerland, 2014; pp. 31–34. ISBN 9783037858769. [Google Scholar]
- Merson, E.; Brydson, R.; Brown, A. The effect of crystallographic orientation on the mechanical properties of titanium. J. Phys. Conf. Ser. 2008, 126, 12020. [Google Scholar] [CrossRef]
- Zahedi, A.; Demiral, M.; Roy, A.; Babitsky, V.; Silberschmidt, V. Indentation in F.C.C. single crystals. In Solid State Phenomena; Trans Teck Publ.: Zürich, Switzerland, 2012; pp. 219–225. ISBN 9783037853917. [Google Scholar]
- Geng, Y.; Zhang, J.; Yan, Y.; Yu, B.; Geng, L.; Sun, T. Experimental and theoretical investigation of crystallographic orientation dependence of nanoscratching of single crystalline copper. PLoS ONE 2015, 10. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Varghese, S.; Ma, J.; Yoshino, M.; Lu, H.; Komanduri, R. Orientation effects in nanoindentation of single crystal copper. Int. J. Plast. 2008, 24, 1990–2015. [Google Scholar] [CrossRef]
- Vlassak, J.J.; Nix, W.D.; Vlassak, J.J.; Nix, W.D. Measuring the elastic properties of anisotropic materials by means of indentaion experiments // Measuring the elastic properties of anisotropic materials by means of indentation experiments. J. Mech. Phys. Solids 1994, 42, 1223–1245. [Google Scholar] [CrossRef]
- Rahimian Koloor, S.; Karimzadeh, A.; Tamin, M.; Abd Shukor, M. Effects of Sample and Indenter Configurations of Nanoindentation Experiment on the Mechanical Behavior and Properties of Ductile Materials. Metals 2018, 8, 421. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, J.; Hassan, H.u.; Zhang, J.; Yan, Y.; Hartmaier, A.; Sun, T. Coupled effect of crystallographic orientation and indenter geometry on nanoindentation of single crystalline copper. Int. J. Mech. Sci. 2018, 148, 531–539. [Google Scholar] [CrossRef]
- Worch, H. (Ed.) Werkstoffwissenschaft; 10., vollst. überarb. Aufl.; Wiley-VCH-Verl.: Weinheim, Germany, 2011; ISBN 978-3-527-32323-4. [Google Scholar]
- Rösler, J.; Harders, H.; Bäker, M. Elastisches Verhalten: Kubisches Kristallgitter. Mechanisches Verhalten der Werkstoffe; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2012; pp. 51–60. ISBN 978-3-658-13794-6. [Google Scholar]
- Hornbogen, E.; Warlimont, H. Elastizität. In Metalle: Struktur und Eigenschaften der Metalle und Legierungen; Springer: Berlin/Heidelberg, Germany, 2016; pp. 120–123. [Google Scholar]
- Inamura, T.; Hosoda, H.; Wakashima, K.; Miyazaki, S. Anisotropy and Temperature Dependence of Young’s Modulus in Textured TiNbAl Biomedical Shape Memory Alloy. Mater. Trans. 2005, 46, 1597–1603. [Google Scholar] [CrossRef]
- Simmons, G.; Wang, H. Single Crystal Elastic Constants and Calculated Aggregate Properties: A Handbook, 2nd ed.; M.I.T. Press: Cambridge, MA, USA, 1971; ISBN 978-0262190923. [Google Scholar]
- Göken, M. Nanoindentierungsprüfung. In Moderne Methoden der Werkstoffprüfung, 2nd ed.; Biermann, H., Krüger, L., Eds.; Wiley-CVH: Hoboken, NJ, USA, 2015; pp. 299–351. [Google Scholar]
- Vlassak, J.J.; Nix, W.D. Indentation modulus of elastically anisotropic half spaces. Philos. Mag. A 1993, 67, 1045–1056. [Google Scholar] [CrossRef]
- Delafargue, A.; Ulm, F.-J. Explicit approximations of the indentation modulus of elastically orthotropic solids for conical indenters. Int. J. Solids Struct. 2004, 41, 7351–7360. [Google Scholar] [CrossRef]
- Delobelle, P.; Dali, S.; Richard, F. Interprétation du module d’indentation dans le cas des matériaux anisotropes et/ou actifs. Matériaux Tech. 2011, 99, 185–196. [Google Scholar] [CrossRef]
- Chung, D.H.; Buessem, W.R. The Voigt–Reuss–Hill Approximation and Elastic Moduli of Polycrystalline MgO, CaF 2, β-ZnS, ZnSe, and CdTe. J. Appl. Phys. 1967, 38, 2535–2540. [Google Scholar] [CrossRef]
- DIN Deutsches Institut für Normung e. V. Metallische Werkstoffe—Instrumentierte Eindringprüfung zur Bestimmung der Härte und Anderer Werkstoffparameter. Teil 1: Prüfverfahren, 5th ed.; 77.040.10 (DIN EN ISO 14577-1); Beuth Verlag GmbH: Berlin, Germany, 2015. [Google Scholar]
- Field, J.E.; Telling, R.H. The Young Modulus and Poisson Ratio of Diamond; PCS Cavendish Laboratory: Cambridge, UK, 1999. [Google Scholar]
- Schuh, C.A. Nanoindentation studies of materials. Mater. Today 2006, 9, 32–40. [Google Scholar] [CrossRef]
- Göken, M.; Kempf, M.; Bordenet, M.; Vehoff, H. Nanomechanical characterizations of metals and thin films. Surf. Interface Anal. 1999, 27, 302–306. [Google Scholar] [CrossRef]
- Wang, Z.; Bei, H.; George, E.P.; Pharr, G.M. Influences of surface preparation on nanoindentation pop-in in single-crystal Mo. Scr. Mater. 2011, 65, 469–472. [Google Scholar] [CrossRef]
- McElhaney, K.W.; Vlassak, J.J.; Nix, W.D. Determination of indenter tip geometry and indentation contact area for depth-sensing indentation experiments. J. Mater. Res. 1998, 13, 1300–1306. [Google Scholar] [CrossRef]
- Tuck, J.R.; Korsunsky, A.M.; Bull, S.J.; Davidson, R.I. On the application of the work-of-indentation approach to depth-sensing indentation experiments in coated systems. Surf. Coat. Technol. 2001, 137, 217–224. [Google Scholar] [CrossRef]
- Legendre, P.; Dutilleul, P. Introduction to the analysis of periodic phenomena. In Rhythms in Fishes; Ali, M.A., Ed.; Springer US: Boston, MA, USA, 1992; pp. 11–25. ISBN 978-1-4613-6326-2. [Google Scholar]
- Meschede, D.; Vogel, H.; Gerthsen, C. (Eds.) Gerthsen Physik; 24., überarb. Aufl.; Springer: Berlin, Germany, 2010; ISBN 978-3-642-12894-3. [Google Scholar]
- Pathak, S.; Michler, J.; Wasmer, K.; Kalidindi, S.R. Studying grain boundary regions in polycrystalline materials using spherical nano-indentation and orientation imaging microscopy. J. Mater. Sci. 2012, 47, 815–823. [Google Scholar] [CrossRef]
- Kucharski, S.; Jarząbek, D. Depth dependence of nanoindentation pile-up patterns in copper single crystals. Met. Mater. Trans. A 2014, 45, 4997–5008. [Google Scholar] [CrossRef]
- Mandel, J. Measurement statistics. In Evaluation and Control of Measurements; Mandel, J., Ed.; Dekker: New York, NY, USA, 1991; pp. 5–13. ISBN 0824785312. [Google Scholar]
- Liu, M. Crystal Plasticity and Experimental Studies of Nano-Indentation of Aluminium and Copper. Ph.D. Thesis, University of Wollongong, Wollongong, Australia, 2014. [Google Scholar]
- Rösler, J.; Harders, H.; Bäker, M. Mechanisches verhalten der metalle: Gleitsysteme. In Mechanisches Verhalten der Werkstoffe; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2012; pp. 176–178. ISBN 978-3-658-13794-6. [Google Scholar]


| Sample Orientation | (100) | (110) | (111) |
|---|---|---|---|
| Influence of crystal orientation | 100% | 98% | 97% |
| Influence of azimuthal indenter orientation | 97% | 100% | 100% |
| 1.24 µm | |
| 1.28 µm | |
| 249.5 MPa | |
| 235.2 MPa |
| Sample Orientation | (100) | (110) |
|---|---|---|
| 1.7% | 2.0% | |
| 1.6% | 1.0% | |
| 2.6% | 2.6% | |
| 1.3% | 1.8% |
| (GPa) | |||||
|---|---|---|---|---|---|
| Calculation Method | (100) | (110) | (111) | Ref. | |
| , Equation (1) | 72.6 | 82.5 | 86.5 | 1.191 () | this study |
| , Equations (2)–(6) | 79.1 | 82.5 | 86.5 | 1.019 | |
| , Equation (8) | 73.6 ± 0.9 | 75.5 ± 1.1 | 77.0 ± 1.4 | 1.046 | |
| , Equation (8) | 71.8 | 81.6 | 85.4 | 1.189 | [8,41] |
| , Equation (8) | 77 | 79 | 1.015 | [16] | |
| numeric approximation | 79 | 80 | 81 | 1.029 | [16] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Filippov, P.; Koch, U. Nanoindentation of Aluminum Single Crystals: Experimental Study on Influencing Factors. Materials 2019, 12, 3688. https://doi.org/10.3390/ma12223688
Filippov P, Koch U. Nanoindentation of Aluminum Single Crystals: Experimental Study on Influencing Factors. Materials. 2019; 12(22):3688. https://doi.org/10.3390/ma12223688
Chicago/Turabian StyleFilippov, Pavel, and Ursula Koch. 2019. "Nanoindentation of Aluminum Single Crystals: Experimental Study on Influencing Factors" Materials 12, no. 22: 3688. https://doi.org/10.3390/ma12223688
APA StyleFilippov, P., & Koch, U. (2019). Nanoindentation of Aluminum Single Crystals: Experimental Study on Influencing Factors. Materials, 12(22), 3688. https://doi.org/10.3390/ma12223688





