Uncertainty Quantification for Mechanical Properties of Polyethylene Based on Fully Atomistic Model
Abstract
1. Introduction
2. Nanoscale Model
2.1. Model System and Molecular Force Field
2.2. Deformation Simulations
3. Stochastic Modeling
4. Surrogate Models
4.1. Kriging Regression
4.1.1. Maximum Likelihood Estimation
4.1.2. Kriging Prediction
4.2. Bayesian Updating
5. Sensitivity Analysis
5.1. First-Order Sensitivity Indices
5.2. Total Effect Sensitivity Indices
6. Numerical Results
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vu-Bac, N.; Areias, P.M.A.; Rabczuk, T. A multiscale multisurface constitutive model for the thermo-plastic behavior of polyethylene. Polymer 2016, 105, 327–338. [Google Scholar] [CrossRef]
- Vu-Bac, N.; Bessa, M.A.; Rabczuk, T.; Liu, W.K. A multiscale model for the quasi-static thermo-plastic behavior of highly cross-linked glassy polymers. Macromolecules 2015, 48, 6713–6723. [Google Scholar] [CrossRef]
- Areias, P.; Vu-Bac, N.; Rabczuk, T. A multisurface constitutive model for highly cross-linked polymers with yield data obtained from molecular dynamics simulations. Int. J. Mech. Mater. Des. 2018, 14, 21–36. [Google Scholar] [CrossRef]
- Binder, K. Monte Carlo and Molecular Dynamics Simulations in Polymer Science; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695. [Google Scholar] [CrossRef] [PubMed]
- Mayo, S.L.; Olafson, B.D.; Goddard, W.A. DREIDING: A generic force field for molecular simulations. J. Phys. Chem. 1990, 94, 8897–8909. [Google Scholar] [CrossRef]
- Brandrup, J.; Immergut, E.H. Polymer Handbook, 3rd ed.; Wiley-Interscience: New York, NY, USA, 1989. [Google Scholar]
- Ramos, J.; Vega, J.F.; Martińez-Salazar, J. Molecular dynamics simulations for the description of experimental molecular conformation, melt dynamics, and phase transitions in polyethylene. Macromolecules 2015, 48, 5016–5027. [Google Scholar] [CrossRef]
- Hartmann, B.; Lee, G.F.; Cole, R.F. Tensile Yield Polyethylene. Polym. Eng. Sci. 1986, 26, 554–559. [Google Scholar] [CrossRef]
- Theodorou, D.N.; Suter, U.W. Atomistic modeling of mechanical properties of polymeric glasses. Macromolecules 1986, 19, 139–154. [Google Scholar] [CrossRef]
- Capaldi, F.M.; Boyce, M.C.; Rutledge, G.C. Molecular response of a glassy polymer to active deformation. Polymer 2004, 45, 1391–1399. [Google Scholar] [CrossRef]
- Brown, D.; Clarke, J. Molecular dynamics simulation of an amorphous polymer under tension. 1. Phenomenology. Macromolecules 1991, 24, 2075–2082. [Google Scholar] [CrossRef]
- Helton, J.C.; Davis, F.J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliab. Eng. Syst. Saf. 2003, 81, 23–69. [Google Scholar] [CrossRef]
- Iman, R.L.; Conover, W.J. Small sample sensitivity analysis techniques for computer models with an application to risk assessment. Commun. Stat. 1980, A9, 1749–1842. [Google Scholar] [CrossRef]
- Vu-Bac, N.; Lahmer, T.; Zhuang, X.; Nguyen-Thoi, T.; Rabczuk, T. A software framework for probabilistic sensitivity analysis for computationally expensive models. Adv. Eng. Softw. 2016, 100, 19–31. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C. Response Surface Methodology Process and Product Optimization Using Designed Experiments, 2nd ed.; John Wiley: New York, NY, USA, 2002. [Google Scholar]
- Vu-Bac, N.; Silani, M.; Lahmer, T.; Zhuang, X.; Rabczuk, T. A unified framework for stochastic predictions of mechanical properties of polymeric nanocomposites. Comput. Mater. Sci. 2015, 96, 520–535. [Google Scholar] [CrossRef]
- Forrester, A.I.J.; Sóbester, A.; Keane, A.J. Engineering Design via Surrogate Modeling: A Practical Guide; John Wiley & Sons: Chichester, UK, 2008; ISBN 978-0-470-06068-1. [Google Scholar]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis. The Primer; John Wiley and Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Vu-Bac, N.; Lahmer, T.; Keitel, H.; Zhao, J.; Zhuang, X.; Rabczuk, T. Stochastic predictions of bulk properties of amorphous polyethylene based on molecular dynamics simulations. Mech. Mater. 2014, 68, 70–84. [Google Scholar] [CrossRef]
- Vu-Bac, N.; Lahmer, T.; Zhang, Y.; Zhuang, X.; Rabczuk, T. Stochastic predictions of interfacial characteristic of polymeric nanocomposites (PNCs). Compos. Part B Eng. 2014, 59, 80–95. [Google Scholar] [CrossRef]
- Vu-Bac, N.; Rafiee, R.; Zhuang, X.; Lahmer, T.; Rabczuk, T. Uncertainty quantification for multiscale modeling of polymer nanocomposites with correlated parameters. Compos. Part B Eng. 2015, 68, 446–464. [Google Scholar] [CrossRef]
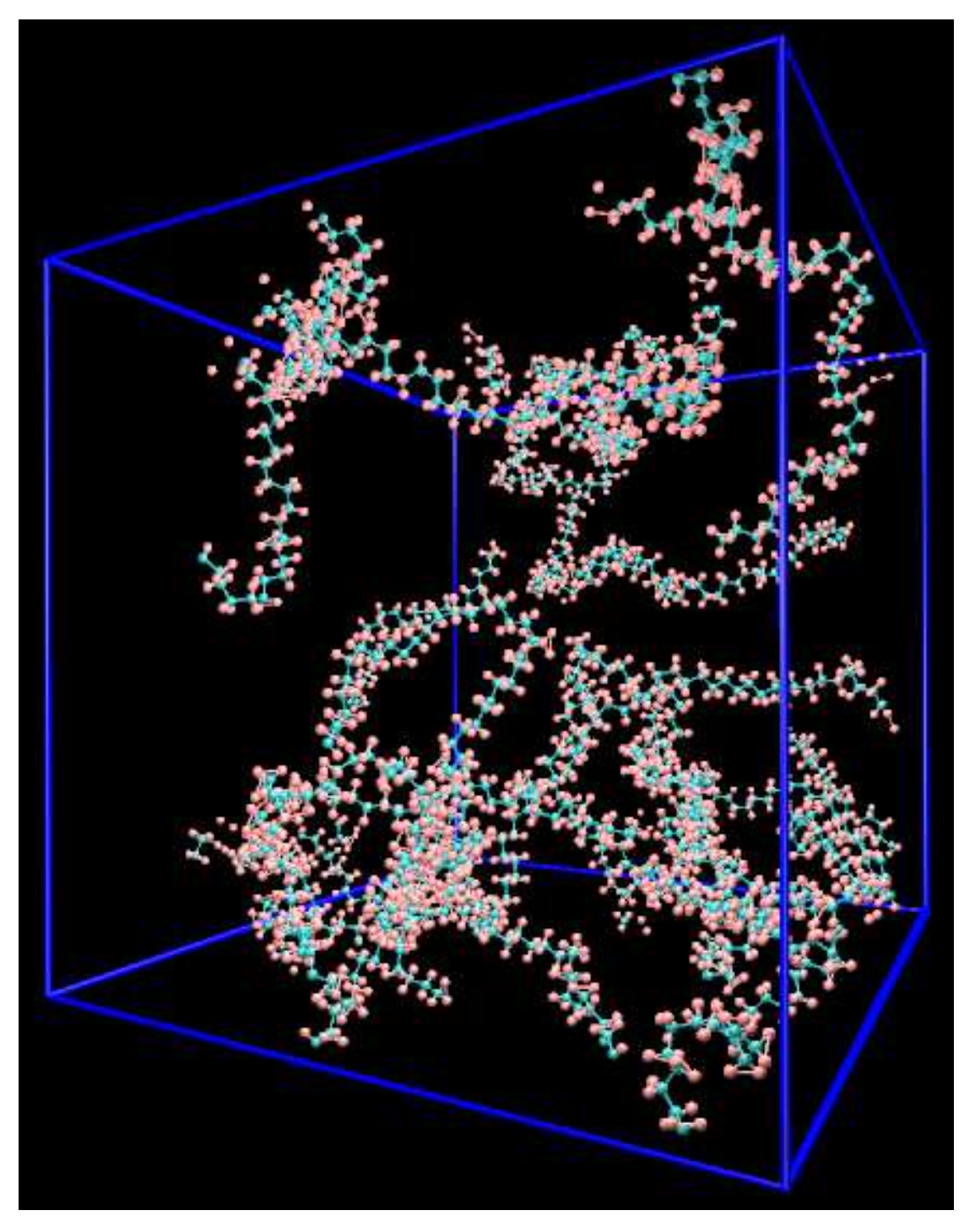
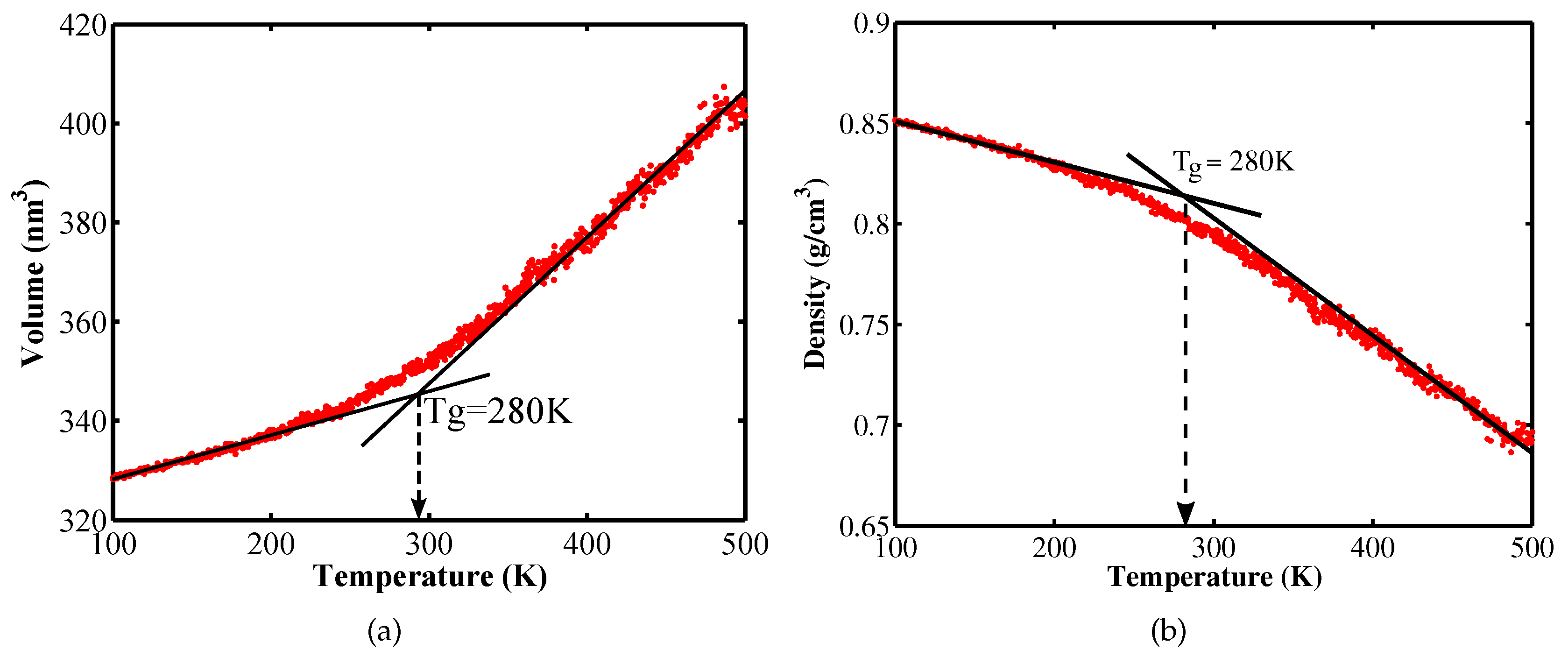

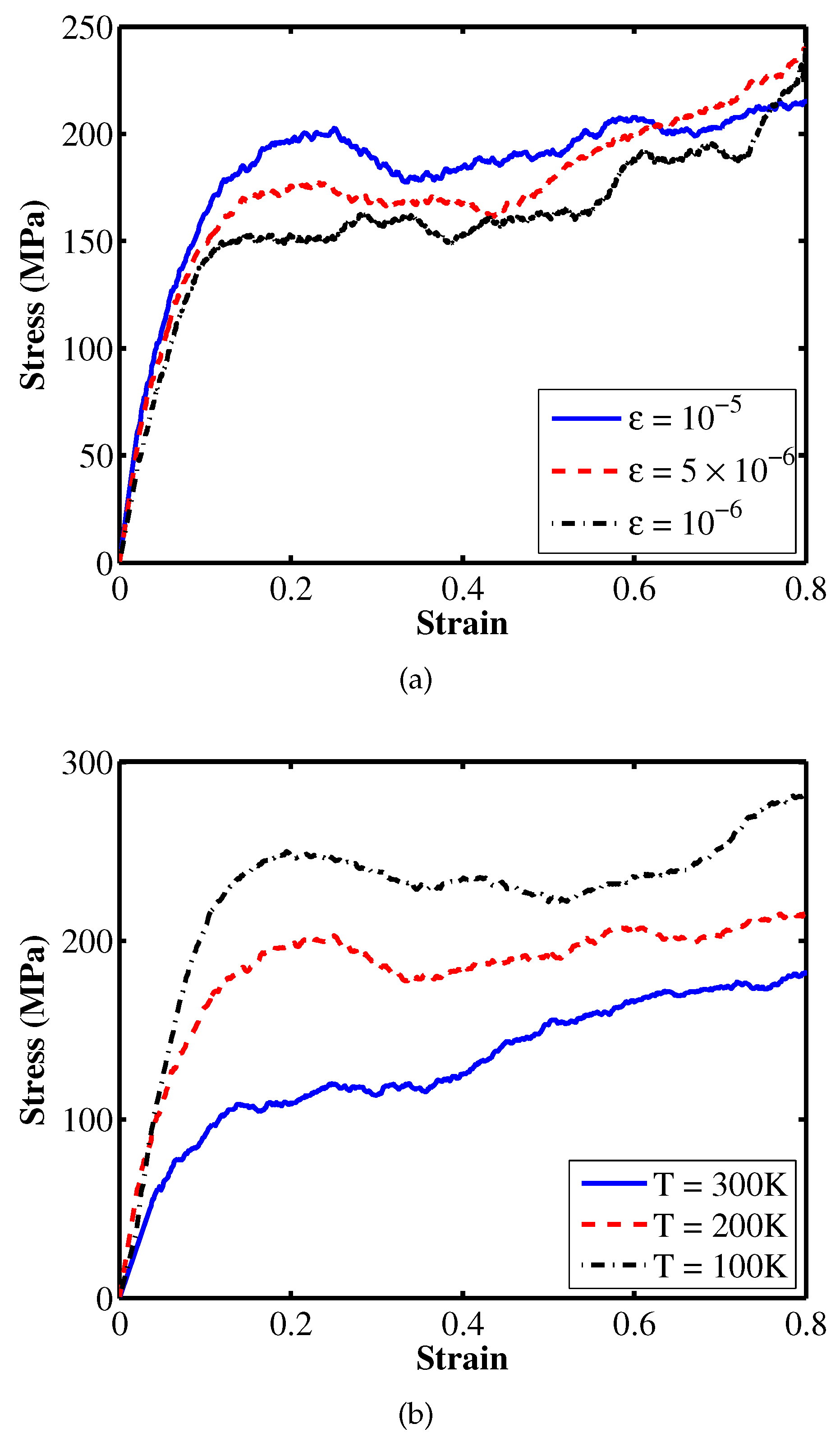
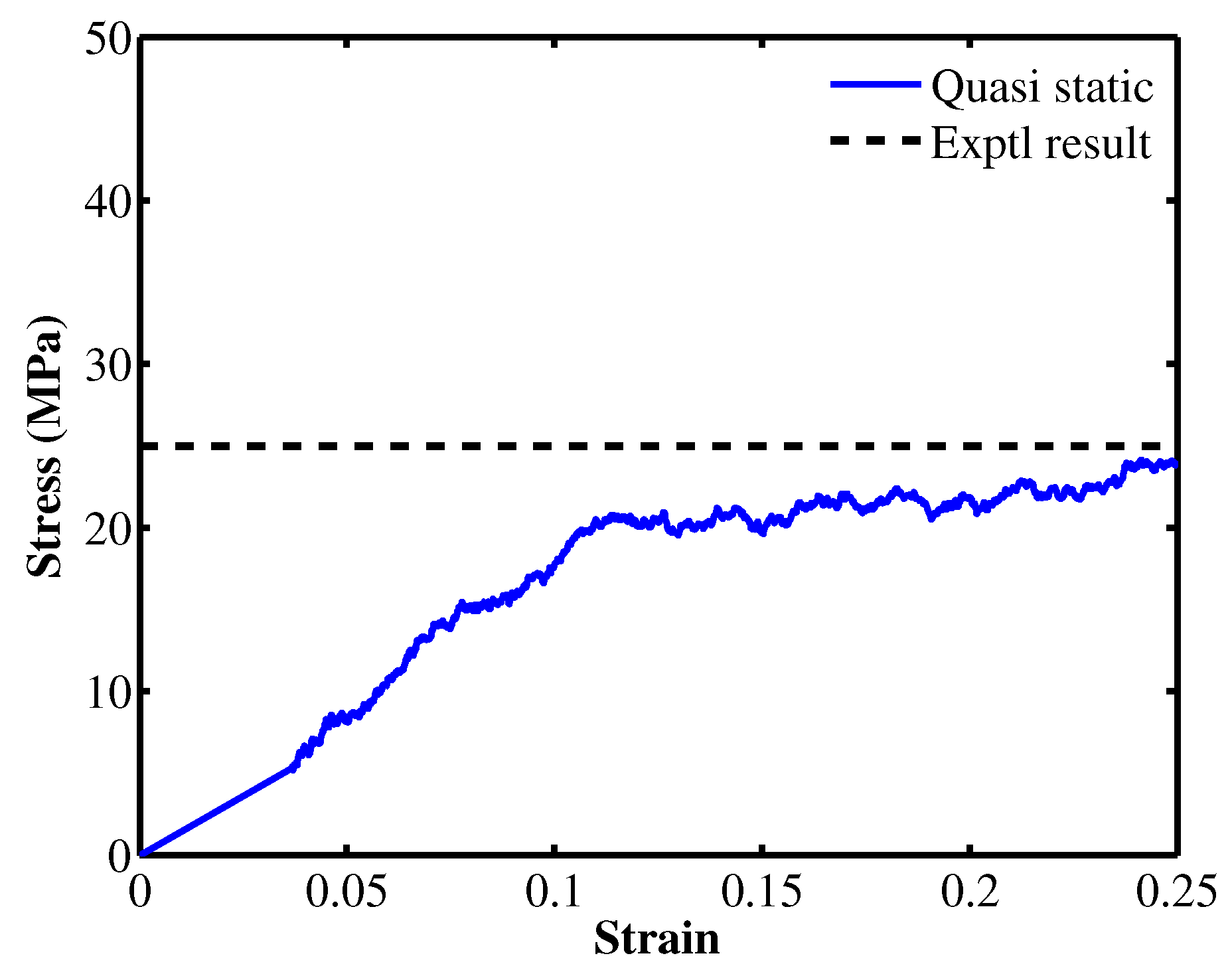
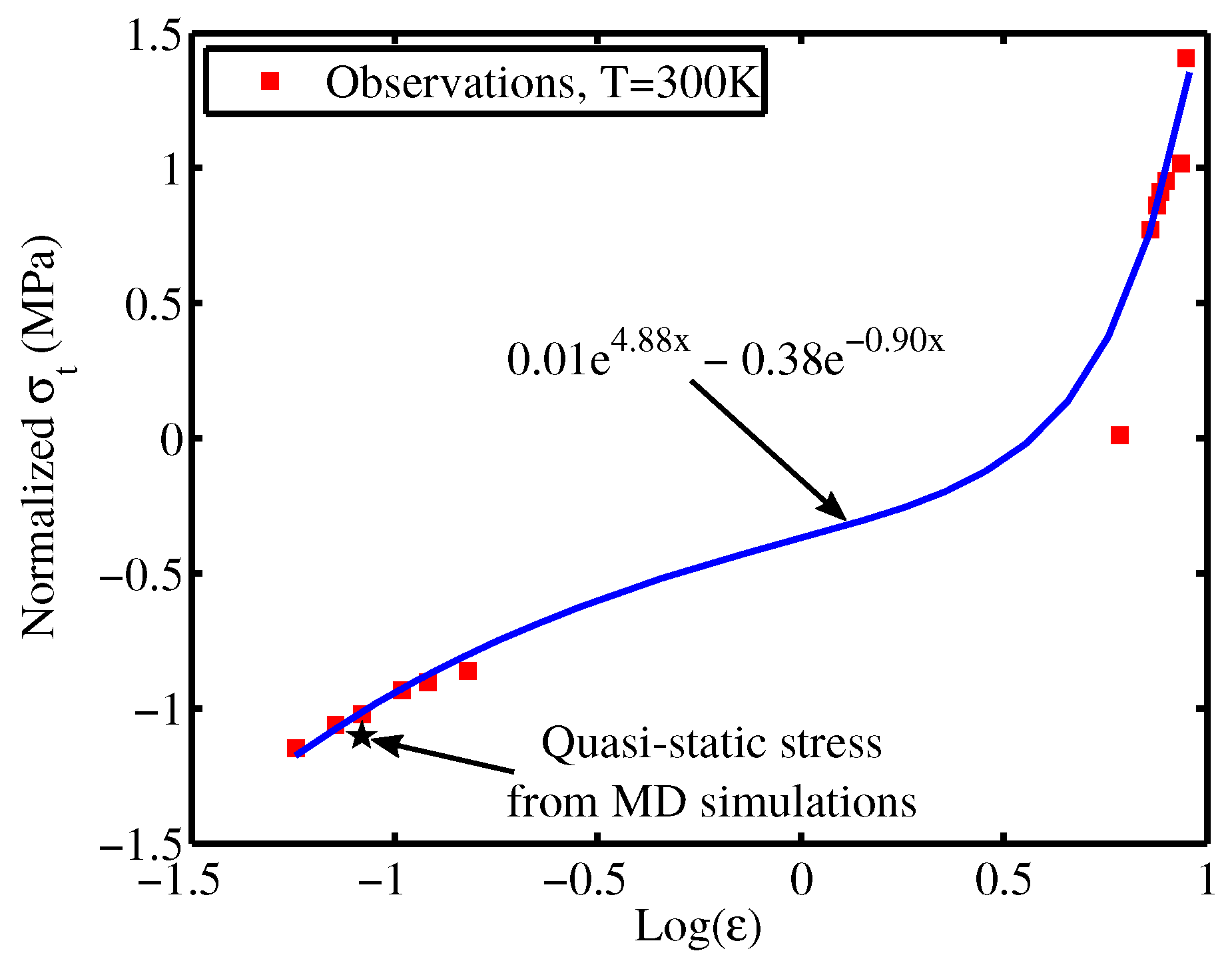


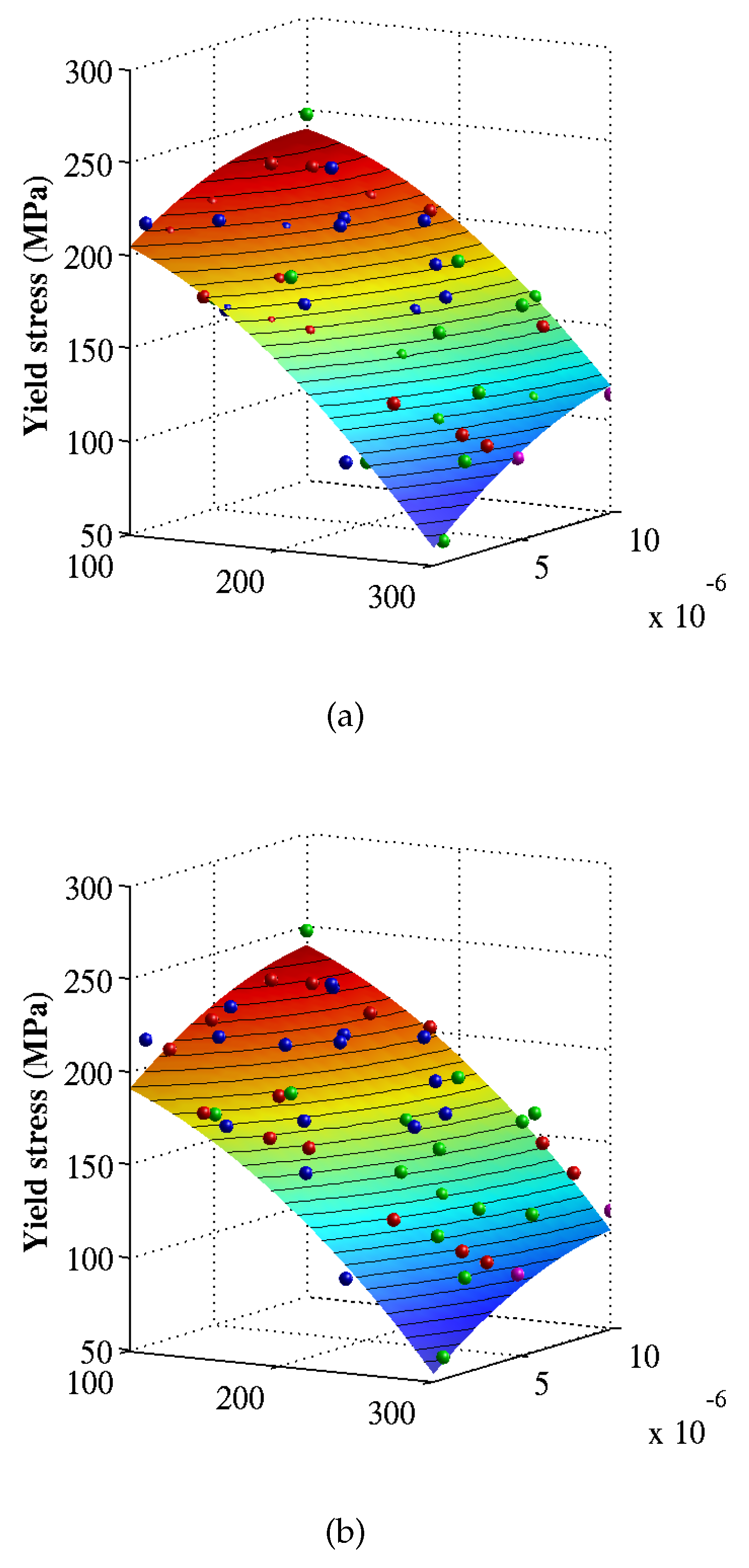

| Tension | ||
|---|---|---|
| Constant | MD | Experimental results |
| simulations | HPDE | |
| Young’s modulus | 1.22 | 1.18 [11] |
| Glass transition temperature | 280 | 250 [9], 255 [10] and 280 [13] |
| Property | ||||
|---|---|---|---|---|
| Young’s modulus | 0.03 | 0.02 | 0.03 | 0.96 |
| Yield stress | 0.03 | 0.01 | 0.005 | 0.96 |
| Property | |||||
|---|---|---|---|---|---|
| Young’s modulus | −0.85 | 0.35 | −0.15 | −0.12 | 0.82 |
| Yield stress | −0.94 | 0.35 | −0.14 | −0.08 | 0.96 |
| Index | ||||
|---|---|---|---|---|
| 0.92 | 0.76 | 0.29 | 0.17 | |
| 0.13 | 0.02 | 0.00 | 0.00 |
| Index | ||||
|---|---|---|---|---|
| 0.92 | 0.76 | 0.29 | 0.17 | |
| 0.13 | 0.02 | 0.00 | 0.00 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vu-Bac, N.; Zhuang, X.; Rabczuk, T. Uncertainty Quantification for Mechanical Properties of Polyethylene Based on Fully Atomistic Model. Materials 2019, 12, 3613. https://doi.org/10.3390/ma12213613
Vu-Bac N, Zhuang X, Rabczuk T. Uncertainty Quantification for Mechanical Properties of Polyethylene Based on Fully Atomistic Model. Materials. 2019; 12(21):3613. https://doi.org/10.3390/ma12213613
Chicago/Turabian StyleVu-Bac, Nam, X. Zhuang, and T. Rabczuk. 2019. "Uncertainty Quantification for Mechanical Properties of Polyethylene Based on Fully Atomistic Model" Materials 12, no. 21: 3613. https://doi.org/10.3390/ma12213613
APA StyleVu-Bac, N., Zhuang, X., & Rabczuk, T. (2019). Uncertainty Quantification for Mechanical Properties of Polyethylene Based on Fully Atomistic Model. Materials, 12(21), 3613. https://doi.org/10.3390/ma12213613




