Creep-Based Reliability Evaluation of Turbine Blade-Tip Clearance with Novel Neural Network Regression
Abstract
:1. Introduction
2. Theory and Methods
2.1. High-Temperature Creep Theory
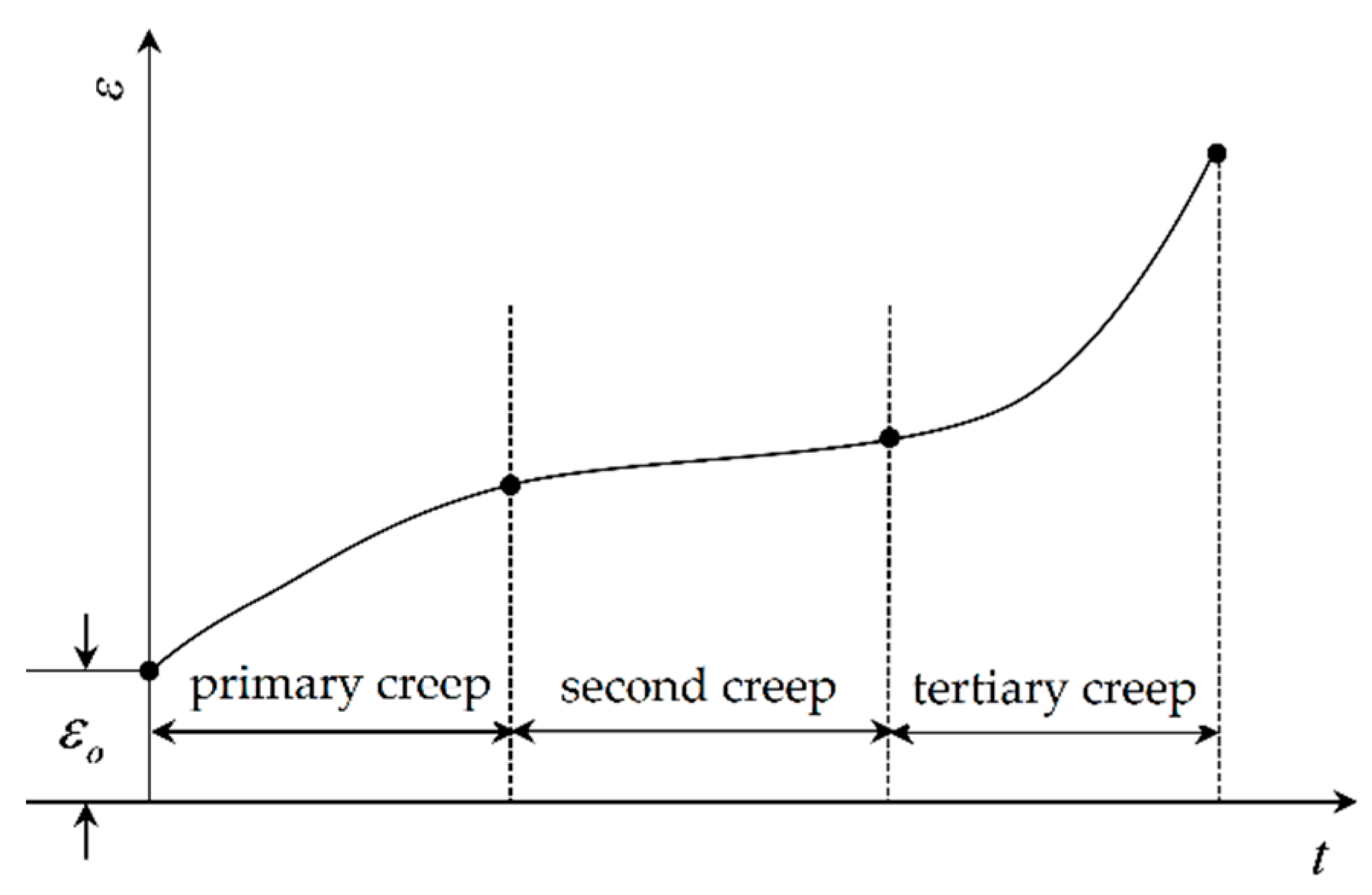
2.2. Generalized Regression Neural Network
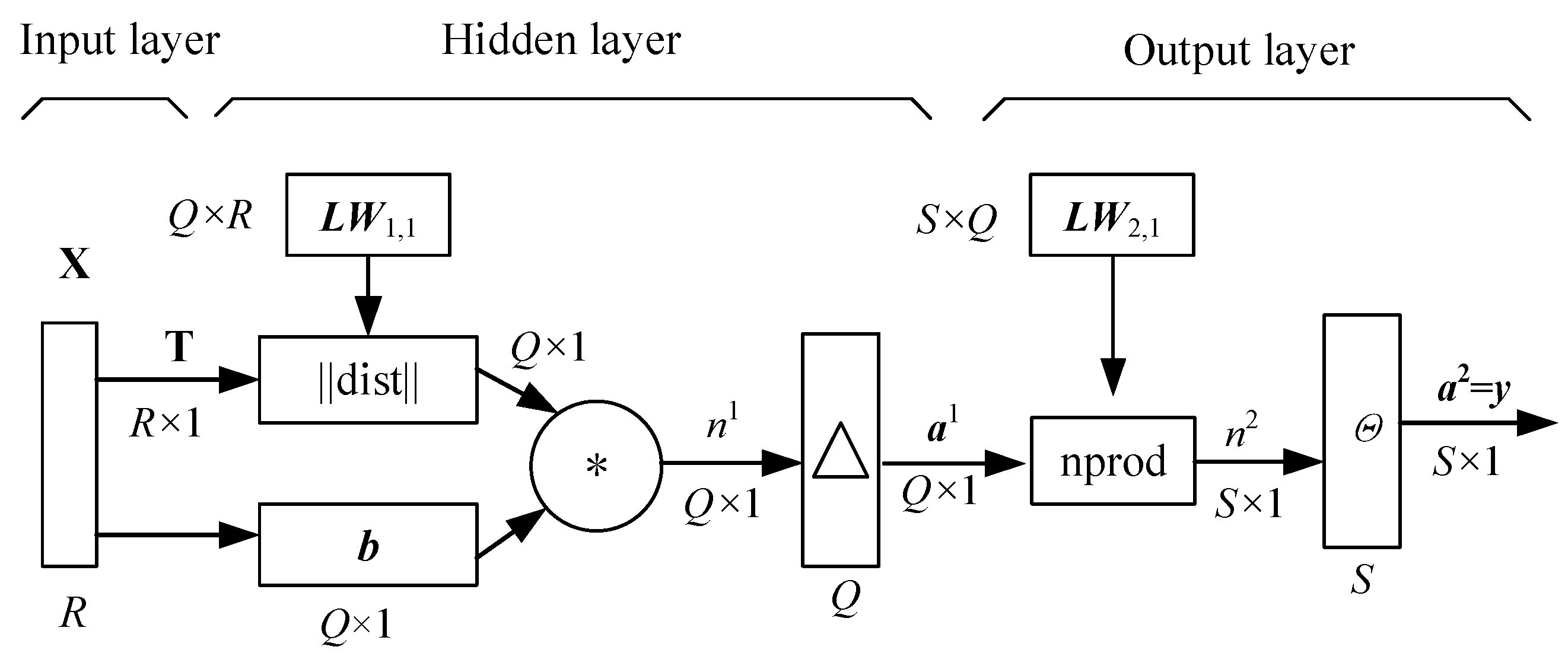
2.3. Generalized Regression Extremum Neural Network Method
2.4. Distributed Collaborative Generalized Regression Extremum Neural Network
2.5. Reliability Calculation Approaches
3. Reliability Analysis of Blade-Tip Radial Running Clearance
3.1. Finite Element Analysis
3.1.1. Finite Element Modeling
3.1.2. Selection of Random Variables
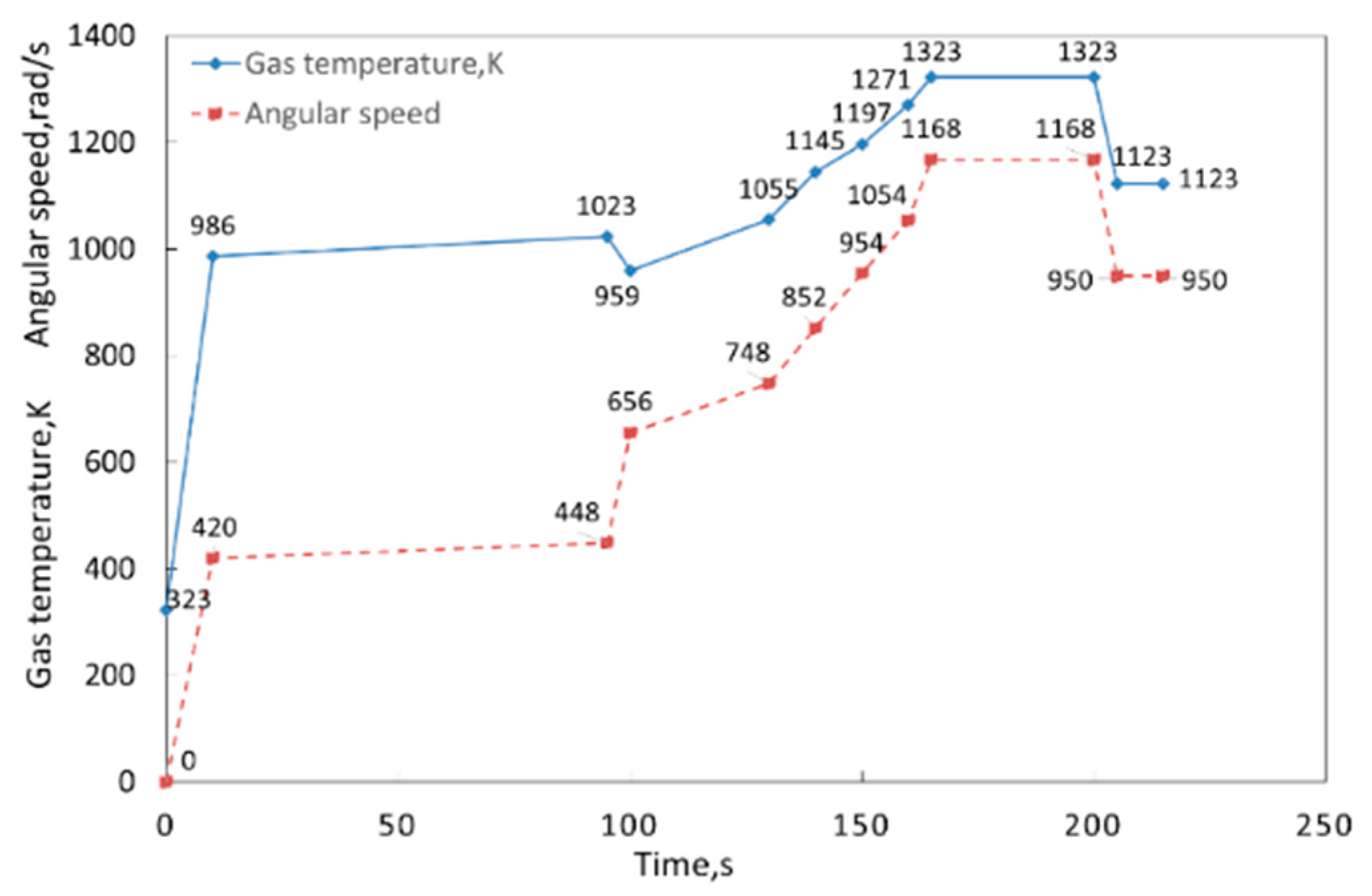
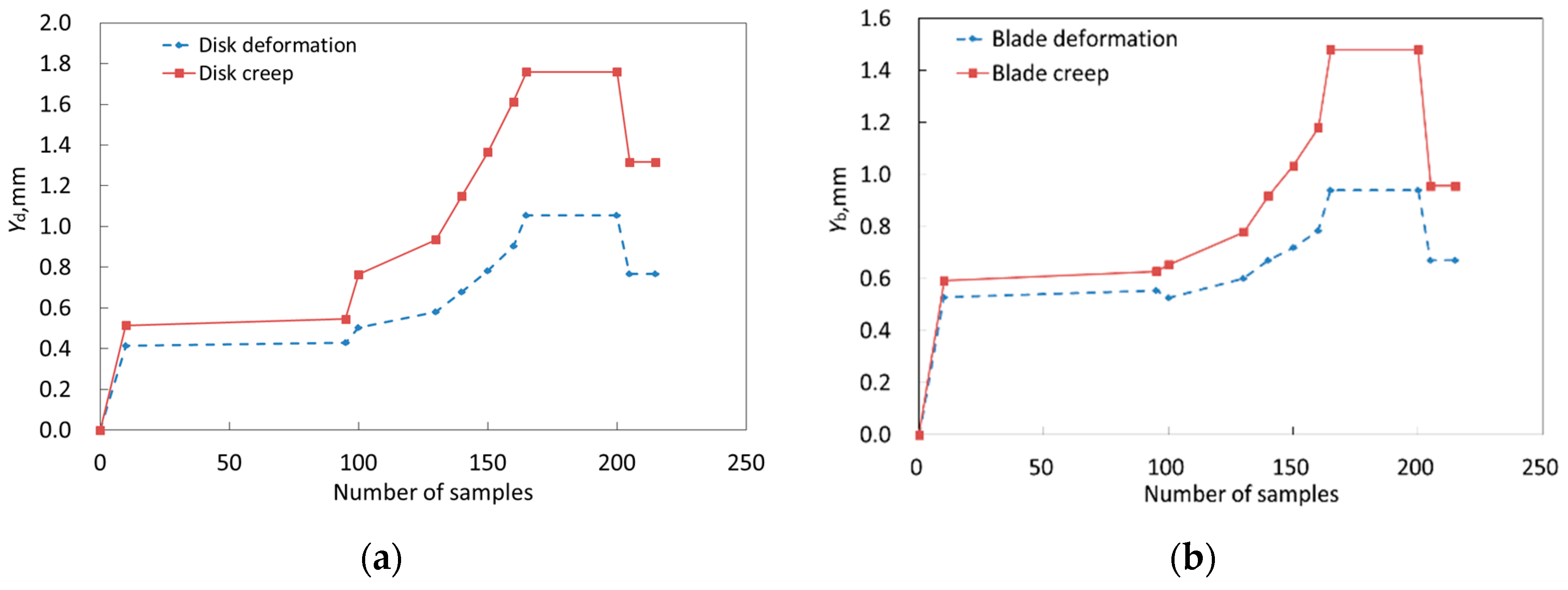
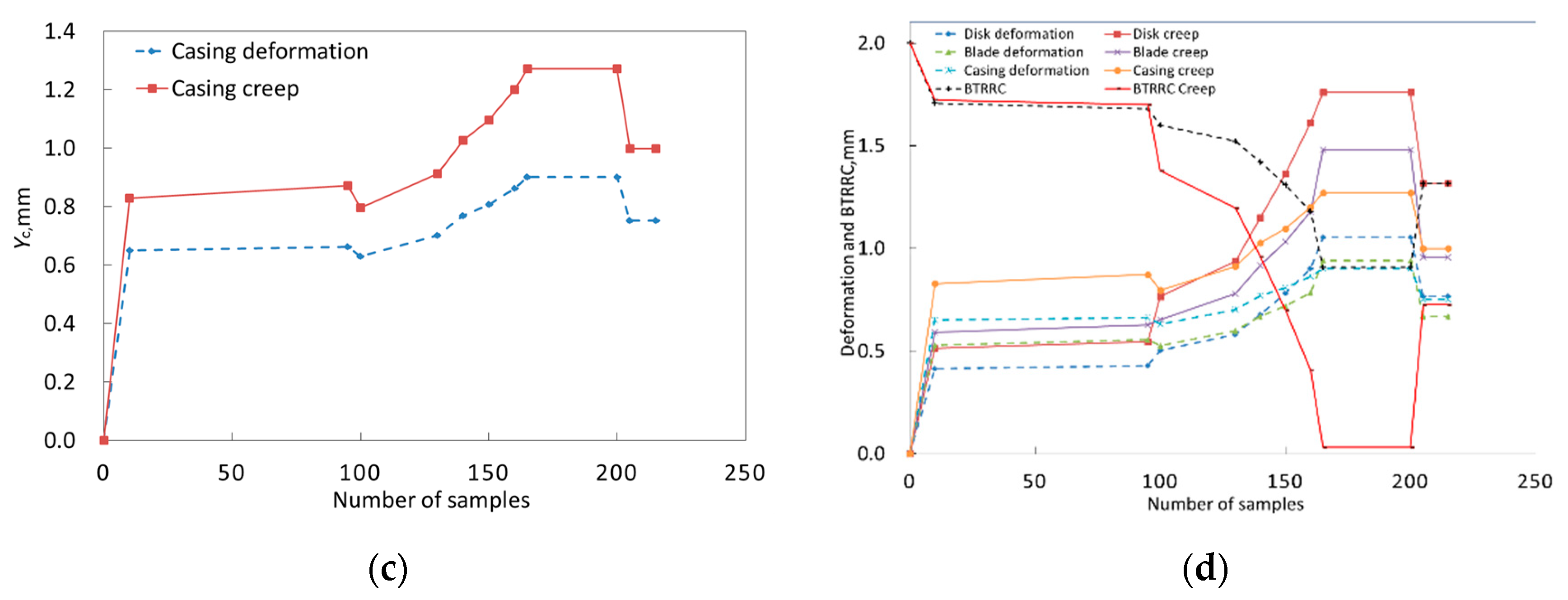
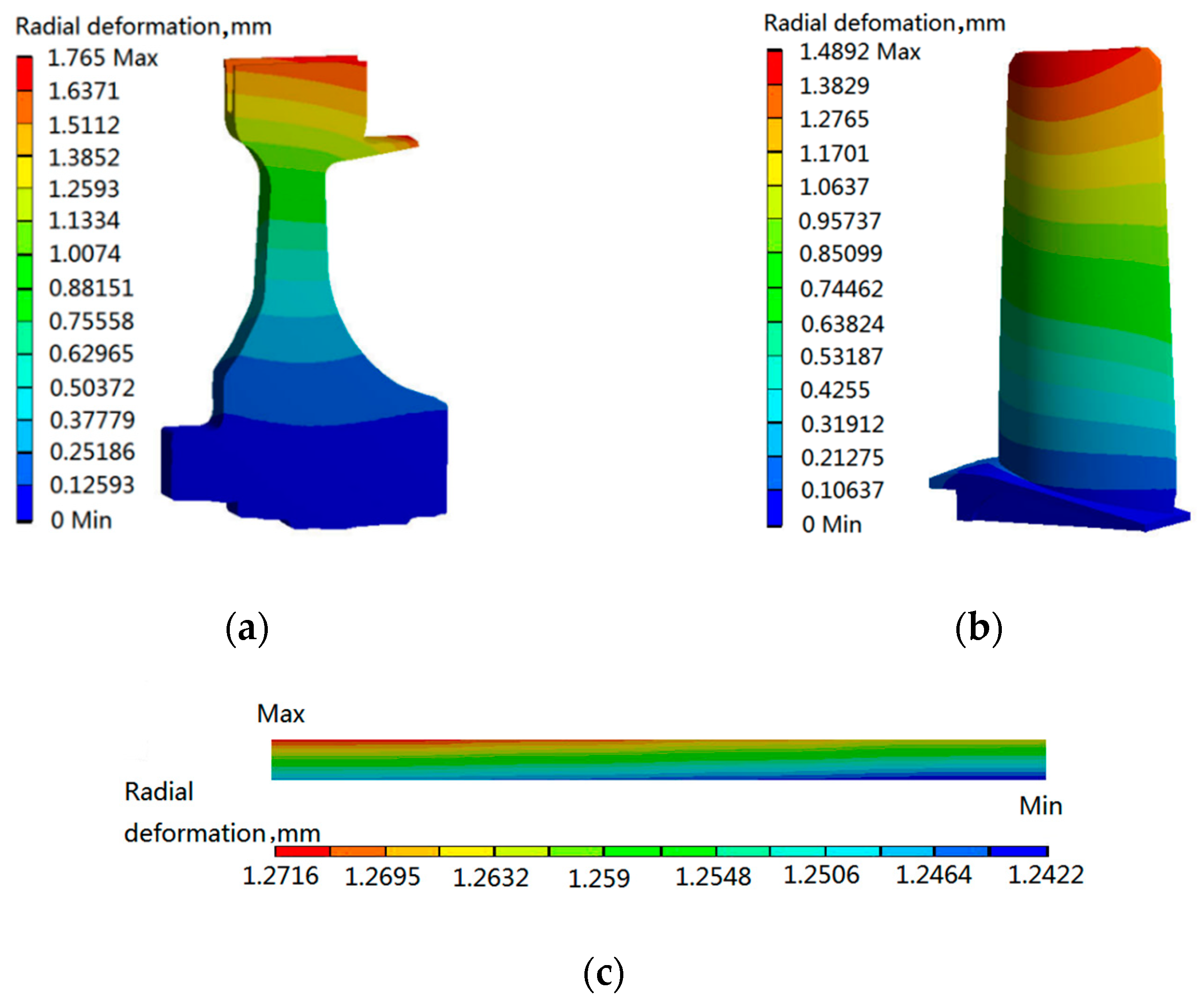
3.1.3. Deterministic Analyses of Three Objects
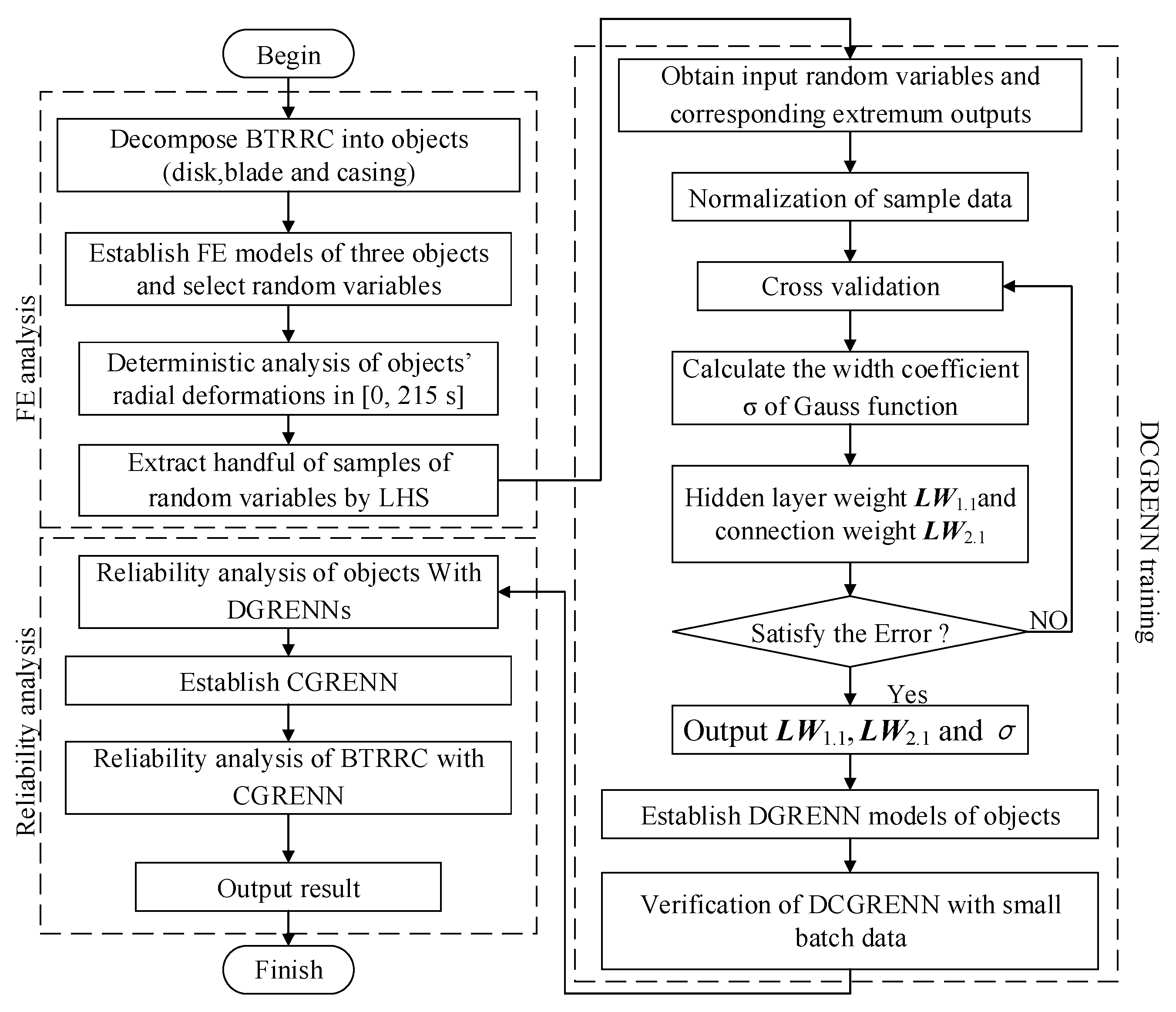
3.2. Modeling of the Distributed Collaborative Generalized Regression Extremum Neural Network
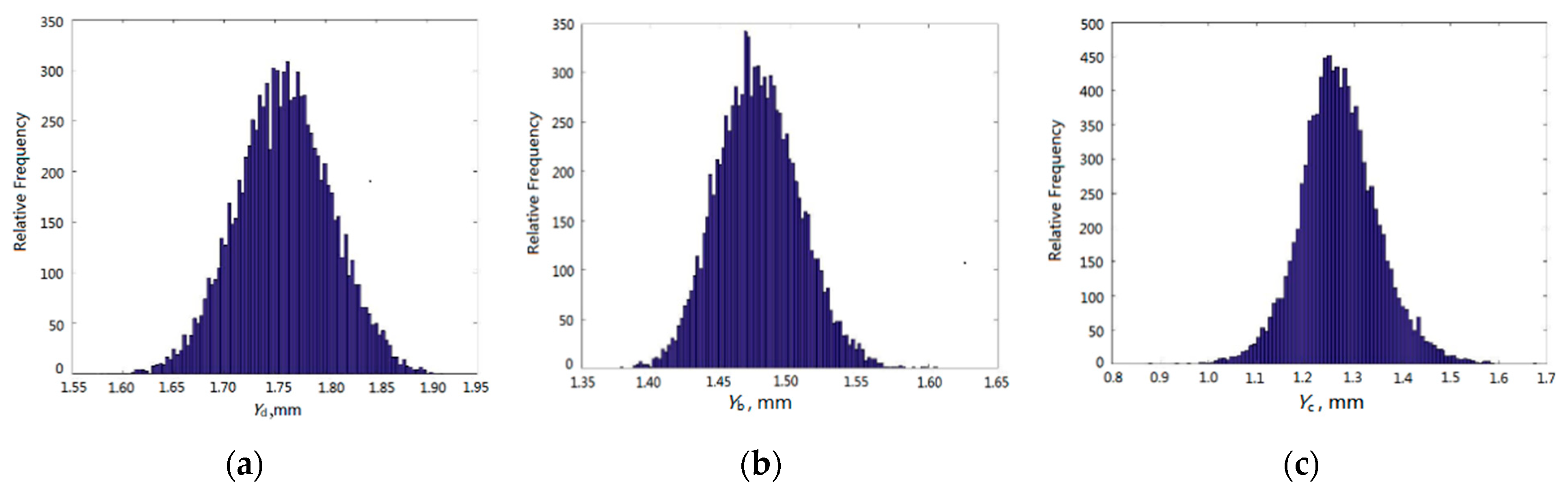
3.3. Creep-Based Reliability Analysis
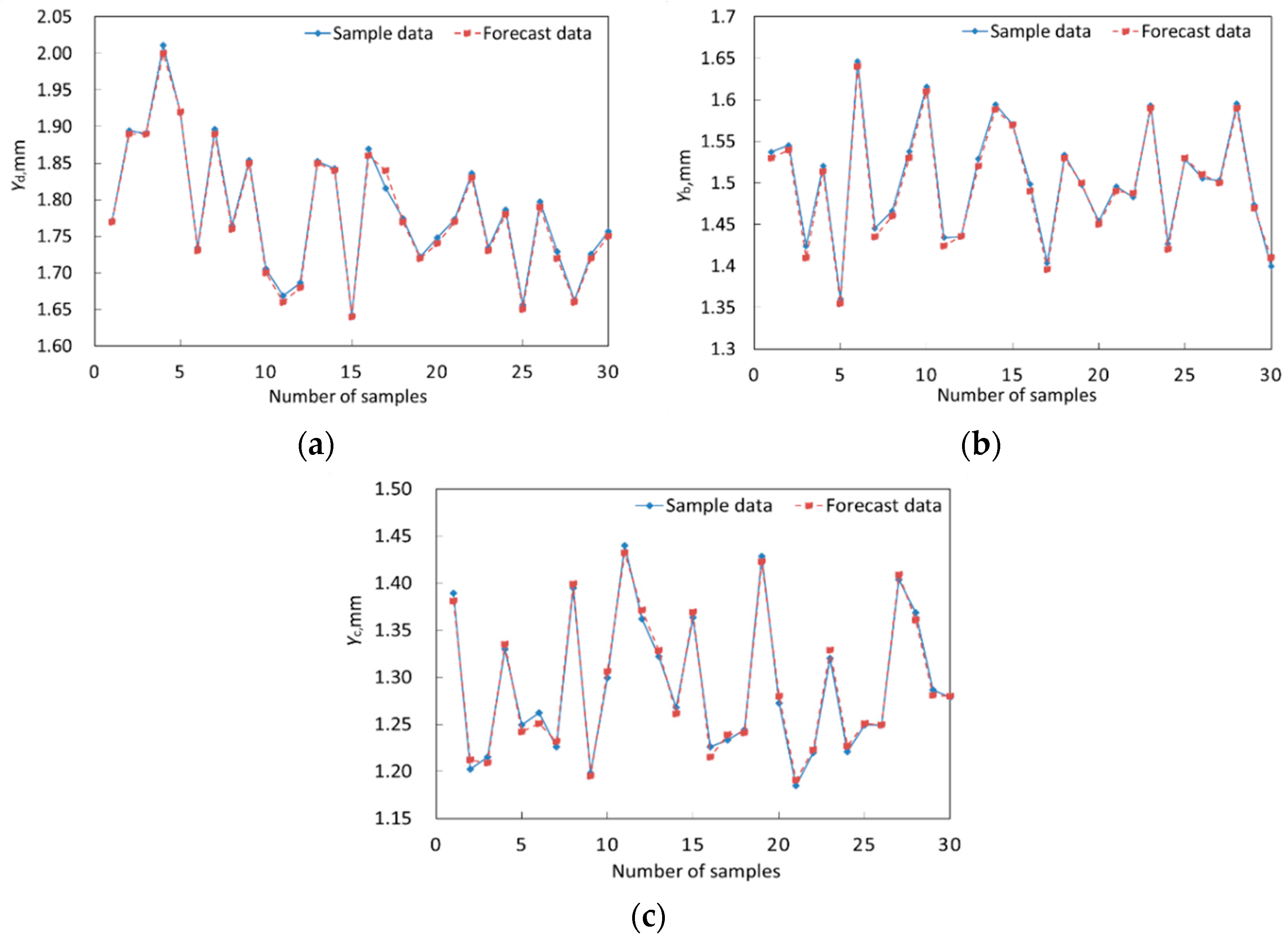
3.4. Validation of Method
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Acronyms
| Acronyms | Explanations |
| BTRRC | Blade-tip radial running clearance |
| MC | Monte Carlo |
| RSM | Response surface method |
| ERSM | Extremum response surface method |
| DC | Distributed collaborative |
| DCRSM | Distributed collaborative response surface method |
| DCERSM | Distributed collaborative extremum response surface method |
| GRNN | Generalized regression neural network |
| GRENN | Generalized regression extremum neural network |
| CGRENN | Collaborative generalized regression extreme neural network |
| DGRENN | Distributed generalized regression extreme neural network |
| DCGRENN | Distributed collaborative generalized regression extreme neural network |
| FE | Finite element |
| LHS | Latin hypercube sampling |
| RMSE | Root-mean-square error |
| SOSD | Single-object single-discipline |
| MOMD | Multi-object multi-discipline |
| RAM | Random access memory |
Nomenclature
| △εcreep | Creep strain |
| ε | Strain |
| t | Time |
| T | Test temperature |
| C1, C2, C3 | Coefficients of material creep |
| exp | Nature exponential function |
| X | Matrix of input samples |
| Q | Number of training samples |
| R | Dimension number of input parameters |
| S | Dimension number of output parameters |
| LW1.1 | Weighted matrix in hide layer |
| Q × R | Dimensions of matrix LW1.1 |
| ||dist|| | Weight (Euclidean distance) function in hide layer |
| △ | Transfer (Gauss) function |
| n1 | Network vector in hide layer |
| a1 | Output of neuro cell in hide layer |
| LW2.1 | Connection threshold value between hide layer and output layer |
| S × Q | Stands for the dimensions of matrix LW2.1 |
| nprod | Weight function of output layer |
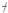 | Purelin transfer function of output layer |
| b | Threshold level vector |
| n2 | Network vector of output layer |
| a2 | Output of neuro cell in output layer |
| y | Output of neuro network |
| aj | Output vectorof Q nerve cells for jth group of input samples |
| The ith element in | |
| E | Mean value of blade-tip clearance |
| D | Variance of blade-tip clearance |
| μY(⋅) | Mean function |
| Disk mean value | |
| Blade mean value | |
| Casing mean value | |
| Disk variance value | |
| Blade variance value | |
| Casing variance value | |
| DY(⋅) | Variance function |
| R | Reliability |
| Φ(⋅) | Accumulative function |
| ω | Rotational speech |
| λ | Heat conductivity coefficient |
| E | Elasticity modulus |
| α | Convective heat transfer coefficient |
| ρ | Material density |
| σ | Smooth factors |
| δ | Allowable value of steady blade-tip clearance |
| γa | Reliability degree computed by MC method |
| γm | Reliability degree calculated by DCRSM or DCGRENN |
| Computing precision | |
| Yi | Output response of ith input sample in time domain [0, T] |
| Yi,max | The maximum of Yi(Xi,t) in time domain |
| i | Number of training samples |
| j | Number of random variables |
| X(pq) | Input sample vector of qth discipline in pth object |
| Y(pq) | Output sample vector of qth discipline in pth object |
| Weight matrix in hidden layer of output layer in the DGRENN model | |
| Weight matrix in output layer of output layer in the DGRENN model | |
| Output vector of output layer in the DGRENN model | |
| X(p) | Input random variables of pth object model |
| Y(q) | Response of pth object |
| Weight matrix in hidden layer of output layer in the DGRENN model | |
| Weight matrix in output layer of output layer in the DGRENN model | |
| Output vector of output layer | |
| Input random variables of the whole coordinative model | |
| Output response of MOMD overall CGRENN model | |
| Weight matrix in hidden layer of output layer | |
| Weight matrix in output layer of output layer | |
| Output vector of output layer in the CGRENN | |
| Radial deformations of turbine disk | |
| Radial deformations of turbine blade | |
| Radial deformations of turbine casings | |
| τ(t) | Deformation of BTRRC |
Appendix A
References
- Lattime, S.B.; Steinetz, B.M. Turbine engine clearance control systems: Current practices and future directions. J. Propuls. Power 2004, 20, 302–311. [Google Scholar] [CrossRef]
- Jia, B.H.; Zhang, X.D. Study on effect of rotor vibration on tip clearance variation and fast active control of tip clearance. Adv. Mater. Res. 2010, 139–141, 2469–2472. [Google Scholar] [CrossRef]
- Pilidis, P.; Maccallum, N.R.L. Models for predicting tip clearance changes in gas turbines. NASA 1983, N83–229258. [Google Scholar]
- Annette, E.N.; Christoph, W.M.; Stehan, S. Modeling and validation of the thermal effects on gas turbine transients. J. Eng. Gas Turbines Power 2005, 127, 564–572. [Google Scholar]
- Fei, C.W.; Bai, G.C. Nonlinear dynamic probabilistic analysis for turbine casing radial deformation based on extremum response surface method-based support vector machine. J. Comput. Nonlinear Dyn. 2013, 8, 041004. [Google Scholar] [CrossRef]
- Song, L.K.; Bai, G.C.; Fei, C.W.; Tang, W.Z. Multi-failure probabilistic design for turbine bladed disks using neural network regression with distributed collaborative strategy. Aerosp. Sci. Technol. 2019, 92, 464–477. [Google Scholar] [CrossRef]
- Fei, C.W.; Lu, C.; Liem, R.P. Decomposed-coordinated surrogate modelling strategy for compound function approximation and a turbine blisk reliability evaluation. Aerosp. Sci. Technol. 2019, 95, 105466. [Google Scholar] [CrossRef]
- Murat, E.K.; Hasan, B.B.; Aledar, B. Probabilistic nonlinear analysis of CFR dams by MCS using response surface method. Appl. Math. Model. 2011, 35, 2752–2770. [Google Scholar]
- Fei, C.W.; Tang, W.Z.; Bai, G.C. Novel method and model for dynamic reliability optimal design of turbine blade deformation. Aerosp. Sci. Technol. 2014, 39, 588–595. [Google Scholar] [CrossRef]
- Puatatsananon, W.; Saouma, V.E. Reliability analysis in fracture mechanics using the first-order reliability method and Monte Carlo simulation. Fatigue Fract. Eng. Mater. Struct. 2010, 29, 959–975. [Google Scholar] [CrossRef]
- Pan, Q.; Dias, D. An efficient reliability method combining adaptive support vector machine and Monte Carlo simulation. Struct. Saf. 2017, 67, 85–95. [Google Scholar] [CrossRef]
- Fei, C.W.; Bai, G.C.; Tian, C. Extremum response surface method for casing radial deformation probabilistic analysis. J. Aerosp. Inf. Syst. 2013, 10, 47–52. [Google Scholar]
- Wei, Z.; Feng, F.; Wei, W. Non-linear partial least squares response surface method for structural reliability analysis. Reliab. Eng. Syst. Saf. 2017, 161, 69–77. [Google Scholar]
- Fei, C.W.; Choy, Y.S.; Hu, D.Y.; Bai, G.C.; Tang, W.Z. Dynamic probabilistic design approach of high-pressure turbine blade-tip radial running clearance. Nonlinear Dyn. 2016, 86, 205–223. [Google Scholar] [CrossRef]
- Song, L.K.; Bai, G.C.; Fei, C.W.; Wen, J. Probabilistic LCF life assessment of turbine discs using DC-based wavelet neural network regression. Int. J. Fatigue 2019, 119, 204–219. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Bai, G.C. Extremum response surface method of reliability analysis on two-link flexible robot manipulator. J. Cent. South Univ. 2012, 19, 101–107. [Google Scholar] [CrossRef]
- Lu, C.; Feng, Y.W.; Liem, R.P.; Fei, C.W. Improved kriging with extremum response surface method for structural dynamic reliability and sensitivity analyses. Aerosp. Sci. Technol. 2018, 76, 164–175. [Google Scholar] [CrossRef]
- Bai, G.C.; Fei, C.W. Distributed collaborative response surface method for mechanical dynamic assembly reliability design. Chin. J. Mech. Eng. 2013, 26, 1160–1168. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Wang, Z.; Fei, C.W.; Yuan, Z.S.; Wei, J.S.; Tang, W.Z. Fuzzy Multi-SVR Learning Model for Reliability-Based Design Optimization of Turbine Blades. Materials 2019, 12, 2341. [Google Scholar] [CrossRef]
- Fei, C.W.; Choy, Y.S.; Hu, D.Y.; Bai, G.C.; Tang, W.Z. Transient probabilistic analysis for turbine blade-tip radial clearance with multiple components and multi-physics fields based on DCERSM. Aerosp. Sci. Technol. 2016, 50, 62–70. [Google Scholar] [CrossRef]
- Nosefilho, K.; Plasencia, L.A.D.; Minussi, C.R. Short-term multinodal load forecasting using a modified general regression neural network. IEEE Trans. Power Deliv. 2011, 26, 2862–2869. [Google Scholar] [CrossRef]
- Adel, M.E.; Salah, G.F. EOS simulation and GRNN modeling of the constant volume depletion behavior of gas condensate reservoirs. Energy Fuels 1998, 12, 353–364. [Google Scholar]
- Zhao, C.; Liu, K.; Li, D.S. Freight volume forecast based on GRNN. J. China Railw. Soc. 2004, 10, 112–113. [Google Scholar]
- Machado, R.N.D.M.; Bezerra, U.H.; Pelaes, E.G.; Oliveira, R.C.L.D.; Tostes, M.E.D.L. Use of wavelet transform and generalized regression neural network (GRNN) to the characterization of short-duration voltage variation in electric power system. IEEE Lat. Am. Trans. 2009, 7, 217–222. [Google Scholar] [CrossRef]
- Li, H.Z.; Guo, S.; Li, C.J.; Sun, J.Q. A hybrid annual power load forecasting model based on generalized regression neural network with fruit fly optimization algorithm. Knowl. Based Syst. 2013, 37, 378–387. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Wei, J.S.; Jing, H.Z.; Fei, C.W.; Tang, W.Z. Reliability-based low fatigue life analysis of turbine blisk with generalized regression extreme neural network method. Materials 2019, 12, 1545. [Google Scholar] [CrossRef]
- Sun, G.; Hoff, S.J.; Zelle, B.C.; Smith, M.A. Development and comparison of backpropagation and generalized regression neural network models to predict diurnal and seasonal gas and PM 10 concentrations and emissions from swine buildings. Trans. Asabe 2008, 51, 685–694. [Google Scholar] [CrossRef]
- Ibanez, A.R.; Srinivasan, V.S.; Saxena, A. Creep deformation and rupture behaviour of directionally solidified GTD 111 superalloy. Fatigue Fract. Eng. Mater. Struct. 2010, 29, 1010–1020. [Google Scholar] [CrossRef]
- Zeng, S.Q.; Zhang, Z.J. The Forced Creep Analysis of Nonmetallic Material. Appl. Mech. Mater. 2012, 1841–1885, 692–695. [Google Scholar] [CrossRef]
- Liu, Y.; Ning, Y.; Nan, Y. Characterization of hot deformation behavior and processing map of FGH4096-GH4133B dual alloys. J. Alloy. Compd. 2015, 633, 505–515. [Google Scholar] [CrossRef]
- Jeon, J.; Panagiotelis, A.; Petropoulos, F. Probabilistic forecast reconciliation with applications to wind power and electric load. Eur. J. Oper. Res. 2019, 279, 364–379. [Google Scholar] [CrossRef]
- Shu, M.A.; Wang, K.M.; Hui, M.; Shuai, Z. Research on turbine blade vibration characteristic under steady state temperature field. J. Shenyang Aerosp. Univ. 2011, 28, 18–21. [Google Scholar]
- Manduhu, M.; Jones, M.W. A work efficient parallel Algorithm for exact Euclidean distance transform. IEEE Trans. Image Process. 2019, 28, 5322–5335. [Google Scholar] [CrossRef] [PubMed]
- Song, L.K.; Bai, G.C.; Fei, C.W. Dynamic surrogate modeling approach for probabilistic creep-fatigue life evaluation of turbine disks. Aerosp. Sci. Technol. 2019, 95, 105439. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Yuan, Z.S.; Wang, Z.; Fei, C.W.; Lu, C. Probabilistic fatigue/creep optimization of turbine bladed disk with fuzzy multi-extremum response surface method. Materials 2019, 12, 3367. [Google Scholar] [CrossRef]


| Coefficient | C1 | C2 | C3 |
|---|---|---|---|
| Creep value | 8.892 × 10−13 | 7.436 | 1.267 |
| Disk | Blade | Casing | ||||||
|---|---|---|---|---|---|---|---|---|
| Random Variable | Mean μ | Standard Deviation | Random Variable | Mean μ | Standard Deviation | Random Variable | Mean μ | Standard Deviation |
| Ta1, K | 813 | 24.39 | Tb1, K | 1303 | 39.09 | Ti, K | 1323 | 39.69 |
| Ta2, K | 483 | 14.49 | Tb2, K | 1253 | 37.59 | To, K | 593 | 17.79 |
| Ta3, K | 473 | 14.19 | Tb3, K | 1093 | 32.79 | αc1, W·m−2·K−1 | 6000 | 180.00 |
| Tb1, K | 518 | 15.54 | Tb4, K | 813 | 24.39 | αc2, W·m−2·K−1 | 5400 | 162.00 |
| Tb2, K | 593 | 17.79 | αb1, W·m−2·K−1 | 11,756 | 352.68 | αc3, W·m−2·K−1 | 4800 | 144.00 |
| αd1, W·m−2·K−1 | 1527 | 45.81 | αb2, W·m−2·K−1 | 8253 | 247.59 | αc4, W·m−2·K−1 | 4200 | 126.00 |
| αd2, W·m−2·K−1 | 1082 | 32.46 | αd3, W·m−2·K−1 | 6547 | 196.41 | αo, W·m−2·K−1 | 2600 | 78.00 |
| αd3, W·m−2·K−1 | 864 | 25.92 | αd4, W·m−2·K−1 | 3130 | 93.90 | ρ, kg·m−3 | 8210 | 246.3 |
| ρ, kg·m−3 | 8210 | 246.3 | ρ, kg·m−3 | 8210 | 246.3 | E, MPa | 163,000 | 4890 |
| E, MPa | 163,000 | 4890 | E, MPa | 163,000 | 4890 | λ, W·m−1·C−1 | 23.7 | 0.711 |
| λ, W·m−1·C−1 | 23.7 | 0.711 | λ, W·m−1·C−1 | 23.7 | 0.711 | |||
| ω, rad·s−1 | 1168 | 35.04 | ω, rad·s−1 | 1168 | 35.04 | |||
| Object | Number of Test Samples | RMSE, ×10−4 |
|---|---|---|
| Disk | 30 | 6.32 |
| Blade | 30 | 3.61 |
| Casing | 30 | 4.73 |
| Distribution Feature | Yd | Yb | Yc |
|---|---|---|---|
| Mean, ×10−3 m | 1.7591 | 1.4774 | 1.2701 |
| Stand deviation, ×10−5 m | 4.6693 | 2.9457 | 8.0059 |
| Distribution | Normal | Normal | Normal |
| Method | Number of Simulations | ||||
|---|---|---|---|---|---|
| 102 | 103 | 104 | 105 | 106 | |
| MC method | 10080 s | 111600 s | 1330560 s | — | — |
| DCRSM | 1.185 s | 1.264 s | 4.071 s | 16.74 s | 141.34 s |
| DCGRENN | 1.176 s | 1.186 s | 1.201 s | 1.451 s | 2.449 s |
| Number of Simulations | Reliability Degree | Improved | ||||
|---|---|---|---|---|---|---|
| MC Method | DCRSM | DCGRENN | DCRSM | DCGRENN | Precision, % | |
| 102 | 0.99 | 0.97 | 0.99 | 97.822 | 99.839 | 2.017 |
| 103 | 0.992 | 0.978 | 0.994 | 98.628 | 99.758 | 1.130 |
| 104 | 0.9916 | 0.9787 | 0.9909 | 98.699 | 99.929 | 1.230 |
| 105 | — | 0.9793 | 0.9898 | 98.759 | 99.818 | 1.059 |
| 106 | — | 0.9779 | 0.9932 | 98.618 | 99.839 | 1.221 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.-Y.; Wei, J.-S.; Wang, Z.; Yuan, Z.-S.; Fei, C.-W.; Lu, C. Creep-Based Reliability Evaluation of Turbine Blade-Tip Clearance with Novel Neural Network Regression. Materials 2019, 12, 3552. https://doi.org/10.3390/ma12213552
Zhang C-Y, Wei J-S, Wang Z, Yuan Z-S, Fei C-W, Lu C. Creep-Based Reliability Evaluation of Turbine Blade-Tip Clearance with Novel Neural Network Regression. Materials. 2019; 12(21):3552. https://doi.org/10.3390/ma12213552
Chicago/Turabian StyleZhang, Chun-Yi, Jing-Shan Wei, Ze Wang, Zhe-Shan Yuan, Cheng-Wei Fei, and Cheng Lu. 2019. "Creep-Based Reliability Evaluation of Turbine Blade-Tip Clearance with Novel Neural Network Regression" Materials 12, no. 21: 3552. https://doi.org/10.3390/ma12213552
APA StyleZhang, C.-Y., Wei, J.-S., Wang, Z., Yuan, Z.-S., Fei, C.-W., & Lu, C. (2019). Creep-Based Reliability Evaluation of Turbine Blade-Tip Clearance with Novel Neural Network Regression. Materials, 12(21), 3552. https://doi.org/10.3390/ma12213552






