Investigations of the Hydrogen Bonds and Vibrational Spectra of Clathrate Ice XVI
Abstract
1. Introduction
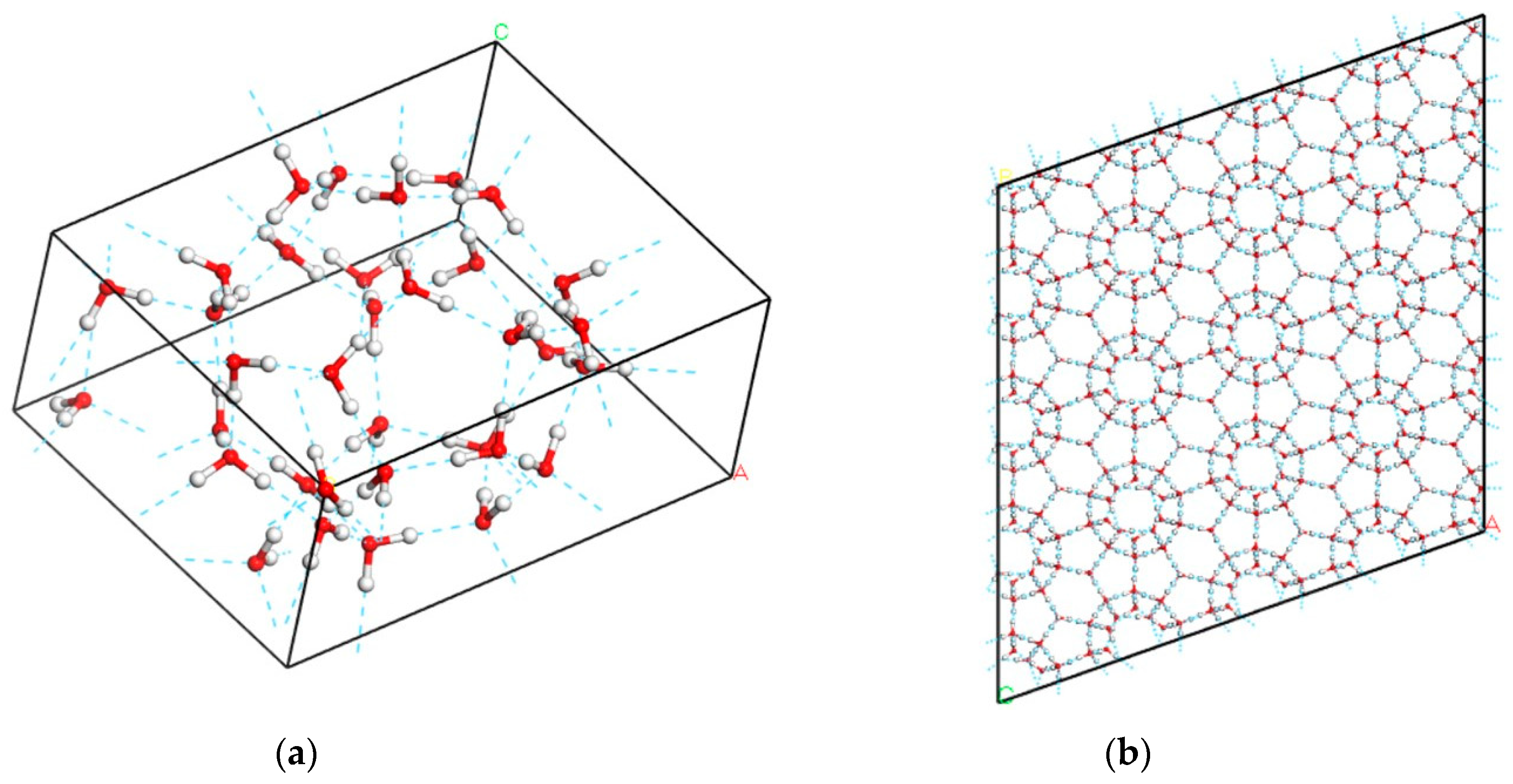
2. Computational Methodology
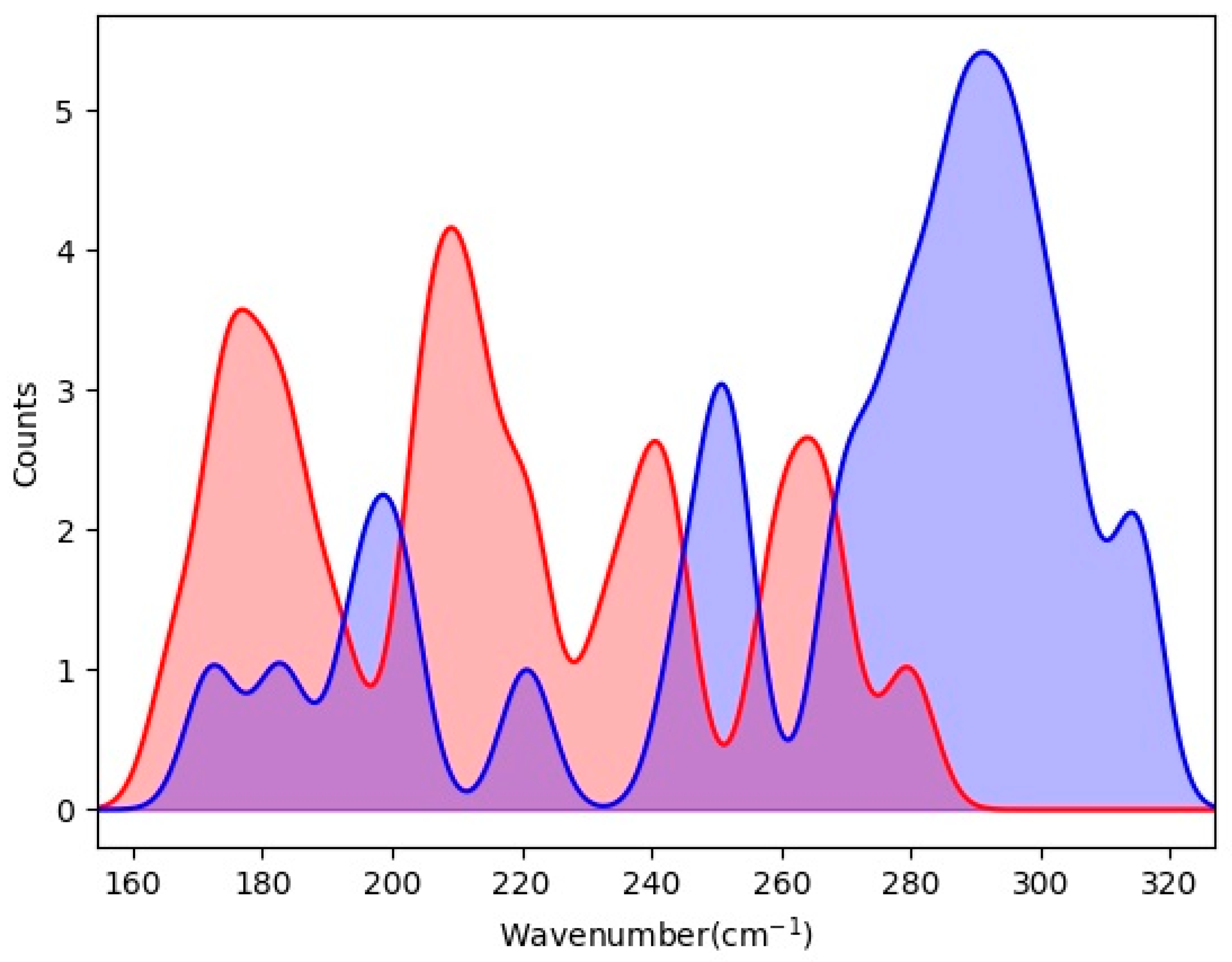
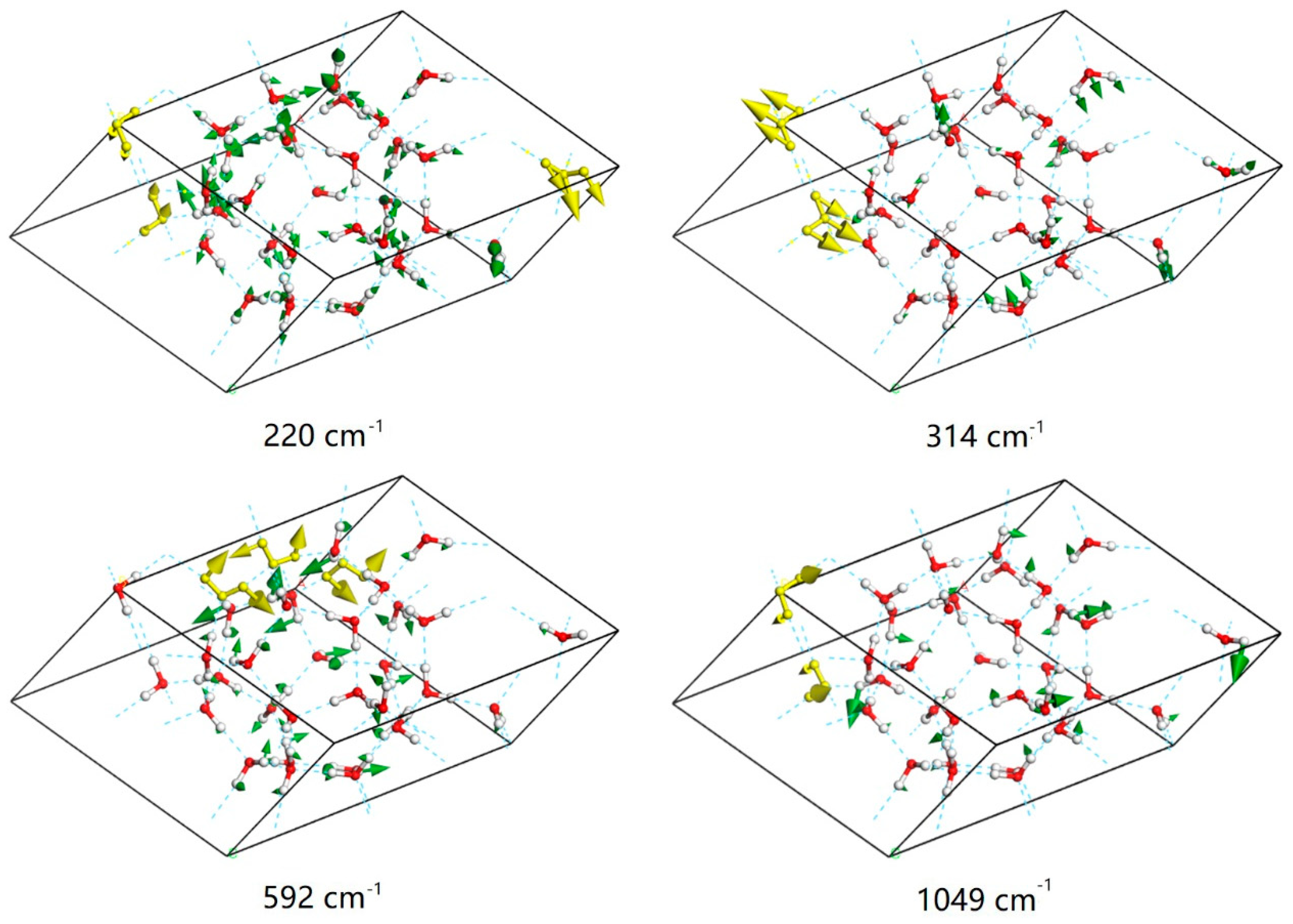
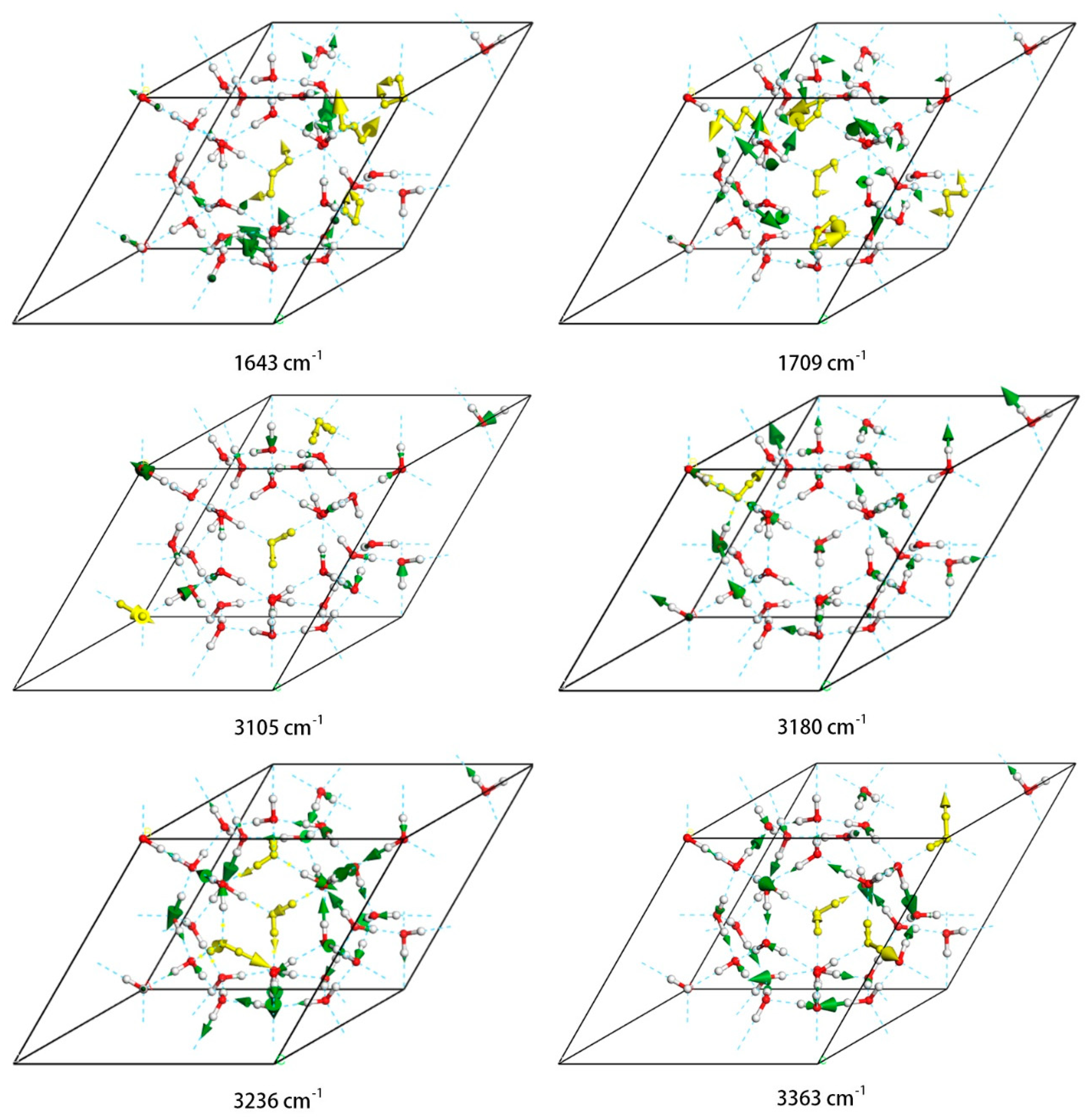
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bertie, J.E.; Calvert, L.D.; Whalley, E. Transformations of ice II, ice III, and ice V at atmospheric pressure. J. Chem. Phys. 1963, 38, 840. [Google Scholar] [CrossRef]
- Bertie, J.E.; Whalley, E. Optical spectra of orientationally disordered crystals. 2. Infrared spectrum of ice Ih and ice Ic from 360 to 50 cm−1. J. Chem. Phys. 1967, 46, 1271. [Google Scholar] [CrossRef]
- Whalley, E.; Heath, J.B.R.; Davidson, D.W. Ice 9—An antiferroelectric phase related to ice 3. J. Chem. Phys. 1968, 48, 2362. [Google Scholar] [CrossRef]
- Tajima, Y.; Matsuo, T.; Suga, H. Phase-transition in KOH-doped hexagonal ice. Nature 1982, 299, 810–812. [Google Scholar] [CrossRef]
- Kuhs, W.F.; Finney, J.L.; Vettier, C.; Bliss, D.V. Structure and hydrogen ordering in ices VI, VII, and VIII by neutron powder diffraction. J. Chem. Phys. 1984, 81, 3612–3623. [Google Scholar] [CrossRef]
- Hirsch, K.R.; Holzapfel, W.B. Effect of high-pressure on the Raman-spectra of ice-VIII and evidence for ice-X. J. Chem. Phys. 1986, 84, 2771–2775. [Google Scholar] [CrossRef]
- Lobban, C.; Finney, J.L.; Kuhs, W.F. The structure of a new phase of ice. Nature 1998, 391, 268–270. [Google Scholar] [CrossRef]
- Salzmann, C.G.; Radaelli, P.G.; Hallbrucker, A.; Mayer, E.; Finney, J.L. The preparation and structures of hydrogen ordered phases of ice. Science 2006, 311, 1758–1761. [Google Scholar] [CrossRef]
- Salzmann, C.G.; Radaelli, P.G.; Mayer, E.; Finney, J.L. Ice XV: A new thermodynamically stable phase of ice. Phys. Rev. Lett. 2009, 103, 105701. [Google Scholar] [CrossRef]
- Falenty, A.; Hansen, T.C.; Kuhs, W.F. Formation and properties of ice XVI obtained by emptying a type sII clathrate hydrate. Nature 2014, 516, 213–233. [Google Scholar] [CrossRef]
- Del Rosso, L.; Celli, M.; Ulivi, L. New porous water ice metastable at atmospheric pressure obtained by emptying a hydrogen-filled ice. Nat. Commun. 2016, 7, 13394. [Google Scholar] [CrossRef]
- Sloan, E.D. Fundamental principles and applications of natural gas hydrates. Nature 2003, 426, 353–359. [Google Scholar] [CrossRef] [PubMed]
- Yin, Z.Y.; Chong, Z.R.; Tan, H.K.; Linga, P. Review of gas hydrate dissociation kinetic models for energy recovery. J. Nat. Gas Sci. Eng. 2016, 35, 1362–1387. [Google Scholar] [CrossRef]
- Chong, Z.R.; Yang, S.H.B.; Babu, P.; Linga, P.; Li, X.S. Review of natural gas hydrates as an energy resource: Prospects and challenges. Appl. Energy 2016, 162, 1633–1652. [Google Scholar] [CrossRef]
- Koh, C.A. Towards a fundamental understanding of natural gas hydrates. Chem. Soc. Rev. 2002, 31, 157–167. [Google Scholar] [CrossRef] [PubMed]
- Davidson, D.W.; Handa, Y.P.; Ratcliffe, C.I.; Tse, J.S.; Powell, B.M. The ability of small molecules to form clathrate hydrates of structure-II. Nature 1984, 311, 142–143. [Google Scholar] [CrossRef]
- VanderWaals, J.H.; Platteeuw, J.C. Clathrate solutions. Adv. Chem. Phys. 1959, 2, 1–57. [Google Scholar]
- Belosludov, V.R.; Inerbaev, T.M.; Subbotin, O.S.; Belosludov, R.V.; Kudoh, J.; Kawazoe, Y. Thermal expansion and lattice distortion of clathrate hydrates of cubic structures I and II. J. Supramol. Chem. 2002, 2, 453–458. [Google Scholar] [CrossRef]
- Matsumoto, M.; Tanaka, H. On the structure selectivity of clathrate hydrates. J. Phys. Chem. B 2011, 115, 8257–8265. [Google Scholar] [CrossRef]
- Jacobson, L.C.; Hujo, W.; Molinero, V. Thermodynamic stability and growth of guest-free clathrate hydrates: A low-density crystal phase of water. J. Phys. Chem. B 2009, 113, 10298–10307. [Google Scholar] [CrossRef]
- Wooldridge, P.J.; Richardson, H.H.; Devlin, J.P. Mobile Bjerrum defects—A criterion for ice-like crystal-growth. J. Chem. Phys. 1987, 87, 4126–4131. [Google Scholar] [CrossRef]
- Yagasaki, T.; Matsumoto, M.; Tanaka, H. Anomalous thermodynamic properties of ice XVI and metastable hydrates. Phys. Rev. B 2016, 93, 054118. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Kristallogr. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Hammer, B.; Hansen, L.B.; Norskov, J.K. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. B 1999, 59, 7413–7421. [Google Scholar] [CrossRef]
- Zhang, P.; Tian, L.; Zhang, Z.P.; Shao, G.; Li, J.C. Investigation of the hydrogen bonding in ice Ih by first-principles density function methods. J. Chem. Phys. 2012, 137, 044504. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Han, S.H.; Yu, H.; Liu, Y. A calculating proof on hydrogen bonding in ordinary ice by the first-principles density functional theory. RSC Adv. 2013, 3, 6646–6649. [Google Scholar] [CrossRef]
- Yuan, Y.Z.; Zhang, P.; Yao, S.K.; Lu, Y.B.; Yang, H.Z.; Lou, H.W.; Zhao, Z.J. Computational assignments of lattice vibrations of ice Ic. RSC Adv. 2017, 7, 36801–36806. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, P.; Wang, Z.R.; Zhu, X.L.; Lu, Y.B.; Guan, C.B.; Li, Y.H. DFT simulations of the vibrational spectrum and hydrogen bonds of ice XI. Molecules 2018, 23, 1781. [Google Scholar] [CrossRef]
- Jiang, L.; Yao, S.K.; Zhang, K.; Wang, Z.R.; Luo, H.W.; Zhu, X.L.; Gu, Y.; Zhang, P. Exotic spectra and lattice vibrations of ice X using the DFT method. Molecules 2018, 23, 2780. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.-R.; Zhu, X.-L.; Jiang, L.; Zhang, K.; Luo, H.-W.; Gu, Y.; Zhang, P. Investigations of the Hydrogen Bonds and Vibrational Spectra of Clathrate Ice XVI. Materials 2019, 12, 246. https://doi.org/10.3390/ma12020246
Wang Z-R, Zhu X-L, Jiang L, Zhang K, Luo H-W, Gu Y, Zhang P. Investigations of the Hydrogen Bonds and Vibrational Spectra of Clathrate Ice XVI. Materials. 2019; 12(2):246. https://doi.org/10.3390/ma12020246
Chicago/Turabian StyleWang, Ze-Ren, Xu-Liang Zhu, Lu Jiang, Kai Zhang, Hui-Wen Luo, Yue Gu, and Peng Zhang. 2019. "Investigations of the Hydrogen Bonds and Vibrational Spectra of Clathrate Ice XVI" Materials 12, no. 2: 246. https://doi.org/10.3390/ma12020246
APA StyleWang, Z.-R., Zhu, X.-L., Jiang, L., Zhang, K., Luo, H.-W., Gu, Y., & Zhang, P. (2019). Investigations of the Hydrogen Bonds and Vibrational Spectra of Clathrate Ice XVI. Materials, 12(2), 246. https://doi.org/10.3390/ma12020246






