Axial Impact Load of a Concrete-Filled Steel Tubular Member with Axial Compression Considering the Creep Effect
Abstract
:1. Introduction
2. Basic Parameters and the Numerical Model
2.1. Geometric Model and Impact Parameters
2.2. Material Properties
2.3. Finite Element Model
3. Results and Discussion
3.1. Impact Speed Effect on Impact Load
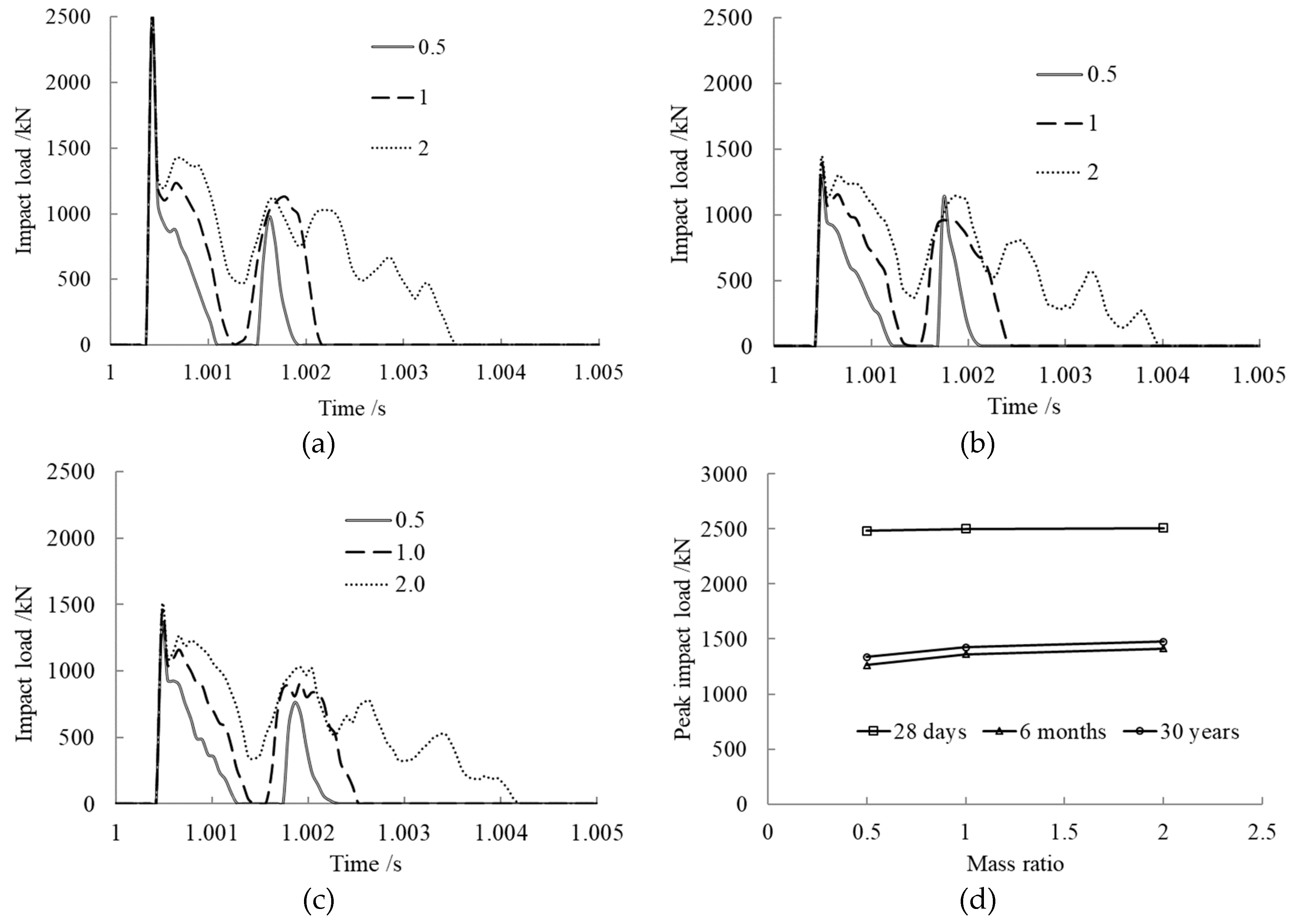
3.2. Mass Ratio Effect on Impact Load
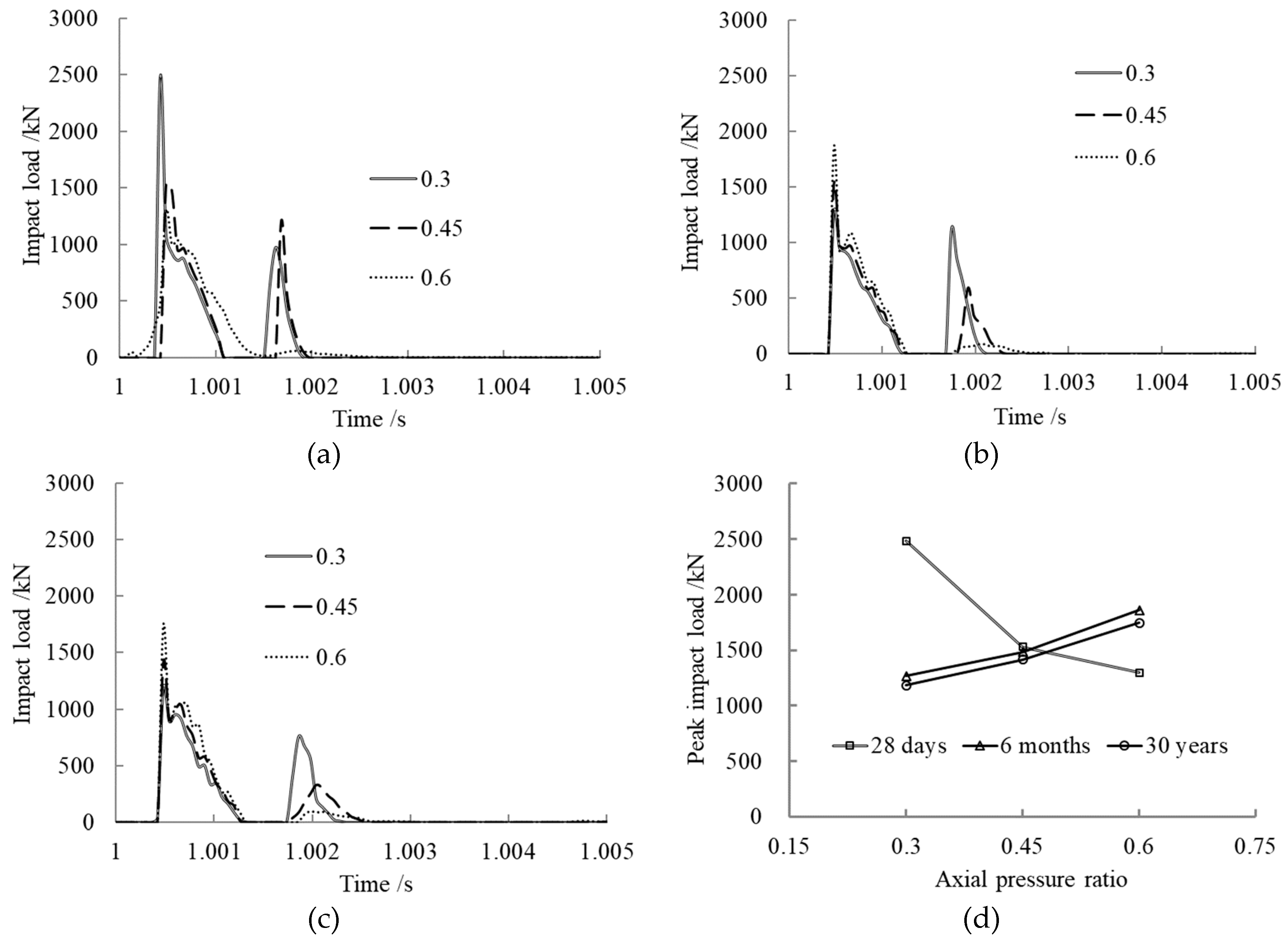
3.3. Axial Pressure Ratio Effect on Impact Load
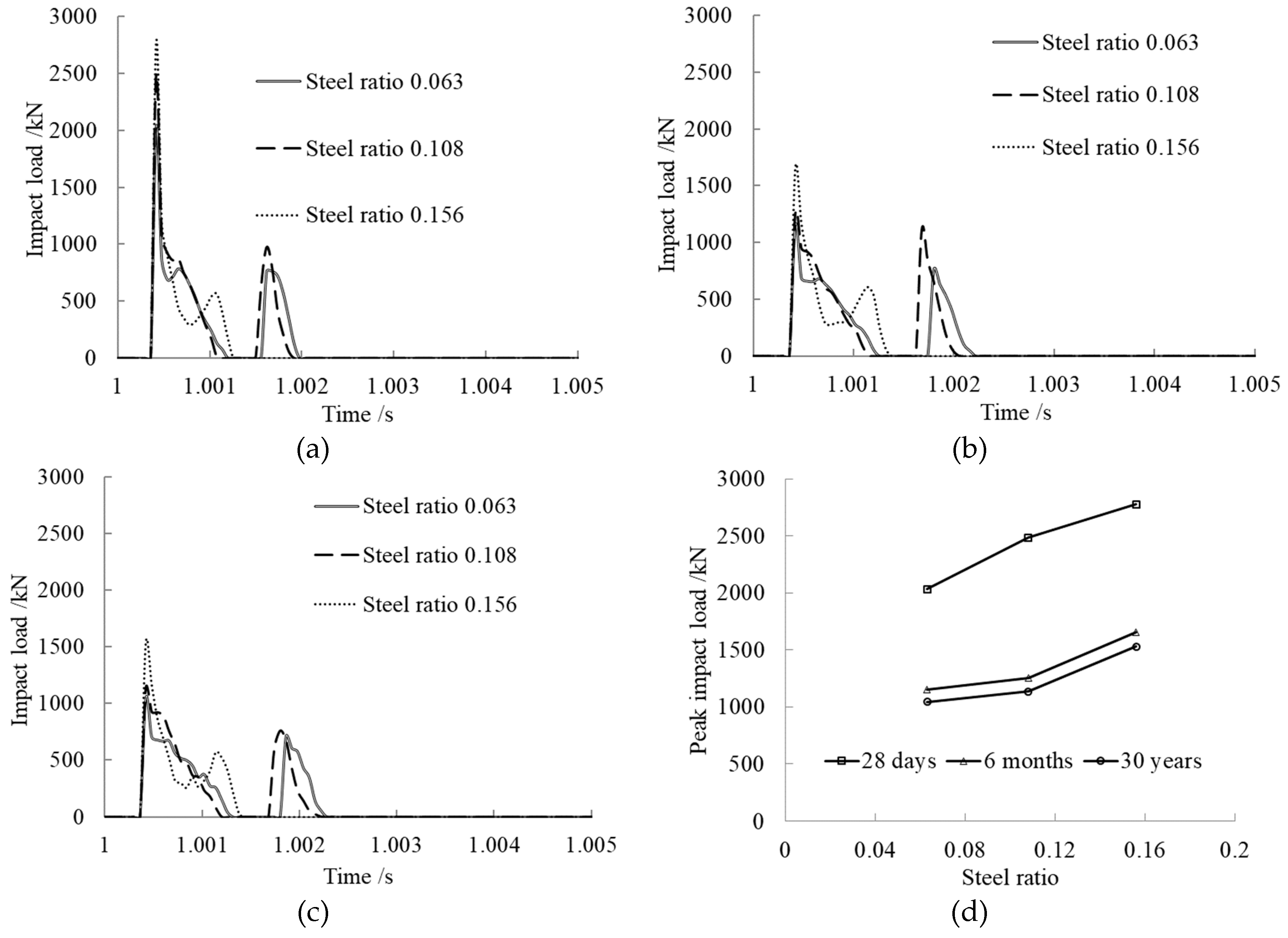
3.4. Steel Ratio Effect on Impact Load
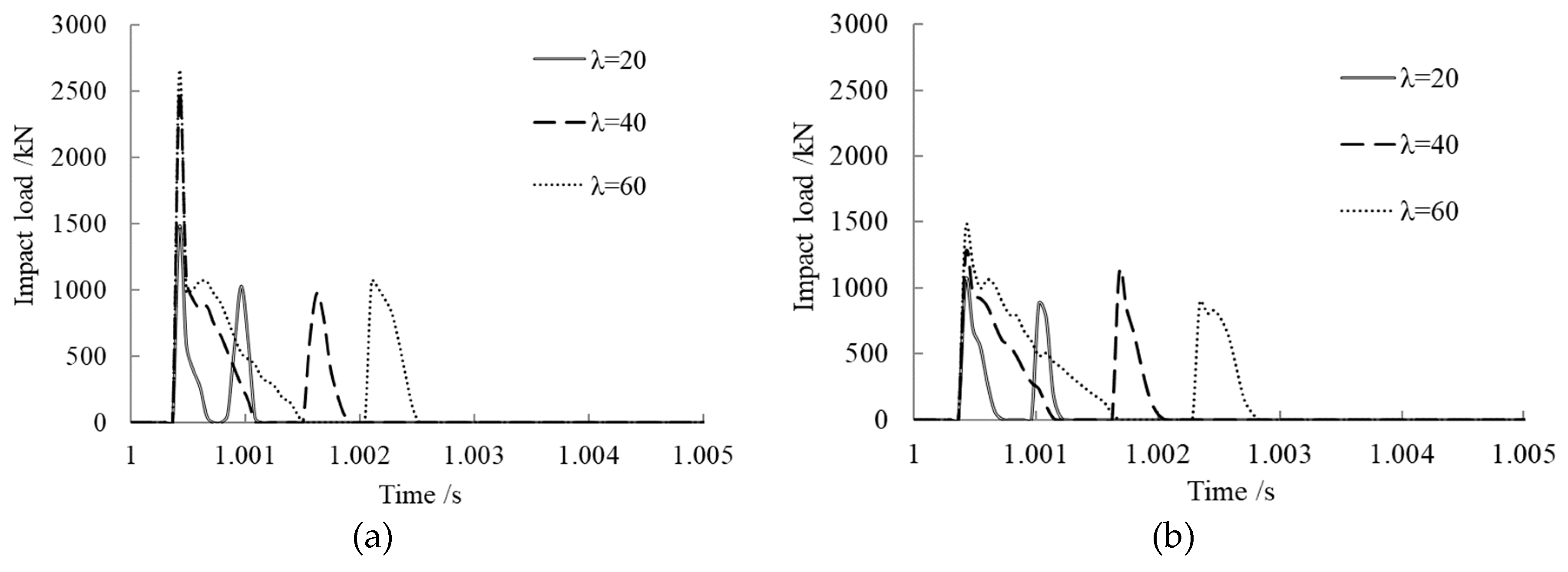
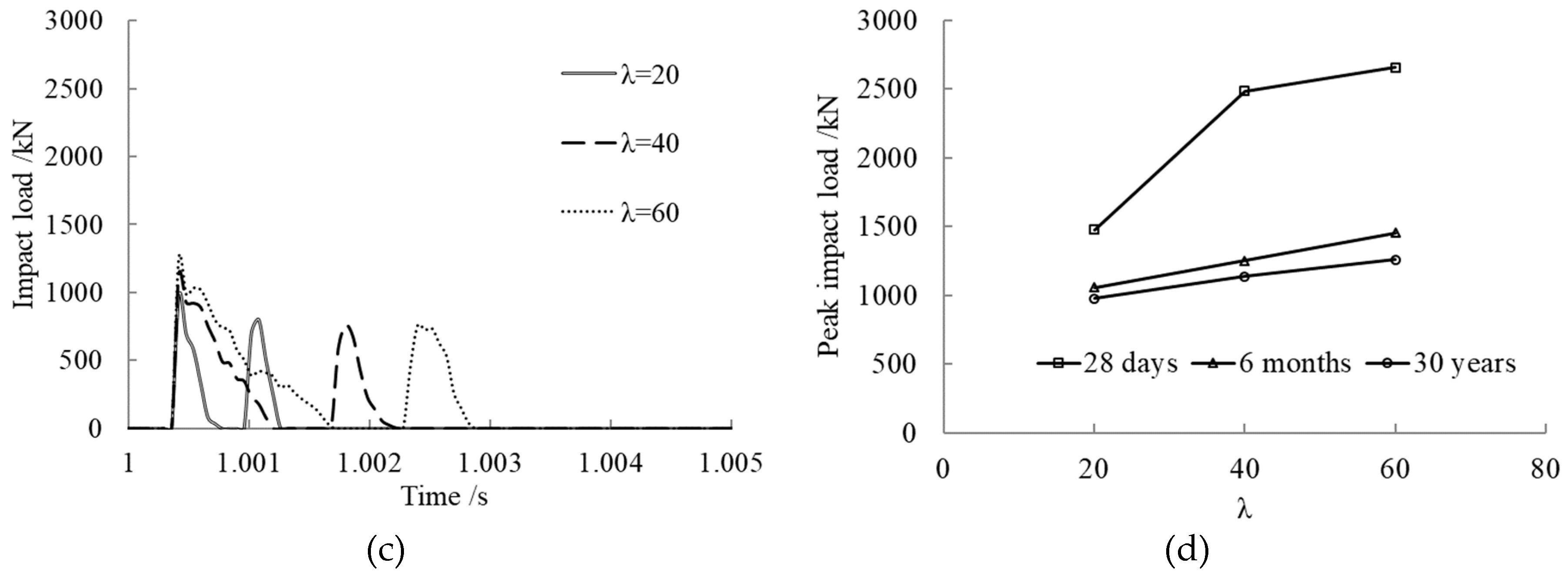
3.5. Slenderness Ratio Effect on Impact Load
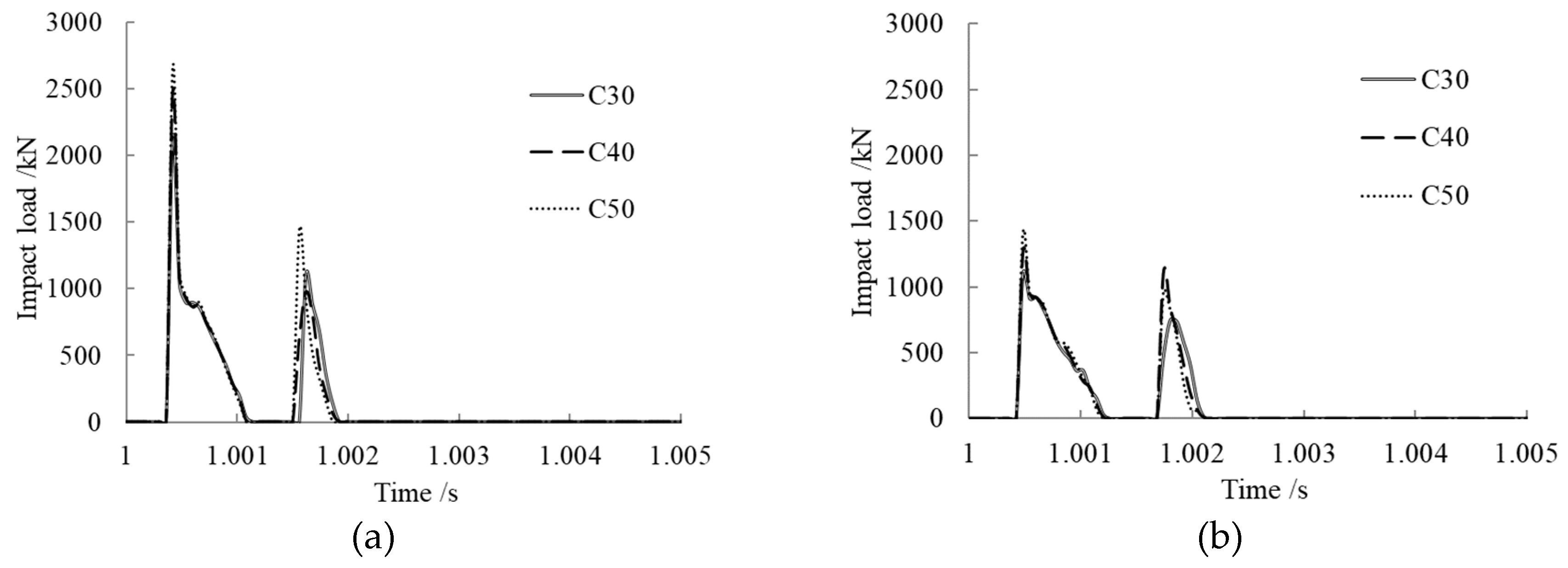
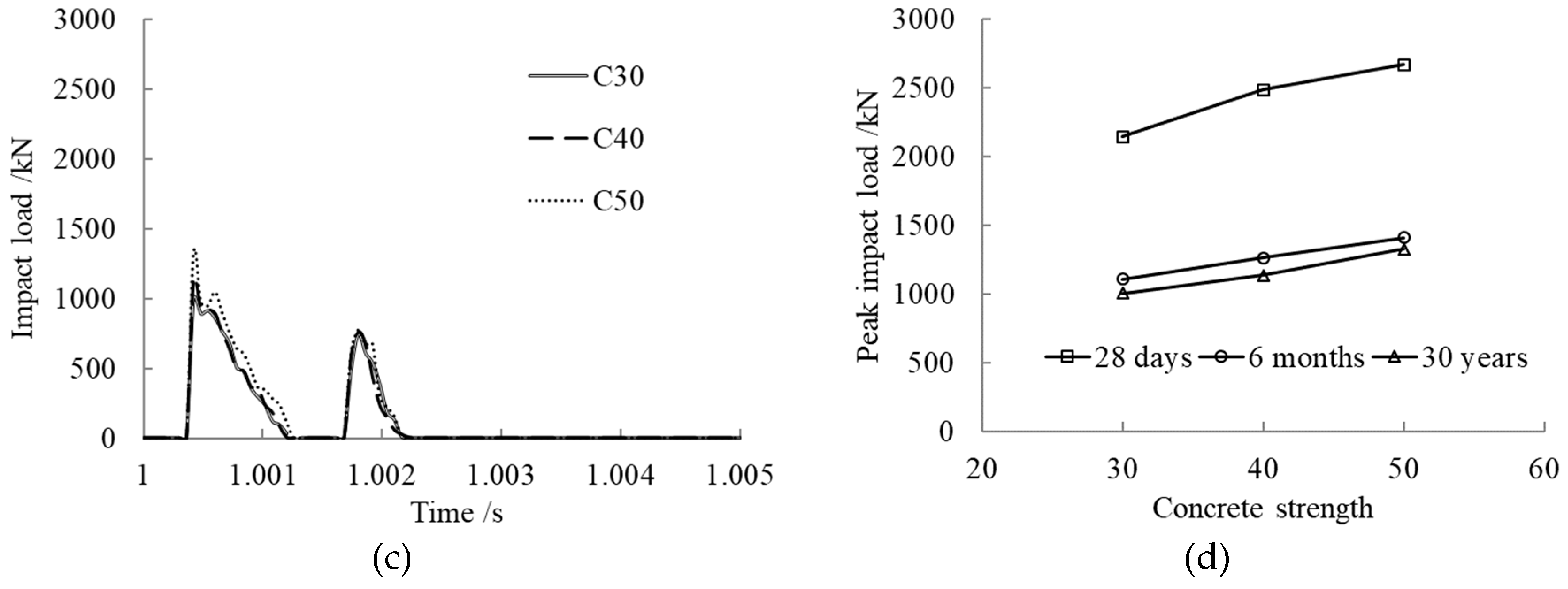
3.6. Concrete Strength Effect on Impact Load
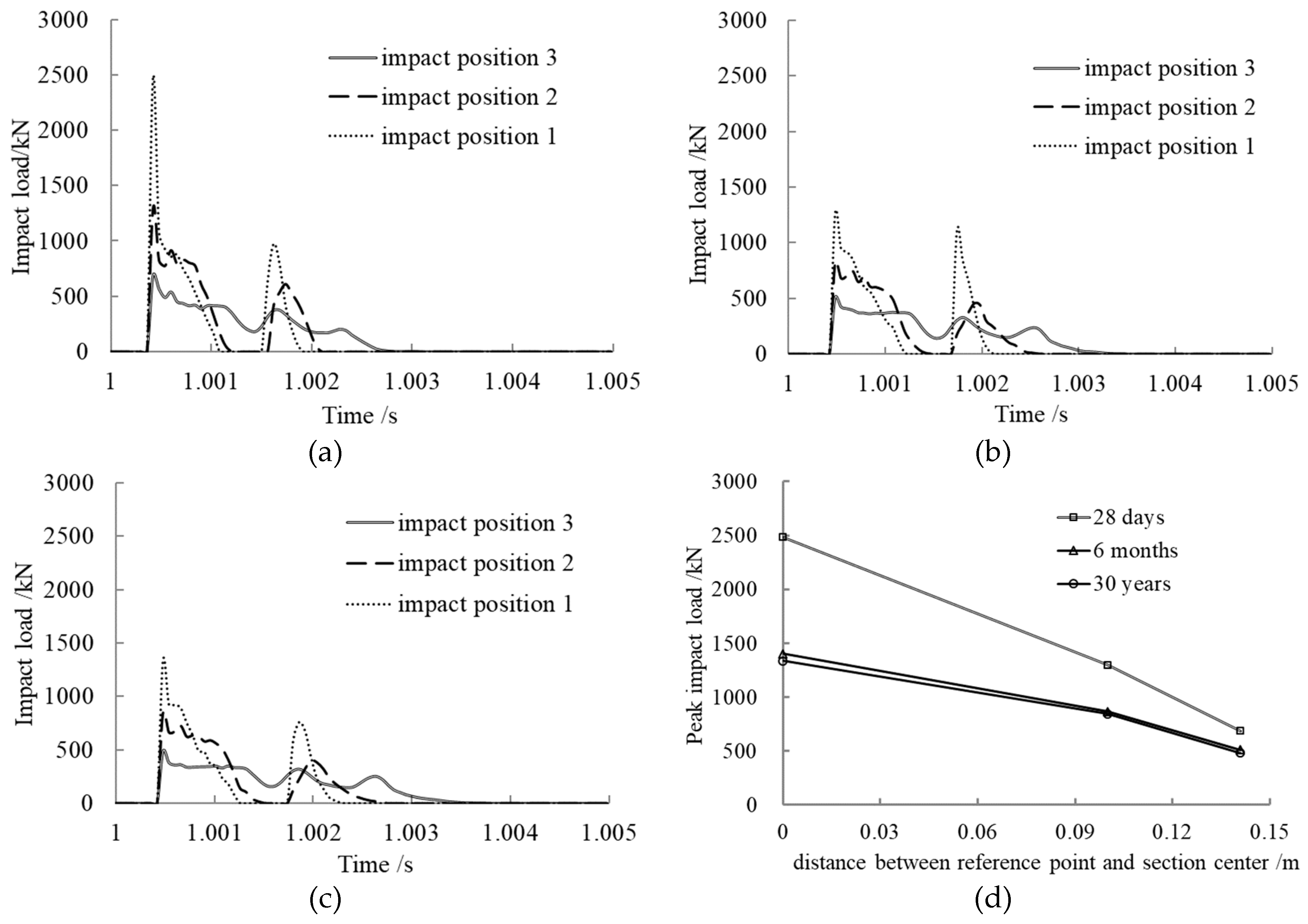
3.7. Eccentricity of Axial Impact Effect on Impact Load
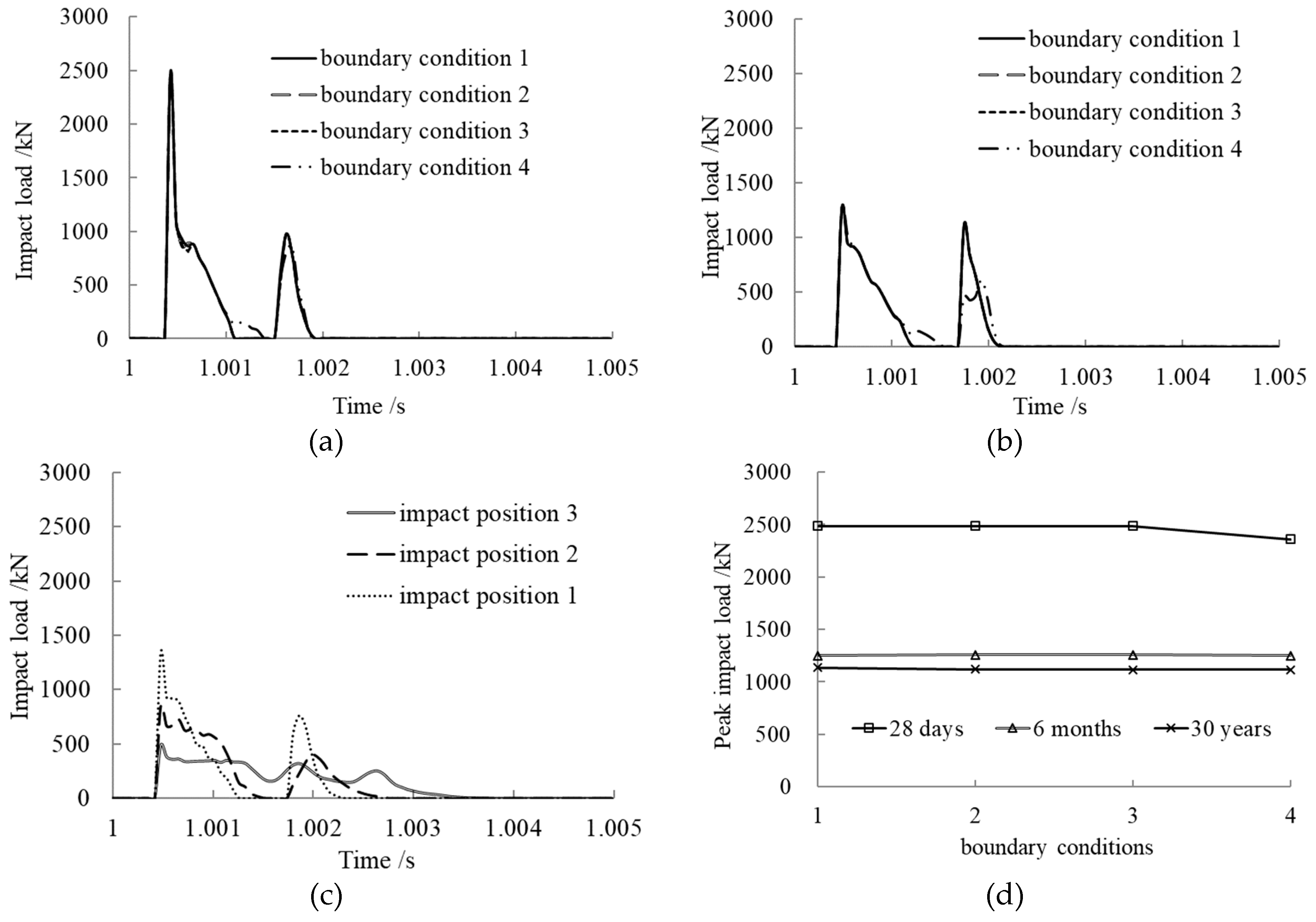
3.8. Boundary Condition Effect on Impact Load
4. Suggestions
4.1. Creep Reduction Coefficient on Peak Impact Load
4.2. Peak Impact Load Calculation Formula Considering Creep
5. Conclusions
- (1)
- The equivalent elasticity modulus was introduced to simulate the dynamic responses of a concrete-filled steel tubular member under the combined action of axial compression, creep, and axial impact. The calculation results show that the finite element model established in this paper is reasonable, accurate, and suitable for the simulation.
- (2)
- The peak impact load and contact time increased with increasing impact speed; when the impact speed was higher, the effect of concrete creep on the impact load was weakened.
- (3)
- The impact load did not change much with increasing mass ratio, while contact time increased with increasing mass ratio. For the same mass ratio, the peak impact load after core concrete creep occurring was far less than that without creep.
- (4)
- After concrete creep occurring, the peak impact load rose with the axial pressure ratio, steel ratio, slenderness ratio, and concrete strength. The axial pressure ratio, within certain limits, had a potentiation effect on the impact resistance of the member.
- (5)
- With increasing eccentricity of the axial impact, the peak impact load decreased linearly. Enhancement of the constraints at the two ends is conducive to improving the impact resistance of the member.
- (6)
- The calculation formula constructed in this paper for the peak impact load of a concrete-filled steel tubular member under axial compression considering creep is easy to use and can help in the impact resistance design of concrete-filled steel tubular members.
Author Contributions
Funding
Conflicts of Interest
References
- Furlong, R.W. Strength of Steel-Encased Concrete Beam Columns. J. Struct. Div. ASCE 1967, 93, 113–124. [Google Scholar]
- Koh, C.G.; Ang, K.K.; Zhang, L. Effects of repeated loading on creep deflection of reinforced concrete beams. Eng. Struct. 1997, 19, 2–18. [Google Scholar] [CrossRef]
- Sapountzakis, E.J.; Katsikadelis, J.T. Elastic deformation of ribbed plates under static, transverse and inplane loading. Comput. Struct. 2000, 74, 571–581. [Google Scholar] [CrossRef]
- Sapountzakis, E.J.; Katsikadelis, J.T. Creep and shrinkage effect on the dynamic analysis of reinforced concrete slab-and-beam structures. J. Sound Vib. 2003, 260, 403–416. [Google Scholar] [CrossRef]
- Sapountzakis, E.J. Dynamic analysis of composite steel–concrete structures with deformable connection. Comput. Struct. 2004, 82, 717–729. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, Y.F. Creep effect on dynamic analysis of concrete-filled steel tubular arch bridge. J. Dalian Univ. Technol. 2006, 46, 82–87. [Google Scholar] [CrossRef]
- Ma, Y.S.; Wang, Y.F. Creep influence on structural dynamic reliability. Eng. Struct. 2015, 99, 1–8. [Google Scholar] [CrossRef]
- Ren, G.; Zhu, L.I. Impact Force Response of Short Concrete Filled Steel Tubular Columns under Axial Load. Int. J. Mod. Phys. B 2008, 22, 0804678. [Google Scholar] [CrossRef]
- Yousuf, M.; Uy, B.; Tao, Z.; Remennikov, A.; Liew, J.R. Transverse impact resistance of hollow and concrete filled stainless steel columns. J. Constr. Steel Res. 2013, 82, 177–189. [Google Scholar] [CrossRef]
- San, J. Experiment Research and Finite Element Analysis on Concrete Filled Steel Tube under Impact; Hunan University: Changsha, China, 2007. [Google Scholar] [CrossRef]
- Han, L.H.; Li, W.; Bjorhovde, R. Developments and advanced applications of concrete-filled steel tubular (CFST) structures: Members. J. Constr. Steel Res. 2014, 100, 211–228. [Google Scholar] [CrossRef]
- Hao, Y.C.; Rui, W. Finite Element Analysis of Concrete Filled Double-Skin (CHS Inner and CHS Outer) Steel Tubes under Lateral Impact. Appl. Mech. Mater. 2014, 501–504, 704–709. [Google Scholar] [CrossRef]
- Tian, Z.; Wu, P.A.; Jia, J. Dynamic Response of RPC-Filled Steel Tubular Columns with High Load Carrying Capacity under Axial Impact Loading. Trans. Tianjin Univ. 2008, 14, 441–449. [Google Scholar] [CrossRef]
- Xue, J.; Liu, Y. Study on the dynamic response of concrete filled steel tubular short columns under axial impact load. In Proceedings of the 2011 International Conference on Electric Technology and Civil Engineering (ICETCE), Lushan, China, 22–24 April 2011. [Google Scholar] [CrossRef]
- Ding, M.; Wang, Y.D.; Dai, C.H.; Ju, J.S.; Jiang, X.G. Creep Calculation and Behavior Analysis of Concrete-Filled Steel Tubular Member under Axial Compression. Eng. Mech. 2017. [Google Scholar] [CrossRef]
- Dai, C. Dynamic Responses Study of Concrete-Filled Steel Tubular Member under Axial Compression and Lateral Impact Considering Creep. Master’s Thesis, China Agricultural University, Beijing, China, 2015. [Google Scholar]

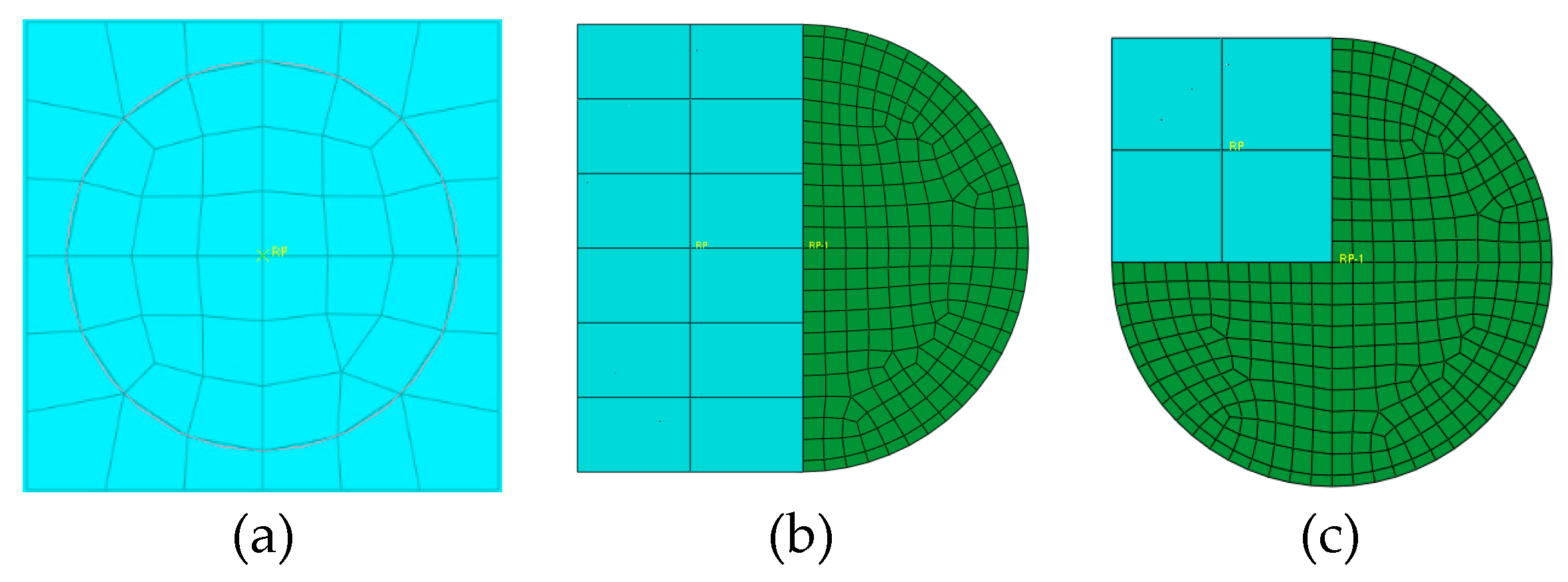


| D/mm | t/mm | L/mm | αs | λ | N/kN | n | x | m/kg | v/(m/s) |
|---|---|---|---|---|---|---|---|---|---|
| 200 | 5 | 2000 | 0.108 | 40 | 423 | 0.3 | 0.5 | 90 | 5 |
| Age | 28 Days | 6 Months | 30 Years |
|---|---|---|---|
| Equivalent elasticity modulus/MPa | 32,500.00 | 20,420.17 | 17,403.85 |
| Compressive Strength/MPa | Inelastic Strain (Compressive) | Tensile Strength/MPa | Inelastic Strain (Tensile) | ||
|---|---|---|---|---|---|
| 10.72 | 0.000000 | 0.000 | 2.39 | 0.00000000 | 0.000 |
| 13.93 | 2.70 × 10−5 | 0.015 | 2.32 | 2.47 × 10−5 | 0.199 |
| 17.42 | 8.10 × 10−5 | 0.035 | 2.03 | 5.65 × 10−5 | 0.393 |
| 20.34 | 1.56 × 10−4 | 0.056 | 1.63 | 1.03 × 10−4 | 0.596 |
| 22.70 | 2.54 × 10−4 | 0.080 | 1.34 | 1.46 × 10−4 | 0.716 |
| 24.53 | 3.72 × 10−4 | 0.105 | 1.08 | 1.97 × 10−4 | 0.809 |
| 26.85 | 8.48 × 10−4 | 0.196 | 0.88 | 2.57 × 10−4 | 0.872 |
| 25.85 | 1.26 × 10−3 | 0.275 | 0.68 | 3.48 × 10−4 | 0.922 |
| 22.49 | 1.96 × 10−3 | 0.403 | 0.58 | 4.25 × 10−4 | 0.945 |
| 20.11 | 2.43 × 10−3 | 0.483 | 0.45 | 5.76 × 10−4 | 0.968 |
| 18.99 | 2.66 × 10−3 | 0.520 | 0.38 | 7.14 × 10−4 | 0.978 |
| 15.24 | 3.56 × 10−3 | 0.644 | 0.28 | 1.03 × 10−3 | 0.988 |
| 13.77 | 3.99 × 10−3 | 0.692 | - | - | - |
| 10.12 | 5.45 × 10−3 | 0.807 | - | - | - |
| 6.82 | 7.83 × 10−3 | 0.899 | - | - | - |
| 2.61 | 1.86 × 10−2 | 0.982 | - | - | - |
| Parameters | 28 Days | 6 Months | 30 Years | ||
|---|---|---|---|---|---|
| Loading Ratio | Loading Ratio | Average Value | Loading Ratio | Average Value | |
| Reference set | 1.00 | 0.50 | 0.60 | 0.46 | 0.55 |
| Impact speed v = 10m/s | 0.56 | 0.41 | |||
| Impact speed v = 15m/s | 0.99 1 | 0.96 1 | |||
| Mass ratio x = 1 | 0.57 | 0.53 | |||
| Mass ratio x = 2 | 0.59 | 0.56 | |||
| Axial pressure ratio n = 0.2 | 0.68 | 0.65 | |||
| Axial pressure ratio n = 0.6 | 0.86 | 0.78 | |||
| Steel ratio αs = 0.063 | 0.57 | 0.51 | |||
| Steel ratio αs = 0.156 | 0.60 | 0.55 | |||
| Slenderness ratio λ = 20 | 0.72 | 0.66 | |||
| Slenderness ratio λ = 60 | 0.55 | 0.47 | |||
| Concrete strength C30 | 0.52 | 0.47 | |||
| Concrete strength C50 | 0.53 | 0.50 | |||
| Impact position 2 | 0.74 | 0.70 | |||
| Impact position 3 | 0.66 | 0.65 | |||
| Boundary condition 2 | 0.51 | 0.45 | |||
| Boundary condition 3 | 0.51 | 0.45 | |||
| Boundary condition 4 | 0.53 | 0.47 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lan, T.; Qin, G.; Zhuang, J.; Wang, Y.; Zheng, Q.; Ding, M. Axial Impact Load of a Concrete-Filled Steel Tubular Member with Axial Compression Considering the Creep Effect. Materials 2019, 12, 3134. https://doi.org/10.3390/ma12193134
Lan T, Qin G, Zhuang J, Wang Y, Zheng Q, Ding M. Axial Impact Load of a Concrete-Filled Steel Tubular Member with Axial Compression Considering the Creep Effect. Materials. 2019; 12(19):3134. https://doi.org/10.3390/ma12193134
Chicago/Turabian StyleLan, Tao, Guangchong Qin, Jinzhao Zhuang, Youdi Wang, Qian Zheng, and Min Ding. 2019. "Axial Impact Load of a Concrete-Filled Steel Tubular Member with Axial Compression Considering the Creep Effect" Materials 12, no. 19: 3134. https://doi.org/10.3390/ma12193134
APA StyleLan, T., Qin, G., Zhuang, J., Wang, Y., Zheng, Q., & Ding, M. (2019). Axial Impact Load of a Concrete-Filled Steel Tubular Member with Axial Compression Considering the Creep Effect. Materials, 12(19), 3134. https://doi.org/10.3390/ma12193134





