Melting Flow in Wire Coating of a Third Grade Fluid over a Die Using Reynolds’ and Vogel’s Models with Non-Linear Thermal Radiation and Joule Heating
Abstract
:1. Introduction
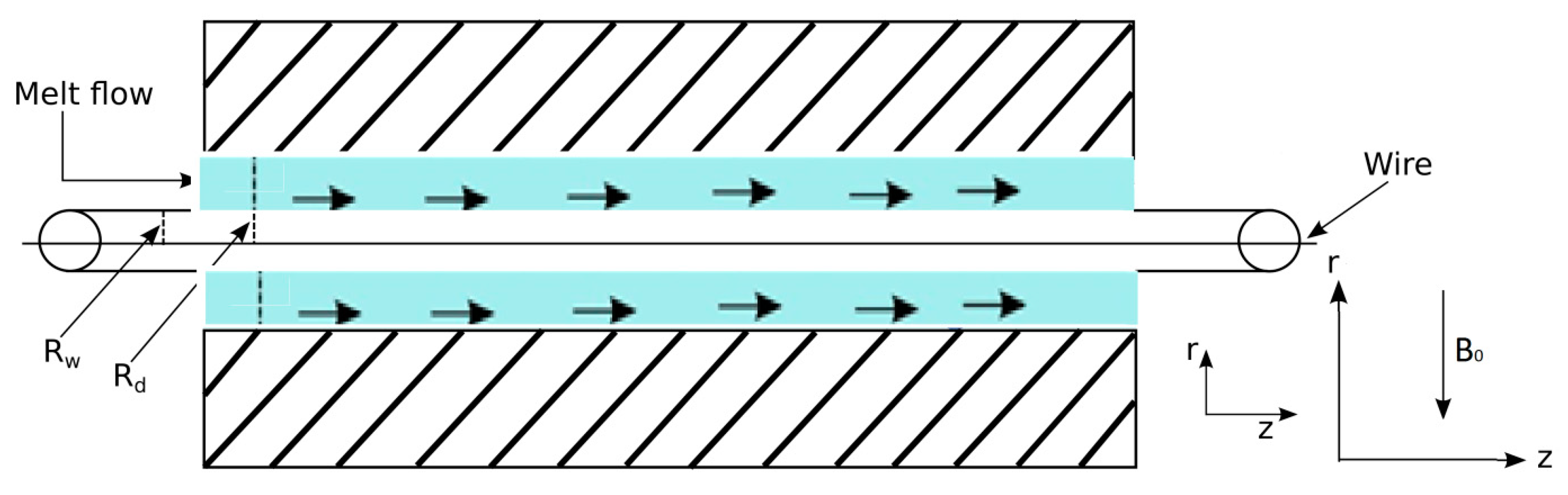
2. Formulation of the Problem
3. Temperature-Dependent Viscosity
3.1. Reynolds’ Model
3.2. Vogel’s Model
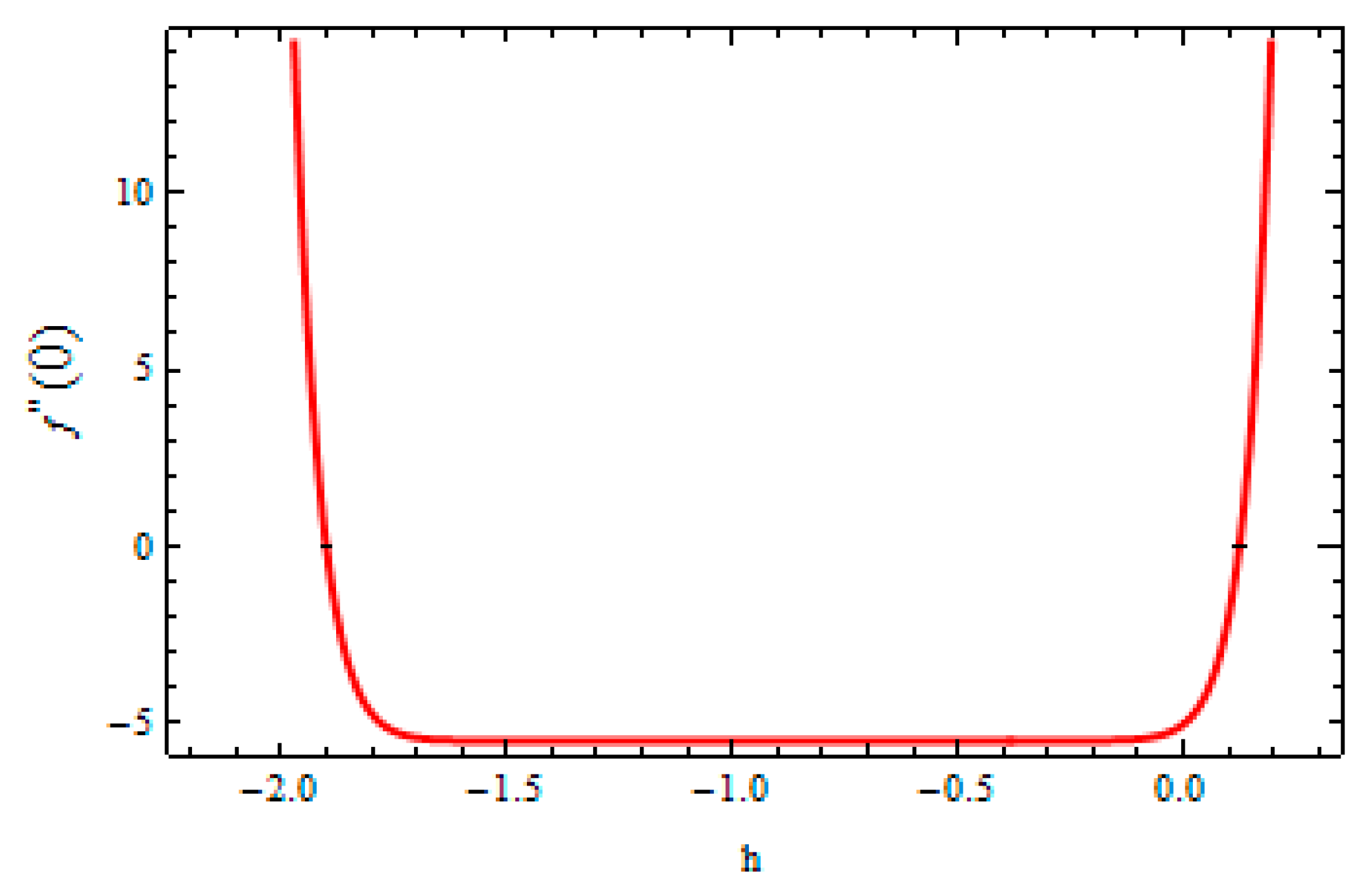
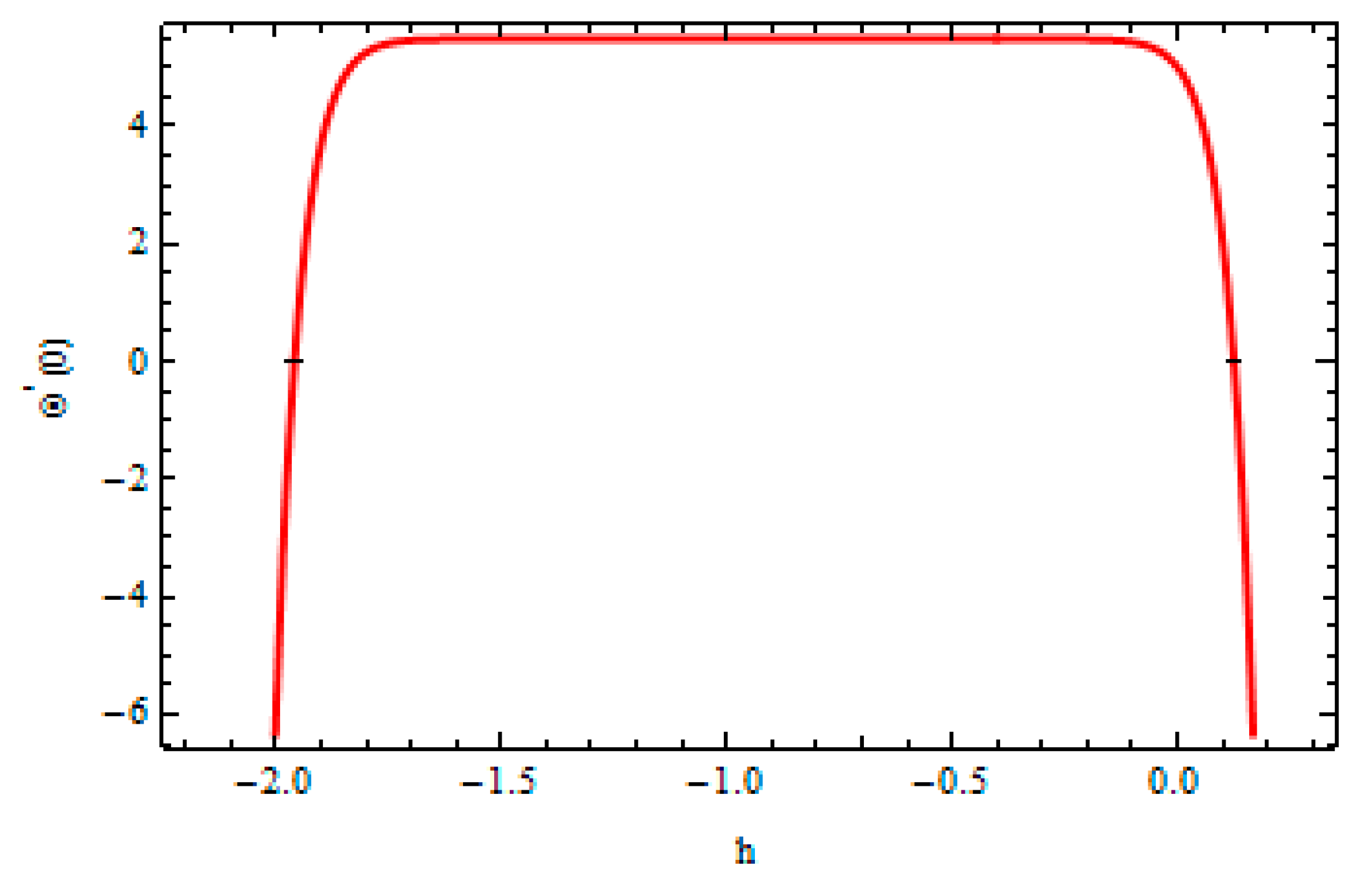
4. Convergence of the Method
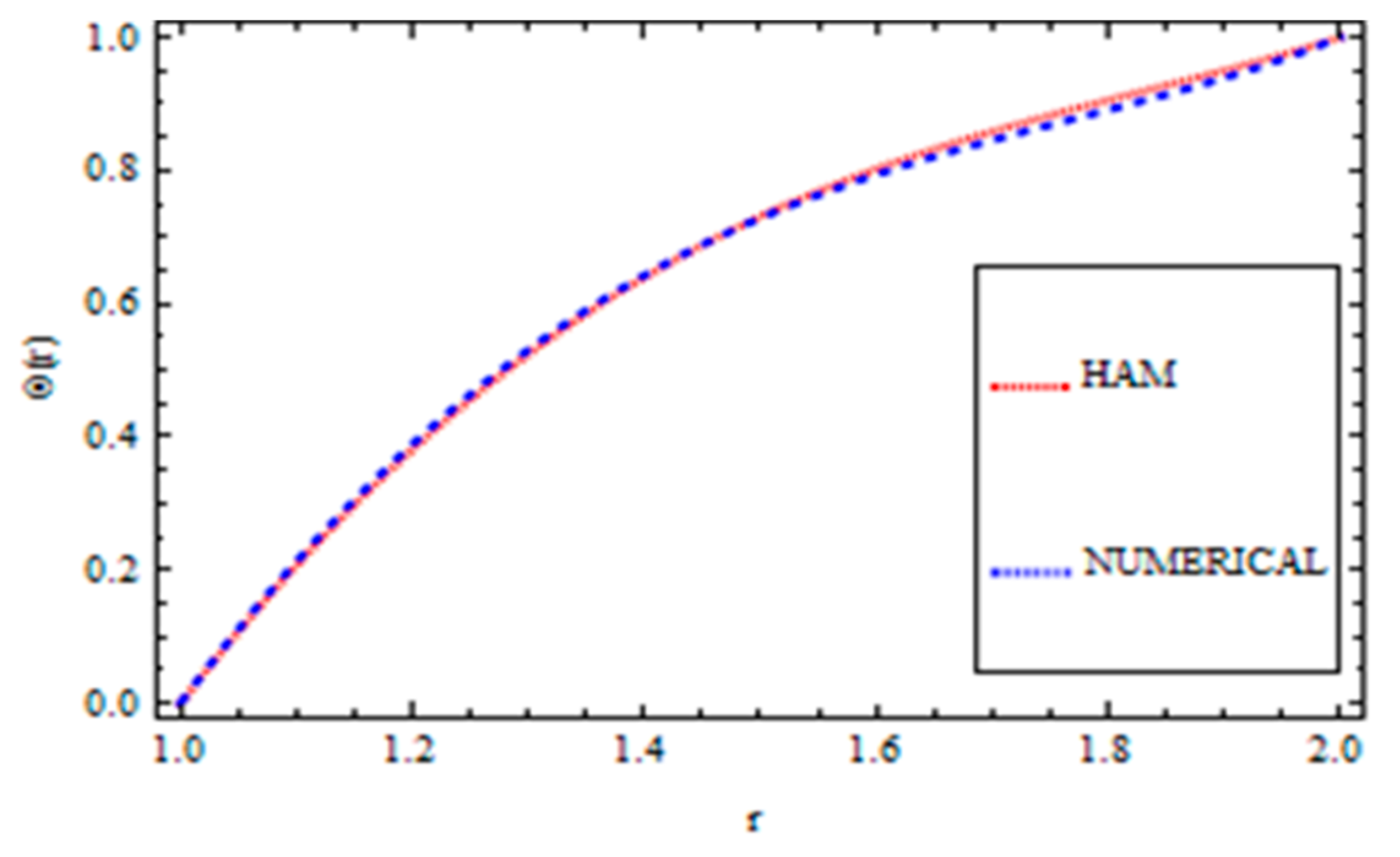
Validation of the Method
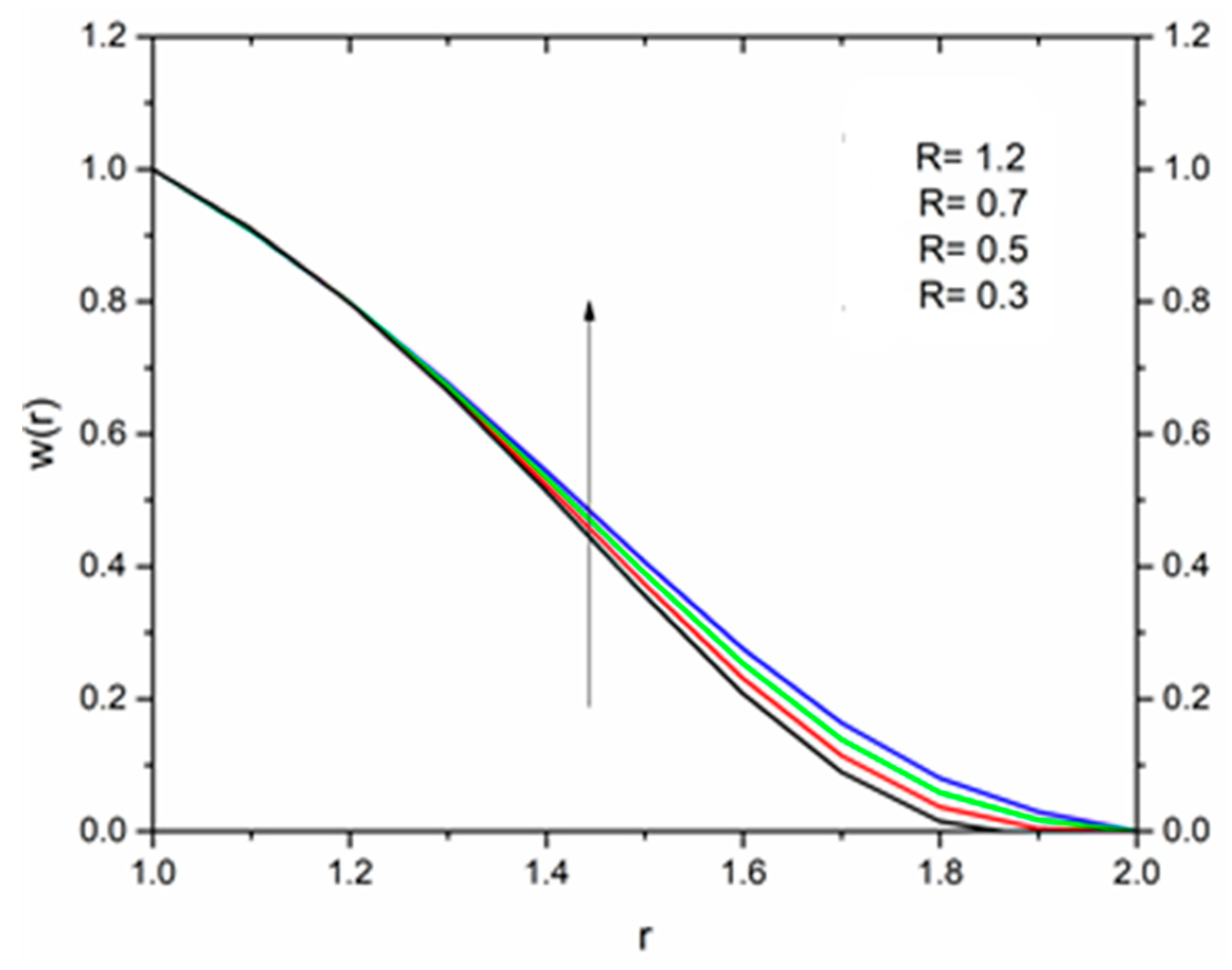
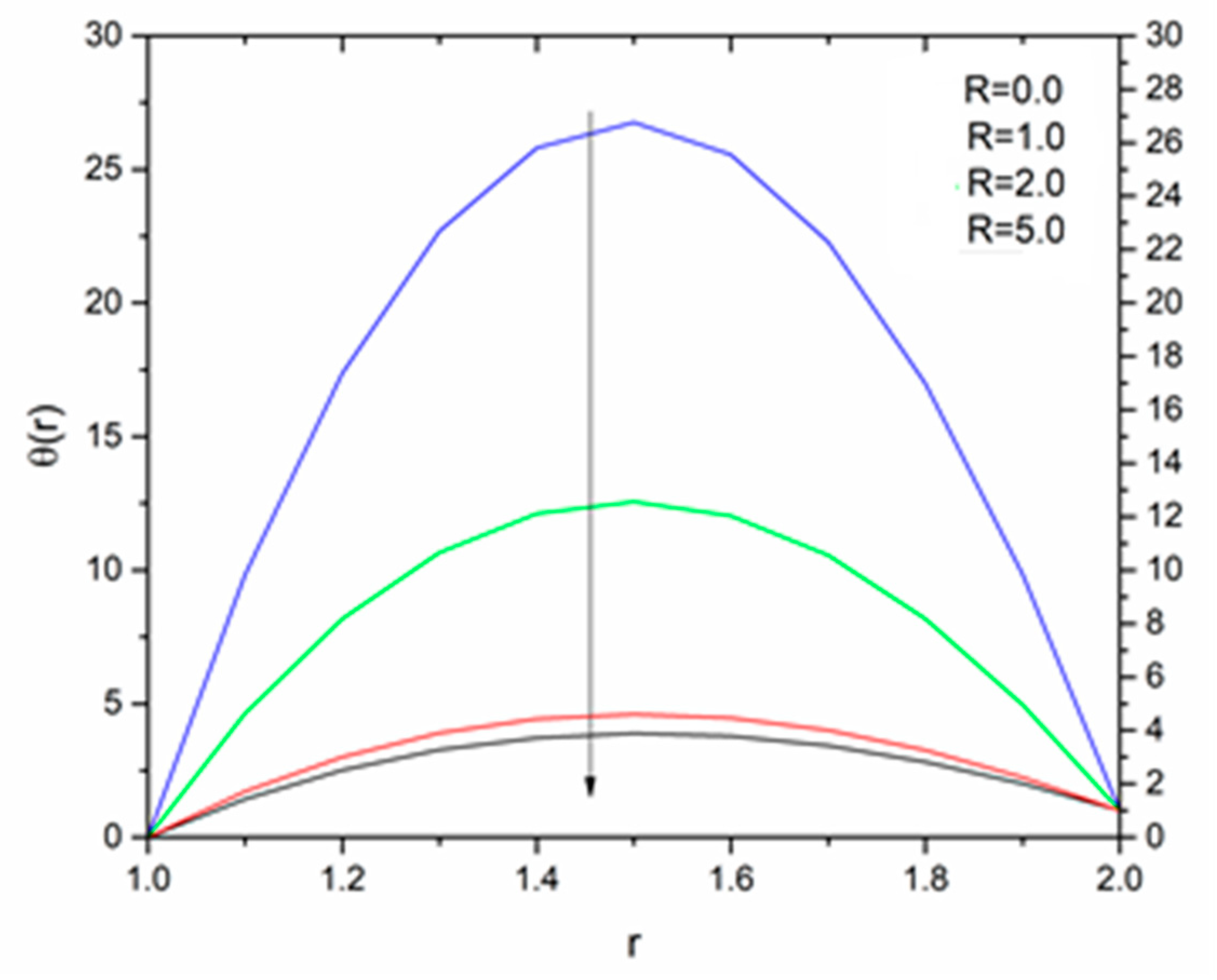
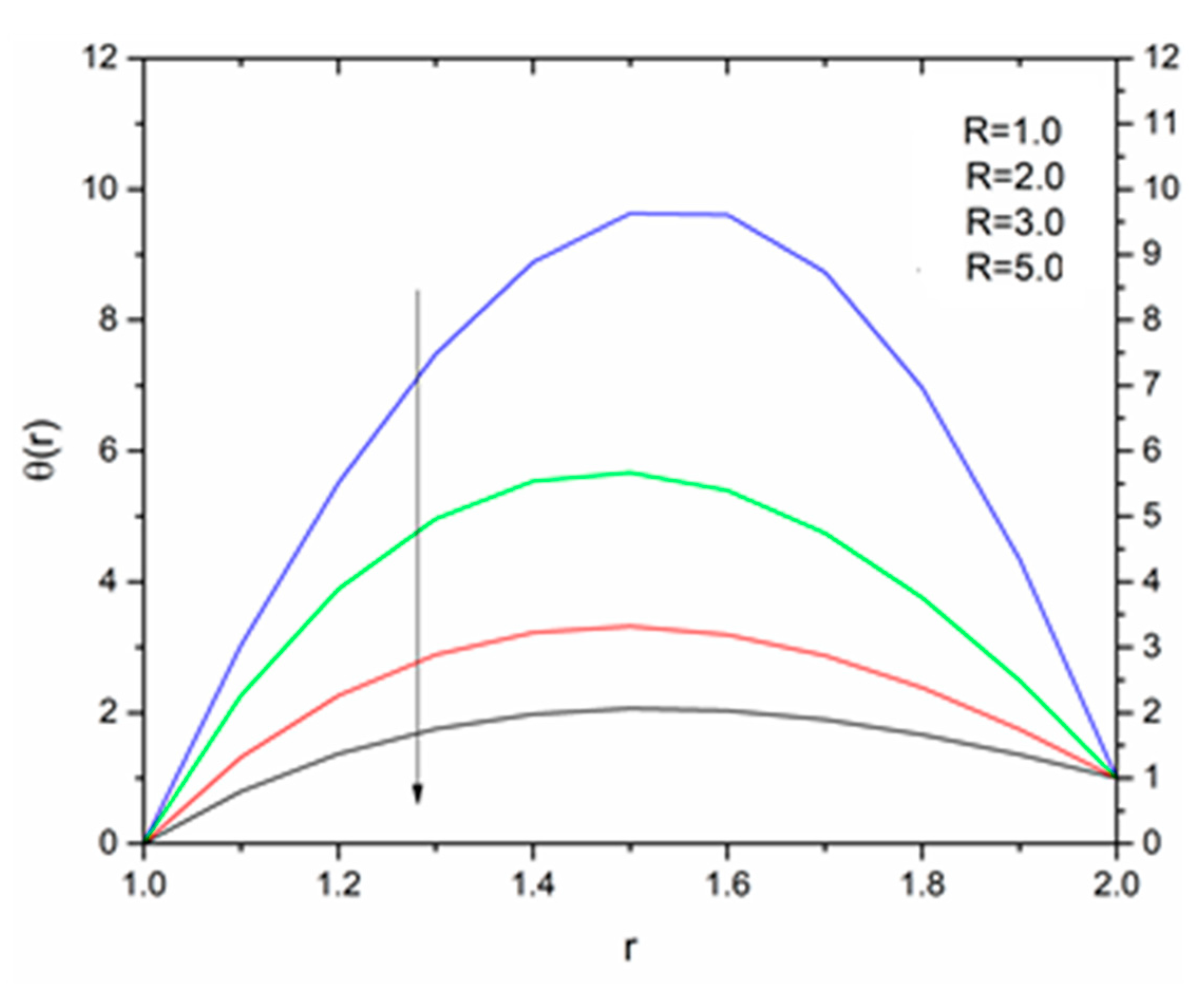
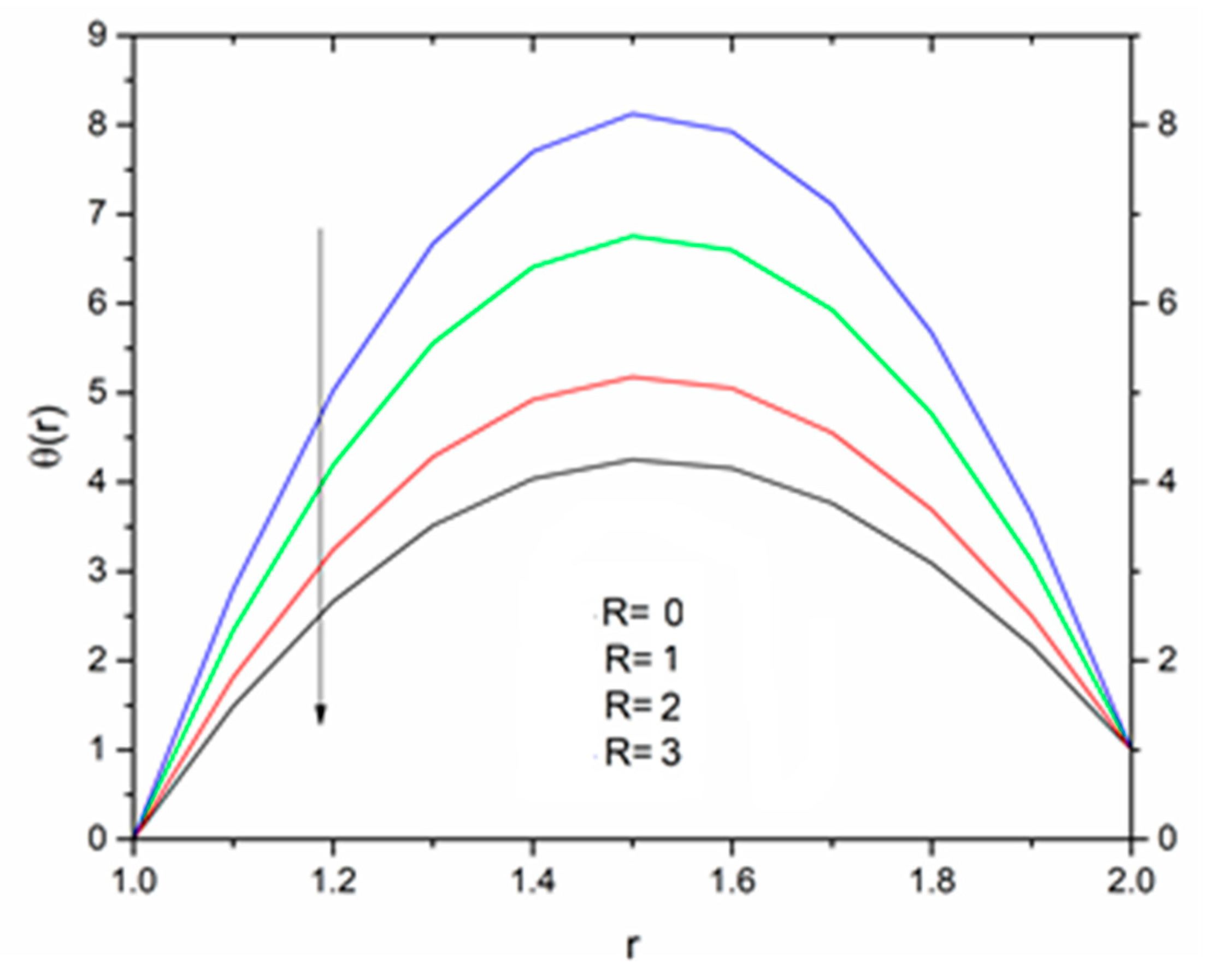
5. Results and Discussion
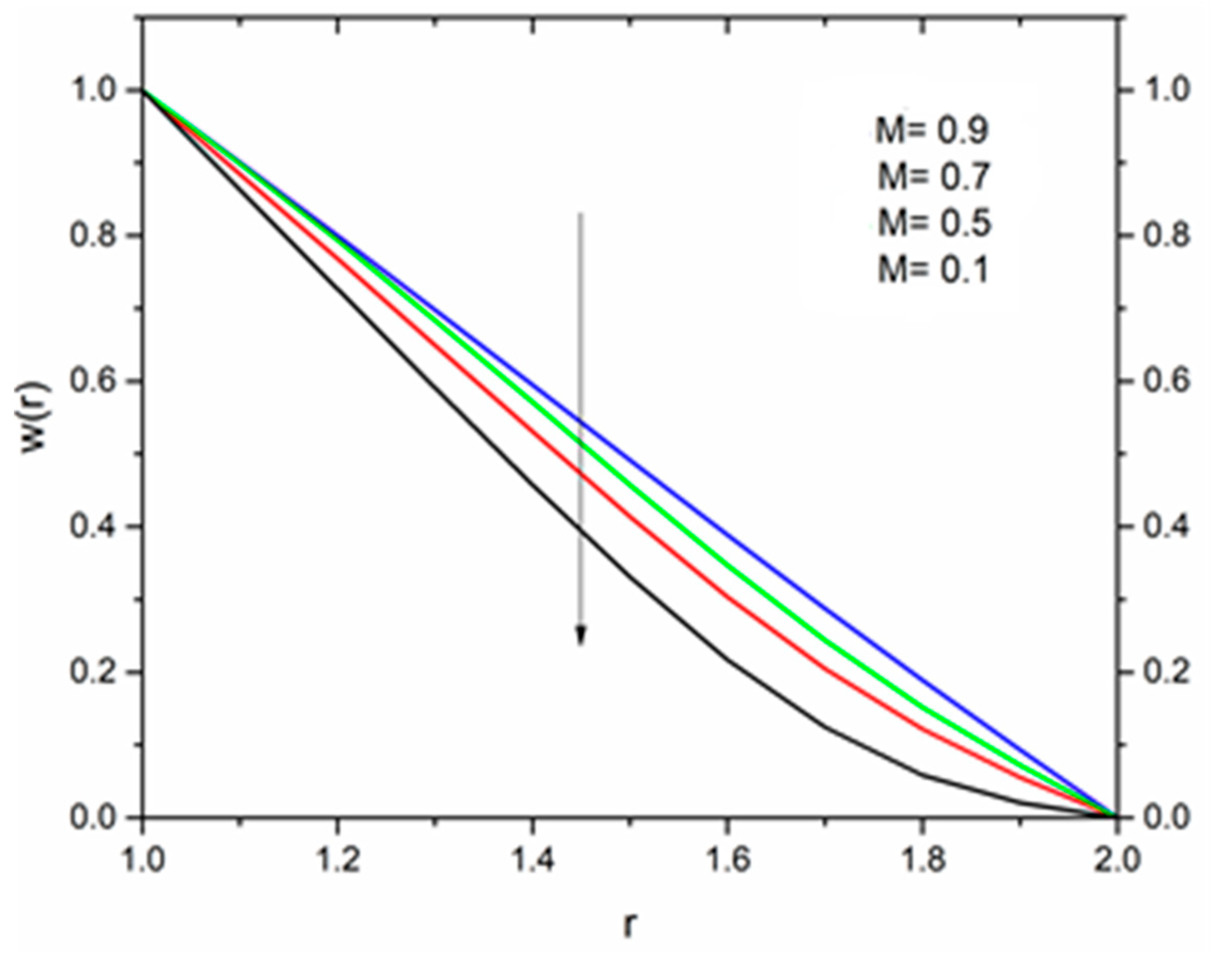
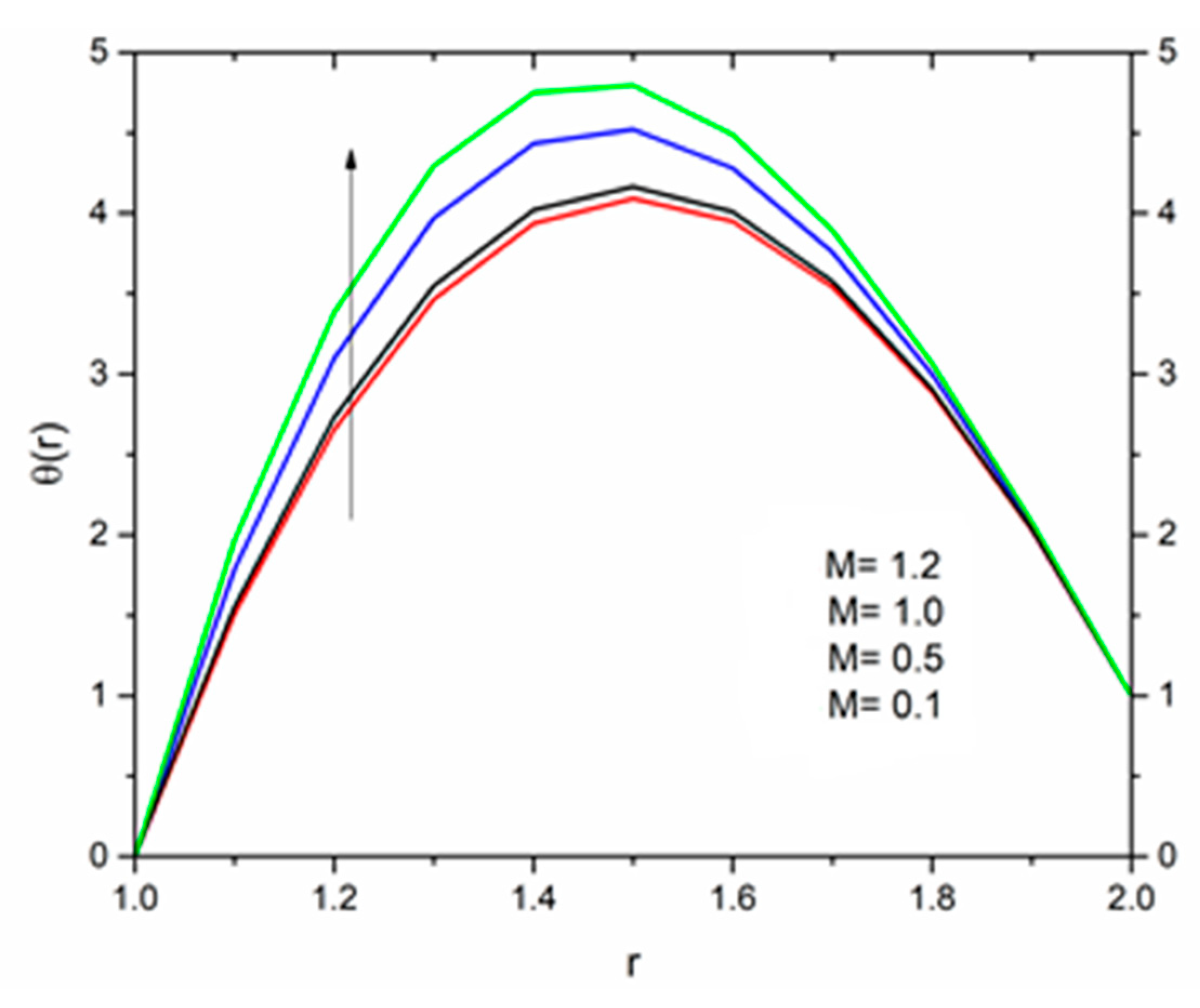
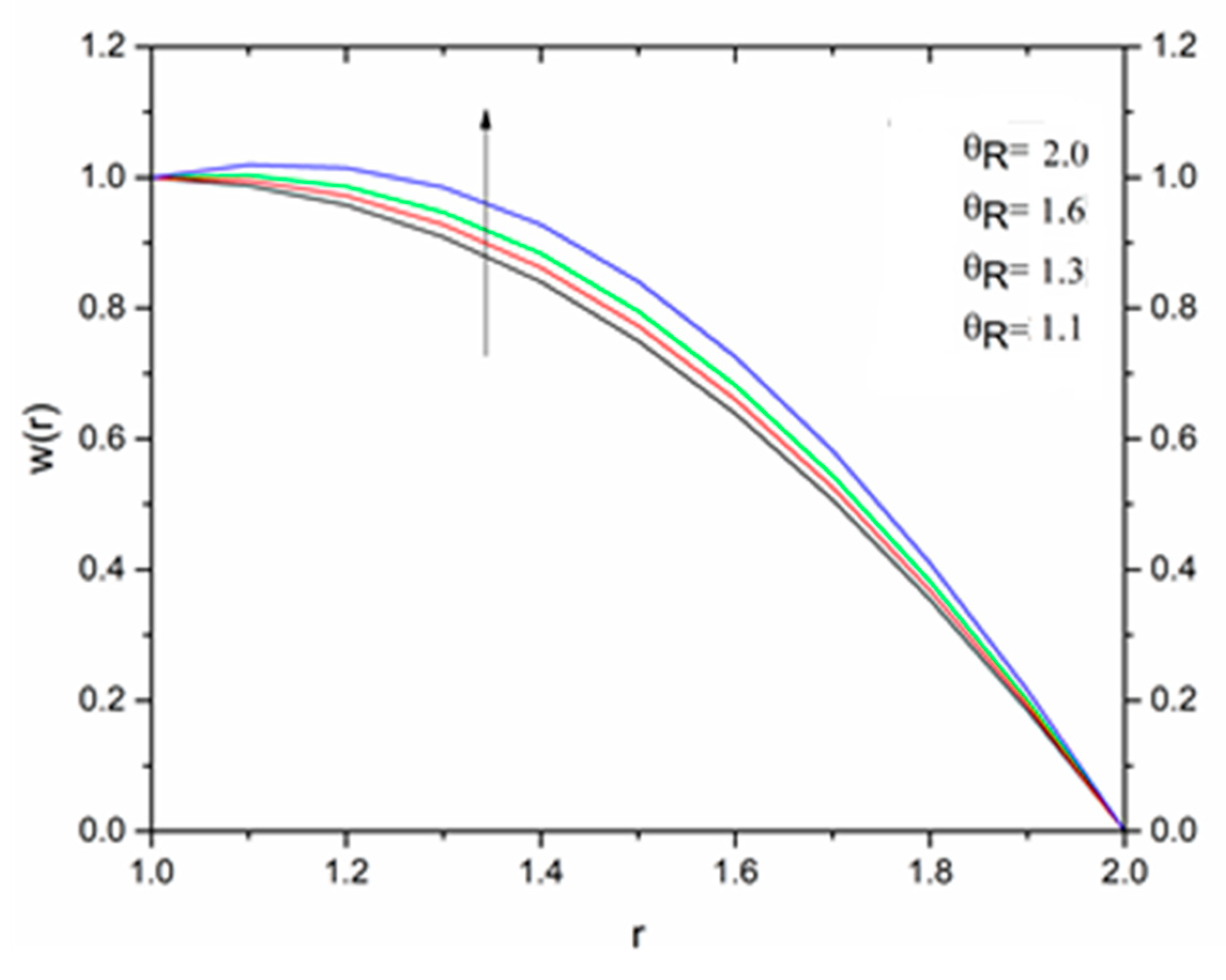
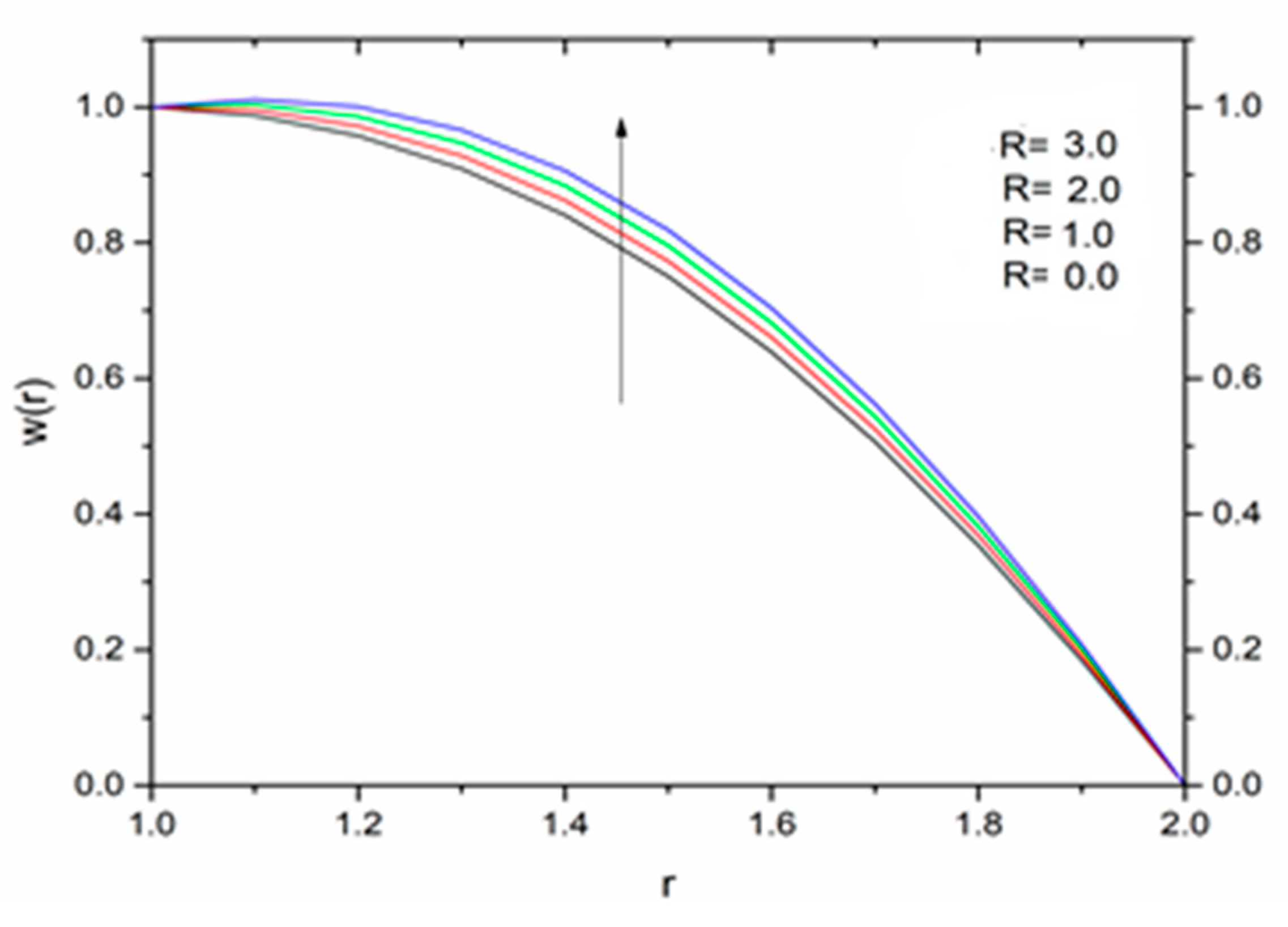
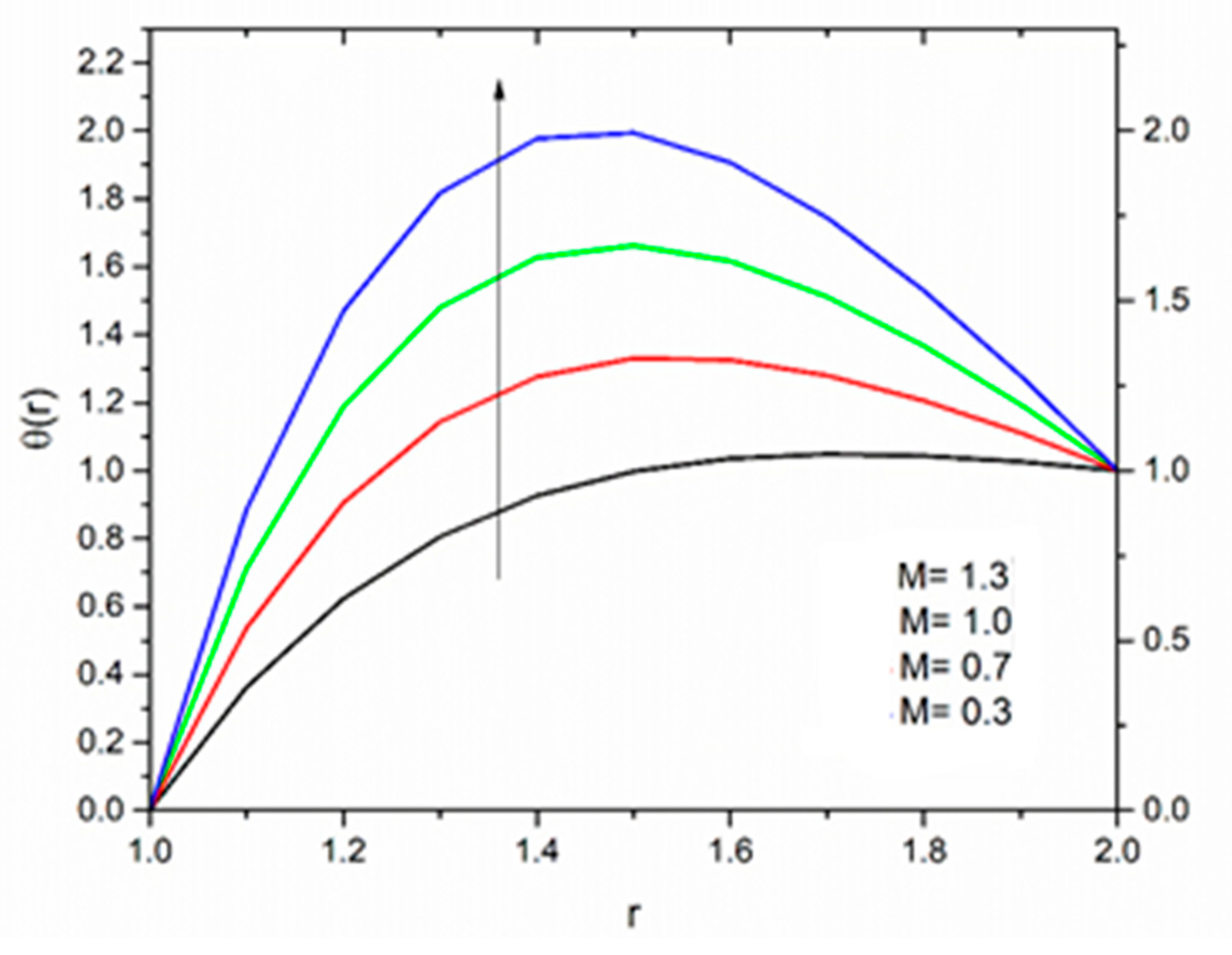
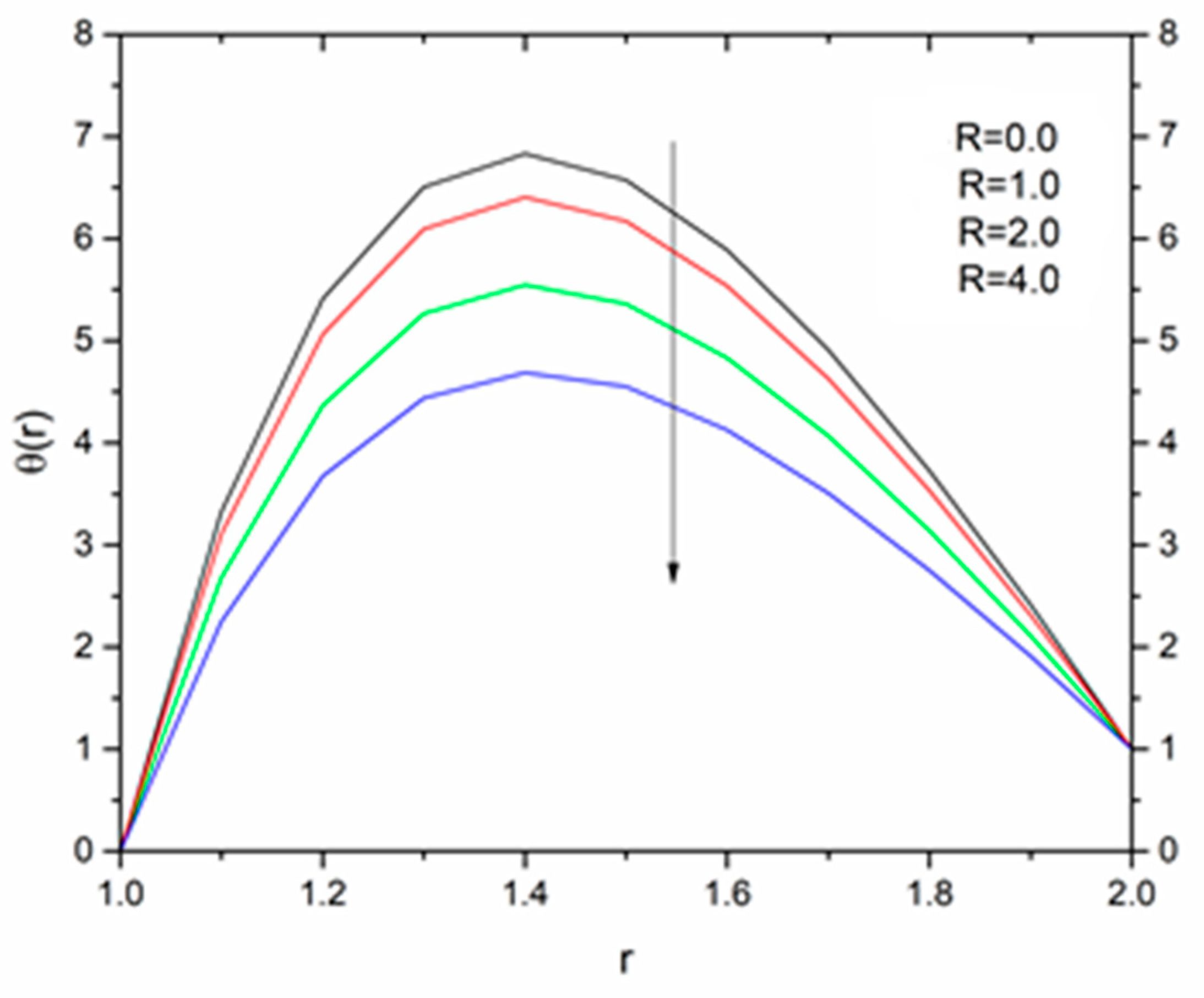
5.1. Reynolds’ Model
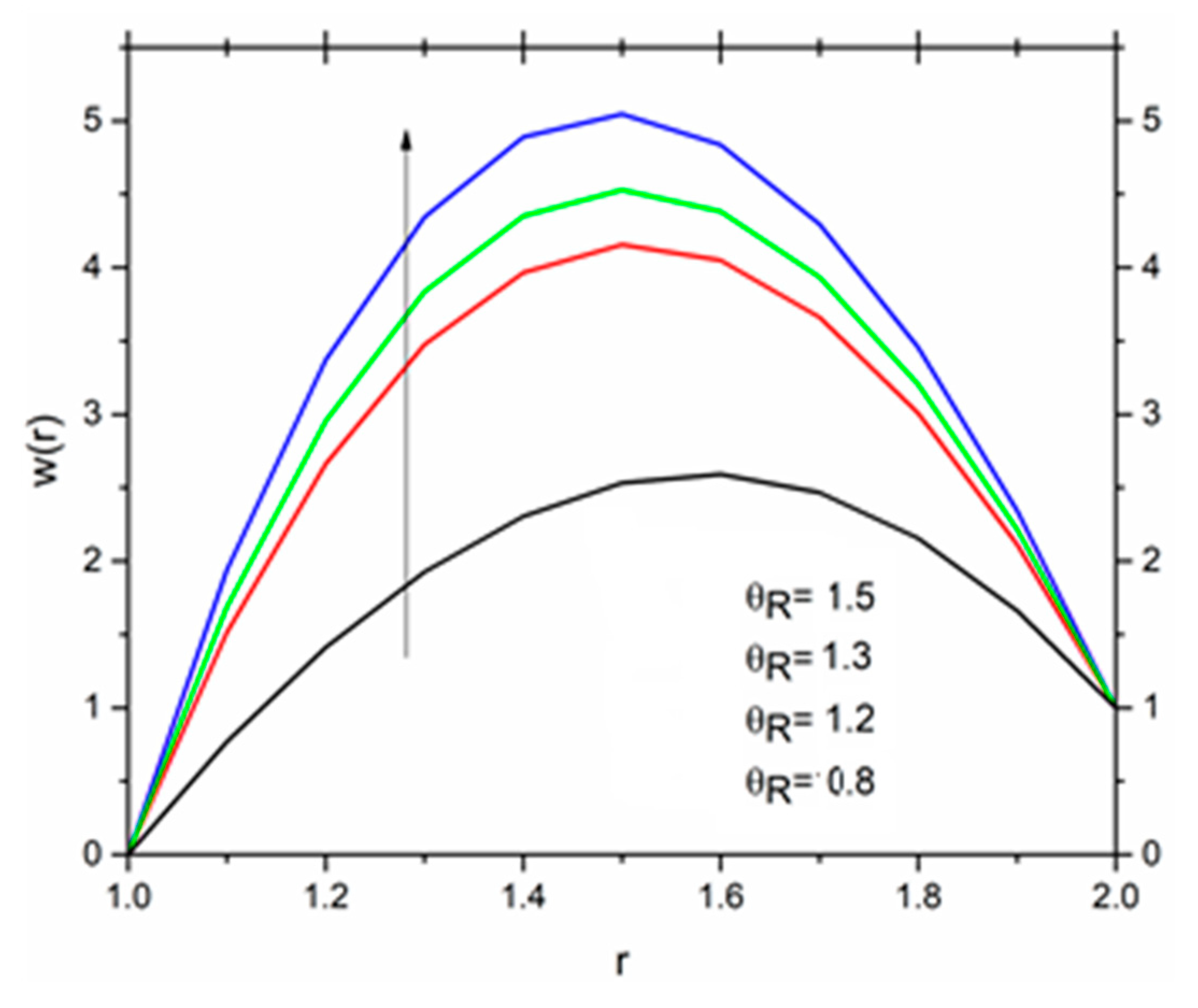
5.2. Vogel’s Model
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Wire radius (m) | M | Magnetic parameter | Co-ordinates system | ||
| Uw | Dragging velocity (ms−1) | Wire temperature (K) | L | Length of the die (m) | |
| Temperature parameter | Stefan-Boltzman constant (Wm−2K−4) | Reference viscosity (N sm−2) | |||
| Radiation parameter | Constant pressure gradient | Uniform magnetic field | |||
| Radius of the die (m) | Non-Newtonian Parameter | Density of the fluid | |||
| Radiative heat flux (Wm−2) | Dissipation function (Wm−2) | w | Velocity of the fluid (ms−1) | ||
| Fluid temperature (K) | Material constants | Substantial derivative | |||
| p | Pressure | Brinkmen number | Joule heating | ||
| Die temperature (k) | Reynolds’ model viscosity parameter | F | Viscous force per unit volume (Nm−3) | ||
| Die temperature (K) | k | Thermal conductivity | Specific heat at constant pressure | ||
| Wire coating aspect ratio | Mean absorption coefficient (m-1) | Dynamic viscosity (N sm−2) |
References
- Bernhardt, E.C. Processing of Thermoplastic Materials; Reinhold Publishing: New York, NY, USA, 1962; pp. 263–269. [Google Scholar]
- McKelvey, J.M. Polymer Processing; John Wiley and Sons: New York, NY, USA, 1962. [Google Scholar]
- Bagley, E.B.; Storey, S.H. Processing of Thermoplastic Materials. Wire Wire Prod. 1963, 38, 1104–1122. [Google Scholar]
- Carley, J.F.; Endo, T.; Krantz, W. Realistic analysis of flow in wire coating dies. Polym. Eng. Sci. 1979, 19, 1178–1187. [Google Scholar] [CrossRef]
- Han, C.D. Rheology and Processing of Polymeric Materials Volume 2 Polymer Processing; Oxford University Press: Oxford, UK, 2007; Volume 2, pp. 235–256. [Google Scholar]
- Middleman, S. Fundamentals of Polymer Processing; McGraw-Hill: New York, NY, USA, 1977. [Google Scholar]
- Khan, Z.; Rasheed, H.; Alharbi, S.O.; Khan, I.; Abbas, T.; Dennis, L.C.C. Manufacturing of double-layer optical fiber coating Phan-Thien-Tanner fluid as coating maerial. Coatings 2019, 9, 147. [Google Scholar] [CrossRef]
- Kasajima, M.; Ito, K. Post-treatment of polymer extrudate in wire coating. Appl. Polym. Symp. 1972, 221, 221–235. [Google Scholar]
- Tadmor, Z.; Bird, R.B. Rheological analysis of stabilizing forces in wire-coating dies. Polym. Eng. Sci. 1974, 14, 124–136. [Google Scholar] [CrossRef]
- Khan, Z.; Islam, S.; Shah, R.A.; Khan, I. Flow and heat transfer of two immiscible fluids in double-layer optical fiber coating. J. Coat. Technol. Res. 2016, 13, 1055–1063. [Google Scholar] [CrossRef]
- Wagner, R.; Mitsoulis, E. Effect of die design on the analysis of wire coating. Adv. Polym. Technol. 1985, 5, 305–325. [Google Scholar] [CrossRef]
- Mitsoulis, E. Fluid flow and heat transfer in wire coating. A review. Adv. Polym. Technol. 1986, 6, 467–487. [Google Scholar] [CrossRef]
- Akter, S.; Hashmi, M.S.J. Modelling of the pressure distribution within a hydrodynamic pressure unit: Effect of the change in viscosity during drawing of wire coating. J. Mater. Process. Technol. 1998, 77, 32–36. [Google Scholar] [CrossRef]
- Akter, S.; Hashmi, M.S.J. Analysis of polymer flow in a conical coating unit: A power law approach. Prog. Org. Coat. 1999, 37, 15–22. [Google Scholar] [CrossRef]
- Akter, S.; Hashmi, M.S.J. Wire drawing and coating using a combined geometry hydrodynamic unit. J. Mater. Process. Technol. 2006, 178, 98–110. [Google Scholar] [CrossRef]
- Caswell, B.; Tanner, R.J. Wire coating die using finite element methods. Polym. Eng. Sci. 1978, 18, 417–421. [Google Scholar] [CrossRef]
- Tucker, C.L. Computer Modeling for Polymer Processing; Hanser: Munich, Germany, 1989; pp. 311–317. [Google Scholar]
- Basu, S. A theoretical analysis of non-isothermal flow in wire coating coextrusion dies. Polym. Eng. Sci. 1981, 21, 1128–1138. [Google Scholar] [CrossRef]
- Tadmor, Z.; Gogos, C.G. Principle of Polymer Processing; John Wiley and Sons: New York, NY, USA, 1979. [Google Scholar]
- Mitsoulis, E. Finite element analysis of wire coating. Polym. Eng. Sci. 1986, 26, 171–186. [Google Scholar] [CrossRef]
- Roy, S.C.; Dutt, D.K. Wire coating by withdrawal from a bath of power law fluid. Chem. Eng. Sci. 1991, 36, 1933–1939. [Google Scholar] [CrossRef]
- Siddiqui, A.M.; Sajjid, M.; Hayat, T. Wire coating by withdrawal from a bath of fourth order fluid. Phys. Lett. A 2008, 372, 2665–2670. [Google Scholar] [CrossRef]
- Khan, Z.; Rasheed, H.; Alkanhal, T.A.; Ullah, M.; Khan, I.; Tlili, I. Effect of magnetic field and heat source on upper-convected-maxwell fluid in a porous channel. Open Phys. 2018, 16, 917–928. [Google Scholar] [CrossRef]
- Symmons, G.R.; Hashmi, M.S.J.; Pervinmehr, H. Plasto-hydrodynamic die less wire drawing, theoretical treatments and experimental results. In Progress Reports in Conference in Developments in Drawing of Metals; Met. Soc.: London, UK, 1992; pp. 54–62. [Google Scholar]
- Fenner, R.T.; Williams, J.G. Rheological analysis of stabilizing forces in wire coating analysis. Trans. Plast. Inst. Lond. 1967, 35, 701–706. [Google Scholar]
- Fenner, R.T. Extruder Screw Design; Iliffe: London, UK, 1970. [Google Scholar]
- Liu, I.-C. Flow and heat transfer of an electrically conducting fluid of second grade fluid over a stretching sheet subject to transverse magnetic field. Int. J. Heat Mass Transf. 2004, 47, 4427–4437. [Google Scholar] [CrossRef]
- Salem, A.M. Variable viscosity and thermal conductivity effects on MHD flow and heat transfer in visco-elastic fluid over a stretching sheet. Phys. Lett. A 2007, 369, 315–322. [Google Scholar] [CrossRef]
- Shah, R.A.; Islam, S.; Ellahi, M.; Siddiqui, A.M.; Haroon, T. Analytical solutions for heat transfer flows of a third grade fluid in post-treatment of wire coating. Int. J. Phys. Sci. 2011, 6, 4213–4223. [Google Scholar]
- Aksoy, Y.; Pakdemirli, M. Approximate analytic solutions for flow of a third grade fluid through a parallel plate channel filled with a porous medium, Transp. Porous Media 2010, 83, 375–395. [Google Scholar] [CrossRef]
- Siddidqui, A.M.; Mahmood, R.; Ghori, Q.K. Thin film flow of a third grade fluid on an inclined plane. Chaos Solitons Fractals 2008, 35, 140–147. [Google Scholar] [CrossRef]
- Siddidqui, A.M.; Zeb, A.; Ghori, Q.K.; Benharbit, A.M. Homotopy perturbation method for heat transfer flow of a third grade fluid between parallel plates. Chaos Solitons Fractals 2008, 36, 182–192. [Google Scholar] [CrossRef]
- Mishra, S.P. Heat transfer by laminar flow of an elastic–viscous liquid in a circular cylinder with linearly varying wall temperature. Appl. Sci. Res. 1965, 14, 182–190. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Kimiaeifar, A. Application of homotopy perturbation method to find an analytical solution for magnetohydrodynamic flows of viscoelastic fluids in converging/diverging channels. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2010. [Google Scholar] [CrossRef]
- Maleki, H.; Safaei, M.R.; Alrashed, A.A.A.A.; Kasaeian, Z. Flow and heat transfer in non-Newtonian nanofluids over porous surfaces. J. Therm. Anal. Calorim. 2019, 135, 1655–1666. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Kimiaeifar, A.; Bagheri, D. Series solution for heat transfer of continuous stretching sheet immersed in a micro polar fluid in the existence of radiation. Int. J. Numer. Meth. Heat Fluid Flow 2013, 23, 289–304. [Google Scholar] [CrossRef]
- Khan, Z.; Khan, I.; Ullah, M.; Tlili, I. Effect of thermal radiation and chemical reaction on non-Newtonian fluid through a vertically stretching porous plate with uniform suction. Results Phys. 2018, 9, 1086–1095. [Google Scholar] [CrossRef]
- Khan, Z.; Rasheed, H.U.; Shah, Q.; Abbas, T.; Ullah, M. Numerical simulation of double-layer optical fiber coating using Oldroyd 8-constant fluid as a coating material. Opt. Eng. 2018, 57, 076104. [Google Scholar] [CrossRef]
- Mabood, F.; Khan, W.A.; Ismail, A.I.M. MHD boundary layer flow and heat transfer of nanofluids over a nonlinear stretching sheet: A numerical study. J. Magn. Magn. Mater. 2015, 374, 569–576. [Google Scholar] [CrossRef]
- Anuar, N.S.; Bachok, N.; Pop, I. A Stability Analysis of Solutions in Boundary Layer Flow and Heat Transfer of Carbon Nanotubes over a Moving Plate with Slip Effect. Energies 2018, 11, 3243. [Google Scholar] [CrossRef]
- Maleki, H.; Safaei, M.R.; Togun, H.; Dahari, M. Heat transfer and fluid flow of pseudo-plastic nanofluid over a moving permeable plate with viscous dissipation and heat absorption/generation. J. Therm. Anal. Calorim. 2019, 135, 1643–1654. [Google Scholar] [CrossRef]
- Nayak, M.K.; Dash, G.C.; Singh, L.P. Steady MHD flow and heat transfer of a third-grade fluid in wire coating analysis with temperature dependent viscosity. Int. J. Heat Mass Transf. 2014, 79, 1087–1095. [Google Scholar] [CrossRef]
- Khan, Z.; Khan, M.A.; Siddiqui, N.; Ullah, M.; Shah, Q. Solution of magnetohydrodynamic flow and heat transfer of radiative viscoelastic fluid with temperature dependent viscosity in wire coating analysis. PLoS ONE 2018, 13, e0194196. [Google Scholar] [CrossRef] [PubMed]
- Khan, Z.; Khan, M.A.; Islam, S.; Jan, B.; Hussain, F.; Rasheed, H.; Khan, W. Analysis of magneto-hydrodynamics flow and heat transfer of a viscoelastic fluid through porous medium in wire coating analysis. Mathematics 2017, 5, 27. [Google Scholar] [CrossRef]

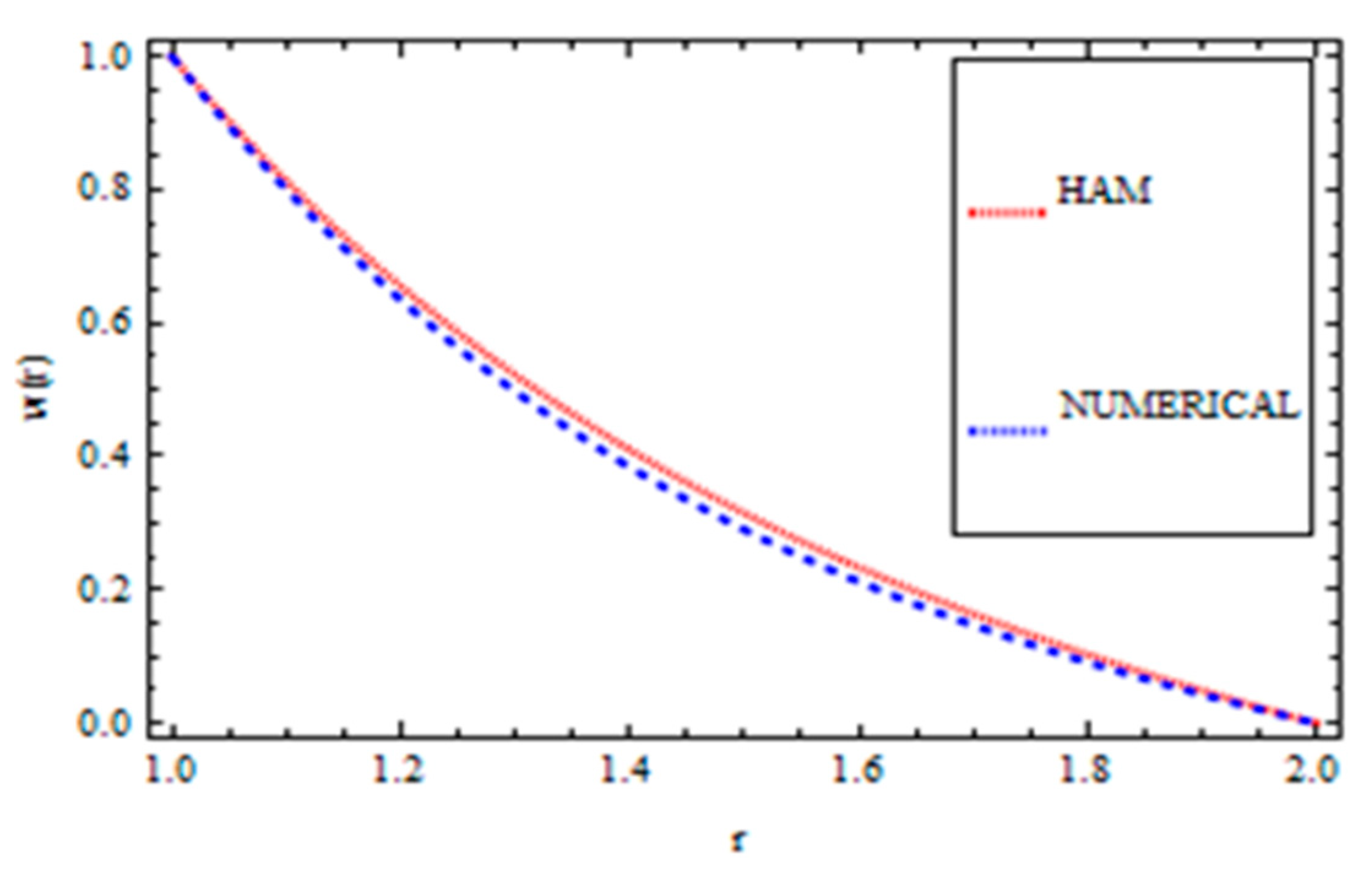





| S. No | Published Work | Present Work |
|---|---|---|
| 1 | 1 | 1 |
| 1.1 | 0.906702201 | 0.906702202 |
| 1.2 | 0.798963328 | 0.798963327 |
| 1.3 | 0.676887100 | 0.676887101 |
| 1.4 | 0.543737426 | 0.543774255 |
| 1.5 | 0.406571921 | 0.4065719210 |
| 1.6 | 0.275849318 | 0.275849317 |
| 1.7 | 0.163688021 | 0.1636880211 |
| 1.8 | 0.080480501 | 0.080480502 |
| 1.9 | 0.0296124455 | 0.0296124456 |
| 2.0 | 1.23245E-26 | 0.2138E-30 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, Z.; Khan, W.A.; Ur Rasheed, H.; Khan, I.; Nisar, K.S. Melting Flow in Wire Coating of a Third Grade Fluid over a Die Using Reynolds’ and Vogel’s Models with Non-Linear Thermal Radiation and Joule Heating. Materials 2019, 12, 3074. https://doi.org/10.3390/ma12193074
Khan Z, Khan WA, Ur Rasheed H, Khan I, Nisar KS. Melting Flow in Wire Coating of a Third Grade Fluid over a Die Using Reynolds’ and Vogel’s Models with Non-Linear Thermal Radiation and Joule Heating. Materials. 2019; 12(19):3074. https://doi.org/10.3390/ma12193074
Chicago/Turabian StyleKhan, Zeeshan, Waqar A. Khan, Haroon Ur Rasheed, Ilyas Khan, and Kottakkaran Sooppy Nisar. 2019. "Melting Flow in Wire Coating of a Third Grade Fluid over a Die Using Reynolds’ and Vogel’s Models with Non-Linear Thermal Radiation and Joule Heating" Materials 12, no. 19: 3074. https://doi.org/10.3390/ma12193074
APA StyleKhan, Z., Khan, W. A., Ur Rasheed, H., Khan, I., & Nisar, K. S. (2019). Melting Flow in Wire Coating of a Third Grade Fluid over a Die Using Reynolds’ and Vogel’s Models with Non-Linear Thermal Radiation and Joule Heating. Materials, 12(19), 3074. https://doi.org/10.3390/ma12193074





