Homogenization and Localization of Ratcheting Behavior of Composite Materials and Structures with the Thermal Residual Stress Effect
Abstract
1. Introduction
- (1)
- The cyclic plastic constitutive model is implemented successfully into the FVDAM theory for the first time, giving the FVDAM the ability to simulate the cyclic behavior of the metal matrix composites.
- (2)
- Not only the homogenized cyclic response of the composites but also the local field distributions are obtained using the proposed model, since most of the mean-field and nongeometrical models cannot obtain the local field response.
- (3)
- The effects of thermal residual stresses induced during the consolidation process, as well as fiber orientations, are considered, which makes the calculation of the cyclic behavior closer to the actual working condition.
- (4)
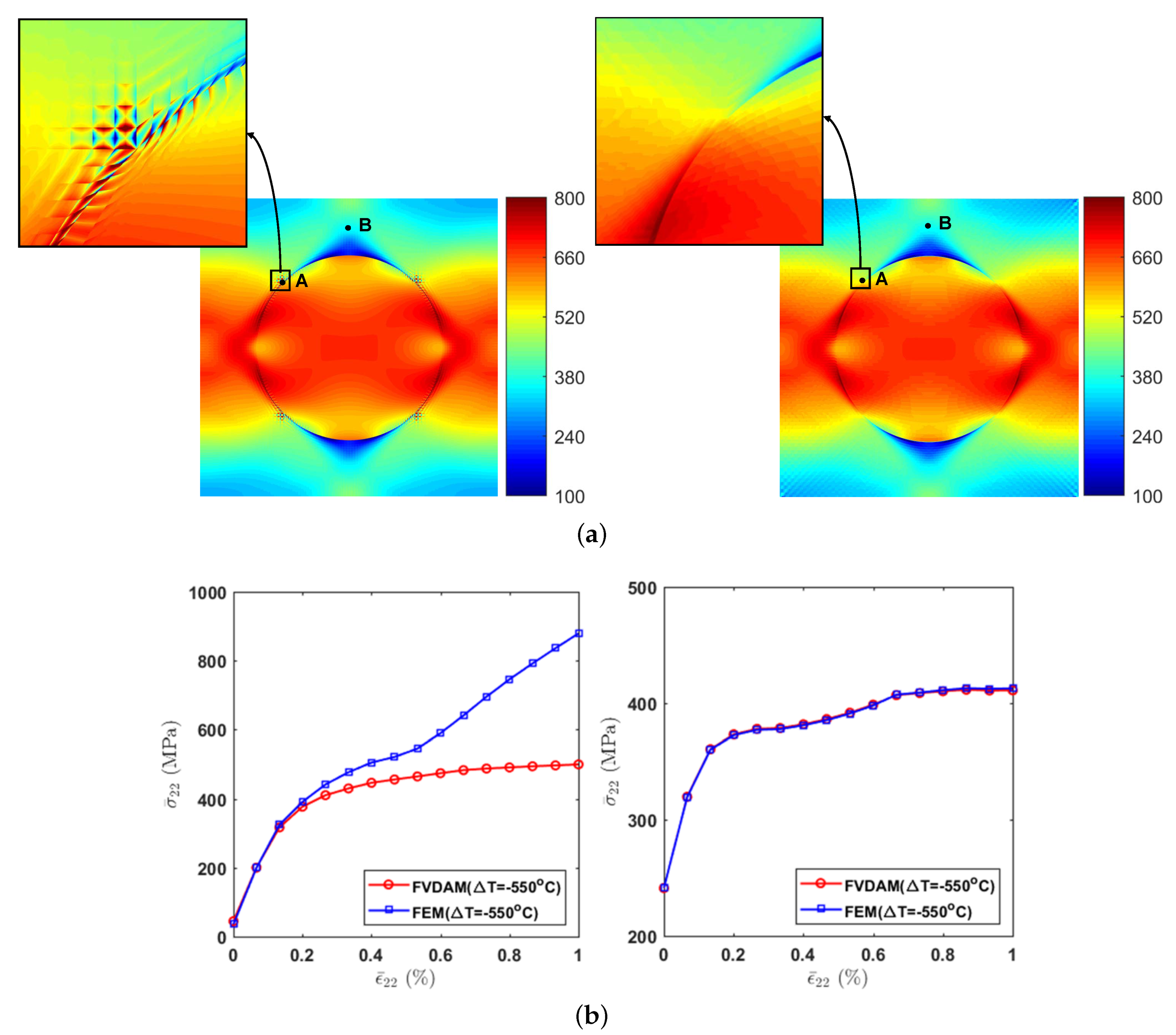
- The effectiveness of the new micromechanical model to accurately simulate both the homogenized stress–strain curve and local field distribution is verified by an FEM model with the same mesh discretizations, providing a golden standard for the simulation. The results also show that the proposed model has a better convergence near the stress concentration region.
2. Finite-Volume Direct Averaging Micromechanics (FVDAM)
3. Implementation of the Cyclic Plasticity Model
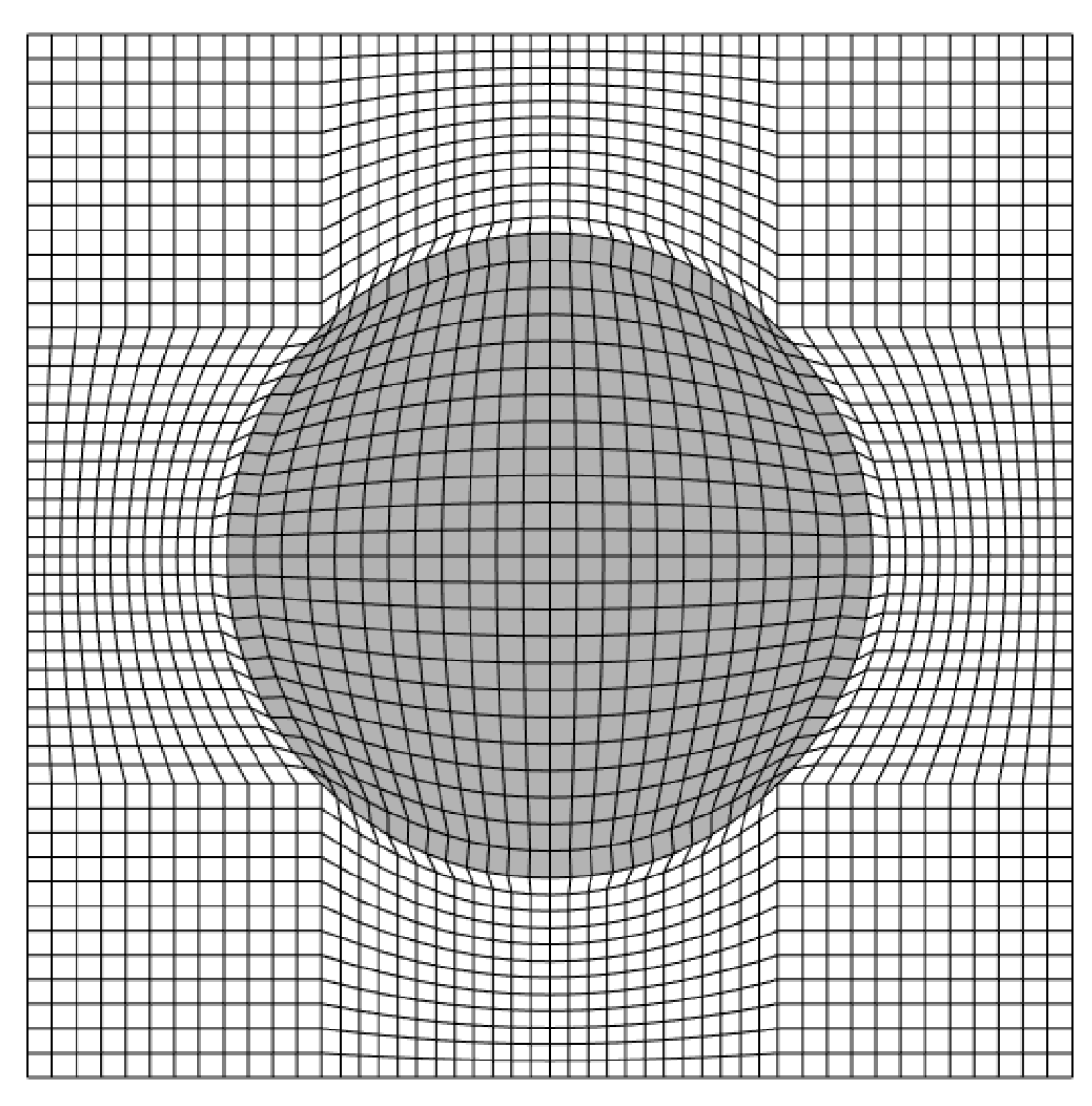
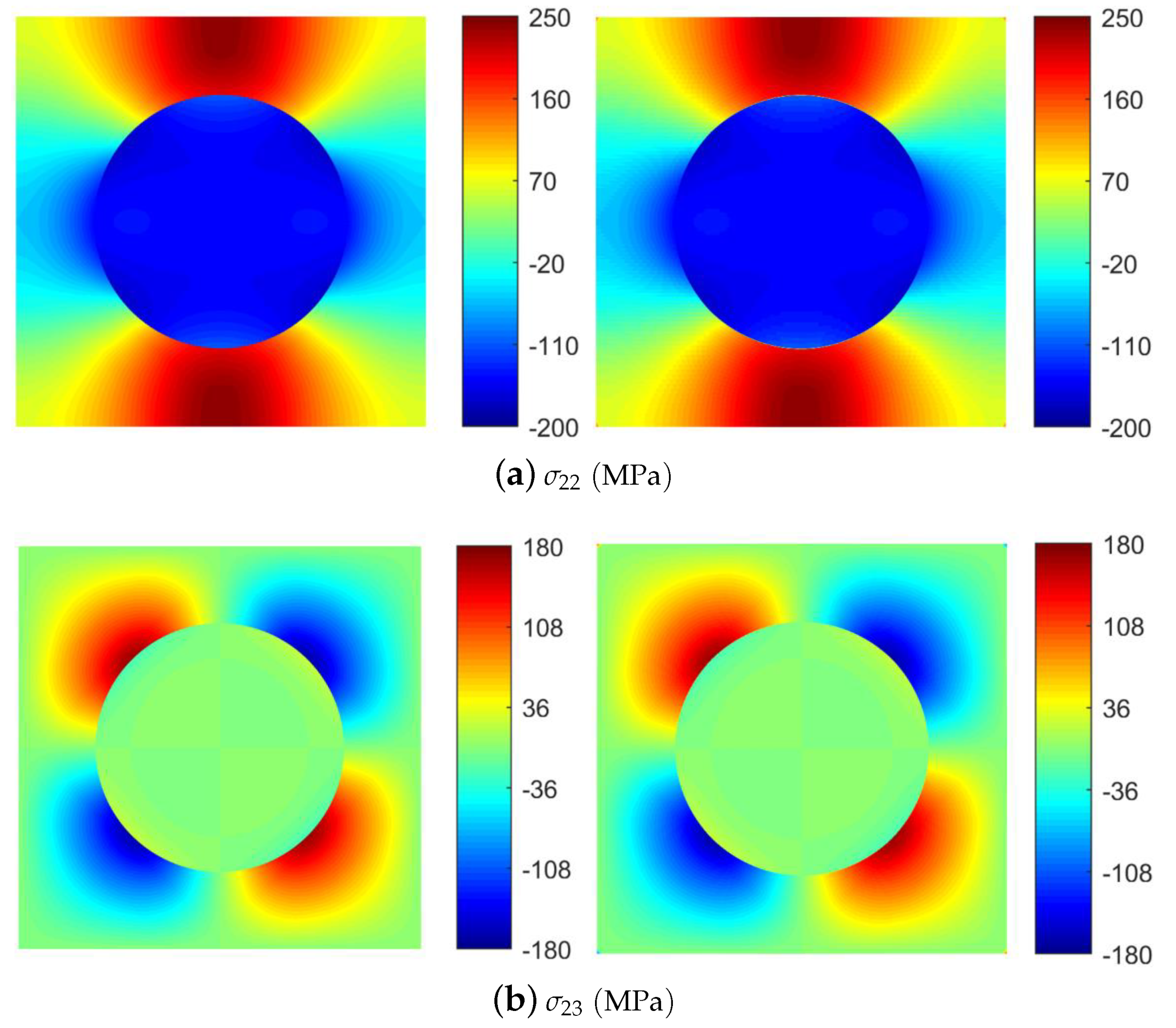
4. Validation and Numerical Results
4.1. Unidirectional Transverse Loading
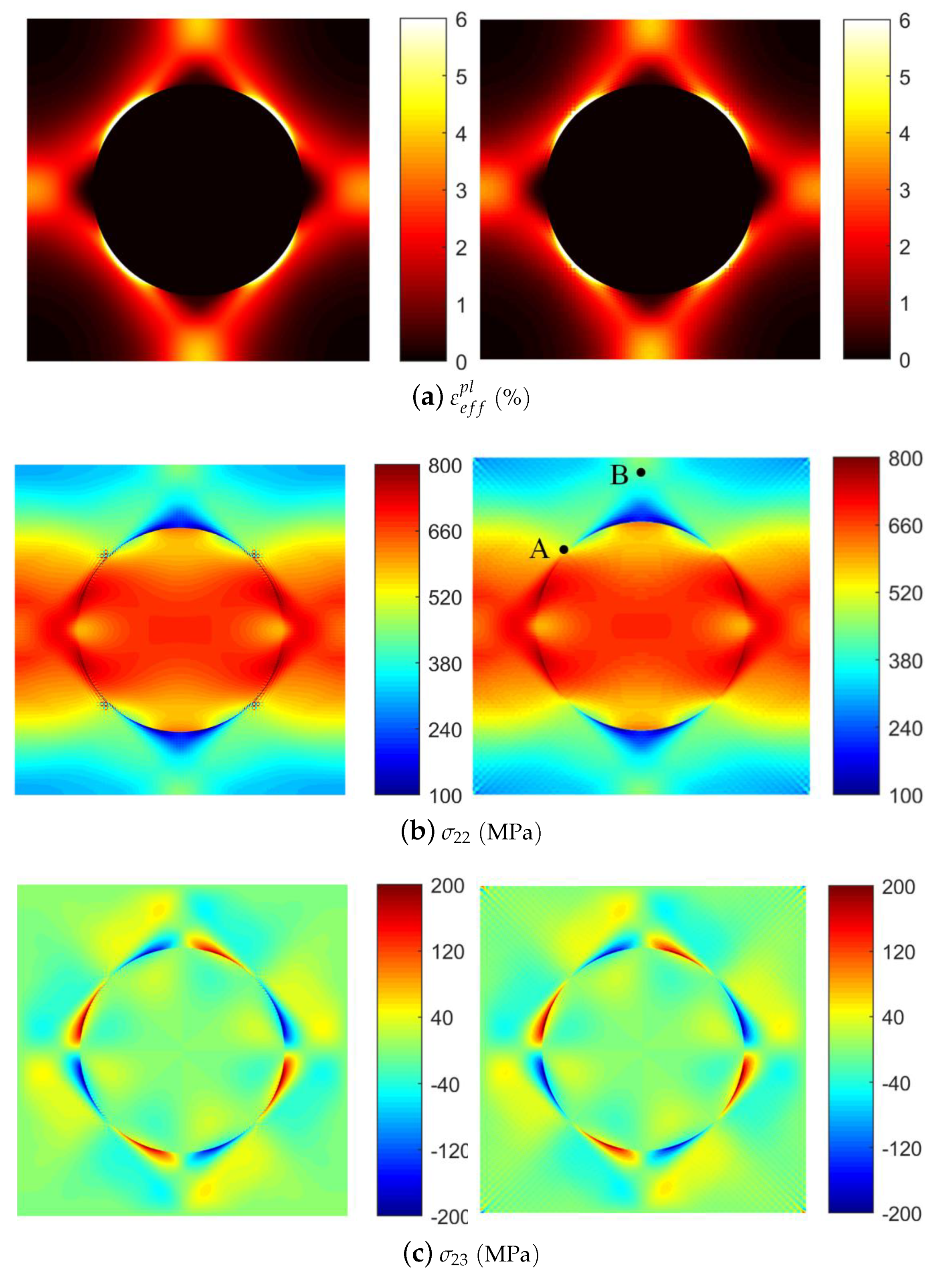
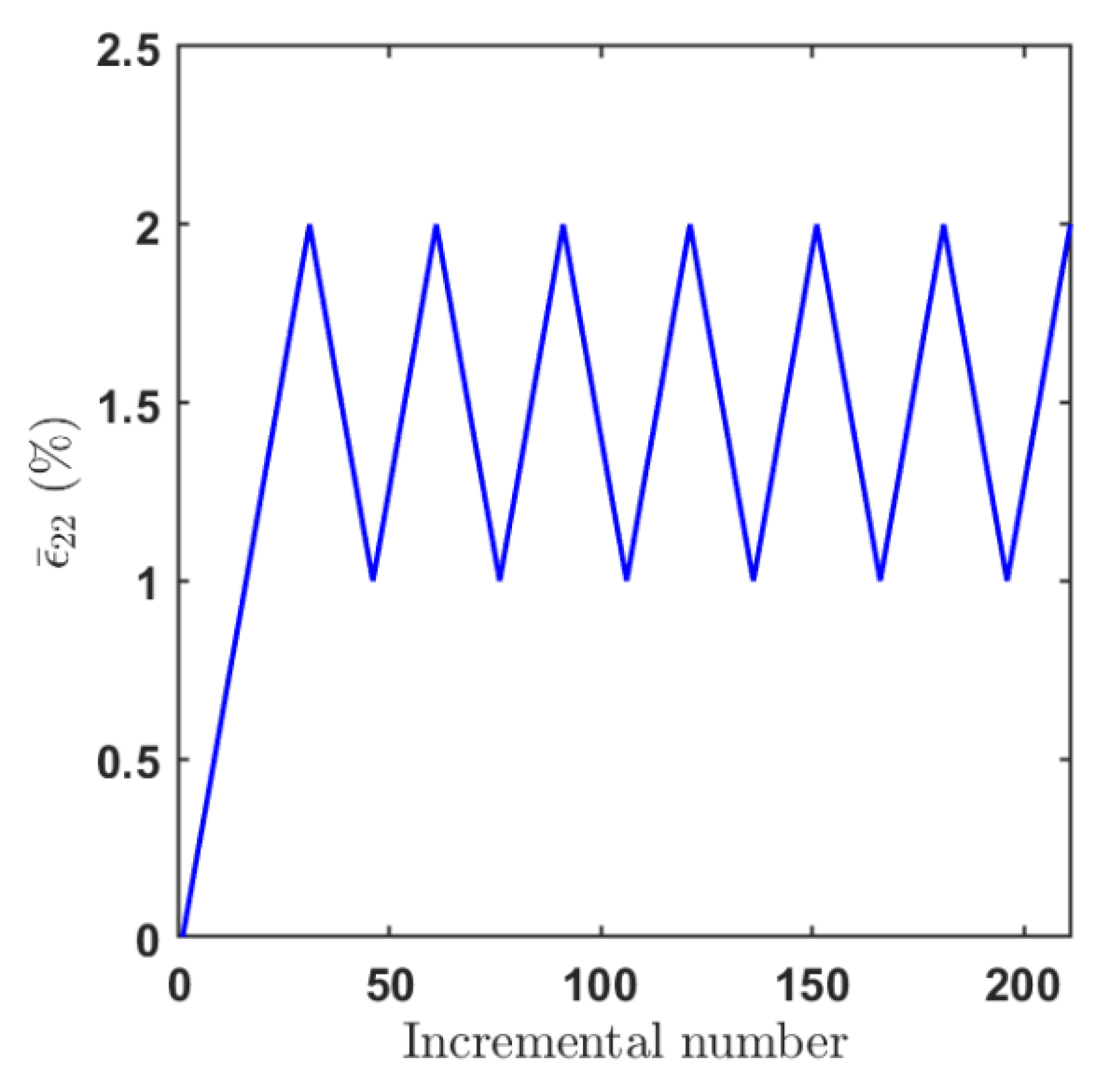
4.2. Cyclic Loading
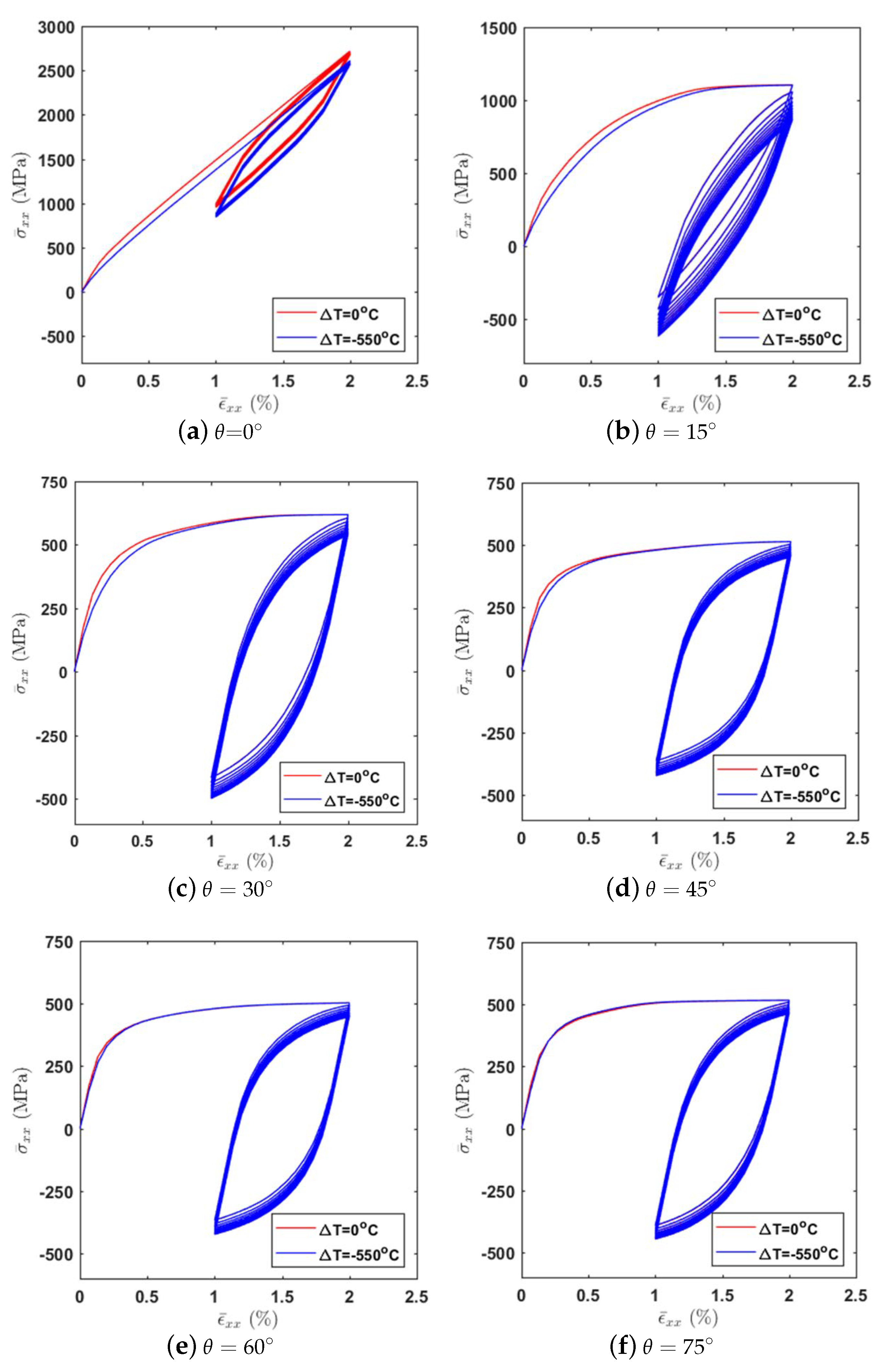
4.3. Off-Axis Loading
5. Discussions
6. Summaries and Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| FVDAM | Finite-volume direct averaging micromechanics |
| FE | Finite element |
| FEM | Finite element method |
References
- Armstrong, P.J.; Frederick, C. A Mathematical Representation of the Multiaxial Bauschinger Effect; Central Electricity Generating Board [and] Berkeley Nuclear Laboratories: London, UK, 1966; Volume 731. [Google Scholar]
- Ohno, N.; Wang, J. Transformation of a nonlinear kinematic hardening rule to a multisurface form under isothermal and nonisothermal conditions. Int. J. Plast. 1991, 7, 879–891. [Google Scholar] [CrossRef]
- Ohno, N.; Wang, J.D. Kinematic hardening rules with critical state of dynamic recovery, part I: Formulation and basic features for ratchetting behavior. Int. J. Plast. 1993, 9, 375–390. [Google Scholar] [CrossRef]
- Ohno, N.; Wang, J.D. Kinematic hardening rules with critical state of dynamic recovery, Part II: Application to experiments of ratchetting behavior. Int. J. Plast. 1993, 9, 391–403. [Google Scholar] [CrossRef]
- Tanaka, E. A nonproportionality parameter and a cyclic viscoplastic constitutive model taking into account amplitude dependences and memory effects of isotropic hardening. Eur. J. Mech. A Solids 1994, 13, 155–173. [Google Scholar]
- Chaboche, J.L. Constitutive equations for cyclic plasticity and cyclic viscoplasticity. Int. J. Plast. 1989, 5, 247–302. [Google Scholar] [CrossRef]
- Chaboche, J.L. On some modifications of kinematic hardening to improve the description of ratchetting effects. Int. J. Plast. 1991, 7, 661–678. [Google Scholar] [CrossRef]
- Chaboche, J.L. A review of some plasticity and viscoplasticity constitutive theories. Int. J. Plast. 2008, 24, 1642–1693. [Google Scholar] [CrossRef]
- Abdel-Karim, M.; Ohno, N. Kinematic hardening model suitable for ratchetting with steady-state. Int. J. Plast. 2000, 16, 225–240. [Google Scholar] [CrossRef]
- Kang, G. A visco-plastic constitutive model for ratcheting of cyclically stable materials and its finite element implementation. Mech. Mater. 2004, 36, 299–312. [Google Scholar] [CrossRef]
- Ohno, N. Recent progress in constitutive modeling for ratchetting. J. Soc. Mater. Sci. Jpn. 1997, 46, 1–9. [Google Scholar] [CrossRef]
- Bari, S.; Hassan, T. An advancement in cyclic plasticity modeling for multiaxial ratcheting simulation. Int. J. Plast. 2002, 18, 873–894. [Google Scholar] [CrossRef]
- Kang, G. Ratchetting: Recent progresses in phenomenon observation, constitutive modeling and application. Int. J. Fatigue 2008, 30, 1448–1472. [Google Scholar] [CrossRef]
- Sajjad, H.M.; Hanke, S.; Güler, S.; Fischer, A.; Hartmaier, A. Modelling Cyclic Behaviour of Martensitic Steel with J2 Plasticity and Crystal Plasticity. Materials 2019, 12, 1767. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Zhang, K.; Kuang, Z.; Hu, G.; Song, Q.; Chang, Y. The Anisotropic Distortional Yield Surface Constitutive Model Based on the Chaboche Cyclic Plastic Model. Materials 2019, 12, 543. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Daehn, G.S.; Wagoner, R. The temperature-cycling deformation of particle reinforced metal matrix composites—A finite element study. Scr. Metall. Mater. 1990, 24, 2151–2155. [Google Scholar] [CrossRef]
- Kang, G. Uniaxial time-dependent ratchetting of SiCP/6061Al composites at room and high temperature. Compos. Sci. Technol. 2006, 66, 1418–1430. [Google Scholar] [CrossRef]
- Han, S.W.; Kang, J.W.; Lee, C.S. Cyclic behavior of diagonally reinforced slender HPFRCC coupling beams with reduced diagonal and transverse reinforcement. Compos. Struct. 2018, 206, 550–562. [Google Scholar] [CrossRef]
- Kimmig, S.; You, J.H. Cyclic plastic behavior of unidirectional SiC fibre-reinforced copper composites under uniaxial loads: An experimental and computational study. Compos. Struct. 2018, 200, 555–564. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Benveniste, Y. A new approach to the application of Mori-Tanaka’s theory in composite materials. Mech. Mater. 1987, 6, 147–157. [Google Scholar] [CrossRef]
- Huang, Z.M. On micromechanics approach to stiffness and strength of unidirectional composites. J. Reinf. Plast. Compos. 2019, 38, 167–196. [Google Scholar] [CrossRef]
- Huang, Z.M. A unified micromechanical model for the mechanical properties of two constituent composite materials. Part I: elastic behavior. J. Thermoplast. Compos. Mater. 2000, 13, 252–271. [Google Scholar] [CrossRef]
- Antin, K.N.; Laukkanen, A.; Andersson, T.; Smyl, D.; Vilaça, P. A Multiscale Modelling Approach for Estimating the Effect of Defects in Unidirectional Carbon Fiber Reinforced Polymer Composites. Materials 2019, 12, 1885. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Huang, Z. Analytical micromechanics models for elastoplastic behavior of long fibrous composites: A critical review and comparative study. Materials 2018, 11, 1919. [Google Scholar] [CrossRef] [PubMed]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1957, 241, 376–396. [Google Scholar]
- Doghri, I.; Ouaar, A. Homogenization of two-phase elastoplastic composite materials and structures: Study of tangent operators, cyclic plasticity and numerical algorithms. Int. J. Solids Struct. 2003, 40, 1681–1712. [Google Scholar] [CrossRef]
- Czarnota, C.; Kowalczyk-Gajewska, K.; Salahouelhadj, A.; Martiny, M.; Mercier, S. Modeling of the cyclic behavior of elastic–viscoplastic composites by the additive tangent Mori–Tanaka approach and validation by finite element calculations. Int. J. Solids Struct. 2015, 56, 96–117. [Google Scholar] [CrossRef]
- Lahellec, N.; Suquet, P. Effective response and field statistics in elastoplastic and elasto-viscoplastic composites under radial and non-radial loadings. Int. J. Plast. 2013, 42, 1–30. [Google Scholar] [CrossRef]
- Bansal, Y.; Pindera, M.J. Finite-volume direct averaging micromechanics of heterogeneous materials with elastic–plastic phases. Int. J. Plast. 2006, 22, 775–825. [Google Scholar] [CrossRef]
- Gattu, M.; Khatam, H.; Drago, A.S.; Pindera, M.J. Parametric finite-volume micromechanics of uniaxial continuously-reinforced periodic materials with elastic phases. J. Eng. Mater. Technol. 2008, 130, 031015. [Google Scholar] [CrossRef]
- Khatam, H.; Pindera, M.J. Parametric finite-volume micromechanics of periodic materials with elastoplastic phases. Int. J. Plast. 2009, 25, 1386–1411. [Google Scholar] [CrossRef]
- Cavalcante, M.A.; Pindera, M.J.; Khatam, H. Finite-volume micromechanics of periodic materials: past, present and future. Compos. Part B Eng. 2012, 43, 2521–2543. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, G. Homogenized and localized responses of coated magnetostrictive porous materials and structures. Compos. Struct. 2018, 187, 102–115. [Google Scholar] [CrossRef]
- Cavalcante, M.A.; Marques, S.P. Homogenization of periodic materials with viscoelastic phases using the generalized FVDAM theory. Comput. Mater. Sci. 2014, 87, 43–53. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, G.; Chen, X.; Geng, J. Finite-volume homogenization of elastic/viscoelastic periodic materials. Compos. Struct. 2017, 182, 457–470. [Google Scholar] [CrossRef]
- Chen, Q.; Chen, X.; Zhai, Z.; Zhu, X.; Yang, Z. Micromechanical modeling of viscoplastic behavior of laminated polymer composites with thermal residual stress effect. J. Eng. Mater. Technol. 2016, 138, 031005. [Google Scholar] [CrossRef]
- Tu, W.; Pindera, M.J. Cohesive zone-based damage evolution in periodic materials via finite-volume homogenization. J. Appl. Mech. 2014, 81, 101005. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, G.; Pindera, M.J. Homogenization and localization of nanoporous composites—A critical review and new developments. Compos. Part B Eng. 2018, 155, 329–368. [Google Scholar] [CrossRef]
- Ye, J.; Chu, C.; Cai, H.; Hou, X.; Shi, B.; Tian, S.; Chen, X.; Ye, J. A multi-scale model for studying failure mechanisms of composite wind turbine blades. Compos. Struct. 2019, 212, 220–229. [Google Scholar] [CrossRef]
- Cavalcante, M.A.; Pindera, M.J. Generalized FVDAM Theory for Periodic Materials Undergoing Finite Deformations—Part I: Framework. J. Appl. Mech. 2014, 81, 021005. [Google Scholar] [CrossRef]
- Cavalcante, M.A.; Pindera, M.J. Generalized FVDAM Theory for Periodic Materials Undergoing Finite Deformations—Part II: Results. J. Appl. Mech. 2014, 81, 021006. [Google Scholar] [CrossRef]
- Chen, Q.; Tu, W.; Liu, R.; Chen, X. Parametric multiphysics finite-volume theory for periodic composites with thermo-electro-elastic phases. J. Intell. Mater. Syst. Struct. 2018, 29, 530–552. [Google Scholar] [CrossRef]
- Ye, J.; Cai, H.; Wang, Y.; Jing, Z.; Shi, B.; Qiu, Y.; Chen, X. Effective mechanical properties of piezoelectric–piezomagnetic hybrid smart composites. J. Intell. Mater. Syst. Struct. 2018, 29, 1711–1723. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, G.; Pindera, M.J. Finite-volume homogenization and localization of nanoporous materials with cylindrical voids. Part 1: Theory and validation. Eur. J. Mech. A Solids 2018, 70, 141–155. [Google Scholar] [CrossRef]
- Kobayashi, M.; Ohno, N. Implementation of cyclic plasticity models based on a general form of kinematic hardening. Int. J. Numer. Methods Eng. 2002, 53, 2217–2238. [Google Scholar] [CrossRef]
- Sauer, T. Numerical Analysis; Pearson Addison Wesley: Boston, MA, USA, 2006. [Google Scholar]
- Levin, V.M. On the coefficients of thermal expansion of heterogeneous materials. Mech. Solids 1967, 2, 58–61. [Google Scholar]
- Aghdam, M.; Pavier, M.; Smith, D. Micro-mechanics of off-axis loading of metal matrix composites using finite element analysis. Int. J. Solids Struct. 2001, 38, 3905–3925. [Google Scholar] [CrossRef]
- Pindera, M.J.; Bansal, Y. On the micromechanics-based simulation of metal matrix composite response. J. Eng. Mater. Technol. 2007, 129, 468–482. [Google Scholar] [CrossRef]





| Matrix | Fiber | |
|---|---|---|
| 215 | 400 | |
| 0.33 | 0.25 | |
| 8 | 4.86 | |
| 220 | ∞ (elastic) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, D.; Yang, Z.; Zhai, Z.; Chen, X. Homogenization and Localization of Ratcheting Behavior of Composite Materials and Structures with the Thermal Residual Stress Effect. Materials 2019, 12, 3048. https://doi.org/10.3390/ma12183048
Yang D, Yang Z, Zhai Z, Chen X. Homogenization and Localization of Ratcheting Behavior of Composite Materials and Structures with the Thermal Residual Stress Effect. Materials. 2019; 12(18):3048. https://doi.org/10.3390/ma12183048
Chicago/Turabian StyleYang, Danhui, Zhibo Yang, Zhi Zhai, and Xuefeng Chen. 2019. "Homogenization and Localization of Ratcheting Behavior of Composite Materials and Structures with the Thermal Residual Stress Effect" Materials 12, no. 18: 3048. https://doi.org/10.3390/ma12183048
APA StyleYang, D., Yang, Z., Zhai, Z., & Chen, X. (2019). Homogenization and Localization of Ratcheting Behavior of Composite Materials and Structures with the Thermal Residual Stress Effect. Materials, 12(18), 3048. https://doi.org/10.3390/ma12183048





