Atomistic Simulations of Plasma-Enhanced Atomic Layer Deposition
Abstract
1. Introduction
2. Method and Implementation
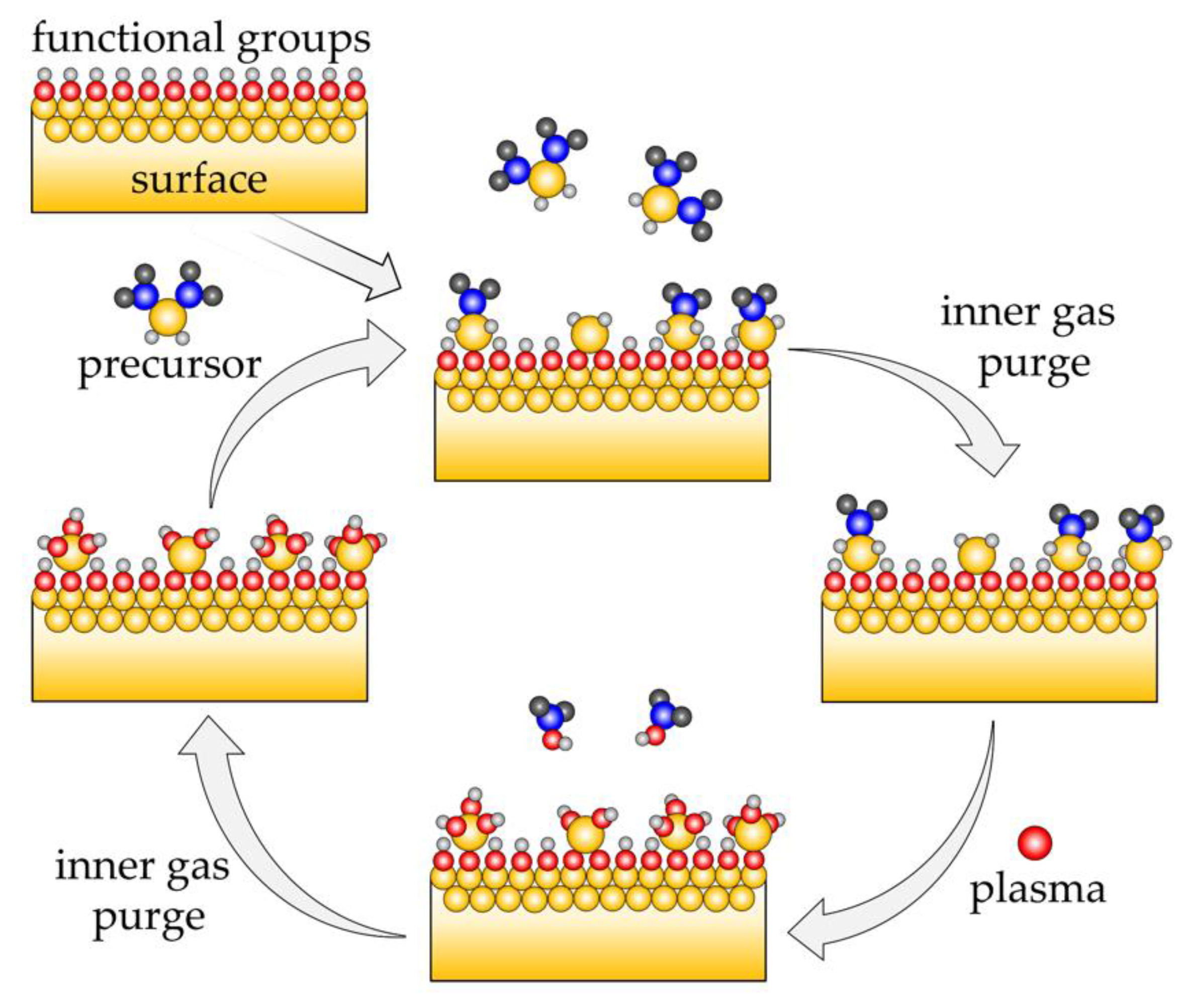
2.1. PEALD Simulation Procedure
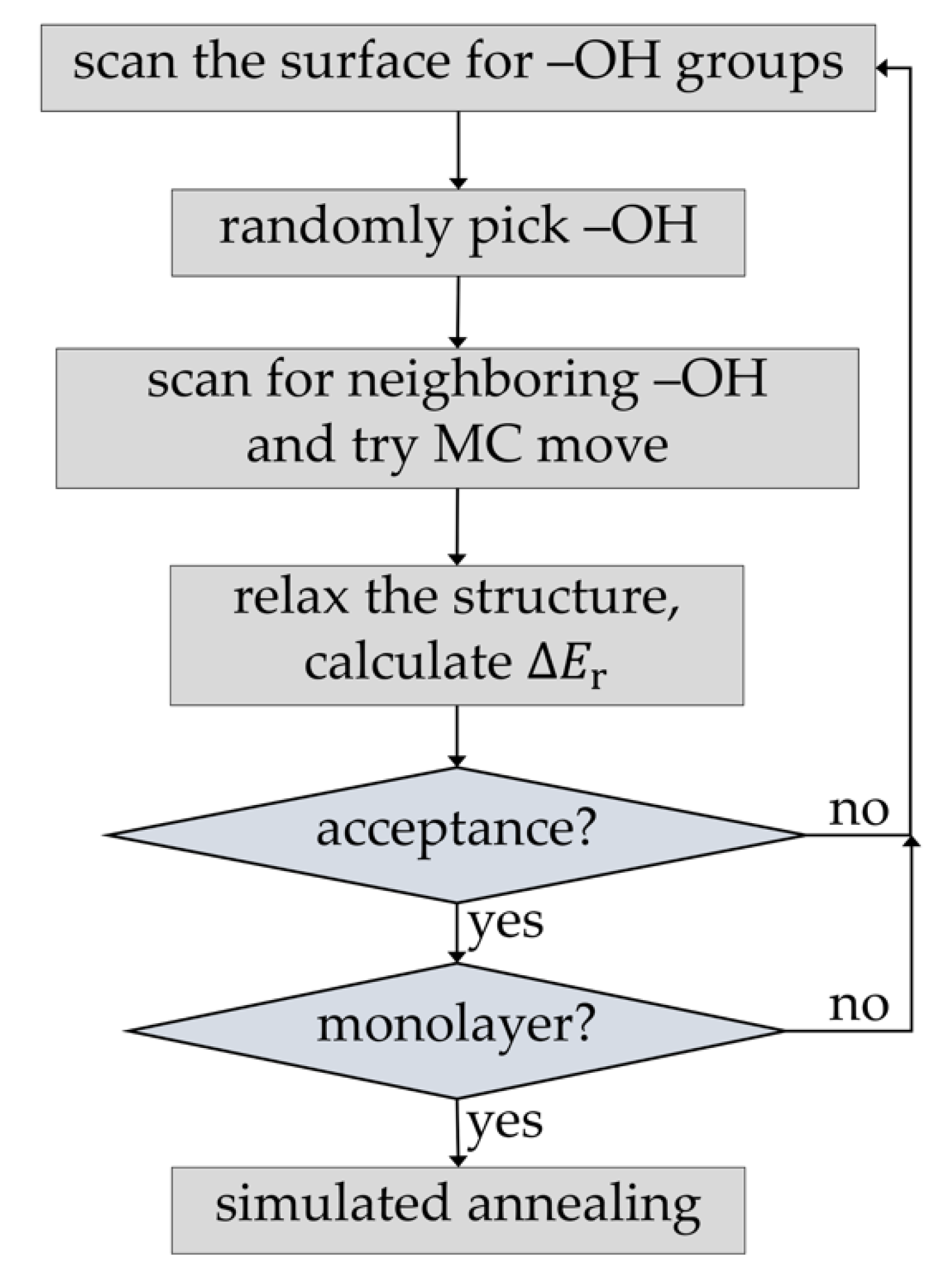
2.2. Implementation
3. Test Application—PEALD of SiO2
3.1. Computational Details
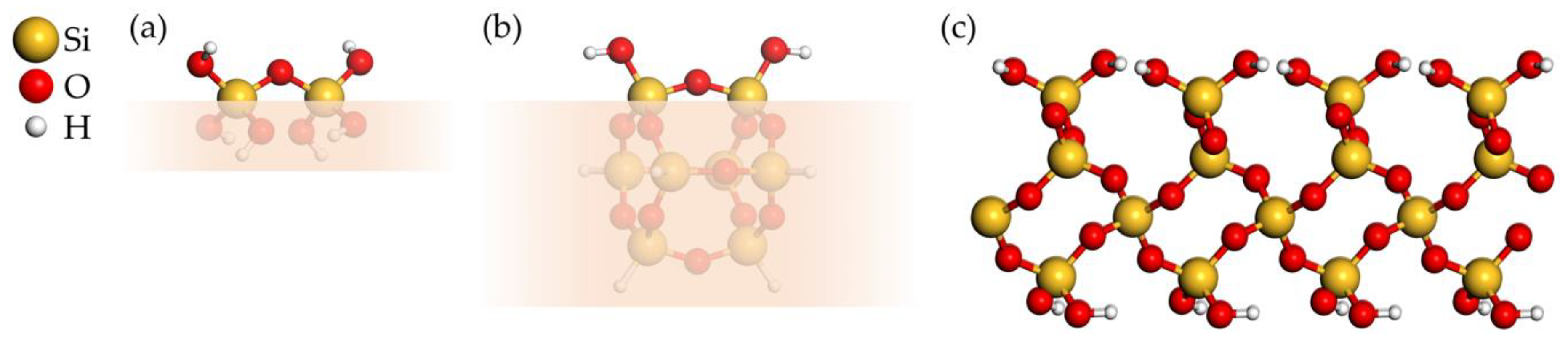
3.1.1. Model Systems
3.1.2. Methods
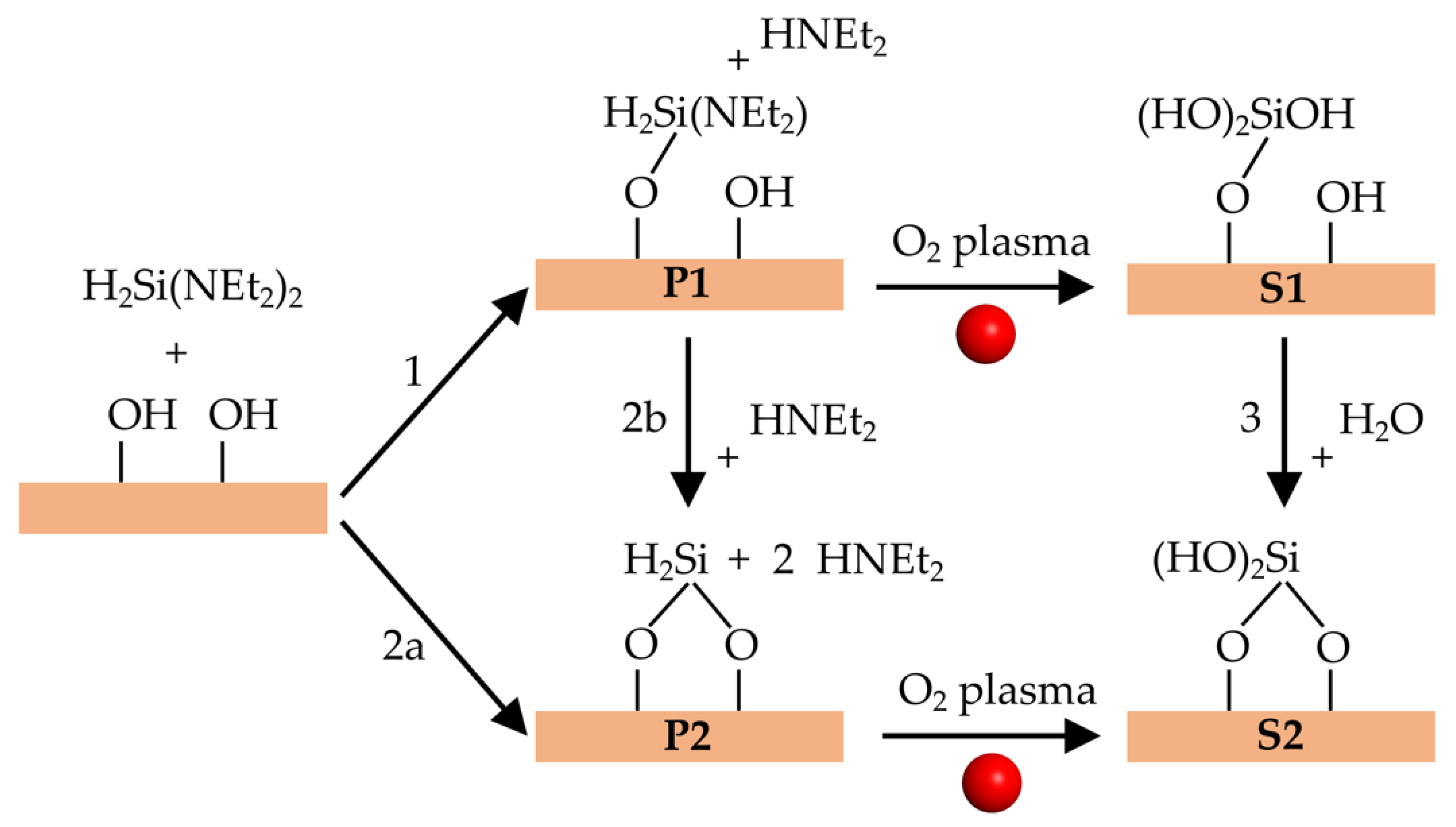
3.2. Surface Reactions and Plasma Pulse Model
3.3. Reaction Energies
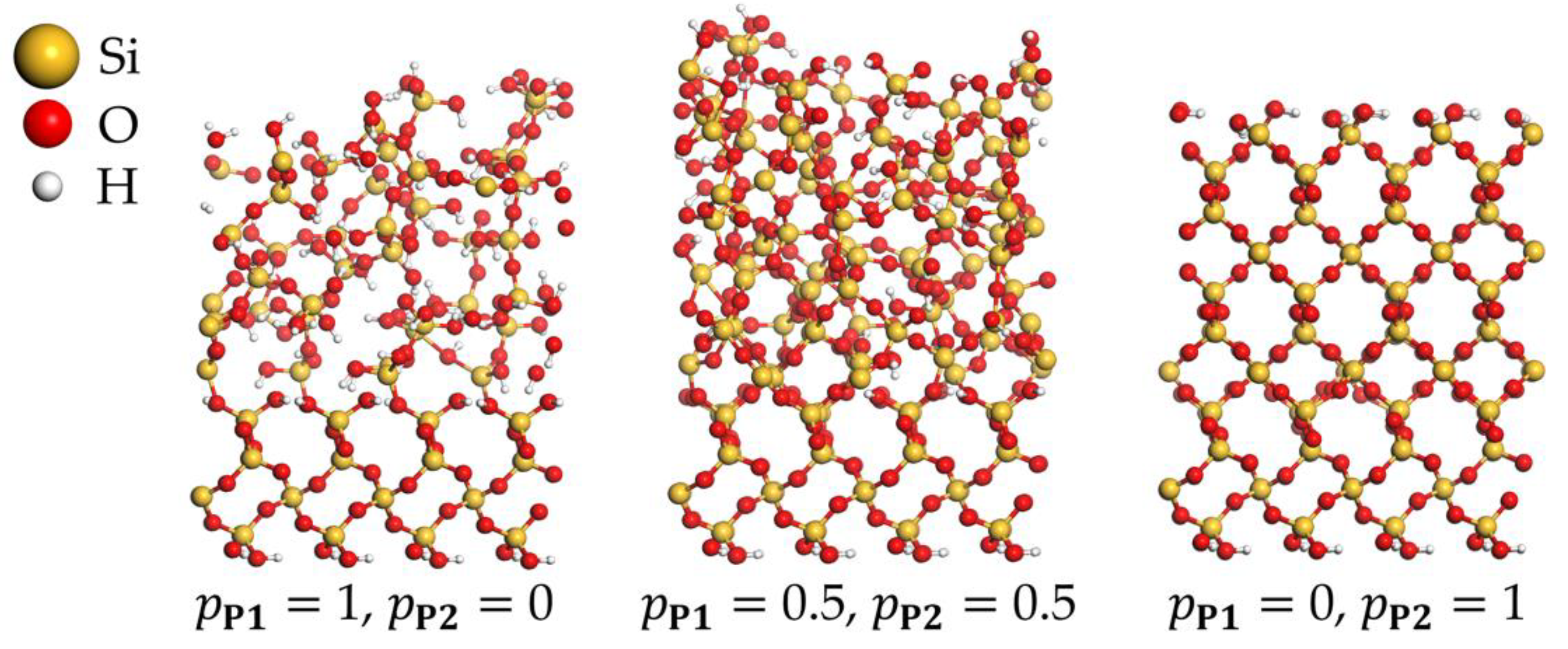
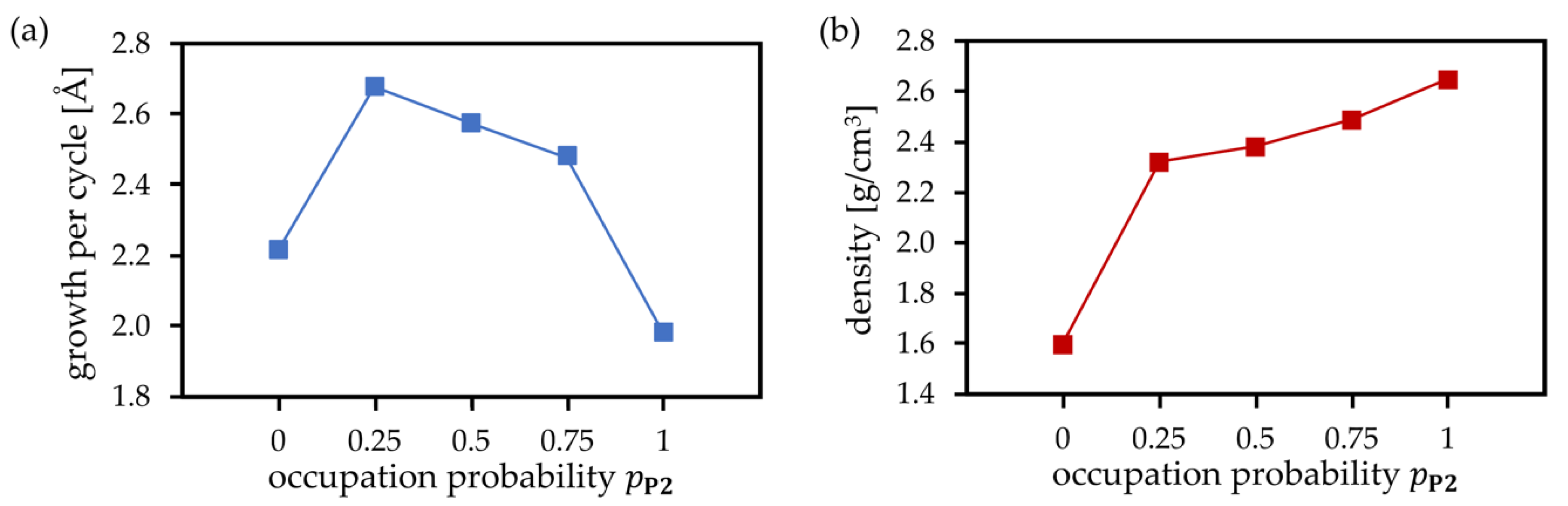
3.4. PEALD Simulations
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ghazaryan, L.; Kley, E.B.; Tünnermann, A.; Szeghalmi, A. Nanoporous SiO2 thin films made by atomic layer deposition and atomic etching. Nanotechnology 2016, 27, 255603. [Google Scholar] [CrossRef] [PubMed]
- Pfeiffer, K.; Schulz, U.; Tünnermann, A.; Szeghalmi, A. Antireflection Coatings for Strongly Curved Glass Lenses by Atomic Layer Deposition. Coatings 2017, 7, 118. [Google Scholar] [CrossRef]
- Pfeiffer, K.; Dewald, W.; Szeghalmi, A. Antireflection coating with consistent near-neutral color on complex-shaped substrates prepared by ALD. Opt. Lett. 2019, 44, 3270–3273. [Google Scholar] [CrossRef] [PubMed]
- Pfeiffer, K.; Ghazaryan, L.; Schulz, U.; Szeghalmi, A. Wide-Angle Broadband Antireflection Coatings Prepared by Atomic Layer Deposition. ACS Appl. Mater. Interfaces 2019, 11, 21887–21894. [Google Scholar] [CrossRef] [PubMed]
- Ghazaryan, L.; Sekman, Y.; Schröder, S.; Mühlig, C.; Stevanovic, I.; Botha, R.; Aghaee, M.; Creatore, M.; Tünnermann, A.; Szeghalmi, A. On the Properties of Nanoporous SiO2 Films for Single Layer Antireflection Coating. Adv. Eng. Mater. 2019, 21, 1801229. [Google Scholar] [CrossRef]
- Profijt, H.B.; Potts, S.E.; van de Sanden, M.C.M.; Kessels, W.M.M. Plasma-Assisted Atomic Layer Deposition: Basics, Opportunities, and Challenges. J. Vac. Sci. Technol. A 2011, 29, 050801. [Google Scholar] [CrossRef]
- Potts, S.E.; Profijt, H.B.; Roelofs, R.; Kessels, W.M.M. Room-Temperature ALD of Metal Oxide Thin Films by Energy-Enhanced ALD. Chem. Vap. Depos. 2013, 19, 125–133. [Google Scholar] [CrossRef]
- Kim, D.H.; Lee, H.J.; Jeong, H.; Shong, B.; Kim, W.H.; Park, T.J. Thermal atomic layer deposition of device-quality SiO2 thin films under 100 °C using an aminodisilane precursor. Chem. Mater. 2019. [Google Scholar] [CrossRef]
- Lee, Y.S.; Choi, D.W.; Shong, B.; Oh, S.; Park, J.S. Low temperature atomic layer deposition of SiO2 thin films using di-isopropylaminosilane and ozone. Ceram. Int. 2017, 43, 2095–2099. [Google Scholar] [CrossRef]
- Faraz, T.; Knoops, H.C.M.; Verheijen, M.A.; van Helvoirt, C.A.A.; Karwal, S.; Sharma, A.; Beladiya, V.; Szeghalmi, A.; Hausmann, D.M.; Henri, J.; et al. Tuning Material Properties of Oxides and Nitrides by Substrate Biasing during Plasma-Enhanced Atomic Layer Deposition on Planar and 3D Substrate Topographies. ACS Appl. Mater. Interfaces 2018, 10, 13158–13180. [Google Scholar] [CrossRef]
- Faraz, T.; Arts, K.; Karwal, S.; Knoops, H.C.M.; Kessels, W.M.M. Energetic ions during plasma-enhanced atomic layer deposition and their role in tailoring material properties. Plasma Sources Sci. Technol. 2019, 28, 024002. [Google Scholar] [CrossRef]
- Ratzsch, S.; Kley, E.B.; Tünnermann, A.; Szeghalmi, A. Influence of the oxygen plasma parameters on the atomic layer deposition of titanium dioxide. Nanotechnology 2015, 26, 024003. [Google Scholar] [CrossRef] [PubMed]
- Elliott, S.D. Atomic-scale simulation of ALD chemistry. Semicond. Sci. Technol. 2012, 27, 074008. [Google Scholar] [CrossRef]
- Shirazi, M.; Elliott, S.D. Atomistic Kinetic Monte Carlo Study of Atomic Layer Deposition Derived from Density Functional Theory. J. Comput. Chem. 2014, 35, 244–259. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; Shi, J.X.; Heath Turner, C. Molecular dynamics simulation of the Al2O3 film structure during atomic layer deposition. Mol. Simulat. 2009, 35, 270–279. [Google Scholar] [CrossRef]
- Fang, G.Y.; Xu, L.N.; Ma, J.; Li, A.D. Theoretical Understanding of the Reaction Mechanism of SiO2 Atomic Layer Deposition. Chem. Mater. 2016, 28, 1247–1255. [Google Scholar] [CrossRef]
- Fang, G.Y.; Xu, L.N.; Cao, Y.Q.; Wang, L.G.; Wu, D.; Li, A.D. Self-catalysis by aminosilanes and strong surface oxidation by O-2 plasma in plasma-enhanced atomic layer deposition of high-quality SiO2. Chem. Commun. 2015, 51, 1341–1344. [Google Scholar] [CrossRef] [PubMed]
- Han, B.; Zhang, Q.; Wu, J.; Han, B.; Karwacki, E.J.; Derecskei, A.; Xiao, M.; Lei, X.; O’Neill, M.L.; Cheng, H. On the Mechanisms of SiO2 Thin-Film Growth by the Full Atomic Layer Deposition Process Using Bis(t-butylamino)silane on the Hydroxylated SiO2(001) Surface. J. Phys. Chem. C 2012, 116, 947–952. [Google Scholar] [CrossRef]
- Huang, L.; Han, B.; Han, B.; Derecskei-Kovacs, A.; Xiao, M.; Lei, X.; O’Neill, M.L.; Pearlstein, R.M.; Chandra, H.; Cheng, H. First-Principles Study of a Full Cycle of Atomic Layer Deposition of SiO2 Thin Films with Di(sec-butylamino)silane and Ozone. J. Phys. Chem. C 2013, 117, 19454–19463. [Google Scholar]
- Baek, S.B.; Kim, D.H.; Kim, Y.C. Adsorption and surface reaction of bis-diethylaminosilane as a Si precursor on an OH-terminated Si (0 0 1) surface. Appl. Surf. Sci. 2012, 258, 6341–6344. [Google Scholar] [CrossRef]
- Jeong, Y.C.; Baek, S.B.; Kim, D.H.; Kim, J.S.; Kim, Y.C. Initial reaction of silicon precursors with a varying number of dimethylamino ligands on a hydroxyl-terminated silicon (0 0 1) surface. Appl. Surf. Sci. 2013, 280, 207–211. [Google Scholar] [CrossRef]
- Li, J.Y.; Wu, J.P.; Zhou, C.G.; Han, B.; Karwacki, E.J.; Xiao, M.C.; Lei, X.J.; Cheng, H.S. On the Dissociative Chemisorption of Tris(dimethylamino)silane on Hydroxylated SiO2(001) Surface. J. Phys. Chem. C. 2009, 113, 9731–9736. [Google Scholar] [CrossRef]
- Murray, C.A.; Elliott, S.D.; Hausmann, D.; Henri, J.; LaVoie, A. Effect of Reaction Mechanism on Precursor Exposure Time in Atomic Layer Deposition of Silicon Oxide and Silicon Nitride. ACS Appl. Mater. Interfaces 2014, 6, 10534–10541. [Google Scholar] [CrossRef] [PubMed]
- Karakasidis, T.E.; Charitidis, C.A. Multiscale modeling in nanomaterials science. Mater. Sci. Eng. C 2007, 27, 1082–1089. [Google Scholar] [CrossRef]
- Dkhissi, A.; Estève, A.; Mastail, C.; Olivier, S.; Mazaleyrat, G.; Jeloaica, L.; Rouhani, M.D. Multiscale Modeling of the Atomic Layer Deposition of HfO2 Thin Film Grown on Silicon: How to Deal with a Kinetic Monte Carlo Procedure. J. Chem. Theory Comput. 2008, 4, 1915–1927. [Google Scholar] [CrossRef]
- Spagnoli, D.; Gale, J.D. Atomistic theory and simulation of the morphology and structure of ionic nanoparticles. Nanoscale 2012, 4, 1051–1067. [Google Scholar] [CrossRef] [PubMed]
- van Duin, A.C.T.; Dasgupta, S.; Lorant, F.; Goddard, W.A. ReaxFF: A reactive force field for hydrocarbons. J. Phys. Chem. A 2001, 105, 9396–9409. [Google Scholar] [CrossRef]
- Deetz, J.D.; Faller, R. Parallel Optimization of a Reactive Force Field for Polycondensation of Alkoxysilanes. J. Phys. Chem. B 2014, 118, 10966–10978. [Google Scholar] [CrossRef] [PubMed]
- Norman, P.; Schwartzentruber, T.E.; Leverentz, H.; Luo, S.J.; Meana-Paneda, R.; Paukku, Y.; Truhlar, D.G. The Structure of Silica Surfaces Exposed to Atomic Oxygen. J. Phys. Chem. C. 2013, 117, 9311–9321. [Google Scholar] [CrossRef]
- Gubbels-Elzas, A.; Thijsse, B.J. Ionic motion during field-assisted oxidation of aluminium studied by molecular dynamics simulations. Comput. Mater. Sci. 2014, 90, 196–202. [Google Scholar] [CrossRef]
- Hühn, C.; Wondraczek, L.; Sierka, M. Dynamics of ultrathin gold layers on vitreous silica probed by density functional theory. PCCP 2015, 17, 27488–27495. [Google Scholar] [CrossRef] [PubMed]
- Amar, J.G. The Monte Carlo method in science and engineering. Comput. Sci. Eng. 2006, 8, 9–19. [Google Scholar] [CrossRef]
- Larsen, A.H.; Mortensen, J.J.; Blomqvist, J.; Castelli, I.E.; Christensen, R.; Dulak, M.; Friis, J.; Groves, M.N.; Hammer, B.; Hargus, C.; et al. The atomic simulation environment-a Python library for working with atoms. J. Phys. Condens. Matter 2017, 29, 273002. [Google Scholar] [CrossRef] [PubMed]
- Gale, J.D.; Rohl, A.L. The General Utility Lattice Program (GULP). Mol. Simulat. 2003, 29, 291–341. [Google Scholar] [CrossRef]
- Kim, H.; Chung, I.; Kim, S.; Shin, S.; Jung, W.; Hwang, R.; Jeong, C.; Hwang, H. Improved film quality of plasma enhanced atomic layer deposition SiO2 using plasma treatment cycle. J. Vac. Sci. Technol. A 2015, 33, 01A146. [Google Scholar] [CrossRef]
- Burow, A.M.; Sierka, M.; Mohamed, F. Resolution of identity approximation for the Coulomb term in molecular and periodic systems. J. Chem. Phys. 2009, 131, 214101. [Google Scholar] [CrossRef] [PubMed]
- Burow, A.M.; Sierka, M. Linear Scaling Hierarchical Integration Scheme for the Exchange-Correlation Term in Molecular and Periodic Systems. J. Chem. Theory Comput. 2011, 7, 3097–3104. [Google Scholar] [CrossRef] [PubMed]
- Lazarski, R.; Burow, A.M.; Sierka, M. Density Functional Theory for Molecular and Periodic Systems Using Density Fitting and Continuous Fast Multipole Methods. J. Chem. Theory Comput. 2015, 11, 3029–3041. [Google Scholar] [CrossRef] [PubMed]
- Lazarski, R.; Burow, A.M.; Grajciar, L.; Sierka, M. Density Functional Theory for Molecular and Periodic Systems Using Density Fitting and Continuous Fast Multipole Method: Analytical Gradients. J. Comput. Chem. 2016, 37, 2518–2526. [Google Scholar] [CrossRef]
- Becker, M.; Sierka, M. Density Functional Theory for Molecular and Periodic Systems Using Density Fitting and Continuous Fast Multipole Method: Stress Tensor. J. Comput. Chem. 2019. [Google Scholar] [CrossRef]
- Ahlrichs, R.; Bär, M.; Häser, M.; Horn, H.; Kölmel, C. Electronic-Structure Calculations on Workstation Computers—The Program System Turbomole. Chem. Phys. Lett. 1989, 162, 165–169. [Google Scholar] [CrossRef]
- Furche, F.; Ahlrichs, R.; Hättig, C.; Klopper, W.; Sierka, M.; Weigend, F. Turbomole. WIREs Comput. Mol. Sci. 2014, 4, 91–100. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. PCCP 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Abolfath, R.M.; van Duin, A.C.T.; Brabec, T. Reactive Molecular Dynamics Study on the First Steps of DNA Damage by Free Hydroxyl Radicals. J. Phys. Chem. A 2011, 115, 11045–11049. [Google Scholar] [CrossRef]
- Rahaman, O.; van Duin, A.C.T.; Goddard, W.A.; Doren, D.J. Development of a ReaxFF Reactive Force Field for Glycine and Application to Solvent Effect and Tautomerization. J. Phys. Chem. B 2011, 115, 249–261. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Becker, M.; Sierka, M. Atomistic Simulations of Plasma-Enhanced Atomic Layer Deposition. Materials 2019, 12, 2605. https://doi.org/10.3390/ma12162605
Becker M, Sierka M. Atomistic Simulations of Plasma-Enhanced Atomic Layer Deposition. Materials. 2019; 12(16):2605. https://doi.org/10.3390/ma12162605
Chicago/Turabian StyleBecker, Martin, and Marek Sierka. 2019. "Atomistic Simulations of Plasma-Enhanced Atomic Layer Deposition" Materials 12, no. 16: 2605. https://doi.org/10.3390/ma12162605
APA StyleBecker, M., & Sierka, M. (2019). Atomistic Simulations of Plasma-Enhanced Atomic Layer Deposition. Materials, 12(16), 2605. https://doi.org/10.3390/ma12162605





