1. Introduction
The compaction of asphalt pavement affects the performance of pavement structure and service life. Rutting, friable, pothole, and other failures usually occur when the pavement layers are not well compacted [
1,
2,
3]. One of the reasons for the poor compaction is that there are no complete theories for the real time rheological properties of asphalt mixture under high temperature and non-compaction conditions. Therefore, it is necessary to establish an actual mechanical model to evaluate the deformation of the asphalt mixture during the construction compaction process.
Asphalt mixture is a kind of thermo-viscoelastic-plastic material; the flow behavior of hot mix asphalt is concluded to be directly related to the rheological properties. Its total strain includes elastic strain, viscoelastic strain, plastic strain, and viscoplastic strain [
4,
5,
6]. Its mechanical properties are related to stress state, temperature, and loading time. There has been a lot of research that is aimed at using the constitutive model to predict the permanent deformation of asphalt mixture [
7,
8,
9]. Various time-dependent constitutive models have been proposed in the past few decades [
10,
11]. Giunta et al. [
12] established a constitutive model that consisted of the Maxwell model and hardened viscoplastic element to simulate the time-dependent non-linear behavior of asphalt mixtures. The model can reflect the experimental characteristics of the material and match thermodynamic requirements. Masad et al. [
13,
14] used the Perzyna viscoplastic model to describe the mechanical behavior of asphalt mixtures in constant strain rate compression tests. However, this model does not lack the ability to represent the recovery behavior during repeated loading-unloading cycles, because the viscoelastic model is not coupled to the viscoplastic model. Sun et al. [
15] used the internal variable theory and the thermodynamic orthogonal principle to establish a continuous two-stage viscoelastic-viscoplastic constitutive model for simulate the aging characteristics of asphalt mixtures.
Other researchers have proposed some models to study the mechanical response of asphalt mixture under high temperature conditions. Huang et al. [
16] proposed a temperature-dependent HiSS plastic model, which can reflect the nonlinear plasticity, temperature, and load rate of asphalt mixture. Darabi et al. [
17] proposed a phenomenological rate-dependent hardening-relaxation model that was coupled with nonlinear Schapery viscoelastic and Perzyna viscoplastic models to accurately predict the permanent deformation of asphalt mixture under cyclic compression loads at high temperatures. However, they did not pay attention to radial strain, so the model could not accurately describe the three-dimensional mechanical properties of the asphalt mixtures. Pasetto et al. [
18] established a viscoelastic-plastic constitutive model by viscoelastic elements and a slider that is connected by elastic springs in parallel with three Maxwell components to analyze the mechanical response and creep deformation ability of asphalt concrete at high temperatures. However, there is a lack of in-depth study regarding the creep mechanism of asphalt mixture and its relationship with viscoelastic response. Chen et al. [
19] proposed a comprehensive constitutive model that is capable of capturing the main mechanical properties of asphalt materials based on the thermodynamic finite strain frame model, which can predict the complex time- and temperature-dependent response of asphalt materials during elongation and compression, and it successfully predicts the permanent deformation of the road.
The constitutive theory to predict the permanent deformation of asphalt mixture has been extensively studied and successfully used in practice. However, the rheological properties of the hot mix asphalt during compaction and the change law of viscoelastic-plastic parameters are seldom studied. Chen [
20] established the viscoelastic-plastic constitutive relation of hot mix asphalt by Material Testing System (MTS) compaction test and SGC (Superpave Gyratory Compactor) gyratory compaction test, while using the basic principles and methods of viscoelastic plastic force. Liu [
21] used the Bodnet–Partom model to simulate the rheological properties of asphalt mixture during compaction and simulated it with finite element software.
The above-mentioned models are complicated to solve the parameters; on the contrary, the Nishihara model is intuitive and theoretically simple, and it can clearly and comprehensively reflect the viscoelastic-plastic in the roller compaction. However, it does not consider the effects of nonlinearity and temperature stress. Therefore, based on the Nishihara model, this paper establishes a nonlinear Nishihara model to simulate the rheological behavior of the asphalt mixture during compaction. Through a MTS compaction test that was designed to simulate the construction compaction process, the rheological parameters were obtained, and the feasibility and rationality of the model were verified. The relation between compaction properties and model parameters was finally discussed based on the real-time parameter analysis.
2. Test Materials and Methods
This chapter describes the asphalt performance, mixture gradations, and MTS compaction test methods. The MTS compaction test is used to obtain the model parameters and verify the model.
Figure 1 shows the flow chart of this article.
2.1. Materials and Mix Design
The asphalt is a CNOOC Taizhou 70# matrix asphalt, and
Table 1 shows its physical properties. The aggregates used in this paper are basalt, and
Table 2 and
Table 3 shows the physical properties. Aggregates with the size larger than 2.36 mm are coarse aggregates, and the aggregates with the size smaller than 2.36 mm are fine aggregates. The mineral filler is ground limestone, and
Table 4 shows the physical properties. All of the tests are requirement Chinese standards [
22,
23,
24].
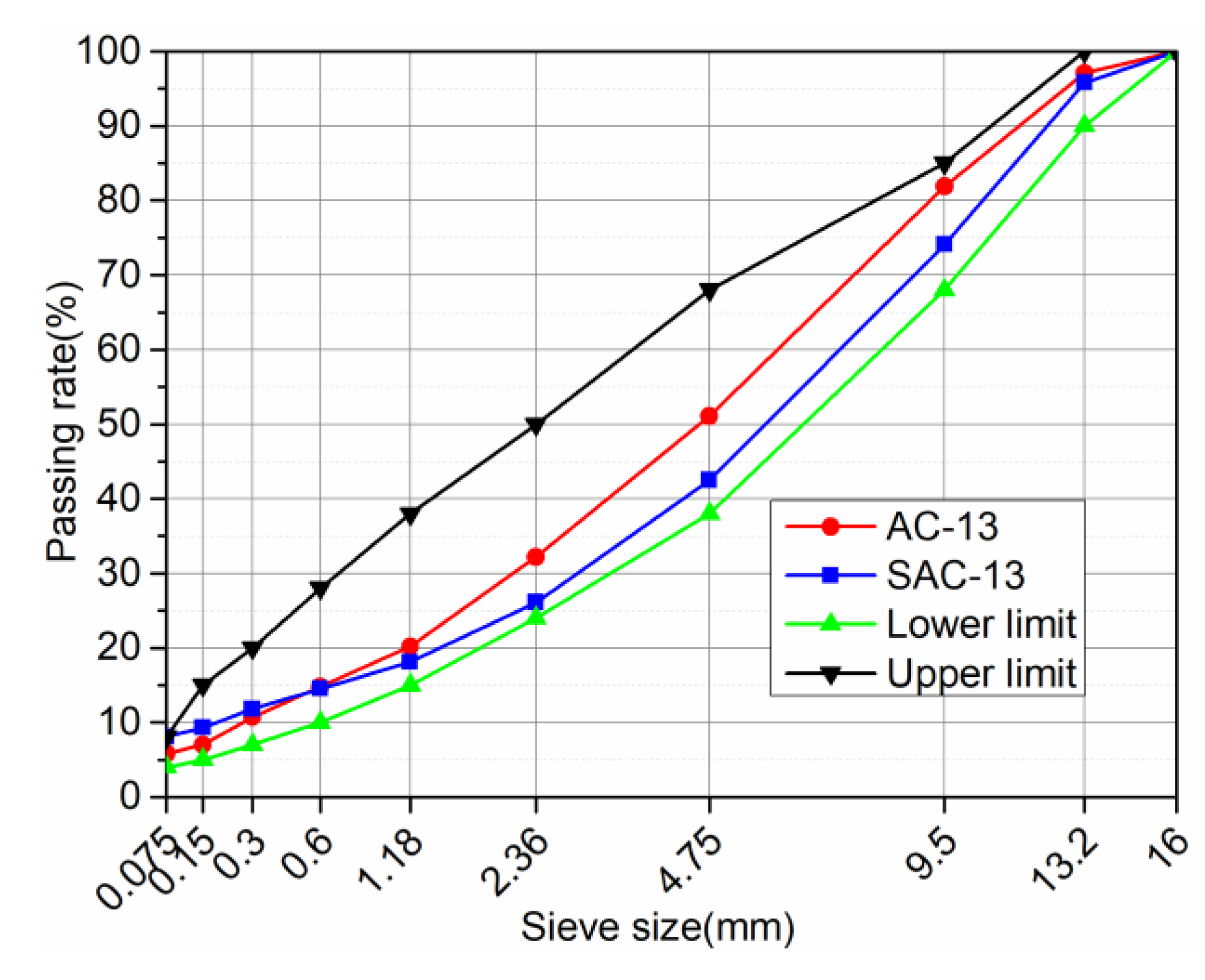
Two different types of asphalt mixtures were used in the test: Fine grain asphalt concrete (AC-13) and multi-gravel asphalt concrete (SAC-13).
Figure 2 shows the gradation. Multi-gravel asphalt concrete (SAC-13) contains more coarse aggregates, which can provide deeper surface structure, smaller voids and less water permeability, and good deformation resistance. The oil-stone ratios of AC-13 and SAC-13 are 5.0% and 5.0%, and the target air voids are 6.7% and 6.5%, respectively.
2.2. MTS Compaction Process
In order to get the complex parameters of the asphalt mixture compaction process and the change law of the temperature field, and to ensure the uniform distribution of aggregate. The test was carried out using a 48 Hz vibration platform, a Pt100 + paperless recorder, and a MTS810 material test system. The test plan mainly simulates pavement compaction. The asphalt mixture mixing temperature is 160 °C and the indoor ambient temperature is controlled to be about 25 °C. The mixed asphalt mixture was placed in a test piece cylinder having a diameter of 150 mm and a temperature sensor (Pt100) was buried in the mixture during the charging process. The mold containing the asphalt mixture was placed on a vibrating table for 10 s, the vibration frequency was 48 Hz, and then the mold was placed on the MTS for loading. Two parallel tests were performed on the same type of asphalt mixture.
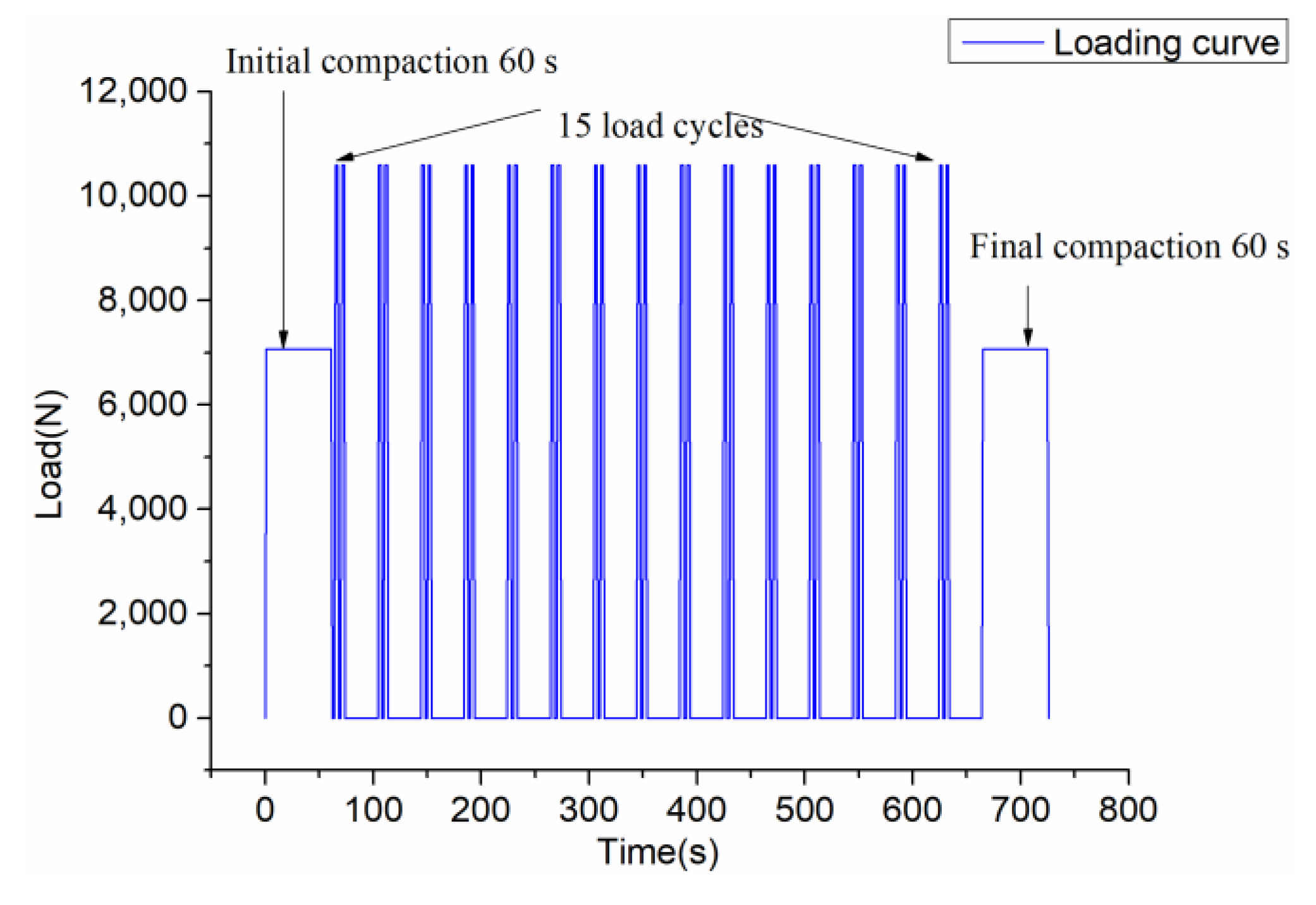
To consider the rolling speed and the interval of the roller in a real construction project,
Figure 3 shows the loading process. First compact for 60 s (initial compaction), then 15 cycles of loading (repeat compaction), and finally compact for 60 s (final compaction). The loading mode of cyclic load is: 1 s loading–2 s dead load–1 s unloading–2 s no load–1 s loading–2 s dead load–1 s unloading–30 s no load. Afterwards, repeat this cycle for 14 times.
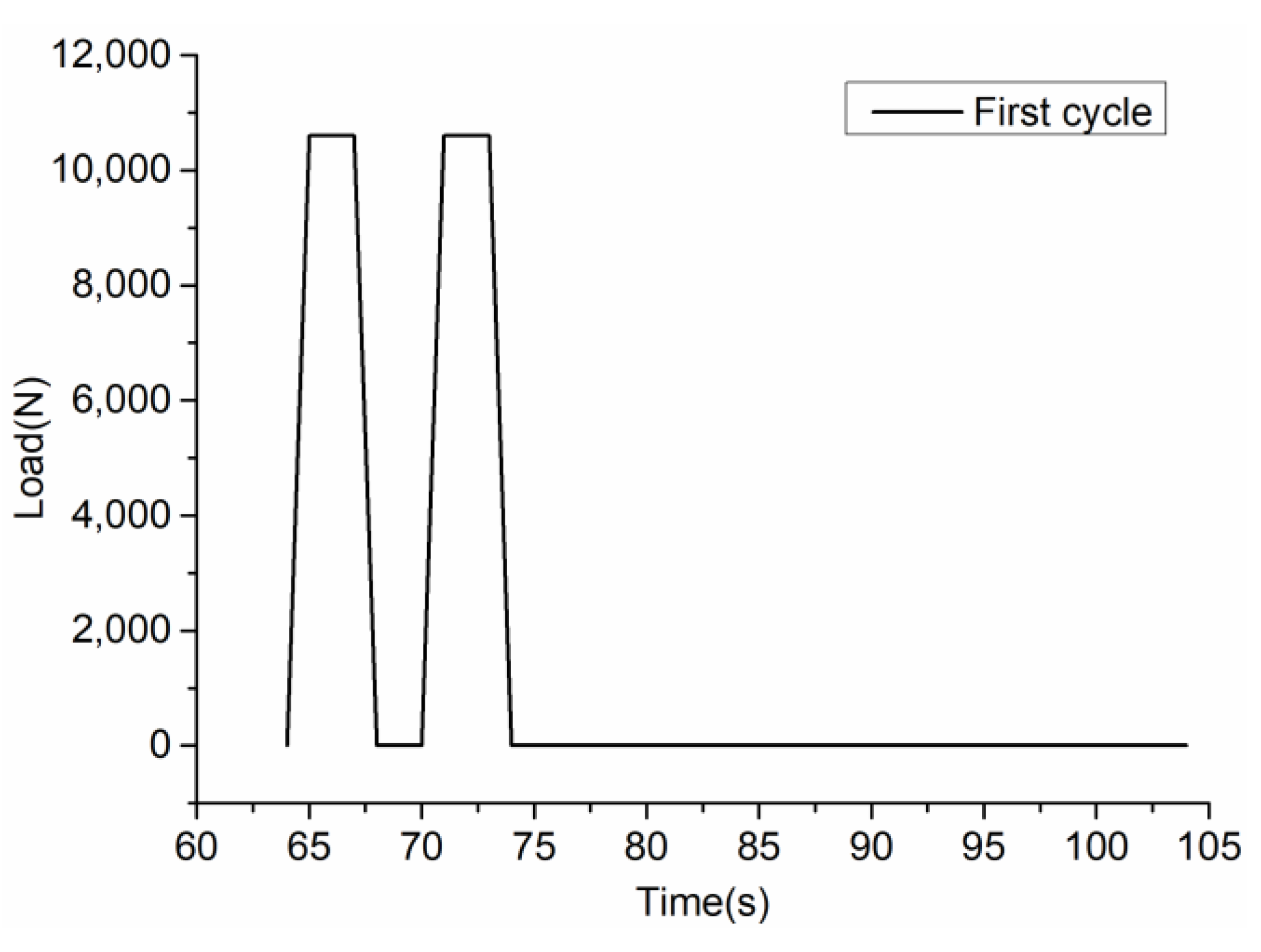
Figure 4 shows the first load cycle. Compaction load design considers SGC compaction load (generally 0.6 MPa) and relevant Chinese standards [
23]. The initial and final compaction loads are 0.4 MPa, the repeated compaction loads are 0.6 MPa, and the total compaction time is 726 s.
The Pt100+ paperless recorder collects the temperature changes during the compaction process at a 1 s interval. The MTS computer is used to automatically record the pressure, time, and deformation during the test at a 0.005 s interval.
3. Viscoelastic-Plastic Rheological Model Theory
3.1. Nonlinear Viscoelastic-Plastic Nishihara Model and Parameter Solving
The Nishihara model is widely used to study the rheological properties of rocks [
25,
26,
27,
28,
29,
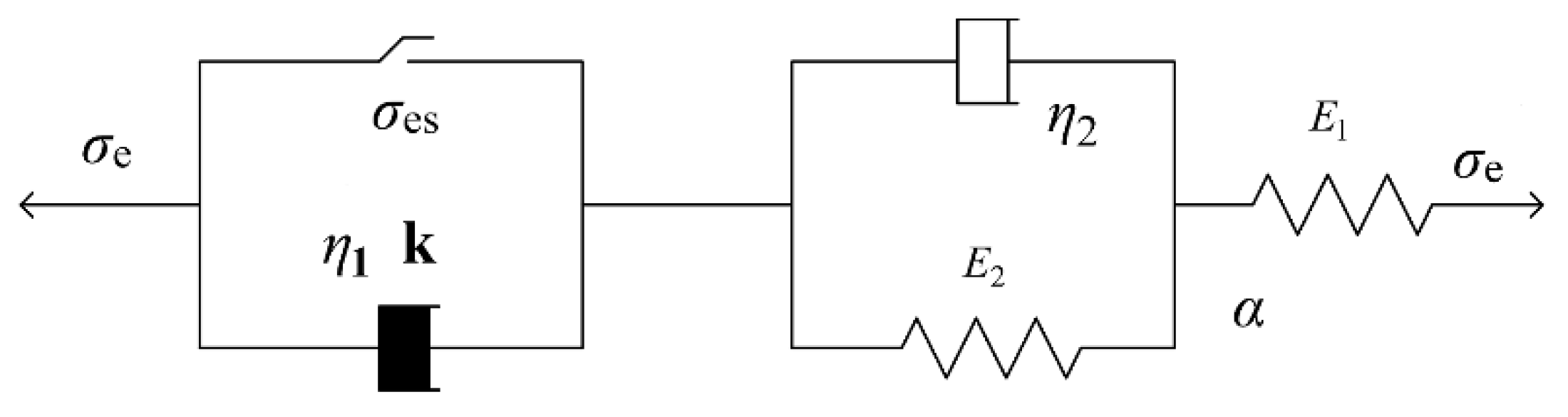
30]. However, it does not consider the effects of nonlinearity and temperature stress. A nonlinear Nishihara model is established to analyze the rheological characteristics of materials based on the theory of viscoelastic-plastic Nishihara model. The nonlinear characteristic uses the power function type
(
A is the test constant,
k is the rheological index. Its value depends on material properties, stress levels, and temperature conditions), as shown in
Figure 5.
When considering the influence of temperature stress and temperature strain on the stress and strain of the material, the constitutive equation of the nonlinear Nishihara model can be written as:
where:
E1 is the elastic modulus of the Hooker body;
E2 is the elastic modulus of the Kelvin body;
η1,
η2 are the viscosity coefficients of the Kelvin body and the Bingham body stick component;
σe is the applied stress;
σes is the material yield stress;
t is time;
k is the rheological index; Δ
T is the calculation of the temperature difference; and, α is the material shrinkage coefficient.
The above formula fully considers the influence of factors, such as nonlinearity, time, and temperature stress of the material. Therefore, the model can more comprehensively reflect the nonlinear viscoelastic-plastic properties of the material.
The material is subjected to compressive stress and it takes a negative value, and the compaction of the hot mix asphalt mix is generally completed above 100 °C, so the asphalt mixture is in a plastic flow dynamic, and the nonlinear viscous property is approximately linear viscous behavior, that is to take
; at the same time, the temperature shrinkage stress
MPa (where
MPa,
°C, Δ
T is the within 2s loading temperature drop range). In addition, studies have shown that the higher temperature asphalt mixture has good stress relaxation performance, and the temperature stress that is generated by cooling can quickly relax to zero [
31]. Therefore, the asphalt mixture pressure has no temperature stress in real time.
The constitutive equation of the nonlinear rheological model of the hot mix asphalt compaction process can be simplified as:
where:
E1 is the elastic modulus of the Hooker body;
E2 is the elastic modulus of the Kelvin body;
η1,
η2 are the viscosity coefficients of the Kelvin body and the Bingham body stick component;
σe is the applied stress;
σes is the material yield stress; and,
t is time.
Equation (2) can ignore the influence of temperature effects during the calculation of stress and strain. It not only simplifies the model theory, but it also makes the determination of model parameters simpler and easier. The meaning of all parameters is shown in
Table A1.
3.2. Model Parameter Solving
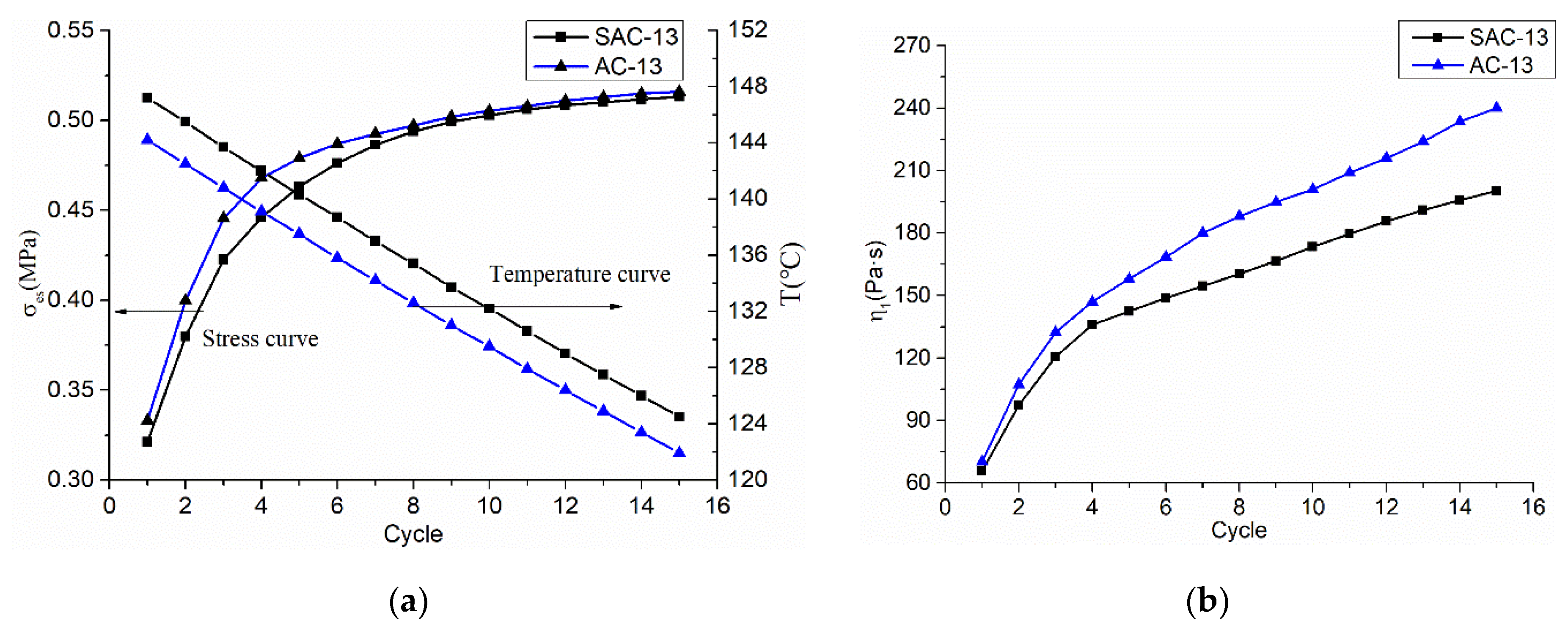
In order to simulate the road compaction process, each load cycle includes two loading and unloading. It is assumed that the temperature is the same in one cycle, but different for different cycle. In Equation (2), there are six model parameters of σe, σes, E1, E2, η1, and η2. Each parameter is a related parameter that varies with the number of load cycles and temperature.
In the analysis of viscoelastic-plastic parameters, the first loading process curve, the second unloading process curve, and the whole viscoplastic deformation in 15 loading cycles are analyzed. Combining the rheological model constitutive equation and the nonlinear regression equation, the solution ideas of each model parameter are presented, as follows:
- (1)
.
- (2)
Under the action of 15 loading cycles, the value of
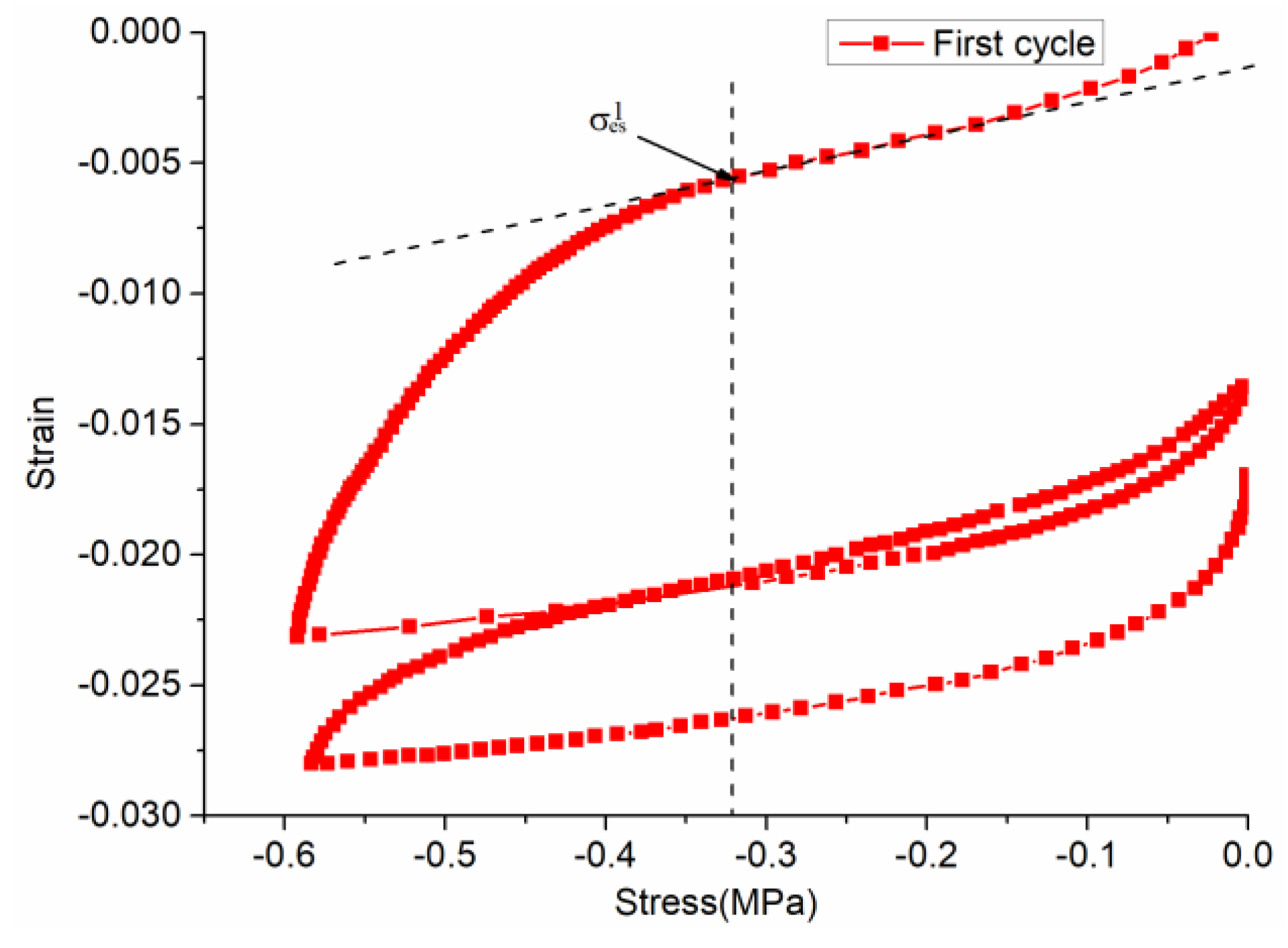
σes in each cycle is during two loading and unloading processes. The tangent stress value at the straight line segment of the stress-strain curve at the first loading and the tangent point at the curve is taken as the
σes of the cyclic process, as shown in
Figure 6.
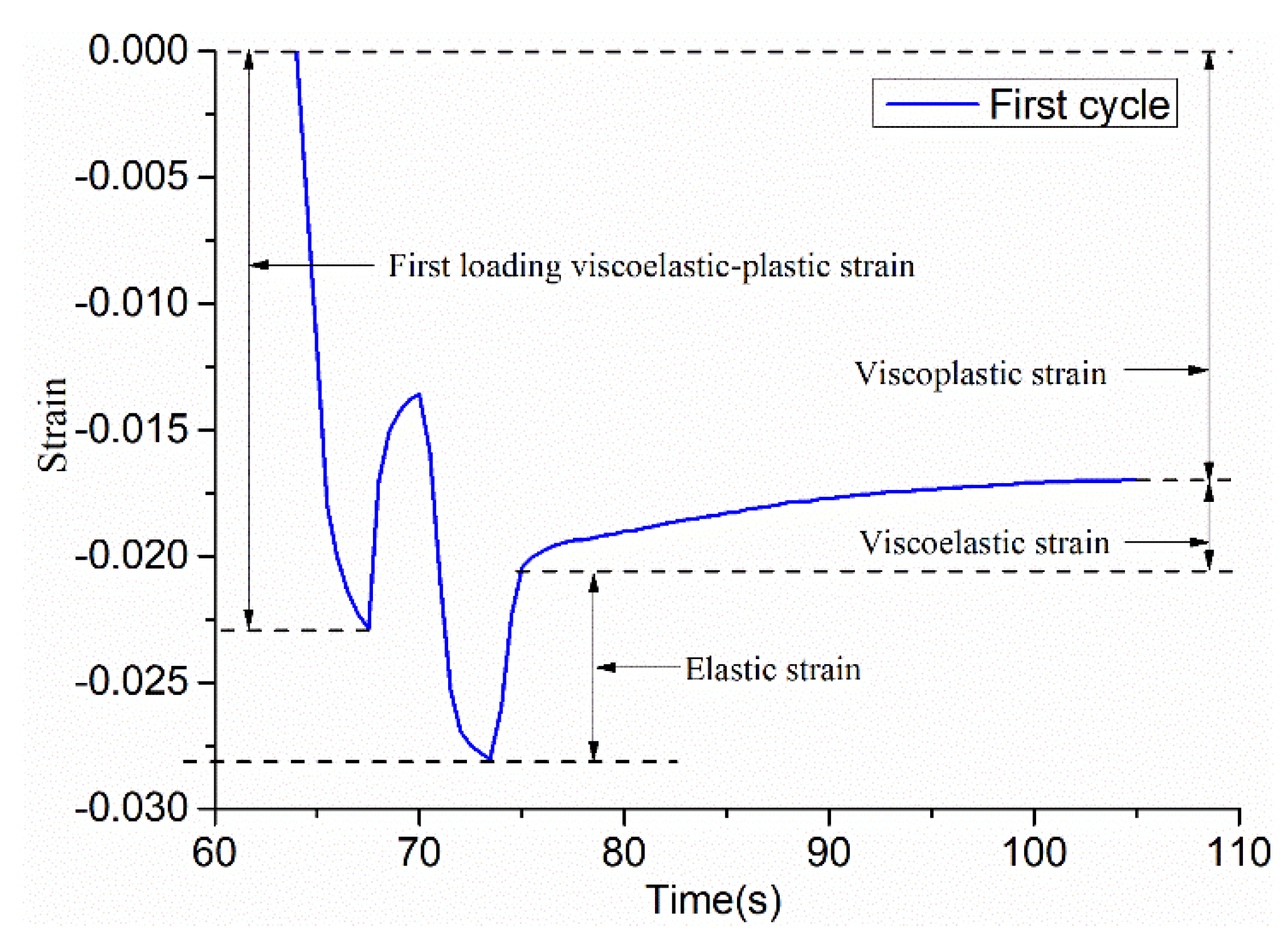
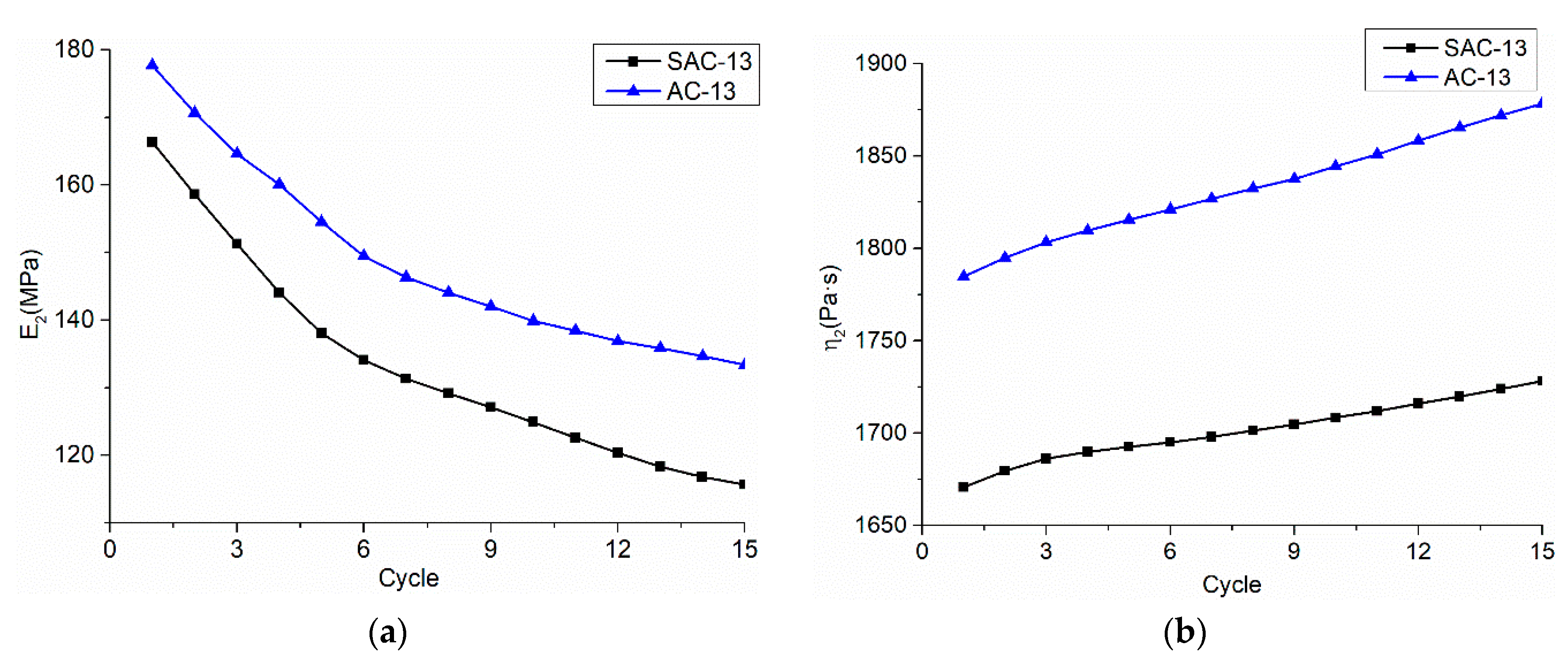
- (3)
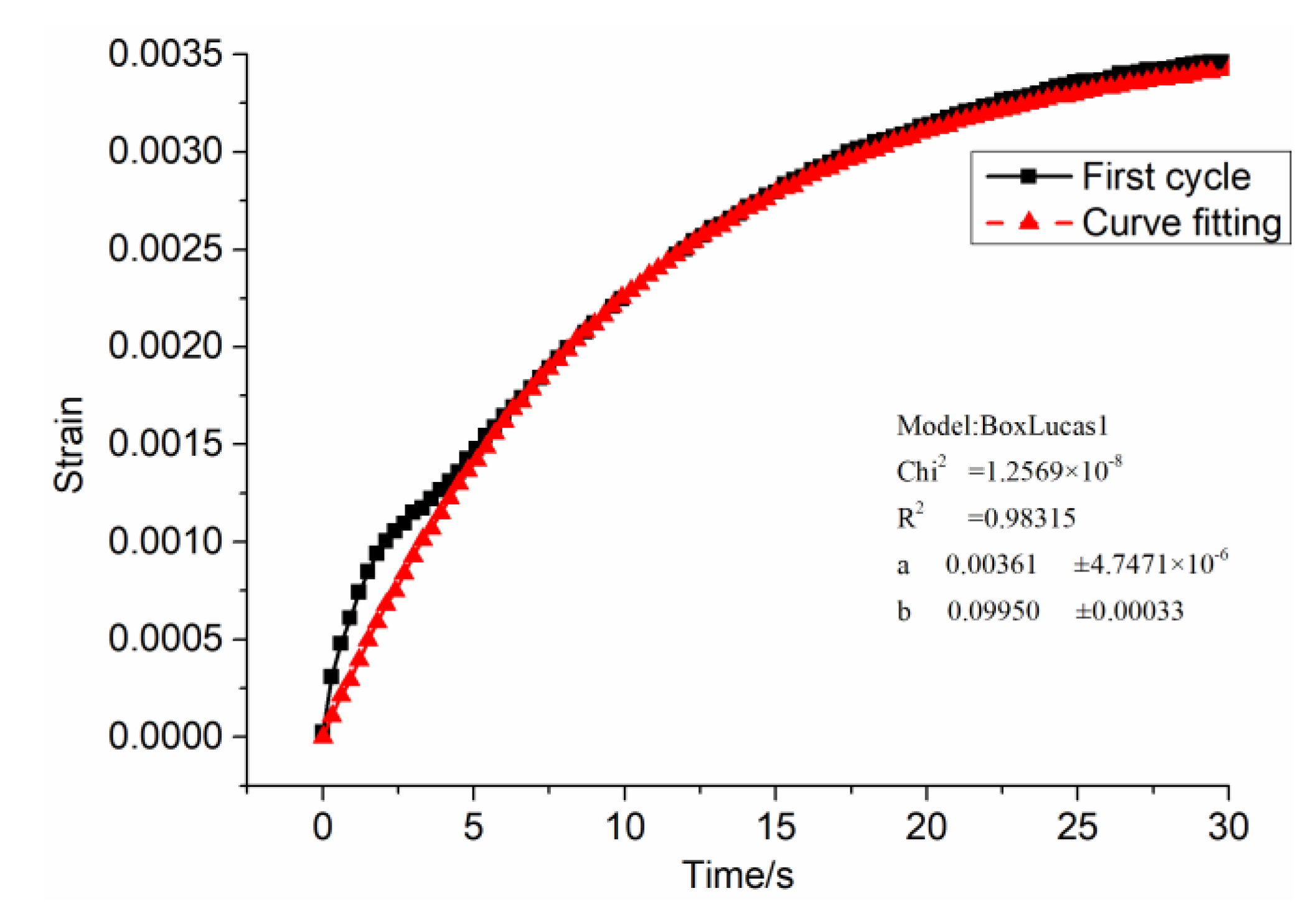
Separating viscoplastic strain, elastic strain, and viscoelastic strain solves the parameters. Firstly, E1 is solved by the “recovery elastic strain” after the second unloading in each cycle: . Secondly, the η1 value is solved by the “median viscoplastic strain” in each cycle:. Thirdly, in the Kelvin body, E2 and η2 use the BoxLucas1 model equation to perform nonlinear regression on the “recover viscoelastic strain time curve” after the second unloading in each cycle, and the parameters of the model are then obtained by calculating.
The stress–strain–time response curves of the SAC-13 matrix asphalt mixture in the first cycle are taken as an example to solve the model parameters.
Table 5 shows the viscoelastic plastic strain results of the SAC-13 asphalt mixture.
The first step is to solve the yield stress
σes. Through the first cyclic stress–strain curve of
Figure 6, the value of the tangent point at the straight line segment of the stress–strain curve at the first loading and the tangent point of the curve is determined, and
is obtained. In the same way,
⋯
can be obtained. The second step is to solve
E1, E2, η1, and
η2. The elastic strain, viscoplastic strain, and viscoelastic strain have been marked in
Figure 7, and the parameters of the table are solved, as follows:
- (a)
, then , in the same way, ⋯ can be obtained.
- (b)
, then , that is , and in the same way, ⋯ can be obtained.
- (c)
The BoxLucas 1 model equation
is used for non-linear regression, as shown in
Figure 8. Where
,
. After calculation,
,
. In the same way,
⋯
and
⋯
can be obtained.